Группы из пяти пар ОДЛК
Message boards :
Science :
Группы из пяти пар ОДЛК
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Найдена первая (в нашей БД) пятёрка! Пятёрку нашёл Demis в эксперименте по поиску решений с симметрией (4,31,31). 0 1 2 3 4 5 6 7 8 9 6 7 5 0 1 9 8 3 2 4 7 3 1 9 6 0 4 8 5 2 9 2 3 4 7 8 1 0 6 5 3 4 9 1 8 6 2 5 7 0 5 9 7 8 3 2 0 6 4 1 8 6 4 7 9 1 5 2 0 3 2 8 0 6 5 4 3 9 1 7 1 5 6 2 0 7 9 4 3 8 4 0 8 5 2 3 7 1 9 6 sq1 - с симметрией 0 1 2 3 4 5 6 7 8 9 6 7 5 9 1 0 8 3 2 4 7 3 1 0 6 9 4 8 5 2 9 2 3 4 7 8 1 0 6 5 3 4 9 1 8 6 2 5 7 0 5 0 7 8 3 2 9 6 4 1 8 6 4 7 0 1 5 2 9 3 2 8 0 6 5 4 3 9 1 7 1 5 6 2 9 7 0 4 3 8 4 9 8 5 2 3 7 1 0 6 sq2 - с симметрией 0 1 2 3 4 5 6 7 8 9 6 7 5 9 1 0 8 3 2 4 7 9 1 0 6 3 4 8 5 2 3 2 9 4 7 8 1 0 6 5 9 4 3 1 8 6 2 5 7 0 5 0 7 8 3 2 9 6 4 1 8 6 4 7 0 1 5 2 9 3 2 8 0 6 5 4 3 9 1 7 1 5 6 2 9 7 0 4 3 8 4 3 8 5 2 9 7 1 0 6 sq3 0 1 2 3 4 5 6 7 8 9 6 7 5 9 1 0 8 3 2 4 7 3 1 5 6 9 4 8 0 2 9 2 3 4 7 8 1 5 6 0 3 4 9 1 8 6 2 0 7 5 5 0 7 8 3 2 9 6 4 1 8 6 4 7 0 1 5 2 9 3 2 8 0 6 5 4 3 9 1 7 1 5 6 2 9 7 0 4 3 8 4 9 8 0 2 3 7 1 5 6 sq4 0 1 2 3 4 5 6 7 8 9 6 7 5 9 1 0 8 3 2 4 7 9 1 5 6 3 4 8 0 2 3 2 9 4 7 8 1 5 6 0 9 4 3 1 8 6 2 0 7 5 5 0 7 8 3 2 9 6 4 1 8 6 4 7 0 1 5 2 9 3 2 8 0 6 5 4 3 9 1 7 1 5 6 2 9 7 0 4 3 8 4 3 8 0 2 9 7 1 5 6 sq5 - с симметрией Square: 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 9 5 7 8 4 8 5 2 9 7 0 3 1 6 8 3 6 7 5 1 4 9 0 2 7 9 0 8 6 2 5 4 3 1 6 5 9 0 1 4 3 8 2 7 2 7 1 6 3 9 8 0 5 4 9 4 8 5 7 3 2 1 6 0 3 0 4 1 2 8 7 6 9 5 5 6 7 9 8 0 1 2 4 3 Основной ДЛК пятёрки (Square) не "симметричный", а вот среди ортогональных соквадратов sqi есть три ДЛК, обладающих симметрией (4,31,31). Я отметила эти соквадраты. Из пяти ортогональных соквадратов пятёрки уникальных только четыре. Позже нарисую конфигурацию для этой пятёрки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Конфигурацию, порождаемую нашей пятёрочкой, изобразила 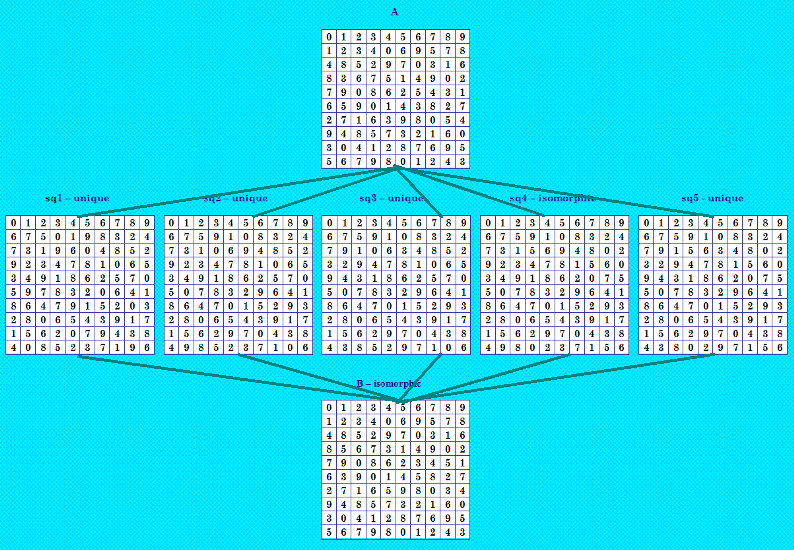 Весьма интересно: все ортогональные соквадраты пятёрки sqi дают двушки, и все эти двушки с ортогональными соквадратами А и В. Но квадраты А и В изоморфны. Были бы пятёрки-близняшки (не полновесные), если бы квадраты А и В не были изоморфными. Имеем же фактически одну не полновесную пятёрку. Полновесная пятёрка должна по идее давать 6 уникальных КФ ОДЛК: основной ДЛК и 5 ортогональных соквадратов. Надеюсь, что полновесную пятёрочку мы тоже найдём, если она существует. А почему бы ей не существовать? PS. Забыла на иллюстрации написать, что квадрат А уникальный, но это и так понятно (основной ДЛК пятёрки). My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 11 Jul 17 Posts: 175 Credit: 5,644,827 RAC: 1 |
Обнаружил, что найденная мной пятерка есть на сайте в сообщении http://forum.boinc.ru/default.aspx?g=posts&m=91270#post91270 При внимательном рассмотрении видно, что со-квадраты там совсем иные. Смотрел по части "6 7 5 0 1 9 8 3 2 4" (вторая строка всех моих со-квадратов). Вопрос такого порядка: Что это тогда за структура? Каким образом оные пересекаются? Под вопросом "каким образом" не имею ввиду сам мой найденный квадрат, с ним и так все понятно. Тут скорее "архитектурный" вопрос. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Обнаружил, что найденная мной пятерка есть на сайте в сообщении http://forum.boinc.ru/default.aspx?g=posts&m=91270#post91270 Demis копирую по указанной вами ссылке КФ ОДЛК конфигурации Unique CFs for combinatorial structure: Да, это найденная вами пятёрка. Основной ДЛК пятёрки - квадрат А в нашей конфигурации, он же в цитате DLS 1: 0123456789123406957848529703168367514902790862543165901438272716398054948573216030412876955679801243 Остальные соквадраты у вашей пятёрки не совпадают потому, что они не переведены в КФ. Переведите их в КФ и они тоже совпадут. Кстати, конфигурация по ссылке опять дырявая (как Венера): два изоморфных ОДЛК в конфигурации присутствуют. Фактически никакого ромба-5 нет, а есть одна не полновесная пятёрка. Я писала: Были бы пятёрки-близняшки (не полновесные), если бы квадраты А и В не были изоморфными. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пропустила через Канонизатор ДЛК все 6 ОДЛК, порождаемые пятёркой (седьмой ОДЛК вторичен - от соквадратов пятёрки происходит, и он не уникален). Получены пять уникальных КФ ОДЛК: 0 1 2 3 4 5 6 7 8 9 1 2 3 0 6 8 9 5 4 7 9 4 5 7 2 3 1 8 6 0 6 8 7 9 5 4 0 2 1 3 8 9 4 1 3 6 7 0 5 2 4 6 9 2 7 1 8 3 0 5 3 0 8 5 9 7 4 1 2 6 7 5 1 8 0 2 3 6 9 4 5 3 0 6 8 9 2 4 7 1 2 7 6 4 1 0 5 9 3 8 0 1 2 3 4 5 6 7 8 9 1 2 3 0 7 9 8 6 5 4 6 8 7 5 9 0 3 2 4 1 5 3 1 4 0 2 7 8 9 6 9 5 8 7 6 1 4 3 2 0 4 6 9 2 3 8 1 0 7 5 3 4 5 6 8 7 9 1 0 2 2 9 4 8 1 6 0 5 3 7 7 0 6 9 2 3 5 4 1 8 8 7 0 1 5 4 2 9 6 3 0 1 2 3 4 5 6 7 8 9 1 2 3 0 7 9 8 6 5 4 6 8 7 5 9 0 3 2 4 1 5 3 1 4 0 2 7 8 9 6 9 5 8 7 6 1 4 3 2 0 4 6 9 2 8 3 1 0 7 5 8 4 5 6 3 7 9 1 0 2 2 9 4 8 1 6 0 5 3 7 7 0 6 9 2 8 5 4 1 3 3 7 0 1 5 4 2 9 6 8 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 9 5 7 8 4 8 5 2 9 7 0 3 1 6 8 3 6 7 5 1 4 9 0 2 7 9 0 8 6 2 5 4 3 1 6 5 9 0 1 4 3 8 2 7 2 7 1 6 3 9 8 0 5 4 9 4 8 5 7 3 2 1 6 0 3 0 4 1 2 8 7 6 9 5 5 6 7 9 8 0 1 2 4 3 0 1 2 3 4 5 6 7 8 9 1 2 3 4 8 6 7 9 0 5 8 7 4 5 9 1 0 2 6 3 6 5 1 7 0 2 8 3 9 4 5 0 9 8 6 7 2 4 3 1 7 9 0 6 5 3 1 8 4 2 4 3 7 1 2 8 9 0 5 6 9 8 6 2 1 4 3 5 7 0 2 4 8 9 3 0 5 6 1 7 3 6 5 0 7 9 4 1 2 8 Из пяти ортогональных соквадратов пятёрки только четыре уникальные. Поэтому пятёрка и называется не полновесной. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 11 Jul 17 Posts: 175 Credit: 5,644,827 RAC: 1 |
Понял, спасибо! Про решето - тоже понял. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пожалуйста :) Осталось поздравить вас с замечательной находкой! Я пятёрку больше двух лет искала и... не нашла. Ещё с Белышевым начинали искать, "рыбалка" у нас была. Много чего нашли в той "рыбалке", но пятёрку не поймали. Теперь нам до полного комплекта не хватает девяточки. Эх, где же она? :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 11 Jul 17 Posts: 175 Credit: 5,644,827 RAC: 1 |
Остальные соквадраты у вашей пятёрки не совпадают потому, что они не переведены в КФ. Так вот это-то и странно тогда. Ведь получается у них винегрет какой-то, мой квадрат в одной форме, а остальные в другой, что сомнительно. Тут скорее всего некий "рикошет". Т.е. у них, предположительно, все в одной форме, но одно значение оказалось в ней точно таким-же. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Demis рикошет - безусловно. Обратите внимание на самый первый ДЛК в сообщении по вашей ссылке 0 1 2 3 4 5 6 7 8 9 1 2 3 0 7 9 8 6 5 4 6 8 7 5 9 0 3 2 4 1 5 3 1 4 0 2 7 8 9 6 9 5 8 7 6 1 4 3 2 0 4 6 9 2 8 3 1 0 7 5 8 4 5 6 3 7 9 1 0 2 2 9 4 8 1 6 0 5 3 7 7 0 6 9 2 8 5 4 1 3 3 7 0 1 5 4 2 9 6 8 Этот ДЛК обладает симметрией (4,31,31) (можно предположить, что он найден в эксперименте по поиску решений с данной симметрией) и даёт двушку. Этот ДЛК у Ватутина как бы порождает конфигурацию. Ну да, он, конечно, её порождает: при полной обработке этой двушки и возникает пятёрка. Точно так же пятёрка была найдена и у вас - рикошетом. Обратите внимание на ортогональные соквадраты вашей пятёрки в моём сообщении: среди них есть три ДЛК с симметрией (4,31,31). (И один из них - тот самый, что у Ватутина стоит самым первым, - "прародитель" конфигурации; только у него этот ДЛК переведён в КФ). Вот они-то и были найдены в выполняемом вами эксперименте по поиску решений с симметрией (4,31,31), а от них уже рикошетом получена пятёрка. Пятёрка-то симметрией не обладает. Но лучше всего конфигурацию проследить по её уникальным ОДЛК, это как раз 5 КФ ОДЛК, которые я уже цитировала. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Удача! В эксперименте с псевдоассоциативными ДЛК мной найдены две уникальные пятёрки! 0 4 5 8 2 9 3 6 7 1 8 1 3 2 5 4 7 9 0 6 9 7 2 5 6 8 4 3 1 0 1 5 9 3 7 0 2 8 6 4 7 8 1 9 4 6 0 5 2 3 2 6 0 1 8 5 9 4 3 7 4 3 8 7 9 1 6 0 5 2 3 0 4 6 1 2 5 7 9 8 6 9 7 4 0 3 1 2 8 5 5 2 6 0 3 7 8 1 4 9 0 4 7 9 6 8 3 2 5 1 7 1 3 6 2 9 8 5 0 4 4 6 2 8 7 0 9 3 1 5 1 0 6 3 5 4 2 8 9 7 2 3 0 5 4 6 1 9 7 8 3 7 9 4 8 5 0 1 2 6 9 5 8 7 1 2 6 4 3 0 8 2 4 0 9 1 5 7 6 3 6 9 5 1 3 7 4 0 8 2 5 8 1 2 0 3 7 6 4 9 Эти пятёрки полновесные, каждая даёт 6 уникальных КФ ОДЛК. Как долго я искала пятёрочки! И вот они, наконец-то! Сразу две. Счёт пятёркам в нашей БД пошёл, это 2-ая и 3-я пятёрки. Эксперимент с псевдоассоциативными ДЛК продолжается! И у меня на ПК, и в автономном подпроекте. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Посмотрим на мои пятёрочки с точки зрения узорчатых ортогоналек. Это иллюстрация для моей первой пятёрки, основной ДЛК пятёрки во втором формате, конфигурация из шести уникальных ОДЛК  Удивительно! Ортогональные соквадраты совершенно так же, как у троек и четвёрок, узорчатые; только здесь переставляются уже пять элементов: 5, 6, 7, 8, 9. Что мы имеем? У троек переставляются три элемента (7, 8, 9), у четвёрок переставляются четыре элемента (6, 7, 8, 9), и у пятёрок переставляются пять элементов (5, 6, 7, 8, 9). Случайно ли это? Или закономерность? Хорошие вопросы! Если это закономерность, то как её можно использовать для поиска групп пар ОДЛК выше двушки? Пятёрок-то у нас найдено всего три на всю многомиллионную БД. Не мешало бы найти ещё пятёрочек, да и других групп пар ОДЛК выше двушки. PS. Интересно! Ранее эта пятёрка была показана в другом виде: основной ДЛК тоже во втором формате, а ортогональные соквадраты найдены программой Беляева  Узорчатость ортогональных соквадратов очевидна. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Немного другие ортогональки у моей второй пятёрки, но они тоже узорчатые [DLK(5)] 0 4 7 9 6 8 3 2 5 1 7 1 3 6 2 9 8 5 0 4 4 6 2 8 7 0 9 3 1 5 1 0 6 3 5 4 2 8 9 7 2 3 0 5 4 6 1 9 7 8 3 7 9 4 8 5 0 1 2 6 9 5 8 7 1 2 6 4 3 0 8 2 4 0 9 1 5 7 6 3 6 9 5 1 3 7 4 0 8 2 5 8 1 2 0 3 7 6 4 9 [mate#1] 3 8 4 1 2 5 0 6 7 9 6 4 1 3 8 9 2 5 0 7 1 6 0 7 9 8 5 4 2 3 0 5 7 9 1 6 3 8 4 2 7 2 9 0 5 1 6 3 8 4 5 3 8 4 6 2 7 1 9 0 2 9 3 5 7 4 8 0 6 1 9 1 2 6 0 3 4 7 5 8 4 7 6 8 3 0 9 2 1 5 8 0 5 2 4 7 1 9 3 6 [mate#2] 3 8 4 1 2 5 0 6 7 9 6 4 1 3 9 8 2 5 0 7 1 6 0 7 8 9 5 4 2 3 0 5 7 9 1 6 3 8 4 2 7 2 8 0 5 1 6 3 9 4 5 3 9 4 6 2 7 1 8 0 2 9 3 5 7 4 8 0 6 1 9 1 2 6 0 3 4 7 5 8 4 7 6 8 3 0 9 2 1 5 8 0 5 2 4 7 1 9 3 6 [mate#3] 7 8 3 2 1 6 0 5 4 9 5 3 2 7 8 9 1 6 0 4 2 5 0 4 9 8 6 3 1 7 0 6 4 9 2 5 7 8 3 1 4 1 9 3 6 2 5 7 8 0 6 7 8 0 5 1 4 2 9 3 1 0 7 6 4 3 8 9 5 2 3 2 1 5 0 7 9 4 6 8 9 4 5 8 7 0 3 1 2 6 8 9 6 1 3 4 2 0 7 5 [mate#4] 7 8 3 2 1 6 0 5 4 9 5 3 2 7 9 8 1 6 0 4 2 5 0 4 8 9 6 3 1 7 0 6 4 9 2 5 7 8 3 1 4 1 8 3 6 2 5 7 9 0 6 7 9 0 5 1 4 2 8 3 1 0 7 6 4 3 8 9 5 2 3 2 1 5 0 7 9 4 6 8 9 4 5 8 7 0 3 1 2 6 8 9 6 1 3 4 2 0 7 5 [mate#5] 7 8 3 2 1 6 0 5 4 9 5 3 2 7 9 8 1 6 0 4 2 5 0 4 8 9 6 3 1 7 0 6 4 9 2 5 7 8 3 1 4 1 8 3 6 2 5 9 7 0 6 9 7 0 5 1 4 2 8 3 1 0 9 6 4 3 8 7 5 2 3 2 1 5 0 7 9 4 6 8 9 4 5 8 7 0 3 1 2 6 8 7 6 1 3 4 2 0 9 5 Иллюстрация  Конфигурация из шести уникальных ОДЛК. Ортогональные соквадраты разделились на две группы узорчатых ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Конфигурация, порождаемая пятёркой, найденной Demis, была показана выше, дублирую  Отличная конфигурация! Здесь основной ДЛК пятёрки в первом формате (квадрат А). Узорчатость ОДЛК не показана на иллюстрации. Квадраты А и В узорчатые, ортогональные соквадраты sqi узорчатые. Исправлю этот недостаток. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот новая иллюстрация для пятёрки, найденной Demis  Конфигурация из пяти уникальных ОДЛК, два ОДЛК изоморфны (на иллюстрации указаны уникальные и изоморфные ОДЛК). В ортогональных соквадратах пятёрки (sqi) переставляются элементы 0, 3, 5, 9. Не забываем, что здесь основной ДЛК пятёрки в первом формате. Во втором формате будет немного другая узорчатость. Можно нарисовать и посмотреть. Пятёрка-близняшка происходит не от уникального ДЛК (квадрат В) Итак, имеем пока всего три пятёрки, узорчатые ОДЛК присутствуют в конфигурациях, порождаемых всеми тремя пятёрками. Ждём новых пятёрок для исследования. Теперь можно посмотреть на шестёрки. |

©2026 (C) Progger