Различные группы пар ОДЛК10
Message boards :
Science :
Различные группы пар ОДЛК10
Message board moderation
Previous · 1 · 2
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Троек в нашей БД на данный момент 69 штук. Какие конфигурации дают нам тройки? Я пока встретила только два вида конфигураций, порождаемых тройками. 1. Стандартная тройка. Такие тройки дают 4 уникальные КФ ОДЛК. Пример уже ставший историческим - первая тройка, найденная Белышевым  Основной ДЛК этой тройки и "симметричный" и является БС, тем не менее, все ортогональные соквадраты тройки уникальные. Симметрии, которыми обладает основной ДЛК данной тройки: (1,31,31) (16,16,16) (16,31,31) 2. Тройки-близняшки. Эти тройки были найдены Demis в эксперименте с псевдоассоциативными ДЛК. Конфигурация содержит 5 уникальных ОДЛК  Конечно, все 69 троек я не проверяла на конфигурацию. Может быть, есть и другие виды конфигураций, порождаемых тройками. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Тройки и четвёрки исследовала на конфигурации и собиралась переходить к шестёркам. А тут... подоспела пятёрочка! Первую пятёрочку в нашей БД нашёл вчера Demis в эксперименте по поиску решений с симметрией (4,31,31). Это не полновесная пятёрка, даёт 5 уникальных КФ ОДЛК. Иллюстрация 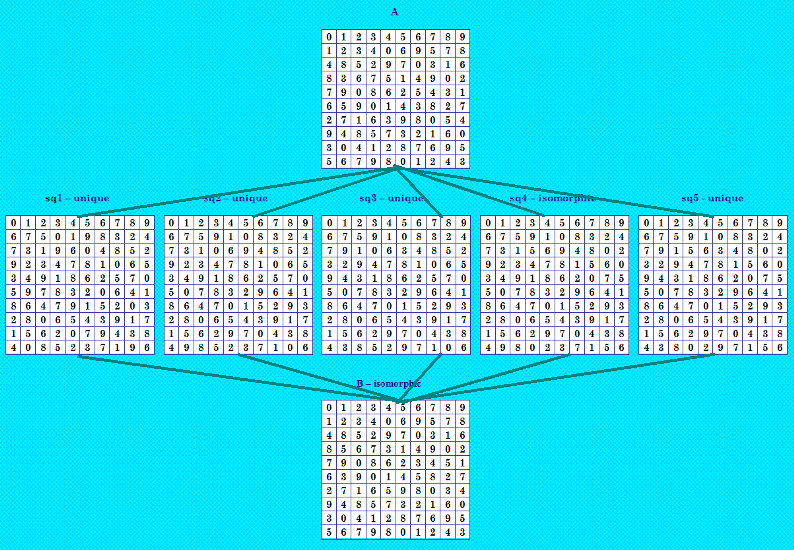 Замечу, что в конфигурации показаны все семь ОДЛК, включая два изоморфных. Изоморфные ОДЛК помечены. (Квадрат А, конечно, уникальный, это основной ДЛК пятёрки.) Если бы квадраты А и В не были изоморфны, были бы пятёрки-близняшки. Пока только одна не полновесная пятёрка. Теперь можно переходить к шестёркам - посмотреть, какие от них происходят конфигурации. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, шестёрки... Первые шесть шестёрок, найденные в нашем с Белышевым эксперименте, все симметричные по Гергели/Брауну и не только Определитель симметрий Введено ЛК : 6 Из них симметричных : 6 Найдено различных симметрий: 4 Время работы : 0.031 сек Список симметрий: (1,1,1) (1,31,31) (16,16,16) (16,31,31) Все эти шестёрки не полновесные, каждая даёт 4 уникальные КФ ОДЛК. Это первый вид конфигураций, порождаемых шестёрками. Иллюстрацию покажу на другой шестёрке, которая тоже "симметричная", но с другой симметрией - (4,31,31). Эта шестёрка найдена мной в эксперименте с псевдоассоциативными ДЛК. Точно так же: из шести ортогональных соквадратов шестёрки три уникальные и три изоморфные. Всего шестёрка даёт 4 уникальные КФ ОДЛК. 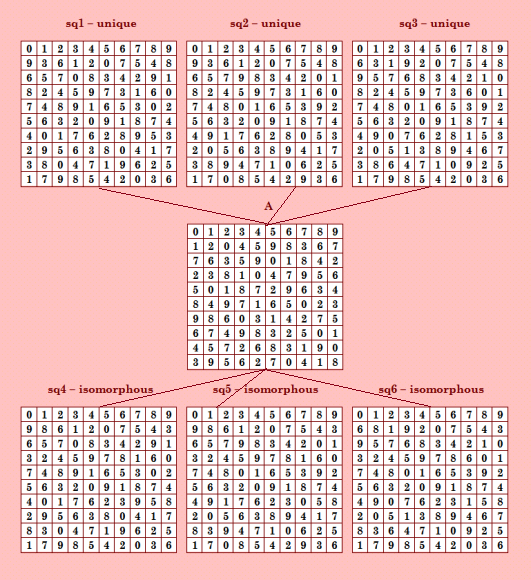 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А это единственная пока в нашей БД полновесная шестёрка 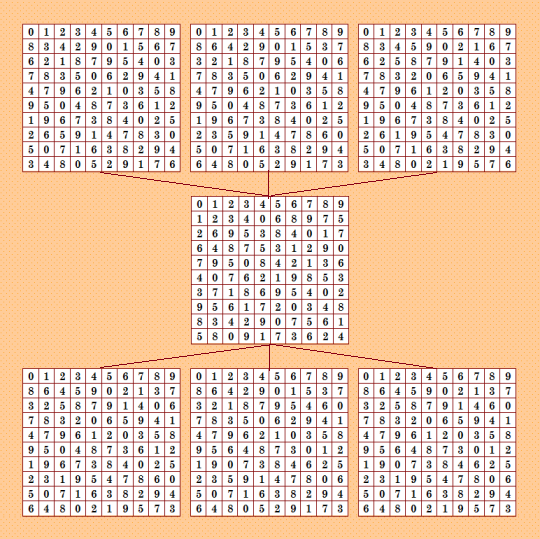 Найдена мной в эксперименте с псевдоассоциативными ДЛК. Все шесть ортогональных соквадратов шестёрки несмотря на свою похожесть уникальные. Это второй вид конфигураций, порождаемых шестёрками. Других конфигураций от шестёрок пока нет. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Единственная пока в нашей БД семёрка 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 9 5 6 8 3 9 4 0 7 1 5 8 2 6 9 0 3 1 8 4 7 6 5 2 5 8 9 7 6 2 0 1 4 3 7 5 6 8 0 9 2 4 3 1 6 4 7 5 1 3 8 2 9 0 2 6 1 9 5 8 4 3 0 7 8 3 5 2 9 6 1 0 7 4 4 7 8 6 2 0 3 9 1 5найдена мной в эксперименте с псевдоассоциативными ДЛК. Эта семёрка полновесная, даёт 8 уникальных КФ ОДЛК. Это и единственная пока конфигурация, порождаемая семёрками. Других семёрок пока нет и конфигураций, понятно, тоже нет. Будем надеяться, что новые семёрки ещё будут найдены. Данную конфигурацию, кажется, не изображала. Ну, тут всё просто: основной ДЛК (его вы видите выше) и семь ортогональных соквадратов. Все ортогональные соквадраты уникальные. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Из семи восьмёрок, имеющихся в нашей БД на данный момент, 5 "симметричных" и две не "симметричные". Это 5 "симметричных" Определитель симметрий Введено ЛК : 5 Из них симметричных : 5 Найдено различных симметрий: 3 Время работы : 0.015 сек Список симметрий: (1,1,1) (1,31,31) (4,31,31) Все "симметричные" восьмёрки не полновесные, дают 5 уникальных КФ ОДЛК. Обе не "симметричные" восьмёрки полновесные, дают 9 уникальных КФ ОДЛК. Соответственно два вида конфигураций. Это две полновесные восьмёрки, обе найдены мной в эксперименте с псевдоассоциативными ДЛК 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 7 3 9 6 8 5 7 3 2 1 9 4 8 0 6 3 0 1 8 9 4 5 6 7 2 8 9 4 6 7 1 0 2 5 3 4 8 5 1 3 6 2 0 9 7 7 5 6 0 8 2 9 1 3 4 9 3 7 5 6 0 8 4 2 1 6 4 8 9 2 3 7 5 1 0 2 6 9 7 0 8 1 3 4 5 0 1 2 3 4 5 6 7 8 9 1 2 0 6 7 9 8 3 4 5 4 6 1 9 5 7 2 8 0 3 7 4 5 8 6 0 3 1 9 2 2 7 3 0 9 6 4 5 1 8 6 8 9 5 2 3 0 4 7 1 9 5 4 1 8 2 7 0 3 6 3 9 7 4 1 8 5 6 2 0 8 0 6 2 3 4 1 9 5 7 5 3 8 7 0 1 9 2 6 4 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А девяточки у нас в БД н-е-е-е-т :( Десяточка зато есть; конфигурация, порождаемая десяточкой, показана выше. Осталось рассмотреть конфигурации, порождаемые двушками. Двушки тоже бывают полновесные (дают 3 уникальные КФ ОДЛК) и не полновесные (дают 2 уникальные КФ ОДЛК). Наверняка есть двушки-близняшки, как полновесные, так и не полновесные. Их надо просто найти среди всех известных двушек. Но двушек очень много и искать надо долго. Двушки и ещё вполне могут какие-то конфигурации порождать. Вот полновесная двушка, которая была найдена мной очень давно в эксперименте со случайным поиском. Очень обрадовалась я тогда этой двушке :)  А теперь у нас двушек в БД полно (несколько тысяч), как полновесных, так и не полновесных. Я их даже и не считаю. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А что вы думаете про однушки? Оказывается, однушки тоже бывают не полновесные, это SODLS. Обычная однушка, понятно, даёт две уникальные КФ ОДЛК. Это полновесная однушка. Таких однушек, конечно, большинство. А вот когда ДЛК ортогонален своему транспонированному - это уже не полновесная однушка, потому что она даёт только один уникальный ОДЛК. Все 30502 SODLS 10-го порядка нашёл Белышев, они были выложены на форуме boinc.ru Пример SODLS (это КФ) 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 8 9 5 7 2 3 6 5 9 8 0 1 7 4 6 4 5 1 7 9 3 8 2 0 5 0 9 7 8 2 4 6 1 3 3 7 8 9 6 4 2 5 0 1 9 5 4 0 1 3 7 2 6 8 8 9 7 2 5 0 1 3 4 6 7 8 3 6 0 1 5 4 9 2 4 6 1 8 2 7 9 0 3 5 Вот и вся тут конфигурация :) один уникальный ОДЛК. Таким образом, от однушек мы имеем два вида конфигураций. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Полновесную однушку покажу историческую, от Брауна с компанией (1992 г.)  Однушка здесь - нижняя ортогональная пара. Две верхние ортогональные пары - двушка, впоследствии дополненная Заикиным до четвёрки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сегодня в эксперименте по поиску решений с симметрией (4,31,31) попались не полновесные двушки-близняшки. 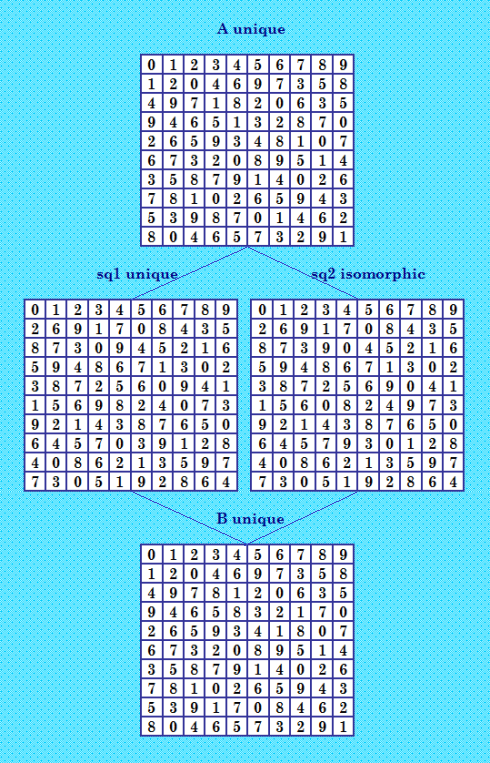 Вот такая конфигурация. Да, в этой конфигурации есть один изоморфный ОДЛК, но это соответствует характеристике двушек: не полновесные. Можно изоморфный ОДЛК в конфигурации и не изображать. В конфигурации содержится 3 уникальных ОДЛК. Главное в том, что основные ДЛК обеих двушек (квадраты А и В на иллюстрации) уникальные. В конфигурации есть и полновесная двушка (не смотрим на изоморфный sq2), она происходит от квадрата sq1; ортогональные соквадраты этой двушки - А и В. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Двушку с аппендиксом нашла  Кажется, такую конфигурацию ещё не показывала. Двушка, происходящая от квадрата А, имеет аппендикс - квадрат В. Все 4 ОДЛК конфигурации уникальные. В конфигурации имеем две двушки и две однушки. Можно так же считать, что аппендикс имеет двушка, происходящая от квадрата sq1. Аппендиксом в этом случае будет квадрат sq2. Ещё можно эту конфигурацию изобразить в виде цепочки. Сейчас изображу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот цепочка: две двушки и две однушки (с квадратами предыдущей конфигурации) 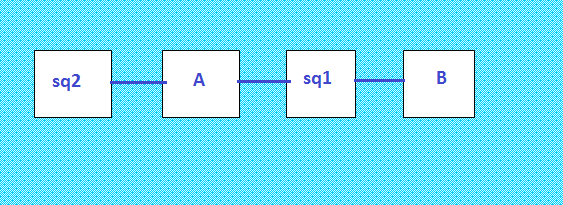 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё одна двушка с аппендиксом 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 8 9 3 5 7 3 5 7 6 1 9 2 8 4 0 5 9 3 1 8 0 4 6 7 2 7 4 5 2 9 1 8 0 3 6 8 6 1 9 0 3 7 5 2 4 6 8 9 7 3 4 5 2 0 1 9 7 6 8 5 2 0 4 1 3 4 3 8 0 2 7 1 9 6 5 2 0 4 5 7 6 3 1 9 8 Наверное, их много в БД. Здесь https://boinc.progger.info/odlk/forum_thread.php?id=46&postid=2334#2334 показана четвёрка с аппендиксом. А вот тройку с аппендиксом я пока не встречала. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А эти однушки родственницы, я назвала их сноха и золовка :)  Выложила давно на форуме MHP http://mathhelpplanet.com/viewtopic.php?p=346944#p346944 Там тема закрыта, но почитать можно, почему так однушки названы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Просматривала группу семейств, которые я проверяла по поиску симметрии (4,31,31) по схеме Белышева. Вот запись в этой группе семейств проверено, 5 марьяжных ДЛК, 4 октября 2018 г. здесь найдены две уникальные "симметричные" четвёрки-близняшки AAAATJBQG AAAATJEDG AAAATJEDO AAAATJENA AAAATJENI AAAATJHFC AAAATJHFO AAAATJHQA AAAATJHQC AAAATJKDA А вот и сами "симметричные" четвёрки-близняшки 0 2 7 9 3 8 5 4 6 1 9 1 6 4 7 2 3 8 0 5 6 8 2 7 5 1 9 3 4 0 7 9 1 3 6 0 4 2 5 8 1 3 0 5 4 6 8 9 7 2 2 6 3 0 8 5 7 1 9 4 8 0 4 2 9 3 6 5 1 7 3 5 9 8 0 4 1 7 2 6 4 7 5 6 1 9 2 0 8 3 5 4 8 1 2 7 0 6 3 9 0 2 7 9 3 8 5 4 6 1 9 1 6 4 7 2 3 8 0 5 6 8 2 7 5 1 9 3 4 0 7 9 1 3 6 0 4 2 5 8 1 3 0 5 4 6 8 9 7 2 2 6 3 1 8 5 7 0 9 4 8 0 4 2 9 3 6 5 1 7 3 5 9 8 1 4 0 7 2 6 4 7 5 6 0 9 2 1 8 3 5 4 8 0 2 7 1 6 3 9 Действительно близняшки, очень похожи! Нарисую иллюстрацию на досуге. Кажется, такую иллюстрацию я ещё не показывала. Вот нарисовала конфигурацию - четвёрки-близняшки с симметрией (4,31,31) 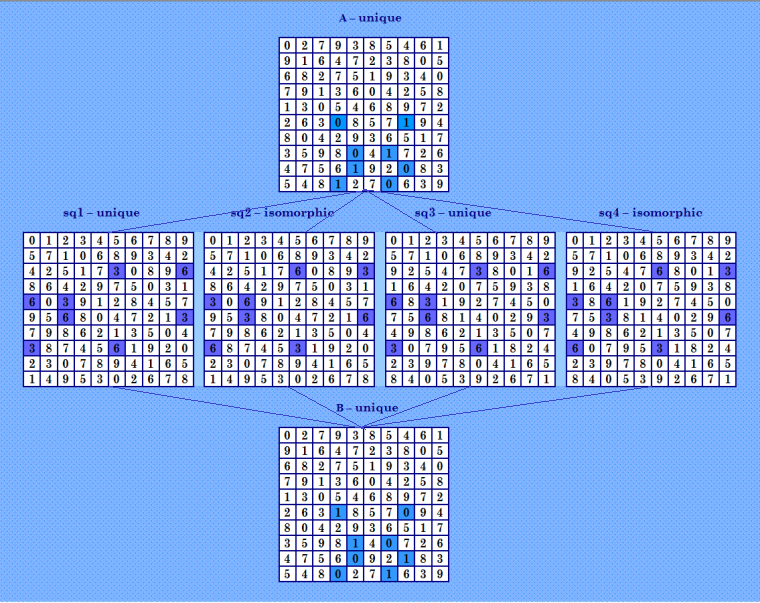 Как утверждает скрипт Белышева zamyk.bat, в этой конфигурации содержится две четвёрки и две двушки, и 4 уникальных ОДЛК Найдено марьяжных КФ: count[2] = 2 count[4] = 2 Всего: 4 Найдено соквадратов: 12 КФ соквадратов: 4 Правильно утверждает :) Раньше вроде показаны "симметричные" четвёрки-близняшки, но с симметрией (1,31,31). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В автономном подпроекте в эксперименте по поиску решений с симметрией (4,31,31) по алгоритму Белышева Tomas Brada нашёл восьмёрку с данной симметрией, которая порождает очень интересную конфигурацию 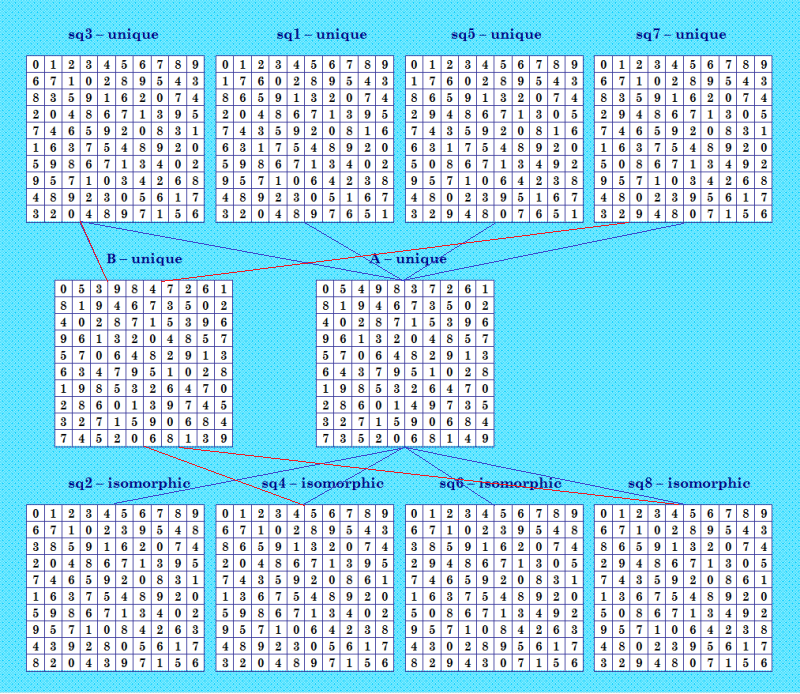 В конфигурации содержится также "симметричная" четвёрка (от квадрата В происходит), тоже с симметрией (4,31,31). Вот такая сложная конфигурация, а уникальных ОДЛК в ней всего 6. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А у меня в эксперименте с псевдоассоциативными ДЛК нашлись две уникальные полновесные пятёрки! 0 4 5 8 2 9 3 6 7 1 8 1 3 2 5 4 7 9 0 6 9 7 2 5 6 8 4 3 1 0 1 5 9 3 7 0 2 8 6 4 7 8 1 9 4 6 0 5 2 3 2 6 0 1 8 5 9 4 3 7 4 3 8 7 9 1 6 0 5 2 3 0 4 6 1 2 5 7 9 8 6 9 7 4 0 3 1 2 8 5 5 2 6 0 3 7 8 1 4 9 0 4 7 9 6 8 3 2 5 1 7 1 3 6 2 9 8 5 0 4 4 6 2 8 7 0 9 3 1 5 1 0 6 3 5 4 2 8 9 7 2 3 0 5 4 6 1 9 7 8 3 7 9 4 8 5 0 1 2 6 9 5 8 7 1 2 6 4 3 0 8 2 4 0 9 1 5 7 6 3 6 9 5 1 3 7 4 0 8 2 5 8 1 2 0 3 7 6 4 9 Ранее Demis нашёл не полновесную пятёрку в эксперименте по поиску решений с симметрией (4,31,31). Эта пятёрка первая в нашей БД. А теперь есть ещё две пятёрки. Я шла до этих пятёрок почти три года! Конфигурации эти пятёрки дают простенькие: основной ДЛК и пять ортогональных соквадратов (ДЛК). Ну, можно нарисовать одну из них. PS. Интересно: обе пятёрки из линейки №10. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Изобразила одну полновесную пятёрочку  Все 6 ОДЛК в конфигурации уникальные. Ортогональные соквадраты весьма забавные. Напоминаю: ортогональные ДЛК найдены по программе коллеги С. Беляева. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В ручном эксперименте мультисимметрия нашлись полновесные двушки-близняшки 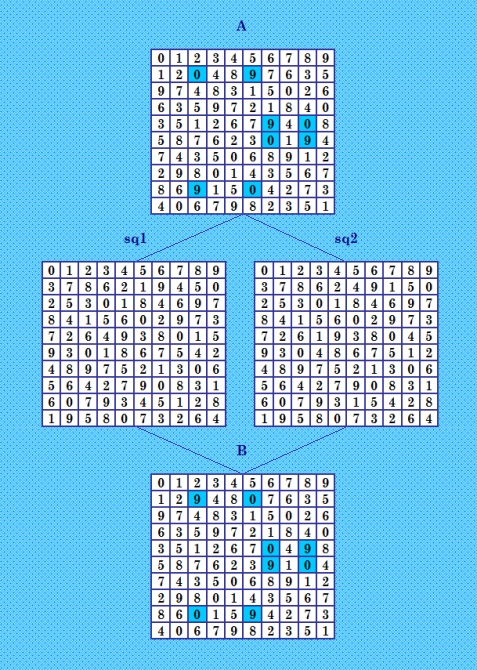 Раньше были показаны не полновесные двушки-близняшки. Интересно: каждая из двушек-близняшек даёт вот такое Замыкание Найдено марьяжных КФ: count[2] = 4 Всего: 4 Найдено соквадратов: 8 КФ соквадратов: 4 То есть здесь две пары двушек-близняшек. Первая пара - двушки от А и В. Вторая пара - двушки от sq1 и sq2. В Замыкании имеем 4 двушки. |

©2026 (C) Progger