Проект gris по кортежу 19-252
Message boards :
Cafe :
Проект gris по кортежу 19-252
Message board moderation
Previous · 1 . . . 30 · 31 · 32 · 33 · 34 · 35 · 36 . . . 54 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программу покажу, которая нашла приближение с valids=14 прямо в этом проходе default(parisizemax,10^9)
default(timer,1)
\l 15unik_pat1_res.txt;
{
\\skipped 221 codes:
sk=[1966, 1967, 2047, 2943, 2991, 3007, 3063, 3069, 3263, 3503, 3510, 3511, 3515, 3519, 3567, 3575, 3582, 3583, 3647, 3663, 3703, 3709, 3711, 3757, 3758, 3759, 3767, 3770, 3775, 3799, 3823, 3831, 3837, 3839, 3895, 3919, 3935, 3947, 3966, 3967, 3983, 3991, 3999, 4007, 4014, 4015, 4019, 4021, 4022, 4023, 4025, 4027, 4029, 4030, 4031, 4046, 4047, 4055, 4059, 4062, 4063, 4071, 4085, 4086, 4095, 5047, 5053, 5119, 5562, 5567, 5631, 5695, 5759, 5807, 5815, 5821, 5823, 5967, 5983, 5999, 6015, 6031, 6059, 6069, 6071, 6077, 6078, 6111, 6135, 6141, 6143, 6591, 6775, 6782, 6846, 6847, 6863, 6895, 7031, 7071, 7093, 7103, 7127, 7134, 7135, 7151, 7159, 7165, 7167, 7350, 7351, 7357, 7359, 7415, 7421, 7423, 7479, 7531, 7535, 7542, 7550, 7583, 7598, 7599, 7606, 7607, 7609, 7610, 7611, 7613, 7614, 7615, 7627, 7639, 7647, 7663, 7669, 7735, 7739, 7741, 7743, 7759, 7767, 7774, 7775, 7790, 7791, 7798, 7807, 7839, 7847, 7851, 7859, 7861, 7862, 7863, 7866, 7867, 7869, 7870, 7871, 7887, 7895, 7902, 7915, 7923, 7926, 7927, 7931, 7934, 7935, 7967, 7983, 7990, 7991, 8015, 8022, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8103, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8159, 8173, 8174, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191];
\\enter pattern
pt=[0, 18, 30, 60, 62, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228];
pt1=[0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228];
w=37;
np1=10521; print(np1," from number");
np2=11021; print(np2," to number");
\\ end
pl=#pt;
nw=primepi(w);
printf("%d \n",pt);
print("patterns length ",pl);
prs=primes(nw);
period=vecprod(prs);
printf("prove by %d#: ",prs[nw]);print(prs);
print(period," period");
vp=vector(np2-np1+1, i, period*(np1-1+i)); lvp=#vp;
printf("search in %d - %d\n",vp[1],vp[lvp]+period);
wd=vector(nw);
vmy=vector(30); pat1=vector(15);
lpr=1;
for( ip=1,nw,
rip=[];
for( r=1,prs[ip]-1,
for( i=1,pl, if( (r+pt[i])%prs[ip]==0, next(2)));
rip =concat(rip,r) );
lpr=lpr*#rip;
wd[ip]=rip;
); \\for ip
print(lpr," formulae expected");
k=0;
forvec(v=vector(#wd,i,[1,#wd[i]]), k++;
form=lift(chinese( vector( #wd,j,Mod( wd[j][v[j]], prs[j]) ) ));
\\ начало проверки кортежа
foreach(vp,bpp,
bpt=form+bpp;
if(ispseudoprime(bpt) && ispseudoprime(bpt+228),
l=0;
forprime(p=bpt,bpt+228, l++; vmy[l]=p; );
if(l==15,
for(m=2,15, pat1[m]=vmy[m]-vmy[1]; );
res=pat1-pt1;
pat2=vector(15,i,(pat1[i]==pt1[i]));
vlds=vecsum(pat2);
ncode=fromdigits(pat2[2..14],2);
if(setsearch(sk,ncode),
print(vmy[1],": ",pat1); print(vmy[1],": ",res);
print(vmy[1],": ",pat2); print("valids=",vlds);
print(" ncode=",ncode);
); \\ if(setsearch
);\\if(l==15
);\\ if ispseudoprime
);\\ foreach
\\ конец проверки кортежа
);\\ forvec
}Совместное с gris творчество. gris написал блок формирования формул, а я - блок проверки кортежа. Вот для каждого паттерна серии работает такая программа. Программа работает на периоде 37#, задаётся 501 период в одном проходе. Ахиллес-3 справляется хорошо, время на один проход time = 13h, 11min, 44,266 ms. В сообщении https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=14364 показана консоль. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ахиллес-3 ещё порадовал приближением с valids=13 79470064895370829: [0, 18, 30, 60, 78, 102, 108, 114, 120, 144, 154, 168, 198, 210, 228] 79470064895370829: [0, 0, 0, 0, 0, 18, 0, 0, 0, 0, 4, 0, 0, 0, 0] 79470064895370829: [1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1] valids=13 ncode=7927 Имеем valids=13, 36 codes 3071, 4079, 4087, 4091, 4093, 4094, 5887, 6079, 6127, 6139, 6142, 6655, 6911, 7039, 7163, 7166, 7551, 7671, 7675, 7677, 7678, 7903, 7919, 7927, 7933, 7999, 8047, 8059, 8150, 8155, 8157, 8167, 8171, 8181, 8185, 8188 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очередная порция Norm-чисел для 19-ки с минимальным диаметром дала следующие приближения при valids>7 10042376902173904853298661: [0, 6, 12, 16, 30, 48, 58, 96, 120, 130, 132, 148, 160, 180, 186, 208, 226, 246, 252] 10042376902173904853298661: [0, 0, 0, -14, -12, -24, -32, 0, 0, 4, 0, -8, -2, 0, -24, -14, -14, 0, 0] valids=9 code=99985 10042376893938139834637767: [0, 6, 16, 30, 70, 76, 90, 114, 124, 126, 132, 136, 180, 196, 210, 232, 234, 244, 252] 10042376893938139834637767: [0, 0, 4, 0, 28, 4, 0, 18, 4, 0, 0, -20, 18, 16, 0, 10, -6, -2, 0] valids=8 code=84360 10042376901273698042937697: [0, 30, 42, 64, 66, 72, 100, 106, 120, 126, 142, 156, 180, 196, 216, 222, 240, 250, 252] 10042376901273698042937697: [0, 24, 30, 34, 24, 0, 10, 10, 0, 0, 10, 0, 18, 16, 6, 0, 0, 4, 0] valids=8 code=4934 10042376900531290743257651: [0, 6, 20, 38, 42, 56, 66, 78, 90, 96, 120, 132, 162, 176, 210, 222, 240, 248, 252] 10042376900531290743257651: [0, 0, 8, 8, 0, -16, -24, -18, -30, -30, -12, -24, 0, -4, 0, 0, 0, 2, 0] valids=8 code=73774 Коды не уникальные. Приближения в спектр добавила. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, нам надо найти следующие 13 приближений к центральной 15-ке с valids=14 4095 14 [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 6143 14 [1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 7167 14 [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 7679 14 [1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 7935 14 [1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1] 8063 14 [1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1] 8127 14 [1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1] 8159 14 [1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1] 8175 14 [1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1] 8183 14 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1] 8187 14 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1] 8189 14 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1] 8190 14 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1] Это приближение известно (из результата г. Петухова для 19-ки) 7679 14 [1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] Это приближение сегодня найдено мной 8159 14 [1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1] Остаётся найти 11 приближений. У меня работает поиск по трём сериям паттернов: [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] [1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] [1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] Кстати, сегодняшнее решение найдено в поиске по третьей серии паттернов. Смотрите об этой серии паттернов сообщение https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=14260 Это вторая серия паттернов [0, 18, 20, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 22, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 24, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 26, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 28, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 32, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 34, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 36, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 38, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 40, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 42, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 44, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 46, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 48, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 50, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 52, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 54, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 56, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 58, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228]; А это первая серия паттернов 0, 2, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 4, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 6, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 8, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 10, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 12, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 14, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 16, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 20, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 22, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 24, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 26, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 0, 28, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228 Первая и вторая серии паттернов запущено недавно, а третья серия паттернов давно; уже много приближений от неё получено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Новости о спектре приближений к центральной 15-ке За сутки найдено 8 уникальных элементов (плохо). Всего найдено 7999 уникальных элементов спектра, 97,64%. Пропущено 193 элемента. В новом списке пропущенных элементов самая верхняя часть спектра (>8000) выглядит так 8015, 8022, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8103, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8173, 8174, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191 За сутки в этой части спектра не найдено ни одного элемента. Список пропущенных элементов (193 шт.) 1967, 2047, 2991, 3007, 3063, 3263, 3503, 3510, 3511, 3515, 3519, 3582, 3583, 3647, 3663, 3711, 3757, 3758, 3759, 3767, 3775, 3799, 3823, 3831, 3839, 3895, 3935, 3947, 3966, 3967, 3983, 3991, 3999, 4007, 4014, 4015, 4019, 4021, 4022, 4023, 4025, 4027, 4029, 4030, 4031, 4047, 4059, 4062, 4063, 4071, 4085, 4086, 4095, 5047, 5053, 5119, 5562, 5567, 5631, 5759, 5807, 5815, 5821, 5823, 5967, 5983, 5999, 6015, 6031, 6059, 6069, 6071, 6077, 6078, 6111, 6135, 6141, 6143, 6775, 6846, 6847, 6895, 7031, 7071, 7093, 7103, 7127, 7134, 7135, 7151, 7159, 7165, 7167, 7350, 7357, 7359, 7415, 7423, 7535, 7542, 7550, 7583, 7598, 7599, 7606, 7607, 7609, 7610, 7611, 7613, 7614, 7615, 7639, 7647, 7663, 7669, 7735, 7739, 7741, 7743, 7767, 7774, 7775, 7790, 7791, 7798, 7807, 7839, 7859, 7861, 7862, 7863, 7866, 7867, 7869, 7870, 7871, 7887, 7895, 7902, 7915, 7926, 7931, 7934, 7935, 7967, 7983, 7990, 8015, 8022, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8103, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8173, 8174, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191 Результаты поиска за сутки 29141263702931473: [0, 18, 46, 60, 78, 84, 108, 118, 120, 144, 150, 184, 198, 210, 228] 29141263702931473: [0, 0, 16, 0, 0, 0, 0, 4, 0, 0, 0, 16, 0, 0, 0] 29141263702931473: [1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1] valids=12 ncode=6075 28684855052471843: [0, 26, 30, 60, 78, 86, 108, 110, 120, 144, 150, 164, 198, 224, 228] 28684855052471843: [0, 8, 0, 0, 0, 2, 0, -4, 0, 0, 0, -4, 0, 14, 0] 28684855052471843: [1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1] valids=10 ncode=3770 82686018236014873: [0, 28, 30, 60, 78, 94, 106, 114, 120, 144, 166, 168, 198, 210, 228] 82686018236014873: [0, 10, 0, 0, 0, 10, -2, 0, 0, 0, 16, 0, 0, 0, 0] 82686018236014873: [1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1] valids=11 ncode=3703 39079010733788573: [0, 18, 30, 60, 78, 86, 108, 116, 120, 150, 158, 168, 198, 210, 228] 39079010733788573: [0, 0, 0, 0, 0, 2, 0, 2, 0, 6, 8, 0, 0, 0, 0] 39079010733788573: [1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1] ncode=7847 38839064786557583: [0, 18, 30, 60, 74, 78, 108, 116, 120, 144, 146, 168, 198, 210, 228] 38839064786557583: [0, 0, 0, 0, -4, -6, 0, 2, 0, 0, -4, 0, 0, 0, 0] 38839064786557583: [1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1] ncode=7351 79470064895370829: [0, 18, 30, 60, 78, 102, 108, 114, 120, 144, 154, 168, 198, 210, 228] 79470064895370829: [0, 0, 0, 0, 0, 18, 0, 0, 0, 0, 4, 0, 0, 0, 0] 79470064895370829: [1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1] valids=13 ncode=7927 448166056275031704989: [0, 18, 42, 68, 78, 84, 98, 114, 120, 144, 192, 194, 198, 210, 228] 448166056275031704989: [0, 0, 12, 8, 0, 0, -10, 0, 0, 0, 42, 26, 0, 0, 0] 448166056275031704989: [1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1] ncode=4979 649489766510585093: [0, 18, 30, 48, 78, 80, 108, 114, 120, 144, 170, 186, 198, 218, 228] 649489766510585093: [0, 0, 0, -12, 0, -4, 0, 0, 0, 0, 20, 18, 0, 8, 0] 649489766510585093: [1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1] ncode=6898 3657133918794129295069: [0, 18, 34, 60, 64, 84, 108, 114, 130, 144, 168, 190, 198, 210, 228] 3657133918794129295069: [0, 0, 4, 0, -14, 0, 0, 0, 10, 0, 18, 22, 0, 0, 0] 3657133918794129295069: [1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1] ncode=5587 11478993030059372706113: [0, 18, 30, 38, 78, 84, 96, 114, 120, 144, 186, 200, 206, 210, 228] 11478993030059372706113: [0, 0, 0, -22, 0, 0, -12, 0, 0, 0, 36, 32, 8, 0, 0] 11478993030059372706113: [1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1] ncode=7025 277118287183753849: [0, 18, 30, 60, 84, 94, 108, 114, 120, 144, 150, 168, 184, 210, 228] 277118287183753849: [0, 0, 0, 0, 6, 10, 0, 0, 0, 0, 0, 0, -14, 0, 0] 277118287183753849: [1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1] ncode=7421 145127183212255183: [0, 24, 30, 60, 76, 84, 108, 114, 120, 144, 148, 168, 198, 210, 228] 145127183212255183: [0, 6, 0, 0, -2, 0, 0, 0, 0, 0, -2, 0, 0, 0, 0] 145127183212255183: [1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1] ncode=3575 60106196304930169: [0, 28, 30, 60, 78, 84, 108, 114, 132, 144, 162, 168, 198, 210, 228] 60106196304930169: [0, 10, 0, 0, 0, 0, 0, 0, 12, 0, 12, 0, 0, 0, 0] 60106196304930169: [1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1] ncode=4055 14053365449884590769: [0, 18, 30, 60, 78, 102, 108, 112, 120, 148, 150, 192, 198, 210, 228] 14053365449884590769: [0, 0, 0, 0, 0, 18, 0, -2, 0, 4, 0, 24, 0, 0, 0] 14053365449884590769: [1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1] ncode=7851 206057869331384449: [0, 12, 30, 60, 78, 82, 100, 114, 120, 144, 150, 168, 184, 210, 228] 206057869331384449: [0, -6, 0, 0, 0, -2, -8, 0, 0, 0, 0, 0, -14, 0, 0] 206057869331384449: [1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1] ncode=3709 354420987890839549: [0, 18, 30, 60, 64, 84, 88, 114, 120, 148, 150, 162, 198, 210, 228] 354420987890839549: [0, 0, 0, 0, -14, 0, -20, 0, 0, 4, 0, -6, 0, 0, 0] 354420987890839549: [1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1] ncode=7531 577884139111393339: [0, 18, 30, 40, 58, 84, 108, 112, 120, 144, 150, 168, 198, 210, 228] 577884139111393339: [0, 0, 0, -20, -20, 0, 0, -2, 0, 0, 0, 0, 0, 0, 0] 577884139111393339: [1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1] ncode=6591 Приближения с valids=10 ещё появляются. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Подготовила ещё одну серию паттернов для поиска приближений с вектором совпадений [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 23 паттерна получилось (включая паттерн центральной 15-ки), представлены в виде матрицы, как в программе 0, 18, 30, 32, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 34, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 36, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 38, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 40, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 42, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 44, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 46, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 48, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 50, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 52, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 54, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 56, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 58, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 62, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 64, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 66, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 68, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 70, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 72, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 74, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 76, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228]; Программу запустила на черепашке в диапазоне больших чисел. (08:39) gp > \r 15unik_v14c.txt logfile = "15unik_v14с_res.txt" 6638368 from number 6638388 to number [0,18,30,32,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 1331394339743307840 - 1331398551513600570 1814400 formulae expected 12638368 from number 12638388 to number [0,18,30,34,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 2534757280523307840 - 2534761492293600570 1036800 formulae expected 18638368 from number 18638388 to number [0,18,30,36,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 3738120221303307840 - 3738124433073600570 2799360 formulae expected . . . . . . . Замечу, что каждый паттерн проверяется в своём диапазоне, то есть диапазоны для всех паттернов различны. Программа работает на периоде 31#. Понятно, что программа ищет не только приближения, но и центральную 15-ку. Собственно, поиск центральной 15-ки и является более важной задачей. Поэтому поиск ведётся в диапазоне больших чисел. [Не очень-то большие числа получились, в следующем проходе увеличу.] PS. 22 паттерна на допустимость не проверяла. 23-й паттерн - паттерн центральной 15-ки - в проверке на допустимость не нуждается. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Следующую серию паттернов приготовила, для поиска приближений с вектором совпадений [1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1] 14 паттернов получилось, включая паттерн центральной 15-ки [0, 18, 30, 60, 78, 80, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 82, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 86, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 88, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 90, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 92, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 94, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 96, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 98, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 100, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 102, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 104, 108, 114, 120, 144, 150, 168, 198, 210, 228; 0, 18, 30, 60, 78, 106, 108, 114, 120, 144, 150, 168, 198, 210, 228]; Пока не запустила в работу. PS. Запущено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Аппроксимация функции, заданной набором значений Посмотрела видео. Открыла Эксель, записала 20 значений, аппроксимировала логарифмической линий. Вот что получилось 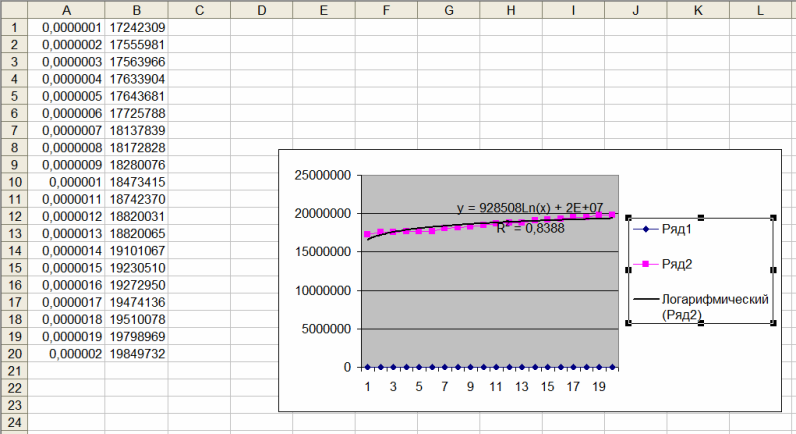 Если ввести 84 значения функции, наверное, аппроксимация точнее будет. Надо попробовать. Аппроксимирующая функция y = 928508Ln(x) + 2E+07 2E+07 надо понимать как 20000000 ? Посчитала по этой формуле, что-то у меня ни одно значение функции даже весьма приближённо не совпадает. Наверное, неправильно я что-то сделала, и аппроксимация у меня неправильная. Господа! Кто-нибудь разбирается в Эксель? Надо помочь разобраться в аппроксимации. Пожалуйста, пишите мне. Адрес не изменился natalimak1@yandex.ru |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сделала другую аппроксимацию для тех же значений функции, полиномом шестой степени 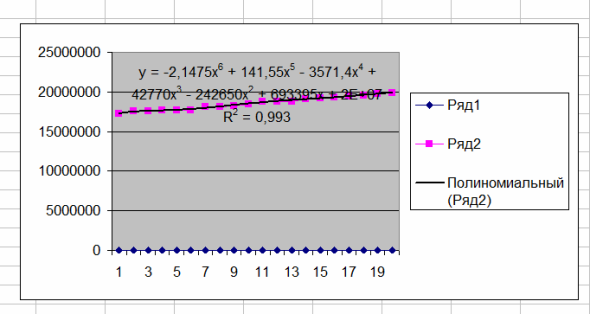 На графике аппроксимирующая линия (линия тренда) очень хорошо совпадает с графиком функции. Но... по формуле у меня ни черта не получаются значения функции :( Чего-то я не понимаю. Для каких х считаются значения аппроксимирующей функции? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ахиллес-3 добавляет новое приближение с valids=13 с уникальным кодом 48236371914410513: [0, 18, 30, 74, 78, 84, 108, 110, 120, 144, 150, 168, 198, 210, 228] 48236371914410513: [0, 0, 0, 14, 0, 0, 0, -4, 0, 0, 0, 0, 0, 0, 0] 48236371914410513: [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1] valids=13 ncode=7103 Имеем valids=13, 37 codes 3071, 4079, 4087, 4091, 4093, 4094, 5887, 6079, 6127, 6139, 6142, 6655, 6911, 7039, 7103, 7163, 7166, 7551, 7671, 7675, 7677, 7678, 7903, 7919, 7927, 7933, 7999, 8047, 8059, 8150, 8155, 8157, 8167, 8171, 8181, 8185, 8188 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Новости о спектре приближений к центральной 15-ке За сутки найдено 8 уникальных элементов (как за предыдущие сутки). Всего найдено 8007 уникальных элементов спектра, 97,74%. Пропущено 185 элементов. В новом списке пропущенных элементов самая верхняя часть спектра (>8000) выглядит так 8015, 8022, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8103, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8173, 8174, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191 За сутки в этой части спектра не найдено ни одного элемента. Список всех пропущенных элементов 1967, 2047, 2991, 3007, 3063, 3263, 3503, 3510, 3511, 3515, 3519, 3582, 3583, 3647, 3663, 3711, 3757, 3758, 3759, 3767, 3775, 3799, 3839, 3895, 3935, 3947, 3966, 3967, 3983, 3991, 3999, 4007, 4014, 4015, 4019, 4021, 4022, 4023, 4025, 4027, 4029, 4030, 4031, 4047, 4059, 4062, 4063, 4071, 4085, 4086, 4095, 5047, 5053, 5119, 5567, 5631, 5759, 5807, 5815, 5821, 5823, 5967, 5983, 5999, 6015, 6031, 6059, 6069, 6071, 6077, 6078, 6111, 6135, 6141, 6143, 6775, 6846, 6847, 6895, 7031, 7093, 7127, 7134, 7135, 7151, 7159, 7165, 7167, 7350, 7357, 7359, 7415, 7423, 7535, 7542, 7550, 7583, 7598, 7599, 7606, 7607, 7609, 7610, 7611, 7614, 7615, 7639, 7647, 7663, 7669, 7735, 7741, 7743, 7767, 7774, 7775, 7790, 7791, 7798, 7807, 7839, 7859, 7861, 7862, 7863, 7866, 7867, 7869, 7870, 7871, 7887, 7895, 7902, 7915, 7926, 7931, 7934, 7935, 7983, 7990, 8015, 8022, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8103, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8173, 8174, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
По вопросу аппроксимации получила вчера письмо. Автор письма прислал график функции f(n) для следующих 84 значений функции {172423091876665,175559810858839,175639662890693,176339041467182,176436819685787,177257881397153,181378395781235,181728285958380,182800763867437,184734156659963,187423708774853,188200313268396,188200657577362,191010672109187,192305100913339,192729500018102,194741369442830,195100782461457,197989694330097,198497329904193,201661946243152,204812550835536,205463344179904,207788797644316,210131169869676,210552855943027,210598026967814,211155964938393,211857917944494,211932520403745,212219596896973,213195211744368,217041524935399,217270661488107,218848252021842,220361763140473,220621357032116,228786752992324,229253874817570,229640148584619,230813154005621,231338259224242,231970518969924,234481859800552,235091716498328,236570130976129,236884017365329,239911561669122,240116192530111,247154506697166,247708201743490,248017230491863,251164239061349,254480410401303,257781118871604,261158836332534,273175932479035,274572861066267,276273554606209,276397601175724,280451307351125,282065570754073,284160902343449,284592848041765,285058843718471,288957866007005,294870963798221,300872781088641,301293973101888,303701569408315,304822061123047,305386210450805,305444920525832,306039909742094,308469796189292,312732138726956,313436823052299,316102754499455,317248565380872,318242428488905,319668462016710,320799447682649,322596443742030,325648131881921} Но это построено не в Эксель, а в MATLAB. Поясню ещё раз. Последняя на данный момент центральная 13-ка, найденная в проекте SPT 9779213400414113221: 0 12 42 60 66 90 96 102 126 132 150 180 192 https://boinc.progger.info/odlk/forum_thread.php?id=282&postid=14323 Для этой 13-ки имеем следующую формулу [9779213400414113221, 0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192, 325648131881921, 30030, 25591] то есть 9779213400414113221 = 325648131881921*30030 + 25591 Рассматриваемая мной Функция f(n) - это значения коэффициентов (при 30030) в формуле. Таким образом, f(84) = 325648131881921. Цель аппроксимации прогнозировать следующие значения функции. Примечание: на красную линию на графике не обращайте внимания. Это пример неправильной аппроксимации. Линия тренда совсем не совпадает с графиком функции. Как я и предполагала, матпакеты решают подобные задачи. Можно попытаться в MATLAB найти хорошую аппроксимацию для изображённой на графике функции. График похоже отображает реальность. Конечно, это не точная линейная зависимость. А если бы она была таковой, то и задача аппроксимации не стояла бы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ахиллес сегодня выполнил суточную норму по приближениям с кодами в самой верхней части спектра 513978500990384809: [0, 18, 30, 60, 78, 84, 100, 114, 130, 144, 162, 168, 198, 222, 228] 513978500990384809: [0, 0, 0, 0, 0, 0, -8, 0, 10, 0, 12, 0, 0, 12, 0] 513978500990384809: [1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1] valids=11 ncode=8022 662200967325561889: [0, 18, 30, 60, 78, 84, 108, 112, 120, 142, 162, 168, 198, 210, 228] 662200967325561889: [0, 0, 0, 0, 0, 0, 0, -2, 0, -2, 12, 0, 0, 0, 0] 662200967325561889: [1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1] valids=12 ncode=8103 Молодец! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очередная порция Norm-чисел для ключевой 17-ки дала следующие приближения при valids>9 10188725888533940943335227: [0, 6, 24, 36, 70, 72, 76, 94, 120, 136, 150, 154, 174, 202, 216, 234, 240] 10188725888533940943335227: [0, 0, 0, 0, 4, -12, -14, -20, 0, 10, 0, -2, 0, -2, 0, 0, 0] valids=10 code=28843 10188725891122580324857267: [0, 6, 22, 36, 66, 84, 90, 94, 124, 126, 136, 154, 162, 204, 216, 234, 240] 10188725891122580324857267: [0, 0, -2, 0, 0, 0, 0, -20, 4, 0, -14, -2, -12, 0, 0, 0, 0] valids=11 code=24135 10188725888079069761059457: [0, 6, 24, 32, 44, 84, 90, 120, 132, 146, 150, 170, 174, 176, 216, 234, 240] 10188725888079069761059457: [0, 0, 0, -4, -22, 0, 0, 6, 12, 20, 0, 14, 0, -28, 0, 0, 0] valids=10 code=26155 Коды не уникальные. Приближения в спектр добавила. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ахиллес ещё раз молодец :) 593499509168175289: [0, 18, 30, 60, 78, 84, 108, 114, 120, 148, 150, 168, 198, 220, 228] 593499509168175289: [0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 10, 0] 593499509168175289: [1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1] valids=13 ncode=8174 Имеем valids=13, 38 codes 3071, 4079, 4087, 4091, 4093, 4094, 5887, 6079, 6127, 6139, 6142, 6655, 6911, 7039, 7103, 7163, 7166, 7551, 7671, 7675, 7677, 7678, 7903, 7919, 7927, 7933, 7999, 8047, 8059, 8150, 8155, 8157, 8167, 8171, 8181, 8185, 8174, 8188 Кстати, этот результат - два в одном: с valids=13 и с кодом в самой верхней части спектра. И по кодам в самой верхней части спектра Ахиллес уже перевыполнил суточную норму! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Новости о спектре приближений к центральной 15-ке За сутки найдено 9 уникальных элементов. Всего найдено 8016 уникальных элементов спектра, 97,85%. Пропущено 176 элементов. В новом списке пропущенных элементов самая верхняя часть спектра (>8000) выглядит так 8015, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8173, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191 Найдено в этой части спектра 150 элементов из 192. Пока продолжаю поиск приближений. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очередная порция Norm-чисел для 19-ки с минимальным диаметром дала следующие приближения при valids>7 10042680925992044274634357: [0, 10, 12, 30, 42, 54, 70, 72, 82, 136, 142, 156, 162, 180, 192, 210, 240, 246, 252] 10042680925992044274634357: [0, 4, 0, 0, 0, -18, -20, -24, -38, 10, 10, 0, 0, 0, -18, -12, 0, 0, 0] valids=10 code=57459 10042680927678183069269351: [0, 6, 12, 30, 42, 56, 86, 90, 98, 110, 126, 156, 176, 180, 198, 222, 240, 248, 252] 10042680927678183069269351: [0, 0, 0, 0, 0, -16, -4, -6, -22, -16, -6, 0, 14, 0, -12, 0, 0, 2, 0] valids=10 code=122966 10042680926979670812442421: [0, 6, 12, 30, 38, 42, 56, 68, 86, 108, 120, 156, 162, 170, 182, 210, 240, 246, 252] 10042680926979670812442421: [0, 0, 0, 0, -4, -30, -34, -28, -34, -18, -12, 0, 0, -10, -28, -12, 0, 0, 0] valids=9 code=114787 10042680929602299848889401: [0, 6, 18, 26, 48, 72, 92, 96, 128, 140, 158, 162, 170, 180, 188, 222, 240, 246, 252] 10042680929602299848889401: [0, 0, 6, -4, 6, 0, 2, 0, 8, 14, 26, 6, 8, 0, -22, 0, 0, 0, 0] valids=9 code=70679 10042680929462198883975491: [0, 6, 18, 20, 68, 72, 90, 92, 120, 128, 132, 152, 158, 176, 198, 210, 218, 246, 252] 10042680929462198883975491: [0, 0, 6, -10, 26, 0, 0, -4, 0, 2, 0, -4, -4, -4, -12, -12, -22, 0, 0] valids=8 code=72321 10042680935366028782843377: [0, 6, 22, 30, 64, 72, 94, 96, 100, 156, 160, 162, 174, 190, 210, 222, 226, 232, 252] 10042680935366028782843377: [0, 0, 10, 0, 22, 0, 4, 0, -20, 30, 28, 6, 12, 10, 0, 0, -14, -14, 0] valids=8 code=87052 10042680935366028782843377: [0, 6, 22, 30, 64, 72, 94, 96, 100, 156, 160, 162, 174, 190, 210, 222, 226, 232, 252] 10042680935366028782843377: [0, 0, 10, 0, 22, 0, 4, 0, -20, 30, 28, 6, 12, 10, 0, 0, -14, -14, 0] valids=8 code=87052 10042680939298680741498097: [0, 6, 12, 30, 54, 72, 90, 96, 106, 114, 120, 132, 156, 160, 162, 222, 240, 250, 252] 10042680939298680741498097: [0, 0, 0, 0, 12, 0, 0, 0, -14, -12, -12, -24, -6, -20, -48, 0, 0, 4, 0] valids=10 code=121862 10042680941709171843441281: [0, 6, 12, 30, 32, 42, 92, 98, 110, 126, 132, 156, 158, 182, 212, 218, 222, 236, 252] 10042680941709171843441281: [0, 0, 0, 0, -10, -30, 2, 2, -10, 0, 0, 0, -4, 2, 2, -4, -18, -10, 0] valids=8 code=115136 10042680958361737699833901: [0, 6, 22, 30, 42, 48, 76, 112, 120, 130, 132, 156, 162, 180, 208, 222, 226, 250, 252] 10042680958361737699833901: [0, 0, 10, 0, 0, -24, -14, 16, 0, 4, 0, 0, 0, 0, -2, 0, -14, 4, 0] valids=11 code=90868 10042680954860544493698577: [0, 4, 40, 42, 70, 72, 76, 96, 120, 132, 144, 156, 166, 180, 202, 222, 232, 240, 252] 10042680954860544493698577: [0, -2, 28, 12, 28, 0, -14, 0, 0, 6, 12, 0, 4, 0, -8, 0, -8, -6, 0] valids=8 code=5716 Найдено одно приближение с уникальным кодом 10042680958361737699833901: [0, 6, 22, 30, 42, 48, 76, 112, 120, 130, 132, 156, 162, 180, 208, 222, 226, 250, 252] 10042680958361737699833901: [0, 0, 10, 0, 0, -24, -14, 16, 0, 4, 0, 0, 0, 0, -2, 0, -14, 4, 0] valids=11 code=90868 Для диапазона больших чисел это редкое приближение. Конечно, 8 "дырок" это много. Но лучше пока не встретилось. В спектре приближений к 19-ке с минимальным диаметром на данный момент содержится 62777 уникальных элементов. Мной добавлено три уникальных элемента, один из них сейчас. Разверну приближение с valids=11 для проверки. {10042680958361737699833901, 10042680958361737699833907, *10042680958361737699833923, 10042680958361737699833931, 10042680958361737699833943, *10042680958361737699833949, *10042680958361737699833977, *10042680958361737699834013, 10042680958361737699834021, *10042680958361737699834031, 10042680958361737699834033, 10042680958361737699834057, 10042680958361737699834063, 10042680958361737699834081, *10042680958361737699834109, 10042680958361737699834123, *10042680958361737699834127, *10042680958361737699834151, 10042680958361737699834153} Всё правильно. PS. У меня поиск ведётся в диапазоне 26-значных чисел. Г. Петухов давно обещал, что до 1Е25 будет 19-ка с минимальным диаметром. Он уже наверняка проверил диапазон до 1Е25, и где 19-ка с минимальным диаметром? Похоже, его прогноз основан на гадании на кофейной гуще. Зато... обо всём г. Петухов рассуждает, как великий эксперт. Примерчик приведу очень интересный. Мне прислали "Некоторые материалы по аппроксимации". Навеяло поговорку: "Кто писал, не знаю, а я, дурак, читаю." :)) Ну, хотя мне имя автора не сообщили, я уверена на 100%, что это писал г. Петухов. Слишком хорошо мне знаком его стиль! Итак, знакомьтесь с мнением эксперта по поводу аппроксимации, в следующем сообщении. Ничего личного, научный трактат :))) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
<….> Знакомьтесь внимательно, господа! Таких умных мыслей вы больше нигде не найдёте. Только одна умная мысль Вот построенный экселем график 13-192 для кортежей больше 5000000000000000000 (ниже есть А кто сказал, что зависимость линейная??? Ежу понятно, что линейная функция не аппроксимирует нашу функцию. Я писала выше. что если бы зависимость была точно линейная, то и задача аппроксимации не стояла бы. Замечу, что я прочитала сей трактат по диагонали. Может, самые умные мысли и пропустила :) А вы, господа, читайте очень внимательно! Когда досконально изучите этот трактат, наверняка сможете аппроксимировать мою функцию :) График показан в сообщении https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=14381 Только учтите: мне аппроксимация нужна поточнее линейной. Желательно с достоверностью R^2=1 или на худой конец - с R^2=0,999 :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, автор письма, приславший мне график функции в MATLAB, писал Нет, в данном случае проблема в Экселе. Я спросила: "Какая проблема?" Ответ: Эксель не подходит для таких задач. В принципе. Тоже экспертное мнение? Или автор письма, как и я, просто не умеет пользоваться Экселем? Ну, хорошо, пусть будет MATLAB, я не против :) Только дальше графика дело пока не пошло. Аппроксимации нет. Хотя автор сказал, что может сделать аппроксимацию. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ой, а черепашка поймала забулдыгу :) 208365200161067783: [0, 30, 56, 60, 78, 84, 108, 116, 120, 138, 150, 168, 198, 210, 228] 208365200161067783: [1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1] valids=11 ncode=1967 Этот элемент давно торчит в начале списка пропущенных элементов. Теперь не будет торчать. Кстати, вот список пропущенных элементов на сегодняшнее утро, 176 штук 1967, 2047, 2991, 3007, 3063, 3263, 3503, 3510, 3511, 3515, 3519, 3583, 3647, 3663, 3711, 3758, 3759, 3767, 3775, 3799, 3839, 3895, 3935, 3947, 3966, 3967, 3983, 3991, 3999, 4007, 4014, 4015, 4019, 4021, 4022, 4023, 4025, 4027, 4029, 4030, 4031, 4047, 4062, 4063, 4071, 4085, 4086, 4095, 5047, 5053, 5119, 5567, 5631, 5759, 5807, 5815, 5821, 5823, 5983, 5999, 6015, 6031, 6059, 6069, 6071, 6077, 6078, 6111, 6135, 6141, 6143, 6775, 6846, 6847, 6895, 7031, 7093, 7127, 7134, 7135, 7151, 7159, 7165, 7167, 7350, 7357, 7359, 7415, 7423, 7535, 7542, 7550, 7583, 7598, 7599, 7606, 7607, 7609, 7610, 7611, 7614, 7615, 7639, 7647, 7663, 7735, 7741, 7743, 7767, 7774, 7775, 7790, 7791, 7798, 7807, 7839, 7859, 7861, 7863, 7866, 7867, 7869, 7870, 7871, 7887, 7895, 7902, 7915, 7926, 7931, 7934, 7935, 7983, 7990, 8015, 8029, 8030, 8031, 8046, 8053, 8055, 8058, 8061, 8062, 8063, 8079, 8087, 8095, 8105, 8106, 8107, 8109, 8110, 8111, 8115, 8119, 8122, 8123, 8125, 8126, 8127, 8142, 8143, 8151, 8154, 8158, 8173, 8175, 8179, 8182, 8183, 8186, 8187, 8189, 8190, 8191 |

©2026 (C) Progger