Для участников форума MHP
Message boards :
Cafe :
Для участников форума MHP
Message board moderation
Previous · 1 . . . 32 · 33 · 34 · 35 · 36 · 37 · 38 . . . 138 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Готово! Показываю частично протокол работы программы Введите через пробел массив модулей: 2 3 5 7 11 13 17 19 Введите через пробел набор остатков по модулю 2: 1 Введите через пробел набор остатков по модулю 3: 1 2 Введите через пробел набор остатков по модулю 5: 1 2 Введите через пробел набор остатков по модулю 7: 4 5 Введите через пробел набор остатков по модулю 11: 2 6 Введите через пробел набор остатков по модулю 13: 4 6 Введите через пробел набор остатков по модулю 17: 1 9 13 14 Введите через пробел набор остатков по модулю 19: 8 11 13 16 19597 21467 44167 65357 69361 79811 85817 123701 129707 155887 190027 200477 . . . . . . . . 9473587 9498781 9509231 9543371 9569551 9575557 9613441 9619447 9629897 9633901 9655091 9677791 9679661 Получено 512 формул. Можно писать новую программу и начинать новый эксперимент по поиску 19-ки с другим паттерном, диаметр побольше, 432 вместо 252. Да, и формул получилось побольше. К тому же, форумчанин Bloodhound считает, что можно получить другую группу формул, если задействовать ещё остатки по модулю 23. Это интересно! Надо попробовать. Ну, и про алгоритм вычисления остатков ответ получен http://mathhelpplanet.com/viewtopic.php?p=445580#p445580 Действительно, всё просто. Тэк-с, сейчас у меня будет 512 формул вида Q = 9699690k + X А если задействовать ещё модуль 23, то формул будет 3072. Ах! Вот откуда у господина Петухова 200 миллионов формул получилось :) И эта группа формул будет следующего вида Q = 223092870k + X В двух группах 3584 формулы. И это только для одного паттерна. А паттернов-то для 19-ки о-ч-е-н-ь много. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Игра "Угадай слово" за 14 июня РУЧКА БАЛЕТ ЗАЛОГ САЛОН Сегодня "неуд" :) Слово хорошее загадано. Большое невезение, плохо буквы ловились, первое проверочное слово ни одной буквы не поймало. Но гимнастика для мозгов отличная получилась :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Игра "Угадай слово" за 15 июня ДЕМОН ШУТКА ЗАКАЗ БАРАК КАПЛЯ Сегодня "четвёрка" :) Слово хорошее загадано. После двух попыток три буквы не на своём месте. И дальше - отличная гимнастика для мозгов! :) Не сразу слово сочинилось, но зато угадано. Куча удовольствия :) Попробуйте-ка быстро угадать. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Вчера много работала над алгоритмами для поиска 19-ки. Ну вот, у меня давно работает алгоритм с паттерном для 19-ки с минимальным диаметром 252 0 6 12 30 42 72 90 96 120 126 132 156 162 180 210 222 240 246 252 Задействовано для поиска 384 формулы, эти формулы были очень давно выложены на форуме dxdy.ru Бегемотом. При составлении этих формул использовались модули до 19 включительно. Решила посмотреть, что будет, если использовать ещё один модуль - 23. Посчитала остатки для всех модулей. 2: 1 3: 1,2 5: 1,2 7: 3,4 11: 4,8 13: 3,5 17: 1,2 19: 2,3,11,12,16,17 23: 3,9,10,14,15,21 Да, если использовать модули 2, 3, ..., 19, формул будет 384, они имеют вид Q = 9699690k + X Эти формулы у меня сейчас и работают в программе. Если добавить ещё модуль 23, формул будет 2304, они будут иметь следующий вид Q = 223092870k + X Пока ещё не применила программу к этим модулям, собираюсь. Интересно, что будет по таким формулам. Сделала и второй алгоритм, в котором 1024 формулы. Тоже интересно покрутить, но... негде все алгоритмы сразу крутить. Собираюсь делать ещё третий алгоритм. Господа! Если вы хотите принять участие в штурме 19-ки, пишите мне natalimak1@yandex.ru Кто зарегистрирован на сайте, можете писать ЛС. Не забывайте смотреть тему "Нерешённая проблема теории чисел" https://boinc.progger.info/odlk/forum_thread.php?id=224 в которой я пишу отчёты о работе программ поиска 19-ки. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Тэк-с, программка лихо отработала, 2304 значения выдала. Покажу начало и конец протокола работы программы Введите через пробел массив модулей: 2 3 5 7 11 13 17 19 23 Введите через пробел набор остатков по модулю 2: 1 Введите через пробел набор остатков по модулю 3: 1 2 Введите через пробел набор остатков по модулю 5: 1 2 Введите через пробел набор остатков по модулю 7: 3 4 Введите через пробел набор остатков по модулю 11: 4 8 Введите через пробел набор остатков по модулю 13: 3 5 Введите через пробел набор остатков по модулю 17: 1 2 Введите через пробел набор остатков по модулю 19: 2 3 11 12 16 17 Введите через пробел набор остатков по модулю 23: 3 9 10 14 15 21 30397 40121 165701 369751 454667 514727 626707 686767 711077 . . . . . . . 221751197 221785231 222042187 222161867 222221927 222255961 222280271 222381541 222405851 222465911 222577891 222637951 222722867 222926917 223052497 223062221 > Можно писать программу на 2304 формулы. Очень интересно, что эта программа найдёт. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Новости "Пентадекатлона мечты" Ой, вот EUgeneUS задал всем задачу с этой 10-ой с 84 делителями :) 850110906168382371216057545387082625772983773608338698713882862297162247190308993041704075477374723603562492: 84, 84, 84, 84, 84, 84, 84, 84, 84, 84 Господин Лецко считает, господин Петухов считает, господин Hugo считает https://dxdy.ru/post1557530.html#p1557530 It had been running for nearly 72 hours on (84, 10, 850...492) when my machine (which tends to suffer from hardware problems) decided to re-mount as readonly the /src partition where I write my log files. So I had to reboot, and sadly that particular process does not write any interim results to recover from. :( Ищет милиция, ищут пожарные... (C) И никак сосчитать не могут делители! А у господина Петухова новые цепочки никак не хотят находиться. Вот же расстройство! :) В общем, мне тема перестала быть интересной, за исключением задачи минимизации, которую решает Антон и Hugo, кажется, тоже. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Господин Лецко писал в сообщении https://dxdy.ru/post1557543.html#p1557543 Написал программку для поиска пятерки чисел по 318 делителей. Запустил пару раз. Она даже нашла несколько четверок. Ха-ха! Даже PARI/GP отказывается считать эти извращения :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Вот ещё. Господин Лецко в сообщении https://dxdy.ru/post1557572.html#p1557572 отвечает на вопрос EUgeneUS А Вы факторизуете в PARI/GP или на https://www.alpertron.com.ar/ECM.HTM ? Пробовал и там, и там. Я же писал. Сложность, как я понимаю, в том, что факторизуемое число содержит очень большие простые множители 850110 906168 382371 216057 545387 082625 772983 773608 338698 713882 862297 162247 190308 993041 704075 477374 723603 562500 (108 digits) = 2^2 × 5^6 × 1699 445829 859553 411400 105322 065849 864679 (40 digits) × 8003 652873 018143 615563 236294 297839 985832 184458 343462 982419 746783 (64 digits) Вот такая задача! Вчетвером несколько суток не могут посчитать делители в двух полученных числах. Интересная задача? :) Ну, опять же - на вкус, на цвет... Для господина Лецко и господина Петухова - очень интересная! Будет несколько тысяч цепочек, состоящих из более 100-значных натуральных чисел, имеющих по несколько сотен (и даже тысяч) делителей. А что? Супер! Для меня, например, интересно найти симметричную 19-ку из последовательных простых чисел, которую не можем найти уже 8 лет. И господин Петухов к поиску руку приложил, аж до 200 миллионов формул у него работало одновременно :) И что? А результат где? Такой штурм был и - ничего? Ярослав Врублевский (ас по кортежам и арифметическим прогрессиям из простых чисел!) тоже руку приложил. Ну, он, по крайней мере, не хвастался своими алгоритмами и "200 миллионами формул". Просто не нашёл - и все дела. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Черепашка ищет 19-ку 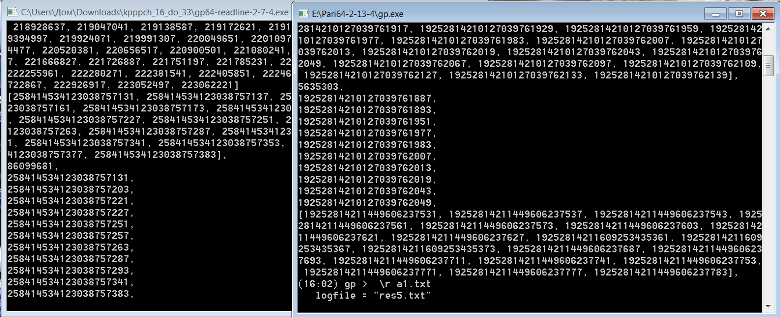 Два потока, два алгоритма, две области диапазона чисел. Подробнее написала в теме "Нерешённая проблема теории чисел" https://boinc.progger.info/odlk/forum_thread.php?id=224&postid=8940 и далее. Эх! Развернуть бы штурм! Негде :( Черепашка работает на пределе своих возможностей. Ой, вспомнила :) Давно это было, писала я на форуме dxdy.ru про ядра и про потоки. Так вот, господин Петухов, как всегда, выступил в том смысле, что я несу чушь про то, что на одно ядро одну программу можно посадить. По его мнению, можно и 10 программ посадить. Угу! Посадить-то можно, да толку что? Нету у процессора ресурсов на 10 потоков! Нету! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Игра "Угадай слово" за 16 июня РЫВОК ДРОЖЬ ПОЖАР Сегодня "двойка" :) Слово хорошее загадано, не сразу в голову пришло. Ну, и многовариантность... |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Алгоритм №3 для поиска 19-ки Цитата из сообщения https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=8928 Получено 512 формул. Ну вот, только добралась до этого алгоритма. В этом алгоритме новый паттерн 0 12 36 90 96 132 162 180 210 216 222 252 270 300 336 342 396 420 432 Формулы имеют вид Q = 9699690k + X Пока попробую 512 формул (для модулей 2, 3, ..., 19). Если задействовать ещё модуль 23, то формул будет 3072. Эти формулы буду иметь вид Q = 223092870k + X 512 формул у меня уже получены, сейчас нашлёпаю программу и буду пробовать. Очень интересно, каков будет эффект от увеличения диаметра. Программу запустила. Жду результатов. Результат смотрите в сообщении https://boinc.progger.info/odlk/forum_thread.php?id=224&postid=8946 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Господин Лецко писал в сообщении https://dxdy.ru/post1557705.html#p1557705 В частности, мне казалось, что цепочку из 11 чисел по 60 делителей мы нашли, но я не нашел сообщения о том, что мы ее нашли :( EUgeneUS ответил в сообщении https://dxdy.ru/post1557708.html#p1557708 Она у меня нашлась, и обязательно было сообщение в этой теме. Кстати, она есть в файле Хуго с датой 18-05-2022, соответственно, близко к этой дате и было сообщенние о нахождении от меня. Ой, совсем растерялись господа :) Причина, на мой взгляд, в бессистемной публикации найденных результатов. Дальше ещё две цепочки потеряны Hugo, он их не видел, потому что господин Петухов опубликовал их под тегом оффтопа. Ну да, длинные цепочки решили прятать в тег, чтобы они не изменяли формат страницы. Но! Результаты надо публиковать не так. Не в той теме, где абсолютный винегрет из всего на свете (бесконечные фрагменты доказательств, "ускорители", минимизация, таблицы Антона Никонова, таблицы господина Лецко по разным пунктам и т. д.). Немудрено в этой теме потерять нужные результаты, и даже EUgeneUS, который опубликовал результат, теперь не знает, где же он. Лень искать? Ну, пусть посмотрит моё сообщение о его 11-ке с 60 делителями :) https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=8716 Я нашла это сообщение за 5 минут. Вот и господин Петухов постарался, нашёл сообщение EUgeneUS о второй 11-ке с 60 делителями https://dxdy.ru/post1557735.html#p1557735 Эта 11-ка состоит из меньших чисел. Со временем, если не изменить систему публикации результатов, находить их в общей теме будет всё сложнее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Кстати, о фрагментах доказательств. Их ну очень много, это только в теме "Пентадекатлон мечты", не говоря уж о специальной теме, созданной для доказательства. Господин Hugo писал в сообщении https://dxdy.ru/post1557783.html#p1557783 I'm definitely interested - I think I've seen parts of it in the forum already, but I wasn't able to find the full proof in one place. Да уж... Найти доказательство в одно месте чрезвычайно трудно, по той простой причине, что его просто нет в одном месте, оно есть десятками фрагментов в разных местах двух (!) тем. Ну, обещают ведь написать статью в arXiv, в которой уж, наверное, соберут всё в одном месте. Хотя... фрагменты от трёх авторов... надо всё это осмыслить, объединить, согласовать, перевести на английский. Плюс ещё фрагмент господина Петухова об "ускорителях" (четвёртый автор). В общем, я не завидую читателям этой будущей статьи. Как-то господин Ватутин высказался в OEIS, что с моими плохо структурированными сообщениями (в разделе "Science" форума) очень трудно работать. Стараюсь структурировать, выражаясь языком господина Ватутина. По крайней мере, стремлюсь в каждой теме писать только по данной теме, а если уже чувствую, что вылезаю за рамки темы, то открываю новую. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Игра "Угадай слово" за 17 июня ВЕСЛО КЛОУН ЗАЛОГ ПИЛОТ ХОЛОД Сегодня "троечка" :) Безобразная игра! Первое проверочное слово поймало три буквы и все на своём месте. А дальше - ужасная многовариантность! И только четвёртой попыткой слово отгадано. К тому же, две одинаковые буквы в загаданном слове, да ещё - Е вместо Ё. Почему не включена буква Ё? Она же есть на клавиатуре! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
О моих алгоритмах для поиска 19-ки Решила попробовать объединить две программы в одну. Первая программа - алгоритм №2, 128 формул вида Q = 510510k + X вторая программа - алгоритм №2а, 1024 формулы вида Q = 9699690k + X Диапазон изменения k в этих программах разный. Поэтому пока просто присоединила вторую программу к первой. Вот что у меня получилось \l res5.txt
{c=[19693,21563,30403,40127,45433,55597,56143,64283,81623,89477,90023,90463,103777,115657,116203,124057,140513,165553,165707,200573,210143,223897,225767,226313,236323,241783,244177,260347,266093,268487,284657,300127,301843,326153,334007,344563,346433,360187,369757,404623,404777,410083,429817,446273,454127,454673,470297,479867,480307,480853,488707,506047,514733,530203,539927,540473,548767,550637,555943,574507,590263,590963,592133,600973,610697,614287,616003,616157,626167,626713,660593,674347,686773,694627,711083,726113,736123,736277,736823,770857,771143,784457,794467,795167,796337,796883,812353,830917,836663,855227,870697,872413,896723,904577,905123,915133,917003,930317,930757,931303,939157,940327,956497,975347,980653,980807,1025243,1040867,1050437,1050983,1051423,1059277,1076617,1085017,1085303,1100773,1110497,1111043,1116943,1119337,1121207,1126513,1145077,1161533,1184857,1186573,1186727,1197283,1231163,1236623,1244917,1255187,1257343,1262803,1265197,1281653,1294967,1296683,1306847,1307393,1321147,1341427,1355027,1365737,1367453,1382923,1401487,1407233,1425797,1431103,1441267,1441813,1442983,1467007,1467293,1475147,1475693,1500887,1501327,1501873,1509727,1527067,1551223,1551377,1576963,1595813,1611437,1611983,1621007,1621553,1621993,1627453,1629847,1637177,1646017,1647187,1655587,1681613,1687513,1697083,1715647,1732103,1755427,1757143,1757297,1757843,1765697,1767853,1791877,1807193,1815487,1825757,1833373,1865537,1867253,1877963,1891717,1901833,1911997,1925597,1926143,1936307,1938023,1941613,1951337,1953493,1960177,1972057,1977803,1996367,2001673,2001827,2011837,2012383,2037577,2046263,2071457,2072443,2080297,2097637,2106037,2111783,2121793,2121947,2122493,2147533,2147687,2156527,2182007,2182553,2192123,2198023,2207747,2216587,2226157,2252183,2257643,2258083,2267653,2283823,2286217,2302673,2315987,2325997,2327867,2328413,2336267,2342167,2362447,2377763,2396327,2403943,2412343,2436107,2436653,2437823,2448533,2461847,2462287,2470687,2472403,2482567,2496167,2496713,2506877,2512183,2521907,2530747,2572243,2572397,2582953,2597983,2608147,2616833,2622293,2640857,2642027,2643013,2648473,2650867,2668207,2676607,2682353,2692517,2693063,2718103,2718257,2727097,2753123,2762693,2768593,2778317,2778863,2786717,2787157,2794333,2796727,2812897,2828213,2828653,2852677,2854393,2886557,2898983,2906837,2912737,2933017,2948333,2962633,2964503,2966897,2974513,2982913,3006677,3007223,3022847,3032417,3032857,3041257,3042973,3067283,3082753,3092477,3101317,3108493,3127057,3142813,3142967,3143513,3151367,3153523,3168553,3168707,3177547,3178717,3192863,3211427,3219043,3247177,3252923,3263633,3278663,3287503,3288673,3288827,3289373,3297667,3312697,3323407,3323693,3337007,3339163,3348887,3349433,3357287,3357727,3364903,3383467,3398783,3423247,3424963,3433363,3457127,3469553,3475013,3477407,3483307,3491707,3493577,3503587,3533203,3533357,3535073,3553483,3577793,3593417,3602987,3611827,3613543,3637567,3637853,3643313,3653323,3663047,3669493,3671887,3679063,3697627,3713537,3714083,3721937,3739123,3739277,3748117,3763433,3781997,3789173,3789613,3798013,3807737,3815353,3817747,3823207,3823493,3834203,3847517,3849233,3858073,3859397,3859943,3868237,3883267,3893977,3907577,3920003,3927857,3935473,3954037,3969353,3983653,3993817,3995533,4003933,4004087,4027697,4045583,4053877,4062277,4064147,4103773,4103927,4105643,4124053,4140223,4148363,4163987,4164533,4172387,4173557,4180003,4182397,4189727,4198567,4208137,4213883,4240063,4249633,4268197,4284653,4292507,4309693,4309847,4318247,4318687,4334003,4344427,4350173,4352567,4359743,4360183,4368583,4378307,4385923,4393777,4418087,4419803,4428643,4430513,4453837,4454383,4464547,4478147,4490573,4494163,4496033,4498427,4506043,4512727,4524607,4554223,4554377,4564387,4574503,4574657,4616153,4632847,4634717,4650733,4664333,4674343,4674497,4675043,4676213,4698367,4700237,4709077,4710793,4734557,4735103,4742957,4750573,4760297,4769137,4778707,4784453,4810193,4810633,4819033,4820203,4836373,4838767,4844227,4855223,4860683,4863077,4879247,4880417,4888817,4889257,4914997,4920743,4930313,4939153,4948877,4956493,4964347,4964893,4988657,4990373,4999213,5001083,5023237,5024407,5024953,5025107,5035117,5048717,5064733,5066603,5083297,5124793,5124947,5135063,5145073,5145227,5174843,5186723,5193407,5201023,5203417,5205287,5208877,5221303,5234903,5245067,5245613,5268937,5270807,5279647,5281363,5305673,5313527,5321143,5330867,5339267,5339707,5346883,5349277,5355023,5365447,5380763,5381203,5389603,5389757,5406943,5414797,5431253,5449817,5459387,5485567,5491313,5500883,5509723,5517053,5519447,5525893,5527063,5534917,5535463,5551087,5559227,5575397,5593807,5595523,5595677,5635303,5637173,5645573,5653867,5671753,5695363,5695517,5703917,5705633,5715797,5730097,5745413,5763977,5771593,5779447,5791873,5805473,5816183,5831213,5839507,5840053,5841377,5850217,5851933,5865247,5875957,5876243,5881703,5884097,5891713,5901437,5909837,5910277,5917453,5936017,5951333,5960173,5960327,5977513,5985367,5985913,6001823,6020387,6027563,6029957,6036403,6046127,6056137,6061597,6061883,6085907,6087623,6096463,6106033,6121657,6145967,6164377,6166093,6166247,6195863,6205873,6207743,6216143,6222043,6224437,6229897,6242323,6266087,6274487,6276203,6300667,6315983,6334547,6341723,6342163,6350017,6350563,6360287,6362443,6375757,6376043,6386753,6401783,6410077,6410623,6410777,6411947,6420787,6435817,6446527,6452273,6480407,6488023,6506587,6520733,6521903,6530743,6530897,6545927,6548083,6555937,6556483,6556637,6572393,6590957,6598133,6606973,6616697,6632167,6656477,6658193,6666593,6667033,6676603,6692227,6692773,6716537,6724937,6732553,6734947,6736817,6751117,6766433,6786713,6792613,6800467,6812893,6845057,6846773,6870797,6871237,6886553,6902723,6905117,6912293,6912733,6920587,6921133,6930857,6936757,6946327,6972353,6981193,6981347,7006387,7006933,7017097,7022843,7031243,7048583,7050977,7056437,7057423,7058593,7077157,7082617,7091303,7101467,7116497,7127053,7127207,7168703,7177543,7187267,7192573,7202737,7203283,7216883,7227047,7228763,7237163,7237603,7250917,7261627,7262797,7263343,7287107,7295507,7303123,7321687,7337003,7357283,7363183,7371037,7371583,7373453,7383463,7396777,7413233,7415627,7431797,7441367,7441807,7447267,7473293,7482863,7491703,7501427,7507327,7516897,7517443,7542923,7551763,7551917,7576957,7577503,7577657,7587667,7593413,7601813,7619153,7627007,7627993,7653187,7661873,7687067,7687613,7697623,7697777,7703083,7721647,7727393,7739273,7745957,7748113,7757837,7761427,7763143,7773307,7773853,7787453,7797617,7807733,7821487,7832197,7833913,7866077,7873693,7883963,7892257,7907573,7931597,7933753,7941607,7942153,7942307,7944023,7967347,7983803,8002367,8011937,8017837,8043863,8052263,8053433,8062273,8069603,8071997,8077457,8077897,8078443,8087467,8088013,8103637,8122487,8148073,8148227,8172383,8189723,8197577,8198123,8198563,8223757,8224303,8232157,8232443,8256467,8257637,8258183,8268347,8273653,8292217,8297963,8316527,8331997,8333713,8344423,8358023,8378303,8392057,8392603,8402767,8404483,8417797,8434253,8436647,8442107,8444263,8454533,8462827,8468287,8502167,8512723,8512877,8514593,8537917,8554373,8572937,8578243,8580113,8582507,8588407,8588953,8598677,8614147,8614433,8622833,8640173,8648027,8648467,8649013,8658583,8674207,8718643,8718797,8724103,8742953,8759123,8760293,8768147,8768693,8769133,8782447,8784317,8794327,8794873,8802727,8827037,8828753,8844223,8862787,8868533,8887097,8902567,8903113,8904283,8904983,8914993,8928307,8928593,8962627,8963173,8963327,8973337,8988367,9004823,9012677,9025103,9038857,9072737,9073283,9083293,9083447,9085163,9088753,9098477,9107317,9108487,9109187,9124943,9143507,9148813,9150683,9158977,9159523,9169247,9184717,9193403,9210743,9218597,9219143,9219583,9229153,9244777,9245323,9253177,9269633,9289367,9294673,9294827,9329693,9339263,9353017,9354887,9365443,9373297,9397607,9399323,9414793,9430963,9433357,9439103,9455273,9457667,9463127,9473137,9473683,9475553,9489307,9498877,9533743,9533897,9558937,9575393,9583247,9583793,9595673,9608987,9609427,9609973,9617827,9635167,9643307,9643853,9654017,9659323,9669047,9677887,9679757];
a=[4223,19693,19847,21563,29417,29963,30403,38257,39973,40127,45433,55597,56143,63997,64283,69743,79753,79907,80453,81623,88307,89477,90023,90463,95923,98317,100187,103777,105493,105647,114487,115657,116203,124057,129803,139967,140513,148367,150083,155983,163837,165553,165707,174547,176263,184117,189863,200573,208427,210143,215603,216043,223897,224443,225613,225767,226313,234167,234607,236323,241783,244177,249637,249923,260347,260633,266093,268487,273947,275663,276103,283957,284503,284657,285827,286373,294227,294667,300127,301843,309697,320407,326153,334007,335723,344563,344717,346433,354287,360187,361903,369757,370303,380467,386213,394067,394613,395783,404623,404777,406493,410083,411953,414347,419807,420247,420793,421963,428647,429817,430363,430517,440527,445987,446273,454127,454673,464837,470143,470297,472013,479867,480307,480853,488707,490423,490577,506047];
w=vector(19);
for (i=37712903181000001, 37712903182000000,
for (n=1, 128,
b=510510*i+a[n];
if(ispseudoprime(b), v=b-6;
if(ispseudoprime(v),
if(nextprime(v+1)==b,
w[9]=v+120; w[10]=v+126; w[11]=v+132;
if(ispseudoprime(w[9]),
if(nextprime(w[9]+1)==w[10],
if(nextprime(w[10]+1)==w[11], w[1]=v; w[2]=v+6; w[3]=v+12; w[4]=v+30; w[5]=v+42; w[6]=v+72; w[7]=v+90; w[8]=v+96; w[12]=v+156; w[13]=v+162; w[14]=v+180; w[15]=v+210; w[16]=v+222; w[17]=v+240; w[18]=v+246; w[19]=v+252;
if(ispseudoprime(w[8]),
if(nextprime(w[8]+1)==w[9],
if(nextprime(w[11]+1)==w[12],
if(ispseudoprime(w[7]),
if(nextprime(w[7]+1)==w[8],
if(nextprime(w[12]+1)==w[13], print(w,", "); print(a[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(ispseudoprime(w[6]),
if(nextprime(w[6]+1)==w[7], print(w,", "); print(a[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(nextprime(w[13]+1)==w[14], print(w,", "); print(a[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(ispseudoprime(w[5]),
if(nextprime(w[5]+1)==w[6], print(w,", "); print(a[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(nextprime(w[14]+1)==w[15], print(w,", "); print(a[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(ispseudoprime(w[4]),
if(nextprime(w[4]+1)==w[5], print(w,", "); print(a[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(nextprime(w[15]+1)==w[16], print(w,", ") )))))))))))))))))))))));
print(w,", ");
for (i=1984889644000001, 1984889645000000,
for (n=1, 1024,
b=9699690*i+c[n];
if(ispseudoprime(b), v=b-6;
if(ispseudoprime(v),
if(nextprime(v+1)==b,
w[9]=v+120; w[10]=v+126; w[11]=v+132;
if(ispseudoprime(w[9]),
if(nextprime(w[9]+1)==w[10],
if(nextprime(w[10]+1)==w[11], w[1]=v; w[2]=v+6; w[3]=v+12; w[4]=v+30; w[5]=v+42; w[6]=v+72; w[7]=v+90; w[8]=v+96; w[12]=v+156; w[13]=v+162; w[14]=v+180; w[15]=v+210; w[16]=v+222; w[17]=v+240; w[18]=v+246; w[19]=v+252;
if(ispseudoprime(w[8]),
if(nextprime(w[8]+1)==w[9],
if(nextprime(w[11]+1)==w[12],
if(ispseudoprime(w[7]),
if(nextprime(w[7]+1)==w[8],
if(nextprime(w[12]+1)==w[13], print(w,", "); print(c[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(ispseudoprime(w[6]),
if(nextprime(w[6]+1)==w[7], print(w,", "); print(c[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(nextprime(w[13]+1)==w[14], print(w,", "); print(c[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(ispseudoprime(w[5]),
if(nextprime(w[5]+1)==w[6], print(w,", "); print(c[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(nextprime(w[14]+1)==w[15], print(w,", "); print(c[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(ispseudoprime(w[4]),
if(nextprime(w[4]+1)==w[5], print(w,", "); print(c[n],", "); forprime(k = w[1], w[19], print(k,", ") );
if(nextprime(w[15]+1)==w[16], print(w,", ") )))))))))))))))))))))));
print(w,", ")
}Ой, где господин Петухов :) Он разнёс бы сейчас в пух и прах мою программу, случалось... Ну, я не претендую на геройские подвиги :) Пишу, как умею. Худо-бедно программа работает. Я к чему веду речь. Надо бы оптимизировать программу насколько это возможно, а оптимизировать почти всегда возможно. Лозунг программиста: "Нет предела оптимизации!" Так что, знатоки PARI/GP, пожалуйста, пишите мне. Первое, что можно сделать: взять один и тот же диапазон изменения параметра цикла i. Тогда будет один внешний цикл по i и два вложенных цикла по n. Это, наверное, будет быстрее выполняться, нежели отдельно два цикла по i, так мне думается. Что ещё можно оптимизировать? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Теперь хочу расширить алгоритм №3. Это для паттерна с диаметром 432 0 12 36 90 96 132 162 180 210 216 222 252 270 300 336 342 396 420 432 Это мне посчитал форумчанин на форуме MHP 2 (1,) 3 (1, 2) 5 (1, 2) 7 (4, 5) 11 (2, 6) 13 (4, 6) 17 (1, 9, 13, 14) 19 (8, 11, 13, 16) 23 (7, 12, 13, 15, 16, 21) Пока я задействовала модули до 19 включительно, что дало 512 формул следующего вида Q = 9699690k + X Теперь хочу попробовать задействовать ещё модуль 23. Это даст 3072 формулы следующего вида Q = 223092870k + X |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Да, самое важное :) Приглашаю всех на штурм 19-ки! Вам нужно скачать и установить PARI/GP. Ссылку сейчас найду на форуме dxdy.ru Алгоритмов можно сделать кучу, программ - тоже. Ну, помните про "200 миллионов формул" господина Петухова? :) Макс Алексеев писал в теме "Интерактивный курс: введение в программирование на PARI/GP" https://dxdy.ru/post120724.html#p120724 Буду предполагать, что с установкой PARI/GP вы справитесь. Берется он на официальной страничке. Я недавно скачала и установила новую версию, у меня была давнишняя версия. Но работают они, кажется, совершенно одинаково (по времени). Кстати, по этой теме Макса я осваивала PARI/GP. Спасибо ему! Познания мои самые минимальные. Документацию, конечно, не читала. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Тэк-с, отложила расширение алгоритма №3 до 3072 формул. Решила сделать другую модификацию: добавить к этому алгоритму ещё один паттерн 0 6 12 30 42 72 90 102 132 156 180 210 222 240 270 282 300 306 312 Тут диаметр 312, больше минимального диаметра 252. Мне этот паттерн понравился; во-первых, у него первые две разности равны 6, такое часто встречается. Во-вторых, для этого паттерна тоже получилось 512 формул вида Q = 9699690k + X Посчитала остатки для модулей 2: 1 3: 1, 2 5: 1, 2 7: 4, 6 11: 1, 6 13: 5, 8 17: 1, 3, 8, 10 19: 2, 9, 14, 16 Сейчас получу формулы и добавлю их в программу алгоритма №3. Будет считаться сразу для двух паттернов по 512 формулам. Диапазон изменения параметра цикла i взяла одинаковый для обоих паттернов. Таким образом, циклы (и внешний, и вложенный) получились одинаковые, что очень удобно. Можно и дальше поискать паттерны с 512 формулами и добавить их в эту программу. Чем больше будет разных паттернов, тем больше шансов найти решение. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Новости "Пентадекатлона мечты" Hugo писал в сообщении https://dxdy.ru/post1557869.html#p1557869 ... for now, I'm particularly interested in satisfying myself that Значит, пока он так и не увидел это совершенно простое доказательство :) А уже и народ доказал и господин Лецко передоказал. Но всё это ещё где-то бродит: то ли в черновиках, то ли в готовящейся статье. Ага, вот господин Лецко ответил Hugo, I also couldn't find the whole proof of Всё понятно :) Странно, что господин Лецко пишет  Ведь для 70 делителей доказано точное равенство. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16460 Credit: 0 RAC: 0 |
Игра "Угадай слово" за 18 июня БЕЛКА МЕТКА СЕТКА ТЕТКА Безобразная ТЕТКА :) Сегодня опять "троечка" :) Однако слово загадано хорошее, пришлось подумать, и потому куча удовольствия. |

©2025 (C) Progger
