Ассоциативные ДЛК
Message boards :
Science :
Ассоциативные ДЛК
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Начну с цитаты Кстати, методом составных квадратов можно строить не только дважды симметричные ДЛК. Я много писала об ассоциативных ДЛК в теме "Дважды симметричные ДЛК"; из этой темы приведённая цитата. В цитате вы видите ассоциативные ДЛК 5-го, 7-го и 35-го порядков. Эти ДЛК не только ассоциативные, но и пандиагональные, то есть идеальные. Заинтересовал вопрос: существуют ли ассоциативные ДЛК 10-го порядка? Предполагаю, что не существуют. Но как это доказать? Что мешает, например, этому ДЛК 10-го порядка  быть ассоциативным? Это СН ДЛК из линейки №15. Пока всё очень хорошо; в шаблон записала первый вариант строки в этой линейке, и записала последнюю строку по условию ассоциативности. Противоречий нет - пока. Если по этому шаблону написать программу построения ассоциативного ДЛК, не выдаст программа решений? В 1939 году Россер доказал, что для классических магических квадратов порядков n=4k+2 (k=1, 2, 3, ...) не существует ни ассоциативных, ни пандиагональных. Но это для классических! ДЛК тоже магический квадрат, но нетрадиционный. А для нетрадиционных магических квадратов порядков n=4k+2 существуют и ассоциативные, и пандиагональные, и даже идеальные. Вот, например, нетрадиционный идеальный магический квадрат 10-го порядка из различных простых чисел (построен мной): 9133 2017 1069 1669 3583 4999 8629 1489 6343 7219 5209 4219 5101 6793 43 6841 7951 2683 5557 1753 7603 7369 6883 8059 8863 919 1471 769 4111 103 163 8179 4723 4243 4663 5869 1741 6553 1723 8293 2833 4051 709 1021 7177 5701 1993 6991 8101 7573 1657 1129 2239 7237 3529 2053 8209 8521 5179 6397 937 7507 2677 7489 3361 4567 4987 4507 1051 9067 9127 5119 8461 7759 8311 367 1171 2347 1861 1627 7477 3673 6547 1279 2389 9187 2437 4129 5011 4021 2011 2887 7741 601 4231 5647 7561 8161 7213 97 Ещё проще построить идеальный квадрат 10-го порядка (как и других порядков) из произвольных натуральных чисел. У меня есть статья о построении таких нетрадиционных магических квадратов. А как же для ДЛК 10-го порядка: существует или не существует ассоциативный ДЛК? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ассоциативные ДЛК 9-го порядка существуют. Вот, например, найденная мной в линейке №1 ассоциативная КФ ОДЛК 0 2 3 4 5 6 7 8 1 6 1 4 7 2 3 8 0 5 8 4 2 1 7 0 3 5 6 4 5 6 3 8 2 0 1 7 5 6 7 0 4 8 1 2 3 1 7 8 6 0 5 2 3 4 2 3 5 8 1 7 6 4 0 3 8 0 5 6 1 4 7 2 7 0 1 2 3 4 5 6 8 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Заинтересовал вопрос: существуют ли ассоциативные ДЛК 10-го порядка? Пишу программу :) С замиранием сердца делаю каждый шаг. Две пары строк программа заполнила без проблем: 0 2 3 4 5 6 7 8 9 1 2 1 4 7 6 8 3 9 0 5 1 5 2 0 9 7 8 3 6 4 x x x 3 x x 4 x x x x x x x 4 2 x x x x x x x x 7 5 x x x x x x x 5 x x 6 x x x 5 3 6 1 2 0 9 7 4 8 4 9 0 6 1 3 2 5 8 7 8 0 1 2 3 4 5 6 7 9 Вроде всё правильно пока. Осталось заполнить две пары строк. Получится??? Для линейки №15 у нас имеется 6164 варианта первой строки. Сейчас у меня шаблон для первого варианта строки в этой линейке. Если с этим вариантом не получится, можно пробовать ещё 6163 варианта. Кроме того, линейка с центрально-симметричной побочной диагональю не единственная. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И вот уже заполнена ещё одна пара строк, кажется, и здесь всё правильно 0 2 3 4 5 6 7 8 9 1 2 1 4 7 6 8 3 9 0 5 1 5 2 0 9 7 8 3 6 4 6 7 5 3 8 9 4 0 1 2 x x x x 4 2 x x x x x x x x 7 5 x x x x 7 8 9 5 0 1 6 4 2 3 5 3 6 1 2 0 9 7 4 8 4 9 0 6 1 3 2 5 8 7 8 0 1 2 3 4 5 6 7 9 Осталось заполнить всего одну пару строк. Неужели не получится? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Увы! Не получилось. Почти до конца всё заполнялось, конфликт возник в последних двух ячейках 0 2 3 4 5 6 7 8 9 1 2 1 4 7 6 8 3 9 0 5 1 5 2 0 9 7 8 3 6 4 6 7 5 3 8 9 4 0 1 2 3 6 7 8 4 2 x 1 5 0 9 4 8 x 7 5 1 2 3 6 7 8 9 5 0 1 6 4 2 3 5 3 6 1 2 0 9 7 4 8 4 9 0 6 1 3 2 5 8 7 8 0 1 2 3 4 5 6 7 9 И дальше программа быстро пробежала полный перебор и не нашла решения. Сильно подозреваю, что решения не будет и с другими вариантами первых строк, а также в других линейках с центрально-симметричной побочной диагональю.. Моё первоначальное предположение, кажется, подтверждается: ассоциативные ДЛК 10-го порядка не существуют. Но, конечно, для полного подтверждения надо проверить все линейки и со всеми вариантами первых строк в них. Проверила со вторым вариантом первой строки в этой же линейке (№15), нет решения. Ну если ещё я в программе не наврала. Программа длинная, а тестировать её не на чем: решений-то известных нет. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Немного о терминологии. Смотрим статью А. Чернова "Метод Гергели построения диагональных латинских квадратов" http://alex-black.ru/article.php?content=123 В этой статье автор ссылается на следующую статью: Ervin Gergely. A Simple Method for Constructing Doubly Diagonalized Latin Squares. 1972. Цитирую статью Чернова: В методе используются трансверсали (transversal), поэтому, прежде всего, определение: трансверсаль квадрата - это коллекция n его элементов, таких, что все они расположены в разных строках, колонках и содержат ровно по одному разу все элементы используемого множества чисел. Ну, тут связано с трансверсалями. Но и без этой связи я часто встречала в англоязычных статьях термин "doubly diagonalized", то есть "дважды диагональный". Иными словами: если в ЛК только главная диагональ состоит из различных элементов, то это "диагональный" ЛК. А вот если и главная, и побочная диагонали состоят из различных элементов, тогда это "дважды диагональный" ЛК. А по-нашему (в русскоязычном сообществе квадратистов) "дважды диагональный" ЛК это и есть "диагональный" ЛК. Не знаю, как сейчас иностранцы пишут в статьях о ДЛК, как-то не обращала на это внимание в последнее время. Во избежание путаницы, мы будем считать диагональным такой ЛК, в котором и главная, и побочная диагонали состоят из различных элементов. Пример "диагонального" ЛК 3-го порядка по терминологии иностранцев 0 2 1 2 1 0 1 0 2 Но это не ДЛК по нашему определению. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Теперь об определении ассоциативных ДЛК. Прежде всего подчеркну, что я даю определение ассоциативных ДЛК, а не ассоциативных ЛК. Оставляю в стороне вопрос об ассоциативных ЛК, так как считаю, что для произвольных ЛК данное определение ассоциативности не имеет смысла. Определение ДЛК порядка n называется ассоциативным, если он имеет ассоциативную КФ второго формата, то есть с естественной перестановкой 0,1, 2,..., n-1 в главной диагонали. Ассоциативная КФ - это такой ДЛК, в котором сумма любых двух центрально-симметричных элементов постоянна и равна (n-1). Пример ассоциативной КФ 9-го порядка 0 2 3 4 5 6 7 8 1 6 1 4 7 2 3 8 0 5 4 6 2 1 7 8 3 5 0 5 7 8 3 0 2 1 4 6 1 5 6 8 4 0 2 3 7 2 4 7 6 8 5 0 1 3 8 3 5 0 1 7 6 2 4 3 8 0 5 6 1 4 7 2 7 0 1 2 3 4 5 6 8 Все ДЛК 9-го порядка, которые имеют данную КФ, являются ассоциативными, например, такой ДЛК: 0 1 2 3 4 5 6 7 8 1 2 0 4 5 7 8 3 6 5 0 3 1 8 6 2 4 7 2 5 7 6 0 1 3 8 4 4 8 1 5 7 2 0 6 3 3 6 4 0 1 8 7 2 5 7 3 5 8 6 0 4 1 2 8 4 6 7 2 3 1 5 0 6 7 8 2 3 4 5 0 1 Пример ассоциативного ДЛК 9-го порядка 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 0 1 2 6 7 8 0 1 2 3 4 5 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 Этот ассоциативный ДЛК имеет следующую ассоциативную КФ: 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Смотрим на примеры ассоциативных ДЛК 7-го порядка 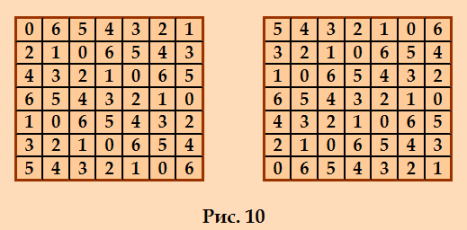 ДЛК справа точно не КФ, а ДЛК слева - не знаю (у меня нет канонизатора для ДЛК 7-го порядка). Но я уверена, что оба эти ДЛК имеют ассоциативную КФ второго формата. PS. У меня есть программка нормализации главной диагонали в ДЛК (Harry White прислал). Так вот, для приведённых выше ассоциативных ДЛК эта программка выдаёт следующие ДЛК с нормализованной главной диагональю: 0 6 5 4 3 2 1 2 1 0 6 5 4 3 4 3 2 1 0 6 5 6 5 4 3 2 1 0 1 0 6 5 4 3 2 3 2 1 0 6 5 4 5 4 3 2 1 0 6 0 5 3 1 6 4 2 3 1 6 4 2 0 5 6 4 2 0 5 3 1 2 0 5 3 1 6 4 5 3 1 6 4 2 0 1 6 4 2 0 5 3 4 2 0 5 3 1 6 Ну, первый ДЛК уже и был с нормализованной главной диагональю. Этот пример привёл к мысли, что ассоциативные ДЛК можно определить и через процедуру нормализации главной диагонали, а не через КФ, как я это сделала выше. Ну, пусть пока будет приведённое выше определение - на правах экспериментального определения. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это цитата
Кстати, интересно. У приведённой ассоциативной КФ есть ортогональный диагональный соквадрат, и он тоже ассоциативный! [DLK(1)] 0 2 3 4 5 6 7 8 1 6 1 4 7 2 3 8 0 5 4 6 2 1 7 8 3 5 0 5 7 8 3 0 2 1 4 6 1 5 6 8 4 0 2 3 7 2 4 7 6 8 5 0 1 3 8 3 5 0 1 7 6 2 4 3 8 0 5 6 1 4 7 2 7 0 1 2 3 4 5 6 8 [mate#1] 3 4 5 2 6 7 8 1 0 5 1 3 0 7 2 6 8 4 7 0 8 4 5 3 1 2 6 1 3 4 6 2 5 7 0 8 8 5 6 7 4 1 0 3 2 2 6 1 3 8 0 4 5 7 0 8 7 5 3 4 2 6 1 4 2 0 8 1 6 5 7 3 6 7 2 1 0 8 3 4 5 Ортогональный соквадрат mate#1 имеет следующую ассоциативную КФ: 0 2 3 7 5 6 4 8 1 3 1 8 5 7 4 2 0 6 1 6 2 8 0 7 3 5 4 5 4 7 3 6 2 8 1 0 6 5 1 0 4 8 7 3 2 8 7 0 6 2 5 1 4 3 4 3 5 1 8 0 6 2 7 2 8 6 4 1 3 0 7 5 7 0 4 2 3 1 5 6 8 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сейчас получила статью Franklinian Diagonal Latin Squares Очень кстати :) В статье есть примеры ассоциативных ДЛК 8-го порядка, причём ортогональные пары. Показано, как из ортогональной пары ДЛК получается магический квадрат. 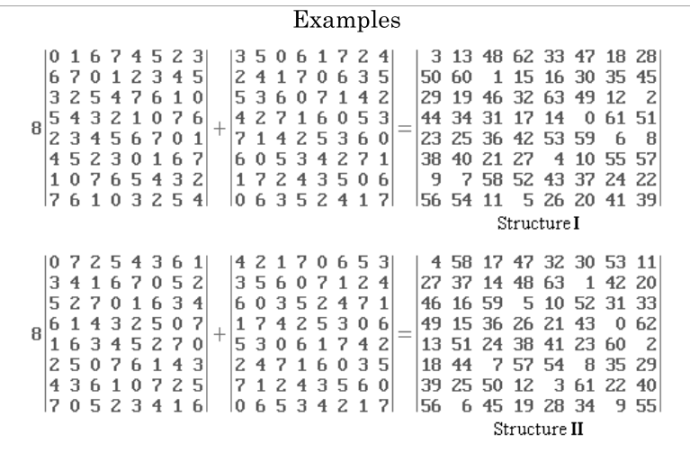 Вот что даёт программа нормализации главной диагонали для двух верхних ассоциативных ДЛК 0 5 4 1 7 2 3 6 4 1 0 5 3 6 7 2 6 3 2 7 1 4 5 0 2 7 6 3 5 0 1 4 3 6 7 2 4 1 0 5 7 2 3 6 0 5 4 1 5 0 1 4 2 7 6 3 1 4 5 0 6 3 2 7 0 4 6 2 3 7 5 1 5 1 3 7 6 2 0 4 4 0 2 6 7 3 1 5 1 5 7 3 2 6 4 0 7 3 1 5 4 0 2 6 2 6 4 0 1 5 7 3 3 7 5 1 0 4 6 2 6 2 0 4 5 1 3 7 Всё верно. Какие КФ (второго формата) у этих ДЛК, я не знаю, у меня нет канонизатора ДЛК 8-го порядка. Но они без сомнения будут ассоциативными. PS. Сейчас выложу статью "Franklinian Diagonal Latin Squares" на Яндекс.Диск. Интересная статья. Автор Miguel Angel Amela. Загрузила, вот ссылка https://yadi.sk/i/4yQLEKfB3Qsjg2 Попутно. В своё время я много занималась магическими квадратами Франклина. Вот ссылка на мой сборник статей "Квадраты Франклина" https://yadi.sk/d/-0u4VKR55pXGa Это очень интересные квадраты. Мне удалось на основе пандиагонального квадрата Франклина 16-го порядка построить идеальный магический квадрат. Жемчужина коллекции магических квадратов Франклина 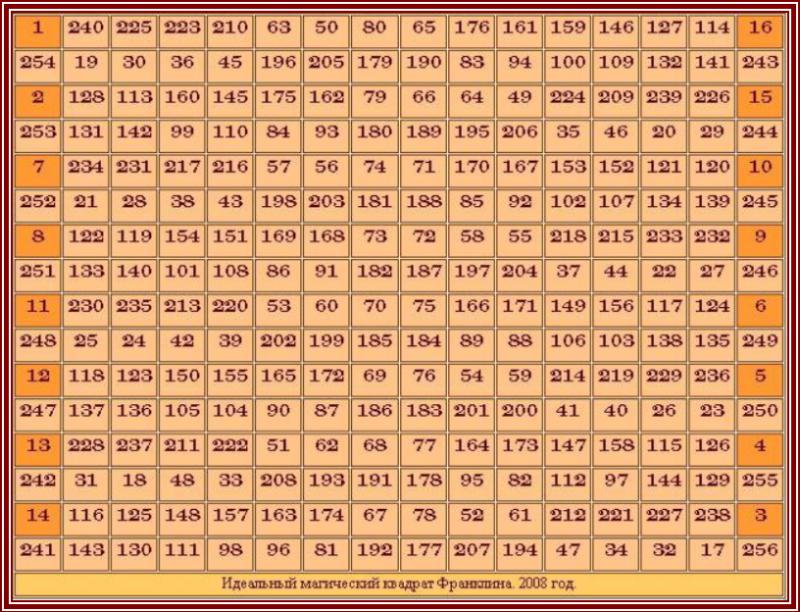 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это цитата Увы! Не получилось. Решила "отпустить" последнюю пару строк, то есть не выполнять в этих строках требование ассоциативности. Так программа выдала решения, много. Вот самое первое 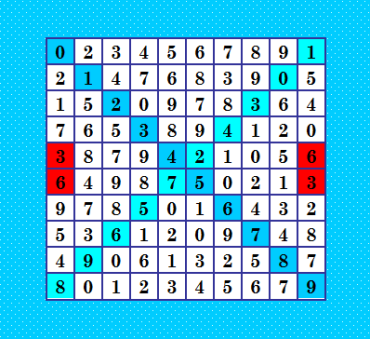 Встречайте - псевдоассоциативный ДЛК 10-го порядка. Вот, значит, как: конфликт возник в 4-х ячейках (они выделены красным цветом) и элементы в этих ячейках расположились не центрально-симметрично, а вертикально-симметрично. А всё остальное в полном соответствии с ассоциативностью. Квадратик волне себе хороший :) Как сообщает программа А. Белышева Ортогон_У, он имеет 107 диагональных трансверсалей; правда, ОДЛК не имеет. Как сообщила программа С. Беляева, этот ДЛК имеет 952 общих трансверсали и 6 ортогональных ЛК Name:a.txt 1 - only the diagonal Max=100 1 100 106 101 88 92 90 88 106 86 95 :952 sq=6 61 63 64 65 cm=65 cmm=65 END Интересный вопрос: псевдоассоциативные ДЛК имеют какое-то преимущество при построении ортогоналек к ним? Надо проверять. Для первого варианта первой строки в линейке №15 программа выдала 38120 псевдоассоциативных ДЛК. Все они СН ДЛК (по построению), но не все, понятное дело, являются КФ. Эти ДЛК проверила, решений они не дали. Но... в линейке №15 ещё 6163 варианта первой строки. Если для каждого варианта первой строки будет примерно столько же псевдоассоциатвиных ДЛК, это много проверять придётся. А потом ещё для двух линеек, в которых центрально-симметричная побочная диагональ. Но проверить стоит. А вдруг всё же преимущества есть. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Спросила Harry White о существовании ассоциативного ДЛК 10-го порядка. Вот что он ответил: I think there are none for singly even orders, but I don’t have a proof. Ну вот и выстроилась цепочка порядков n = 4k + 2. Видимо, гипотеза моя верна: не существует для данных порядков ассоциативных ДЛК. Но доказательства у Harry нет. У меня тоже нет доказательства. Конечно, можно сделать полный перебор для порядка 10, это будет считаться доказательством. Но полный перебор - сложно для меня. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Новое письмо от Harry White. Цитирую: The proof is essentially the same as the one I give for no Я пока не смотрела это доказательство. Можно также посмотреть и доказательство Россера несуществования ассоциативных и пандиагональных магических квадратов порядков n = 4k + 2, k = 1, 2, 3, ... Статью Россера можно скачать с Яндекс.Диска https://yadi.sk/d/tl-_Ab-o5AYhS My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё интересная информация из письма Harry White An elegant proof for pandiagonal and associative was given by Dr. Charles Planck in My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю исследовать псевдоассоциативные ДЛК 10-го порядка. Весьма интересный класс ДЛК. Выяснилось, что нарушение ассоциативности может возникать в различных ячейках в паре центральных строк ДЛК (в которых разрешено нарушение ассоциативности). При этом не только в четырёх ячейках, но и, например, в восьми. Вот покажу ещё пример 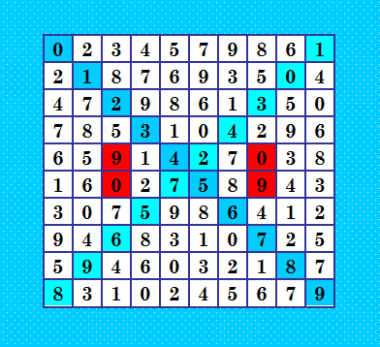 Здесь нарушение ассоциативности в 4-х ячейках, но не в тех, что были показаны выше. И элементы в этих ячейках другие. В общем, программа делает полный перебор, и в этих двух строках как получится. Только в 4-х ячейках, расположенных на диагоналях ДЛК, ассоциативность будет всегда выполняться. Далее, интересный момент: проверила 20 вариантов первой строки в линейке №15, оказалось, что далеко не все варианты первой строки дают псевдоассоциативные ДЛК. Все сгенерированные псевдоассоциативные ДЛК проверила на ОДЛК, пока не нашла решений, но ещё мало сгенерировала ДЛК. Потом решила попробовать обработать псевдоассоциативные ДЛК Канонизатором ЛК по ДЛК. И здесь удача! Решения есть. Даже одна двушка нашлась. Но обработала пока чуть-чуть, эта обработка не шустрая у меня. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю обработку псевдоассоциативных ДЛК программой Белышева Канонизатор ЛК по ДЛК. Интересен вот какой момент: сами псевдоассоциативные ДЛК (подвергающиеся вторичной обработке) ОДЛК не имеют, а при вторичной обработке Канонизатором ЛК по ДЛК решения появляются. Покажу только что найденные решения - двушка и однушка 0 1 2 3 4 5 6 7 8 9 3 6 0 9 1 7 8 4 2 5 7 5 3 6 0 8 4 1 9 2 1 3 9 8 2 6 7 5 0 4 2 7 8 5 9 3 1 6 4 0 9 8 1 2 5 4 0 3 6 7 4 2 7 0 3 9 5 8 1 6 5 0 6 4 7 1 9 2 3 8 6 4 5 1 8 0 2 9 7 3 8 9 4 7 6 2 3 0 5 1 sq1 0 1 2 3 4 5 6 7 8 9 3 6 0 9 1 7 8 4 2 5 7 9 3 6 0 8 4 1 5 2 1 3 5 8 2 6 7 9 0 4 2 7 8 5 9 3 1 6 4 0 9 8 1 2 5 4 0 3 6 7 4 2 7 0 3 9 5 8 1 6 5 0 6 4 7 1 9 2 3 8 6 4 9 1 8 0 2 5 7 3 8 5 4 7 6 2 3 0 9 1 sq2 Square: 0 2 5 7 3 4 8 6 9 1 4 1 9 6 5 3 0 8 2 7 9 8 2 0 6 7 1 3 5 4 6 9 8 3 1 2 4 5 7 0 3 5 1 2 4 0 7 9 6 8 7 6 0 8 9 5 3 1 4 2 2 0 7 5 8 9 6 4 1 3 1 4 6 9 0 8 2 7 3 5 5 7 3 4 2 1 9 0 8 6 8 3 4 1 7 6 5 2 0 9 --------------------- 0 1 2 3 4 5 6 7 8 9 1 6 3 5 0 9 8 4 2 7 8 7 5 0 2 1 4 3 9 6 2 4 7 8 9 3 5 1 6 0 6 5 9 7 1 4 0 2 3 8 5 2 4 9 8 7 3 6 0 1 9 3 0 1 5 6 2 8 7 4 4 8 6 2 3 0 7 9 1 5 3 0 1 6 7 8 9 5 4 2 7 9 8 4 6 2 1 0 5 3 sq1 Square: 0 3 5 2 6 7 8 9 4 1 7 1 4 8 3 9 0 5 2 6 1 4 2 6 7 8 9 3 0 5 9 2 0 3 5 1 4 6 7 8 3 9 8 7 4 0 5 1 6 2 6 8 3 4 9 5 7 2 1 0 2 0 9 5 1 4 6 8 3 7 4 5 6 0 8 2 1 7 9 3 5 7 1 9 2 6 3 0 8 4 8 6 7 1 0 3 2 4 5 9 Оба решения уникальные, двушка полновесная, 5 КФ в БД добавлены. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Удивительно хороши псевдоассоциативные ДЛК при обработке Канонизатором ЛК по ДЛК. При этом сами они "пустышки"! Выход КФ ОДЛК довольно приличный. Даже двушки попадаются. Вот сейчас попалась двушка 0 1 2 3 4 5 6 7 8 9 7 8 6 9 0 2 5 1 3 4 3 2 7 8 5 9 0 4 1 6 6 9 0 5 1 8 2 3 4 7 2 7 8 4 6 1 3 9 0 5 9 6 3 1 7 4 8 0 5 2 5 4 9 6 2 3 1 8 7 0 4 3 5 7 8 0 9 2 6 1 1 0 4 2 3 6 7 5 9 8 8 5 1 0 9 7 4 6 2 3 sq1 0 1 2 3 4 5 6 7 8 9 7 8 6 9 1 2 5 0 3 4 3 2 7 8 5 9 0 4 1 6 6 9 1 5 0 8 2 3 4 7 2 7 8 4 6 1 3 9 0 5 9 6 3 0 7 4 8 1 5 2 5 4 9 6 2 3 1 8 7 0 4 3 5 7 8 0 9 2 6 1 1 0 4 2 3 6 7 5 9 8 8 5 0 1 9 7 4 6 2 3 sq2 Square: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 9 3 8 6 7 7 8 4 0 1 6 9 2 3 5 4 5 8 6 2 7 0 1 9 3 3 6 1 8 9 4 5 0 7 2 2 7 9 5 8 3 4 6 0 1 8 0 3 1 6 2 7 9 5 4 6 4 7 9 3 1 8 5 2 0 9 3 5 7 0 8 2 4 1 6 5 9 6 2 7 0 1 3 4 8 Уникальная и полновесная, 3 уникальные КФ добавила в БД. Однушки, конечно, гораздо чаще попадаются, нежели двушки. Троек и четвёрок пока не было. Псевдоассоциативных ДЛК много, обрабатывать хватит очень надолго. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И это ещё не всё! Обработала эту двушку ещё раз Канонизатором ЛК по ДЛК и... ещё 4 уникальные КФ! 0 1 2 3 4 5 6 7 8 9 1 2 3 0 5 8 7 9 4 6 2 8 6 5 9 4 1 3 0 7 7 9 8 1 6 0 5 4 3 2 3 4 0 7 8 2 9 6 1 5 4 6 9 8 0 7 2 1 5 3 5 0 4 6 7 9 3 8 2 1 9 3 1 4 2 6 8 5 7 0 6 7 5 2 1 3 4 0 9 8 8 5 7 9 3 1 0 2 6 4 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 9 5 8 2 6 5 8 3 7 9 0 4 1 9 5 1 7 6 8 4 3 2 0 8 7 4 0 9 2 1 6 3 5 7 3 6 9 1 4 8 5 0 2 4 0 8 6 5 1 3 2 9 7 5 9 7 1 2 3 0 8 6 4 6 8 0 2 7 9 5 4 1 3 3 4 9 5 8 0 2 1 7 6 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 9 5 8 7 9 1 8 6 0 5 4 2 3 8 3 7 9 5 4 0 2 6 1 6 5 9 2 7 1 8 3 0 4 9 0 5 1 2 8 4 6 3 7 5 8 4 6 9 7 3 0 1 2 4 6 8 7 3 2 1 5 9 0 2 7 6 0 8 3 9 1 4 5 3 4 0 5 1 9 2 8 7 6 0 1 2 3 4 5 6 7 8 9 1 2 3 7 0 8 4 9 6 5 3 7 5 9 2 4 0 8 1 6 7 8 4 6 5 9 3 1 0 2 6 5 9 4 1 0 7 2 3 8 8 9 0 1 7 3 2 6 5 4 4 0 6 5 9 7 8 3 2 1 9 6 1 8 3 2 5 4 7 0 5 4 7 2 8 6 1 0 9 3 2 3 8 0 6 1 9 5 4 7 Вот это да! Это очень напоминает симметричные (по Гергели/Брауну) ДЛК, только они так здорово клонировались. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю генерацию псевдоассоциативных ДЛК своим простеньким генератором и проверку их на ОДЛК - первичную и вторичную. При первичной обработке пока не найдено ни одного решения. А при вторичной решения стабильно появляются, в каждой порции сгенерированных ДЛК есть несколько решений, изредка встречаются двушки. Вот сейчас опять двушка попалась 0 1 2 3 4 5 6 7 8 9 2 3 9 6 8 7 0 4 1 5 1 9 4 8 7 6 3 0 5 2 3 6 5 1 9 4 7 8 2 0 7 2 0 5 6 8 1 9 4 3 4 8 1 0 2 9 5 6 3 7 5 7 8 4 3 0 2 1 9 6 9 0 3 7 1 2 8 5 6 4 8 5 6 9 0 3 4 2 7 1 6 4 7 2 5 1 9 3 0 8 sq1 0 1 2 3 4 5 6 7 8 9 2 3 9 6 8 7 4 0 1 5 1 9 4 8 7 6 3 2 5 0 3 6 5 1 9 4 7 8 0 2 7 4 0 5 6 8 1 9 2 3 4 8 1 2 0 9 5 6 3 7 5 7 8 4 3 0 2 1 9 6 9 0 3 7 1 2 8 5 6 4 8 5 6 9 2 3 0 4 7 1 6 2 7 0 5 1 9 3 4 8 sq2 Square: 0 1 2 3 4 5 6 7 8 9 1 2 3 0 7 8 5 9 4 6 6 5 8 2 1 9 0 3 7 4 5 4 0 9 6 7 2 1 3 8 4 9 6 1 3 0 8 2 5 7 2 6 7 4 5 1 3 8 9 0 9 3 4 6 8 2 7 5 0 1 8 7 1 5 0 6 9 4 2 3 3 8 5 7 9 4 1 0 6 2 7 0 9 8 2 3 4 6 1 5 Уникальная и полновесная. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю генерацию псевдоассоциативных ДЛК и проверку их на ОДЛК. Сейчас сгенерировала порцию с 17-ым вариантом первой строки в линейке №15. Сгенерировалось 67110 псевдоассоциативных ДЛК. Первичная обработка решений не дала, эта обработка быстро выполняется. А вот со вторичной обработкой (программой Белышева Канонизатор ЛК по ДЛК) проблемы со скоростью; программа-то работает нормально, но ДЛК для проверки получается несколько миллионов. Но как раз эта обработка псевдоассоциативных ДЛК и даёт решения! Это очень интересный момент. В каждой порции решений (а генерирую я их по каждому варианту первой строки, правда, не для каждого варианта они есть почему-то) вторичная обработка даёт несколько КФ ОДЛК, попадаются даже двушки, причём есть очень хорошие двушки, которые дают решения и ещё при одной обработке Канонизатором ЛК по ДЛК (выше такая двушка показана). Покажу первые три псевдоассоциативных ДЛК в последней сгенерированной порции (для 17-го варианта первой строки линейки №15) 0 2 3 4 6 8 7 5 9 1 2 1 5 6 3 7 8 9 0 4 1 4 2 7 8 0 9 3 6 5 6 7 8 3 5 9 4 2 1 0 7 5 1 9 4 2 0 8 3 6 3 6 9 8 7 5 1 0 4 2 9 8 7 5 0 4 6 1 2 3 4 3 6 0 9 1 2 7 5 8 5 9 0 1 2 6 3 4 8 7 8 0 4 2 1 3 5 6 7 9 0 2 3 4 6 8 7 5 9 1 2 1 5 6 3 7 8 9 0 4 1 4 2 7 8 0 9 3 6 5 6 7 8 3 5 9 4 2 1 0 7 5 9 8 4 2 1 0 3 6 3 6 1 9 7 5 0 8 4 2 9 8 7 5 0 4 6 1 2 3 4 3 6 0 9 1 2 7 5 8 5 9 0 1 2 6 3 4 8 7 8 0 4 2 1 3 5 6 7 9 0 2 3 4 6 8 7 5 9 1 2 1 5 6 3 7 8 9 0 4 1 4 2 7 8 0 9 3 6 5 6 8 7 3 5 9 4 1 2 0 7 5 1 9 4 2 0 8 3 6 3 6 9 8 7 5 1 0 4 2 9 7 8 5 0 4 6 2 1 3 4 3 6 0 9 1 2 7 5 8 5 9 0 1 2 6 3 4 8 7 8 0 4 2 1 3 5 6 7 9 Интересные квадратики: нарушение ассоциативности в 8 ячейках двух центральных строк, при этом элементы в этих ячейках расположились вертикально-симметрично 7 5 1 9 4 2 0 8 3 6 3 6 9 8 7 5 1 0 4 2 Запустила вторичную обработку этой порции псевдоассоциативных ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger