БД КФ ОДЛК 9-го порядка
Message boards :
Science :
БД КФ ОДЛК 9-го порядка
Message board moderation
Previous · 1 . . . 8 · 9 · 10 · 11 · 12 · 13 · 14 . . . 34 · Next
| Author | Message |
|---|---|
 Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Вот 128-ки дуплетом [DLK(128):48036] 0 2 5 4 8 6 7 3 1 6 1 7 8 2 3 4 0 5 7 4 2 5 6 1 3 8 0 8 6 0 3 5 7 2 1 4 1 8 3 7 4 0 5 6 2 3 0 4 6 1 5 8 2 7 5 7 8 1 0 2 6 4 3 4 5 1 2 3 8 0 7 6 2 3 6 0 7 4 1 5 8 [DLK(128):48164] 0 2 5 4 8 6 7 3 1 6 1 7 8 2 3 4 0 5 7 4 2 5 6 1 3 8 0 8 6 0 3 5 7 2 1 4 1 8 3 7 4 0 5 6 2 4 0 1 6 3 5 8 2 7 5 7 8 1 0 2 6 4 3 3 5 4 2 1 8 0 7 6 2 3 6 0 7 4 1 5 8 и 138-ки дуплетом [DLK(138):48884] 0 2 5 4 8 6 7 3 1 7 1 6 8 2 3 4 0 5 6 4 2 5 7 1 3 8 0 8 6 0 3 5 7 2 1 4 1 8 3 7 4 0 5 6 2 4 0 1 6 3 5 8 2 7 5 7 8 1 0 2 6 4 3 3 5 4 2 1 8 0 7 6 2 3 7 0 6 4 1 5 8 [DLK(138):49022] 0 2 5 4 8 6 7 3 1 7 1 6 8 2 3 4 0 5 6 4 2 5 7 1 3 8 0 8 6 0 3 5 7 2 1 4 3 8 1 7 4 0 5 6 2 4 0 3 6 1 5 8 2 7 5 7 8 1 0 2 6 4 3 1 5 4 2 3 8 0 7 6 2 3 7 0 6 4 1 5 8 Может, и ещё есть интересные решения, но... надоело бегать по массиву поиском. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6285 · Rating: 0 · rate:
 /   |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Уф! Черепашка бегом бегала :) Обработала уже шахматным алгоритмом всю имеющуюся у нас БД. В итоге БД у нас выросла до 37493 КФ ОДЛК (+5112). Круто! А теперь эти новые КФ ОДЛК надо обработать Канонизатором ЛК по ДЛК. Отдохнёт немножко черепашка, замучилась бедненькая :) Хм... А потом новые КФ ОДЛК (если они будут) надо снова обработать шахматным алгоритмом. Вот такая карусель! Возникла 310-ка, кажется, не было раньше [DLK(310):102589] 0 3 5 4 6 7 8 2 1 8 1 7 5 3 4 2 0 6 6 4 2 8 7 0 3 1 5 7 8 1 3 0 6 4 5 2 3 5 0 2 4 8 1 6 7 2 6 4 7 1 5 0 8 3 1 7 8 0 5 2 6 3 4 4 2 6 1 8 3 5 7 0 5 0 3 6 2 1 7 4 8 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6286 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Господа! У вас уже есть БД КФ ОДЛК 9-го порядка? Ну, хоть какая-то её часть. Тогда мы идём к вам :) Мы можем вашу БД обработать двумя алгоритмами постобработки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6287 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Запостила просьбу о программе сортировки массива марьяжных ДЛК на форуме Math Help Planet http://mathhelpplanet.com/viewtopic.php?p=397460#p397460 Может, там кто-нибудь поможет. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6288 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Тэк-с, черепашка отдохнула, и я вместе с ней :) Берём 5112 новых КФ ОДЛК и обрабатываем программой Канонизатор ЛК по ДЛК. И... получаем 380 уникальных КФ ОДЛК. БД выросла до 37873 КФ ОДЛК. Интересно: посмотрите на хвостик массива марьяжных КФ . . . . . . [DLK(4):230427] 0 8 7 4 6 2 5 3 1 6 1 5 8 3 4 7 0 2 1 6 2 0 8 7 3 5 4 8 7 4 3 1 6 0 2 5 3 5 0 2 4 8 1 6 7 2 3 1 7 0 5 4 8 6 7 4 8 5 2 0 6 1 3 4 2 6 1 5 3 8 7 0 5 0 3 6 7 1 2 4 8 [DLK(2):230431] 0 8 7 4 6 2 5 3 1 6 1 5 8 3 4 7 0 2 4 6 2 1 8 7 3 5 0 8 7 0 3 1 6 4 2 5 3 5 1 2 4 8 0 6 7 2 3 4 7 0 5 1 8 6 7 0 8 5 2 1 6 4 3 1 2 6 0 5 3 8 7 4 5 4 3 6 7 0 2 1 8 [DLK(2):230433] 0 8 7 4 6 2 5 3 1 6 1 5 8 3 4 7 0 2 4 6 2 1 8 7 3 5 0 8 7 1 3 0 6 4 2 5 3 5 0 2 4 8 1 6 7 2 3 4 7 1 5 0 8 6 7 0 8 5 2 1 6 4 3 1 2 6 0 5 3 8 7 4 5 4 3 6 7 0 2 1 8 [DLK(2):230435] 0 8 7 4 6 2 5 3 1 6 1 5 8 3 4 7 0 2 4 6 2 1 8 7 3 5 0 8 7 4 3 0 6 1 2 5 3 5 1 2 4 8 0 6 7 2 3 0 7 1 5 4 8 6 7 0 8 5 2 1 6 4 3 1 2 6 0 5 3 8 7 4 5 4 3 6 7 0 2 1 8 [DLK(2):230437] 0 8 7 4 6 2 5 3 1 6 1 5 8 3 4 7 0 2 4 6 2 1 8 7 3 5 0 8 7 4 3 1 6 0 2 5 3 5 0 2 4 8 1 6 7 2 3 1 7 0 5 4 8 6 7 0 8 5 2 1 6 4 3 1 2 6 0 5 3 8 7 4 5 4 3 6 7 0 2 1 8 На число 230437 обратите внимание. Это все ортогональки (они выводятся программой в файл mates.txt)! Круто! А ещё обратите внимание на последнюю КФ. Эта двушечка уже вечность стоит тут - на последнем месте. Глобальный максимум БД??? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6289 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Да, и это ещё не всё. Теперь надо обработать 380 новых КФ ОДЛК шахматным алгоритмом. Авось ещё будет добавление. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6290 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Обработка 380 новых КФ ОДЛК шахматным алгоритмом дала ещё 33 уникальные КФ ОДЛК. Теперь у нас БД содержит 37906 КФ ОДЛК. Стратегия грубой силы работает плохо: очень редко встречаются продуктивные области. Следовательно, надо придумывать новые алгоритмы: поиска и/или постобработки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6291 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
С марьяжными ДЛК поработала вручную - в Ворде поиском. Тяжело, конечно, но лучшего варианта пока нет. Составила статистику. Весьма интересная статистика. От 1 до 50 показываю все DLK(1) - 7709 DLK(2) - 11215 DLK(3) - 629 DLK(4) - 6446 DLK(5) - 294 DLK(6) - 791 DLK(7) - 27 DLK(8) - 4759 DLK(9) - 77 DLK(10) - 1329 DLK(11) - 11 DLK(12) - 585 DLK(13) - 60 DLK(14) - 143 DLK(15) - 25 DLK(16) - 1671 DLK(17) - 10 DLK(18) - 54 DLK(19) - 9 DLK(20) - 511 DLK(21) - 7 DLK(22) - 13 DLK(23) - 0 DLK(24) - 104 DLK(25) - 1 DLK(26) - 32 DLK(27) - 3 DLK(28) - 162 DLK(29) - 1 DLK(30) - 6 DLK(31) - 1 DLK(32) - 552 DLK(33) - 7 DLK(34) - 23 DLK(35) - 1 DLK(36) - 153 DLK(37) - 0 DLK(38) - 11 DLK(39) - 0 DLK(40) - 167 DLK(41) - 18 DLK(42) - 5 DLK(43) - 2 DLK(44) - 40 DLK(45) - 2 DLK(46) - 23 DLK(47) - 2 DLK(48) - 44 DLK(49) - 7 DLK(50) - 2 От 50 до 100 показываю только те, которые не нули DLK(52) - 9 DLK(54) - 9 DLK(55) - 1 DLK(56) - 22 DLK(58) - 2 DLK(59) - 1 DLK(60) - 12 DLK(61) - 1 DLK(64) - 22 DLK(66) - 1 DLK(67) - 1 DLK(68) - 3 DLK(69) - 2 DLK(70) - 2 DLK(71) - 1 DLK(72) - 6 DLK(74) - 1 DLK(76) - 1 DLK(78) - 1 DLK(80) - 3 DLK(82) - 1 DLK(86) - 4 DLK(88) - 2 DLK(92) - 1 DLK(99) - 1 DLK(100) - 9 И вот что осталось в сухом остатке (это группы из более 100 пар ОДЛК) [DLK(196):955] [DLK(188):1163] [DLK(204):1351] [DLK(220):1563] [DLK(196):1805] [DLK(190):2001] [DLK(560):6886] [DLK(560):7446] [DLK(560):8006] [DLK(104):11990] [DLK(104):17460] [DLK(194):22891] [DLK(147):29906] [DLK(112):37018] [DLK(111):38921] [DLK(112):43146] [DLK(329):44079] [DLK(576):47812] [DLK(614):48392] [DLK(580):49006] [DLK(144):50557] [DLK(144):50701] [DLK(128):50849] [DLK(128):50977] [DLK(144):51113] [DLK(128):51277] [DLK(128):51409] [DLK(128):51569] [DLK(138):51697] [DLK(138):51835] [DLK(188):60016] [DLK(194):60204] [DLK(308):72078] [DLK(360):73303] [DLK(120):82132] [DLK(106):85386] [DLK(310):103311] [DLK(576):112707] [DLK(576):113317] [DLK(576):113935] [DLK(516):172476] Не ранжировала. Тут интересно - 329-ка, которую я раньше не видела. Сейчас я её найду и покажу. Вот она голубушка [DLK(329):44079] 0 2 5 4 6 3 7 8 1 3 1 4 6 5 8 2 0 7 4 8 2 1 7 6 3 5 0 7 4 0 3 8 2 5 1 6 8 7 6 5 4 0 1 3 2 6 0 1 7 2 5 8 4 3 1 5 8 0 3 7 6 2 4 2 6 3 8 0 1 4 7 5 5 3 7 2 1 4 0 6 8 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6292 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Ну, теперь вроде бы видела все группы пар ОДЛК. Чуть-чуть наша БД не дотянула до 38 тысяч КФ. Интересно: в БД есть минимальная КФ и, кажется, есть максимальная КФ (хотя это пока не факт). Сколько марьяжных КФ может быть между минимальной и максимальной КФ в БД КФ ОДЛК 9-го порядка? 10 миллионов? 100 миллионов? Миллиард? Трудно ответить на этот вопрос. Ну, сколько бы их ни было, задача составления БД КФ ОДЛК 9-го порядка видится мне вполне решаемой за реальное время. Разумеется, не на одном ПК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6293 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Топ-20 групп пар ОДЛК 9-го порядка №1 [DLK(614)] 0 2 5 4 7 3 8 6 1 5 1 6 7 8 2 4 0 3 8 4 2 5 6 0 3 1 7 6 8 0 3 2 7 1 5 4 1 0 3 8 4 6 7 2 5 4 7 1 6 3 5 2 8 0 7 3 8 0 5 1 6 4 2 3 5 4 2 1 8 0 7 6 2 6 7 1 0 4 5 3 8 Д-трансверсалей: 140 №2 [DLK(580)] 0 2 5 4 7 3 8 6 1 5 1 6 7 8 2 4 0 3 8 4 2 5 6 0 3 1 7 6 8 0 3 5 7 1 2 4 1 0 3 8 4 6 7 5 2 4 7 1 6 3 5 2 8 0 7 3 8 0 2 1 6 4 5 3 5 4 2 1 8 0 7 6 2 6 7 1 0 4 5 3 8 Д-трансверсалей: 108 №3 [DLK(576)] 0 2 5 4 7 3 8 6 1 5 1 6 7 8 2 4 0 3 8 4 2 5 6 0 3 1 7 6 8 0 3 2 7 1 4 5 1 0 3 8 4 6 7 5 2 4 7 1 6 3 5 2 8 0 7 3 8 0 5 1 6 2 4 3 5 4 2 1 8 0 7 6 2 6 7 1 0 4 5 3 8 Д-трансверсалей: 112 №4 [DLK(576)] 0 3 5 8 2 7 4 6 1 3 1 6 5 7 4 8 0 2 1 0 2 4 6 8 3 5 7 7 4 1 3 5 6 2 8 0 6 2 8 1 4 0 7 3 5 8 7 3 2 0 5 1 4 6 2 5 7 0 8 3 6 1 4 4 8 0 6 1 2 5 7 3 5 6 4 7 3 1 0 2 8 Д-трансверсалей: 112 №5 [DLK(576)] 0 3 5 8 2 7 4 6 1 3 1 6 5 7 4 8 0 2 4 0 2 1 6 8 3 5 7 7 4 1 3 5 6 2 8 0 1 2 8 6 4 0 7 3 5 8 7 3 2 0 5 1 4 6 2 5 7 0 8 3 6 1 4 6 8 0 4 1 2 5 7 3 5 6 4 7 3 1 0 2 8 Д-трансверсалей: 94 №6 [DLK(576)] 0 3 5 8 2 7 4 6 1 3 1 6 5 7 4 8 0 2 4 0 2 6 1 8 3 5 7 7 4 1 3 5 6 2 8 0 6 2 8 1 4 0 7 3 5 8 7 3 2 0 5 1 4 6 2 5 7 0 8 3 6 1 4 1 8 0 4 6 2 5 7 3 5 6 4 7 3 1 0 2 8 Д-трансверсалей: 88 №7 [DLK(560)] 0 2 3 5 6 4 7 8 1 6 1 4 2 5 7 8 0 3 1 7 2 0 8 6 3 4 5 4 0 8 3 7 2 1 5 6 3 5 1 7 4 8 0 6 2 8 3 7 6 0 5 2 1 4 2 4 5 8 1 0 6 3 7 5 8 6 1 2 3 4 7 0 7 6 0 4 3 1 5 2 8 Д-трансверсалей: 132 №8 [DLK(560)] 0 2 3 5 6 4 7 8 1 6 1 4 2 5 7 8 0 3 1 7 2 0 8 6 3 4 5 4 0 8 3 7 2 1 5 6 3 5 1 7 4 8 0 6 2 8 3 7 6 2 5 4 1 0 2 4 5 8 1 0 6 3 7 5 8 6 1 0 3 2 7 4 7 6 0 4 3 1 5 2 8 Д-трансверсалей: 108 №9 [DLK(560)] 0 2 3 5 6 4 7 8 1 6 1 4 2 5 7 8 0 3 1 7 2 0 8 6 3 4 5 4 0 8 3 7 2 1 5 6 3 5 1 7 4 8 2 6 0 8 3 7 6 2 5 0 1 4 2 4 5 8 1 0 6 3 7 5 8 6 1 0 3 4 7 2 7 6 0 4 3 1 5 2 8 Д-трансверсалей: 108 №10 (ассоциативный ДЛК из полной системы MOLS) [DLK(516)] 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 Д-трансверсалей: 323 №11 [DLK(360)] 0 2 8 7 6 3 5 4 1 4 1 0 6 3 7 2 8 5 1 7 2 8 0 4 3 5 6 8 5 4 3 7 6 1 0 2 5 6 1 0 4 8 7 2 3 6 8 7 2 1 5 4 3 0 2 3 5 4 8 0 6 1 7 3 0 6 1 5 2 8 7 4 7 4 3 5 2 1 0 6 8 Д-трансверсалей: 269 №12 [DLK(329)] 0 2 5 4 6 3 7 8 1 3 1 4 6 5 8 2 0 7 4 8 2 1 7 6 3 5 0 7 4 0 3 8 2 5 1 6 8 7 6 5 4 0 1 3 2 6 0 1 7 2 5 8 4 3 1 5 8 0 3 7 6 2 4 2 6 3 8 0 1 4 7 5 5 3 7 2 1 4 0 6 8 Д-трансверсалей: 271 №13 [DLK(310)] 0 3 5 4 6 7 8 2 1 8 1 7 5 3 4 2 0 6 6 4 2 8 7 0 3 1 5 7 8 1 3 0 6 4 5 2 3 5 0 2 4 8 1 6 7 2 6 4 7 1 5 0 8 3 1 7 8 0 5 2 6 3 4 4 2 6 1 8 3 5 7 0 5 0 3 6 2 1 7 4 8 Д-трансверсалей: 257 №14 (совершенный ДЛК) [DLK(308)] 0 2 7 8 6 3 5 4 1 4 1 6 0 5 2 7 8 3 6 8 2 7 1 4 3 5 0 2 5 4 3 8 6 0 1 7 3 6 0 1 4 7 8 2 5 1 7 8 2 0 5 4 3 6 8 3 5 4 7 1 6 0 2 5 0 1 6 3 8 2 7 4 7 4 3 5 2 0 1 6 8 Д-трансверсалей: 333 №15 [DLK(220)] 0 2 3 4 5 7 8 6 1 5 1 0 6 3 2 4 8 7 1 4 2 5 7 8 3 0 6 2 8 7 3 1 6 0 5 4 6 5 8 7 4 0 1 2 3 4 3 6 2 8 5 7 1 0 3 7 5 8 0 1 6 4 2 8 0 4 1 6 3 2 7 5 7 6 1 0 2 4 5 3 8 Д-трансверсалей: 117 №16 [DLK(204)] 0 2 3 4 5 7 8 6 1 5 1 0 6 3 2 4 8 7 1 4 2 0 7 8 3 5 6 2 8 7 3 1 6 5 0 4 8 5 6 7 4 0 1 2 3 4 3 8 2 6 5 7 1 0 3 7 5 8 0 1 6 4 2 6 0 4 1 8 3 2 7 5 7 6 1 5 2 4 0 3 8 Д-трансверсалей: 269 №17 [DLK(196)] 0 2 3 4 5 7 8 6 1 5 1 0 6 3 2 4 8 7 1 4 2 5 7 8 3 0 6 2 8 7 3 1 6 0 5 4 6 5 8 7 4 0 1 2 3 8 3 4 2 6 5 7 1 0 3 7 5 8 0 1 6 4 2 4 0 6 1 8 3 2 7 5 7 6 1 0 2 4 5 3 8 Д-трансверсалей: 125 №18 [DLK(196)] 0 2 3 4 5 7 8 6 1 5 1 0 6 3 2 4 8 7 1 4 2 0 7 8 3 5 6 2 8 7 3 1 6 5 0 4 6 5 8 7 4 0 1 2 3 4 3 6 2 8 5 7 1 0 3 7 5 8 0 1 6 4 2 8 0 4 1 6 3 2 7 5 7 6 1 5 2 4 0 3 8 Д-трансверсалей: 133 №19 [DLK(194)] 0 2 3 6 8 4 7 5 1 2 1 4 5 6 7 0 8 3 8 6 2 0 7 1 3 4 5 4 7 8 3 1 6 5 2 0 5 8 0 7 4 2 1 3 6 6 3 7 2 0 5 8 1 4 3 4 5 1 2 8 6 0 7 1 0 6 8 5 3 4 7 2 7 5 1 4 3 0 2 6 8 Д-трансверсалей: 121 №20 [DLK(194)] 0 2 6 7 3 4 8 5 1 6 1 4 5 2 0 7 8 3 8 7 2 6 0 1 3 4 5 4 8 0 3 1 6 5 2 7 5 3 8 0 4 7 1 6 2 3 6 7 2 8 5 0 1 4 2 4 5 1 7 8 6 3 0 1 0 3 8 5 2 4 7 6 7 5 1 4 6 3 2 0 8 Д-трансверсалей: 117 Интересно проанализировать каждую группу ОДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6294 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Приведу небольшой анализ группы ОДЛК от рекордного квадратика [DLK(614)] 0 2 5 4 7 3 8 6 1 5 1 6 7 8 2 4 0 3 8 4 2 5 6 0 3 1 7 6 8 0 3 2 7 1 5 4 1 0 3 8 4 6 7 2 5 4 7 1 6 3 5 2 8 0 7 3 8 0 5 1 6 4 2 3 5 4 2 1 8 0 7 6 2 6 7 1 0 4 5 3 8 Утилита Harry White GetType никаких свойств у квадратов этой группы не обнаружила Order? 9
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt
Counts
------
614 diagonal LatinОртогональных пар ДЛК в этой группе нет, как утверждает программа Harry White Order? 9 Enter the name of the squares file: inp ..output file inpPairs_2.txt ..output file inpPairNos_2.txt squares 614 orthogonal pairs 0 614 ОДЛК группы дают 166 КФ ОДЛК, как утверждает программа Белышева Канонизатор ДЛК9 Введено ДЛК: 614 Найдено КФ: 166 КФ записаны в файл: output.txt Общее время работы: 0.015 сек Вместе с исходным ДЛК получается конфигурация из 167 уникальных ОДЛК. Среди этих ОДЛК есть представители четырёх линеек Order? 9 File? inp Input file is inp.txt .. writing squares to file inpDiags_5.txt Which \ 1 or / 2? 2 squares 167 diags 4 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6295 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Покажу ещё раз иллюстрацию 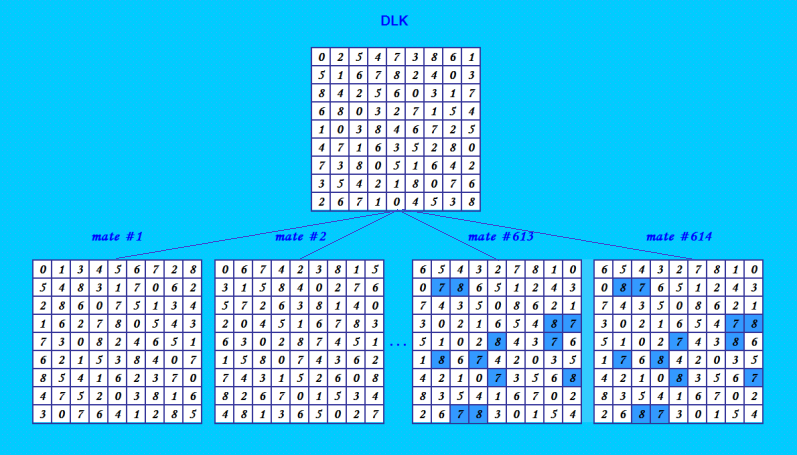 Но! Конфигурация на этой иллюстрации далеко не полная. Каждая КФ ОДЛК из 166 имеет ортогональные диагональные соквадраты. Начинается дерево. Переверните иллюстрацию и рисуйте дерево. На втором уровне от 166 КФ получено 1508 ОДЛК. Самая большая группа ОДЛК на этом уровне - 32-ка [DLK(32):1360] 0 5 3 7 8 2 4 6 1 2 1 5 4 7 6 8 0 3 7 0 2 5 1 4 3 8 6 8 6 0 3 5 7 1 4 2 6 3 1 8 4 0 7 2 5 3 8 4 6 0 5 2 1 7 1 7 8 0 2 3 6 5 4 4 2 6 1 3 8 5 7 0 5 4 7 2 6 1 0 3 8 Теперь можно исследовать эту группу ОДЛК. Затем будет третий уровень. Сколько всего будет уровней? Сколько КФ ОДЛК порождает рекордный ДЛК? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6296 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Более интересна группа ОДЛК от этого ДЛК [DLK(516)] 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 В этой группе есть взаимно ортогональные ДЛК. Программа Harry White говорит, что в этой группе есть 116 ортогональных пар Order? 9 Enter the name of the squares file: inp ..output file inpPairs_2.txt ..output file inpPairNos_2.txt squares 516 orthogonal pairs 116 Программа выводит список этих ортогональных пар 316: 125 344: 196 391: 125 316 426: 196 344 481: 196 344 426 505: 125 316 391 513: 73 75 84 85 89 96 102 125 132 135 138 144 147 179 180 185 187 191 192 193 195 196 198 199 200 201 310 312 313 314 315 316 317 318 320 322 323 324 325 331 332 333 339 340 342 344 345 346 351 352 359 360 380 382 384 386 387 388 389 390 391 392 393 394 396 400 401 402 403 405 409 420 421 422 426 430 433 435 452 454 457 464 468 469 471 473 474 481 483 484 486 494 496 499 501 502 503 504 505 506 507 509 510 511 Нарисуйте конфигурацию. Это очень интересная конфигурация - уже на первом уровне. В общем, исследуйте, господа, не ленитесь :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6297 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Кстати, по поводу рисования конфигураций. В проекте Rake Search очень увлекались этим рисованием. Вот скопипастила отсюда http://mathhelpplanet.com/viewtopic.php?p=331533#p331533  Как писали на форуме boinc.ru, это рисовалось с помощью программы Gephi. Разумеется, конфигурацию из тысяч ОДЛК вручную не нарисуешь. Можно ли с помощью этой программы нарисовать конфигурацию от ДЛК 9-го порядка, дающего 516 ОДЛК? Думаю, что можно. Кто-нибудь нарисует? Очень интересно посмотреть. Хотя бы первый уровень. Между прочим, эту конфигурацию в проекте Rake Search, наверное, рисовали, потому что она содержит "перестановочные" ОДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6298 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
А вот и моё сообщение об этой группе "перестановочных" ОДЛК. Цитата Ночью и ранним утром 15 декабря 2017 года, с разницей в 2 часа и 22 минуты, сервер проекта получил два результата от workunit-а R9_000478253 - обработанных компьютерами участника damotbe (из команды L'Alliance Francophone) и Bryan (из SETI.USA). Оба файла (как и полагается правильным результатам) были одинаковы и содержали 8 квадратов. Восемь (и даже больше!) квадратов есть в результатах обработки немалого числа workunit-ов. Но в этом случае, только первые два квадрата относились к обычной паре ОДЛК (ортогональных диагональных латинских квадратов), а остальные 6... были взаимно отогональны! (И, конечно же, они все были "перестановочными" - т.е. получены друг из друга перестановкой строк). Так была в проекте Rake Search иллюстрация этой конфигурации? Наверное, была. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6299 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Да, конечно, иллюстрация была; скопипастила её по указанной в цитате ссылке 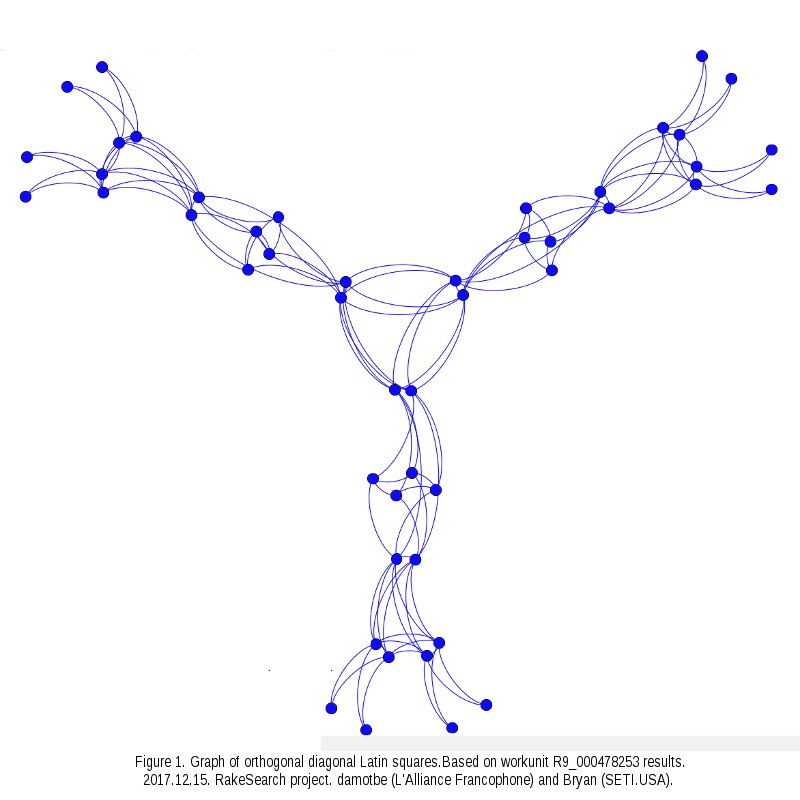 Не совсем понимаю принцип этой конфигурации, но пар ОДЛК здесь явно мало. Где здесь 516 ОДЛК, среди которых есть 116 ортогональных пар??? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6300 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Итак, господа, жду красивую иллюстрацию конфигурации, порождаемой показанной выше группой из 10 "перестановочных" ОДЛК 9-го порядка, которые найдены мной, начиная от известных давным-давно шести "перестановочных" ОДЛК из полной системы MOLS. Может быть, вы рисовать захотите :) Писать программы не хотите, считать тоже не хотите... Порисуйте тогда уж что ли :) В моём понимании конфигурация, порождаемая данной группой ОДЛК, должна быть совсем не такая, как представлена в проекте Rake Search. Там какая-то урезанная конфигурация. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6301 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Повторю эту группу из 10 "перестановочных" ОДЛК 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 0 1 2 6 7 8 0 1 2 3 4 5 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 0 1 2 3 4 5 6 7 8 6 7 8 0 1 2 3 4 5 3 4 5 6 7 8 0 1 2 5 3 4 8 6 7 2 0 1 2 0 1 5 3 4 8 6 7 8 6 7 2 0 1 5 3 4 7 8 6 1 2 0 4 5 3 4 5 3 7 8 6 1 2 0 1 2 0 4 5 3 7 8 6 0 1 2 3 4 5 6 7 8 6 7 8 0 1 2 3 4 5 3 4 5 6 7 8 0 1 2 8 6 7 2 0 1 5 3 4 5 3 4 8 6 7 2 0 1 2 0 1 5 3 4 8 6 7 4 5 3 7 8 6 1 2 0 1 2 0 4 5 3 7 8 6 7 8 6 1 2 0 4 5 3 0 1 2 3 4 5 6 7 8 7 8 6 1 2 0 4 5 3 5 3 4 8 6 7 2 0 1 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 6 7 8 0 1 2 3 4 5 8 6 7 2 0 1 5 3 4 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 0 1 2 3 4 5 6 7 8 7 8 6 1 2 0 4 5 3 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 6 7 8 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 4 5 3 7 8 6 1 2 0 8 6 7 2 0 1 5 3 4 1 2 0 4 5 3 7 8 6 5 3 4 8 6 7 2 0 1 6 7 8 0 1 2 3 4 5 2 0 1 5 3 4 8 6 7 3 4 5 6 7 8 0 1 2 7 8 6 1 2 0 4 5 3 0 1 2 3 4 5 6 7 8 4 5 3 7 8 6 1 2 0 8 6 7 2 0 1 5 3 4 5 3 4 8 6 7 2 0 1 6 7 8 0 1 2 3 4 5 1 2 0 4 5 3 7 8 6 7 8 6 1 2 0 4 5 3 2 0 1 5 3 4 8 6 7 3 4 5 6 7 8 0 1 2 0 1 2 3 4 5 6 7 8 5 3 4 8 6 7 2 0 1 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 3 4 5 6 7 8 0 1 2 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 4 5 3 7 8 6 1 2 0 6 7 8 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 5 3 4 8 6 7 2 0 1 7 8 6 1 2 0 4 5 3 4 5 3 7 8 6 1 2 0 6 7 8 0 1 2 3 4 5 2 0 1 5 3 4 8 6 7 8 6 7 2 0 1 5 3 4 1 2 0 4 5 3 7 8 6 3 4 5 6 7 8 0 1 2 0 1 2 3 4 5 6 7 8 8 6 7 2 0 1 5 3 4 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 7 8 6 1 2 0 4 5 3 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 6 7 8 0 1 2 3 4 5 5 3 4 8 6 7 2 0 1 Кстати, только внутри этой группы программа Harry White обнаружила 29 ортогональных пар! Order? 9 Enter the name of the squares file: inp ..output file inpPairs_3.txt ..output file inpPairNos_3.txt squares 10 orthogonal pairs 29 Это список ортогональных пар, выданный программой 2: 1 3: 1 4: 1 3 5: 1 2 6: 1 2 5 7: 1 3 4 8: 1 3 4 7 9: 1 2 5 6 10: 1 2 3 4 5 6 7 8 9 Нумерация квадратов в точном соответствии их порядковому номеру в списке. Взаимно ортогональными являются квадраты №№ 1, 3, 4, 7, 8, 10. Повторю: это только внутри данной группы из 10 "перестановочных" ОДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6302 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Согласно этой таблице ортогональных пар в моей группе "перестановочных" ОДЛК, показанной выше, нарисовала конфигурацию 2: 1 3: 1 4: 1 3 5: 1 2 6: 1 2 5 7: 1 3 4 8: 1 3 4 7 9: 1 2 5 6 10: 1 2 3 4 5 6 7 8 9 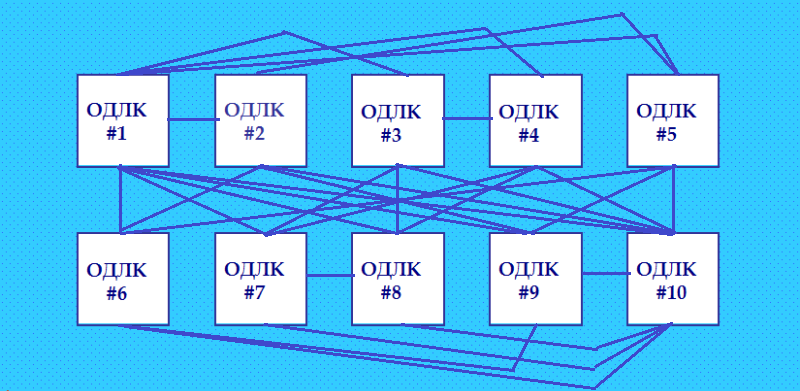 29 орогональных пар должны насчитать, я соединила все квадраты, которые между собой ортогональны. Вот такая замкнутая в себе группа из 10 ОДЛК, которые образовали 29 ортогональных пар. А теперь выходим наружу - за пределы этой группы. И тут уже вручную ничего невозможно нарисовать. Первый же ОДЛК группы имеет 516 ортогональных диагональных соквадратов. Тут, конечно, нужна программа-рисовальщик. Такой должна быть конфигурация, порождаемая этими 10 "перестановочными" ОДЛК, в моём понимании. Что представили в проекте Rake Search, я не понимаю. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6303 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14339 Credit: 0 RAC: 0 |
Никто не нарисовал картинку :) Ладно, будем воображать её мысленно, у кого богатое воображение. Мы с черепашкой продолжаем поиск новых КФ ОДЛК. Черепашке нужны хорошие алгоритмы. Ну, алгоритмов постобработки можно придумать десятки и даже сотни. Я это уже отмечала, когда писала об алгоритмах постобработки ОДЛК 10-го порядка. У меня их куча уже есть для ОДЛК 10-го порядка. Всеми пользуюсь. Для ОДЛК порядка 9 написала вчера вариант шахматного алгоритма. Это дало небольшое прибавление. БД подросла до 38361 КФ ОДЛК (+455). [А вариантов шахматного алгоритма можно десятки написать. И каждый будет работать и давать добавление, хотя и не сильно большое.] Теперь пишу следующую программу постобработки; ничего не надо придумывать, взяла последний алгоритм постобработки для ОДЛК 10-го порядка и переписываю его для ОДЛК порядка 9. Завтра допишу программу и посмотрю на результаты, которые даст этот алгоритм. Придумала хитрый ход - как увидеть все новые группы пар ОДЛК. Это прекрасно делает программа Harry White GetOrthogonal. Небольшие группы ОДЛК эта программа быстренько проверяет на ортогональные пары и выводит статистику. Выше показан пример работы этой программы. Конечно, проверить всю имеющуюся БД этой программой довольно долго будет (потому что слишком много ОДЛК). А вот для небольших групп ОДЛК (для новых добавлений) замечательно программа работает. В общем, инструментарий у меня огромный, спасибо Белышеву и Harry White! Ну и мне тоже спасибо :) А главное - спасибо черепашке!! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg ID: 6306 · Rating: 0 · rate:
/ |
©2024 (C) Progger