Возвращаюсь к фрагменту спектра.

Посмотрим на оранжевые квадратики в нижней строке квадратов А и В.
Это элементы спектра с valids15

32719, 15
28639, 15

Оба они не найдены.

Смотрим на вектора совпадений этих элементов

28639
[1,1,1,0,1,1,1,1,1,1,0,1,1,1,1,1,1]
32719
[1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1]

Расстояние Хэмминга между этими элементами тоже равно 2 !

gris,
для вас есть хорошая задачка :)

Это квадрат А

 24784 24785 24786 24787 24788 24789 24790 24791 24792 24793 24794 24795 24796 24797 24798 24799
 25040 25041 25042 25043 25044 25045 25046 25047 25048 25049 25050 25051 25052 25053 25054 25055
 25296 25297 25298 25299 25300 25301 25302 25303 25304 25305 25306 25307 25308 25309 25310 25311
 25552 25553 25554 25555 25556 25557 25558 25559 25560 25561 25562 25563 25564 25565 25566 25567
 25808 25809 25810 25811 25812 25813 25814 25815 25816 25817 25818 25819 25820 25821 25822 25823
 26064 26065 26066 26067 26068 26069 26070 26071 26072 26073 26074 26075 26076 26077 26078 26079
 26320 26321 26322 26323 26324 26325 26326 26327 26328 26329 26330 26331 26332 26333 26334 26335
 26576 26577 26578 26579 26580 26581 26582 26583 26584 26585 26586 26587 26588 26589 26590 26591
 26832 26833 26834 26835 26836 26837 26838 26839 26840 26841 26842 26843 26844 26845 26846 26847
 27088 27089 27090 27091 27092 27093 27094 27095 27096 27097 27098 27099 27100 27101 27102 27103
 27344 27345 27346 27347 27348 27349 27350 27351 27352 27353 27354 27355 27356 27357 27358 27359
 27600 27601 27602 27603 27604 27605 27606 27607 27608 27609 27610 27611 27612 27613 27614 27615
 27856 27857 27858 27859 27860 27861 27862 27863 27864 27865 27866 27867 27868 27869 27870 27871
 28112 28113 28114 28115 28116 28117 28118 28119 28120 28121 28122 28123 28124 28125 28126 28127
 28368 28369 28370 28371 28372 28373 28374 28375 28376 28377 28378 28379 28380 28381 28382 28383
 28624 28625 28626 28627 28628 28629 28630 28631 28632 28633 28634 28635 28636 28637 28638 28639

Это квадрат В

 28864 28865 28866 28867 28868 28869 28870 28871 28872 28873 28874 28875 28876 28877 28878 28879
 29120 29121 29122 29123 29124 29125 29126 29127 29128 29129 29130 29131 29132 29133 29134 29135
 29376 29377 29378 29379 29380 29381 29382 29383 29384 29385 29386 29387 29388 29389 29390 29391
 29632 29633 29634 29635 29636 29637 29638 29639 29640 29641 29642 29643 29644 29645 29646 29647
 29888 29889 29890 29891 29892 29893 29894 29895 29896 29897 29898 29899 29900 29901 29902 29903
 30144 30145 30146 30147 30148 30149 30150 30151 30152 30153 30154 30155 30156 30157 30158 30159
 30400 30401 30402 30403 30404 30405 30406 30407 30408 30409 30410 30411 30412 30413 30414 30415
 30656 30657 30658 30659 30660 30661 30662 30663 30664 30665 30666 30667 30668 30669 30670 30671
 30912 30913 30914 30915 30916 30917 30918 30919 30920 30921 30922 30923 30924 30925 30926 30927
 31168 31169 31170 31171 31172 31173 31174 31175 31176 31177 31178 31179 31180 31181 31182 31183
 31424 31425 31426 31427 31428 31429 31430 31431 31432 31433 31434 31435 31436 31437 31438 31439
 31680 31681 31682 31683 31684 31685 31686 31687 31688 31689 31690 31691 31692 31693 31694 31695
 31936 31937 31938 31939 31940 31941 31942 31943 31944 31945 31946 31947 31948 31949 31950 31951
 32192 32193 32194 32195 32196 32197 32198 32199 32200 32201 32202 32203 32204 32205 32206 32207
 32448 32449 32450 32451 32452 32453 32454 32455 32456 32457 32458 32459 32460 32461 32462 32463
 32704 32705 32706 32707 32708 32709 32710 32711 32712 32713 32714 32715 32716 32717 32718 32719

Вы считали :)
Глупая шестиклассница только до 100 умеет считать :)

Посчитайте, пожалуйста, расстояние Хэмминга между соответствующими элементами этих квадратов, сообщите результаты.
Я для трёх пар соответствующих элементов посчитала расстояние Хэмминга, оно получилось равно 2 во всех трёх случаях.

Не забываем, что все соответствующие элементы квадратов А и В имеют одинаковый valids.
А valids - это количество единичек в векторе совпадений.

Ещё для наших элементов k имеем такую формулу

valids(k) = hammingweight(k) + 2,
где hammingweight(k) - расстояние Хэмминга элемента k до нуля.

Пример

k = 28639
hammingweight(k) = 13
valids(k) = 15

В новой порции приближений всего один элемент в верхней части спектра

22536
25273630156280070813397

Элемент дало это приближение

25273630156280070813397: [0, 6, 30, 36, 66, 70, 100, 136, 142, 144, 162, 172, 174, 190, 196, 204, 240]
25273630156280070813397: [0, 0, 6, 0, 0, -14, 10, 22, 22, 18, 12, 16, 0, -14, -20, -30, 0]
6

Для тех, кто ещё не знает, что означает число 6.
Это количество правильных элементов в приближении, то есть совпадающих с паттерном.

Это
[0, 0, 6, 0, 0, -14, 10, 22, 22, 18, 12, 16, 0, -14, -20, -30, 0]
у меня вектор разностей между паттерном приближения и паттерном ключевой 17-ки.
Для совпадающих элементов паттернов разности равны 0.

Чтобы получить вектор совпадений в метрике gris, надо в моём векторе разностей заменить нули на единички, а не нули на нули.
Вот вектор совпадений для рассматриваемого элемента 22536
[1,1,0,1,1,0,0,0,0,0,0,0,1,0,0,0,1]

А и Б сидели на трубе :)

Цитата из письма gris

совсем чуть чуть про эти наши забавные квадратики 16*16. Отмечу особенность таковых: если вы возьмём любой квадратик 16*16 в матрице 256*128 чисел от 0 до 32768 и квадратик, соседний по диагонали вверх и вправо, то мы увидим, что соответственные элементы квадратиков отличаются на 4080. Вторая особенность, касающаяся квадратиков А и В, состоит в том, что если взять элементы в двоичном виде, то мы увидим, что у всех элементов квадрата А в пятой позиции слева стоит 1, а в тринадцатой — 0, а у всех элементов квадрата Б в пятой позиции слева стоит 0, а в тринадцатой — 1, а все остальные элемента одинаковы. Например,
А 28624 110111111010000
Б 32704 111111111000000
То есть двоичные коды соответственных элементов отличаются ровно в двух позициях: пятой и тринадцатой. А как мы переходим от двоичных кодов квадрата Б к А: меняем в пятой позиции 1 на 0, что в десятичном виде означает вычитание 16, а в тринадцатой позиции меняем 0 на 1, что означает прибавление 4096. То есть в итоге мы просто прибавляем 4080, что по диагональному правилу означает смещение А на 16 позиций влево и 16 вниз, то есть ровно на место квадрата Б.

Ну вот имеем полное теоретическое объяснение совпадающей структуры квадратов А и В.
Понятно, что расстояние Хэмминга между любыми двумя соответствующими элементами квадратов А и В равно 2.

Сначала была картинка gris для элементов с valids=11 и valids=12, потом было моё небольшое исследование двух квадратов с одинаковой структурой, наконец, теоретическое объяснение от gris.

Ну, что скажете, господа: нужна визуализация или она совершенно бесполезна?

Кстати, смотрим внимательно на картинку полного спектра приближений к ключевой 17-ке



Тут много пар подквадратов 16х16 с одинаковой структурой!
И не только с такой структурой, как в рассмотренных мной подквадратах.
Я рассмотрела только одну пару таких подквадратов.
Эта пара подквадратов находится в квадрате 32х32 - втором слева от правого нижнего квадрата 32х32.

PS. Цитата из сообщения
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13767

Если вы посмотрите на весь спектр для valids11 и valids12 в сообщении
https://dxdy.ru/post1631393.html#p1631393
то увидите, что описанная выше закономерность с подквадратами 16х16 имеет место во всём спектре.

Конечно, теоретическое объяснение этому факту может быть найдено (не только г. Петуховым!).
Но в любом случае закономерность интересная, даже если она совсем не удивительная.

Кстати, о птичках...

Метрика, введённая gris, дала возможность применять расстояние Хэмминга.
Количество правильных элементов в приближении (что по сути и есть valids) очень хорошо увязалось с расстоянием Хэмминга элемента спектра до нуля.

Повторю формулу

valids(k) = hammingweight(k) + 2,
где hammingweight(k) - расстояние Хэмминга элемента k до нуля.

Смотрите пример в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13797

Удивительно, что ключевые 17-ки не находятся!
Мной найдено около 5000 приближений к ключевой 17-ке от приближения с 15 "дырками" до приближения с 3 "дырками".
Но до полной ключевой 17-ки. как я понимаю, мне не добраться за всю оставшуюся жизнь.

Пример приближения с 15 "дырками"
0
117920780706464625549246043

Пример приближения с 3 "дырками"
32741
17490495325553024845924787

Это приближение было неоднократно показано, например, в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13730
Лучшее из найденных мной приближений к ключевой 17-ке.

Как Врублевский умудрился найти шесть ключевых 17-ок?!
При этом он не 10 лет искал, а всего два или три месяца, только в рамках конкурса по кортежам.
Ну, понятно, что у него было очень много вычислительных ресурсов.
Однако этого мало.
Думаю, что у него ещё был какой-то очень хороший алгоритм и хорошая программная реализация, точно не на PARI/GP.

Я стараюсь делать большой разброс по диапазону.
Выше показывала географию поиска.
Ничего не помогает!
Ключевых 17-ок нет.

Новая визуализация спектра.
Это правый нижний квадрат 32х32.
Есть и полная картинка.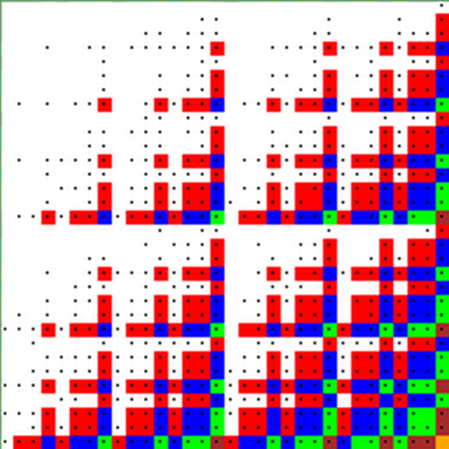



На картинке раскрашены элементы с valids13, valids14, valids15, valids16, valids17.
Элемент с valids17 единственный (32767), это оранжевый квадратик в самом нижнем правом углу картинки.
Он помечен, как найденный, потому что мы имеем приближения с valids17 (это известные ключевые 17-ки).

valids13 - красные квадратики;
valids14 - синие квадратики;
valids15 - зелёные квадратики;
valids16 - коричневые квадратики.

По-прежнему точка внутри квадратика означает, что данный элемент спектра не найден.

Исследуйте, господа!
Как много нам открытий чудных...

В правом нижнем подквадрате 16х16 мы видим один коричневый квадратик без точки.
Найден элемент с valids16?

Я не скачивала последний вариант спектра г. Петухова.
В том варианте, который я скачала, элемента с valids16 нет.

Элемент этот (с valids16) - 31743.
Скачала файл г. Петухова, там нет этого элемента.

А, поняла: gris, наверное, использовал другие результаты г. Петухова (приближения к 19-ке с минимальным диаметром).
Я их тоже использовала, и в моём спектре этот элемент есть

31743
548934853673670454695071

Вектор совпадений у этого элемента

31743

[1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1]

Да, отличное приближение!
Одна "дырка".

Это, наверное, из приближения к 19-ке с минимальным диаметром с одной "дыркой", найденного г. Петуховым.

Ну, и в этом фрагменте тоже видим два подквадрата 16х16 (правый верхний и левый нижний) с совершенно одинаковой структурой.
Назовём их, как и раньше, квадрат А и квадрат В соответственно.

Интересно посмотреть на расстояние Хэмминга между соответствующими элементами квадратов А и В.

Рассмотрим коричневые квадратики в правом нижнем углу квадратов А и В.
Это элементы с valids16, оба они не найдены.

Вот эти элементы с векторами совпадений

28671
[1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1]
32751
[1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1]

Да, расстояние Хэмминга между этими элементами равно 2 !
И разность между десятичными кодами тоже равна 4080.

Верхняя часть спектра пополнилась следующими элементами

28833
17490495418835727913718767
20145
17490495419826218328853687
29377
17490495420663426736270237
28561
17490495420191770142640407
30848
17490495419881128989159903
20896
17490495419842256220525203
26754
17490495421924520583255887
28865
17490495423958557134032117

Ещё один фрагмент вырезала из картинки полного спектра приближений к ключевой 17-ке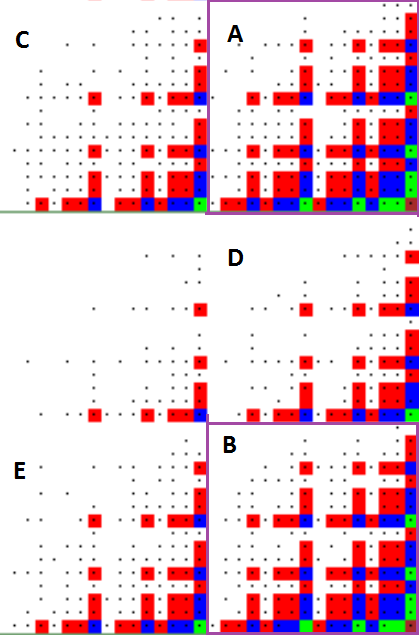



На этом фрагменте сразу три подквадрата 16х16 имеют одинаковую структуру: C, D и E.
И ещё два подквадрата 16х16 - А и В - тоже имеют одинаковую структуру (другую)

Завтра посмотрю на элементы подквадратов А и В.

Сразу бросаются в глаза два зелёных квадратика без точки в нижней строке квадрата В.
Это элементы с valids15.
Соответствующие элементы в квадрате А не найдены.

gris писал в сообщении
https://dxdy.ru/post1631958.html#p1631958

А при любой перестановке двоичных цифр valids не меняется.

<…>

Закон: От перемены мест двоичных цифр цвет квадрата не меняется!

Первое утверждение очевидно.
Второе следует из первого.

Там новый критик появился.
Он абсолютно не в теме!
Но критиковать ведь надо обязательно, даже если ни ухом, ни рылом.

Вот он пишет:

Это уже гипотеза. Не могли бы сформулировать ее в терминах простых кортежей?

https://dxdy.ru/post1631966.html#p1631966

(Это про утверждение "Закон: От перемены мест двоичных цифр цвет квадрата не меняется!")
Какая же это гипотеза?!
Ёжик рассмеялся! :)))

Теме симметричных кортежей из последовательных простых чисел пошёл десятый год.
Хоть что-нибудь из темы почитал бы этот критик!
На dxdy.ru есть ведь основная тема о кортежах, в которой даны все определения.
Надо ли влезать в новую тему, не ознакомившись с самыми основными понятиями и определениями?

Пожалуйста, дайте ему ссылку, господа, на основную тему о кортежах - "Симметричные кортежи из последовательных простых чисел".
Пусть почитает, прежде чем с умным видом влезать в тему.
А также и на этот комментарий киньте ему ссылку.

Из последней порции приближений к ключевой 17-ке нашлись такие элементы в верхней части спектра

20496
25801771909000067134303
26752
25960214434816590987677
24736
31166313216185938895778607
24772
31166313217107668815204663
20616
33171918118399282539731633
22144
33171918118409196004104313

А это из последней порции приближений от Стефана

23143893564678849298916953: [0, 6, 24, 36, 66, 76, 114, 118, 120, 126 136, 178, 184, 190, 204, 234, 240]
23143893564678849298916953: [0, 0, 0, 0, 0, -8, 24, 4, 0, 0, -14, 22 10, -14, -12, 0, 0]
9

Приближение дало элемент в верхней части спектра

30913
23143893564678849298916953

В спектре г. Петухова такой элемент тоже есть

19777735567: [0,6,24,36,66,72,84,100,120,126,132,160,172,174,204,234,240], num15=30913, valids=9

Возвращаюсь к фрагменту



Рассмотрим два зелёных квадратика в нижней строке квадратов А и В - первый слева и первый справа.
В квадрате В эти элементы найдены, а в квадрате А не найдены.
Это элементы с valids15.

Итак, первый слева зелёный квадратик в нижней строке квадрата В это элемент 24567.
Этот элемент спектра найден

24567
432021824240632917437227

Вектор совпадений для этого элемента

[1,1,0,1,1,1,1,1,1,1,1,1,0,1,1,1,1]

Соответствующий элемент в квадрате А - 16375.
Этот элемент не найден.

Вектор совпадений для этого элемента

[1,0,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1]

Расстояние Хэмминга между этими элементами равно 2.

Первый справа зелёный квадратик в нижней строке квадрата В это элемент 24574.
Этот элемент найден

24574
760217846235120764791667

Вектор совпадений для этого элемента

[1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1]

Соответствующий элемент в квадрате В - 16382.
Этот элемент не найден.

Вектор совпадений для этого элемента

[1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]

Один из очень редких элементов - центральная 13-ка!

Расстояние Хэмминга между этой парой соответствующих элементов тоже равно 2.

Может быть, закономерности вполне тривиальные, но всё равно весьма интересные.

За ночь во всех потоках найдено около 400 приближений к ключевой 17-ке!

Хорошо пополнилась верхняя часть спектра

30148
31166313217662307095971233
26247
33171918119805944529740363
24710
29160708317220507850769033
29072
29160708317165530153292617
24728
33171918119336884574266667
20708
33171918119678975802609817
29056
29160708316760703737550037
20868
29160708316707559230638933
24965
29160708316679960721816503
24971
33171918119180029049186413
22152
33171918118634339018558957
24774
33171918118490443032906553
20736
26699612888624783502497
21920
31166313217318501588722443
24773
17490495431015386156382833
24711
17490495431427076743733267
24993
17490495429348644914592923
20688
17490495428761032180819403
24740
17490495428165342121473153
28803
17490495428403686580905947
22913
27155103367072850949503657
21888
25149498465976271265974923
21656
25149498466106510203373753
25826
27155103367250109500839963
26080
27155103366801591180230773
20720
271551033668540204151594563
26768
17490495425819057392615237
27072
17490495424497567565737863
21633
17490495426492308668454093
20352
17490495426173101259137583
23168
17490495425926462782023723
29058
17490495427853257757857997
28032
17490495427256775721351487

Это вкусная десяточка :)
(10 правильных элементов)

30148
[1,1,1,1,0,1,0,1,1,1,0,0,0,1,0,0,1]

Приближение
30148
31166313217662307095971233

Приближения с 10 правильными элементами довольно часто встречаются.
Изредка встречаются приближения с 11 и 12 правильными элементами.
С 13 правильными элементами не было, насколько помню.
Найденное ранее приближение с 14 правильными элементами - крупная удача!

Цитата

Вектор совпадений для этого элемента

[1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]

Один из очень редких элементов - центральная 13-ка!

Запомним это.
Идея есть, как поискать этот редкий элемент - 16382.

Просто классная иллюстрация от gris (один из фрагментов полного спектра приближений к ключевой 17-ке)
из сообщения
https://dxdy.ru/post1631958.html#p1631958



Это правый нижний угол.
В самом уголочке фрагмента (справа внизу) видим оранжевый квадратик - элемент 32767 (единственный оранжевого цвета!)
Это полная ключевая 17-ка (valids17).

32767
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

Чтобы изобразить полный спектр приближений к ключевой 17-ке, надо 16 цветов для всех valids: 2, 3, 4, ..., 16, 17.
Наверное, будет очень красивая картина.