Итак, элементы с valids13 находятся плохо.

Вот проанализировала, что мы можем найти, исходя из центральной 11-ки.

8188
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,1]
найден
61909098512627: [0,2,6,36,66,84,90,114,120,126,150,156,174,204,212,230,240], num15=8188, valids=13
---

8189
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,0,1,1]
нет
---

8190
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
нет
---

8191
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
найден
8191
689032376626445458382311
---

16380
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1]
нет
---

16381
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1]
нет
---

24572
[1,1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,1]
нет
---

24574
[1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
найден
24574
760217846235120764791667
---

24575
[1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
нет
---

32764
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1]
нет
---

32765
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1]
нет
---

Может быть, пропустила какой-нибудь вариант.

Совсем забыла, есть ли в БД проекта Томаша 11-ки.
Оказывается, есть!
Отлично.
Можно поискать.
Не знаю, сколько их у него; мне кажется, что в какой-то момент он перестал их выводить.

Вот ссылка на первую страницу 11-ок в проекте Томаша
https://boinc.tbrada.eu/spt/tuples.php?spt=11&p=1

200000 11-ок!
Может, что-то удастся найти из наших редких элементов.

Вторая страница 11-ок тоже открылась
https://boinc.tbrada.eu/spt/tuples.php?spt=11&p=2

Это ещё 200000 11-ок!
Дальше не смотрела.

Конечно, нужно выбрать 11-ки с паттерном

0 30 48 54 78 84 90 114 120 138 168

Это подпаттерн ключевой 17-ки, а также 19-ки с минимальным диаметром.

Ещё пополнилась верхняя часть спектра приближений к ключевой 17-ке

27026
31166313221428608895896157
[1,1,1,0,1,0,0,1,1,0,0,1,0,0,1,0,1]

28809
31166313221550823699853843
[1,1,1,1,0,0,0,0,1,0,0,0,1,0,0,1,1]

24741
33171918122685581002988597
[1,1,1,0,0,0,0,0,1,0,1,0,0,1,0,1,1]

20867
29160708320431123473162953
[1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,1,1]

20483
181183381468036998707295697
[1,1,0,1,0,0,0,0,0,0,0,0,0,0,1,1,1]

20489
30226748456576834992217
[1,1,0,1,0,0,0,0,0,0,0,0,1,0,0,1,1]

28808
25149498466502970650195647
[1,1,1,1,0,0,0,0,1,0,0,0,1,0,0,0,1]

20615
23143893564377521671717523
[1,1,0,1,0,0,0,0,1,0,0,0,0,1,1,1,1]

20545
9208864767347683604524753
[1,1,0,1,0,0,0,0,0,1,0,0,0,0,0,1,1]

20546
9286835477628376553657573
[1,1,0,1,0,0,0,0,0,1,0,0,0,0,1,0,1]

28804
17490495446751150511211197
[1,1,1,1,0,0,0,0,1,0,0,0,0,1,0,0,1]

26000
17490495446497079420848367
[1,1,1,0,0,1,0,1,1,0,0,1,0,0,0,0,1]

20704
17490495449816153575000277
[1,1,0,1,0,0,0,0,1,1,1,0,0,0,0,0,1]

26804
17490495453302610627890543
[1,1,1,0,1,0,0,0,1,0,1,1,0,1,0,0,1]

Максимальный valids равен 9.

Интересно: нашлись два элемента подряд

20545
9208864767347683604524753
[1,1,0,1,0,0,0,0,0,1,0,0,0,0,0,1,1]

20546
9286835477628376553657573
[1,1,0,1,0,0,0,0,0,1,0,0,0,0,1,0,1]

Оба элемента с valids=6.
Расстояние Хэмминга между ними равно 2.

Нашла область скопления высоковалидных элементов

16300, 12
16301, 13
16302, 13
16303, 14
16304, 11
16305, 12
16306, 12
16307, 13
16308, 12
16309, 13
16310, 13
16311, 14
16312, 12
16313, 13
16314, 13
16315, 14
16316, 13
16317, 14
16318, 14
16319, 15
16320, 10
16321, 11
16322, 11
16323, 12
16324, 11
16325, 12
16326, 12
16327, 13
16328, 11
16329, 12
16330, 12
16331, 13
16332, 12
16333, 13
16334, 13
16335, 14
16336, 11
16337, 12
16338, 12
16339, 13
16340, 12
16341, 13
16342, 13
16343, 14
16344, 12
16345, 13
16346, 13
16347, 14
16348, 13
16349, 14
16350, 14
16351, 15
16352, 11
16353, 12
16354, 12
16355, 13
16356, 12
16357, 13
16358, 13
16359, 14
16360, 12
16361, 13
16362, 13
16363, 14
16364, 13
16365, 14
16366, 14
16367, 15
16368, 12
16369, 13
16370, 13
16371, 14
16372, 13
16373, 14
16374, 14
16375, 15
16376, 13
16377, 14
16378, 14
16379, 15
16380, 14
16381, 15
16382, 15
16383, 16

Найден из этого списка только один элемент - 16383.
Вот где надо потрудиться!

PS. В спектре г. Петухова найдены некоторые элементы из этого списка.
Все не проверила.

Векторы совпадений для показанных выше высоковалидных элементов (частично)

16300
[1,0,1,1,1,1,1,1,1,0,1,0,1,1,0,0,1]
16301
[1,0,1,1,1,1,1,1,1,0,1,0,1,1,0,1,1]
16302
[1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,0,1]
16303
[1,0,1,1,1,1,1,1,1,0,1,0,1,1,1,1,1]
16304
[1,0,1,1,1,1,1,1,1,0,1,1,0,0,0,0,1]
16305
[1,0,1,1,1,1,1,1,1,0,1,1,0,0,0,1,1]
16306
[1,0,1,1,1,1,1,1,1,0,1,1,0,0,1,0,1]
16307
[1,0,1,1,1,1,1,1,1,0,1,1,0,0,1,1,1]
16308
[1,0,1,1,1,1,1,1,1,0,1,1,0,1,0,0,1]
16309
[1,0,1,1,1,1,1,1,1,0,1,1,0,1,0,1,1]
16310
[1,0,1,1,1,1,1,1,1,0,1,1,0,1,1,0,1]
. . . . . . .

16374
[1,0,1,1,1,1,1,1,1,1,1,1,0,1,1,0,1]
16375
[1,0,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1]
16376
[1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1]
16377
[1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1]
16378
[1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1]
16379
[1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1]
16380
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1]
16381
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1]
16382
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
16383
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

Вернусь к двум зелёным квадратикам в квадратах А и В в фрагменте, показанном в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13844

В квадрате А зелёный квадратик с точкой, это элемент 16344, он не найден.
В квадрате В соответствующий квадратик без точки, это элемент 16360, он найден

41174702957: [0,12,24,36,66,84,90,114,120,126,150,170,174,192,194,212,240], num15=16360, valids=12

(из спектра г. Петухова).

Показываю векторы совпадений этих элементов

16344
[1,0,1,1,1,1,1,1,1,1,0,1,1,0,0,0,1]

16360
[1,0,1,1,1,1,1,1,1,1,1,0,1,0,0,0,1]

Очень мало отличаются векторы совпадений.
Расстояние Хэмминга между этими элементами равно 2.

Поскольку в последнем фрагменте два подквадрата 16х16 совершенно одинаковой структуры, я отрезала левый подквадрат и получила такой фрагмент



Провела в этом квадрате диагональ.
И наблюдаю интересную симметрию по цветам относительно этой диагонали!

Жёлтые квадратики симметричны розовым квадратикам (valids9 <--> valids13).
Синие квадратики симметричны зелёным квадратикам (valids10 <--> valids12).
Оранжевые квадратики симметричны оранжевым же квадратикам (valids11 <--> valids11).
Можно предположить, что красные квадратики симметричны элементам с valids14, они не окрашены в этом фрагменте (белые), то есть valids8 <--> valids14.

Очень интересно!
Обратите внимание на сумму valids симметричных по цветам элементов, она равна 22.

Если не ошиблась, вот матрица данного фрагмента

14432, 14433, 14434, 14435, 14436, 14437, 14438, 14439, 14440, 14441, 14442, 14443, 14444, 14445, 14446, 14447
14560, 14561, 14562, 14563, 14564, 14565, 14566, 14567, 14568, 14569, 14570, 14571, 14572, 14573, 14574, 14575
14688, 14689, 14690, 14691, 14692, 14693, 14694, 14695, 14696, 14697, 14698, 14699, 14700, 14701, 14702, 14703
14816, 14817, 14818, 14819, 14820, 14821, 14822, 14823, 14824, 14825, 14826, 14827, 14828, 14829, 14830, 14831
14944, 14945, 14946, 14947, 14948, 14949, 14950, 14951, 14952, 14953, 14954, 14955, 14956, 14957, 14958, 14959
15072, 15073, 15074, 15075, 15076, 15077, 15078, 15079, 15080, 15081, 15082, 15083, 15084, 15085, 15086, 15087
15200, 15201, 15202, 15203, 15204, 15205, 15206, 15207, 15208, 15209, 15210, 15211, 15212, 15213, 15214, 15215
15328, 15329, 15330, 15331, 15332, 15333, 15334, 15335, 15336, 15337, 15338, 15339, 15340, 15341, 15342, 15343
15456, 15457, 15458, 15459, 15460, 15461, 15462, 15463, 15464, 15465, 15466, 15467, 15468, 15469, 15470, 15471
15584, 15585, 15586, 15587, 15588, 15589, 15590, 15591, 15592, 15593, 15594, 15595, 15596, 15597, 15598, 15599
15712, 15713, 15714, 15715, 15716, 15717, 15718, 15719, 15720, 15721, 15722, 15723, 15724, 15725, 15726, 15727
15840, 15841, 15842, 15843, 15844, 15845, 15846, 15847, 15848, 15849, 15850, 15851, 15852, 15853, 15854, 15855
15968, 15969, 15970, 15971, 15972, 15973, 15974, 15975, 15976, 15977, 15978, 15979, 15980, 15981, 15982, 15983
16096, 16097, 16098, 16099, 16100, 16101, 16102, 16103, 16104, 16105, 16106, 16107, 16108, 16109, 16110, 16111
16224, 16225, 16226, 16227, 16228, 16229, 16230, 16231, 16232, 16233, 16234, 16235, 16236, 16237, 16238, 16239
16352, 16353, 16354, 16355, 16356, 16357, 16358, 16359, 16360, 16361, 16362, 16363, 16364, 16365, 16366, 16367

Сейчас проверю верхнюю строку.

14432, 7
14433, 8
14434, 8
14435, 9
14436, 8
14437, 9
14438, 9
14439, 10
14440, 8
14441, 9
14442, 9
14443, 10
14444, 9
14445, 10
14446, 10
14447, 11

Всё соответствует раскраске.

Ну, теперь у нас есть все элементы, можно анализировать.
Особенно интересна симметрия цветов относительно диагонали квадрата.
Надо посмотреть на симметричные элементы.

О!
Центральные 11-ки у gris пошли в проверку на вхождение в ключевую 17-ку.
Цитирую его письмо

На второй и третьей странице ничего нет
На четвёртой
}
111833871030817847 [1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1]
386 120-138-168 vectors

Нашёлся элемент с valids=14.
Отлично!

А элемент найден такой
8190
111833871030817847
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1]

Сейчас разверну его для проверки.

Готово!

{111833871030817847, *111833871030817849, *111833871030817879, 111833871030817883,
111833871030817913, 111833871030817931, 111833871030817937, 111833871030817961,
111833871030817967, 111833871030817973, 111833871030817997, 111833871030818003,
111833871030818021, 111833871030818051, 111833871030818063, *111833871030818071,
111833871030818087}

На 46-й странице 11-ок (последней) найдено такое приближение к ключевой 17-ке

2120657254193816473 [1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1]

Такой элемент уже есть в спектре г. Петухова

8188
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,1]
найден
61909098512627: [0,2,6,36,66,84,90,114,120,126,150,156,174,204,212,230,240], num15=8188, valids=13

То есть теперь этот элемент имеет два приближения

8188
(61909098512627, 2120657254193816473)

Эх, жаль, что Томаш прервал вывод 11-ок.
Может быть, ещё что-нибудь нашлось бы.

PS. Э-э-э...
gris все 46 страниц 11-ок не проверил.
Ну, может быть, я сама проверю (по его программе), если будет время.

Г. Петухов писал в сообщении
https://dxdy.ru/post1632544.html#p1632544

А эти нашёл среди данных боинка:
1554944739656527: [0, 4, 16, 46, 66, 84, 90, 114, 120, 126, 150, 156, 174, 186, 204, 234, 240], num15=4089, valids=12
3692939714570017: [0, 4, 36, 46, 66, 84, 90, 114, 120, 126, 150, 156, 174, 192, 216, 234, 240], num15=4091, valids=13
4066905498223787: [0, 14, 24, 60, 66, 84, 90, 114, 120, 126, 150, 156, 174, 200, 216, 230, 240], num15=12282, valids=13
5787548433002737: [0, 10, 22, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 192, 220, 232, 240], num15=8184, valids=12
7184298747301217: [0, 6, 24, 62, 66, 84, 90, 114, 120, 126, 150, 156, 174, 194, 222, 224, 240], num15=28664, valids=13
7849758790696217: [0, 6, 14, 42, 66, 84, 90, 114, 120, 126, 150, 156, 174, 176, 204, 234, 240], num15=20473, valids=13
9297384447350933: [0, 14, 24, 26, 66, 84, 90, 114, 120, 126, 150, 156, 174, 224, 230, 234, 240], num15=12281, valids=13
111833871030817847: [0, 2, 32, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 224, 240], num15=8190, valids=14
3241648437603927893: [0, 14, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 234, 240], num15=16383, valids=16

Вставила векторы совпадений, чтобы видеть, какие кортежи использовались при поиске

1554944739656527: [0, 4, 16, 46, 66, 84, 90, 114, 120, 126, 150, 156, 174, 186, 204, 234, 240], num15=4089, valids=12
[1,0,0,0,1,1,1,1,1,1,1,1,1,0,0,1,1]
3692939714570017: [0, 4, 36, 46, 66, 84, 90, 114, 120, 126, 150, 156, 174, 192, 216, 234, 240], num15=4091, valids=13
[1,0,0,0,1,1,1,1,1,1,1,1,1,0,1,1,1]
4066905498223787: [0, 14, 24, 60, 66, 84, 90, 114, 120, 126, 150, 156, 174, 200, 216, 230, 240], num15=12282, valids=13
[1,0,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1]
5787548433002737: [0, 10, 22, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 192, 220, 232, 240], num15=8184, valids=12
[1,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1]
7184298747301217: [0, 6, 24, 62, 66, 84, 90, 114, 120, 126, 150, 156, 174, 194, 222, 224, 240], num15=28664, valids=13
[1,1,1,0,1,1,1,1,1,1,1,1,1,0,0,0,1]
7849758790696217: [0, 6, 14, 42, 66, 84, 90, 114, 120, 126, 150, 156, 174, 176, 204, 234, 240], num15=20473, valids=13
[1,1,0,0,1,1,1,1,1,1,1,1,1,0,0,1,1]
9297384447350933: [0, 14, 24, 26, 66, 84, 90, 114, 120, 126, 150, 156, 174, 224, 230, 234, 240], num15=12281, valids=13
[1,0,1,0,1,1,1,1,1,1,1,1,1,0,0,1,1]
111833871030817847: [0, 2, 32, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 224, 240], num15=8190, valids=14
[1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1]
3241648437603927893: [0, 14, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 234, 240], num15=16383, valids=16
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

Всё понятно.

По последнему приближению было
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13825

По предпоследнему приближению было
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13854

Остальные не проверяла.

Вот теперь не знаю, проверять ли мне 46 страниц 11-ок с проекта Томаша, или г. Петухов их все уже проверил.
Не мешало бы указать, какие именно кортежи "среди данных боинка" использовались при поиске.
По векторам совпадений видно, что использовались и 9-ки, и 11-ки, и 13-ки.

Новое пополнение верхней части спектра приближений к ключевой 17-ке

20674
17490495447505016212888153
[1,1,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1]

24753
29160708321600191173247237
[1,1,1,0,0,0,0,0,1,0,1,1,0,0,0,1,1]

26241
33171918124770254722973453
[1,1,1,0,0,1,1,0,1,0,0,0,0,0,0,1,1]

20870
31166313223924925835008153
[1,1,0,1,0,0,0,1,1,0,0,0,0,1,1,0,1]

28849
33171918125428371796820987
[1,1,1,1,0,0,0,0,1,0,1,1,0,0,0,1,1]

Вот вкусная 11-ка найдена (11 правильных элементов, valids=11)

17490495459311140013558183: [0, 6, 8, 36, 48, 74, 104, 114, 120, 126, 150, 156, 174, 228, 230, 234, 240]
17490495459311140013558183: [0, 0, -16, 0, -18, -10, 14, 0, 0, 0, 0, 0, 0, 24, 14, 0, 0]
11

20985
17490495459311140013558183

Этот элемент в спектре г. Петухова

2285925426487: [0,6,22,36,40,70,106,114,120,126,150,156,174,184,204,234,240], num15=20985, valids=11

Таким образом, этот элемент имеет уже два приближения

20985
(2285925426487, 17490495459311140013558183)

Явно к редким элементам не относится.

PS. Приближения с 11 правильными элементами у меня редко появляются.
Ещё реже с бОльшим количеством правильных элементов (12 - 16).
Максимум был - 14 правильных элементов.

Это исследуемый фрагмент спектра приближений к ключевой 17-ке



А это матрица данного фрагмента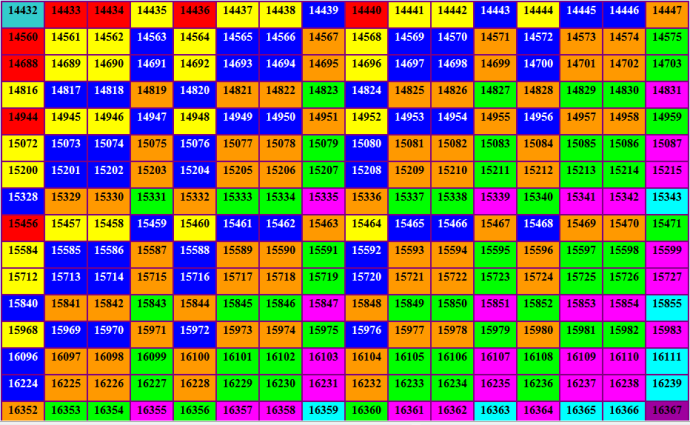



Красивый магический квадрат? :)

В матрице я раскрасила все квадратики, которые были белыми в спектре.
Верхний левый угловой квадратик - это элемент с valids=7; правый нижний угловой квадратик - это элемент с valids=15.
И опять сумма valids симметричных относительно показанной диагонали квадрата элементов равна 22.
Да, красным квадратикам (valids=8) симметричны бирюзовые квадратики (valids=14), как я и предполагала.
И снова та же сумма valids!

Итак, первая пара симметричных относительно диагонали квадрата элементов с векторами совпадений

14432 (valids=7)
[1,0,1,1,1,0,0,0,0,1,1,0,0,0,0,0,1]

16367 (valids=15)
[1,0,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1]

Пока вижу только то, что расстояние Хэмминга между этими элементами равно 8.

Вот проанализировала четыре пары симметричных квадратиков - синих (valids=10) и зелёных (valids=12)

14563
[1,0,1,1,1,0,0,0,1,1,1,0,0,0,1,1,1]
15982
[1,0,1,1,1,1,1,0,0,1,1,0,1,1,1,0,1]

14691
[1,0,1,1,1,0,0,1,0,1,1,0,0,0,1,1,1]
15982
[1,0,1,1,1,1,1,0,0,1,1,0,1,1,1,0,1]

14817
[1,0,1,1,1,0,0,1,1,1,1,0,0,0,0,1,1]
16236
[1,0,1,1,1,1,1,1,0,1,1,0,1,1,0,0,1]

14718
[1,0,1,1,1,0,0,1,0,1,1,1,1,1,1,0,1]
16108
[1,0,1,1,1,1,1,0,1,1,1,0,1,1,0,0,1]

Пока вижу только то, что расстояние Хэмминга между симметричными элементами данной группы равно 6 во всех показанных примерах.

Очень вкусная десяточка нашлась (десять правильных элементов)

17490495455037222595877573: [0, 6, 24, 36, 104, 108, 114, 116, 120, 126, 150, 164, 186, 204, 216, 218, 240]
17490495455037222595877573: [0, 0, 0, 0, 38, 24, 24, 2, 0, 0, 0, 8, 12, 0, 0, -16, 0]
10

28902
17490495455037222595877573
[1,1,1,1,0,0,0,0,1,1,1,0,0,1,1,0,1]

Для моего спектра уникальный элемент.

В спектре г. Петухова имеется

353175855937: [0,6,24,36,46,66,100,112,120,126,150,186,190,204,216,220,240], num15=28902, valids=10

Таким образом, элемент не является редким, уже имеет два приближения

28902
(353175855937, 17490495455037222595877573)

Очередное пополнение верхней части спектра приближений к ключевой 17-ке

20632
17490495455917686562029757
[1,1,0,1,0,0,0,0,1,0,0,1,1,0,0,0,1]

21665
17490495457773199202574907
[1,1,0,1,0,1,0,0,1,0,1,0,0,0,0,1,1]

25797
17490495457449789375460793
[1,1,1,0,0,1,0,0,1,1,0,0,0,1,0,1,1]

20679
17490495459411057580048093
[1,1,0,1,0,0,0,0,1,1,0,0,0,1,1,1,1]

20869
17490495458940423386973593
[1,1,0,1,0,0,0,1,1,0,0,0,0,1,0,1,1]

20680
17490495460044432165125327
[1,1,0,1,0,0,0,0,1,1,0,0,1,0,0,0,1]

29376
17490495455199441365158687
[1,1,1,1,0,0,1,0,1,1,0,0,0,0,0,0,1]

28813
17490495454628946237113713
[1,1,1,1,0,0,0,0,1,0,0,0,1,1,0,1,1]

24770
17490495455039134604405717
[1,1,1,0,0,0,0,0,1,1,0,0,0,0,1,0,1]

28902
17490495455037222595877573
[1,1,1,1,0,0,0,0,1,1,1,0,0,1,1,0,1]

20163
31166313224221352821103287
[1,1,0,0,1,1,1,0,1,1,0,0,0,0,1,1,1]

22977
33171918125479096989946007
[1,1,0,1,1,0,0,1,1,1,0,0,0,0,0,1,1]

29345
29160708323520852983124307
[1,1,1,1,0,0,1,0,1,0,1,0,0,0,0,1,1]

22709
33171918126224804636563787
[1,1,0,1,1,0,0,0,1,0,1,1,0,1,0,1,1]

22667
31166313225067922727128977
[1,1,0,1,1,0,0,0,1,0,0,0,1,0,1,1,1]

20681
33171918126626732412379793
[1,1,0,1,1,0,0,0,1,0,0,1,1,0,0,1,1]

Много элементов с valids=9, только один элемент с valids=10, он был показан в предыдущем сообщении.

В спектре г. Петухова элементы с valids=9 найдены все, элементы с valids=10 найдены не все, кажется, нет 167 шт.

Загрузила спектр приближений к ключевой 17-ке на Яндекс.Диск
https://disk.yandex.ru/d/CzIzf3xW2JORpA
115 КБ.

В файле после строки
1111111111111111111111111111111
следует первая часть, которую я временно открепила.
В этой части элементы отсортированы в порядке возрастания; кроме того, для каждого элемента выписаны все найденные приближения.
Так заполнять спектр очень трудно.
Поэтому прекратила эту часть.

В новой (текущей) части элементы не отсортированы и приближения для одного элемента не выписываются.

Две части спектра пересекаются!

В обеих частях содержится примерно 1500 уникальных элементов.
Всего приближений к ключевой 17-ке найдено около 10000.
Как видим, очень много приближений имеют одинаковый десятичный код (по метрике gris).

Ой, в теме "кортежи последовательных простых. ключ к 19-252" захватывающая дух дискуссия! :))

Ядряра пишет за всех

Мы в курсе.

https://dxdy.ru/post1632633.html#p1632633

Г. Петухов горячится

Это я погорячился, рост далеко не линейный, а примерно как корень (например до 1e12 их не 40млн, а всего 13.8млн), так что до 1e15 количество будет порядка 400млн.

https://dxdy.ru/post1632643.html#p1632643

vicvolf вообще чёрт знает о чём пишет

Если Вы под цепочкой понимаете бесконечную последовательностей простых кортежей определенного вида, то это неверно для простых близнецов.

https://dxdy.ru/post1632638.html#p1632638

Автор темы благоразумно помалкивает.

vicvolf писал в сообщении
https://dxdy.ru/post1632638.html#p1632638

Если Вы под цепочкой понимаете бесконечную последовательностей простых кортежей определенного вида, то это неверно для простых близнецов.

Г. Петухов писал в сообщении
https://dxdy.ru/post1632643.html#p1632643

vicvolf
Повторю, нас интересуют симметричные цепочки нечётной длины и именно про них я и говорил (и это чётко указано в изначальном моём сообщении), а таковые могут быть только на одной (но любой) последовательности 6n+/-1.

Ну вот, чёрт те чё

...под цепочкой понимаете бесконечную последовательностей простых кортежей определенного вида...

Может, наконец, г. Петухов перестанет лепить свои "цепочки" и будет называть кортежи кортежами?!

Упёртость зашкаливает!

Возвращаюсь к визуализации спектра приближений к ключевой 17-ке, смотрите сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13862

Давайте посмотрим на диагональные элементы, которые все оранжевые, то есть с valids=11:

14447
14574
14701
14828
14955
15082
15209
15336
15463
15590
15717
15844
15971
16098
16225
16352

Разность между любыми соседними элементами равна 127.
Сейчас вставлю сюда векторы совпадений.