Задача века
Message boards :
Cafe :
Задача века
Message board moderation
Previous · 1 . . . 6 · 7 · 8 · 9 · 10 · 11 · 12 . . . 13 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё с q=17 [0, 4, 6, 10, 48, 54, 60, 64, 108, 126, 130, 174, 246, 250, 270, 276, 294, 330,396, 490, 496, 516, 550, 616, 736] 6565135591116793: [0, 6, 48, 64, 108, 174, 196, 246, 250, 270, 276, 280, 286, 316, 330, 340, 360, 396, 424, 490, 516, 550, 564, 616, 736] q=17 Опять популярный диаметр 736. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Репост https://mathhelpplanet.com/viewtopic.php?p=485515#p485515 "Nataly-Mak" wrote: Уважаемые коллеги! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Да, выше показано, как я реализовала генерацию простых чисел генератором primesieve. Это очень круто! Генерирую простые числа сразу на интервале 50 миллионов (натуральных чисел). Это генерируется за 2-3 секунды. [Напомню: Белышев в свой программе для поиска кортежей генерировал этим генератором на интервале 2 миллиарда (натуральных чисел).] А вот проверка на построение квадрата Стенли пока реализована хорошо на Бейсике - практически мгновенно проверяется. Никаких предпроверок! Сразу проверяется заданный набор из 25 чисел и выдаётся квадрат Стенли, если его возможно построить из этих чисел. Что-то мне запомнилось из последнего сообщения г. Петухова, которое я комментировала, что он искал с довольно медленным генератором простых чисел. А зачем искать с медленным генератором, когда есть очень быстрый?! Надо только написать хорошую программу проверки на построение квадрата Стенли, чтобы она выполнялось мгновенно, как моя программа на Бейсике выполняется. Ответ программы чёткий: есть квадрат либо его нет. Без всяких "дырок"! Я тоже писала выше программу предпроверки на PARI/GP. Не надо никаких предпроверок! Сразу надо строить квадрат Стенли полностью; он либо строится, либо нет, третьего не дано. gris, ау! Вы вернулись из страны коз и енотов? Тут вот задачка для вас очень хорошая :) Подключайтесь, пожалуйста. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё с q=17 [0, 2, 18, 20, 30, 48, 96, 98, 126, 140, 158, 170, 188, 236, 266, 528, 530, 558, 576, 578, 606, 668, 698, 716, 746] 74877540253070981: [0, 2, 18, 20, 48, 96, 98, 138, 158, 170, 200, 236, 258, 312, 326, 342, 528, 530, 576, 590, 606, 668, 716, 726, 746] q=17 [0, 4, 6, 10, 48, 54, 60, 64, 108, 126, 130, 174, 246, 250, 270, 276, 294, 330,396, 490, 496, 516, 550, 616, 736] 8274318181728163: [0, 10, 48, 60, 64, 108, 130, 180, 190, 210, 244, 246, 250, 270, 276, 318, 330, 346, 396, 496, 516, 550, 588, 606, 736] q=17 Для паттерна с диаметром 746, кажется, не проверяла построение квадрата Стенли. Вот проверила 0 170 2 30 140 96 266 98 126 236 18 188 20 48 158 528 698 530 558 668 576 746 578 606 716 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
[0, 2, 12, 14, 30, 42, 60, 62, 90, 102, 104, 132, 134, 146, 194, 236, 260, 272, 320, 362, 480, 482, 510, 614, 740] 7247010896985227: [0, 2, 12, 42, 60, 90, 92, 96, 134, 194, 236, 272, 320, 350, 372, 480, 482, 510, 536, 552, 554, 572, 614, 686, 740] q=16 Этот паттерн, кажется, не проверяла на построение квадрата Стенли. Вот 0 2 30 134 260 12 14 42 146 272 60 62 90 194 320 102 104 132 236 362 480 482 510 614 740 У следующего приближения довольно большой диаметр паттерна [0, 6, 14, 20, 30, 44, 68, 74, 98, 168, 174, 180, 194, 198, 224, 230, 248, 254, 348, 404, 660, 674, 728, 828, 884] 75888530480384243: [0, 20, 74, 96, 98, 116, 146, 156, 168, 174, 194, 198, 224, 248, 254, 276, 290, 300, 348, 380, 584, 660, 728, 828, 884] q=16 Проверила на построение квадрата Стенли 0 6 30 180 660 14 20 44 194 674 68 74 98 248 728 168 174 198 348 828 224 230 254 404 884 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё приближение с q=17 [0, 4, 36, 40, 64, 66, 70, 100, 130, 144, 180, 210, 252, 256, 270, 274, 294, 316, 330, 334, 360, 396, 414, 546, 564] 9788606755429027: [0, 36, 40, 42, 66, 70, 100, 130, 136, 180, 210, 252, 294, 316, 330, 334, 360, 364, 406, 474, 480, 502, 544, 546, 564] q=17 Паттерн с диаметром 564 даёт много приближений. Не помню, проверяла ли я его на построение квадрата Сиенли. Ещё раз проверю. Квадрат Стенли построился 0 4 64 144 294 36 40 100 180 330 66 70 130 210 360 252 256 316 396 546 270 274 334 414 564 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ой, вспомнила о проверке паттерна на допустимость. Паттерн, который я получила из неверного квадрата Стенли г. Петухова (исправив его), оказался недопустимым 0, 30, 72, 130, 132, 160, 202, 210, 244, 262, 270, 274, 300, 316, 340, 342, 376, 402, 420, 450, 454, 480, 492, 552, 630 Выбрасываю его из списка теоретических паттернов для квадрата Стенли. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё два приближения с 8 "дырками" [0, 4, 36, 40, 64, 66, 70, 100, 130, 144, 180, 210, 252, 256, 270, 274, 294, 316, 330, 334, 360, 396, 414, 546, 564] 13030833244998787: [0, 4, 30, 52, 64, 70, 100, 130, 150, 210, 252, 256, 270, 294, 316, 322, 334, 352, 396, 414, 436, 444, 466, 546, 564] q=17 [0, 6, 20, 26, 48, 68, 92, 98, 102, 108, 140, 150, 186, 206, 216, 236, 278, 288, 308, 318, 440, 446, 488, 626, 656] 12189413143097321: [0, 6, 20, 48, 62, 66, 68, 92, 102, 108, 140, 186, 278, 288,318, 336, 372, 440, 476, 488, 500, 522, 612, 626, 656] q=17 Паттерн с диаметром 656 вроде не проверяла на построение квадрата Стенли. Вот 0 6 48 186 216 20 26 68 206 236 92 98 140 278 308 102 108 150 288 318 440 446 488 626 656 Кстати, счёт превысил 1е16. Замечу ещё раз: данный алгоритм поиска по паттерну не является брутфорсом. Понятно, что проверка всего нескольких паттернов даёт малую толику результатов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ой. вчера смотрела программу проверки на построение квадрата Стенли из набора, состоящего из 25 чисел, которая у меня написана давным-давно на Бейсике. Немножко модифицировала программу, убрала запрос на ввод индекса квадрата Стенли, он считается в программе. Ещё кое-что изменила, квадрат Стенли сейчас более красивым выводится. Итак, вот начало списка теоретических паттернов для квадратов Стенли (которые мне известны, здесь нет четырёх паттернов с минимальным диаметром 156, которые нашёл Andersen), паттерны отсортированы по диаметру 0, 12, 30, 36, 42, 54, 64, 66, 76, 84, 90, 94, 96, 100, 106, 120, 124, 132, 136, 150, 154, 156, 160, 162, 166 0, 4, 18, 22, 48, 52, 60, 64, 70, 78, 82, 84, 88, 90, 102, 108, 118, 130, 132, 138, 144, 148, 150, 162, 168 0, 12, 30, 36, 42, 46, 58, 60, 72, 76, 82, 88, 90, 96, 102, 126, 130, 138, 142, 156, 160, 162, 166, 168, 172 0, 6, 10, 16, 30, 66, 72, 76, 82, 84, 90, 94, 96, 100, 114, 126, 132, 136, 142, 144, 150, 154, 156, 160, 174 0, 10, 24, 34, 48, 60, 66, 70, 76, 84, 90, 94, 100, 108, 114, 120, 126, 130, 136, 144, 150, 154, 160, 168, 174 0, 20, 30, 36, 38, 48, 56, 60, 66, 74, 80, 84, 90, 98, 108, 120, 126, 140, 146, 150, 156, 158, 164, 168, 174 0, 6, 18, 24, 28, 30, 34, 40, 46, 48, 54, 58, 60, 70, 84, 96, 114, 124, 126, 136, 144, 150, 154, 166, 180 . . . . . . В программу паттерн вводится без запятых, вот так 0 12 30 36 42 54 64 66 76 84 90 94 96 100 106 120 124 132 136 150 154 156 160 162 166 Вводится всего один паттерн. Проверка выполняется примерно 3-4 секунды. Тут ещё можно оптимизировать, сейчас программа выводит все варианты квадрата Стенли, то есть переставляет в квадрате строки и столбцы, это совсем не нужно делать, нам достаточно получить один вариант квадрата. Тогда проверка будет выполняться практически мгновенно. Вот квадрат Стенли для первого паттерна 0 12 30 36 42 54 66 84 90 96 64 76 94 100 106 120 132 150 156 162 124 136 154 160 166 Разумеется, надо ещё сделать, чтобы паттерны проверялись сразу все, а не по одному. Для всех 55 известных мне теоретических паттернов квадрат Стенли должен строиться, если не ошиблась. В общем, вспомнила старый добрый Бейсик :) Много программ я на нём написала и много результатов нашла - в магических квадратах, в магических кубах и даже в тессерактах третьего порядка, а также в ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А теперь смотрим репост https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=15117 Паттерны для 25-к из последовательных простых чисел получаются за несколько секунд с помощью генератора primesieve (порционально, конечно). Дальше надо эти паттерны проверять на построение квадрата Стенли. Это будет брутфорс. Кстати, есть программа Белышева, тоже брутфорс. К сожалению, не сохранился код. Я эту программу немножко крутила. Плохо то, что она ничего не выводит, работает молча. Что она там находит, что проверяет, - не видно. Зато есть чекпоинт, это очень хорошо. Я эту программу выше выложила. Думаю, что у Алексея такой алгоритм и есть, как я описала: генерация паттернов 25-к из последовательных простых чисел с последующей проверкой на построение квадрата Стенли. Эх, куда же пропал Алексей? :( А что там у Progger было? Progger, ау! Не хотите ли порешать задачу века? :) Вы ведь начинали! Это было больше 10 лет назад. А задача-то не решена. Пожалуйста, напишите что-нибудь, вы совсем форум забросили. Я прямо жутко соскучилась :) Макс Алексеев тоже начинал и... бросил. Неизвестно, докуда он досчитал. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
О! Порывшись в архивах программ на Бейсике нашла программу построения примитивного квадрата 5-го порядка из 25 заданных чисел. Кто не в курсе, примитивный квадрат = антимагический квадрат Стенли. Эта программа практически мгновенно строит квадрат Стенли, если это возможно, и выводит, "Решение не найдено", если квадрат построить невозможно. Для первого паттерна в моём списке теоретических паттернов программа выдала квадрат Стенли в таком виде 0 12 30 36 42 54 66 84 90 96 64 76 94 100 106 120 132 150 156 162 124 136 154 160 166 482 За квадратом следует его индекс. Квадрат выведен в строку, решение полностью совпадает с приведённым выше, покажу его 0 12 30 36 42 54 66 84 90 96 64 76 94 100 106 120 132 150 156 162 124 136 154 160 166 Отличная программулька! Только надо сделать, чтобы она проверяла сразу несколько наборов из 25 чисел. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
С q=16 , паттерн с довольно большим диаметром [0, 48, 86, 114, 134, 140, 188, 200, 204, 254, 260, 290, 308, 330, 344, 374, 378, 444, 464, 468, 534, 554, 608, 728, 798] 78501247032943373: [0, 48, 56, 66, 84, 114, 134, 140, 144, 146, 188, 200, 204, 290, 330, 344, 350, 374, 386, 408, 444, 534, 554, 668, 798] q=16 Сейчас проверю этот паттерн программулькой, которую только что раскопала в архиве. Вот, готов квадрат Стенли 0 48 114 204 468 86 134 200 290 554 140 188 254 344 608 260 308 374 464 728 330 378 444 534 798 1650 Индекс квадрата Стенли S=1650. Глазом не успела моргнуть :) Запишу квадрат Стенли в привычном виде 0 48 114 204 468 86 134 200 290 554 140 188 254 344 608 260 308 374 464 728 330 378 444 534 798 Всё замечательно! Кто не в курсе: квадрат Стенли не магический, он антимагический. Зато сумма чисел во всех диагоналях квадрата Стенли (главных и разломанных) равна индексу квадрата. Проверьте! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Заглянула на Ахиллесе-3 в папку, где считала давно по программе Белышева. В файле start.txt записана конечная точка, до которой было посчитано: 1026075545933699. Замечательно! Запустила дальше считать. Пусть считает в один поток. Это бесконечная программа, даже без кавычек. Но огромное преимущество её в том, что при любом прерывании конечная точка проверенного интервала сохраняется. Таким образом, никакое прерывание не страшно. Вот что сейчас в консоли Поиск антимага Стенли 5-го порядка 0:06:18 Текущий интервал: [1026083545930482 ... 1026085545930482] Проверено: 1235%% Скорость: 79 Всего: 57856791 Подходящих: 11571656 Я понимаю так: всего сгенерировано в порции 57856791 паттернов для 25-к из последовательных простых чисел, из них 11571656 подходящих для построения квадрата Стенли, то есть, например, выполняется необходимое условие для суммы чисел в паттерне (эта сумма должна быть кратна 5). Наверное, Алексей по-прежнему генерирует простые числа генератором primesieve в интервале 2 миллиарда (натуральных чисел). Генерация простых чисел мгновенная, проверка на построение квадрат Стенли тоже довольно быстрая. Так что, программа есть, ничего не надо придумывать заново, изобретать велосипед. Конечно, можно придумать другой алгоритм (не брутфорс). Ну, я вот придумала поиск по паттерну. Г. Петухов свой вердикт вынес: искать по паттерну бессмысленно. Ну пусть найдёт, что не бессмысленно! Как уже сказано, программа Белышева выложена. Все желающие берите и считайте. Только желательно сообщить, что считаете, чтобы не считать один и тот же диапазон. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё раз подчеркну: как и в случае с симметричной 19-й из последовательных простых чисел, задача разбивается на две подзадачи: а) поиск минимального пандиагонального квадрата 5-го порядка из последовательных простых чисел; б) поиск пандиагонального квадрата 5-го порядка из последовательных простых чисел, построенного из кортежа с минимальным диаметром 156. Как мы знаем, для 19-ки первая подзадача решена. А вот найти 19-ку с минимальным диаметром 252 пока не удалось. Точно так же для пандиагонального квадрата 5-го порядка - первая подзадача вполне реально решаема, по моему мнению. Со второй подзадачей гораздо сложнее. Andersen писал на форуме dxdy.ru, что до 10^20 решения по паттернам с минимальным диаметром 156 точно нет. Просто серьёзно ещё никто задачу не решал. Так, по чуть-чуть попробовали, не получается наскоком, и бросили. PS. Поясню для тех, кто не в теме, что значит минимальный пандиагональный квадрат 5-го порядка из последовательных простых чисел. Это значит, что квадрат составлен из минимально возможных 25 последовательных простых чисел; он будет иметь минимальную магическую константу. Диаметр кортежа, из которого он будет построен, может быть любым. Ну, вот для примера минимальный пандиагональный квадрат 4-го порядка из последовательных простых чисел, найденныё Максом Алексеевым  |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
С q=16, довольно маленький диаметр паттерна [0, 2, 6, 8, 12, 18, 30, 36, 48, 50, 60, 78, 90, 92, 102, 120, 126, 128, 138, 156, 252, 258, 300, 342, 378] 79525881013977521: [0, 2, 6, 8, 12, 18, 30, 60, 68, 90, 92, 102, 128, 198, 216, 230, 258, 272, 288, 300, 312, 320, 330, 342, 378] q=16 Редко находятся приближения для этого паттерна. Квадратик Стенли для этого паттерна сейчас покажу. Готов! 0 2 12 30 252 6 8 18 36 258 48 50 60 78 300 90 92 102 120 342 126 128 138 156 378 566 В привычном виде 0 2 12 30 252 6 8 18 36 258 48 50 60 78 300 90 92 102 120 342 126 128 138 156 378 Индекс S=566 Может встретиться кортеж из 25 последовательных простых чисел с таким паттерном? А почему нет? Паттерн допустимый. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Эх, люблю я квадраты рисовать! :) Вот квадрат Стенли с 9 "дырками" из примера, показанного выше 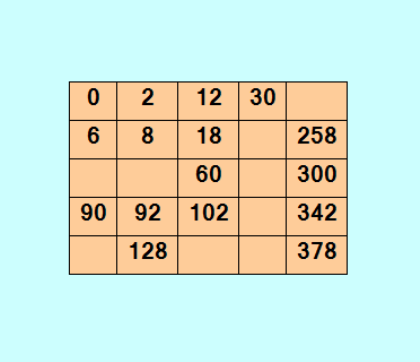 Квадрат построен из чисел кортежа 79525881013977521: [0, 2, 6, 8, 12, 18, 30, 60, 68, 90, 92, 102, 128, 198, 216, 230, 258, 272, 288, 300, 312, 320, 330, 342, 378] Да, конечно, сильно дырявый. Ну, будет и менее дырявый и даже совсем не дырявый :)) Может быть, из кортежа с другим паттерном. PS. Если мне не изменяет память, что-то там г. Петухов писал про квадраты Стенли именно с таким началом: 0, 2, 6, 8. Он писал, что таких и близко нет. Ну, близко, может, и нет, а вот с 9 "дырками" есть. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
С q=16, довольно большой диаметр паттерна [0, 4, 6, 10, 34, 40, 66, 70, 100, 126, 130, 160, 174, 180, 240, 300, 360, 364,394, 510, 516, 534, 576, 636, 870] 80129800057507297: [0, 4, 6, 34, 42, 70, 84, 126, 130, 154, 174, 252, 292, 300,364, 394, 426, 454, 510, 516, 576, 636, 672, 814, 870] q=16 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Найдены два приближения с 8 "дырками" [0, 4, 6, 10, 48, 54, 60, 64, 108, 126, 130, 174, 246, 250, 270, 276, 294, 330,396, 490, 496, 516, 550, 616, 736] 15773795899482493: [0, 4, 10, 48, 54, 60, 108, 124, 126, 130, 136, 174, 178, 186, 276, 330, 334, 396, 490, 496, 516, 556, 696, 708, 736] q=17 [0, 4, 18, 22, 30, 34, 48, 52, 144, 162, 198, 202, 228, 232, 342, 378, 382, 408, 412, 522, 564, 568, 594, 598, 708] 15381821962850359: [0, 4, 18, 30, 34, 52, 58, 100, 102, 150, 162, 198, 202, 232, 342, 382, 408, 412, 448, 522, 550, 564, 610, 672, 708] q=17 Покажу квадрат Стенли для второго приближения 0 4 30 34 *144 18 *22 *48 52 162 198 202 *228 232 342 *378 382 408 412 522 564 *568 *594 *598 708 Звёздочкой помечены элементы, которых нет в паттерне найденного кортежа, то есть "дырки". С q=18 пока не найдено ни одного приближения. Ладно, пусть будет сразу с q=19, а ещё лучше - с q=25 :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
После того, как посмотрела на программы построения квадрата Стенли 5-го порядка, написанные на Бейсике, стало совсем понятно, как написать программу на PARI/GP. Без всяких предпроверок! Кстати, в теме "Антимагические квадраты" на форуме dxdy.ru есть общие формулы квадратов Стенли для всех порядков, кажется, до 10-го. Ну, берём общую формулу квадрата Стенли 5-го порядка и вперёд. Я ещё не смотрела формулы в указанной теме. Сейчас прикинула: в общей формуле квадрата Стенли 5-го порядка при заданном индексе получается 7 независимых переменных. Может быть, ошиблась. Надо посмотреть общую формулу. В программе Алексея Белышева проверка на построение квадрата Стенли очень быстро выполняется. Там проверяются миллионы наборов за несколько секунд. Супер! Жалко, что не сохранился код его программы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё с q=17, для довольно большого диаметра [0, 48, 86, 114, 134, 140, 188, 200, 204, 254, 260, 290, 308, 330, 344, 374, 378, 444, 464, 468, 534, 554, 608, 728, 798] 80428434661684643: [0, 48, 50, 74, 86, 114, 134, 140, 188, 200, 276, 290, 308, 338, 374, 378, 468, 534, 554, 638, 650, 674, 728, 794, 798] q=17 А вот ещё больше диаметр, q=16 [0, 6, 8, 14, 18, 26, 78, 84, 96, 140, 146, 158, 278, 284, 296, 426, 434, 504, 546, 554, 566, 624, 686, 704, 824] 17527768842994463: [0, 8, 18, 26, 84, 86, 140, 144, 146, 158, 176, 210, 284, 320, 384, 546, 548, 554, 566, 624, 686, 704, 708, 774, 824] q=16 Интересненько! Всё чаще находятся приближения для паттернов с довольно большими диаметрами. Квадрат Стенли для этого приближения 0 6 18 426 546 8 14 26 434 554 78 84 96 504 624 140 146 158 566 686 278 284 296 704 824 И ещё больше диаметр! [0, 4, 6, 10, 34, 40, 66, 70, 100, 126, 130, 160, 174, 180, 240, 300, 360, 364, 394, 510, 516, 534, 576, 636, 870] 16795403341767763: [0, 10, 34, 40, 48, 66, 70, 100, 124, 126, 160, 240, 280, 360, 364, 394, 406, 426, 510, 534, 550, 556, 564, 690, 870] q=16 Квадрат Стенли для этого приближения 0 4 34 174 510 6 10 40 180 516 66 70 100 240 576 126 130 160 300 636 360 364 394 534 870 |

©2026 (C) Progger