Уважаемые наши помощники!

Спасибо, что вы с нами!

Как уже сказано в соседнем топике, данный BOINC-проект является продолжением моего «ручного» проекта, который действует уже больше года на форуме Math Help Planet в теме «Ортогональные латинские квадраты 10-го порядка»
http://mathhelpplanet.com/viewtopic.php?f=57&t=46638

Если очень кратко: в проекте составляется база данных канонических форм (КФ) диагональных латинских квадратов (ДЛК) 10-го порядка, имеющих ортогональные диагональные латинские квадраты (ОДЛК).

Проект постоянно развивается. Разработано несколько алгоритмов и схем поиска ОДЛК.
Мне сложно описать весь проект в несколько строк.
Может быть, вы хотите задать вопросы? Я постараюсь на них ответить.

В проекте работали и работают замечательные программисты, назову их ещё раз:

С. Беляев (Россия)
А. Белышев (Россия)
В. Чирков (Россия)
S. Tognon (Италия)
H. White (Канада)

А. Белышев - главный теоретик проекта. Ему принадлежит теория канонических форм ДЛК.
Он также написал много программ для проекта и выполнил несколько важных экспериментов.

Мы начали BOINC-проект с самой последней теории Белышева – о сильно нормализованных ДЛК (СН ДЛК).
Задания генерируются программой, автор которой Белышев.
Задания обрабатываются программой, которая была создана С. Беляевым. Потом авторский вариант дважды модифицировался программистами проекта.

На момент старта BOINC-проекта БД, составленная в проекте, содержала 44642 уникальные КФ ОДЛК.
Теперь мы будем продолжать составление БД, добавляя в неё новые решения, найденные в BOINC-проекте.
Но и наши «ручные» вычисления также продолжаются.
Теперь это будет один общий проект.

Покажу одно интересное решение, найденное мной не так давно в одном из экспериментов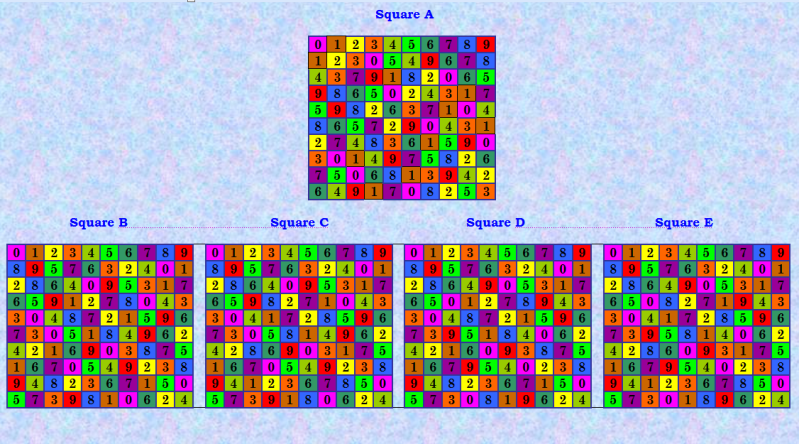



Это группа из четырёх ортогональных пар ДЛК (кратко называемая «четвёрка»).
Ортогональные пары: A – B, A – C, A – D, A – E,

Группы ортогональных пар ДЛК на сегодня известны из двух, трёх, четырёх, шести и восьми пар.
Ортогональная пара, состоящая только из двух ортогональных друг другу ДЛК, называется одиночной ортогональной парой (кратко «однушкой»).
Однушки встречаются гораздо чаще, нежели группы ортогональных пар.
Группа из трёх ортогональных пар ДЛК на сегодня известна мне всего одна, групп из шести пар – 6, групп из восьми пар – 2. Редкие жемчужины в коллекции :)

Историческое сообщение нашла в своей теме «Латинские квадраты» на форуме dxdy.ru
2012 год!
Письмо автора научного BOINC-проекта SAT@home Олега Заикина, оставленное в гостевой книге моего сайта

Здравствуйте. Я научный сотрудник ИДСТУ СО РАН, программист проекта SAT@home. Мы сейчас ищем пары ОДЛК порядка 10, один уже нашли. В одной из Вашей замечательной статье нашел упоминание, что известны 3 пары ОДЛК порядка 10. Подскажите пожалуйста, какие именно пары известны и откуда эта информация. И насколько будет значимо если найдутся ранее неизвестные пары ОДЛК порядка 10?
http://sat.isa.ru/pdsat/

См. http://dxdy.ru/post639174.html#p639174

Кстати, о проекте SAT@home. За всё время его действия было найдено 77 одиночных ортогональных пар, которые дали 154 уникальные КФ. Проект был первым проектом по данной теме.
Эти 154 КФ включены в БД, составляемую в моём проекте.

Первые три ортогональные пары диагональных латинских квадратов 10-го порядка были опубликованы в 1992 году в статье
“Completion of the Spectrum of Orthogonal Diagonal Latin Squares” (J. W. Brown и другие).
Смотрите сообщение в теме "Ортогональные латинские квадраты 10-го порядка"
http://mathhelpplanet.com/viewtopic.php?p=277638#p277638
и ещё мою статью
http://www.natalimak1.narod.ru/aspekty7.htm

Покажу эти три исторические ортогональные пары ДЛК 10-го порядка



Эти ортогональные пары - первые в составляемой сейчас БД КФ ОДЛК.

Представляю предыдущую версию БД по состоянию на 31 марта 2017 г.

A database of unique CF DLS of order 10 having orthogonal DLS
as of March 31, 2017 (38711 unique CF)

The database is composed of the results obtained in three projects:

1. BOINC project SAT@home (154 CF)
http://sat.isa.ru/pdsat/index.php
https://ru.wikipedia.org/wiki/SAT@home

2. "Manual" project "Development of the DB from CF DLS of order 10 having orthogonal DLS" (36387 CF)
Details about the project in the forum
http://mathhelpplanet.com/viewtopic.php?f=57&t=46638

Author of project Natalia Makarova.
Participants of the project are listed in the specified topic.

3. BOINC project Gerasim@Home (2170 CF)
http://gerasim.boinc.ru/
https://ru.wikipedia.org/wiki/Gerasim@Home

Download DB from here
https://yadi.sk/d/2qQ5B7dS3GYEgD

Готовлюсь выложить новую версию БД. На сегодня в БД содержится 45002 уникальные КФ ОДЛК.
Хорошее добавление поступило с данного BOINC-проекта.
Спасибо участникам проекта!

Следите за информацией.

Выложена текущая БД
https://progger.info/files/DB_45347.rar

Описание
A database of unique CF DLS of order 10 having orthogonal DLS
as of May 24, 2017 (45347 unique CF)

The database is composed of the results obtained in three projects:

1. BOINC project SAT@home (154 CF)
http://sat.isa.ru/pdsat/index.php
https://ru.wikipedia.org/wiki/SAT@home

2. BOINC project Gerasim@Home (5865 CF)
http://gerasim.boinc.ru/
https://ru.wikipedia.org/wiki/Gerasim@Home

3. "Manual" project "Development of the DB from CF DLS of order 10 having orthogonal DLS"
Details about the project in the forum
http://mathhelpplanet.com/viewtopic.php?f=57&t=46638
and
BOINC project
https://boinc.progger.info/odlk/
(39328 CF)

Что такое линейка

Сейчас в нашем BOINC-проекте задействовано 3 линейки - №№ 62, 63, 65.
Кратко поясню, что такое линейка.

На этой иллюстрации вы видите нормализованный ДЛК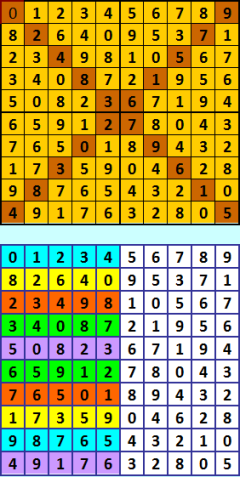



Этот ДЛК построен методом Гергели.
На иллюстрации ещё показана особая структура этого ДЛК (нижний вариант квадрата). Такую структуру имеют так называемые "брауны", но о "браунах" в другой раз расскажу, может быть :)
В нормализованном ДЛК в первой строке находится тождественная перестановка

0 1 2 3 4 5 6 7 8 9

Переобозначением элементов любой ДЛК можно привести к нормализованному виду. Поэтому без потери общности можно рассматривать только нормализованные ДЛК, что мы и делали в первой части нашего "ручного" проекта.
Кстати, БД и сейчас продолжается в КФ нормализованных ДЛК.

Недавно А. Белышев ввёл новый класс ДЛК - сильно нормализованные ДЛК (СН ДЛК).
В СН ДЛК тождественная перестановка (0 1 2 3 4 5 6 7 8 9) находится в главной диагонали квадрата, а побочная диагональ может иметь один из 67 вариантов; смотрите варианты здесь
http://forum.boinc.ru/default.aspx?g=posts&m=87504#post87504

Вот эти 67 побочных диагоналей и определяют номер линейки, которой принадлежит СН ДЛК.
Если некоторый ДЛК не имеет вид СН ДЛК, он всё равно принадлежит одному из классов эквивалентности СН ДЛК, то есть изоморфен КФ, представляющей этот класс эквивалентности.

На следующей иллюстрации вы видите СН ДЛК, принадлежащий линейке №63



Это я получила первый СН ДЛК своим генератором.
Остаётся добавить, что между КФ нормализованных ДЛК и КФ СН ДЛК существует строгое соответствие.
Если мы имеем в БД 40000 КФ нормализованных ДЛК, то и в соответствующей БД КФ СН ДЛК будет 40000 КФ.

Рассказала очень кратко. Если есть вопросы, прошу задавать. На что смогу, отвечу.

И очень интересный вопрос: сколько СН ДЛК в одной линейке?
Вы можете попробовать посчитать :)

Вот что написал мне Harry White по этому поводу:

Regarding an estimate of the number of DLS for each /diagonal variant:

With /diagonal variant 1 and its first row variant 1,
the count is 13,003,902,633 DLS for one second row.

The number of second row variants with this /diagonal and first row is
computed as 2,143.
The computed number of variants for the first row with this /diagonal is
6,166.

So, based on the count for just one first row and one second row, the total
DLS for this /diagonal
variant would be 6,166 * 2,143 * 13,003,902,633 = 1.7 x 10e17,
(170,000,000,000,000,000).

The average computed number of variants for the first row for all the 67
/diagonal variants
is 6,193+.

Вот здесь
http://forum.boinc.ru/default.aspx?g=posts&m=87664#post87664
сообщение А. Белышева на форуме boinc.ru, в котором он рассказывает о своей программе Генератор КФ ОДЛК и других (попутных).
В сообщении есть ссылка, где можно эти программы скачать
https://yadi.sk/d/yQZpCCXo3HWzGe
(это на Яндекс.Диске)

Программу Белышева Генератор КФ ОДЛК мы используем в Приложении 2.
Подчеркну ещё раз: если кто-то хочет найти ортогональные соквадраты к найденным в проекте КФ ОДЛК, воспользуйтесь программой Белышева Ортогон. Программа в архиве dlk_ortogon.zip, прикреплённом к указанному посту.

Я использую для этой цели другую программу, созданную давно коллегой С. Беляевым и дважды модифицированную; последний раз модифицировал Progger.

Пример работы программы А. Белышева dlk_ortogon.exe

вводим в программу следующую КФ ОДЛК, найденную в нашем проекте:

0 2 3 4 5 7 8 6 9 1
4 1 0 5 3 9 7 8 2 6
8 7 2 6 9 1 5 0 3 4
5 9 8 3 0 2 4 1 6 7
7 3 1 0 4 6 9 2 5 8
6 8 4 9 7 5 2 3 1 0
9 4 7 8 1 3 6 5 0 2
2 6 9 1 8 0 3 7 4 5
1 5 6 7 2 4 0 9 8 3
3 0 5 2 6 8 1 4 7 9

В выходном файле output.txt получаем:

DLK(2):
0 2 3 4 5 7 8 6 9 1
4 1 0 5 3 9 7 8 2 6
8 7 2 6 9 1 5 0 3 4
5 9 8 3 0 2 4 1 6 7
7 3 1 0 4 6 9 2 5 8
6 8 4 9 7 5 2 3 1 0
9 4 7 8 1 3 6 5 0 2
2 6 9 1 8 0 3 7 4 5
1 5 6 7 2 4 0 9 8 3
3 0 5 2 6 8 1 4 7 9
mate#1:
2 8 0 9 5 6 1 3 7 4
0 3 6 7 1 9 8 4 2 5
8 5 1 0 4 2 6 7 9 3
1 2 9 4 0 3 5 6 8 7
4 6 5 8 7 1 0 9 3 2
6 7 2 3 9 8 4 5 0 1
5 1 3 6 8 7 9 2 4 0
7 4 8 1 3 5 2 0 6 9
9 0 7 2 6 4 3 1 5 8
3 9 4 5 2 0 7 8 1 6
mate#2:
2 8 0 9 5 6 1 3 7 4
0 3 6 7 1 8 9 4 2 5
9 5 1 0 4 2 6 7 8 3
1 2 8 4 0 3 5 6 9 7
4 6 5 8 7 1 0 9 3 2
6 7 2 3 8 9 4 5 0 1
5 1 3 6 9 7 8 2 4 0
7 4 9 1 3 5 2 0 6 8
8 0 7 2 6 4 3 1 5 9
3 9 4 5 2 0 7 8 1 6

Введённая КФ ОДЛК имеет два ортогональных диагональных соквадрата - mate#1 и mate#2.
Кстати, очень интересная двушка, найденная в проекте, она получена непосредственно от КФ из линейки №65.

И для сравнения - для той же КФ ОДЛК программа С. Беляева выдаёт:

 0 1 2 3 4 5 6 7 8 9
 2 7 5 8 6 1 3 9 0 4
 3 4 6 2 9 0 5 8 1 7
 6 0 1 9 2 7 4 5 3 8
 9 5 4 1 8 6 2 3 7 0
 5 8 0 7 1 3 9 4 2 6
 4 6 7 5 3 8 1 0 9 2
 8 9 3 6 7 4 0 2 5 1
 1 2 8 0 5 9 7 6 4 3
 7 3 9 4 0 2 8 1 6 5
sq1

 0 1 2 3 4 5 6 7 8 9
 2 7 5 8 6 3 1 9 0 4
 1 4 6 2 9 0 5 8 3 7
 6 0 3 9 2 7 4 5 1 8
 9 5 4 1 8 6 2 3 7 0
 5 8 0 7 3 1 9 4 2 6
 4 6 7 5 1 8 3 0 9 2
 8 9 1 6 7 4 0 2 5 3
 3 2 8 0 5 9 7 6 4 1
 7 3 9 4 0 2 8 1 6 5
sq2

Square:
 0 2 3 4 5 7 8 6 9 1
 4 1 0 5 3 9 7 8 2 6
 8 7 2 6 9 1 5 0 3 4
 5 9 8 3 0 2 4 1 6 7
 7 3 1 0 4 6 9 2 5 8
 6 8 4 9 7 5 2 3 1 0
 9 4 7 8 1 3 6 5 0 2
 2 6 9 1 8 0 3 7 4 5
 1 5 6 7 2 4 0 9 8 3
 3 0 5 2 6 8 1 4 7 9

Здесь ортогональные соквадраты sq1 и sq2.
Другие ортогональные соквадраты (по сравнению с ортогональными соквадратами, выданными программой Белышева)? :)
Нет, они изоморфные. Просто программа Беляева находит ортогональные соквадраты в нормализованном виде.

Сейчас в нашем BOINC-проекте задействовано 3 линейки - №№ 62, 63, 65.

В моём «ручном» проекте я занимаюсь поиском решений в линейке №13.
Почему выбрала именно эту линейку?
Проверив первые КФ во всех 67 линейках, я нашла минимальную КФ в линейке №13:

0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 7 4 9 3 5 8
5 6 0 3 8 9 4 1 2 7
3 7 8 9 4 2 0 6 1 5
8 9 1 0 6 5 2 4 7 3
9 3 7 8 0 1 6 5 4 2
6 8 9 1 2 0 5 7 3 4
4 5 6 7 9 3 1 2 8 0
7 4 5 2 1 8 3 0 6 9

Эта КФ не имеет ортогональных диагональных соквадратов.
Тогда я начала искать КФ ОДЛК, начав поиск с минимальной КФ.
На сегодня я нашла 15 первых КФ ОДЛК.

КФ #1
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 7 4 9 3 5 8
8 7 6 3 9 0 4 5 1 2
6 9 8 1 4 2 5 0 7 3
3 8 0 9 6 5 1 2 4 7
9 4 7 8 0 3 6 1 2 5
5 6 9 2 8 1 0 7 3 4
4 5 1 7 2 9 3 6 8 0
7 3 5 0 1 8 2 4 6 9

КФ #2
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 8 4 9 3 5 7
8 9 6 3 7 0 4 2 1 5
5 8 7 9 4 2 3 1 6 0
9 7 1 0 6 5 2 4 3 8
4 3 5 8 9 1 6 0 7 2
6 4 9 1 0 8 5 7 2 3
3 5 0 7 2 9 1 6 8 4
7 6 8 2 1 3 0 5 4 9

КФ #3
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 8 4 9 3 7 5
9 8 6 3 7 1 4 5 2 0
5 9 0 7 4 2 3 1 6 8
8 4 1 9 6 5 2 0 3 7
3 7 5 8 0 9 6 2 1 4
4 6 9 0 2 8 1 7 5 3
6 5 7 1 9 3 0 4 8 2
7 3 8 2 1 0 5 6 4 9
. . . . . . . . 

КФ #14
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 4 2 6 7 9 0 3 5 8
9 6 0 3 2 8 4 1 7 5
5 8 6 9 4 2 1 0 3 7
8 9 7 1 6 5 3 4 2 0
3 7 5 8 9 0 6 2 1 4
6 0 9 2 8 1 5 7 4 3
4 5 1 7 0 3 9 6 8 2
7 3 8 0 1 4 2 5 6 9

КФ #15
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 4 2 6 8 0 9 3 7 5
8 0 5 3 9 1 4 2 6 7
6 9 0 7 4 2 3 5 1 8
3 7 8 9 6 5 1 0 2 4
5 3 7 8 0 9 6 1 4 2
4 6 9 1 2 8 5 7 3 0
9 5 1 2 7 4 0 6 8 3
7 8 6 0 1 3 2 4 5 9

На моём ПК поиск выполняется медленно. Тем не менее, есть некоторые результаты.
Я использую программу А. Белышева "Генератор КФ ОДЛК".
Продолжаю поиск.

--------

In my "manual" project, I'm looking for solutions in the ruler # 13.
Why did I choose this ruler?
Checking the first CF in all 67 rulers, I found the minimal CF in the ruler # 13:

0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 7 4 9 3 5 8
5 6 0 3 8 9 4 1 2 7
3 7 8 9 4 2 0 6 1 5
8 9 1 0 6 5 2 4 7 3
9 3 7 8 0 1 6 5 4 2
6 8 9 1 2 0 5 7 3 4
4 5 6 7 9 3 1 2 8 0
7 4 5 2 1 8 3 0 6 9

This CF does not have orthogonal diagonal squares.
Then I began to look for the CF of the ODLS, starting the search with a minimal CF.
For today, I found the first 15 KF ODLS.

CF #1
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 7 4 9 3 5 8
8 7 6 3 9 0 4 5 1 2
6 9 8 1 4 2 5 0 7 3
3 8 0 9 6 5 1 2 4 7
9 4 7 8 0 3 6 1 2 5
5 6 9 2 8 1 0 7 3 4
4 5 1 7 2 9 3 6 8 0
7 3 5 0 1 8 2 4 6 9

CF #2
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 8 4 9 3 5 7
8 9 6 3 7 0 4 2 1 5
5 8 7 9 4 2 3 1 6 0
9 7 1 0 6 5 2 4 3 8
4 3 5 8 9 1 6 0 7 2
6 4 9 1 0 8 5 7 2 3
3 5 0 7 2 9 1 6 8 4
7 6 8 2 1 3 0 5 4 9

CF #3
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 0 2 6 8 4 9 3 7 5
9 8 6 3 7 1 4 5 2 0
5 9 0 7 4 2 3 1 6 8
8 4 1 9 6 5 2 0 3 7
3 7 5 8 0 9 6 2 1 4
4 6 9 0 2 8 1 7 5 3
6 5 7 1 9 3 0 4 8 2
7 3 8 2 1 0 5 6 4 9
. . . . . . . . 

CF #14
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 4 2 6 7 9 0 3 5 8
9 6 0 3 2 8 4 1 7 5
5 8 6 9 4 2 1 0 3 7
8 9 7 1 6 5 3 4 2 0
3 7 5 8 9 0 6 2 1 4
6 0 9 2 8 1 5 7 4 3
4 5 1 7 0 3 9 6 8 2
7 3 8 0 1 4 2 5 6 9

CF #15
0 2 3 4 5 6 7 8 9 1
2 1 4 5 3 7 8 9 0 6
1 4 2 6 8 0 9 3 7 5
8 0 5 3 9 1 4 2 6 7
6 9 0 7 4 2 3 5 1 8
3 7 8 9 6 5 1 0 2 4
5 3 7 8 0 9 6 1 4 2
4 6 9 1 2 8 5 7 3 0
9 5 1 2 7 4 0 6 8 3
7 8 6 0 1 3 2 4 5 9

On my PC the search is slow. Nevertheless, there are some results.
I use the program of A. Belyshev "The generator of the CF of ODLS".
I continue the search.

Итак, у нас в работе сейчас находятся 4 линейки.
Каждый может заняться поиском решений в одной из оставшихся 63 линеек.
Для этого нужно желание и технические возможности.

Если вы хотите получить подробные инструкции, пишите мне.

--------

So, we currently have 4 rulers in our work.
Everyone can look for solutions in one of the remaining 63 rulers.
This requires the desire and technical capabilities.

If you want detailed instructions, write to me.

Harry White написал мне:

I checked all the remaining diagonal variants for a bigger CF. I didn't find any.
None of the last 1,000,000 biggest DLS for each was in canonical form.

Смотрите
http://mathhelpplanet.com/viewtopic.php?p=302619#p302619

Итак, максимальная КФ принадлежит линейке №66 (если Harry не ошибся):

0 9 8 7 6 4 5 2 3 1
9 1 7 8 5 3 4 6 2 0
7 8 2 6 9 0 1 3 5 4
6 7 5 3 8 9 0 4 1 2
5 3 1 9 4 6 2 8 0 7
4 6 0 2 7 5 8 1 9 3
3 2 4 5 0 1 6 9 7 8
2 0 9 4 1 8 3 7 6 5
1 4 3 0 2 7 9 5 8 6
8 5 6 1 3 2 7 0 4 9

В текущей БД, составляемой в моём проекте (на данный момент 53685 КФ) максимальная КФ:

0 9 8 7 6 4 5 2 3 1
4 1 7 5 2 9 3 6 0 8
1 0 2 6 9 8 7 3 4 5
9 8 0 3 1 7 4 5 2 6
8 3 5 0 4 6 9 1 7 2
2 6 3 4 7 5 1 8 9 0
3 4 1 8 0 2 6 9 5 7
6 5 9 2 3 0 8 7 1 4
7 2 6 9 5 1 0 4 8 3
5 7 4 1 8 3 2 0 6 9

Эта КФ принадлежит линейке №59.
Теперь нам нужно искать бОльшие КФ ОДЛК, начиная с текущей максимальной КФ ОДЛК и заканчивая максимальной КФ.
Это одно из направлений поиска.

-------------

Harry White wrote to me:

I checked all the remaining diagonal variants for a bigger CF. I didn't find any.
None of the last 1,000,000 biggest DLS for each was in canonical form.

See
http://mathhelpplanet.com/viewtopic.php?p=302619#p302619

So, the maximal CF belongs to the ruler # 66 (if Harry was not mistaken):

0 9 8 7 6 4 5 2 3 1
9 1 7 8 5 3 4 6 2 0
7 8 2 6 9 0 1 3 5 4
6 7 5 3 8 9 0 4 1 2
5 3 1 9 4 6 2 8 0 7
4 6 0 2 7 5 8 1 9 3
3 2 4 5 0 1 6 9 7 8
2 0 9 4 1 8 3 7 6 5
1 4 3 0 2 7 9 5 8 6
8 5 6 1 3 2 7 0 4 9

In the current database, compiled in my project (at the moment 53685 CF) the maximal CF:

0 9 8 7 6 4 5 2 3 1
4 1 7 5 2 9 3 6 0 8
1 0 2 6 9 8 7 3 4 5
9 8 0 3 1 7 4 5 2 6
8 3 5 0 4 6 9 1 7 2
2 6 3 4 7 5 1 8 9 0
3 4 1 8 0 2 6 9 5 7
6 5 9 2 3 0 8 7 1 4
7 2 6 9 5 1 0 4 8 3
5 7 4 1 8 3 2 0 6 9

This CF belongs to the ruler # 59.
Now we need to look for larger CFs of the ODLS, starting from the current maximal CF of the ODLS and ending with the maximal CF.
This is one of the areas of search.

Дорогие участники проекта!

Команда проекта продолжает активно трудиться с вашей помощью.
Два BOINC-проекта (ODLK и ODLK1) стабильно работают и выдают новые результаты.
Я ежемесячно обрабатываю результаты и выкладываю их
https://boinc.progger.info/odlk/forum_thread.php?id=86
https://boinc.progger.info/odlk/forum_thread.php?id=67

Активно продолжает работу мой ручной проект.
К сожалению, у меня пока только один помощник в этом проекте - Demis.

Я приглашаю всех к выполнению индивидуальных заданий!
https://boinc.progger.info/odlk/forum_thread.php?id=84
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=45

В ручном проекте мы выполняем ряд интереснейших экспериментов по алгоритмам, разработанным мной и Белышевым.
И мы нашли в этих экспериментах немало интересных решений, например, уникальные группы из 5, 7 и 10 пар ОДЛК.
Группа из 10 пар ОДЛК отмечена в OEIS
https://oeis.org/A287695

Спасибо вам за ваш огромный труд в наших проектах!

****
Dear participants of the project!

The project team continues to work actively with your help.
Two BOINC projects (ODLK and ODLK1) work stably and produce new results.
I process the results on a monthly basis and spread them out
https://boinc.progger.info/odlk/forum_thread.php?id=86
https://boinc.progger.info/odlk/forum_thread.php?id=67

Actively continues to work my manual project.
Unfortunately, I have only one assistant in this project - Demis.

I invite everyone to perform individual jobs!
https://boinc.progger.info/odlk/forum_thread.php?id=84
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=45

In the manual project we perform a number of interesting experiments on algorithms developed by me and Belyshev.
And we found in these experiments a lot of interesting solutions, for example, unique groups of 5, 7 and 10 pairs of ODLS.
A group of 10 pairs of ODLS is marked in OEIS
https://oeis.org/A287695

Thank you for your great work in our projects!

Цитата

Весьма интересен такой момент: первые пары ОДЛК 10-го порядка были опубликованы в 1992 году.
И что? Поиском таких пар ОДЛК больше никто не занимался?
Целых 20 лет, до 2012 года, когда поиск ОДЛК 10-го порядка начали в BOINC-проекте SAT@home.
Странно как-то.

отсюда
https://boinc.progger.info/odlk/forum_thread.php?id=116&postid=3543#3543

Косвенно ко мне пришёл вопрос: а нет ли у кого-нибудь в мире БД КФ ОДЛК 10-го порядка?
В приведённой цитате я сказала о том же, несколько иначе.

Может быть, эта БД давно составлена, но мы о ней просто не знаем?
Но... проекту ODLK пошёл третий год, проекту ODLK1 в ноябре т. г. будет два года.
В проектах участники из многих стран мира.
Странным кажется полное неведение всех о существовании БД КФ ОДЛК 10-го порядка.

Я пыталась писать к Wanless в Австралию. На два письма не получила ни одного ответа.

Задаю этот же вопрос снова.
ВСЕМ! ВСЕМ! ВСЕМ!
Кто что знает о поиске ОДЛК 10-го порядка в мировом научном сообществе, кроме того, что нам известно (проект SAT@home)?
Пожалуйста, сообщите.