Ржу не могу :)))
За то, что Верховная самодура "охренела", Захар сказал ей "Спасибо", и продолжает в теме
http://mathhelpplanet.com/viewtopic.php?p=441477#p441477

Booker48
Я нашёл поистине чудесное и не менее лаконичное доказательство для параметризации с чётным делителем q. Будет статья II часть.

Чудесная мыльная опера! Шедевр!
Я таких ещё не встречала за многие годы участия в форумах.

Обратите внимание: самодура "охренела", однако тему не закрыла.
Продолжай, дорогой жополиз!
"Спасибо" поставил за пост, ещё в репутацию поставь плюсик. И цены тебе не будет на форуме.
И самодура будет тебя лелеять.
Все форумчане будут восхищаться и поздравлять, благодарить и уважать, помогать поправить гениальные доказательства и т. д.
Ну, может быть, кроме одного форумчанина - ferma-T.
Он вроде понял, что "персонаж невменяем".

Наверное, я что-то не так понимаю.
Вот три 15-ки по 12 делителей

66387422053662391209161093722597723545: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12
75847648332862724576017454918623133145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12
91340991749658028244987380473874205145: 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12

Я понимала так, что это цепочка из 15 последовательных натуральных чисел, каждое из которых имеет 12 делителей.
Раскладываю на множители число 66387422053662391209161093722597723545

[3, 2; 5, 1; 1475276045636942026870246527168838301, 1]

Если факторизацию выполняю правильно, здесь вижу всего 4 делителя: 3 в квадрате, 5 и 1475276045636942026870246527168838301.
Где 12 делителей?
Точно такая же ситуация с числами в двух других 15-ах, первые числа цепочек имеют по 4 делителя.

Для следующего числа первой 15-ки ( факторизация даёт 66387422053662391209161093722597723546)

[2, 1; 37, 2; 24246684460797074948561392886266517, 1]

И опять 4 делителя!
Делаю проверку. Ввожу в программу число

b=2*37^2*24246684460797074948561392886266517;

Прошу программу напечатать это число, программа выводит

(05:35) gp > \r a1.txt
66387422053662391209161093722597723546
(05:39) gp >

Да, это исходное число, которое разложено на множители.

Ничего не понимаю!
Где 12 делителей? У каких чисел показанных 15-ек?
Может быть, эти числа надо домножить на какое-то известное число, которое имеет 8 делителей?
И тогда результирующее число будет иметь 12 делителей.
Например, число 2^8 имеет 8 делителей. Правильно?
Тогда все числа 15-ек домножить на 2^8 и дело в шляпе :)

Вот, домножила первое число первой 15-ки на 2^8, получилось число, которое имеет 12 делителей

[2, 8; 3, 2; 5, 1; 1475276045636942026870246527168838301, 1]
16995180045737572149545239992985017227520

Но это, скорее всего, неправильно.
Ведь с таким же успехом можно домножить числа и на 2^9, и тогда все числа цепочки будут иметь по 13 делителей.
И т. д.
Нет, что-то я тут совсем не понимаю.

Игра "Угадай слово" за 16 апреля

КОШКА
НАРОД
ГАЛОП
САПОГ

В сегодняшней игре "отлично"!
Первое проверочное слово поймало две буквы и обе на своём месте. Удача!
А дальше... комбинация этих двух букв именно на этом месте содержится во многих словах.
Пришлось долго выбирать из всех вариантов более подходящее слово. И угадала!

Ой, вот же состарилась как - всё забыла про делители :)
Ну, такой заскок: думала, что считаются только простые делители.
В кортежах из простых чисел у меня нет никаких делителей, вот я и забыла про них начисто.
Написала другу, чтобы просветил, где 12 делителей.
Он просветил:

Имеются в виду, конечно, не простые делители, а все, включая 1 и само число.
Например 60=2² * 3 * 5
А делители 1,2,3,4,5,6,10,12,15,20,30,60
как раз 12 штук.

УФ!
Теперь понятно.

Итак, число 66387422053662391209161093722597723545 так раскладывается на простые множители
[3, 2; 5, 1; 1475276045636942026870246527168838301, 1]
Конечно, если посчитать и составные делители, то всего будет 12 делителей.

Цитата

Разложила на множители число, которое мне программа нарисовала
5110145662825543332475140141244972679378639054064347
Вот что получилось

[7, 1; 29, 2; 149, 1; 9699152146384651, 1; 600646849575045503832342134419, 1]

Интересно: это число имеет всего 6 делителей.
А я думала, что оно является началом цепочки чисел, имеющих по 48 делителей :)
Ну, трудно понять, что ищет и находит чужая программа.

И далее, любопытно.
Следующие числа тоже имеют по 6 делителей.

[2, 2; 3, 1; 2833, 1; 647417, 1; 232178157344080911202893830719785435347989, 1]
(22:51) gp > \r a1.txt
[13, 1; 17, 2; 79, 1; 2559495594991, 1; 6726832393926766280095814123096113, 1]
(22:52) gp >

______________________
конец цитаты

Это найденная мной цепочка чисел

5110145662825543332475140141244972679378639054064347
# [1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1] 17

Ой, не буду выписывать все 48 делителей в факторизованных числах; поверю, что их ровно 48.
Значит, первые четыре числа цепочки имеют по 48 делителей, а следующее (пятое) число не имеет 48 делителей. Так?
Сейчас проверю.

Вот, факторизация четвёртого и пятого чисел в цепочке

%1 = 5110145662825543332475140141244972679378639054064347
[2, 1; 5, 2; 3461, 1; 16927, 1; 1744543013452225841989888575951857133230021, 1]
[3, 2; 139, 1; 479, 1; 521, 1; 525148567, 1; 30059944487, 1; 1036889255766041057
815091, 1]

Вроде всё правильно.

Теперь начну с шестого числа и до последнего; последнее тут 17-ое, так как в векторе всего 17 нулей и единичек.
Готово!

%4 = 5110145662825543332475140141244972679378639054064347
[2, 5; 2316463, 1; 77533538519, 1; 889136274317788787631866950464463, 1]
[19, 2; 105101156742293452577, 1; 134684798822723385102759863449, 1]
[2, 1; 3, 1; 7, 2; 11, 1; 1580131621158176664339870173545136882924749243681, 1]
[5, 1; 31, 2; 19778053991, 1; 684822823757, 1; 78519604522174186166305253, 1]
[2, 2; 1099636251457345066261, 1; 1161780919838965059141423331349, 1]
[3, 1; 47, 2; 492673, 1; 5800699, 1; 269821912653607880592198702520675733, 1]
[2, 1; 41, 2; 199, 1; 125858881, 1; 60687413473540721275627901744259711461, 1]
[23, 2; 239, 1; 1097, 1; 842112277134503, 1; 43752520824968637856073784679, 1]
[2, 3; 3, 2; 5, 1; 14194849063404287034653167059013812998273997372401, 1]
[7, 1; 43, 2; 825701, 1; 5144309, 1; 92949802384724069556293879329907503, 1]
[2, 1; 13, 2; 107, 1; 196709, 1; 718304473493172678753044953285780646032123, 1]
[3, 1; 37, 2; 56401, 1; 1297271, 1; 17005564893971977353656750135915132279, 1]

Предлагаю читателям самостоятельно проверить эти факторизации но количество делителей.
Надеюсь, что тут всё правильно.
Последние 8 чисел подряд в этой цепочке должны иметь по 48 делителей.
Ну, а также первое и третье числа в этой цепочке из 12 чисел.

Итак, если бы я нашла не такую цепочку

# [1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1] 17

а цепочку, состоящую из всех 17 единичек, это что было бы?
Всего 17-ка, а ищется 20-ка.
Опять не понимаю. Где брать ещё три числа цепочки?

О-о-о!
Антон Никонов писал в сообщении
https://dxdy.ru/post1552778.html#p1552778

И коммент специально для Саратова.
66387422053662391209161093722597723545 имеет 4 простых множителя в разложении, но 12 делителей.

5110145662825543332475140141244972679378639054064347 имеет 6 простых множителей в разложении, но 48 делителей.

Здесь нет противоречия.

Спасибо, Антон!
Но меня уже просветил gris :)
Да, конечно, здесь нет противоречия, был просто у меня заскок в мозгах :)
Я с делителями лет 50 не встречалась, вот и забыла, что делители - это не только простые множители в разложении числа.
Ну, вот такой заскок случился.

А сейчас вспомнила, что вроде есть специальная функция в PARI/GP для подсчёта делителей в числе, и не надо их вручную считать.
Опробую.

PS. Антон, а не наложат ли на вас санкции за комментарии "для Саратова"? :)
Предлагаю вам зарегистрироваться здесь и писать ваши комментарии.
Регистрация на сайте свободная.
Искренне за вас волнуюсь. Вы же знаете, что упоминание забаненной Макаровой (прямое или косвенное) на форуме dxdy.ru категорически запрещено.

Опробовала функцию numdiv.
Вот цепочка, выданная программой господина Лецко, и проверка чисел цепочки на количество делителей (первое число цепочки в моей программке выведено)

# [1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1] 17
%9 = 5110145662825543332475140141244972679378639054064347
48, 48, 48, 48, 192, 48, 12, 48, 48, 12, 48, 48, 48, 48, 48, 48, 48,

Что-то не совпадает в 9-й и 10-й позициях.
У меня ошибка или в программе господина Лецко ошибка?

Перезапустила тот интервал, в котором была получена показанная в предыдущем посте цепочка (17).
Программу скопировала из последней инструкции (pdf).
Может быть, ошибка была, и господин Лецко её исправил.
Посмотрю, что выведет программа в этом сеансе.

Сделала скриншот консоли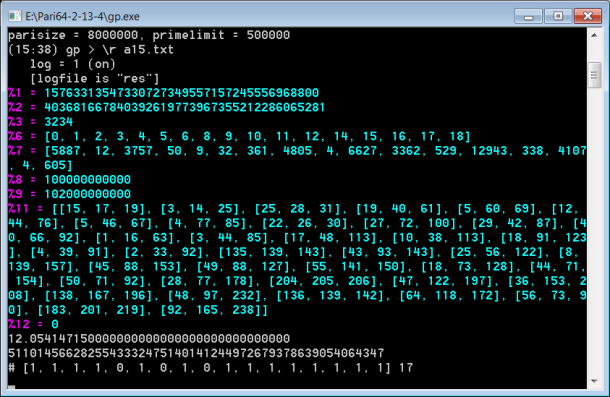



Цепочка выведена точно такая же и через такое же время от начала запуска.
Пока ничего не понимаю :)
Может быть, это не так важно - в какой последовательности нули и единички выводятся, лишь бы количество нулей и количество единичек было правильное?
Но... как-то не совсем красиво получается: какие-то нули и единички соответствуют количествам делителей (48 или не 48), а какие-то не соответствуют.
На мой взгляд, должны все соответствовать.
Может, у меня в элементарной программке подсчёта делителей ошибка?
Вроде и ошибаться в этой программке негде.

Программу прервала.
На этом заканчиваю эксперименты с программой господина Лецко.

Господа!
Отдохнём от математики :)
Весна пришла!
По этому поводу - моё стихотворение

58-ая весна

Какая боль и грусть – в надежде
Ещё одну весну узнать!
И. А. Бунин

А в природе буйствует весна.
Вчера лишь были почки –
Сегодня уж листва.
Ах, какая ты волшебница, весна!
Тебе ведь всё равно,
Что, может, для меня
Ты будешь уж последняя весна…

Я с каждым годом пристальней гляжу,
Хочу запомнить листик каждый.
Благословляю с нежностью судьбу,
Что на Земле пришлось прожить однажды.
Мы все уйдём, придут другие.
Лишь об одном молю я Провиденье:
Чтобы им всем увидеть довелось
Такое же чудесное цветенье!

21 мая 2007 г.
https://stihi.ru/2007/05/21-1366

А сейчас у меня уже 73-я весна :)



Фото друга.

Так, возвращаемся к делителям.
Попросила друга gris проверить мои подсчёты по делителям.
Он начал с 4-й позиции в цепочке, используя приведённую мной в теме факторизацию чисел цепочки.
Вот что у него получилось (первая колонка - номер позиции, последняя колонка - количество делителей)

 4 [1; 2; 1; 1;  1] 2 3 2 2 2 = 48
 5 [2; 1; 1;  1;  1; 1;  1] 3 2 2 2 2 2 2 =192
 6 [5; 1;  1;  1]  6 2 2 2 = 48
 7 [2; 1;  1] 3 2 2 = 12
 8 [1; 1; 2; 1; 1] 2 2 3 2 2 = 48
 9 [1; 2; 1;  1;  1] 2 3 2 2 2 = 48  
10 [2; 1; 1] 3 2 2 = 12
11 [1; 2;  1;  1;  1] 2 3 2 2 2 = 48 
12 [1;  2; 1;  1;  1] 2 3 2 2 2 = 48
13 [2; 1; 1; 1;  1] = 3 2 2 2 2 = 48
14 [3; 2; 1; 1] 4 3 2 2 = 48
15 [1; 2; 1; 1;  1] 2 3 2 2 2 =48
16 [1; 2;  1;  1; 1] 2 3 2 2 = 48
17 [1; 2; 1; 1;  1] 2 3 2 2 2 = 48

Это в точности совпадает с моими результатами.
Спасибо, gris!

Таким образом, несоответствие количества делителей нулю и единичке (не 48 и 48 делителей) в 9-й и 10-й позициях налицо.
Как объяснить это несоответствие, я не знаю.
Является ли это ошибкой программы господина Лецко, или это несоответствие не имеет значения.
Хорошо, если второе.

Ещё выяснила, почему выводится цепочка из 17 чисел.
Как я и предположила в самом начале, это 20-ка.
Фокус в том, что следующие три числа за числами цепочки 17 тоже имеют по 48 делителей.
В-о-о-о-т!

%16 = 5110145662825543332475140141244972679378639054064347
48, 48, 48, 48, 192, 48, 12, 48, 48, 12, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48,

Это 20-ка с тремя "дырками".
Замечательно!
Я не ожидала такого успеха :)
Эта 20-ка появилась через час после запуска программы.
Смотрите скриншот в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=8556

Господин Лецко тоже использует термин "дырка", только он говорит более грубо - "дыра" :)
Он сообщил, что ему удалось найти 20-ку с одной "дыркой".

Это 19-ка, найденная господином Лецко

%19 = 5908388043825578351730345292813071711296723319324
48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48,

Сравните начальные числа этой 19-ки и найденной мной 20-ки с тремя "дырками"
5908388043825578351730345292813071711296723319324
5110145662825543332475140141244972679378639054064347

На форуме MHP появилась интересная тема "Диофантовы пятёрки"
http://mathhelpplanet.com/viewtopic.php?f=48&t=77151

Мыльная опера "Совершенный кубоид" продолжается!
Не читаю. Скучно!

Игра "Угадай слово" за 17 апреля

МЕСТЬ
МЕШОК

Ой!
В сегодняшней игре "двойка" (пять попыток).
С первым проверочным словом не повезло, поймалась всего одна буква и та не на своём месте.
А дальше опять получила комбинацию двух букв (на своём месте), которая содержится в огромном количестве слов.
Вот раньше такое встречалось редко в русской игре, а в английской - часто.
Сейчас и в русской стало часто встречаться.
Не нравится мне это!
Начинается тупой и очень нудный перебор вариантов слов (которых много!) с этой жёсткой комбинацией букв.
Никакой уже логики.

Кажется, я поняла причину несоответствия строки из нулей и единичек количеству делителей в последовательности чисел.
Вот на этот вектор посмотрите

uu = [0,1,2,3,4,5,6,8,9,10,11,12,14,15,16,17,18]

и далее на строку, которая формирует цепочку нулей и единичек - вектор Е.

if(f3, E=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0];ss=0;t=t+1; for(j=1,17,if(numdiv(n+uu[j])==48,E[j]=1;ss=ss+1));

Начальное число n не всегда увеличивается каждый раз на 1 (то есть проверяются на делители не последовательные числа), оно увеличивается на координаты вектора uu.

Таким образом, цепочка из нулей и единиц (вектор Е) формируется по количеству делителей следующих чисел

5110145662825543332475140141244972679378639054064347+0
5110145662825543332475140141244972679378639054064347+1
5110145662825543332475140141244972679378639054064347+2
5110145662825543332475140141244972679378639054064347+3
5110145662825543332475140141244972679378639054064347+4
5110145662825543332475140141244972679378639054064347+5
5110145662825543332475140141244972679378639054064347+6
5110145662825543332475140141244972679378639054064347+8
5110145662825543332475140141244972679378639054064347+9
5110145662825543332475140141244972679378639054064347+10
5110145662825543332475140141244972679378639054064347+11
5110145662825543332475140141244972679378639054064347+12
5110145662825543332475140141244972679378639054064347+14
5110145662825543332475140141244972679378639054064347+15
5110145662825543332475140141244972679378639054064347+16
5110145662825543332475140141244972679378639054064347+17
5110145662825543332475140141244972679378639054064347+18

Сейчас проверю, какая получится цепочка из количества делителей для этих чисел.

Да, всё правильно.
Вот полученная цепочка делителей для показанного набора чисел

48, 48, 48, 48, 192, 48, 12, 48, 12, 48, 48, 48, 48, 48, 48, 48, 48,

что полностью соответствует цепочке из нулей и единиц, выведенной программой

# [1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1] 17

Вот такая хитрая проверка цепочки чисел на делители.
Почему она такая хитрая, знает только господин Лецко.

Однако это не отменяет найденной мной 20-ки с тремя "дырками" :)

%16 = 5110145662825543332475140141244972679378639054064347
48, 48, 48, 48, 192, 48, 12, 48, 48, 12, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48,

Я проверяю на делители цепочку последовательных чисел, начинающуюся с числа 5110145662825543332475140141244972679378639054064347.

Игра "Угадай слово" за 18 апреля

ЧИСЛО
ОТВЕТ
ОТАРА
ОТПАД
ОТКАЗ

Вот он - тупой, нудный перебор!
Вторым ходом получена комбинация букв ОТ***.
Сколько слово имеют такую комбинацию!!
Хорошо ещё, что в 5 попыток уложилась, можно было и в 6 попыток не уложиться.
Это безобразие!
Надо заметить, что второе и третье проверочные слова не очень хороши, так как содержат одинаковые буквы.
Это увеличивает и без того большой перебор.

В сегодняшней игре "четвёрка".
Игра длилась три минуты.

Ну вот, я исправилась - из двоечницы в хорошистки :)
Гимнастика для ума закончилась, надо работать.
Ну, черепашка-то уже работает, это я развлекаюсь :)

Итак, в теме "Пентадекатлон мечты" в данный момент ищут 20-ку чисел по 48 делителей.
Для этого используют программу господина Лецко, написанную на PARI/GP.
Выше я рассказала, как опробовала эту программу.
Господин Петухов сетует, что его "ускорители" в данной задаче плохо работают: вместо 1000-кратного ускорения получается всего 6-кратное.
Антон Никонов писал в сообщении
https://dxdy.ru/post1553023.html#p1553023

Кстати, при переходе от 11 одиночных простых к 3-м, по грубой прикидке оно и должно было из 1000-кратного стать 6-7-кратным:

Подумалось: эти три одиночных простых не объясняют ту хитрую проверку чисел на делители, о которой рассказано выше?
Я ведь в алгоритм не вникала.

В общем, пришли к выводу, что не стОит делать "ускорители" для поиска 20-ки по 48 делителей.
Господин Лецко уверен, что 20-ка и так вот-вот найдётся (по его программе).
Он уже нашёл несколько 19-ок, а также 20-ку с одной "дыркой".

А я всего за один час работы программы нашла 20-ку с тремя "дырками" :)

"Ускорители" будут делать, наверное, для поиска цепочек по 36 делителей.
Господин Лецко писал в сообщении
https://dxdy.ru/post1552974.html#p1552974

В случае отыскания цепочек из чисел по 36 делителей параллелить придется (без этого реально отыскать, разве что, цепочку из 12 чисел).
Полагаю, разумно разбить поиск на две части. Сначала искать цепочку из 13 чисел (12 найдутся по ходу). А в случае не слишком трудозатратного успеха искать 15 чисел (14 по ходу). Для 13 чисел могу предоставить 384 паттерна, которые кажутся мне наиболее перспективными. Уверен такой ширины захвата достаточно.

Цепочка из 20 чисел по 48 делителей, весьма вероятно, найдется в ближайшее время (даже если Лев не "раскошелится" хотя бы на один поток :) )
Только за сегодня нашел еще две цепочки по 19 чисел.

Господин Петухов получил, наконец, паттерны и приступил к созданию "ускорителей".

PS. Хорошо, если с 20-ой действительно повезёт, и она будет быстро найдена.
В моей нерешённой проблеме - 19-ка (симметричный кортеж из последовательных простых чисел)...
17-ки давно найдены, несколько 19-ок с одной "дыркой" давно найдены, однако 19-ки до сих пор нет!
Она ищется уже 8 лет.
И в данный момент ищется.

И сегодня в искомой 19-ке нашлась первая полная 11-ка!
Вот она - красавица

258410073778468021379: 0 30 48 54 78 84 90 114 120 138 168

Подробности смотрите в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=224&postid=8570
Ну вот, из 19 последовательных простых чисел, найдено уже 11, удовлетворяющих паттерну. Осталось всего 8 неправильных чисел.
То есть найдена 19-ка с восемью "дырками", по четыре "дырки" в начале и в конце кортежа.
Вот эта 19-ка

{258410073778468021099*, 258410073778468021303*, 258410073778468021307*, 258410073778468021357*, 258410073778468021379,
258410073778468021409, 258410073778468021427, 258410073778468021433, 258410073778468021457, 258410073778468021463,
258410073778468021469, 258410073778468021493, 258410073778468021499, 258410073778468021517, 258410073778468021547,
258410073778468021561*, 258410073778468021633*, 258410073778468021643*, 258410073778468021651*}

Неправильные элементы помечены звёздочкой.
Все числа в этом кортеже простые и последовательные, но 8 чисел не легли на паттерн.
Конечно, до 19-ки ещё очень далеко, но полная 11-ка - это уже маленький прогресс.
До этого находились только полные 9-ки.
Мы с черепашкой очень рады полной 11-ке, она долго не находилась.
Теперь будем ждать полную 13-ку.
Пока даже 13-ки с одной "дыркой" не было, только с двумя "дырками".

Напомню, что кроме этого эксперимента, который я пока выполняю одна, у нас выполняется другой эксперимент, в котором тоже может найтись 19-ка.
В этом эксперименте в данный момент работают четверо, включая меня.
Тут тотальная проверка (алгоритм грубой силы)! И если на пути этой тотальной проверки 19-ка встретится, то она никуда она от нас не денется.
Вопрос только в том, когда она встретится.

Черепашка ищет кортежи

Поиск ассоциативных наборов простых              5:58:42
Текущий интервал: [3539064725785867666 ... 3539064727785867666]
Проверено :      0%
Скорость  :    247
Найдено 12:   1265
Найдено 13:      0
Найдено 14:     54
Найдено 15:      0
Найдено 16:      2
Найдено 17:      0
Найдено 18:      0
Найдено 19:      0
Найдено 20:      0
Найдено 21:      0
Найдено 22:      0
Найдено 23:      0
Найдено 24:      0
Найдено 25:      0
Найдено 26:      0
Найдено 27:      0
Найдено 28:      0
Найдено 29:      0
Найдено 30:      0
Найдено 31:      0
Найдено 32:      0
Найдено 33:      0

Стабильный набор длин найденных кортежей: 12, 14, 16.
Редко попадаются 13-ки и 18-ки.
У других участников встречаются 20-ки, даже одна 22-ка попалась.
Пока ни 15-ки, ни 17-ки не попались - в этом ручном эксперименте.
Как видим, даже тотальная проверка изредка находит 13-ки, и совсем редки 15-ки и 17-ки.
17-ок за всё время действия проекта (8 лет) найдено всего 9 штук (не считая 17-ок, найденных Ярославом Врублевским в конкурсе по кортежам, эти 17-ки с огромными точками входа).

Замечательная программа Алексея Белышева!
Он сделал её в самом начале проекта по кортежам.
Потом адаптировал под BOINC-платформу.
Это ещё тогда, когда был запущен первый BOINC-проект - Stop@home.
Где сейчас Алексей?
Я не вижу его ни на форуме boinc.ru, ни на форуме dxdy.ru, ни на форуме MHP.

Дорогой Алексей!
Если вы читаете это, пожалуйста, отзовитесь.
Надо снова запустить проект по кортежам в BOINC.
Вы можете в этом помочь.
Tomas Brada, похоже, закончил свою деятельность. Проект стоит больше двух месяцев.
В ручном проекте мы много не насчитаем.

Как вы можете помочь?
Вы можете сделать готовый расчётный модуль для BOINC-проекта, который можно предложить для запуска на yoyo@home.
Они это могут принять.
Смотрите темы
https://boinc.progger.info/odlk/forum_thread.php?id=49
https://boinc.progger.info/odlk/forum_thread.php?id=224
https://boinc.progger.info/odlk/forum_thread.php?id=225
Пишите мне, адрес не изменился.

Игра "Угадай слово" за 19 апреля

МИТРА
КУМАЧ
ЗАМОК

Сегодня опять "двойка" :(
Первые два проверочных слова поймали всего одну букву, и та не на своём месте. Не повезло.
Пришлось сделать ещё три попытки. И долго думать.
А слово загадано очень простое.

Игра "Угадай слово" за 20 апреля

ОБЪЕМ
ПУШКА
ЧАСТЬ
ВИРАЖ
ДИВАН

Сегодня "тройка".
Думать что-то сильно не хотелось, в третьем проверочном слове явная ошибка, можно было вполне написать загаданное слово, если подумать.
Ну, зато быстро сыграла, за три минуты.

У господина Петухова проблема в программе; он подозревает, что в PARI/GP какая-то ошибка, что вряд ли.
Скорее, у него в программе какая-то ошибка.
https://dxdy.ru/post1553140.html#p1553140

Главное не понимаю почему не ту ошибку вываливает, или даже вообще не ошибку (ошибки я как раз перехватываю и обрабатываю). Смахивает на глюк CPU/RAM или самого PARI.

В общем, застопорилось создание "ускорителей".

Антон Никонов продолжает искать меньший пентадекатлон.
И нафиг он ему нужен, если больше никому не нужен?
Хочет доказать, что он существует?

kotenok gav считать, похоже, отказался.
Что-то у него с потоками непонятки. Он считает, что одна программа на PARI/GP на одно ядро - это "слишком расточительно".
https://dxdy.ru/post1552920.html#p1552920

Если это так, то... это как-то уж слишком расточительно выполнять одну программу в одном PARI/GP потоке.

Он хочет посадить на одно ядро несколько программ? :)

Мыльная опера "Совершенный кубоид" на форуме MHP чуть-чуть прервалась.
Но, думаю, не надолго.
Скоро Захар родит (N+2)-ое доказательство несуществования совершенного кубоида или очередную параметризацию, которая уж точно будет полной.
И тогда совершенный кубоид будет у него в кармане, несмотря на то, что он доказал его несуществование :)))