ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · 7 . . . 27 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Смотрит ли эту тему Белышев? Ау, Алексей! Тут для вас столько грандиозных задач! :) Пожалуйста, решайте, не ленитесь :) Нам покажите, пожалуйста, что нарешаете. Вот, к примеру, ДЛК 20-го порядка, показанный чуть выше. Неужели у такого гармоничного ДЛК нет других ортогональных диагональных соквадратов??? Что-то не верится в это. А найти их как? Ваша программа не хочет искать :) Говорит, что слишком много диагональных транверсалей. Так это же хорошо, что их много! Значит, есть шансы построить ортогональные диагональные соквадраты. А какая оригинальная блочная структура в этом ДЛК! Залюбуетесь :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И в заключение о ОДЛК 20-го порядка Я построила уже сейчас ещё две ортогональные пары ДЛК 20-го порядка методом составных квадратов. Первая ортогональная пара ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 Свойства этих ОДЛК, выданные утилитой Harry White Tuesday 2020-06-16 08:04:42 ¦юёъютёъюх тЁхь (чшьр)
Order? 20
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
2 diagonal Latin
1 weakly pandiagonal
2 center symmetric
2 nfr
1 orthogonal pair
2 self-orthogonalВторая ортогональная пара ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 Свойства этих ОДЛК, выданные утилитой Harry, точно такие же Tuesday 2020-06-16 08:06:47 ¦юёъютёъюх тЁхь (чшьр)
Order? 20
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
2 diagonal Latin
1 weakly pandiagonal
2 center symmetric
2 nfr
1 orthogonal pair
2 self-orthogonalОДЛК все нормализованные и вроде различные. Но вот насчёт изоморфности... Нет у меня канонизатора для ДЛК 20-го порядка, пока ещё не сделал Алексей :) Вполне возможно, что эти ортогональные пары изоморфные и ещё изоморфны подобной ортогональной паре, показанной выше. Очень интересное в показанных ортогональных парах: ОДЛК в каждой ортогональной паре получаются друг из друга перестановкой строк! Ортогональных пар ДЛК с таким свойством для порядка 10, по-моему, не существует; по крайней мере, мне такие ортогональные пары ДЛК 10-го порядка неизвестны. Для порядка 9 ортогональным парам ДЛК с таким свойством посвящён BOINC-проект Rake Search. Смотрите тему об этом проекте здесь https://boinc.progger.info/odlk/forum_thread.php?id=31 Вроде бы в этом проекте искали и ортогональные пары ДЛК 10-го порядка с таким свойством. Нашли ли? А вот ортогональные пары ЛК 10-го порядка с таким свойством есть! Кажется, всё написала о ДЛК и ОДЛК 20-го порядка. Далее расскажу о порядке 21. PS. Забыла сказать об ортогональных парах ДЛК 20-го порядка, построенных Алексеем Черновым методом Ли Жу. В его статье http://alex-black.ru/article.php?content=126 есть Приложение. Скачайте его, в нём вы найдёте папку с ортогональными парами ДЛК, построенными методом Ли Жу. Там есть ортогональные пары ДЛК не только для порядка 20. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Порядок 21 проблемный - для ортогональных пар ДЛК. Для ортогональных пар ЛК - нет, потому что 21=3*7, и ортогональны пары ЛК порядков 3 и 7 существуют. Следовательно, можно построить ортогональную пару ЛК 21-го порядка методом составных квадратов. А вот ортогональных пар ДЛК 3-го порядка не существует. В статье ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ http://www.natalimak1.narod.ru/dlk.htm ДЛК 21-го порядка, построенный методом Гергели, изображён на рис.30. Показываю этот ДЛК 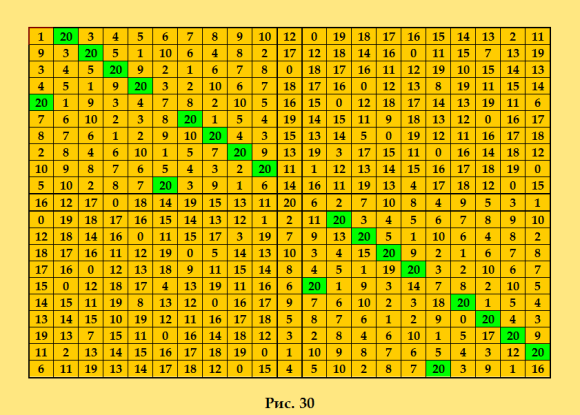 Утилита Harry White никаких свойств в этом ДЛК не обнаружила. Поискать ортогональные диагональные соквадраты к этому ДЛК с помощью программы Белышева ortogon_u, конечно, не удалось: слишком много диагональных трансверсалей у этого ДЛК. В общем, ортогональной пары с квадратом Гергели 21-го порядка пока не имеем. Даже и не знаем, существует ли она в природе. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Хм.. Просмотрела свои статьи и... не нашла ни одной ортогональной пары ДЛК 21-го порядка. Тогда расскажу о интересном ЛК 21-го порядка. В статье ГРУППЫ MOLS 20-го и 21-го ПОРЯДКА http://www.natalimak1.narod.ru/mols20_21.htm построила группу MOLS 21-го порядка, состоящую из 5 взаимно ортогональных ЛК по квази-разностной матрице из книги “Handbook of Combinatorial Designs”. Пятый ЛК в этой группе MOLS показан в статье на рис. 24. Этот ЛК мне помогли построить на форуме dxdy.ru, я сразу не поняла, как его построить по заданной квази-разностной матрице. Вот в этом ЛК сразу бросается в глаза очень интересное свойство. Этим свойством обладают и другие ЛК данной группы MOLS. Покажу пятый ЛК с рис. 24 в традиционной форме 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 Закономерность в этом ЛК ну очень очевидна! Этот ЛК пандиагональный в одном направлении; своего рода псевдопандиагональность. А теперь вспомним, что такое пандиагональный квадрат. Да, мы имеем набор готовых трансверсалей! И выписав этот набор трансверсалей, мы получим ЛК ортогональный исходному. Вот прямо сразу - ничего не делая. Показываю этот готовый ортогональный ЛК, полученный из готового набора трансверсалей в исходном ЛК 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 14 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 15 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 16 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 17 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 18 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 19 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 20 19 17 15 13 11 9 7 5 3 1 20 18 16 14 12 10 8 6 4 2 0 20 18 16 14 12 10 8 6 4 2 0 19 17 15 13 11 9 7 5 3 1 Проверяю эти ЛК утилитой Harry White Wednesday 2020-06-17 08:24:43 ╠юёъютёъюх тЁхь (чшьр)
Order? 21
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt
Counts
------
2 Latin
2 center symmetric
1 nfr
1 nfc
1 orthogonal pairВсё правильно: ЛК ортогональные; ещё оба они ассоциативные. И ещё: оба пандиагональные в одном направлении (причём направления эти разные в двух ЛК, в одном - для прямых разломанных диагоналей, а в другом - для обратных), что утилита Harry не отмечает. Закономерность построения этого ЛК обалденная! Интересно: для каких ещё порядков ЛК эта закономерность работает? Кстати, очень давно я пыталась построить ЛК 10-го порядка пандиагональный в одном направлении. Начала писать программу, но с некоторого момента программа начала впадать в ступор. Пришлось бросить. То ли ошиблась где-то, то ли для порядка 10 ЛК с таким свойством не существуют. А жаль, если не существуют. Очень полезное свойство при построении ортогональных пар ЛК. Пыталась и ДЛК 10-го порядка построить с таким свойством. Тоже ничего не получилось. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Да, но где же нам взять хотя бы одну ортогональную пару ДЛК 21-го порядка? Как её построить? В моей статье http://www.natalimak1.narod.ru/dolk.htm описаны эксперименты с Приложением Чернова для построения ортогональных пар ДЛК методом Ли Жу (ссылка на статью Чернова чуть выше). Цитирую Для порядка 19 программа что-то надолго задумалась. Не стала ждать результатов. Далее попробовала построить с подквадратом 5х5. Цитирую Пара ортогональных квадратов построилась, но они не диагональные. Так что, пока ортогональной пары ДЛК 21-го порядка у нас нет. Есть отличная задача! Дерзайте, господа! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Погуляла в Интернете, искала ортогональную пару ДЛК 21-го порядка. Не нашла :( Никто не построил? Зато нашла интересную статью New Bounds For Pairwise Orthogonal Diagonal Latin Squares B.Du https://pdfs.semanticscholar.org/8fbc/493f8a0c436298ba0b85727e22e328339ed5.pdf А в статье нашла очень интересную теорему, покажу скриншот  Напишу и текст на всякий случай (картинка может исчезнуть) Theorem 1.1 Перевод в Google Существует пять попарно ортогональных диагональных латинских квадратов каждого порядок n, где n > 164. Вот, значит, как. Для порядка 15 существование пяти пар попарно ортогональных ДЛК не установлено. Я нашла группу из четырёх попарно ортогональных ДЛК 15-го порядка, о чём рассказано выше. Расширить эту группу до пяти попарно ортогональных ДЛК мне не удалось. Но не факт, что расширение не существует. Это надо доказать. Ну, с порядком 10 всё понятно: для этого порядка даже трёх попарно ортогональных ДЛК пока не найдено. Порядок 21 тоже проблемный; да уж, где там пять попарно ортогональных ДЛК - я никак не найду одну ортогональную пару ДЛК для этого порядка. Господа! Давайте вместе поищем :) PS. В списке литературы в указанной статье есть такая статья [3] B. Du, Four pairwise orthogonal diagonal Latin squares, Utilitas Math. Тот же автор. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, для порядка 21 я пока не нашла ни одной ортогональной пары ДЛК. Наверное, плохо искала. Свои статьи вроде внимательно просмотрела. В Интернете поискала. Ну, не попалась мне. Поищите вы, кто хочет, конечно. Она, разумеется, существует; математики доказали это. Перехожу к порядку 22. Как всегда, начну с ДЛК, построенного методом Гергели. Смотрим мою статью ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ ДЛК 22-го порядка вы видите в статье на рис. 17. Утилита Harry White отметила в этом ДЛК только симметричность по Гергели/Брауну. Но это такая красивая симметрия! Хоть ковры начинай изготавливать :) Показываю ДЛК с частичной раскраской вертикальной симметрии  Да, гармоничный ДЛК. А есть ли у него ортогональные ДЛК? Хороший вопрос! Ответ я не знаю. Кто знает, скажите :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Построению ортогональных пар ДЛК 22-го порядка посвящена моя статья http://www.natalimak1.narod.ru/diagon22.htm Варьируя известную квази-разностную матрицу я построила 576 неизоморфных ортогональных пар ДЛК 22-го порядка. Однако факт неизоморфности этих ортогональных пар надо доказать (или опровергнуть). Да, по виду эти ортогональные пары различны. Но это ещё не означает, что они неизоморфны. Ну, в любом случае одна ортогональная пара ДЛК 22-го порядка у нас уже есть. Сейчас посмотрю статьи с экспериментами по методам Чернова, там вроде тоже есть ортогональная пара ДЛК 22-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Да, вот ортогональная пара ДЛК 22-го порядка из статьи http://www.natalimak1.narod.ru/dolk.htm (статья с абракадабрами на сайте; у нас есть теперь перекодированный нормальный вариант) построенная методом Ли Жу, описанным подробно Черновым 0 21 20 19 18 17 15 14 16 8 6 5 4 3 9 2 11 12 10 7 13 1 4 1 21 20 19 18 0 16 15 9 7 6 5 10 3 12 13 11 8 14 2 17 11 5 2 21 20 19 18 1 17 10 8 7 6 4 13 14 12 9 15 3 0 16 5 12 6 3 21 20 19 18 2 11 9 8 7 14 15 13 10 16 4 1 17 0 15 6 13 7 4 21 20 19 18 12 10 9 8 16 14 11 17 5 2 0 1 3 17 16 7 14 8 5 21 20 19 13 11 10 9 15 12 0 6 3 1 2 4 18 16 0 17 8 15 9 6 21 20 14 12 11 10 13 1 7 4 2 3 5 18 19 14 17 1 0 9 16 10 7 21 15 13 12 11 2 8 5 3 4 6 18 19 20 3 15 0 2 1 10 17 11 8 16 14 13 12 9 6 4 5 7 18 19 20 21 13 14 15 16 17 0 1 2 3 19 18 21 20 12 11 10 9 8 7 6 5 4 6 7 8 9 10 11 12 13 14 20 21 18 19 5 4 3 2 1 0 17 16 15 2 3 4 5 6 7 8 9 10 18 19 20 21 1 0 17 16 15 14 13 12 11 1 2 3 4 5 6 7 8 9 21 20 19 18 0 17 16 15 14 13 12 11 10 21 20 19 18 16 14 13 15 0 7 5 4 3 17 2 8 1 10 11 9 6 12 20 19 18 15 13 12 14 17 11 6 4 3 2 21 16 1 7 0 9 10 8 5 19 18 14 12 11 13 16 10 4 5 3 2 1 20 21 15 0 6 17 8 9 7 18 13 11 10 12 15 9 3 6 4 2 1 0 19 20 21 14 17 5 16 7 8 12 10 9 11 14 8 2 5 7 3 1 0 17 18 19 20 21 13 16 4 15 6 9 8 10 13 7 1 4 6 5 2 0 17 16 11 18 19 20 21 12 15 3 14 7 9 12 6 0 3 5 4 13 1 17 16 15 8 10 18 19 20 21 11 14 2 8 11 5 17 2 4 3 12 1 0 16 15 14 6 7 9 18 19 20 21 10 13 10 4 16 1 3 2 11 0 12 17 15 14 13 7 5 6 8 18 19 20 21 9 0 17 16 15 14 21 20 19 18 1 8 10 11 6 4 12 5 3 7 13 9 2 7 1 0 17 16 15 21 20 19 2 9 11 12 5 13 6 4 8 14 10 3 18 6 8 2 1 0 17 16 21 20 3 10 12 13 14 7 5 9 15 11 4 18 19 15 7 9 3 2 1 0 17 21 4 11 13 14 8 6 10 16 12 5 18 19 20 9 16 8 10 4 3 2 1 0 5 12 14 15 7 11 17 13 6 18 19 20 21 8 10 17 9 11 5 4 3 2 6 13 15 16 12 0 14 7 18 19 20 21 1 13 9 11 0 10 12 6 5 4 7 14 16 17 1 15 8 18 19 20 21 2 3 2 14 10 12 1 11 13 7 6 8 15 17 0 16 9 18 19 20 21 3 4 5 17 3 15 11 13 2 12 14 8 9 16 0 1 10 18 19 20 21 4 5 6 7 3 4 5 6 7 8 9 10 11 20 21 18 19 2 1 0 17 16 15 14 13 12 4 5 6 7 8 9 10 11 12 18 19 20 21 3 2 1 0 17 16 15 14 13 1 2 3 4 5 6 7 8 9 19 18 21 20 0 17 16 15 14 13 12 11 10 5 6 7 8 9 10 11 12 13 21 20 19 18 4 3 2 1 0 17 16 15 14 16 15 14 13 21 20 19 18 1 0 7 9 10 17 5 3 11 4 2 6 12 8 14 13 12 21 20 19 18 0 7 17 6 8 9 15 16 4 2 10 3 1 5 11 12 11 21 20 19 18 17 6 10 16 5 7 8 13 14 15 3 1 9 2 0 4 10 21 20 19 18 16 5 9 3 15 4 6 7 11 12 13 14 2 0 8 1 17 21 20 19 18 15 4 8 2 16 14 3 5 6 9 10 11 12 13 1 17 7 0 20 19 18 14 3 7 1 15 17 13 2 4 5 21 8 9 10 11 12 0 16 6 19 18 13 2 6 0 14 16 5 12 1 3 4 20 21 7 8 9 10 11 17 15 18 12 1 5 17 13 15 4 14 11 0 2 3 19 20 21 6 7 8 9 10 16 11 0 4 16 12 14 3 13 15 10 17 1 2 18 19 20 21 5 6 7 8 9 Утилита Harry White не обнаружила у этих ОДЛК никаких свойств Thursday 2020-06-18 07:00:56 ╠юёъютёъюх тЁхь (чшьр)
Order? 22
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt
Counts
------
2 diagonal Latin
1 orthogonal pairКонстатирует, что ДЛК ортогональны; ну, это мы сами знаем :) Кажется, всё у меня об ортогональных парах ДЛК 22-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Для ДЛК 22-го порядка программа Белышева ortogon_u тоже ничего не хочет строить, ругается - и всё. Переходим к порядку 23. Тут всё просто, уф - отдыхаем :) Число 23 простое. Существует полная система MOLS 23-го порядка, состоящая из 22 взаимно ортогональных ЛК. Два ЛК в этой системе не являются ДЛК. Все ЛК этой полной системы элементарно строятся методом циклического сдвига, как и полные системы для всех порядков, являющихся простым числом. Сейчас построю и покажу первые два ДЛК этой полной системы. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Готово! 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Утилита Harry White сообщает от этих ОДЛК следуюшее: Thursday 2020-06-18 07:45:45 ╠юёъютёъюх тЁхь (чшьр)
Order? 23
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
2 diagonal Latin
2 pandiagonal
2 center symmetric
2 nfr
1 orthogonal pair
2 self-orthogonalОтличные свойства! Квадраты ассоциативные и пандиагональные (то есть ultra), ещё они self orthogonal. Все ЛК и ДЛК полной системы MOLS 23-го порядка получаются друг из друга перестановкой строк (этим свойством обладают все ЛК и ДЛК полной системы MOLS любого порядка, являющегося простым числом). Осталось посмотреть на ДЛК Гергели 23-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это ДЛК 23-го порядка, построенный методом Гергели 1 22 3 4 5 6 7 8 9 10 11 13 0 21 20 19 18 17 16 15 14 2 12 2 3 22 5 6 7 8 9 10 11 1 15 12 0 21 20 19 18 17 16 4 14 13 3 4 5 22 7 8 9 10 11 1 2 17 13 12 0 21 20 19 18 6 16 15 14 4 5 6 7 22 9 10 11 1 2 3 19 14 13 12 0 21 20 8 18 17 16 15 5 6 7 8 9 22 11 1 2 3 4 21 15 14 13 12 0 10 20 19 18 17 16 6 7 8 9 10 11 22 2 3 4 5 12 16 15 14 13 1 0 21 20 19 18 17 7 8 9 10 11 1 2 22 4 5 6 14 17 16 15 3 13 12 0 21 20 19 18 8 9 10 11 1 2 3 4 22 6 7 16 18 17 5 15 14 13 12 0 21 20 19 9 10 11 1 2 3 4 5 6 22 8 18 19 7 17 16 15 14 13 12 0 21 20 10 11 1 2 3 4 5 6 7 8 22 20 9 19 18 17 16 15 14 13 12 0 21 22 1 2 3 4 5 6 7 8 9 10 0 21 20 19 18 17 16 15 14 13 12 11 0 13 15 17 19 21 12 14 16 18 20 22 10 8 6 4 2 11 9 7 5 3 1 21 0 12 13 14 15 16 17 18 19 9 8 20 22 7 6 5 4 3 2 1 11 10 20 21 0 12 13 14 15 16 17 7 19 6 8 18 22 5 4 3 2 1 11 10 9 19 20 21 0 12 13 14 15 5 17 18 4 7 6 16 22 3 2 1 11 10 9 8 18 19 20 21 0 12 13 3 15 16 17 2 6 5 4 14 22 1 11 10 9 8 7 17 18 19 20 21 0 1 13 14 15 16 11 5 4 3 2 12 22 10 9 8 7 6 16 17 18 19 20 10 0 12 13 14 15 9 4 3 2 1 11 21 22 8 7 6 5 15 16 17 18 8 20 21 0 12 13 14 7 3 2 1 11 10 9 19 22 6 5 4 14 15 16 6 18 19 20 21 0 12 13 5 2 1 11 10 9 8 7 17 22 4 3 13 14 4 16 17 18 19 20 21 0 12 3 1 11 10 9 8 7 6 5 15 22 2 12 2 14 15 16 17 18 19 20 21 0 1 11 10 9 8 7 6 5 4 3 13 22 11 12 13 14 15 16 17 18 19 20 21 10 22 9 8 7 6 5 4 3 2 1 0 Никаких свойств в этом ДЛК утилита Harry White не обнаружила. Мне неизвестно, есть ли у этого ДЛК ортогональные ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Рассмотрим теперь порядок 24. Для ортогональных пар ДЛК этот порядок проблемный, а для ортогональных пар ЛК - нет, потому что 24=3*8, и ортогональны пары ЛК 3-го и 8-го порядков существуют. В статье http://www.natalimak1.narod.ru/dlk.htm на рис. 11 изображён ДЛК 24-го порядка, построенный методом составных квадратов. ДЛК 24-го порядка методом Гергели я в статье не построила, написала, что можно построить. Ну, это одиночные ДЛК 24-го порядка. Посмотрю, что у меня с ортогональными парами ДЛК 24-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ура-а-а-а! Есть ортогональная пара ДЛК 24-го порядка. В моей статье http://www.natalimak1.narod.ru/ddolk.htm (статья тоже с абракадабрами на сайте, но я её перекодировала). Цитирую Пример № 2. Построение пары ОДЛК 24-го порядка Это порядок, для которого я не могла ранее построить ни одной пары ОДЛК. В качестве исходной пары ОДЛК 8-го пордка выбрала такую пару: 0 1 2 3 4 5 6 7 2 3 0 1 6 7 4 5 4 5 6 7 0 1 2 3 6 7 4 5 2 3 0 1 5 4 7 6 1 0 3 2 7 6 5 4 3 2 1 0 1 0 3 2 5 4 7 6 3 2 1 0 7 6 5 4 0 1 2 3 4 5 6 7 3 2 1 0 7 6 5 4 6 7 4 5 2 3 0 1 5 4 7 6 1 0 3 2 1 0 3 2 5 4 7 6 2 3 0 1 6 7 4 5 7 6 5 4 3 2 1 0 4 5 6 7 0 1 2 3 Это полученная пара ОДЛК 24-го порядка: 8 2 1 0 7 6 5 4 3 9 10 11 12 13 14 16 23 22 21 20 19 18 17 15 1 11 3 2 5 4 7 6 10 0 8 9 14 15 19 13 21 20 23 22 17 16 12 18 7 6 14 4 3 2 1 0 12 13 5 15 8 22 10 11 19 18 17 16 23 9 21 20 5 4 7 13 1 0 3 2 14 15 12 6 21 11 8 9 17 16 19 18 10 20 23 22 6 7 4 5 9 3 0 1 13 12 15 17 2 8 11 10 18 19 16 14 22 23 20 21 4 5 6 7 0 10 2 3 15 14 18 12 11 1 9 8 16 17 13 19 20 21 22 23 2 3 0 1 6 7 15 5 9 23 11 10 13 12 4 14 22 8 20 21 18 19 16 17 0 1 2 3 4 5 6 12 20 10 9 8 15 14 13 7 11 21 22 23 16 17 18 19 10 17 8 9 14 15 12 13 16 11 6 19 20 21 22 23 4 5 18 7 0 1 2 3 18 9 10 11 12 13 14 15 8 19 16 5 22 23 20 21 6 7 4 17 2 3 0 1 14 15 12 23 10 11 8 9 0 21 22 13 16 17 18 19 20 1 2 3 4 5 6 7 12 13 20 15 8 9 10 11 22 3 14 21 18 19 16 17 2 23 0 1 6 7 4 5 15 14 13 12 11 16 9 8 21 20 23 22 17 10 7 18 1 0 3 2 5 4 19 6 13 12 15 14 19 8 11 10 23 22 21 20 9 18 17 4 3 2 1 0 7 6 5 16 11 10 9 8 15 14 13 22 17 16 19 18 1 20 23 12 5 4 7 6 21 0 3 2 9 8 11 10 13 12 21 14 19 18 17 16 23 2 15 20 7 6 5 4 3 22 1 0 17 16 19 18 21 20 23 7 11 1 2 3 4 5 6 22 0 10 9 8 15 14 13 12 19 18 17 16 23 22 4 20 2 8 0 1 6 7 21 5 9 3 11 10 13 12 15 14 21 20 23 22 17 1 19 18 4 5 13 7 0 16 2 3 15 14 6 12 11 10 9 8 23 22 21 20 2 18 17 16 6 7 4 14 19 3 0 1 13 12 15 5 9 8 11 10 20 21 22 6 16 17 18 19 5 4 7 23 10 0 3 2 14 15 12 13 1 11 8 9 22 23 5 21 18 19 16 17 7 6 20 4 3 9 1 0 12 13 14 15 8 2 10 11 16 0 18 19 20 21 22 23 1 17 3 2 5 4 12 6 10 11 8 9 14 15 7 13 3 19 16 17 22 23 20 21 18 2 1 0 7 6 5 15 8 9 10 11 12 13 14 4 16 2 1 0 7 6 5 4 3 17 18 19 20 21 22 11 12 13 14 15 8 9 10 23 0 18 2 3 4 5 6 7 19 1 17 16 23 22 9 20 15 14 13 12 11 10 21 8 5 4 20 6 1 0 3 2 22 23 7 21 18 15 16 17 10 11 8 9 14 19 12 13 6 7 4 22 2 3 0 1 21 20 23 5 13 16 19 18 9 8 11 10 17 12 15 14 2 3 0 1 21 7 4 5 17 16 19 14 6 20 23 22 13 12 15 18 9 8 11 10 1 0 3 2 5 23 7 6 18 19 12 17 22 4 20 21 14 15 16 13 10 11 8 9 4 5 6 7 0 1 17 3 23 10 21 20 19 18 2 16 11 22 9 8 15 14 13 12 7 6 5 4 3 2 1 19 8 21 22 23 16 17 18 0 20 9 10 11 12 13 14 15 15 1 13 12 11 10 9 8 0 14 16 3 4 5 6 7 18 19 2 17 22 23 20 21 3 13 14 15 8 9 10 11 12 2 1 18 7 6 5 4 17 16 19 0 21 20 23 22 9 8 11 5 13 12 15 14 20 7 4 10 2 3 0 1 6 21 22 23 16 17 18 19 10 11 7 9 14 15 12 13 5 22 8 6 1 0 3 2 23 4 21 20 19 18 17 16 14 15 12 13 10 4 8 9 1 0 3 2 5 11 21 6 19 18 17 16 23 22 7 20 13 12 15 14 6 8 11 10 2 3 0 1 9 7 4 23 16 17 18 19 20 21 22 5 8 9 10 11 12 13 14 0 7 6 5 4 17 2 1 15 21 20 23 22 3 16 19 18 11 10 9 8 15 14 2 12 4 5 6 7 0 19 13 3 22 23 20 21 18 1 16 17 20 21 22 23 16 17 18 15 6 9 10 11 12 13 14 19 8 7 4 5 2 3 0 1 23 22 21 20 19 18 13 16 11 4 9 8 15 14 17 12 5 10 7 6 1 0 3 2 18 19 16 17 22 11 20 21 14 15 2 13 10 23 8 9 0 1 12 3 4 5 6 7 17 16 19 18 9 20 23 22 13 12 15 0 21 8 11 10 3 2 1 14 7 6 5 4 21 20 23 10 17 16 19 18 9 8 11 22 3 12 15 14 7 6 5 4 13 2 1 0 22 23 8 21 18 19 16 17 10 11 20 9 14 1 12 13 4 5 6 7 0 15 2 3 19 14 17 16 23 22 21 20 15 18 13 12 11 10 7 8 1 0 3 2 5 4 9 6 12 17 18 19 20 21 22 23 16 13 14 15 8 9 10 5 2 3 0 1 6 7 4 11 Ортогональная пара построена методом Пелегрино-Ланселотти, описанным в статье Чернова http://alex-black.ru/article.php?content=124 Никаких свойств у этих ОДЛК утилита Harry White не обнаружила Thursday 2020-06-18 08:44:02 ╠юёъютёъюх тЁхь (чшьр)
Order? 24
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_3.txt
Counts
------
2 diagonal Latin
1 orthogonal pairМожно переходить к порядку 25. Этот порядок не проблемный, потому что 25=5^2. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Интересно строятся ортогональные пары ДЛК 24-го порядка программой Чернова. Мгновенно! Скачайте Приложение в указанной статье, попробуйте. И интересно, что можно построить таких ортогональных пар ДЛК много. Для показанной выше ортогональной пары ДЛК я выбрала первые два ДЛК 8-го порядка из полной системы MOLS. Обозначим ОДЛК этой показанной выше пары: A и B. Теперь взяла следующие два ДЛК 8-го порядка из той же полной системы MOLS и построила на их основе ортогональную пару ДЛК 24-го порядка. С 8 7 4 5 2 3 0 1 6 9 10 11 12 13 14 20 19 18 17 16 23 22 21 15 2 13 0 1 6 7 4 5 12 3 14 15 8 9 17 11 23 22 21 20 19 18 10 16 3 2 15 0 7 6 5 4 13 12 1 14 9 19 11 10 22 23 20 21 18 8 16 17 7 6 5 10 3 2 1 0 9 8 11 4 22 12 15 14 18 19 16 17 13 23 20 21 1 0 3 2 11 4 7 6 15 14 13 23 5 10 9 8 20 21 22 12 16 17 18 19 5 4 7 6 1 14 3 2 11 10 18 8 15 0 13 12 16 17 9 19 20 21 22 23 4 5 6 7 0 1 12 3 10 16 8 9 14 15 2 13 17 11 19 18 21 20 23 22 0 1 2 3 4 5 6 9 21 15 12 13 10 11 8 7 14 20 23 22 17 16 19 18 12 17 14 15 8 9 10 11 16 13 7 19 20 21 22 23 5 4 18 6 1 0 3 2 20 9 10 11 12 13 14 15 8 21 22 2 16 17 18 19 1 0 3 23 5 4 7 6 9 8 11 22 13 12 15 14 0 20 23 10 17 16 19 18 21 1 2 3 4 5 6 7 13 12 19 14 9 8 11 10 17 5 15 18 21 20 23 22 4 16 6 7 0 1 2 3 11 10 9 8 15 18 13 12 23 22 21 20 19 14 4 16 2 3 0 1 6 7 17 5 15 14 13 12 23 10 9 8 19 18 17 16 11 22 21 1 6 7 4 5 2 3 0 20 14 15 12 13 10 11 8 21 18 19 16 17 3 23 20 9 7 6 5 4 22 2 1 0 10 11 8 9 14 15 16 13 22 23 20 21 18 6 12 17 3 2 1 0 7 19 5 4 18 19 16 17 22 23 20 7 14 1 2 3 4 5 6 21 0 15 12 13 10 11 8 9 22 23 20 21 18 19 2 17 4 11 6 7 0 1 16 3 10 5 8 9 14 15 12 13 23 22 21 20 19 0 17 16 5 4 9 6 1 18 3 2 11 10 7 8 15 14 13 12 19 18 17 16 5 22 21 20 1 0 3 12 23 4 7 6 15 14 13 2 11 10 9 8 21 20 23 4 17 16 19 18 7 6 5 22 13 2 1 0 9 8 11 10 3 12 15 14 17 16 1 18 21 20 23 22 3 2 19 0 7 8 5 4 13 12 15 14 9 6 11 10 16 3 18 19 20 21 22 23 2 17 0 1 6 7 10 5 12 13 14 15 8 9 4 11 6 21 22 23 16 17 18 19 20 7 4 5 2 3 0 15 8 9 10 11 12 13 14 1 D 16 4 7 6 1 0 3 2 5 17 18 19 20 21 22 14 9 8 11 10 13 12 15 23 0 20 2 3 4 5 6 7 21 1 23 22 17 16 10 18 12 13 14 15 8 9 19 11 2 3 21 1 6 7 4 5 23 22 0 20 19 11 17 16 14 15 12 13 10 18 8 9 7 6 5 17 3 2 1 0 18 19 16 4 15 23 20 21 11 10 9 8 22 14 13 12 6 7 4 5 23 3 0 1 19 18 17 9 2 22 21 20 10 11 8 16 14 15 12 13 3 2 1 0 7 19 5 4 22 23 13 21 18 6 16 17 15 14 20 12 11 10 9 8 1 0 3 2 5 4 18 6 20 12 22 23 16 17 7 19 13 21 15 14 9 8 11 10 4 5 6 7 0 1 2 22 8 16 19 18 21 20 23 3 17 9 10 11 12 13 14 15 12 1 14 15 8 9 10 11 0 13 20 3 4 5 6 7 22 23 2 21 18 19 16 17 5 8 11 10 13 12 15 14 9 4 7 16 1 0 3 2 19 18 17 6 23 22 21 20 11 10 9 4 15 14 13 12 17 6 5 8 3 2 1 0 7 16 19 18 21 20 23 22 14 15 0 13 10 11 8 9 2 21 12 1 6 7 4 5 20 3 22 23 16 17 18 19 15 14 13 12 11 6 9 8 3 2 1 0 7 10 19 4 21 20 23 22 17 16 5 18 10 11 8 9 2 15 12 13 6 7 4 5 14 3 0 23 16 17 18 19 20 21 22 1 8 9 10 11 12 13 14 3 4 5 6 7 22 1 2 15 18 19 16 17 0 23 20 21 13 12 15 14 9 8 7 10 1 0 3 2 5 18 11 6 23 22 21 20 19 4 17 16 17 16 19 18 21 20 23 15 7 9 10 11 12 13 14 22 8 6 5 4 3 2 1 0 20 21 22 23 16 17 11 19 13 3 15 14 9 8 18 10 2 12 0 1 6 7 4 5 22 23 20 21 18 10 16 17 15 14 2 12 11 19 9 8 0 1 13 3 4 5 6 7 19 18 17 16 14 22 21 20 10 11 8 6 23 15 12 13 5 4 7 9 1 0 3 2 18 19 16 8 22 23 20 21 11 10 9 17 0 14 13 12 4 5 6 7 15 1 2 3 23 22 12 20 19 18 17 16 14 15 21 13 10 4 8 9 1 0 3 2 5 11 7 6 21 13 23 22 17 16 19 18 12 20 14 15 8 9 5 11 3 2 1 0 7 6 10 4 9 17 18 19 20 21 22 23 16 8 11 10 13 12 15 1 6 7 4 5 2 3 0 14 Обозначила ОДЛК этой ортогональной пары С и D. Обнаружила, что квадрат А (из предыдущей ортогональной пары) ортогонален квадрату D. Это уже двушка в нашей терминологии. Далее взяла последние два ДЛК 8-го порядка из той же системы MOLS и построила на их основе ещё одну ортогональную пару ДЛК 24-го порядка E 8 4 7 6 1 0 3 2 5 9 10 11 12 13 14 19 20 21 22 23 16 17 18 15 3 15 1 0 7 6 5 4 14 2 12 13 10 11 20 9 18 19 16 17 22 23 8 21 4 5 11 7 0 1 2 3 9 8 6 10 13 16 15 14 21 20 23 22 17 12 19 18 2 3 0 12 6 7 4 5 15 14 13 1 23 10 9 8 19 18 17 16 11 22 21 20 7 6 5 4 14 2 1 0 10 11 8 21 3 15 12 13 22 23 20 9 18 19 16 17 1 0 3 2 5 9 7 6 12 13 18 15 8 4 10 11 16 17 14 19 20 21 22 23 6 7 4 5 2 3 13 1 11 22 9 8 15 14 0 12 23 10 21 20 19 18 17 16 0 1 2 3 4 5 6 10 17 12 15 14 9 8 11 7 13 16 19 18 21 20 23 22 14 17 12 13 10 11 8 9 16 15 3 19 20 21 22 23 1 0 18 2 5 4 7 6 22 9 10 11 12 13 14 15 8 23 20 4 18 19 16 17 7 6 5 21 3 2 1 0 15 14 13 18 11 10 9 8 0 16 19 12 21 20 23 22 17 1 2 3 4 5 6 7 9 8 21 10 13 12 15 14 23 7 11 20 19 18 17 16 6 22 4 5 2 3 0 1 12 13 14 15 8 23 10 11 18 19 16 17 22 9 5 21 3 2 1 0 7 6 20 4 10 11 8 9 16 15 12 13 20 21 22 23 14 17 18 2 5 4 7 6 1 0 3 19 13 12 15 14 9 8 11 20 19 18 17 16 6 22 21 10 2 3 0 1 23 7 4 5 11 10 9 8 15 14 19 12 21 20 23 22 17 1 13 18 4 5 6 7 0 16 2 3 19 18 17 16 23 22 21 7 13 1 2 3 4 5 6 20 0 12 15 14 9 8 11 10 21 20 23 22 17 16 0 18 6 10 4 5 2 3 19 1 11 7 9 8 15 14 13 12 18 19 16 17 22 4 20 21 1 0 14 2 5 23 7 6 12 13 3 15 8 9 10 11 20 21 22 23 3 17 18 19 7 6 5 9 16 2 1 0 10 11 8 4 14 15 12 13 17 16 19 1 21 20 23 22 2 3 0 18 11 7 4 5 15 14 13 12 6 10 9 8 23 22 6 20 19 18 17 16 4 5 21 7 0 12 2 3 9 8 11 10 13 1 15 14 16 2 18 19 20 21 22 23 3 17 1 0 7 6 8 4 14 15 12 13 10 11 5 9 5 23 20 21 18 19 16 17 22 4 7 6 1 0 3 15 8 9 10 11 12 13 14 2 F 16 6 5 4 3 2 1 0 7 17 18 19 20 21 22 13 10 11 8 9 14 15 12 23 0 22 2 3 4 5 6 7 23 1 21 20 19 18 11 16 13 12 15 14 9 8 17 10 4 5 17 7 0 1 2 3 19 18 6 16 23 12 21 20 9 8 11 10 13 22 15 14 3 2 1 23 7 6 5 4 20 21 22 0 10 17 18 19 14 15 12 13 16 11 8 9 1 0 3 2 18 4 7 6 22 23 20 15 5 19 16 17 12 13 14 21 8 9 10 11 6 7 4 5 2 20 0 1 17 16 9 18 21 3 23 22 11 10 19 8 15 14 13 12 2 3 0 1 6 7 19 5 21 14 23 22 17 16 4 18 15 20 13 12 11 10 9 8 5 4 7 6 1 0 3 21 8 19 16 17 22 23 20 2 18 9 10 11 12 13 14 15 13 1 15 14 9 8 11 10 0 12 19 3 4 5 6 7 17 16 2 18 21 20 23 22 7 11 8 9 14 15 12 13 10 6 5 21 3 2 1 0 22 23 20 4 18 19 16 17 14 15 12 0 10 11 8 9 18 2 1 13 7 6 5 4 3 19 16 17 22 23 20 21 9 8 6 10 13 12 15 14 4 20 11 7 0 1 2 3 21 5 23 22 17 16 19 18 11 10 9 8 15 3 13 12 6 7 4 5 2 14 17 1 23 22 21 20 19 18 0 16 12 13 14 15 5 9 10 11 1 0 3 2 8 4 7 23 16 17 18 19 20 21 22 6 8 9 10 11 12 13 14 2 5 4 7 6 16 0 3 15 20 21 22 23 1 17 18 19 15 14 13 12 11 10 4 8 2 3 0 1 6 22 9 5 19 18 17 16 23 7 21 20 18 19 16 17 22 23 20 15 3 9 10 11 12 13 14 21 8 2 1 0 7 6 5 4 21 20 23 22 17 16 9 18 15 5 13 12 11 10 19 8 4 14 6 7 0 1 2 3 17 16 19 18 21 14 23 22 11 10 2 8 15 20 13 12 0 1 9 3 4 5 6 7 22 23 20 21 8 19 16 17 12 13 14 4 18 9 10 11 7 6 5 15 3 2 1 0 20 21 22 13 16 17 18 19 14 15 12 23 1 11 8 9 5 4 7 6 10 0 3 2 19 18 11 16 23 22 21 20 9 8 17 10 13 7 15 14 2 3 0 1 6 12 4 5 23 12 21 20 19 18 17 16 13 22 15 14 9 8 0 10 6 7 4 5 2 3 11 1 10 17 18 19 20 21 22 23 16 11 8 9 14 15 12 6 1 0 3 2 5 4 7 13 Обозначила ОДЛК этой ортогональной пары E и F. Обнаружила, что квадрат А ортогонален квадрату F. Это уже тройка в нашей терминологии. У квадрата А три ортогональных диагональных соквадрата: B, D, F. К сожалению, взаимной ортогональности в этой тройке не получилось. Интересно: какие ортогональные пары ДЛК 24-го порядка построятся, если перебрать все возможные пары ДЛК 8-го порядка из полной системы MOLS? Можно поиграться. Вариантов пар будет 15. Три варианта я уже использовала. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Перехожу к построению ортогональной пары ДЛК 25-го порядка. Самое простое тут - метод составных квадратов. Берём ортогональную пару ДЛК 5-го порядка 0 1 2 3 4 2 3 4 0 1 4 0 1 2 3 1 2 3 4 0 3 4 0 1 2 0 1 2 3 4 3 4 0 1 2 1 2 3 4 0 4 0 1 2 3 2 3 4 0 1 и на её основе строим ортогональную пару ДЛК 25-го порядка методом составных квадратов. Я не помню, есть ли это построение в моих давних статьях; искать не стала, а построила сейчас, это делается очень просто. Готовая ортогональная пара ДЛК 25-го порядка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 Проверка этих ОДЛК утилитой Harry White выдаёт Thursday 2020-06-18 19:33:16 ╠юёъютёъюх тЁхь (чшьр)
Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
2 diagonal Latin
2 pandiagonal
2 center symmetric
2 nfr
1 orthogonal pair
2 self-orthogonalОтличные квадратики получились! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Теперь интересно, как строится полная система MOLS 25-го порядка. У кого есть матпакет Maple, могут построить эту систему в матпакете. Предполагаю, что для порядка 25 полная система MOLS строится аналогично полной системе MOLS 9-го порядка, покажу её  Смотрите мою статью http://www.natalimak1.narod.ru/grolk.htm (рис. 7) По аналогии должно быть два ЛК не диагональных, остальные диагональные. Таким образом, полная система MOLS 25-го порядка состоит из 24 взаимно ортогональных ЛК, 22 из которых диагональные. Надеюсь, что аналогия не подводит. Если кто-нибудь построит полную систему MOLS 25-го порядка в матпакете, покажите, пожалуйста. Сейчас попробую построить первые два ДЛК в полной системе MOLS 25-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Построила вручную первую пару ОДЛК в полной системе MOLS 25-го порядка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 23 24 20 21 22 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 21 22 23 24 20 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 24 20 21 22 23 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 22 23 24 20 21 2 3 4 0 1 7 8 9 5 6 Сдаётся мне, что эти ОДЛК сильно похожи на ОДЛК, построенные методом составных квадратов. Схема построения легко прослеживается. Проверка построенных ОДЛК утилитой Harry White выдаёт Thursday 2020-06-18 20:57:08 ╠юёъютёъюх тЁхь (чшьр)
Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
2 diagonal Latin
2 pandiagonal
2 center symmetric
2 nfr
1 orthogonal pair
2 self-orthogonalИ свойства ОДЛК точно такие же, как у ОДЛК, построенных методом составных квадратов (см. выше). В общем, с ОДЛК 25-го порядка нет никаких проблем. Далее у нас идёт порядок 26 - проблемный порядок. Ортогональную пару ДЛК данного порядка я искала очень долго. Продолжение следует My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В статье http://www.natalimak1.narod.ru/dlk.htm на рис. 18 изображён ДЛК 26-го порядка, построенный методом Гергели. Показываю этот ДЛК 1 15 3 4 5 6 7 8 9 10 11 12 13 0 25 24 23 22 21 20 19 18 17 16 2 14 2 3 17 5 6 7 8 9 10 11 12 13 1 14 0 25 24 23 22 21 20 19 18 4 16 15 3 4 5 19 7 8 9 10 11 12 13 1 2 15 14 0 25 24 23 22 21 20 6 18 17 16 4 5 6 7 21 9 10 11 12 13 1 2 3 16 15 14 0 25 24 23 22 8 20 19 18 17 5 6 7 8 9 23 11 12 13 1 2 3 4 17 16 15 14 0 25 24 10 22 21 20 19 18 6 7 8 9 10 11 25 13 1 2 3 4 5 18 17 16 15 14 0 12 24 23 22 21 20 19 7 8 9 10 11 12 13 14 2 3 4 5 6 19 18 17 16 15 1 0 25 24 23 22 21 20 8 9 10 11 12 13 1 2 16 4 5 6 7 20 19 18 17 3 15 14 0 25 24 23 22 21 9 10 11 12 13 1 2 3 4 18 6 7 8 21 20 19 5 17 16 15 14 0 25 24 23 22 10 11 12 13 1 2 3 4 5 6 20 8 9 22 21 7 19 18 17 16 15 14 0 25 24 23 11 12 13 1 2 3 4 5 6 7 8 22 10 23 9 21 20 19 18 17 16 15 14 0 25 24 12 13 1 2 3 4 5 6 7 8 9 10 24 11 23 22 21 20 19 18 17 16 15 14 0 25 0 1 2 3 4 5 6 7 8 9 10 11 12 25 24 23 22 21 20 19 18 17 16 15 14 13 25 0 14 15 16 17 18 19 20 21 22 23 11 24 10 9 8 7 6 5 4 3 2 1 13 12 24 25 0 14 15 16 17 18 19 20 21 9 23 10 22 8 7 6 5 4 3 2 1 13 12 11 23 24 25 0 14 15 16 17 18 19 7 21 22 9 8 20 6 5 4 3 2 1 13 12 11 10 22 23 24 25 0 14 15 16 17 5 19 20 21 8 7 6 18 4 3 2 1 13 12 11 10 9 21 22 23 24 25 0 14 15 3 17 18 19 20 7 6 5 4 16 2 1 13 12 11 10 9 8 20 21 22 23 24 25 0 1 15 16 17 18 19 6 5 4 3 2 14 13 12 11 10 9 8 7 19 20 21 22 23 24 12 0 14 15 16 17 18 5 4 3 2 1 13 25 11 10 9 8 7 6 18 19 20 21 22 10 24 25 0 14 15 16 17 4 3 2 1 13 12 11 23 9 8 7 6 5 17 18 19 20 8 22 23 24 25 0 14 15 16 3 2 1 13 12 11 10 9 21 7 6 5 4 16 17 18 6 20 21 22 23 24 25 0 14 15 2 1 13 12 11 10 9 8 7 19 5 4 3 15 16 4 18 19 20 21 22 23 24 25 0 14 1 13 12 11 10 9 8 7 6 5 17 3 2 14 2 16 17 18 19 20 21 22 23 24 25 0 13 12 11 10 9 8 7 6 5 4 3 15 1 13 14 15 16 17 18 19 20 21 22 23 24 25 12 11 10 9 8 7 6 5 4 3 2 1 0 Утилита Harry White отметила в этом ДЛК только симметричность по Гергели/Брауну Thursday 2020-06-18 21:37:26 ╠юёъютёъюх тЁхь (чшьр)
Order? 26
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt
Counts
------
1 diagonal Latin
1 axial symmetricИмеет ли этот ДЛК ортогональные ДЛК, мне неизвестно. Это был первый ДЛК 26-го порядка, который мне удалось построить. Ортогональную пару ДЛК данного порядка в этот момент я ещё не знала. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Первая ортогональная пара ДЛК 26-го порядка была построена в статье http://www.natalimak1.narod.ru/dolk.htm (статья на сайте с абракадабрами. Смотрите перекодированную статью тут https://boinc.progger.info/odlk/forum_thread.php?id=54&postid=5721#5721) на основе алгоритма, разработанного Черновым для метода Ли Жу, и с помощью его программы. Вот эта ортогональная пара 0 25 24 23 22 21 20 18 17 19 16 12 9 6 4 3 5 2 13 8 15 11 7 14 10 1 4 1 25 24 23 22 0 21 19 18 20 13 10 7 5 6 3 14 9 16 12 8 15 11 2 17 7 5 2 25 24 23 22 1 0 20 19 14 11 8 6 4 15 10 17 13 9 16 12 3 18 21 5 8 6 3 25 24 23 22 2 1 21 15 12 9 7 16 11 18 14 10 17 13 4 19 0 20 17 6 9 7 4 25 24 23 22 3 2 16 13 10 8 12 19 15 11 18 14 5 20 1 21 0 13 18 7 10 8 5 25 24 23 22 4 17 14 11 9 20 16 12 19 15 6 21 2 0 1 3 21 14 19 8 11 9 6 25 24 23 22 18 15 12 10 17 13 20 16 7 0 3 1 2 4 5 18 0 15 20 9 12 10 7 25 24 23 19 16 13 11 14 21 17 8 1 4 2 3 5 6 22 15 19 1 16 21 10 13 11 8 25 24 20 17 14 12 0 18 9 2 5 3 4 6 7 22 23 1 16 20 2 17 0 11 14 12 9 25 21 18 15 13 19 10 3 6 4 5 7 8 22 23 24 20 2 17 21 3 18 1 12 15 13 10 0 19 16 14 11 4 7 5 6 8 9 22 23 24 25 19 20 21 0 1 2 3 4 5 6 7 23 22 25 24 18 17 16 15 14 13 12 11 10 9 8 8 9 10 11 12 13 14 15 16 17 18 24 25 22 23 7 6 5 4 3 2 1 0 21 20 19 3 4 5 6 7 8 9 10 11 12 13 22 23 24 25 2 1 0 21 20 19 18 17 16 15 14 2 3 4 5 6 7 8 9 10 11 12 25 24 23 22 1 0 21 20 19 18 17 16 15 14 13 25 24 23 22 20 19 17 16 18 15 0 11 8 5 3 21 2 4 1 12 7 14 10 6 13 9 24 23 22 19 18 16 15 17 14 21 8 10 7 4 2 25 20 1 3 0 11 6 13 9 5 12 23 22 18 17 15 14 16 13 20 7 11 9 6 3 1 24 25 19 0 2 21 10 5 12 8 4 22 17 16 14 13 15 12 19 6 10 3 8 5 2 0 23 24 25 18 21 1 20 9 4 11 7 16 15 13 12 14 11 18 5 9 2 6 7 4 1 21 22 23 24 25 17 20 0 19 8 3 10 14 12 11 13 10 17 4 8 1 5 9 6 3 0 20 15 22 23 24 25 16 19 21 18 7 2 11 10 12 9 16 3 7 0 4 8 1 5 2 21 19 13 14 22 23 24 25 15 18 20 17 6 9 11 8 15 2 6 21 3 7 0 5 4 1 20 18 10 12 13 22 23 24 25 14 17 19 16 10 7 14 1 5 20 2 6 21 4 15 3 0 19 17 8 9 11 12 22 23 24 25 13 16 18 6 13 0 4 19 1 5 20 3 14 17 2 21 18 16 9 7 8 10 11 22 23 24 25 12 15 12 21 3 18 0 4 19 2 13 16 14 1 20 17 15 5 8 6 7 9 10 22 23 24 25 11 0 21 20 19 18 25 24 23 22 17 15 7 6 14 11 8 9 12 3 1 4 5 16 10 13 2 9 1 0 21 20 19 25 24 23 22 18 8 7 15 12 10 13 4 2 5 6 17 11 14 3 16 11 10 2 1 0 21 20 25 24 23 22 9 8 16 13 14 5 3 6 7 18 12 15 4 17 19 15 12 11 3 2 1 0 21 25 24 23 10 9 17 14 6 4 7 8 19 13 16 5 18 20 22 7 16 13 12 4 3 2 1 0 25 24 11 10 18 15 5 8 9 20 14 17 6 19 21 22 23 6 8 17 14 13 5 4 3 2 1 25 12 11 19 16 9 10 21 15 18 7 20 0 22 23 24 10 7 9 18 15 14 6 5 4 3 2 13 12 20 17 11 0 16 19 8 21 1 22 23 24 25 12 11 8 10 19 16 15 7 6 5 4 14 13 21 18 1 17 20 9 0 2 22 23 24 25 3 2 13 12 9 11 20 17 16 8 7 6 15 14 0 19 18 21 10 1 3 22 23 24 25 4 5 19 3 14 13 10 12 21 18 17 9 8 16 15 1 20 0 11 2 4 22 23 24 25 5 6 7 1 20 4 15 14 11 13 0 19 18 10 17 16 2 21 12 3 5 22 23 24 25 6 7 8 9 3 4 5 6 7 8 9 10 11 12 13 24 25 22 23 2 1 0 21 20 19 18 17 16 15 14 21 0 1 2 3 4 5 6 7 8 9 22 23 24 25 20 19 18 17 16 15 14 13 12 11 10 17 18 19 20 21 0 1 2 3 4 5 23 22 25 24 16 15 14 13 12 11 10 9 8 7 6 4 5 6 7 8 9 10 11 12 13 14 25 24 23 22 3 2 1 0 21 20 19 18 17 16 15 20 19 18 17 25 24 23 22 16 14 1 6 5 13 10 21 7 8 11 2 0 3 4 15 9 12 18 17 16 25 24 23 22 15 13 0 11 5 4 12 9 19 20 6 7 10 1 21 2 3 14 8 16 15 25 24 23 22 14 12 21 10 7 4 3 11 8 17 18 19 5 6 9 0 20 1 2 13 14 25 24 23 22 13 11 20 9 6 12 3 2 10 7 15 16 17 18 4 5 8 21 19 0 1 25 24 23 22 12 10 19 8 5 11 0 2 1 9 6 13 14 15 16 17 3 4 7 20 18 21 24 23 22 11 9 18 7 4 10 21 20 1 0 8 5 25 12 13 14 15 16 2 3 6 19 17 23 22 10 8 17 6 3 9 20 19 16 0 21 7 4 24 25 11 12 13 14 15 1 2 5 18 22 9 7 16 5 2 8 19 18 15 17 21 20 6 3 23 24 25 10 11 12 13 14 0 1 4 8 6 15 4 1 7 18 17 14 16 3 20 19 5 2 22 23 24 25 9 10 11 12 13 21 0 5 14 3 0 6 17 16 13 15 2 21 19 18 4 1 7 22 23 24 25 8 9 10 11 12 20 13 2 21 5 16 15 12 14 1 20 19 18 17 3 0 4 6 22 23 24 25 7 8 9 10 11 Утилита Harry White никаких свойств у ОДЛК этой пары не обнаружила Thursday 2020-06-18 21:51:55 ╠юёъютёъюх тЁхь (чшьр)
Order? 26
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_2.txt
Counts
------
2 diagonal Latin
1 orthogonal pairКонстатирует, что ДЛК ортогональны, ну это мы сами знаем :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger