Пока все дома...
Message boards :
Number crunching :
Пока все дома...
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Прежде всего обращаюсь к соотечественникам. В страну пришла беда, она пришла во многие страны мира. Правительство России, в частности, правительство Москвы, ищет способы противостоять распространению инфекции среди жителей. Вводится самоизоляция граждан. Без нужды не гуляем по паркам и скверам, не ходим в театры, кинотеатры и т. п. места развлечений. Стараемся больше находиться дома, насколько это возможно. Да, конечно, надо проявить сознательность и думать не только о своём здоровье, но и о здоровье окружающих. Очень плохая ситуация в Италии. Администратор проекта ODLK1 ice00 пишет мне, что у них карантин и они все сидят дома. Сервер он пока не остановил, проект работает. Из-за коронавируса Tomas Brada остановил подпроект PADLS TOTAL в своём BOINC-проекте. Мне, конечно, очень жаль. Это была единственная живая нить в поиске ОДЛК. Теперь её нет. Пока держится проект ОДЛК. Progger как вы там? Я читала, что в вашем городе уже есть случаи заражения. Ну, и пока держится мой ручной проект. XAVER работает, недавно прислал новую порцию решений. Я тоже работаю. У нас в регионе два случая заражения. Для меня самоизоляция привычна, я давно самоизолировалась :) Хожу только за продуктами в магазин, за пенсией в банк и платежи сделать. В общем, держитесь все! Будьте бдительны и сознательны, не подвергайте себя и окружающих опасности заражения. И да, если в самоизоляции вам станет скучно, приходите в мой ручной проект https://boinc.progger.info/odlk/forum_thread.php?id=155&postid=5390#5390 По интернету коронавирус, слава Богу, не передаётся. PS. Горячая тема о коронавирусе на форуме dxdy.ru https://dxdy.ru/topic138706.html |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
"reCAPTCHA broken" https://boinc.progger.info/odlk/forum_thread.php?id=157 Вчера видела сообщение на эту же тему на форуме boinc.ru https://boinc.ru/forum/topic/recaptcha/#postid-1712 Теперь понятно это сообщение. Ну вот, господа, самое время поучаствовать в моём ручном проекте :) Для ручного проекта не нужен BOINC! Конечно, администратор проекта может вскоре изменить код на сервере, и всё снова будет работать. Ну, а вдруг это случится не вскоре :) Тогда подключайтесь к ручному проекту. Уверяю вас: это ничуть не хуже вычислений в BOINC, а в чём-то даже лучше - для пользователей. Подключение к BOINC со всеми его заморочками требует определённых усилий и гораздо большего слежения за процессом. Там очень часто что-то идёт не так (много видела подобного на форуме boinc.ru). В ручном проекте нет никаких подводных камней. Запустили скрипт и забыли. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вслед за Москвой многие регионы ввели режим обязательной самоизоляции. Об этом сообщается в новостях Яндекса. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ох, в Сети сплошные страшилки... Для поднятия настроения: Владимир Высоцкий "Утренняя гимнастика" (шуточная песня) https://yandex.ru/video/preview?filmId=12539668270091852804&text=%D0%B2%D1%8B%D1%81%D0%BE%D1%86%D0%BA%D0%B8%D0%B9%20%D1%83%D1%82%D1%80%D0%B5%D0%BD%D0%BD%D1%8F%D1%8F%20%D0%B3%D0%B8%D0%BC%D0%BD%D0%B0%D1%81%D1%82%D0%B8%D0%BA%D0%B0&path=wizard&parent-reqid=1586844887534064-431600783069459409000158-prestable-app-host-sas-web-yp-178&redircnt=1586844924.1 Ссылка тут километровая, сработает ли? А я выложила новый тест, читайте подробности тут https://boinc.progger.info/odlk/forum_thread.php?id=155&postid=5459#5459 Тестируйте, господа! Для поднятия настроения и укрепления иммунитета! :) PS. Ссылка на песню работает. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Tomas Brada выложил ссылку на видеоролик https://www.youtube.com/watch?v=qu04xLNrk94 отсюда https://boinc.tbrada.eu/forum_thread.php?id=3075&postid=4093#4093 Смотрите, читайте комментарии к видеоролику. Я тоже хотела оставить комментарий https://boinc.progger.info/odlk/forum_thread.php?id=1&postid=1742#1742 но у меня нет аккаунта в Google. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Tomas Brada выложил ссылку на видеоролик Популярный видеоролик! Комментариев там уже более 700. Tomas Brada оставил мой комментарий  Спасибо! Озадачили весь мир вопросом: существует ли одиннадцатка, или двенадцатка, или тринадцатка :) Ну, или любое другое решение a(10)>10. Вдруг уже найдено, а мы и не знаем :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Дублирую сообщение из темы "Новый эксперимент в ручном проекте" Друг изобразил мою черепашку :) Далее покажу, как я изобразила на панцире черепашки греко-латинский квадрат. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Поскольку у меня нет возможности записать греческие буквы, я записала латинские маленькие буквы: d, l, k. Вот что у меня получилось  Теперь осталось присвоить буквам значения 0, 1, 2 и получить следующий греко-латинский числовой квадрат 10 22 01 02 11 20 21 00 12 Из этого числового греко-латинского квадрата получается магический квадрат Ло Шу по известному методу латинских квадратов. Ознакомиться с этим методом можно, например, в моей книге "Волшебный мир магических квадратов" (смотрите 4.1.5 Метод Делаира или метод латинских квадратов, стр. 60-70) Скачайте книгу с Яндекс.Диска https://yadi.sk/d/ehakE2V6S5TzG Неплохой учебник по магическим квадратам для начинающих. Книга написана очень давно (2009 г.). Готовилась к изданию, но не получилось. Издатель резко ограничил объём книги, поэтому она такая маленькая. Уже в то время у меня было написано о магических квадратах гораздо больше. Всё это вы можете найти на моём сайте http://www.klassikpoez.narod.ru/glavnaja.htm Кстати, там статьи не только о магических, но и о латинских квадратах. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, греко-латинские квадраты ввёл в математику Эйлер. Он без труда построил греко-латинские квадраты порядков 3, 4, 5, а вот построить греко-латинский квадрат 6-го порядка ему не удалось. Эйлер высказал гипотезу, что греко-латинские квадраты не существуют для всех порядков n=4k+2, k=1, 2, 3, ... Гипотеза оказалась верной только для порядка 6. Для порядка 10 гипотезу опроверг Паркер, построив первый греко-латинский квадрат 10-го порядка в 1959 г. Завтра я его покажу. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это греко-латинский квадрат 10-го порядка, построенный Паркером в 1959 г. 00 47 18 76 29 93 85 34 61 52 86 11 57 28 70 39 94 45 02 63 95 80 22 67 38 71 49 56 13 04 59 96 81 33 07 48 72 60 24 15 73 69 90 82 44 17 58 01 35 26 68 74 09 91 83 55 27 12 46 30 37 08 75 19 92 84 66 23 50 41 14 25 36 40 51 62 03 77 88 99 21 32 43 54 65 06 10 89 97 78 42 53 64 05 16 20 31 98 79 87 Я скопировала данный квадрат из книги "Математические досуги" (Мартин Гарднер, М., Мир 1972 г.) Интересно в этой книге описывается доказательство гипотезы Эйлера для греко-латинского квадрата порядка 6. Цитирую
Далее сообщается, что Паркер написал программу для электронно-вычислительной машины UNIVAC-1206, которой требовалось от 28 до 45 минут рабочего времени, чтобы осуществить полный поиск квадратов, ортогональных заданному латинскому квадрату десятого порядка... И завершающий итог: Проведённые в последнее время исследования греко-латинских квадратов с помощью машин принесли сильнейшее разочарование, потому что никому так и не удалось найти трёх взаимно ортогональных латинских квадратов десятого порядка. Это было написано в 1972 г. Ничего не изменилось и по сей день! Но есть и хороший результат: доказано, что греко-латинский квадрат существует для любого порядка n=4k+2, если n>6. Таким образом, гипотеза Эйлера оказалась верной только для n=6. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Tomas Brada выложил ссылку на видеоролик Посмотрите этот видеоролик. В нём интересно рассказывается о построении греко-латинских квадратов. Кто-то в комментариях спросил: "Почему невозможно для n=6?" В самом деле, почему? :) А фиг его знает. Не складывается - и всё тут. Нет даже теоретического доказательства этого факта, есть только доказательство методом полного перебора, причём ручного! Впрочем, может быть, позже и нашли теоретическое доказательство, вот когда доказали, что для всех n>6 гипотеза Эйлера неверна. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А у меня в 2009 г. были долгие мучения с построением трёх взаимно ортогональных ЛК 14-го порядка. Смотрите страницу на моём сайте http://www.natalimak1.narod.ru/zadacha.htm ЗАДАЧА О СОСТАВЛЕНИИ ТРЁХ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ ЧЕТЫРНАДЦАТОГО ПОРЯДКА Цитирую В 1985 г. D. T. Todorov опубликовал статью “Three Mutually Orthogonal Latin Squares of Order 14” (Ars Combinatoria, 20 (1985), pp. 45-48). В этой статье рассказывается о составлении группы из трёх взаимно ортогональных латинских квадратов 14-го порядка. Эту статью я выложила здесь: Посмотрела сейчас, статья там лежит. Интересующиеся могут статью увидеть. В моей статье приведён перевод статьи Тодорова на русский язык, сделанный форумчанкой форума dxdy.ru. Но даже получив этот хороший перевод, я всё равно ничего не поняла и построить эти взаимно ортогональные ЛК мне не удалось в тот момент. Я долго искала ответ; наконец, на форуме dxdy.ru мне объяснили доходчиво, что такое квази-разностная матрица. Только тогда я поняла, как построить эти ЛК 14-го порядка с помощью квази-разностной матрицы. Кстати, интересные вехи: 1959 год - первый греко-латинский квадрат 10-го порядка, 1985 год - первая группа из трёх взаимно ортогональных ЛК 14-го порядка. А затем: 1992 год - первые пары ортогональных ДЛК 10-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И вскоре (после долгих мучений) я написала статью ПОСТРОЕНИЕ ГРУПП MOLS ЧЕТЫРНАДЦАТОГО ПОРЯДКА http://www.natalimak1.narod.ru/mols14.htm Цитирую В статье “Построение ортогональных латинских квадратов из ортогонального массива” (http://www.natalimak1.narod.ru/arry.htm) было показано построение пары ОЛК 14-го порядка по описанию, приведённому в книге М. Холла. Здесь будет показано построение групп взаимно ортогональных латинских квадратов 14-го порядка, состоящих из трёх квадратов. При написании статьи использовалась следующая литература: Интересно: для порядка 6 не существует даже пары ортогональных ЛК; для порядка 10 существуют пары ортогональных ЛК, но никак не могут найти тройку взаимно ортогональных ЛК (существует ли такая тройка?); для порядка 14 уже нашли и тройку взаимно ортогональных ЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И уже в марте 2009 г. я написала статью О ГРУППАХ MOLS ВОСЕМНАДЦАТОГО ПОРЯДКА http://www.natalimak1.narod.ru/mols18.htm Здесь тоже не сразу всё получилось. Читайте статью! А статья ПОСТРОЕНИЕ ГРУПП MOLS 22-го ПОРЯДКА http://www.natalimak1.narod.ru/mols22.htm написана раньше, ещё в феврале. Видимо, о группе MOLS 18-го порядка статья запоздала из-за непоняток. Ну, и далее там много ещё статей написано о построении разных групп MOLS. Кому интересно, заходите, читайте http://www.klassikpoez.narod.ru/glavnaja.htm My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
"MODLS groups of order 15" https://boinc.progger.info/odlk/forum_thread.php?id=152#5354 Эта тема уже здесь, на форуме. Мне удалось построить группу из 4-х взаимно ортогональных ДЛК 15-го порядка (я использовала для этого известную группу MOLS). Показываю группу MODLS 1 7 12 10 9 3 15 8 2 14 11 4 13 5 6 3 2 8 13 11 10 4 9 1 12 5 14 6 7 15 2 4 3 9 14 12 11 10 13 6 1 7 8 15 5 14 3 5 4 10 1 13 11 7 2 8 9 15 6 12 8 1 4 6 5 11 2 12 3 9 10 15 7 13 14 4 9 2 5 7 6 12 13 10 11 15 8 14 1 3 11 5 10 3 6 8 7 14 12 15 9 1 2 4 13 9 10 11 12 13 14 1 15 8 7 6 5 4 3 2 6 11 9 8 2 15 5 7 14 1 13 10 3 12 4 10 8 7 1 15 4 3 6 5 13 14 12 9 2 11 7 6 14 15 3 2 10 5 9 4 12 13 11 8 1 5 13 15 2 1 9 14 4 6 8 3 11 12 10 7 12 15 1 14 8 13 6 3 4 5 7 2 10 11 9 15 14 13 7 12 5 8 2 11 3 4 6 1 9 10 13 12 6 11 4 7 9 1 15 10 2 3 5 14 8 1 11 8 3 6 12 9 14 7 2 10 5 15 13 4 8 2 12 9 4 7 13 1 3 11 6 15 14 5 10 4 9 3 13 10 5 8 2 12 7 15 1 6 11 14 13 5 10 4 14 11 6 3 8 15 2 7 12 1 9 9 14 6 11 5 1 12 4 15 3 8 13 2 10 7 15 10 1 7 12 6 2 5 4 9 14 3 11 8 13 5 15 11 2 8 13 7 6 10 1 4 12 9 14 3 12 13 14 1 2 3 4 15 11 10 9 8 7 6 5 10 7 2 5 11 8 3 13 14 6 1 9 4 15 12 6 1 4 10 7 2 11 12 9 13 5 14 8 3 15 14 3 9 6 1 10 15 11 5 8 12 4 13 7 2 2 8 5 14 9 15 1 10 13 4 7 11 3 12 6 7 4 13 8 15 14 5 9 1 12 3 6 10 2 11 3 12 7 15 13 4 10 8 6 14 11 2 5 9 1 11 6 15 12 3 9 14 7 2 5 13 10 1 4 8 1 9 7 13 3 2 12 5 8 15 4 14 11 6 10 9 2 10 8 14 4 3 6 15 5 1 12 7 11 13 15 10 3 11 9 1 5 7 6 2 13 8 12 14 4 7 15 11 4 12 10 2 8 3 14 9 13 1 5 6 4 8 15 12 5 13 11 9 1 10 14 2 6 7 3 2 5 9 15 13 6 14 10 11 1 3 7 8 4 12 12 3 6 10 15 14 7 11 2 4 8 9 5 13 1 14 1 2 3 4 5 6 15 13 12 11 10 9 8 7 8 6 12 2 1 11 9 4 14 7 15 3 13 10 5 5 11 1 14 10 8 4 3 7 13 6 15 2 12 9 10 14 13 9 7 3 8 2 4 6 12 5 15 1 11 13 12 8 6 2 7 10 1 9 3 5 11 4 15 14 11 7 5 1 6 9 13 14 12 8 2 4 10 3 15 6 4 14 5 8 12 15 13 10 11 7 1 3 9 2 3 13 4 7 11 15 1 12 5 9 10 6 14 2 8 1 6 13 7 12 5 8 3 9 10 15 2 4 11 14 10 2 7 14 8 13 6 4 11 15 3 5 12 1 9 12 11 3 8 1 9 14 5 15 4 6 13 2 10 7 15 13 12 4 9 2 10 6 5 7 14 3 11 8 1 6 15 14 13 5 10 3 7 8 1 4 12 9 2 11 9 7 15 1 14 6 11 8 2 5 13 10 3 12 4 3 10 8 15 2 1 7 9 6 14 11 4 13 5 12 13 14 1 2 3 4 5 15 12 11 10 9 8 7 6 5 12 6 11 4 7 13 2 14 8 9 15 1 3 10 11 5 10 3 6 12 9 1 4 13 7 8 15 14 2 4 9 2 5 11 8 1 14 10 3 12 6 7 15 13 8 1 4 10 7 14 12 13 3 9 2 11 5 6 15 14 3 9 6 13 11 15 12 7 2 8 1 10 4 5 2 8 5 12 10 15 4 11 13 6 1 7 14 9 3 7 4 11 9 15 3 2 10 1 12 5 14 6 13 8 У меня вопрос: можно ли расширить эту группу MODLS 15-го порядка? То есть требуется найти ещё хотя бы один ДЛК 15-го порядка, который ортогонален всем четырём ДЛК группы. Я пыталась решить эту задачу с помощью программы Белышева ortogon_u, но ничего не получилось. Программа вроде бы работает, но решения не находит. Господа! Попробуйте, может, вам повезёт. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Далее рекомендую очень интересную статью о построении ортогональных пар ЛК и ДЛК 14-го порядка ОРТОГОНАЛЬНЫЕ ДИАГОНАЛЬНЫЕ ЛАТИНСКИЕ КВАДРАТЫ http://www.natalimak1.narod.ru/diagon.htm Я использовала для этого построения алгоритм, изложенный в статье “ORTOGONAL DIAGONAL LATIN SQUARES OF ORDER FOURTEEN” (L. Zhu, 1982 г.) Снова квази-разностная матрица! Построив по этому алгоритму ортогональную пару ЛК, я затем превратила её в ортогональную пару ДЛК и не одну! Это была счастливая находка. Ведь ортогональная пара ДЛК сразу даёт магический квадрат, а для меня тогда главным во всех ортогональных парах ЛК была возможность построить с их помощью магические квадраты. Показываю эту очень красивую ортогональную пару ДЛК 14-го порядка 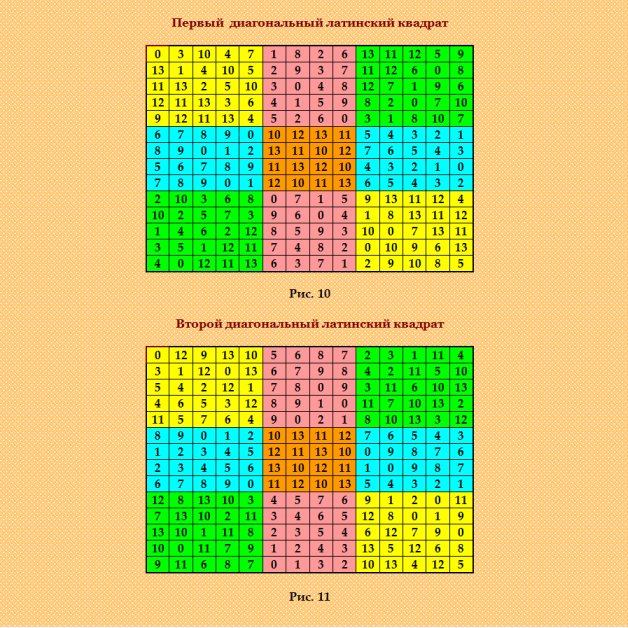 И снова вопрос: можно ли расширить эту ортогональную пару до группы MODLS хотя бы из трёх ОДЛК? То есть существует ли третий ДЛК 14-го порядка, который ортогонален обоим показанным ДЛК? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, указанная статья L.Zhu. Orthogonal Diagonal Latin Squares of order fourteen. 1982 выложена мной давно на Яндекс.Диск https://yadi.sk/i/vXQhLKYY3RFUYi И ещё: по данной статье написана статья А. Чернова "ОДЛК. Метод Ли Жу" http://alex-black.ru/article.php?content=126 В общем, мы с Алексеем хорошо поработали по этой статье :) Вот какая пара ОДЛК 14-го порядка получилась у Алексея  Читайте эту статью Чернова, она очень полезна! Особая полезность в этом Ниже приложение, которое позволяет сгенерировать последовательности и сформировать по ним латинские квадраты. При запуске нужно указать три параметра - порядок квадратов, имя файла с DDOLS(4) (пример файла прилагается) и имя файла для вывода: test 16 DDOLK_4.txt 16.txt My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger
