ЛК блочной структуры с блоками 5х5
Message boards :
Science :
ЛК блочной структуры с блоками 5х5
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
О ЛК блочной структуры с блоками (интеркалятами, или же подквадратами) 5х5, кажется, не рассказывала в специальной теме. Вчера наткнулась на рабочий файл с таким названием. Это самый первый ЛК блочной структуры с блоками (интеркалятами) 5х5, который я построила  Интереснейший ЛК! Этот ЛК диагонально-симметричный. Он имеет также блочную структуру с блоками 2х2; семейство БС вида 5х5 с каноническим шаблоном 0 1 2 3 4 1 2 3 4 0 2 3 4 0 1 3 4 0 1 2 4 0 1 2 3  (иллюстрации из темы «ЛК блочной структуры») Программа Белышева Интеркалятор выдаёт для этого ЛК (показываю один срез) срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 6 7 8 9 5
2 3 4 0 1 7 8 9 5 6
3 4 0 1 2 8 9 5 6 7
4 0 1 2 3 9 5 6 7 8
5 6 7 8 9 0 1 2 3 4
6 7 8 9 5 1 2 3 4 0
7 8 9 5 6 2 3 4 0 1
8 9 5 6 7 3 4 0 1 2
9 5 6 7 8 4 0 1 2 3
{0,5} = 5 : (0,5,0,5) (1,6,4,9) (2,7,3,8) (3,8,2,7) (4,9,1,6)
{1,6} = 5 : (0,5,1,6) (1,6,0,5) (2,7,4,9) (3,8,3,8) (4,9,2,7)
{2,7} = 5 : (0,5,2,7) (1,6,1,6) (2,7,0,5) (3,8,4,9) (4,9,3,8)
{3,8} = 5 : (0,5,3,8) (1,6,2,7) (2,7,1,6) (3,8,0,5) (4,9,4,9)
{4,9} = 5 : (0,5,4,9) (1,6,3,8) (2,7,2,7) (3,8,1,6) (4,9,0,5)
Классическая блочная структура! Данный ЛК марьяжных ДЛК не производит. Однако семейство БС, которое он порождает, даёт много марьяжных ДЛК. Это как раз то самое семейство БС, которое описано Белышевым тут http://mathhelpplanet.com/viewtopic.php?p=276832#p276832 Это наш совместный эксперимент. В заключение покажу КФ этого ЛК 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 5 6 7 8 9 0 1 3 4 5 6 7 8 9 0 1 2 4 5 6 7 8 9 0 1 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 0 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 9 0 1 2 3 4 5 6 7 8 Ну, ещё можно отметить, что этот ЛК обладает многими симметриями. Вот (1,1,1): 1 (1,31,31): 3 (1,41,41): 12 (1,42,42): 12 (16,16,16): 25 (16,31,31): 75 (21,21,21): 50 (21,36,36): 150 (31,41,42): 24 (41,41,41): 12 (41,42,42): 36 (1,1,1)+: 1 (1,1,16)+: 2 (1,16,16)+: 10 (1,16,41)+: 16 (1,31,31)+: 17 (1,31,42)+: 16 (1,41,41)+: 12 (1,42,42)+: 12 (16,16,16)+: 25 (16,16,41)+: 40 (16,31,31)+: 97 (16,31,42)+: 96 (16,41,41)+: 32 (16,42,42)+: 32 (21,21,21)+: 150 (21,36,36)+: 450 (31,31,41)+: 56 (31,41,42)+: 88 (41,41,41)+: 12 (41,42,42)+: 36 (1,1,16)++: 2 (1,16,16)++: 10 (1,16,41)++: 16 (1,31,31)++: 14 (1,31,42)++: 16 (16,16,41)++: 40 (16,31,31)++: 22 (16,31,42)++: 96 (16,41,41)++: 32 (16,42,42)++: 32 (21,21,21)++: 100 (21,36,36)++: 300 (31,31,41)++: 56 (31,41,42)++: 64 Теперь вроде всё рассказала об этом чудесном ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Второй ЛК блочной структуры с блоками 5х5 строю по схеме Белышева, описанной тут http://mathhelpplanet.com/viewtopic.php?p=277196#p277196 0 1 2 3 4 1 0 3 4 2 2 4 0 1 3 3 2 4 0 1 4 3 1 2 0 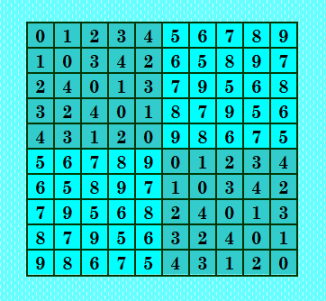 Этот ЛК тоже является блочной структурой с блоками 2х2; семейство БС вида 5х5. Базовый ЛК этого семейства 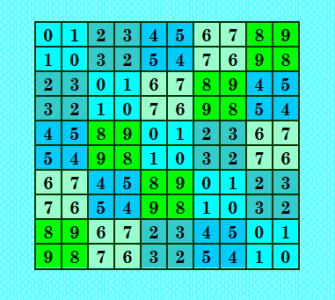 Это второе семейство данного вида; в отличие от рассмотренного выше семейства БС вида 5х5, это семейство не даёт ни одного марьяжного ДЛК. КФ этого ЛК 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 5 4 1 8 7 0 9 6 3 3 4 1 0 7 8 9 6 5 2 4 3 0 7 6 9 8 5 2 1 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 0 9 6 3 2 5 4 1 8 8 9 6 5 2 3 4 1 0 7 9 8 5 2 1 4 3 0 7 6 Симметрии, которыми обладает этот ЛК (1,1,1): 1 (1,31,31): 3 (10,10,10): 8 (10,34,34): 24 (16,16,16): 3 (16,31,31): 9 (4,4,4)+: 6 (4,16,16)+: 6 (4,31,31)+: 24 (4,41,41)+: 6 (4,42,42)+: 6 (10,21,41)+: 12 (10,36,42)+: 12 (16,31,31)+: 12 (21,21,21)+: 6 (21,34,42)+: 12 (21,36,36)+: 18 (31,41,42)+: 12 (34,36,41)+: 12 (1,33,33)++: 2 (1,34,34)++: 2 (4,10,33)++: 4 (4,34,34)++: 4 (10,21,33)++: 12 (10,31,34)++: 4 (10,34,36)++: 12 (16,21,21)++: 6 (16,36,36)++: 6 (21,31,36)++: 12 (21,34,34)++: 12 (31,33,34)++: 8 (33,34,36)++: 12 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У меня в рабочем файле есть ещё ЛК блочной структуры с блоками 5х5. Разбираться с ними буду позже. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата В заключение покажу КФ этого ЛК Обалденная КФ! Этот ЛК построен методом циклического сдвига с шагом 1. Смотрим мою статью "Методы построения латинских квадратов" http://www.natalimak1.narod.ru/metod2.htm Цитирую ЦИКЛИЧЕСКИЙ СДВИГ Статья написана в 2009 году. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А если построить ЛК 10-го порядка циклическим сдвигом с шагом 3, например: 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 0 1 2 6 7 8 9 0 1 2 3 4 5 9 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 0 1 5 6 7 8 9 0 1 2 3 4 8 9 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 0 4 5 6 7 8 9 0 1 2 3 7 8 9 0 1 2 3 4 5 6 Получился ЛК изоморфный построенному с циклическим сдвигом с шагом 1 (ЛК получаются друг из друга перестановкой строк). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А на ЛК блочной структуры с блоками 2х2 посмотрите (нижний квадрат)  Этот ЛК тоже строится методом циклического сдвига с шагом 1, только сдвигаются блоки 2х2. PS. Верхний ЛК на иллюстрации тоже является БС, просто по-другому составлен: он изоморфен нижнему ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И этот ЛК  тоже строится методом циклического сдвига с шагом 1; тут сдвигаются блоки 5х5. И каждый блок 5х5 в этом ЛК тоже строится этим методом! Циклический сдвиг в циклическом сдвиге :) [циклический сдвиг]^2. PS. И в ЛК, показанном в предыдущем посте, тоже [циклический сдвиг]^2. Каждый блок 2х2 (как ЛК2) строится методом циклического сдвига с шагом 1 (в ЛК2 шаг 1 единственно возможный) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю рассказ о ЛК блочной структуры с блоками 5х5. ЛК №3 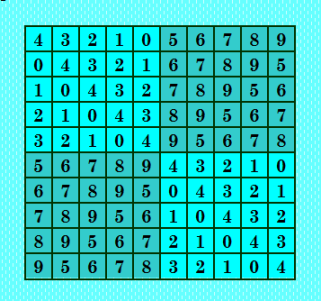 Сравните этот ЛК с ЛК №1. Интересно построен ЛК. И получился он знаменитый - изоморфен ЛК Агриппы. КФ этого ЛК 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 8 9 5 2 3 4 0 1 7 8 9 5 6 3 4 0 1 2 8 9 5 6 7 4 0 1 2 3 9 5 6 7 8 5 9 8 7 6 0 4 3 2 1 6 5 9 8 7 1 0 4 3 2 7 6 5 9 8 2 1 0 4 3 8 7 6 5 9 3 2 1 0 4 9 8 7 6 5 4 3 2 1 0 Этот ЛК является БС вида 10х5 с каноническим шаблоном 0 1 2 3 4 0 2 1 4 3 1 0 3 2 4 1 3 0 4 2 2 0 4 1 3 2 4 0 3 1 3 1 4 0 2 3 4 1 2 0 4 2 3 0 1 4 3 2 1 0 Программа Интеркалятор выдаёт (показываю один срез) срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
2 3 4 0 1 8 9 5 6 7
3 4 0 1 2 7 8 9 5 6
4 0 1 2 3 6 7 8 9 5
5 6 7 8 9 0 1 2 3 4
6 7 8 9 5 4 0 1 2 3
7 8 9 5 6 3 4 0 1 2
8 9 5 6 7 2 3 4 0 1
9 5 6 7 8 1 2 3 4 0
{0,5} = 5 : (0,5,0,5) (1,6,4,6) (2,7,3,7) (3,8,2,8) (4,9,1,9)
{0,6} = 5 : (0,6,0,6) (1,7,4,7) (2,8,3,8) (3,9,2,9) (4,5,1,5)
{0,7} = 5 : (0,7,0,7) (1,8,4,8) (2,9,3,9) (3,5,2,5) (4,6,1,6)
{0,8} = 5 : (0,8,0,8) (1,9,4,9) (2,5,3,5) (3,6,2,6) (4,7,1,7)
{0,9} = 5 : (0,9,0,9) (1,5,4,5) (2,6,3,6) (3,7,2,7) (4,8,1,8)
{1,5} = 5 : (0,9,1,5) (1,5,0,6) (2,6,4,7) (3,7,3,8) (4,8,2,9)
{1,6} = 5 : (0,5,1,6) (1,6,0,7) (2,7,4,8) (3,8,3,9) (4,9,2,5)
{1,7} = 5 : (0,6,1,7) (1,7,0,8) (2,8,4,9) (3,9,3,5) (4,5,2,6)
{1,8} = 5 : (0,7,1,8) (1,8,0,9) (2,9,4,5) (3,5,3,6) (4,6,2,7)
{1,9} = 5 : (0,8,1,9) (1,9,0,5) (2,5,4,6) (3,6,3,7) (4,7,2,8)
{2,5} = 5 : (0,8,2,5) (1,9,1,6) (2,5,0,7) (3,6,4,8) (4,7,3,9)
{2,6} = 5 : (0,9,2,6) (1,5,1,7) (2,6,0,8) (3,7,4,9) (4,8,3,5)
{2,7} = 5 : (0,5,2,7) (1,6,1,8) (2,7,0,9) (3,8,4,5) (4,9,3,6)
{2,8} = 5 : (0,6,2,8) (1,7,1,9) (2,8,0,5) (3,9,4,6) (4,5,3,7)
{2,9} = 5 : (0,7,2,9) (1,8,1,5) (2,9,0,6) (3,5,4,7) (4,6,3,8)
{3,5} = 5 : (0,7,3,5) (1,8,2,6) (2,9,1,7) (3,5,0,8) (4,6,4,9)
{3,6} = 5 : (0,8,3,6) (1,9,2,7) (2,5,1,8) (3,6,0,9) (4,7,4,5)
{3,7} = 5 : (0,9,3,7) (1,5,2,8) (2,6,1,9) (3,7,0,5) (4,8,4,6)
{3,8} = 5 : (0,5,3,8) (1,6,2,9) (2,7,1,5) (3,8,0,6) (4,9,4,7)
{3,9} = 5 : (0,6,3,9) (1,7,2,5) (2,8,1,6) (3,9,0,7) (4,5,4,8)
{4,5} = 5 : (0,6,4,5) (1,7,3,6) (2,8,2,7) (3,9,1,8) (4,5,0,9)
{4,6} = 5 : (0,7,4,6) (1,8,3,7) (2,9,2,8) (3,5,1,9) (4,6,0,5)
{4,7} = 5 : (0,8,4,7) (1,9,3,8) (2,5,2,9) (3,6,1,5) (4,7,0,6)
{4,8} = 5 : (0,9,4,8) (1,5,3,9) (2,6,2,5) (3,7,1,6) (4,8,0,7)
{4,9} = 5 : (0,5,4,9) (1,6,3,5) (2,7,2,6) (3,8,1,7) (4,9,0,8)
125 интеркалятов, как в ЛК Агриппы. ЛК Агриппы смотрите в моей статье http://www.natalimak1.narod.ru/metod2.htm Вот он 0 1 2 3 4 5 6 7 8 9 9 8 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 9 8 8 9 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 0 1 1 0 9 8 7 6 5 4 3 2 5 4 3 2 1 0 9 8 7 6 6 7 8 9 0 1 2 3 4 5 4 5 6 7 8 9 0 1 2 3 3 2 1 0 9 8 7 6 5 4 Ну вот, от показанных трёх ЛК блочной структуры с блоками 5х5 семейства БС (с блоками 2х2) уже исследованы. Здесь нечего искать (в смысле ОДЛК), всё уже найдено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ЛК №4 а теперь взяла ЛК №2 и точно так же перевернула (отразила) в нём левый верхний и правый нижний блоки 5х5, получился такой ЛК 4 3 2 1 0 5 6 7 8 9 2 4 3 0 1 6 5 8 9 7 3 1 0 4 2 7 9 5 6 8 1 0 4 2 3 8 7 9 5 6 0 2 1 3 4 9 8 6 7 5 5 6 7 8 9 4 3 2 1 0 6 5 8 9 7 2 4 3 0 1 7 9 5 6 8 3 1 0 4 2 8 7 9 5 6 1 0 4 2 3 9 8 6 7 5 0 2 1 3 4 КФ этого ЛК 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 5 6 7 8 9 0 1 3 0 1 2 9 8 5 6 7 4 4 7 0 1 8 9 2 5 6 3 5 8 9 6 7 0 3 4 1 2 6 5 8 9 2 1 0 3 4 7 7 4 5 8 1 2 9 0 3 6 8 9 6 7 0 3 4 1 2 5 9 6 7 0 3 4 1 2 5 8 Этот ЛК является БС вида 10х5 с каноническим шаблоном 0 1 2 3 4 0 1 2 4 3 1 0 3 2 4 1 0 3 4 2 2 3 4 0 1 2 4 0 3 1 3 2 4 1 0 3 4 1 2 0 4 2 0 1 3 4 3 1 0 2 Программа Интеркалятор выдаёт 89 интеркалятов срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 3 4 5 6 7 8 9 0 1
3 0 1 2 9 8 5 6 7 4
4 7 0 1 8 9 2 5 6 3
5 8 9 6 7 0 3 4 1 2
6 5 8 9 2 1 0 3 4 7
7 4 5 8 1 2 9 0 3 6
8 9 6 7 0 3 4 1 2 5
9 6 7 0 3 4 1 2 5 8
{0,1} = 1 : (7,8,4,7)
{0,3} = 1 : (1,4,2,9)
{0,6} = 1 : (0,6,0,6)
{0,8} = 1 : (3,5,1,5)
{1,2} = 1 : (6,7,4,5)
{1,5} = 1 : (0,6,1,5)
{1,7} = 1 : (2,6,5,9)
{1,9} = 1 : (4,6,3,5)
{2,6} = 1 : (2,6,0,4)
{2,8} = 1 : (3,7,3,5)
{3,4} = 1 : (3,4,0,9)
{3,5} = 1 : (3,5,0,6)
{3,7} = 1 : (3,7,0,8)
{3,9} = 1 : (3,9,0,4)
{4,6} = 1 : (4,6,0,8)
{4,8} = 1 : (3,9,5,9)
{5,6} = 1 : (7,8,2,9)
{5,8} = 1 : (1,4,4,7)
{6,7} = 1 : (6,7,0,9)
{8,9} = 1 : (3,4,4,5)
{0,7} = 2 : (0,7,0,7) (1,6,6,9)
{0,9} = 2 : (3,8,1,4) (4,5,2,5)
{1,3} = 2 : (1,3,0,2) (6,8,5,7)
{2,5} = 2 : (0,7,2,5) (1,6,1,4)
{4,5} = 2 : (3,8,6,9) (4,5,0,7)
{6,8} = 2 : (1,3,5,7) (6,8,0,2)
{1,4} = 3 : (0,7,1,4) (1,4,0,3) (2,3,2,9)
{2,3} = 3 : (4,5,6,9) (6,9,4,7) (7,8,5,8)
{6,9} = 3 : (0,7,6,9) (1,4,5,8) (2,3,4,7)
{7,8} = 3 : (4,5,1,4) (6,9,2,9) (7,8,0,3)
{0,5} = 5 : (0,5,0,5) (1,8,4,9) (2,9,3,8) (3,6,1,6) (4,7,2,7)
{1,6} = 5 : (0,9,1,6) (1,6,0,5) (2,7,4,9) (3,8,2,7) (4,5,3,8)
{1,8} = 5 : (0,5,1,8) (1,8,0,7) (2,9,6,9) (3,6,2,5) (4,7,3,4)
{2,7} = 5 : (0,9,2,7) (1,4,1,6) (2,7,0,5) (3,8,3,8) (5,6,4,9)
{2,9} = 5 : (0,5,2,9) (1,8,1,8) (2,9,0,7) (3,6,3,4) (4,7,5,6)
{3,6} = 5 : (0,5,3,6) (1,8,2,5) (2,9,1,4) (3,6,0,7) (4,7,8,9)
{3,8} = 5 : (0,7,3,8) (1,6,2,7) (2,5,1,6) (3,8,0,5) (4,9,4,9)
{4,7} = 5 : (0,5,4,7) (1,8,3,6) (2,9,2,5) (3,6,8,9) (4,7,0,1)
{4,9} = 5 : (0,3,4,9) (1,6,3,8) (2,5,2,7) (4,9,0,5) (7,8,1,6)
Ну, семейства БС вида 10х5 все были проверены. Но... такой вопрос возник: а программа tzs_lk уже не даст для этого ЛК ничего нового? Тут много интеркалятов, не то что в чистой БС, имеющей только 25 интеркалятов. Как насчёт транзитивного замыкания? Стоит пробовать или не стоит? Без понятия, что это за зверь такой :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Прежде чем перейти к следующему ЛК, введу обозначения. Блочная структура ЛК, состоящего из блоков 2х2, будет далее обозначаться БС2. Блочная структура ЛК, состоящего из блоков 5х5, будет далее обозначаться БС5. Мы знаем, что в ЛК, являющихся БС2, можно поворачивать блоки 2х2. В ЛК, являющихся БС5, тоже можно поворачивать блоки, только это блоки 5х5. ЛК №5 получен как раз поворотом двух блоков 5х5 (левого верхнего и правого нижнего); остальные два блока остались такими же, как были в исходном ЛК №1. Смотрим иллюстрацию 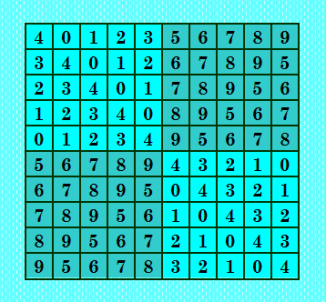 Полученный ЛК не является БС2, что отличает его от всех ранее рассмотренных ЛК. Программа Интеркалятор выдаёт для этого ЛК 25 интеркалятов срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 6 7 8 9 5
2 3 4 0 1 7 8 9 5 6
3 4 0 1 2 8 9 5 6 7
4 0 1 2 3 9 5 6 7 8
5 6 7 8 9 0 1 2 3 4
6 7 8 9 5 4 0 1 2 3
7 8 9 5 6 3 4 0 1 2
8 9 5 6 7 2 3 4 0 1
9 5 6 7 8 1 2 3 4 0
{0,5} = 1 : (0,5,0,5)
{0,6} = 1 : (0,6,0,6)
{0,7} = 1 : (0,7,0,7)
{0,8} = 1 : (0,8,0,8)
{0,9} = 1 : (0,9,0,9)
{1,5} = 1 : (0,9,1,5)
{1,6} = 1 : (0,5,1,6)
{1,7} = 1 : (0,6,1,7)
{1,8} = 1 : (0,7,1,8)
{1,9} = 1 : (0,8,1,9)
{2,5} = 1 : (0,8,2,5)
{2,6} = 1 : (0,9,2,6)
{2,7} = 1 : (0,5,2,7)
{2,8} = 1 : (0,6,2,8)
{2,9} = 1 : (0,7,2,9)
{3,5} = 1 : (0,7,3,5)
{3,6} = 1 : (0,8,3,6)
{3,7} = 1 : (0,9,3,7)
{3,8} = 1 : (0,5,3,8)
{3,9} = 1 : (0,6,3,9)
{4,5} = 1 : (0,6,4,5)
{4,6} = 1 : (0,7,4,6)
{4,7} = 1 : (0,8,4,7)
{4,8} = 1 : (0,9,4,8)
{4,9} = 1 : (0,5,4,9)
Программы Harry White находят в этом ЛК 5 независимых блоков и 25 всех блоков 2х2 (так же, как в программе Интеркалятор). Поворот всех блоков по программе Harry ничего не дал в смысле поиска ОДЛК. А вот программа Белышева tzs_lk для этого ЛК дала уникальную однушку. Я остановилась на глубине поиска 12. Можно, наверное, увеличить глубину поиска. Пробуйте! Вот найденная однушка 0 8 5 2 7 9 3 4 6 1 4 1 8 9 5 7 2 6 0 3 9 5 2 7 1 0 8 3 4 6 5 0 6 3 2 8 4 9 1 7 7 9 3 8 4 6 0 1 2 5 3 6 4 1 8 5 7 2 9 0 8 3 1 5 9 2 6 0 7 4 1 2 9 0 6 4 5 7 3 8 6 7 0 4 3 1 9 5 8 2 2 4 7 6 0 3 1 8 5 9 Итак, сочиняем ЛК, являющиеся БС5; крутим в них блоки 5х5, получаем новые БС5. Применяем к этим ЛК алгоритм Белышева, реализованный в программе tzs_lk. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ЛК №5 обладает следующими симметриями (1,1,1): 1 (1,41,41): 4 (4,31,31): 10 (4,42,42): 20 (7,7,7): 8 (7,41,41): 12 (16,16,16): 25 (21,21,21): 50 (21,36,36): 50 (24,42,42): 20 (1,1,4)+: 1 (1,31,31)+: 5 (4,16,16)+: 25 (4,41,41)+: 4 (7,7,24)+: 8 (7,42,42)+: 20 (16,31,31)+: 5 (16,42,42)+: 20 (21,21,21)+: 50 (21,36,36)+: 50 (24,41,41)+: 12 Интересно: симметрия (16,16,16) аж 25-кратная. А что там выдаётся как предствители очевидной симметрии для симметрии (16,16,16)? Сейчас посмотрю. Вот (16,16,16) 0 7 8 5 6 3 4 1 2 9 2 0 1 4 9 5 6 7 8 3 1 8 0 9 5 6 3 2 7 4 5 4 9 0 8 7 2 6 3 1 6 9 5 1 0 8 7 3 4 2 3 5 6 2 1 0 8 4 9 7 4 6 3 7 2 1 0 9 5 8 8 2 7 6 3 4 9 0 1 5 7 1 2 3 4 9 5 8 0 6 9 3 4 8 7 2 1 5 6 0 0 1 5 4 3 2 9 8 7 6 1 0 6 7 8 9 3 2 5 4 4 6 0 3 2 5 8 7 1 9 5 7 2 0 4 3 6 9 8 1 2 8 3 5 0 4 1 6 9 7 3 9 4 2 5 0 7 1 6 8 9 2 8 6 1 7 0 4 3 5 8 3 7 9 6 1 5 0 4 2 7 4 1 8 9 6 2 5 0 3 6 5 9 1 7 8 4 3 2 0 И весьма интересный очевидный представитель симметрии (7,7,7) (7,7,7) 4 3 2 1 0 5 6 7 8 9 0 4 3 2 1 6 7 8 9 5 1 0 4 3 2 7 8 9 5 6 2 1 0 4 3 8 9 5 6 7 3 2 1 0 4 9 5 6 7 8 5 6 7 8 9 4 0 1 2 3 6 7 8 9 5 3 4 0 1 2 7 8 9 5 6 2 3 4 0 1 8 9 5 6 7 1 2 3 4 0 9 5 6 7 8 0 1 2 3 4 Сравните с самим ЛК №5. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ЛК блочной структуры с блоками 5х5 прибыли! Здесь были показаны такие ЛК, построенные мной. А вчера в проекте PADLS rule 51 были найдены ещё 6 таких ЛК, смотрите сообщение https://boinc.progger.info/odlk/forum_thread.php?id=107&postid=3612#3612 Продублирую эти ЛК 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 0 1 7 8 9 5 6 3 4 0 1 2 8 9 5 6 7 4 0 1 7 8 9 5 6 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 5 6 2 3 4 0 1 8 9 5 6 7 3 4 0 1 2 9 5 6 2 3 4 0 1 7 8 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 0 1 7 8 9 5 6 3 4 0 1 2 8 9 5 6 7 4 5 1 7 8 9 0 6 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 5 6 2 3 4 0 1 8 9 5 6 7 3 4 0 1 2 9 0 6 2 3 4 5 1 7 8 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 0 1 7 8 9 5 6 3 4 0 1 7 8 9 5 6 2 4 5 6 2 3 9 0 1 7 8 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 5 6 2 3 4 0 1 8 9 5 6 2 3 4 0 1 7 9 0 1 7 8 4 5 6 2 3 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 0 1 7 8 9 5 6 3 4 0 6 2 8 9 5 1 7 4 0 1 7 8 9 5 6 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 5 6 2 3 4 0 1 8 9 5 1 7 3 4 0 6 2 9 5 6 2 3 4 0 1 7 8 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 0 1 7 8 9 5 6 3 4 0 6 7 8 9 5 1 2 4 5 6 2 3 9 0 1 7 8 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 5 6 2 3 4 0 1 8 9 5 1 2 3 4 0 6 7 9 0 1 7 8 4 5 6 2 3 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 0 6 7 8 9 5 1 3 4 5 1 2 8 9 0 6 7 4 5 1 7 8 9 0 6 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 5 1 2 3 4 0 6 8 9 0 6 7 3 4 5 1 2 9 0 6 2 3 4 5 1 7 8 Чудесные квадратики! Все они мультисимметричные и дают 22 мультисимметричные четвёрки! Четвёрки показаны здесь https://boinc.progger.info/odlk/forum_thread.php?id=107&postid=3618#3618 Интересно испытать эти ЛК программой Белышева tzs_lk. И весьма интересный вопрос возникает сам собой: сколько существенно различных БС5 можно построить? Вот я построила всего 5 таких ЛК, тут неожиданно ещё 6 нашлись. Сильно подозреваю, что их м-н-о-о-о-г-о можно настроить. Но как? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Эх, как интересно! Определитель семейств блочных ЛК Введено ЛК : 6 Из них блочных : 6 Найдено семейств блочных ЛК 5x5 : 1 Время работы : 0.015 сек Все найденные 6 ЛК блочной структуры с блоками 5х5 оказались из семейства БС2 вида 5х5. Смотрите показанный протокол работы программы Белышева Определитель семейств блочных ЛК. Значит, это не уникальные БС5. Тэк-с, задача: построить уникальные БС5, которые я ещё не построила. |

©2026 (C) Progger