Ещё раз о повороте блоков
Message boards :
Science :
Ещё раз о повороте блоков
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Как я уже отмечала, вторичная обработка результатов включает на сегодня несколько алгоритмов. Самый главный (алгоритм №1) - это программа Белышева Канонизатор ЛК по ДЛК. Алгоритм был разработан на заре поиска ОДЛК. Не так давно Белышев создал замечательный скрипт zamyk.bat. который по сути включил эту обработку в первичную. Алгоритм №2 - это алгоритм поворота блоков. Этот алгоритм разработан тоже давно, у меня он был реализован в программе Карусель. Долгое время я обрабатывала результаты (вторичная обработка) этой программой. Затем поставила эту задачу Harry White, он написал более совершенную программу поворота блоков, которой я теперь пользуюсь. Все результаты, полученные в ручном проекте, обрабатываю этой программой. Недавно Белышев на boinc.ru выложил программу, которая тоже (как мне кажется) поворачивает блоки, но там какая-то привязка к графам. Не знаю теорию графов, поэтому не вникала в эту программу: что и как она крутит-вертит. Моя программа поворота блоков мне абсолютно понятна: что и как поворачивается. Далее я покажу примеры из замечательной последовательности КФ ОДЛК, составленной мной недавно. Смотрите об этой последовательности тему https://boinc.progger.info/odlk/forum_thread.php?id=111 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, в замечательной последовательности есть член КФ3 0 2 6 9 5 7 8 4 3 1 8 1 5 6 3 2 4 9 0 7 4 5 2 0 8 9 1 3 7 6 7 6 4 3 9 8 2 5 1 0 3 0 9 7 4 6 5 1 2 8 2 4 1 8 7 5 9 0 6 3 1 7 0 4 2 3 6 8 9 5 9 3 8 1 6 4 0 7 5 2 6 9 3 5 1 0 7 2 8 4 5 8 7 2 0 1 3 6 4 9 Эта КФ ОДЛК даёт десятку, которая найдена мной в апреле прошлого года; первая десятка в нашей БД (и не только в нашей, как видно из OEIS https://oeis.org/A287695). А теперь обработайте эту КФ ОДЛК программой поворота блоков. И... вы получите три четвёрки! Эти четвёрки тоже содержатся в замечательной последовательности. Завтра покажу иллюстрации. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А вот что мы имеем от КФ3 при обработке скриптом zamyk.bat Найдено марьяжных КФ: count[1] = 26 count[2] = 8 count[4] = 1 count[10] = 1 Всего: 36 Найдено соквадратов: 56 КФ соквадратов: 36 Круто! Одна КФ ОДЛК дала 36 уникальных КФ ОДЛК, при этом четвёрку и 8 двушек. Кстати, одна из трёх четвёрок (которые получаются обработкой поворотом блоков) и при этой обработке получена, вот эта 0 2 6 9 5 7 8 4 3 1 8 1 5 6 3 2 4 9 0 7 4 5 2 1 8 9 0 3 7 6 7 6 4 3 9 8 2 5 1 0 3 0 9 7 4 6 5 1 2 8 2 4 1 8 7 5 9 0 6 3 1 7 0 4 2 3 6 8 9 5 9 3 8 0 6 4 1 7 5 2 6 9 3 5 0 1 7 2 8 4 5 8 7 2 1 0 3 6 4 9 В замечательной последовательности эта четвёрка КФ13. Отмечу, что эта четвёрка получается даже без обработки Канонизатором ЛК по ДЛК, то есть при первичной обработке КФ ОДЛК, дающей десятку. Помните кубок Грааля, с помощью которого Demis представил конфигурацию, порождаемую десяткой? Вот он 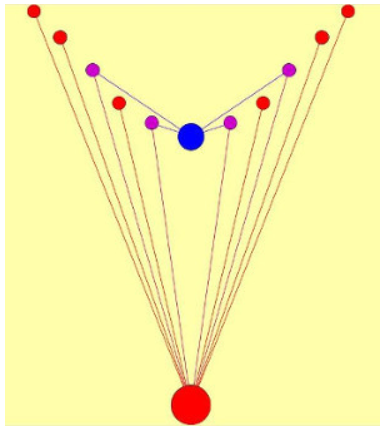 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, показываю иллюстрации - преобразование КФ ОДЛК поворотом блоков. Первая иллюстрация 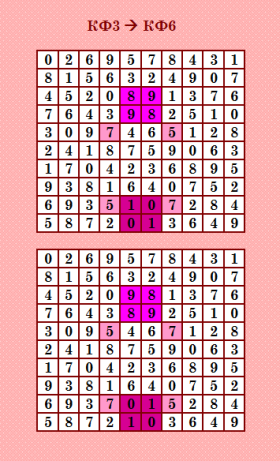 Красиво! В КФ3 (десятка) повёрнуты три блока и получена КФ6 (четвёрка). Или наоборот: от КФ6 к КФ3 поворотом тех же трёх блоков. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вторая иллюстрация 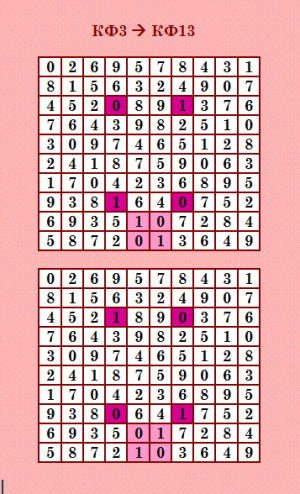 Здесь в КФ3 (десятка) повёрнуты всего два блока и получена КФ13 (четвёрка). Самая знаменитая четвёрка, которая содержится в кубке Грааля :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Третья иллюстрация 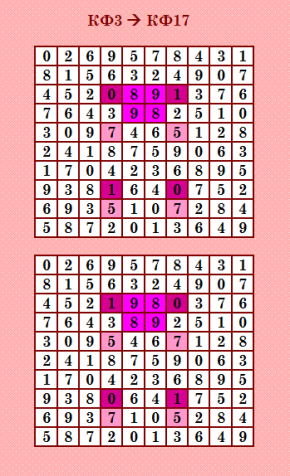 Здесь в КФ3 (десятка) повёрнуты три блока и получена КФ17 (четвёрка). Следует отметить разницу в блоках: есть цельные блоки 2х2, а есть разорванные блоки 2х2. На показанной здесь иллюстрации блок {8,9} цельный, а блоки {0,1} и {5,7} разорванные. Поворачиваются блоки - цельные и разорванные - одинаково. У Белышева блоки называются ещё интеркалятами. Есть у него программа Интеркалятор, которая может определить все интеркаляты в ДЛК (ЛК). Вот, например, все интеркаляты в КФ3 (показываю один срез) срез #1
0 1 2 3 4 5 6 7 8 9
1 7 9 6 5 4 3 0 2 8
2 3 8 4 9 0 5 1 6 7
3 8 6 9 2 7 0 5 4 1
4 6 5 1 0 9 8 2 7 3
5 2 7 8 3 6 1 4 9 0
6 9 4 2 8 1 7 3 0 5
7 4 1 0 6 3 9 8 5 2
8 0 3 5 7 2 4 9 1 6
9 5 0 7 1 8 2 6 3 4
{0,1} = 1 : (3,5,6,9)
{0,3} = 1 : (4,5,4,9)
{0,4} = 1 : (0,4,0,4)
{0,8} = 1 : (2,9,2,5)
{2,3} = 1 : (1,9,6,8)
{2,9} = 1 : (4,8,5,7)
{3,8} = 1 : (1,4,6,9)
{4,7} = 1 : (2,9,3,9)
{5,9} = 1 : (3,8,3,7)
{6,7} = 1 : (3,5,2,5)
{6,9} = 1 : (1,3,2,3)
{0,9} = 2 : (2,4,4,5) (3,7,3,6)
{3,6} = 2 : (0,1,3,6) (5,7,4,5)
{3,7} = 2 : (3,7,0,5) (5,8,2,4)
{4,5} = 2 : (0,1,4,5) (2,8,3,6)
{4,8} = 2 : (1,9,5,9) (4,8,0,6)
{5,7} = 2 : (0,3,5,7) (2,6,6,9)
{1,8} = 3 : (2,7,2,7) (4,5,3,6) (6,9,4,5)
{2,7} = 3 : (2,7,0,9) (3,8,4,5) (6,9,3,6)
{5,8} = 3 : (1,6,4,9) (2,4,2,6) (5,8,0,3)
32 интеркалята. В своей новой программе Белышев как раз работает с интеркалятами-графами. Ну уж... интеркаляты да ещё и графы :) У меня просто блоки 2х2, так понятнее. Кто хочет интеркаляты-графы, смотрите новую программу Белышева. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А теперь стоит посмотреть, как четвёрка КФ6 превращается в четвёрку КФ17 преобразованием поворота блоков. Эти четвёрки ещё и близняшки. Превращение четвёрки КФ6 в четвёрку КФ17  |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ортогональные соквадраты четвёрок КФ6 и КФ17 не совпадают, они изоморфны. Аналогичный случай с тройками-близняшками смотрите здесь https://boinc.progger.info/odlk/forum_thread.php?id=42&postid=3171#3171 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Алгоритм №3 вторичной обработки результатов не связан с поворотом блоков. У меня рабочее название этого алгоритма - алгоритм Х. Этот алгоритм тоже применяю ко всем результатам БД ручного проекта. Недавно применила его к обработке результатов, полученных в BOINC-проекте Tomas Brada. Нашлась уникальная тройка и много других решений. Смотрите сообщение https://boinc.progger.info/odlk/forum_thread.php?id=42&postid=3238#3238 Теперь перехожу к алгоритму №4 вторичной обработки результатов. Этот алгоритм связан с поворотом блоков. Рабочее название алгоритма - алгоритм Y. Я применяю этот алгоритм только к основным ДЛК солидных групп пар ОДЛК. Алгоритм основан на моей теме "ЛК с частичной блочной структурой". Идея моя, программная реализация Harry White. Он написал две программы для этой обработки: 1. Поворот независимых блоков (лёгкая программа); 2. Поворот всех блоков. Идея состоит в следующем: смотрим на КФ ОДЛК как на ЛК. Ну и далее всё понятно. Можно пропускать поиск программой 1 (поворот независимых блоков), сразу выполнять поворот всех блоков. Получив порцию ЛК таким образом, далее проверяем её программой Белышева family_mar. Что такое независимые блоки, хорошо объяснено в указанной теме "ЛК с частичной блочной структурой". Повторять не буду здесь. Смотрите, например, сообщение https://boinc.progger.info/odlk/forum_thread.php?id=63&postid=1689#1689 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Приведу пример применения алгоритма Y к КФ1 замечательной последовательности (эта КФ ОДЛК даёт восьмёрку) 0 2 6 9 5 7 8 4 3 1 8 1 5 6 3 2 4 9 0 7 4 5 2 0 8 9 1 3 7 6 7 0 4 3 9 1 2 6 5 8 3 8 9 7 4 6 0 5 1 2 2 4 1 8 7 5 9 0 6 3 1 7 0 4 2 3 6 8 9 5 9 3 8 1 6 4 5 7 2 0 6 9 3 5 1 0 7 2 8 4 5 6 7 2 0 8 3 1 4 9 Вот протокол выполнения первой программы Harry - поворот независимых блоков .. writing LS to file 10LS_2.txt
1: blocks 13
LS out 8192
blocks
{0,5} : [ 1][ 1] [ 1][ 5] [10][ 1] [10][ 5]
{2,3} : [ 1][ 2] [ 1][ 9] [ 8][ 2] [ 8][ 9]
{6,4} : [ 1][ 3] [ 1][ 8] [ 4][ 3] [ 4][ 8]
{9,8} : [ 1][ 4] [ 1][ 7] [ 6][ 4] [ 6][ 7]
{8,7} : [ 2][ 1] [ 2][10] [ 4][ 1] [ 4][10]
{5,9} : [ 2][ 3] [ 2][ 8] [ 5][ 3] [ 5][ 8]
{6,4} : [ 2][ 4] [ 2][ 7] [ 7][ 4] [ 7][ 7]
{3,2} : [ 2][ 5] [ 2][ 6] [ 7][ 5] [ 7][ 6]
{4,9} : [ 3][ 1] [ 3][ 6] [ 8][ 1] [ 8][ 6]
{2,3} : [ 3][ 3] [ 3][ 8] [ 9][ 3] [ 9][ 8]
{3,2} : [ 4][ 4] [ 4][ 7] [10][ 4] [10][ 7]
{3,2} : [ 5][ 1] [ 5][10] [ 6][ 1] [ 6][10]
{8,6} : [ 5][ 2] [ 5][ 6] [10][ 2] [10][ 6]
elapsed time 0:00:00
Press a key to close the consoleЭто лёгкая программа, независимых блоков найдено всего 13 (все эти блоки выведены), поворотом этих независимых блоков получено 8192 ЛК (2^13). Эти ЛК необходимо канонизировать программой Белышева kanonizator_lk. Затем полученные КФ ЛК проверить программой family_mar. Как уже сказано выше, лёгкую программу можно вообще пропустить, потому что повороты независимых блоков будут сделаны следующей программой поворота всех блоков. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это протокол работы второй программы Harry .. writing LS to file 10LS_2.txt
1: blocks 34 intersections 78
LS out 785672
blocks
{0,5} : [ 1][ 1] [ 1][ 5] [10][ 1] [10][ 5]
{2,3} : [ 1][ 2] [ 1][ 9] [ 8][ 2] [ 8][ 9]
{6,4} : [ 1][ 3] [ 1][ 8] [ 4][ 3] [ 4][ 8]
{9,8} : [ 1][ 4] [ 1][ 7] [ 6][ 4] [ 6][ 7]
{5,4} : [ 1][ 5] [ 1][ 8] [ 5][ 5] [ 5][ 8]
{5,7} : [ 1][ 5] [ 1][ 6] [ 6][ 5] [ 6][ 6]
{7,4} : [ 1][ 6] [ 1][ 8] [ 8][ 6] [ 8][ 8]
{8,7} : [ 2][ 1] [ 2][10] [ 4][ 1] [ 4][10]
{5,9} : [ 2][ 3] [ 2][ 8] [ 5][ 3] [ 5][ 8]
{6,4} : [ 2][ 4] [ 2][ 7] [ 7][ 4] [ 7][ 7]
{3,7} : [ 2][ 5] [ 2][10] [ 6][ 5] [ 6][10]
{3,2} : [ 2][ 5] [ 2][ 6] [ 7][ 5] [ 7][ 6]
{4,7} : [ 2][ 7] [ 2][10] [ 9][ 7] [ 9][10]
{4,9} : [ 3][ 1] [ 3][ 6] [ 8][ 1] [ 8][ 6]
{4,6} : [ 3][ 1] [ 3][10] [ 9][ 1] [ 9][10]
{2,3} : [ 3][ 3] [ 3][ 8] [ 9][ 3] [ 9][ 8]
{1,3} : [ 3][ 7] [ 3][ 8] [10][ 7] [10][ 8]
{7,3} : [ 4][ 1] [ 4][ 4] [ 5][ 1] [ 5][ 4]
{4,9} : [ 4][ 3] [ 4][ 5] [ 5][ 3] [ 5][ 5]
{3,8} : [ 4][ 4] [ 4][10] [ 6][ 4] [ 6][10]
{3,2} : [ 4][ 4] [ 4][ 7] [10][ 4] [10][ 7]
{2,5} : [ 4][ 7] [ 4][ 9] [ 8][ 7] [ 8][ 9]
{3,2} : [ 5][ 1] [ 5][10] [ 6][ 1] [ 6][10]
{8,6} : [ 5][ 2] [ 5][ 6] [10][ 2] [10][ 6]
{4,6} : [ 5][ 5] [ 5][ 6] [ 8][ 5] [ 8][ 6]
{4,6} : [ 6][ 2] [ 6][ 9] [10][ 2] [10][ 9]
{1,8} : [ 6][ 3] [ 6][ 4] [ 8][ 3] [ 8][ 4]
{5,3} : [ 6][ 6] [ 6][10] [ 7][ 6] [ 7][10]
{9,6} : [ 6][ 7] [ 6][ 9] [ 7][ 7] [ 7][ 9]
{9,3} : [ 6][ 7] [ 6][10] [10][ 7] [10][10]
{0,3} : [ 7][ 3] [ 7][ 6] [ 9][ 3] [ 9][ 6]
{4,5} : [ 7][ 4] [ 7][10] [ 9][ 4] [ 9][10]
{4,0} : [ 8][ 6] [ 8][10] [ 9][ 6] [ 9][10]
{3,7} : [ 9][ 3] [ 9][ 7] [10][ 3] [10][ 7]
elapsed time 0:00:02
Press a key to close the console
Всего в КФ1 найдено 34 блока; блоки выведены. Получено поворотом этих блоков 785672 ЛК. После канонизации останется гораздо меньше КФ ЛК. Ну и дальше - проверка программой family_mar полученной порции КФ ЛК. Я проверила КФ1 этим алгоритмом, решения найдены. PS. Не знаю, насколько мой алгоритм пересекается с алгоритмом Белышева, где интеркаляты-графы, но думаю, что как-то всё-таки пересекается. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, программа Белышева Интеркалятор находит в КФ1 тоже 34 интеркалята (то бишь - блоков) Программа поиска интеркалятов в ЛК10: 0 2 6 9 5 7 8 4 3 1 8 1 5 6 3 2 4 9 0 7 4 5 2 0 8 9 1 3 7 6 7 0 4 3 9 1 2 6 5 8 3 8 9 7 4 6 0 5 1 2 2 4 1 8 7 5 9 0 6 3 1 7 0 4 2 3 6 8 9 5 9 3 8 1 6 4 5 7 2 0 6 9 3 5 1 0 7 2 8 4 5 6 7 2 0 8 3 1 4 9 Найдено: 34 Так что, программа Белышева и программа Harry согласны друг с другом в части количества блоков. А вот что там дальше у Белышева - в части поворота интеркалятов-графов - сие мне не известно. Ну, программа Harry тоже неплохо поворачивает блоки. Так что, можно пользоваться вполне этой программой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программу Белышева tzs_lk.exe я скачала с форума boinc.ru, когда она появилась. К сожалению, ссылку не могу дать, так как у меня уже больше недели форум boinc.ru не открывается. Пару раз её попробовала тогда же, но ничего не поняла, то есть опробовала вслепую. Важное: программа запрашивает глубину поиска. И какой её задавать - ХЗ :) Наугад? Ну вот покажу пример опять с КФ1 (восьмёрка). Записала этот ДЛК в файл input.txt и запустила программу; на запрос о глубине поиска ввела 5. Протокол работы программы Частичное транзитивное замыкание связанности ЛК Задайте глубину поиска: 5 36524 96 72250 92 108515 53 143759 42 Построено КФ ЛК: 149132 Сохранение : выполнено Время работы : 25.443 сек Какие-то КФ ЛК программа построила, аж 149132 шт. Завтра проверю эти КФ ЛК. Вдруг что-то новое найдётся. И потом попробую задать глубину поиска 6. Что будет? В файле readme.txt написано Если задать слишком большую глубину поиска, то программа исчерпает всю память после чего будет принудительно закрыта ОС. В-о-о-о-т! Не хапайте слишком много :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очень интересные дела у меня! :) Решила сравнить КФ ЛК, полученные от КФ1 программами Harry (поворот всех блоков) и Белышева (tzs_lk). Вот результаты вычитания, в файле output.txt - 515820 КФ ЛК, полученные программой Harry, в файле input.txt - 149132 КФ ЛК, полученные программой Белышева. Вычитание выполняется программой В. Чиркова. Имя входного файла ИСТОЧНИК (без расширения):output Имя входного файла ВЫЧИТАЕМОЕ (без расширения):input output.txt Всего 515820 квадратов (вход) в output.txt input.txt Всего 149132 квадратов (вход) в input.txt Уникальных 490400 квадратов (выход). Для продолжения нажмите любую клавишу . . . Имя входного файла ИСТОЧНИК (без расширения):input Имя входного файла ВЫЧИТАЕМОЕ (без расширения):output input.txt Всего 149132 квадратов (вход) в input.txt output.txt Всего 515820 квадратов (вход) в output.txt Уникальных 123712 квадратов (выход). Для продолжения нажмите любую клавишу . . . Да! Пересечения есть! Теперь запускаю проверку 123712 КФ ЛК, которые в порции от программы Белышева новые. Получаю Поиск марьяжных ДЛК (кроме симметричных) для семейства ЛК Введено ЛК: 123712 Найдено марьяжных ДЛК: 2 они записаны в файл output.txt Время работы в сек : 7893.42 Найденные КФ ОДЛК 0 2 9 7 5 3 8 6 4 1 9 1 6 2 3 7 5 4 0 8 6 7 2 5 8 1 4 3 9 0 8 0 4 3 6 9 2 5 1 7 7 5 0 8 4 6 1 9 3 2 3 6 1 9 7 5 0 8 2 4 1 8 5 4 9 0 6 2 7 3 4 3 8 1 0 2 9 7 5 6 2 9 3 6 1 4 7 0 8 5 5 4 7 0 2 8 3 1 6 9 0 4 5 2 7 6 8 9 3 1 4 1 7 9 5 8 2 6 0 3 5 8 2 6 9 1 0 3 4 7 7 9 8 3 6 0 4 1 2 5 9 5 3 8 4 7 1 2 6 0 1 3 6 4 8 5 7 0 9 2 2 7 0 5 3 9 6 4 1 8 8 6 9 0 1 2 3 7 5 4 3 2 1 7 0 4 9 5 8 6 6 0 4 1 2 3 5 8 7 9 Уникальные однушки. Итак, программы Белышева и Harry дают пересекающиеся множества КФ ЛК, но не совпадающие. И решения получаются от обоих множеств! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Тэк-с, пробую изменить глубину поиска в программе Белышева. Глубина 6 проходит Частичное транзитивное замыкание связанности ЛК Задайте глубину поиска: 6 36011 60 71343 96 107515 58 142891 61 177876 93 212191 59 246245 62 281110 64 Построено КФ ЛК: 283321 Сохранение : выполнено Время работы : 44.46 сек Глубина 7 тоже проходит . . . . . . . 1664298 85 1697109 54 1731818 99 1765781 63 1799957 34 1834093 79 1867952 57 1900968 95 1933048 60 1966596 77 2001368 42 2036836 46 2070909 57 2105483 59 Построено КФ ЛК: 2116504 Сохранение : выполнено Время работы : 312.484 секДальше не буду пробовать. Уже есть 2116504 КФ ЛК, можно проверять их. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Только добралась до порции КФ ЛК, полученной программой Белышева tzs_lk от КФ1. Вычла те КФ ЛК, которые уже были проверены (от программы Harry и от программы Белышева), осталось 1954244 КФ ЛК. Проверила первую махонькую порцию 50000 КФ ЛК, и сразу уникальное решение (однушечка)! Поиск марьяжных ДЛК (кроме симметричных) для семейства ЛК Введено ЛК: 50000 Найдено марьяжных ДЛК: 1 они записаны в файл output.txt Время работы в сек : 2152.46 Ну, что можно сказать? Вывод радостный, ободряющий: мой алгоритм вторичной обработки (алгоритм Y) получил очень хорошее добавление (развитие) в виде алгоритма Белышева, реализованного в программе tzs_lk. Я ещё называю алгоритм Y - "поворот блоков в ДЛК как в ЛК", если смотреть на этот алгоритм как на алгоритм вторичной обработки результатов, где он применяется к известным КФ ОДЛК. Порцию из 1954244 КФ ЛК проверю постепенно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очевидно, что алгоритм Y, а также программу Белышева tzs_lk, можно применять не только ко вторичной обработке результатов, то есть к известным КФ ОДЛК. Берём любой ЛК, например, из темы "ЛК с частичной блочной структурой" и применяем к нему алгоритм. Большинство ЛК из указанной темы я проверяла этим алгоритмом. А теперь можно все их проверить программой Белышева. Наверняка найдутся новые решения. У меня в рабочем файле ЛК с частичной блочной структурой гораздо больше, чем выложено в теме, не все ЛК выкладывала. Так что, проверки прибыло ох как много. Цитирую из указанной темы Показываю ЛК с частичной блочной структурой, в котором 19 блоков, представленный мной на форуме Math Help Planet Этот ЛК с частичной блочной структурой был выложен давным-давно на форуме Math Help Planet. А ну-ка покрутите в нём интеркаляты-графы :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот, например, для глубины поиска 5 Частичное транзитивное замыкание связанности ЛК Задайте глубину поиска: 5 33358 113 69957 112 104720 117 141012 125 175075 126 207931 79 243139 152 275263 57 306135 118 340305 96 371566 72 404700 55 439349 139 470745 78 504736 81 538303 42 Построено КФ ЛК: 565966 Сохранение : выполнено Время работы : 88.389 сек Хорошая порция КФ ЛК получена. Можно проверять. Дерзайте, господа! У кого есть техника. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, программа Белышева Интеркалятор находит в этом ЛК 47 интеркалятов! Показываю один срез. срез #1
0 1 2 3 4 5 6 7 8 9
1 0 8 9 5 4 7 6 2 3
2 3 5 0 7 6 9 8 4 1
3 2 6 7 8 9 1 4 0 5
4 5 0 1 2 3 8 9 6 7
5 4 9 8 6 7 3 2 1 0
6 7 4 5 9 8 0 1 3 2
7 6 1 4 3 2 5 0 9 8
8 9 3 2 1 0 4 5 7 6
9 8 7 6 0 1 2 3 5 4
{0,2} = 1 : (1,3,1,8)
{1,2} = 1 : (4,8,3,4)
{1,3} = 1 : (7,8,2,4)
{1,6} = 1 : (1,6,0,7)
{1,7} = 1 : (0,6,1,7)
{1,9} = 1 : (5,7,2,8)
{2,4} = 1 : (3,5,1,7)
{2,9} = 1 : (2,9,0,6)
{3,4} = 1 : (0,7,3,4)
{3,8} = 1 : (2,9,1,7)
{6,8} = 1 : (0,4,6,8)
{7,9} = 1 : (0,4,7,9)
{0,1} = 2 : (0,1,0,1) (8,9,4,5)
{0,3} = 2 : (4,8,2,5) (7,9,4,7)
{0,7} = 2 : (0,7,0,7) (1,6,1,6)
{2,8} = 2 : (0,1,2,8) (6,7,5,9)
{3,9} = 2 : (0,1,3,9) (6,7,4,8)
{4,5} = 2 : (0,1,4,5) (4,5,0,1)
{4,8} = 2 : (1,6,2,5) (4,8,0,6)
{0,6} = 3 : (0,6,0,6) (1,7,1,7) (3,4,2,8)
{5,9} = 3 : (0,3,5,9) (1,6,3,4) (4,8,1,7)
{2,3} = 5 : (0,8,2,3) (1,6,8,9) (2,3,0,1) (4,7,4,5) (5,9,6,7)
{6,7} = 5 : (0,1,6,7) (2,5,4,5) (3,9,2,3) (4,8,8,9) (6,7,0,1)
{8,9} = 5 : (0,7,8,9) (1,5,2,3) (2,4,6,7) (3,6,4,5) (8,9,0,1)
Есть что покрутить. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программа Harry находит в этом ЛК 19 независимых блоков (выводятся все) .. writing LS to file 10LS_1.txt
1: blocks 19
LS out 524288
blocks
{0,9} : [ 1][ 1] [ 1][ 2] [ 2][ 1] [ 2][ 2]
{1,8} : [ 1][ 3] [ 1][ 4] [ 9][ 3] [ 9][ 4]
{2,7} : [ 1][ 5] [ 1][ 6] [ 2][ 5] [ 2][ 6]
{3,6} : [ 1][ 7] [ 1][ 8] [ 2][ 7] [ 2][ 8]
{4,5} : [ 1][ 9] [ 1][10] [ 8][ 9] [ 8][10]
{4,5} : [ 2][ 3] [ 2][ 4] [ 6][ 3] [ 6][ 4]
{1,8} : [ 2][ 9] [ 2][10] [ 7][ 9] [ 7][10]
{1,8} : [ 3][ 1] [ 3][ 2] [ 4][ 1] [ 4][ 2]
{6,3} : [ 3][ 5] [ 3][ 6] [ 6][ 5] [ 6][ 6]
{5,4} : [ 3][ 7] [ 3][ 8] [ 5][ 7] [ 5][ 8]
{3,6} : [ 4][ 3] [ 4][ 4] [10][ 3] [10][ 4]
{4,5} : [ 4][ 5] [ 4][ 6] [ 7][ 5] [ 7][ 6]
{2,7} : [ 5][ 1] [ 5][ 2] [ 6][ 1] [ 6][ 2]
{1,8} : [ 5][ 5] [ 5][ 6] [ 8][ 5] [ 8][ 6]
{3,6} : [ 5][ 9] [ 5][10] [ 9][ 9] [ 9][10]
{8,1} : [ 6][ 7] [ 6][ 8] [10][ 7] [10][ 8]
{3,6} : [ 7][ 1] [ 7][ 2] [ 8][ 1] [ 8][ 2]
{4,5} : [ 9][ 1] [ 9][ 2] [10][ 1] [10][ 2]
{9,0} : [ 9][ 5] [ 9][ 6] [10][ 5] [10][ 6]
elapsed time 0:00:01
Press a key to close the console
Можно сравнить с иллюстрацией. Независимые блоки могут быть выбраны и по-другому (из 47 блоков), но количество их должно быть 19 в любом варианте. А программа Harry для всех блоков находит тоже 47 блоков, как и программа Белышева. Программа тоже их все выводит, но не буду показывать - много. В общем, отличный квадратик для алгоритма поворота блоков или как их там... интеркалятов-графов :) Интеркаляты-графы, может, и не так поворачиваются, как у меня блоки, но как-то поворачиваются, ИМХО. |

©2026 (C) Progger
