Весьма интересной оказалась эта четвёрка

 0 1 2 3 4 5 6 7 8 9
 3 7 4 0 8 1 9 5 2 6
 8 2 6 4 0 9 5 3 7 1
 6 5 1 9 2 7 0 8 4 3
 7 3 0 5 1 8 4 9 6 2
 9 8 3 7 5 4 2 6 1 0
 2 0 5 1 6 3 8 4 9 7
 1 4 7 6 9 0 3 2 5 8
 5 6 9 8 7 2 1 0 3 4
 4 9 8 2 3 6 7 1 0 5
sq1

 0 1 2 3 4 5 6 7 8 9
 3 7 5 0 8 1 9 4 2 6
 8 2 6 4 0 9 5 3 7 1
 6 4 1 9 2 7 0 8 5 3
 7 3 0 5 1 8 4 9 6 2
 9 8 3 7 5 4 2 6 1 0
 2 0 4 1 6 3 8 5 9 7
 1 5 7 6 9 0 3 2 4 8
 5 6 9 8 7 2 1 0 3 4
 4 9 8 2 3 6 7 1 0 5
sq2

 0 1 2 3 4 5 6 7 8 9
 3 7 4 0 8 1 9 5 2 6
 8 2 6 4 0 9 5 3 7 1
 6 5 1 9 7 2 0 8 4 3
 2 3 0 5 1 8 4 9 6 7
 9 8 3 2 5 4 7 6 1 0
 7 0 5 1 6 3 8 4 9 2
 1 4 7 6 9 0 3 2 5 8
 5 6 9 8 2 7 1 0 3 4
 4 9 8 7 3 6 2 1 0 5
sq3

 0 1 2 3 4 5 6 7 8 9
 3 7 5 0 8 1 9 4 2 6
 8 2 6 4 0 9 5 3 7 1
 6 4 1 9 7 2 0 8 5 3
 2 3 0 5 1 8 4 9 6 7
 9 8 3 2 5 4 7 6 1 0
 7 0 4 1 6 3 8 5 9 2
 1 5 7 6 9 0 3 2 4 8
 5 6 9 8 2 7 1 0 3 4
 4 9 8 7 3 6 2 1 0 5
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 3 4 0 9 5 6 7 8
 3 4 1 7 9 0 2 8 5 6
 5 9 7 6 8 1 3 4 0 2
 9 7 5 8 3 6 1 2 4 0
 4 5 6 0 1 8 9 3 2 7
 6 8 0 5 2 4 7 9 1 3
 8 6 4 9 7 2 0 5 3 1
 7 0 8 2 6 3 4 1 9 5
 2 3 9 1 5 7 8 0 6 4

Основной ДЛК четвёрки не является ЛК блочной структуры. Однако… все ортогональные соквадраты этой четвёрки блочные, причём симметричные по Гергели/Брауну.
Очень интересно! Все эти ортогональки принадлежат одному семейству БС с каноническим шаблоном

0 1 2 3 4
0 1 2 4 3
1 2 0 3 4
1 2 3 4 0
2 3 4 1 0
2 4 3 0 1
3 0 4 1 2
3 4 0 2 1
4 0 1 2 3
4 3 1 0 2

и все они дают двушки.
Вот такая весьма интересная конфигурация получается: четвёрка и 4 двушки.

Таким образом, показанная четвёрка напрямую от ЛК блочной структуры не происходит, но… она происходит от семейства ЛК блочной структуры рикошетом – от двушек, происходящих от ЛК блочной структуры.
Основной ДЛК четвёрки не имеет блочную структуру, но в нём имеется 15 блоков. Такие ЛК будем называть ЛК с частичной блочной структурой.
Показываю иллюстрацию основного ДЛК четвёрки с раскрашенными 15 блоками (в ДЛК переставлены строки и столбцы для более компактного представления блоков)



Семейство ЛК блочной структуры, которое дало эту четвёрку рикошетом, я планирую проверить полностью. Интересное семейство!
Полный паспорт этого семейства

Семейство BGJRWETA содержит 65536 ЛК
Они записаны в файл lk_10x5_BGJRWETA_65536.txt

Канонический шаблон:
0 1 2 3 4
0 1 2 4 3
1 2 0 3 4
1 2 3 4 0
2 3 4 1 0
2 4 3 0 1
3 0 4 1 2
3 4 0 2 1
4 0 1 2 3
4 3 1 0 2

Базовый квадрат:
0 1 2 3 4 5 6 7 8 9
1 0 3 2 5 4 8 9 6 7
2 3 4 5 0 1 7 6 9 8
3 2 5 4 6 7 9 8 0 1
4 5 6 7 8 9 2 3 1 0
5 4 8 9 7 6 0 1 2 3
6 7 0 1 9 8 3 2 4 5
7 6 9 8 1 0 4 5 3 2
8 9 1 0 2 3 5 4 7 6
9 8 7 6 3 2 1 0 5 4

Понятно, что данное семейство даёт несколько двушек, от которых ещё и четвёрка получается (может, и не одна!). Что ещё даст это семейство?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

О ЛК с частичной блочной структурой я немного писала здесь
https://boinc.progger.info/odlk/forum_thread.php?id=41&postid=1620#1620

В этом сообщении указаны ссылки на форум Math Help Planet, где представлены ЛК с частичной блочной структурой.
Мне удалось найти ЛК, в котором имеется 19 блоков.
Вот думаю: а не проверить ли это семейство? Может быть, семейства ЛК с частичной блочной структурой тоже дадут что-нибудь интересное (в смысле пар ОДЛК). Правда, семейств таких у меня пока мало.

Есть ли ЛК с частичной блочной структурой, в которых больше 19 блоков?
На форуме Math Help Planet показан ЛК, в котором 21 блок, но этот ЛК легко превращается в полную блочную структуру поворотом одного из двух одиночных блоков.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Показываю ЛК с частичной блочной структурой, в котором 19 блоков, представленный мной на форуме Math Help Planet



Вполне себе блочная структура, 6 блоков не хватает до полного комплекта.
Можно точно так же поворачивать 19 блоков и получать новые ЛК. Потом все эти ЛК обработать программой Белышева Канонизатор ЛК по ДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это цитата

Весьма интересной оказалась эта четвёрка

 0 1 2 3 4 5 6 7 8 9
 3 7 4 0 8 1 9 5 2 6
 8 2 6 4 0 9 5 3 7 1
 6 5 1 9 2 7 0 8 4 3
 7 3 0 5 1 8 4 9 6 2
 9 8 3 7 5 4 2 6 1 0
 2 0 5 1 6 3 8 4 9 7
 1 4 7 6 9 0 3 2 5 8
 5 6 9 8 7 2 1 0 3 4
 4 9 8 2 3 6 7 1 0 5
sq1

 0 1 2 3 4 5 6 7 8 9
 3 7 5 0 8 1 9 4 2 6
 8 2 6 4 0 9 5 3 7 1
 6 4 1 9 2 7 0 8 5 3
 7 3 0 5 1 8 4 9 6 2
 9 8 3 7 5 4 2 6 1 0
 2 0 4 1 6 3 8 5 9 7
 1 5 7 6 9 0 3 2 4 8
 5 6 9 8 7 2 1 0 3 4
 4 9 8 2 3 6 7 1 0 5
sq2

 0 1 2 3 4 5 6 7 8 9
 3 7 4 0 8 1 9 5 2 6
 8 2 6 4 0 9 5 3 7 1
 6 5 1 9 7 2 0 8 4 3
 2 3 0 5 1 8 4 9 6 7
 9 8 3 2 5 4 7 6 1 0
 7 0 5 1 6 3 8 4 9 2
 1 4 7 6 9 0 3 2 5 8
 5 6 9 8 2 7 1 0 3 4
 4 9 8 7 3 6 2 1 0 5
sq3

 0 1 2 3 4 5 6 7 8 9
 3 7 5 0 8 1 9 4 2 6
 8 2 6 4 0 9 5 3 7 1
 6 4 1 9 7 2 0 8 5 3
 2 3 0 5 1 8 4 9 6 7
 9 8 3 2 5 4 7 6 1 0
 7 0 4 1 6 3 8 5 9 2
 1 5 7 6 9 0 3 2 4 8
 5 6 9 8 2 7 1 0 3 4
 4 9 8 7 3 6 2 1 0 5
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 3 4 0 9 5 6 7 8
 3 4 1 7 9 0 2 8 5 6
 5 9 7 6 8 1 3 4 0 2
 9 7 5 8 3 6 1 2 4 0
 4 5 6 0 1 8 9 3 2 7
 6 8 0 5 2 4 7 9 1 3
 8 6 4 9 7 2 0 5 3 1
 7 0 8 2 6 3 4 1 9 5
 2 3 9 1 5 7 8 0 6 4

Кстати, на эту четвёрку я обратила внимание давно, смотрите сообщение на форуме Math Help Planet
http://mathhelpplanet.com/viewtopic.php?p=293883#p293883
В сообщении приведены две четвёрки:

#1
0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 4 9 6 7 8
4 3 7 9 1 8 2 0 6 5
9 8 6 5 0 2 4 3 1 7
5 9 8 2 6 3 7 1 0 4
8 6 5 7 2 9 0 4 3 1
2 7 4 8 3 6 1 5 9 0
3 0 1 4 9 7 5 8 2 6
7 5 0 6 8 1 3 9 4 2
6 4 9 1 7 0 8 2 5 3

#2
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 1 7 9 0 2 8 5 6
5 9 7 6 8 1 3 4 0 2
9 7 5 8 3 6 1 2 4 0
4 5 6 0 1 8 9 3 2 7
6 8 0 5 2 4 7 9 1 3
8 6 4 9 7 2 0 5 3 1
7 0 8 2 6 3 4 1 9 5
2 3 9 1 5 7 8 0 6 4

Обе они происходят от двушек, происходящих от ЛК блочной структуры.
И основные ДЛК обеих четвёрок содержат 15 блоков.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это цитата

Показываю ЛК с частичной блочной структурой, в котором 19 блоков, представленный мной на форуме Math Help Planet



Вполне себе блочная структура, 6 блоков не хватает до полного комплекта.
Можно точно так же поворачивать 19 блоков и получать новые ЛК. Потом все эти ЛК обработать программой Белышева Канонизатор ЛК по ДЛК.

Проверила семейство, порождаемое данным ЛК с частичной блочной структурой.
Согласно теории Белышева можно 9 блоков (на пересечении с первой строкой и с первым столбцом ЛК) не поворачивать.
Остаётся повернуть всего 10 блоков, вариантов преобразованных ЛК 2^10=1024. Всего-то! Проверяется очень быстро.
Решения от семейства найдены! Однушки и две двушки. Показываю двушки:

0 2 4 9 6 3 5 8 7 1 
2 1 9 8 3 7 4 5 0 6 
8 7 2 6 5 9 0 3 1 4 
4 0 5 3 1 2 7 9 6 8 
7 6 0 5 4 8 9 1 3 2 
6 8 3 0 9 5 1 2 4 7 
1 9 8 2 7 0 6 4 5 3 
3 5 6 1 8 4 2 7 9 0 
9 4 1 7 2 6 3 0 8 5 
5 3 7 4 0 1 8 6 2 9 

0 2 6 5 8 9 7 4 3 1 
5 1 9 6 3 2 4 8 0 7 
6 7 2 1 9 8 0 3 5 4 
7 0 8 3 6 4 2 9 1 5 
3 5 1 8 4 6 9 0 7 2 
4 3 0 9 7 5 8 1 2 6 
1 8 3 4 5 7 6 2 9 0 
9 6 5 2 0 1 3 7 4 8 
2 9 4 7 1 0 5 6 8 3 
8 4 7 0 2 3 1 5 6 9 

Интересно: одна двушка симметричная по Гергели/Брауну, а вторая - нет.
Но все найденные решения в БД уже есть.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот этот ЛК с частичной блочной структурой, содержащий 15 блоков, очень симпатичный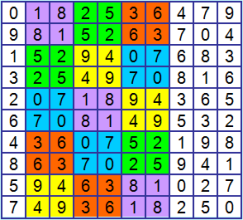



отсюда
http://mathhelpplanet.com/viewtopic.php?p=284913#p284913

Блоки в нём компактные. Сейчас преобразую этот ЛК немножко и проверю семейство ЛК, которое он порождает.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Готово! Проверила это семейство.
Решения нашлись. Вот двушечка такая нашлась

 0 1 2 3 4 5 6 7 8 9
 6 3 4 9 7 1 2 8 5 0
 1 9 7 8 0 3 4 6 2 5
 5 6 9 1 2 8 0 4 7 3
 4 0 8 6 9 7 5 2 3 1
 2 7 5 0 8 4 3 9 1 6
 7 5 6 2 1 0 8 3 9 4
 8 2 1 4 3 6 9 5 0 7
 9 4 3 7 5 2 1 0 6 8
 3 8 0 5 6 9 7 1 4 2
sq1

 0 1 2 3 4 5 6 7 8 9
 6 3 4 9 7 1 2 8 5 0
 1 9 7 8 0 3 4 6 2 5
 9 6 5 1 2 8 0 4 7 3
 4 0 8 6 5 7 9 2 3 1
 2 7 9 0 8 4 3 5 1 6
 7 5 6 2 1 0 8 3 9 4
 8 2 1 4 3 6 5 9 0 7
 5 4 3 7 9 2 1 0 6 8
 3 8 0 5 6 9 7 1 4 2
sq2

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 6 7 9 5 3 8
 9 3 4 6 5 8 7 2 1 0
 7 5 6 8 3 2 4 9 0 1
 5 6 9 0 7 1 2 8 4 3
 4 9 8 2 0 3 5 1 6 7
 8 4 3 7 2 9 1 0 5 6
 3 0 5 1 9 4 8 6 7 2
 2 8 7 5 1 6 0 3 9 4
 6 7 1 9 8 0 3 4 2 5

Удивительно, что из трёх ДЛК этой двушки какой-то - блочная структура семейства вида 5х5, которое дало море решений.
И при вторичной обработке этой двушки программой Канонизатор ЛК по ДЛК море решений находится.

В общем, рассматриваемое семейство ЛК с частичной блочной структурой непостижимым образом выходит на полную блочную структуру. Пока не поняла механизм этой связи частичных блочных структур с полными блочными структурами.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Показываю иллюстрацию основного ДЛК четвёрки с раскрашенными 15 блоками (в ДЛК переставлены строки и столбцы для более компактного представления блоков)

Проверила семейство, порождаемое этим ЛК частичной блочной структуры.
Решение нашлось одно - та самая четвёрка, от которой я это семейство получила:

0 5 3 6 9 8 4 2 7 1 
3 1 9 7 6 4 8 5 0 2 
7 6 2 1 5 9 0 3 4 8 
9 8 4 3 1 0 2 6 5 7 
1 7 5 2 4 6 3 8 9 0 
2 4 1 8 7 5 9 0 6 3 
8 0 7 4 3 2 6 9 1 5 
6 3 8 9 0 1 5 7 2 4 
4 9 0 5 2 3 7 1 8 6 
5 2 6 0 8 7 1 4 3 9 

Итак, что мы имеем? Семейства ЛК с частичной блочной структурой решения дают.
Но все проверенные семейства были получены от известных решений.
Теперь надо идти обратным путём: строить семейства ЛК с частичной блочной структурой и искать от них решения.
Только вот вопрос: как эти семейства строить?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Взяла ещё ЛК с частичной блочной структурой из 16 блоков с форума Math Help Planet, преобразовала его немножко, вот такой симпатичный квадратик получился



Тут очень интересно: 16 блоков различных, не пересекающихся и один блок одиночный, смотрите на иллюстрации розовый блок {0,9}.
Этот блок тоже можно всегда беспрепятственно поворачивать, он ни с чем не пересекается, ничему не мешает.
В программе заложила поворот 11 блоков, включая одиночный.
Получилось 2048 ЛК в результате полного перебора всех возможных вариантов поворотов 11 блоков.
Проверила эти ЛК программой Белышева Канонизатор ЛК по ДЛК, нашлась всего одна однушка:

0 1 2 3 4 5 6 7 8 9
9 4 3 8 2 7 1 6 5 0
8 2 6 5 9 0 4 3 7 1
1 3 4 9 7 2 0 5 6 8
7 8 5 0 3 6 9 4 1 2
2 6 9 4 8 1 5 0 3 7
6 5 8 2 0 9 7 1 4 3
3 9 1 7 5 4 2 8 0 6
5 7 0 1 6 3 8 9 2 4
4 0 7 6 1 8 3 2 9 5
sq1

Square:
 0 3 4 9 6 8 7 5 2 1
 9 1 5 6 3 2 4 8 0 7
 5 7 2 4 0 1 8 3 9 6
 8 6 0 3 7 9 2 1 5 4
 3 0 7 8 4 6 5 9 1 2
 1 9 6 2 8 5 3 4 7 0
 4 2 1 5 9 7 6 0 3 8
 2 8 9 1 5 4 0 7 6 3
 6 4 3 7 1 0 9 2 8 5
 7 5 8 0 2 3 1 6 4 9

Но посмотрите на эту однушку! Ортогональный соквадрат sq1 опять блочная структура! И даёт эта блочная структура двушку.

Вот такая мистическая связь блочных структур с частичными блочными структурами.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посмотрела на ДЛК, от которых получила ЛК с частичной блочной структурой.
Покажу два ДЛК



Очевидно, что эти ДЛК почти симметричные по Гергели/Брауну, но с несколькими нарушениями симметричности (нарушения выделены красным цветом).
И даже нарушения вполне гармоничные.
Назовём такие ДЛК псевдосимметричными по Гергели/Брауну (аналогично псевдоассоциативным ДЛК).
Интересно, дадут ли что-нибудь ЛК с частичной блочной структурой. Настроить таких ЛК можно огромную кучу, но есть ли смысл?
То, что решения от псевдосимметричных ДЛК есть, сомнению не подлежит: решения перед вами - показанные ДЛК не "пустышки".
Много ли решений? Ответ на этот вопрос может дать только эксперимент.

Взяла свою программу генерации симметричных по Гергели/Брауну ДЛК и «отпустила» в ней две последние строки, то есть в этих строках условие симметричности не выполняется.
Нагенерировала псевдосимметричные ДЛК, 200000 штук, проверила их на ОДЛК, пусто.
Их надо ещё обрабатывать программой Канонизатор ЛК по ДЛК, тогда, может быть, будут решения.
Именно так я получаю решения от псевдоассоциативных ДЛК.

Интересно: проверила сгенерированные псевдосимметричные ДЛК программой определитель семейств БС и … некоторые из них оказались блочными структурами. Вот протокол работы программы

Определитель семейств блочных ЛК

Введено ЛК    : 200000
Из них блочных  : 14944

Найдено семейств блочных ЛК

10x5       : 1
10x9       : 6
10x10      : 17

Это как раз тот случай, о котором рассказано выше: ЛК с частичной блочной структурой из 21 блока.
Там достаточно повернуть один из одиночных блоков и получается полная блочная структура.
Вот аналогичные примеры

0 1 2 3 4 5 6 7 8 9 
1 2 0 4 3 6 5 9 7 8 
2 0 1 5 6 3 4 8 9 7 
3 4 7 8 0 9 1 2 5 6 
4 6 8 2 9 0 7 1 3 5 
8 5 3 0 2 7 9 6 4 1 
7 8 9 6 5 4 3 0 1 2 
6 7 4 9 8 1 0 5 2 3 
9 3 5 1 7 8 2 4 6 0 
5 9 6 7 1 2 8 3 0 4 

0 1 2 3 4 5 6 7 8 9 
1 2 0 4 3 6 5 9 7 8 
2 0 1 5 6 3 4 8 9 7 
3 4 7 8 0 9 1 2 5 6 
4 6 8 2 9 0 7 1 3 5 
8 5 3 0 2 7 9 6 4 1 
7 8 9 6 5 4 3 0 1 2 
6 7 4 9 8 1 0 5 2 3 
9 3 5 7 1 2 8 4 6 0 
5 9 6 1 7 8 2 3 0 4 

0 1 2 3 4 5 6 7 8 9 
1 2 0 4 3 6 5 9 7 8 
2 0 1 5 6 3 4 8 9 7 
3 4 7 8 0 9 1 2 5 6 
4 6 8 2 9 0 7 1 3 5 
8 5 3 9 2 7 0 6 4 1 
7 8 9 6 5 4 3 0 1 2 
6 7 4 0 8 1 9 5 2 3 
9 3 5 1 7 8 2 4 6 0 
5 9 6 7 1 2 8 3 0 4

В последних двух строках нарушения симметричности есть, но если повернуть один из блоков - {1,7} или {2,8} - получается полная блочная структура, нарушений симметричности уже не будет.

Но это у меня только один вид нарушений симметричности: в двух последних строках. А ведь таких нарушений можно море соорудить.
И каждый ДЛК с такими нарушениями симметричности будет давать частичную блочную структуру, а иногда даже и полную блочную структуру, как видим из приведённых выше примеров.

PS. Хм... Проверила три показанных выше псевдосимметричных по Гергели/Брауну ДЛК.
Программа нашла только одну блочную структуру:

Определитель семейств блочных ЛК

Введено ЛК       : 3
Из них блочных   : 1

Найдено семейств блочных ЛК

10x10            : 1

Вроде все три ДЛК подобные, однако не все являются ЛК блочной структуры.
Ну, зато все они являются ЛК с частичной блочной структурой, а именно такие ЛК моя программа и генерировала. Я не преследовала цель получить полные блочные структуры, они сами получились.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это цитата

Взяла ещё ЛК с частичной блочной структурой из 16 блоков с форума Math Help Planet, преобразовала его немножко, вот такой симпатичный квадратик получился



Тут очень интересно: 16 блоков различных, не пересекающихся и один блок одиночный, смотрите на иллюстрации розовый блок {0,9}.
Этот блок тоже можно всегда беспрепятственно поворачивать, он ни с чем не пересекается, ничему не мешает.
В программе заложила поворот 11 блоков, включая одиночный.
Получилось 2048 ЛК в результате полного перебора всех возможных вариантов поворотов 11 блоков.
Проверила эти ЛК программой Белышева Канонизатор ЛК по ДЛК, нашлась всего одна однушка:

На примере этого ЛК с частичной блочной структурой впервые применила условный поворот одиночного блока.
Поясню, что это значит. Выбрала для условного поворота блок {4,6}, этот блок расположен в первой и третьей строках.
Очевидно, что данный блок нельзя повернуть всегда, потому что он пересекается с другим блоком - {3,6}. Поэтому этот блок поворачивается только в том случае, когда блок {3,6} не повёрнут. Вот это и называется условным поворотом блока.
[Угловой блок {0,4} не поворачивается.]

Мысль о таком повороте блоков сидела в голове давно.
А не теряем ли мы решения, не поворачивая одиночные блоки в полных блочных структурах?
Интересный вопрос! Разве при дополнительных поворотах одиночных блоков не могут появиться уникальные ЛК - то есть не изоморфные всем остальным ЛК, которые мы получаем поворотом основных блоков?

Ну, а пока вот маленький экспериментик с ЛК частичной блочной структуры.
Сейчас это уже проверится. Кстати, получилось у меня в результате поворота 12 блоков 3072 ЛК. 11 блоков поворачиваются без условий, а один блок поворачивается при условии, что блок, с которым он пересекается, не повёрнут.
Хочу выполнить такой эксперимент с ЛК (полной) блочной структуры.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Возвращаюсь к четвёркам, которые дают ЛК с частичной блочной структурой.
В сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=40&postid=1556#1556
показаны 7 четвёрок из нашей БД, которые не происходят от ЛК блочной структуры.
Покажу их ещё раз (это основный ДЛК четвёрок во втором формате)

**0 2 4 7 9 8 3 6 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 0 4 5 2 6 1 3 7
2 0 8 9 6 4 5 7 1 3
3 9 6 5 1 0 7 4 8 2
5 6 1 2 3 7 8 0 4 9

**0 2 6 7 9 8 3 4 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 1 4 5 2 6 0 3 7
2 0 8 9 6 4 5 7 1 3
3 9 4 5 1 0 7 6 8 2
5 6 0 2 3 7 8 1 4 9

*0 4 3 7 8 9 5 2 6 1
7 1 5 2 6 4 3 9 0 8
9 0 2 6 5 8 4 3 1 7
1 8 6 3 9 7 2 4 5 0
2 5 9 1 4 6 0 8 7 3
6 2 0 9 7 5 8 1 3 4
8 7 1 4 3 2 6 0 9 5
3 6 8 5 0 1 9 7 4 2
4 9 7 0 2 3 1 5 8 6
5 3 4 8 1 0 7 6 2 9

*0 5 3 6 9 8 4 2 7 1
3 1 9 7 6 4 8 5 0 2
7 6 2 1 5 9 0 3 4 8
9 8 4 3 1 0 2 6 5 7
1 7 5 2 4 6 3 8 9 0
2 4 1 8 7 5 9 0 6 3
8 0 7 4 3 2 6 9 1 5
6 3 8 9 0 1 5 7 2 4
4 9 0 5 2 3 7 1 8 6
5 2 6 0 8 7 1 4 3 9

0 5 4 6 3 7 8 2 9 1
8 1 5 7 6 3 0 9 2 4
6 0 2 5 9 8 1 3 4 7
9 2 6 3 7 1 4 8 5 0
7 3 1 2 4 6 9 5 0 8
2 4 8 9 0 5 7 6 1 3
1 9 7 8 5 0 6 4 3 2
4 8 9 0 1 2 3 7 6 5
3 7 0 4 2 9 5 1 8 6
5 6 3 1 8 4 2 0 7 9

0 2 3 7 5 9 8 4 6 1
4 1 8 6 9 7 3 5 0 2
6 5 2 9 1 0 4 3 7 8
5 8 6 3 0 1 2 9 4 7
2 7 9 8 4 6 0 1 3 5
3 6 0 1 7 5 9 8 2 4
1 4 7 5 8 3 6 2 9 0
9 0 4 2 3 8 5 7 1 6
7 9 5 0 2 4 1 6 8 3
8 3 1 4 6 2 7 0 5 9

0 3 4 2 7 8 5 9 6 1
3 1 7 9 2 4 8 5 0 6
6 4 2 7 8 9 1 3 5 0
5 2 1 3 9 0 4 6 7 8
9 8 0 6 4 2 7 1 3 5
1 7 3 4 6 5 0 8 9 2
2 9 5 8 1 7 6 0 4 3
8 0 9 1 5 6 3 7 2 4
4 5 6 0 3 1 9 2 8 7
7 6 8 5 0 3 2 4 1 9

Как выяснилось, две из этих четвёрок происходят от ЛК блочной структуры косвенным образом - от двушек, которые находятся от семейства БС. Я пометила эти четвёрки звёздочкой.
Осталось исследовать 5 четвёрок - откуда они происходят.
Отмечу, что две четвёрки в этом списке происходят от псевдоассоциативных ДЛК. Вряд ли тут замешаны семейства БС даже косвенным образом.

Исследую эту четвёрку

0 2 4 7 9 8 3 6 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 0 4 5 2 6 1 3 7
2 0 8 9 6 4 5 7 1 3
3 9 6 5 1 0 7 4 8 2
5 6 1 2 3 7 8 0 4 9

Нашла ортогональные соквадраты четвёрки (программа С. Беляева):

0 1 2 3 4 5 6 7 8 9
4 3 0 8 2 7 1 9 6 5
6 0 8 5 7 2 4 1 9 3
9 4 1 2 3 6 7 8 5 0
7 5 6 1 9 0 8 3 4 2
8 7 9 6 5 4 3 0 2 1
1 9 7 4 6 3 5 2 0 8
5 2 3 0 1 8 9 6 7 4
3 8 4 7 0 9 2 5 1 6
2 6 5 9 8 1 0 4 3 7
sq1

 0 1 2 3 4 5 6 7 8 9
 4 3 0 8 7 2 1 9 6 5
 6 0 8 5 2 7 4 1 9 3
 9 4 1 7 3 6 2 8 5 0
 2 5 6 1 9 0 8 3 4 7
 8 7 9 6 5 4 3 0 2 1
 1 9 7 4 6 3 5 2 0 8
 5 2 3 0 1 8 9 6 7 4
 3 8 4 2 0 9 7 5 1 6
 7 6 5 9 8 1 0 4 3 2
sq2

 0 1 2 3 4 5 6 7 8 9
 4 3 9 8 2 7 1 0 6 5
 6 9 8 5 7 2 4 1 0 3
 9 4 1 2 3 6 7 8 5 0
 7 5 6 1 9 0 8 3 4 2
 8 7 0 6 5 4 3 9 2 1
 1 0 7 4 6 3 5 2 9 8
 5 2 3 9 1 8 0 6 7 4
 3 8 4 7 0 9 2 5 1 6
 2 6 5 0 8 1 9 4 3 7
sq3

 0 1 2 3 4 5 6 7 8 9
 4 3 9 8 7 2 1 0 6 5
 6 9 8 5 2 7 4 1 0 3
 9 4 1 7 3 6 2 8 5 0
 2 5 6 1 9 0 8 3 4 7
 8 7 0 6 5 4 3 9 2 1
 1 0 7 4 6 3 5 2 9 8
 5 2 3 9 1 8 0 6 7 4
 3 8 4 2 0 9 7 5 1 6
 7 6 5 0 8 1 9 4 3 2
sq4

Эти ортогональки не оставляют никаких сомнений, что случай совершенно аналогичный. Все они принадлежат одному и тому же семейству БС вида 10х5 - DBIFSRVT и дают двушки, от которых рикошетом получается рассматриваемая четвёрка.

Сильно подозреваю, что должна быть вторая четвёрка, происходящая от двушек данного семейства БС. Сейчас буду искать эту четвёрку.
Забегая вперёд: рассматриваемая четвёрка тоже дала ЛК с частичной блочной структурой - 13 блоков. Далее покажу этот ЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Всё правильно: эта четвёрка

0 2 6 7 9 8 3 4 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 1 4 5 2 6 0 3 7
2 0 8 9 6 4 5 7 1 3
3 9 4 5 1 0 7 6 8 2
5 6 0 2 3 7 8 1 4 9

тоже от семейства БС DBIFSRVT происходит рикошетом.
Пометила эти две четвёрки в списке выше двумя звёздочками.

В списке ещё три четвёрки не исследованные.
Две четвёрки происходят от псевдоассоциативных ДЛК, а откуда происходит третья четвёрка? Если вдруг она тоже происходит от семейства БС косвенным образом, должна быть парная ей четвёрка. Сейчас буду смотреть на эти четвёрки.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверила оставшиеся три четвёрки. Нет, тут не такой случай: никакой связи с семействами БС не видно.

Таким образом, в классификации четвёрок произошли изменения. Добавился класс четвёрок, которые происходят от семейств БС косвенным образом. Имеем примеры таких четвёрок из нашей БД, примеры показаны выше.

Откуда ещё происходят четвёрки, предстоит выяснить.
Ну, ещё они происходят от псевдоассоциативных ДЛК, такие четвёрки тоже у нас имеются, две штуки.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Показываю обещанный ЛК с частичной блочной структурой, полученный от рассмотренной выше четвёрки



В ЛК 13 блоков, это основные. Но есть ещё одиночные блоки.
Вот вывод программы Белышева Интеркалятор

срез #2

{0,8} = 1 : (2,5,1,3) 
{1,3} = 1 : (2,7,2,6) 
{1,4} = 1 : (2,3,2,5) 
{1,9} = 1 : (2,5,2,8) 
{2,3} = 1 : (1,8,1,4) 
{2,5} = 1 : (1,6,1,6) 
{3,4} = 1 : (0,1,3,4) 
{3,5} = 1 : (1,2,4,6) 
{3,7} = 1 : (1,9,4,8) 
{3,8} = 1 : (1,6,4,9) 
{3,9} = 1 : (0,6,3,9) 
{4,8} = 1 : (0,6,4,8) 
{0,6} = 2 : (4,8,5,8) (5,7,3,4) 
{2,7} = 2 : (1,3,1,8) (2,7,0,9) 
{3,6} = 2 : (3,6,0,9) (8,9,1,8) 
{5,8} = 2 : (0,7,5,8) (1,4,6,9) 
{0,9} = 3 : (0,9,0,9) (2,4,1,8) (5,6,2,3) 
{1,8} = 3 : (0,5,1,8) (1,8,0,9) (2,9,2,3) 
{4,5} = 3 : (0,2,4,5) (4,5,0,9) (6,7,1,8) 

Здесь хорошо видно все блоки: и основные, и одиночные. Основные блоки характеризуются тем, что они не пересекающиеся и поворачивать их можно беспрепятственно и безусловно. Одиночные блоки можно поворачивать только условно (редко встречаются такие одиночные блоки, которые тоже можно поворачивать безусловно).
Я выполнила для этого ЛК эксперимент с условным поворотом блоков. Ничего нового, кроме известной четвёрки, не нашлось в эксперименте.

Ещё не добралась до эксперимента с условным поворотом блоков в ЛК полной блочной структуры.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg