Вот последний из проверенных 10 ЛК

 0  1  2  3  4  5  6  7  8  9 
 1  0  3  2  5  6  7  8  9  4 
 2  3  0  1  7  4  9  6  5  8 
 3  2  1  0  9  8  5  4  7  6 
 4  5  6  8  0  1  2  9  3  7 
 5  8  9  7  6  0  4  3  1  2 
 6  7  8  4  3  9  0  1  2  5 
 7  4  5  9  1  2  8  0  6  3 
 8  9  4  6  2  7  3  5  0  1 
 9  6  7  5  8  3  1  2  4  0 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123678945 0123678945 0123894567 -> (10,10,10)
** 0123894567 0123894567 0123678945 -> (10,10,10)
** 0231496587 3102854769 2130658749 -> (10,10,10)
** 0231658749 3102476985 2130496587 -> (10,10,10)
** 0231874965 3102698547 2130874965 -> (27,27,27)
** 0312476985 2130658749 3102854769 -> (10,10,10)
** 0312698547 2130874965 3102698547 -> (27,27,27)
** 0312854769 2130496587 3102476985 -> (10,10,10)

Симметрия (27,27,27) двукратная, симметрия (10,10,10) шестикратная.
У этого ЛК самый скромный набор симметрий (из проверенных).

Ещё 10 ЛК проверила, у всех симметрия (27,27,27) как минимум двукратная!
Вот ЛК с самым скромным набором симметрий

 0  1  2  3  4  5  6  7  8  9 
 1  0  3  4  2  6  7  8  9  5 
 2  3  0  1  5  4  8  9  6  7 
 3  2  1  0  7  8  9  4  5  6 
 4  6  9  8  0  7  1  5  3  2 
 5  7  6  9  8  2  4  1  0  3 
 6  4  5  2  1  9  0  3  7  8 
 7  8  4  6  9  3  5  2  1  0 
 8  9  7  5  3  0  2  6  4  1 
 9  5  8  7  6  1  3  0  2  4 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0742369815 8136572490 9162743508 -> (27,27,27)
** 0834295176 9162743508 8136572490 -> (27,27,27)
R* 0132496875 0132476598 0132476598 -> (8,8,8)+
R* 0724359186 8163542709 8163542709 -> (8,8,8)+
R* 0843265719 9126753480 9126753480 -> (8,8,8)+

А вот у этого ЛК очень интересно

 0  1  2  3  4  5  6  7  8  9 
 1  0  3  2  5  6  7  8  9  4 
 2  3  0  4  6  8  9  1  7  5 
 3  2  4  0  7  9  5  6  1  8 
 4  5  6  7  0  2  8  9  3  1 
 5  6  8  9  2  0  1  3  4  7 
 6  7  9  5  8  1  0  4  2  3 
 7  8  1  6  9  3  4  0  5  2 
 8  9  7  1  3  4  2  5  0  6 
 9  4  5  8  1  7  3  2  6  0 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 2186075493 2186075493 0541987263 -> (30,30,30)
** 3164920857 3164920857 0716529348 -> (30,30,30)
** 4109763528 4109763528 0379218654 -> (30,30,30)
** 5172698340 5172698340 0482691537 -> (27,27,27)
** 6150382974 6150382974 0257843196 -> (30,30,30)
** 7148539602 7148539602 0964735812 -> (30,30,30)
** 8195247036 8195247036 0895362471 -> (30,30,30)
** 9137804265 9137804265 0638174925 -> (27,27,27)
*T 0123456789 0123456789 0123456789 -> (1,1,1)+
*T 2186075493 2186075493 0541987263 -> (30,30,30)+
*T 3164920857 3164920857 0716529348 -> (30,30,30)+
*T 4109763528 4109763528 0379218654 -> (30,30,30)+
*T 5172698340 5172698340 0482691537 -> (27,27,27)+
*T 6150382974 6150382974 0257843196 -> (30,30,30)+
*T 7148539602 7148539602 0964735812 -> (30,30,30)+
*T 8195247036 8195247036 0895362471 -> (30,30,30)+
*T 9137804265 9137804265 0638174925 -> (27,27,27)+

Симметрия (27,27,27) двукратная.
А ещё симметрия (27,27,27)+ тоже двукратная.
Присмотрелась я к этой симметрии.
Тут только транспонирование надо выполнить сначала.
Уже собралась выполнить, как увидела, что ЛК этот диагонально-симметричный и его транспонированный ЛК совпадает с ним самим.
О!! Вот теперь и понятно. Если этот ЛК транспонировать, то он снова будет обладать симметрией (27,27,27).
Конечно, будет! Потому что транспонирование его не изменит.
Сравните

** 5172698340 5172698340 0482691537 -> (27,27,27)
*T 5172698340 5172698340 0482691537 -> (27,27,27)+

и

** 9137804265 9137804265 0638174925 -> (27,27,27)
*T 9137804265 9137804265 0638174925 -> (27,27,27)+

То же самое имеем для симметрии (30,30,30) в данном ЛК.

Ой, никак не уйду от симметрии (27,27,27) :)
Но уже начала поглядывать в сторону другой симметрии.
Пока присматриваюсь, обкатываю.
Я уже начинала эту симметрию разрабатывать и тема есть этой симметрии посвящённая.
И генератор уже есть, Harry White написал.

Кстати, для примера Белышева, приведённого им при описании симметрии (27,27,27)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 0 1 5 8 3 9 4 7 6
3 9 4 7 2 8 5 0 6 1
4 6 9 1 0 7 3 5 2 8
5 7 0 8 6 4 2 9 1 3
6 8 7 9 1 2 4 3 0 5
7 5 6 0 3 9 8 1 4 2
8 4 5 2 9 0 1 6 3 7
9 3 8 6 7 1 0 2 5 4

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0734268951 3071592684 1360947285 -> (27,27,27)
** 0942385167 1360947285 3071592684 -> (27,27,27)

Симметрия двукратная!
Значит, такая вот она и есть - двукратная симметрия (как минимум) :)

Цитата

А вообще мой генератор ЛК с симметрией (27,27,27) даёт много мультисимметричных ЛК.
Список симметрий такой:

(8,8,8)
(10,10,10)
(15,15,15)
(16,16,16)
(19,19,19)
(21,21,21)
(22,22,22)
(27,27,27)
(28,28,28)
(30,30,30)

Это те, которые я увидела. Может быть, есть и ещё.
Да и симметрии с кодом с плюсом, наверное, тоже имеются.

Весьма интересна симметрия (28,28,28). Часто совместна с симметрией (27,27,27).
Пытаюсь расколоть эту симметрию, но пока не удаётся. Вижу только, что где-то очень близко к симметрии (27,27,27), но есть какой-то маленький нюансик, которым различаются эти две симметрии. Вот этот нюансик и никак не уловлю.

О-ч-ч-ч-е-н-ь забавный экземплярчик ЛК

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 0 1 5 6 3 8 9 4 7
3 5 6 8 9 4 0 1 7 2
4 6 8 9 0 7 1 5 2 3
5 3 4 6 7 8 9 2 0 1
6 4 0 7 8 9 2 3 1 5
7 8 9 0 1 2 5 6 3 4
8 9 7 1 2 0 3 4 5 6
9 7 5 2 3 1 4 0 6 8

Список симметрий, которыми этот ЛК обладает

(1,1,1)
(8,8,8)
(16,16,16)
(27,27,27)
(28,28,28)

Очевидные симметрии выводятся для всех четырёх симметрий, но! для симметрии (28,28,28) я сама добавила автоморфизм в файл standart.txt и, скорее всего, добавила не тот автоморфизм, который нужно добавить.
Поэтому очевидную симметрию для симметрии (28,28,28) не показываю.
А для трёх других симметрий вот очевидные симметрии

(8,8,8)
0 1 2 3 4 5 6 7 8 9
8 9 7 6 5 4 3 2 0 1
3 7 0 1 8 6 9 4 5 2
2 4 3 0 1 9 7 8 6 5
4 6 1 8 7 0 5 9 2 3
5 3 9 4 0 2 8 1 7 6
7 5 8 2 9 1 0 6 3 4
6 2 5 9 3 8 1 0 4 7
1 8 4 7 6 3 2 5 9 0
9 0 6 5 2 7 4 3 1 8

(16,16,16)
0 1 2 3 4 5 6 7 8 9
3 2 8 4 7 6 9 5 0 1
4 8 1 7 0 9 3 6 2 5
7 4 0 5 6 8 1 9 3 2
1 5 6 2 8 7 0 4 9 3
8 9 5 0 2 1 7 3 4 6
2 6 9 8 1 3 4 0 5 7
5 7 3 6 9 0 2 8 1 4
6 0 4 9 3 2 5 1 7 8
9 3 7 1 5 4 8 2 6 0

(27,27,27)
0 3 1 2 6 4 5 8 9 7
8 1 3 4 5 2 6 0 7 9
9 5 2 1 4 6 3 7 0 8
7 2 6 3 1 5 4 9 8 0
1 4 7 5 0 9 8 3 2 6
2 6 5 8 9 0 7 4 1 3
3 9 4 6 8 7 0 1 5 2
5 0 8 7 2 1 9 6 3 4
6 8 0 9 7 3 2 5 4 1
4 7 9 0 3 8 1 2 6 5

Программа avtoizor выдаёт для показанного в предыдущем посте ЛК 72 автоморфизма, показываю часть автоморфизмов

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0361482957 2603871549 2603871549 -> (16,16,16)
** 0769452183 4183076529 4183076529 -> (8,8,8)
** 0927486351 8643251709 8643251709 -> (8,8,8)
** 2105436879 1025438769 0213654987 -> (8,8,8)
** 2561470938 2815670349 2063178945 -> (28,28,28)
** 2869430175 4065178329 4813670925 -> (27,27,27)
** 2908476531 6845230719 8463152907 -> (16,16,16)
** 6308412597 6207834519 1403892567 -> (28,28,28)
** 6527410398 8217654309 1043298765 -> (16,16,16)
** 6705492813 1487032569 6283094517 -> (27,27,27)
** 6823490715 0467152389 6823490715 -> (8,8,8)
*T 3072965418 1830765294 4183076529 -> (8,37,37)+
*T 3250917864 3510928674 8643251709 -> (8,33,33)+
*T 3458967012 7890125634 0123456789 -> (1,42,42)+
*T 3874915260 9570368214 2603871549 -> (16,36,36)+
*T 5172983406 1752863094 4813670925 -> (27,28,38)+
*T 5231907684 5312907684 8463152907 -> (16,23,23)+
*T 5436987102 8792103654 0213654987 -> (8,39,39)+
. . . . . . 
RT 5672389401 3986521074 4015678923 -> (38,40,42)++
RT 7091325648 5312907684 6487092513 -> (23,40,42)++
RT 7150349826 1752863094 1845290763 -> (25,26,38)++
RT 7658329041 9382567014 6025498713 -> (14,33,40)++
RT 7896345120 8792103654 1207894563 -> (38,39,40)++
RT 9072315468 3510928674 4689071523 -> (31,33,40)++
RT 9250367814 1830765294 8149256703 -> (8,37,40)++
RT 9458317062 9570368214 0629451783 -> (4,36,42)++
RT 9874365210 7890125634 2109876543 -> (16,31,42)++

Очень разнообразен набор симметрий с кодами с плюсом/с двумя плюсами.
Ценный экземпляр для исследования симметрий. Белышеву дарю :)

И очень хотелось бы узнать, чем симметрия (28,28,28) отличается от симметрии (27,27,27).
По той очевидной симметрии, которая у меня выводится, вроде бы квадрат 9х9 тоже должен быть, состоящий из блоков 3х3 с определёнными свойствами.
Но чёрт его знает, что я добавила для этой симметрии. Вот пытаюсь разобраться в этом.

Пытаюсь расколоть самостоятельно симметрию (28,28,28).
На данный момент у меня есть 38 КФ ЛК с данной симметрией.
И! Все они обладают одновременно и симметрией (27,27,27)! Очень интересно!

Дарю Белышеву ещё один очень интересный экземпляр; этот ЛК обладает 90 различными симметриями

 0  1  2  3  4  5  6  7  8  9 
 1  0  3  2  5  6  4  8  9  7 
 2  3  0  1  6  4  5  9  7  8 
 3  2  1  0  7  9  8  4  6  5 
 4  5  6  7  0  8  9  3  1  2 
 5  6  4  9  8  0  7  1  2  3 
 6  4  5  8  9  7  0  2  3  1 
 7  8  9  4  3  1  2  0  5  6 
 8  9  7  6  1  2  3  5  0  4 
 9  7  8  5  2  3  1  6  4  0 

(1,1,1): 	1
(8,8,8): 	36
(10,10,10): 	24
(16,16,16): 	9
(19,19,19): 	72
(21,21,21): 	54
(22,22,22): 	108
(27,27,27): 	56
(28,28,28): 	72
(1,31,31)R: 	1
(2,2,16)R: 	1
(8,16,16)R: 	12
(8,40,40)R: 	24
(10,28,28)R: 	16
(10,34,34)R: 	8
(12,12,28)R: 	24
(14,14,19)R: 	16
(16,38,38)R: 	8
(18,18,19)R: 	8
(19,38,38)R: 	48
(21,29,29)R: 	48
(21,36,36)R: 	6
(22,30,30)R: 	96
(22,37,37)R: 	12
(23,23,27)R: 	8
(26,26,27)R: 	48
(28,39,39)R: 	48
(1,31,31)C: 	1
(2,2,16)C: 	1
(8,16,16)C: 	12
(8,40,40)C: 	24
(10,28,28)C: 	16
(10,34,34)C: 	8
(12,12,28)C: 	24
(14,14,19)C: 	16
(16,38,38)C: 	8
(18,18,19)C: 	8
(19,38,38)C: 	48
(21,29,29)C: 	48
(21,36,36)C: 	6
(22,30,30)C: 	96
(22,37,37)C: 	12
(23,23,27)C: 	8
(26,26,27)C: 	48
(28,39,39)C: 	48
(1,1,1)T: 	1
(8,8,8)T: 	36
(10,10,10)T: 	24
(16,16,16)T: 	9
(19,19,19)T: 	72
(21,21,21)T: 	54
(22,22,22)T: 	108
(27,27,27)T: 	56
(28,28,28)T: 	72
(1,31,31)RT: 	1
(2,2,16)RT: 	1
(8,16,16)RT: 	12
(8,40,40)RT: 	24
(10,28,28)RT: 	16
(10,34,34)RT: 	8
(12,12,28)RT: 	24
(14,14,19)RT: 	16
(16,38,38)RT: 	8
(18,18,19)RT: 	8
(19,38,38)RT: 	48
(21,29,29)RT: 	48
(21,36,36)RT: 	6
(22,30,30)RT: 	96
(22,37,37)RT: 	12
(23,23,27)RT: 	8
(26,26,27)RT: 	48
(28,39,39)RT: 	48
(1,31,31)CT: 	1
(2,2,16)CT: 	1
(8,16,16)CT: 	12
(8,40,40)CT: 	24
(10,28,28)CT: 	16
(10,34,34)CT: 	8
(12,12,28)CT: 	24
(14,14,19)CT: 	16
(16,38,38)CT: 	8
(18,18,19)CT: 	8
(19,38,38)CT: 	48
(21,29,29)CT: 	48
(21,36,36)CT: 	6
(22,30,30)CT: 	96
(22,37,37)CT: 	12
(23,23,27)CT: 	8
(26,26,27)CT: 	48
(28,39,39)CT: 	48

Симметрия (28,28,28) у этого ЛК аж 72-кратная.
Симметрия (27,27,27) 56-кратная, а симметрия (22,22,22) 108-кратная.

Выписала несколько автоморфизмов для симметрии (28,28,28) (при проверке всех 38 КФ ЛК)

** 1203789645 1203789645 0231789645 -> (28,28,28)
** 0245879361 1327698540 9021874365 -> (28,28,28)
** 0247638591 1325874960 9021638547 -> (28,28,28)
** 0236795841 4963810275 6573092841 -> (28,28,28)

Какой из этих автоморфизмов надо добавить в файл standart.txt? ХЗ :)
А какой-то я уже давно добавила.
В общем, ёжик в тумане.

PS. Кстати, этот ЛК диагонально-симметричный, транспонирование его не изменяет.
Обратите внимание на эти симметрии

 (1,1,1)T: 	1
(8,8,8)T: 	36
(10,10,10)T: 	24
(16,16,16)T: 	9
(19,19,19)T: 	72
(21,21,21)T: 	54
(22,22,22)T: 	108
(27,27,27)T: 	56
(28,28,28)T: 	72

Пытаюсь расколоть самостоятельно симметрию (28,28,28).
На данный момент у меня есть 38 КФ ЛК с данной симметрией.
И! Все они обладают одновременно и симметрией (27,27,27)! Очень интересно!
. . .
Выписала несколько автоморфизмов для симметрии (28,28,28) (при проверке всех 38 КФ ЛК)

** 1203789645 1203789645 0231789645 -> (28,28,28)
** 0245879361 1327698540 9021874365 -> (28,28,28)
** 0247638591 1325874960 9021638547 -> (28,28,28)
** 0236795841 4963810275 6573092841 -> (28,28,28)

Какой из этих автоморфизмов надо добавить в файл standart.txt? ХЗ :)
А какой-то я уже давно добавила.

Выудила автоморфизм, который добавила давно в файл standart.txt для симметрии (28,28,28)

** 1203789645 1203789645 0231789645

и удалила.
[Это как раз самый первый автоморфизм из приведённого в цитате списка.]

Сейчас очевидная симметрия для (28,28,28) программой get_standard не выводится, вот

(8,8,8)
0 1 2 3 4 5 6 7 8 9
1 0 3 7 5 4 2 6 9 8
2 3 1 8 7 0 9 5 6 4
3 4 8 5 9 6 1 0 7 2
4 2 6 0 8 1 7 9 5 3
5 7 9 2 1 8 0 3 4 6
6 5 0 1 3 9 4 8 2 7
7 6 4 9 0 2 8 1 3 5
8 9 5 6 2 7 3 4 0 1
9 8 7 4 6 3 5 2 1 0

(27,27,27)
0 1 2 3 4 5 6 7 8 9
7 4 6 5 2 8 0 3 9 1
8 6 5 4 0 3 9 2 1 7
9 5 4 6 7 0 1 8 3 2
3 2 1 0 6 9 8 4 7 5
1 0 3 2 9 4 7 6 5 8
2 3 0 1 8 7 5 9 4 6
4 7 9 8 1 6 2 5 0 3
5 9 8 7 3 2 4 1 6 0
6 8 7 9 5 1 3 0 2 4

(28,28,28)

Значит, правильно выудила и удалила автоморфизм.
А теперь попробую добавить другой автоморфизм

** 0245879361 1327698540 9021874365

Сейчас покажу, что получится с этим автоморфизмом. С удалённым автоморфизмом мне очевидные симметрии не очень нравятся. Посмотрю, что будет с новым автоморфизмом.

С новым автоморфизмом очевидная симметрия такая выдалась

(28,28,28)
0 1 2 3 4 5 6 7 8 9
8 6 1 7 0 2 3 9 5 4
6 4 3 8 9 0 1 5 7 2
5 0 6 9 8 7 2 1 4 3
2 8 7 6 5 9 0 4 3 1
7 9 8 1 6 3 4 0 2 5
1 7 9 2 3 4 5 6 0 8
9 5 4 0 2 1 8 3 6 7
3 2 5 4 7 6 9 8 1 0
4 3 0 5 1 8 7 2 9 6

Н-е-е-е, это ещё хуже.
Возвращаюсь к прежнему автоморфизму, с ним очевидная симметрия такая

(28,28,28)
2 0 1 3 6 9 7 4 5 8
3 1 0 2 9 5 8 7 6 4
0 2 3 1 7 8 4 6 9 5
1 3 2 0 4 6 5 8 7 9
4 5 6 8 2 0 9 3 1 7
5 6 4 7 8 1 0 9 2 3
6 4 5 9 0 7 3 2 8 1
7 8 9 5 3 4 2 1 0 6
8 9 7 4 1 2 6 5 3 0
9 7 8 6 5 3 1 0 4 2

Может быть, это тоже неправильно. Но тут, по крайней мере, что-то просматривается.

Да, симметрия (28,28,28) у меня упёрлась по генерации ЛК: сколько ни генерирую, больше 38 КФ ЛК никак не получается!
Генератора-то специального у меня нет для этой симметрии, я его ещё не написала, потому что никак не могу понять суть симметрии.
А генерирую ЛК с этой симметрией другими генераторами, где она присутствует как совместная.

Внимание! Опыт! Возможны ошибки!

Покажу иллюстрации очевидных симметрий для симметрии (28,28,28), которые я получила добавлением автоморфизма давно, автоморфизм был такой добавлен

** 1203789645 1203789645 0231789645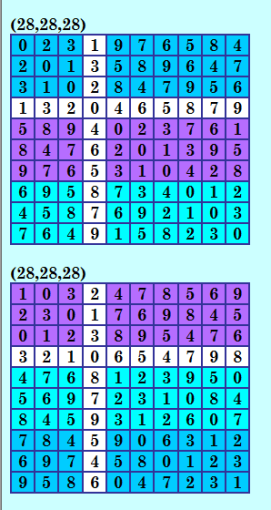

Забавные очевидные симметрии :)
Ну о-ч-ч-ч-е-н-ь похожи на очевидные симметрии для симметрии (27,27,27)!
Но что-то всё-таки не так. Нюансик, нюансик должен быть. В чём-то эти симметрии различны.
Есть у меня одна гипотеза, но озвучивать не буду, чтобы бабушка ситерра с Белышевым не "прибалдели" :)

PS. А не нравится мне в этих очевидных симметриях то, что блоки 3х3 разделены строкой и столбцом. Это же можно легко исправить перестановкой строк и столбцов.
Ну, вот значит, автоморфизм надо добавить другой, чтобы этого разделения блоков 3х3 не было.

Опыты продолжаются!

Добавила в файл standart.txt другой автоморфизм для симметрии (28,28,28)

** 0231789645 0231789645 0231789645

Получила такую очевидную симметрию

(28,28,28)
0 1 3 2 4 6 5 8 7 9
1 0 2 3 7 8 9 6 4 5
3 2 0 1 8 9 7 4 5 6
2 3 1 0 9 7 8 5 6 4
4 9 7 8 0 5 6 3 1 2
6 7 8 9 5 0 4 1 2 3
5 8 9 7 6 4 0 2 3 1
8 5 6 4 3 1 2 0 9 7
7 6 4 5 1 2 3 9 0 8
9 4 5 6 2 3 1 7 8 0

Такая очевидная симметрия мне больше нравится. Здесь блоки 3х3 не разделены, а полностью находятся в ЛК 9х9.

Кстати, у введённого ЛК есть и симметрия (27,27,27), вот очевидная симметрия для данной симметрии

(27,27,27)
0 1 2 3 4 5 6 9 7 8
1 0 3 2 8 7 9 6 5 4
2 3 0 1 7 9 8 5 4 6
3 2 1 0 9 8 7 4 6 5
4 9 8 7 0 6 5 3 2 1
5 8 7 9 6 0 4 2 1 3
6 7 9 8 5 4 0 1 3 2
9 4 6 5 3 2 1 0 8 7
7 6 5 4 2 1 3 8 0 9
8 5 4 6 1 3 2 7 9 0

Сравните эти очевидные симметрии. Ну, где нюансик? :)

Теперь пробую получить очевидные симметрии для другого ЛК, он был показан выше, но не показана очевидная симметрия для (28,28,28)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 0 1 5 6 3 8 9 4 7
3 5 6 8 9 4 0 1 7 2
4 6 8 9 0 7 1 5 2 3
5 3 4 6 7 8 9 2 0 1
6 4 0 7 8 9 2 3 1 5
7 8 9 0 1 2 5 6 3 4
8 9 7 1 2 0 3 4 5 6
9 7 5 2 3 1 4 0 6 8

Вот все 4 очевидные симметрии для данного ЛК

(8,8,8)
0 1 2 3 4 5 6 7 8 9
8 9 7 6 5 4 3 2 0 1
3 7 0 1 8 6 9 4 5 2
2 4 3 0 1 9 7 8 6 5
4 6 1 8 7 0 5 9 2 3
5 3 9 4 0 2 8 1 7 6
7 5 8 2 9 1 0 6 3 4
6 2 5 9 3 8 1 0 4 7
1 8 4 7 6 3 2 5 9 0
9 0 6 5 2 7 4 3 1 8

(16,16,16)
0 1 2 3 4 5 6 7 8 9
3 2 8 4 7 6 9 5 0 1
4 8 1 7 0 9 3 6 2 5
7 4 0 5 6 8 1 9 3 2
1 5 6 2 8 7 0 4 9 3
8 9 5 0 2 1 7 3 4 6
2 6 9 8 1 3 4 0 5 7
5 7 3 6 9 0 2 8 1 4
6 0 4 9 3 2 5 1 7 8
9 3 7 1 5 4 8 2 6 0

(27,27,27)
0 3 1 2 6 4 5 8 9 7
8 1 3 4 5 2 6 0 7 9
9 5 2 1 4 6 3 7 0 8
7 2 6 3 1 5 4 9 8 0
1 4 7 5 0 9 8 3 2 6
2 6 5 8 9 0 7 4 1 3
3 9 4 6 8 7 0 1 5 2
5 0 8 7 2 1 9 6 3 4
6 8 0 9 7 3 2 5 4 1
4 7 9 0 3 8 1 2 6 5

(28,28,28)
0 3 2 1 5 4 6 9 8 7
3 0 1 2 4 5 8 7 6 9
2 1 0 3 7 6 4 8 9 5
1 2 3 0 6 9 5 4 7 8
4 5 6 9 8 1 7 0 2 3
6 8 4 5 9 7 3 2 0 1
5 4 7 6 2 8 9 3 1 0
8 6 9 7 1 2 0 5 3 4
7 9 5 8 0 3 1 6 4 2
9 7 8 4 3 0 2 1 5 6

Ну, процентов на 30 уже расколола симметрию (28,28,28) :)

И ещё для этого ЛК, который обладает 90 симметриями, он тоже показан выше

 0  1  2  3  4  5  6  7  8  9 
 1  0  3  2  5  6  4  8  9  7 
 2  3  0  1  6  4  5  9  7  8 
 3  2  1  0  7  9  8  4  6  5 
 4  5  6  7  0  8  9  3  1  2 
 5  6  4  9  8  0  7  1  2  3 
 6  4  5  8  9  7  0  2  3  1 
 7  8  9  4  3  1  2  0  5  6 
 8  9  7  6  1  2  3  5  0  4 
 9  7  8  5  2  3  1  6  4  0 

Показываю очевидные симметрии не для всех симметрий, хотя у меня все выводятся, но чёрт знает, что я надобавляла для неизвестных симметрий.

(8,8,8)
0 1 2 3 4 5 6 7 8 9
1 0 3 2 5 4 7 6 9 8
2 3 0 1 8 7 4 9 6 5
3 2 1 0 6 9 8 5 4 7
4 5 8 6 0 1 9 2 7 3
5 4 7 9 1 0 3 8 2 6
6 7 4 8 9 3 0 1 5 2
7 6 9 5 2 8 1 0 3 4
8 9 6 4 7 2 5 3 0 1
9 8 5 7 3 6 2 4 1 0

(16,16,16)
0 3 2 1 4 5 8 7 6 9
3 0 1 2 7 8 5 4 9 6
2 1 0 3 8 6 4 9 5 7
1 2 3 0 6 7 9 5 4 8
4 7 8 6 0 9 2 3 1 5
5 8 6 7 9 0 3 1 2 4
8 5 4 9 2 3 0 6 7 1
7 4 9 5 3 1 6 0 8 2
6 9 5 4 1 2 7 8 0 3
9 6 7 8 5 4 1 2 3 0

(27,27,27)
0 7 8 9 4 5 6 1 2 3
7 0 9 8 1 3 2 4 6 5
8 9 0 7 3 2 1 6 5 4
9 8 7 0 2 1 3 5 4 6
4 1 3 2 0 6 5 7 9 8
5 3 2 1 6 0 4 9 8 7
6 2 1 3 5 4 0 8 7 9
1 4 6 5 7 9 8 0 3 2
2 6 5 4 9 8 7 3 0 1
3 5 4 6 8 7 9 2 1 0

(28,28,28)
0 1 3 2 9 8 7 6 5 4
1 0 2 3 4 5 6 7 8 9
3 2 0 1 5 6 4 8 9 7
2 3 1 0 6 4 5 9 7 8
9 4 5 6 0 7 8 2 3 1
8 5 6 4 7 0 9 3 1 2
7 6 4 5 8 9 0 1 2 3
6 7 8 9 2 3 1 0 4 5
5 8 9 7 3 1 2 4 0 6
4 9 7 8 1 2 3 5 6 0

В общем, если вывести теперь очевидные симметрии для всех 38 КФ ЛК с симметрией (28,28,28), которые у меня имеются, то можно, пожалуй, расколоть симметрию до конца :)

Кстати, о птичках псевдотройках.
Если я не ошибаюсь, и симметрия (28,28,28) действительно аналогична симметрии (27,27,27), то... догадались, да?
ЛК с симметрией (28,28,28) тоже могут давать псевдотройки с высокой х. о.

Пробуйте, господа! Дарю идею!
Нагенерируйте много-много-много ЛК с симметрией (28,28,28) и проверьте их все на псевдотройки.

Тут только один интересный вопросик: есть ли такие ЛК, которые обладают симметрией (28,28,28), но не обладают симметрией (27,27,27)?
У меня пока таких ЛК нет.

Обалдеть!
Переделала свой генератор для ЛК с симметрией (27,27,27) для получения ЛК с симметрией (28,28,28).
И вижу просто чудеса!
Сгенерировала 500000 ЛК. Показываю три ЛК полностью, а перед ними и после них специально ЛК обрезала, чтобы не путаться

. . . . . 
 8  6  9  7  2  3  1  5  0  4 
 7  9  5  8  3  1  2  6  4  0 
 9  7  8  4  1  2  3  0  5  6
  
 0  3  2  1  5  4  6  9  8  7 
 3  0  1  2  4  5  8  7  6  9 
 2  1  0  3  7  6  4  8  9  5 
 1  2  3  0  6  9  5  4  7  8 
 4  5  6  9  8  0  7  3  1  2 
 6  8  4  5  9  7  0  1  2  3 
 5  4  7  6  0  8  9  2  3  1 
 8  6  9  7  3  1  2  5  0  4 
 7  9  5  8  1  2  3  6  4  0 
 9  7  8  4  2  3  1  0  5  6 

 0  3  2  1  5  4  6  9  8  7 
 3  0  1  2  4  5  8  7  6  9 
 2  1  0  3  7  6  4  8  9  5 
 1  2  3  0  6  9  5  4  7  8 
 4  5  6  9  8  1  7  0  2  3 
 6  8  4  5  9  7  3  2  0  1 
 5  4  7  6  2  8  9  3  1  0 
 8  6  9  7  1  2  0  5  3  4 
 7  9  5  8  0  3  1  6  4  2 
 9  7  8  4  3  0  2  1  5  6 
 
 0  3  2  1  5  4  6  9  8  7 
 3  0  1  2  4  5  8  7  6  9 
 2  1  0  3  7  6  4  8  9  5 
 1  2  3  0  6  9  5  4  7  8 
 4  5  6  9  8  1  7  2  3  0 
 6  8  4  5  9  7  3  0  1  2 
 5  4  7  6  2  8  9  1  0  3 
 8  6  9  7  0  3  1  5  2  4 
 7  9  5  8  3  0  2  6  4  1 
 9  7  8  4  1  2  0  3  5  6 
 
 0  3  2  1  5  4  6  9  8  7 
 3  0  1  2  4  5  8  7  6  9 
 2  1  0  3  7  6  4  8  9  5 
 1  2  3  0  6  9  5  4  7  8 
 4  5  6  9  8  1  7  3  0  2 
. . . . . 

Смотрим на целые три ЛК. Первые два обладают симметрией (28,28,28), вместе с симметрией (27,27,27), кстати.
А третий ЛК симметрией (27,27,27) обладает, а симметрией (28,28,28) не обладает!
А чем он отличается от первых двух ЛК??? Загадка!
Генерируется одним и тем же генератором, способ составления ЛК одинаковый в программе для всех трёх ЛК. А симметрия (28,28,28) то есть, то нет.
Фантастика!
После канонизации этой порции ЛК получилось 9813 КФ ЛК.
Так вот

Поиск чистых симметрий

Введено ЛК: 9813
Введите код симметрии:
(27,27,27)
Квадратов с симметрией (27,27,27) найдено: 9813
они записаны в файл symm_27_27_27.txt
Время поиска: 1.123 сек

Продолжить? (Y/N): y

Введите код симметрии:
(28,28,28)
Квадратов с симметрией (28,28,28) найдено: 38
они записаны в файл symm_28_28_28.txt
Время поиска: 1.202 сек

Симметрией (27,27,27) обладают все 9813 ЛК, а симметрией (28,28,28) только 38 ЛК; при этом, разумеется, вместе с симметрией (27,27,27).

Пока я в этих чудесах ничего не понимаю.
Симметрия (28,28,28) какой-то извращённый довесок к симметрии (27,27,27).
Каким таким особым свойством обладает этот довесок - чёрт и тот не знает. Только один Белышев знает, но не скажет :)

Забыла сказать: второй ЛК из трёх рассмотренных в предыдущем посте не что иное как очевидная симметрия для симметрии (28,28,28)

(28,28,28)
0 3 2 1 5 4 6 9 8 7
3 0 1 2 4 5 8 7 6 9
2 1 0 3 7 6 4 8 9 5
1 2 3 0 6 9 5 4 7 8
4 5 6 9 8 1 7 0 2 3
6 8 4 5 9 7 3 2 0 1
5 4 7 6 2 8 9 3 1 0
8 6 9 7 1 2 0 5 3 4
7 9 5 8 0 3 1 6 4 2
9 7 8 4 3 0 2 1 5 6

Именно эту очевидную симметрию я взяла в качестве исходного образца для генератора, то есть первая строка и первый столбец заданы в программе из этого ЛК. А потом составляются все возможные ЛК 9х9 из блоков 3х3 с определённым свойством.

Я и стала искать в сгенерированной порции именно этот ЛК, он успешно сгенерировался.

Я нагенерировала своим генератором для ЛК с симметрией (27,27,27) 143264 КФ ЛК с данной симметрией, о чём выше рассказывала.
Смотрите!

Поиск чистых симметрий

Введено ЛК: 143264
Введите код симметрии:
(27,27,27)
45154
91392
136751
Квадратов с симметрией (27,27,27) найдено: 143264
они записаны в файл symm_27_27_27.txt
Время поиска: 15.865 сек

Продолжить? (Y/N): y

Введите код симметрии:
(28,28,28)
42842
86503
129362
Квадратов с симметрией (28,28,28) найдено: 38
они записаны в файл symm_28_28_28.txt
Время поиска: 16.677 сек

И здесь это магическое число 38!
38 ЛК обладают симметрией (28,28,28) вместе с симметрией (27,27,27).

И больше не могу найти ни одного нового ЛК с симметрией (28,28,28). И где их искать? И как их искать? Ежик в тумане :)

Версия только одна пока у меня: неправильно вывожу очевидную симметрию для (28,28,28), не тот добавила автоморфизм.
Допустим.
Но порция ЛК перед нами (143264 КФ ЛК), и в этих ЛК симметрия (27,27,27) есть во всех, а симметрия (28,28,28) только в 38 ЛК. Это факт!

Ура!!!
Белышев подтвердил мой результат по симметрии (27,27,27).
Спасибо!
whitefox;92291 wrote:

Выкладываю список имён всех существенно различных ЛК с симметрией (27,27,27). Всего таких ЛК 143264.

отсюда
http://forum.boinc.ru/default.aspx?g=posts&m=92291#post92291

Значит, мой генератор ЛК с симметрией (27,27,27) правильный, ничего не напутала.

И ещё одно подтверждение моих результатов по симметрии (27,27,27) от Белышева
http://forum.boinc.ru/default.aspx?g=posts&m=92307#post92307

whitefox;92307 wrote:

Выкладываю программу (с исходниками) с помощью которой был получен вчерашний список. Прогресс выводится каждые пять секунд в виде двух чисел. Первое — объём выполненной работы, второе — число найденных ЛК. Поиск завершается когда объём работы достигает значения более 91 миллиона, что заняло 460 секунд.

Также прилагаю архив с 47 марьяжными ДЛК с симметрией (27,27,27), все единицы. Их замыкание содержит 48 единиц (прилагается).

Герасим отдыхает :)
И бабушка ситерра не при делах.

Белышев не отметил, что все КФ ОДЛК Замыкания, кроме одной

 0  7  6  2  3  4  5  8  9  1 
 5  1  3  4  6  9  8  0  2  7 
 7  9  2  1  8  0  4  3  6  5 
 1  2  4  3  9  8  0  5  7  6 
 9  3  1  0  4  6  7  2  5  8 
 3  8  0  9  7  5  1  6  4  2 
 2  0  8  5  1  7  6  9  3  4 
 4  6  9  8  5  3  2  7  1  0 
 6  4  5  7  0  2  9  1  8  3 
 8  5  7  6  2  1  3  4  0  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)

обладают двукратной симметрией (27,27,27).
Например, первые 10 КФ ОДЛК из Замыкания, проверенные программой Белышева avtoizor

 0  2  3  4  6  7  8  5  9  1 
 7  1  9  0  5  4  3  6  2  8 
 6  4  2  8  7  0  9  3  1  5 
 1  5  0  3  2  9  7  8  4  6 
 9  7  8  1  4  6  0  2  5  3 
 3  8  6  7  9  5  2  1  0  4 
 4  9  7  5  1  8  6  0  3  2 
 2  3  4  9  8  1  5  7  6  0 
 5  0  1  6  3  2  4  9  8  7 
 8  6  5  2  0  3  1  4  7  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 2467830519 0785163492 4312690587 -> (27,27,27)
** 6805172349 0496735128 6231074985 -> (27,27,27)
 0  2  3  5  9  4  8  6  7  1 
 4  1  7  0  3  9  5  8  2  6 
 7  6  2  9  5  1  3  0  4  8 
 2  8  1  3  6  7  4  5  9  0 
 8  0  5  7  4  6  9  3  1  2 
 9  4  8  6  7  5  2  1  0  3 
 3  9  4  8  1  0  6  2  5  7 
 6  5  9  1  2  8  0  7  3  4 
 1  3  6  4  0  2  7  9  8  5 
 5  7  0  2  8  3  1  4  6  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 5481392760 9327068154 8540672139 -> (27,27,27)
** 9364108725 4721985360 3768214509 -> (27,27,27)
 0  2  3  7  6  4  8  5  9  1 
 4  1  0  8  3  6  7  9  2  5 
 7  8  2  6  1  9  0  3  5  4 
 6  7  5  3  9  1  4  2  0  8 
 9  5  7  1  4  0  2  8  6  3 
 1  3  8  2  7  5  9  6  4  0 
 3  9  4  5  8  2  6  0  1  7 
 2  4  9  0  5  8  1  7  3  6 
 5  6  1  9  0  7  3  4  8  2 
 8  0  6  4  2  3  5  1  7  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 5284960713 5284960713 6819305724 -> (27,27,27)
** 6819305724 6819305724 5284960713 -> (27,27,27)
 0  2  4  6  9  7  8  5  3  1 
 3  1  7  4  8  9  0  6  2  5 
 6  4  2  9  1  8  7  3  5  0 
 7  9  5  3  6  2  4  0  1  8 
 2  5  3  1  4  0  9  8  7  6 
 9  8  6  0  7  5  2  1  4  3 
 4  3  8  5  0  1  6  2  9  7 
 1  0  9  8  3  4  5  7  6  2 
 5  6  0  7  2  3  1  9  8  4 
 8  7  1  2  5  6  3  4  0  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 5843760291 5843760291 6973205418 -> (27,27,27)
** 6973205418 6973205418 5843760291 -> (27,27,27)
 0  2  4  7  6  8  3  9  5  1 
 6  1  3  5  8  9  7  2  0  4 
 5  4  2  0  9  1  8  3  7  6 
 8  0  6  3  1  2  4  5  9  7 
 9  8  7  2  4  6  1  0  3  5 
 4  3  1  9  7  5  2  8  6  0 
 7  9  5  8  0  3  6  1  4  2 
 3  6  9  1  5  4  0  7  2  8 
 1  5  0  4  2  7  9  6  8  3 
 2  7  8  6  3  0  5  4  1  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0872645391 8064537219 2154907863 -> (27,27,27)
** 0937564218 1875342609 5109328674 -> (27,27,27)
 0  2  4  8  7  3  9  6  5  1 
 9  1  6  4  2  7  8  5  0  3 
 8  0  2  1  6  9  5  3  4  7 
 6  5  1  3  9  8  4  0  7  2 
 2  3  5  0  4  6  7  1  9  8 
 1  6  7  9  8  5  2  4  3  0 
 7  9  3  2  5  0  6  8  1  4 
 3  8  9  6  0  4  1  7  2  5 
 4  7  0  5  1  2  3  9  8  6 
 5  4  8  7  3  1  0  2  6  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0475681932 0475681932 0698134257 -> (27,27,27)
** 0698134257 0698134257 0475681932 -> (27,27,27)
 0  2  5  4  7  3  9  8  6  1 
 3  1  7  0  6  4  5  9  2  8 
 9  6  2  7  0  8  1  3  4  5 
 7  5  9  3  8  1  4  6  0  2 
 6  3  1  8  4  0  2  5  9  7 
 2  8  4  6  9  5  3  1  7  0 
 4  9  8  5  2  7  6  0  1  3 
 1  0  6  9  3  2  8  7  5  4 
 5  7  3  2  1  9  0  4  8  6 
 8  4  0  1  5  6  7  2  3  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 5384160279 0279385164 4506297381 -> (27,27,27)
** 6471305829 0714968253 2947013685 -> (27,27,27)
 0  2  5  4  7  8  9  6  3  1 
 3  1  6  7  9  2  4  5  0  8 
 1  9  2  8  6  0  5  3  4  7 
 8  0  9  3  5  7  2  1  6  4 
 9  3  7  5  4  6  0  8  1  2 
 4  6  1  0  8  5  7  9  2  3 
 7  4  8  9  3  1  6  2  5  0 
 2  5  4  1  0  3  8  7  9  6 
 6  7  0  2  1  9  3  4  8  5 
 5  8  3  6  2  4  1  0  7  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 7354162809 0917385462 6709152438 -> (27,27,27)
** 8461325079 0294768351 2468750193 -> (27,27,27)
 0  2  5  9  8  3  7  4  6  1 
 3  1  4  7  5  6  9  8  0  2 
 8  7  2  6  9  4  1  3  5  0 
 2  6  8  3  1  0  4  9  7  5 
 7  9  1  5  4  2  0  6  3  8 
 4  0  6  2  7  5  8  1  9  3 
 5  4  0  8  3  9  6  2  1  7 
 1  3  9  0  2  8  5  7  4  6 
 9  5  3  1  6  7  2  0  8  4 
 6  8  7  4  0  1  3  5  2  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 1694720385 1694720385 6057391482 -> (27,27,27)
** 6057391482 6057391482 1694720385 -> (27,27,27)
 0  2  6  5  7  3  8  9  4  1 
 6  1  3  2  5  9  7  4  0  8 
 8  7  2  4  1  6  5  3  9  0 
 9  0  7  3  8  1  4  2  6  5 
 3  9  5  7  4  2  0  8  1  6 
 4  8  0  9  6  5  2  1  7  3 
 1  3  4  8  9  7  6  0  5  2 
 5  6  9  1  0  8  3  7  2  4 
 2  5  1  0  3  4  9  6  8  7 
 7  4  8  6  2  0  1  5  3  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 1452039687 1452039687 4035127986 -> (27,27,27)
** 4035127986 4035127986 1452039687 -> (27,27,27)

Вот такая "самоортогональная" симметрия.

И ещё у меня есть следующая гипотеза: все ЛК с данной симметрией обладают ею 2n-кратно (n = 1, 2, 3, ...).
Может быть, Белышев знает, как эту гипотезу доказать или опровергнуть.
Для опровержения гипотезы нужен всего один контрпример из 143264 ЛК с данной симметрией.
[Конечно, все 143264 ЛК я программой avtoizor не проверила.
У меня эта проверка выполняется моим пакетным файлом по 10 ЛК.]