Обобщённые симметрии - 2
Message boards :
Science :
Обобщённые симметрии - 2
Message board moderation
Previous · 1 . . . 9 · 10 · 11 · 12 · 13 · 14 · 15 . . . 24 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В списке у меня осталось 15 симметрий для подтверждения (2,42,42) (4,42,42) (8,42,42) (11,11,11) (11,34,34) (13,42,42) (17,36,36) (18,34,34) (19,34,34) (24,42,42) (31,42,42) (32,36,36) (34,34,34) (36,36,36) (37,37,37) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверяю вывод очевидных симметрий для симметрий (21,21,21) и (21,36,36) у этого ЛК 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 4 7 6 9 8 2 3 4 5 6 7 8 9 0 1 3 2 5 4 7 6 9 8 1 0 4 5 6 7 9 8 0 1 2 3 5 4 7 6 8 9 1 0 3 2 6 7 8 9 0 1 2 3 4 5 7 6 9 8 1 0 3 2 5 4 8 9 0 1 2 3 4 5 6 7 9 8 1 0 3 2 5 4 7 6 Выводятся очевидные симметрии (21,21,21) 0 6 2 8 1 9 7 5 3 4 1 7 3 5 0 4 6 8 2 9 9 5 7 1 4 2 8 0 6 3 6 9 0 2 7 5 4 3 1 8 3 1 5 9 2 6 0 4 8 7 5 3 9 7 8 0 2 6 4 1 7 4 1 3 6 8 9 2 0 5 2 0 8 4 3 7 1 9 5 6 8 2 4 6 5 1 3 7 9 0 4 8 6 0 9 3 5 1 7 2 (21,36,36) 0 8 5 1 4 2 3 9 7 6 5 3 0 6 9 7 8 4 2 1 3 1 8 2 5 9 6 0 4 7 2 9 7 5 6 8 4 1 3 0 1 7 6 4 3 5 2 8 0 9 9 5 4 8 7 1 0 2 6 3 7 4 2 0 1 3 9 6 8 5 6 2 1 9 8 0 7 3 5 4 4 0 9 3 2 6 5 7 1 8 8 6 3 7 0 4 1 5 9 2 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Листаю тему... Очень интересно :) Вот здесь https://boinc.progger.info/odlk/forum_thread.php?id=81&postid=2101#2101 обратила внимание на кратность симметрии (27,27,27). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А вот на этого пупсика посмотрите :) 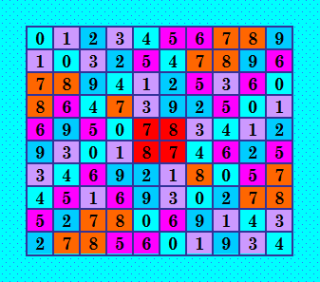 Кого вы в нём узнаёте? Это псевдосимметрия (31,31,31), или псевдоассоциативный ЛК. Всего-то в 4-х ячейках нарушение симметрии. Эти 4 ячейки в центре ЛК находятся, окрашены красным цветом. Этот центральный блок 2х2 можно повернуть на 90 градусов в любом направлении, получится ЛК изоморфный исходному со следующим изоморфизмом ** 9876543210 9876543210 4391065872 Иллюстрация из второй части моей статьи, которая пока лежит в черновиках, надо собрать и дописать. Но никак руки не доходят :( |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата . . . . Точнее Белышевым было написано так: В общем случае, поиск стандартного представления для симметрии полезно начинать с минимальных представителей для соответствующих циклических структур. Такой выбор часто будет удачным, например, для симметрии (27,27,27) минимальный представитель циклической структуры №27 есть 0231564897. Поэтому добавим в файл standart.txt представление: отсюда http://forum.boinc.ru/default.aspx?g=posts&m=91102#post91102 Что такое "минимальные представители для соответствующих циклических структур", я не знаю. Поэтому все мои добавления в файл standart.txt (с целью получения очевидных симметрий) необходимо проверить, они могут быть неправильные. Ну, по крайней мере, ЛК, обладающие всеми указанными выше симметриями (30 штук), действительно существуют, могу их все показать. Что касается расшифровки этих симметрий, получения их очевидных представителей, - это неплохо бы сделать автору теории Белышеву. На данный момент я знаю о симметриях с кодами (х,31,31) (5 штук), (16,16,16) и (27,27,27). Всего семь симметрий я видела с полным описанием Белышева. И всё! Больше ни о каких симметриях ничего не знаю. Из 30 симметрий, которые у меня подтверждены, выбросим тождественную симметрию, остаётся 29 штук. О 7 симметриях знаю, о 22 симметриях не знаю. PS. Что-то ещё краем глаза видела о симметрии (1,41,41). Особо не вникала. Надо снова посмотреть это сообщение. Там, кажется, говорилось, что ЛК, обладающие данной симметрией, не могут иметь ОЛК (по теореме Манна). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот ещё цитирую Белышева В файл standart.txt включены стандартные представления для симметрий: Это были первоначально включены в файл standart.txt стандартные представления симметрий. Чуть позже было добавлено Белышевым стандартное представление для симметрии (27,27,27). Вот для этих симметрий всё правильно. Все остальные симметрии надо проверять в моём файле standart.txt. Чего я там надобавляла :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот нашла сообщение Белышева о симметрии (1,41,41) http://forum.boinc.ru/default.aspx?g=posts&m=91597#post91597 В качестве стандартного представления симметрии (1,41,41) возьмём автоморфизм: Кое-что понятно о данной симметрии. Кстати, посмотрела этот автоморфизм в своём файле standart.txt ** 0123456789 1234067895 4012395678 его там не было, я его добавила. Но там ведь было записано Белышевым какое-то стандартное представление для данной симметрии (?). Теперь вот что получается. Беру пример из цитаты, этот ЛК 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 8 9 5 2 3 4 0 1 7 8 9 5 6 3 4 0 1 2 8 9 5 6 7 4 0 1 2 3 9 5 6 7 8 5 6 7 8 9 0 1 2 3 4 6 7 8 9 5 1 2 3 4 0 7 8 9 5 6 2 3 4 0 1 8 9 5 6 7 3 4 0 1 2 9 5 6 7 8 4 0 1 2 3и вывожу для него очевидные симметрии программой get_standard. (1,31,31) 0 4 3 2 1 8 7 6 5 9 1 0 4 3 2 7 6 5 9 8 2 1 0 4 3 6 5 9 8 7 3 2 1 0 4 5 9 8 7 6 4 3 2 1 0 9 8 7 6 5 9 5 6 7 8 1 2 3 4 0 8 9 5 6 7 2 3 4 0 1 7 8 9 5 6 3 4 0 1 2 6 7 8 9 5 4 0 1 2 3 5 6 7 8 9 0 1 2 3 4 0 1 2 3 4 9 8 7 6 5 1 2 3 4 0 5 9 8 7 6 2 3 4 0 1 6 5 9 8 7 3 4 0 1 2 7 6 5 9 8 4 0 1 2 3 8 7 6 5 9 9 5 6 7 8 3 2 1 0 4 8 9 5 6 7 2 1 0 4 3 7 8 9 5 6 1 0 4 3 2 6 7 8 9 5 0 4 3 2 1 5 6 7 8 9 4 3 2 1 0 (1,41,41) 0 4 3 2 1 5 9 8 7 6 2 1 0 4 3 7 6 5 9 8 4 3 2 1 0 9 8 7 6 5 1 0 4 3 2 6 5 9 8 7 3 2 1 0 4 8 7 6 5 9 5 9 8 7 6 0 4 3 2 1 7 6 5 9 8 2 1 0 4 3 9 8 7 6 5 4 3 2 1 0 6 5 9 8 7 1 0 4 3 2 8 7 6 5 9 3 2 1 0 4 0 5 1 6 2 7 3 8 4 9 3 8 4 9 0 5 1 6 2 7 1 6 2 7 3 8 4 9 0 5 4 9 0 5 1 6 2 7 3 8 2 7 3 8 4 9 0 5 1 6 5 0 6 1 7 2 8 3 9 4 8 3 9 4 5 0 6 1 7 2 6 1 7 2 8 3 9 4 5 0 9 4 5 0 6 1 7 2 8 3 7 2 8 3 9 4 5 0 6 1 0 1 2 3 4 5 6 7 8 9 3 4 0 1 2 8 9 5 6 7 1 2 3 4 0 6 7 8 9 5 4 0 1 2 3 9 5 6 7 8 2 3 4 0 1 7 8 9 5 6 5 6 7 8 9 0 1 2 3 4 8 9 5 6 7 3 4 0 1 2 6 7 8 9 5 1 2 3 4 0 9 5 6 7 8 4 0 1 2 3 7 8 9 5 6 2 3 4 0 1 (1,42,42) 0 5 1 6 2 7 3 8 4 9 1 6 2 7 3 8 4 9 0 5 2 7 3 8 4 9 0 5 1 6 3 8 4 9 0 5 1 6 2 7 4 9 0 5 1 6 2 7 3 8 5 0 6 1 7 2 8 3 9 4 6 1 7 2 8 3 9 4 5 0 7 2 8 3 9 4 5 0 6 1 8 3 9 4 5 0 6 1 7 2 9 4 5 0 6 1 7 2 8 3 0 1 2 3 4 5 6 7 8 9 6 7 8 9 0 1 2 3 4 5 2 3 4 5 6 7 8 9 0 1 8 9 0 1 2 3 4 5 6 7 4 5 6 7 8 9 0 1 2 3 5 6 7 8 9 0 1 2 3 4 1 2 3 4 5 6 7 8 9 0 7 8 9 0 1 2 3 4 5 6 3 4 5 6 7 8 9 0 1 2 9 0 1 2 3 4 5 6 7 8 (16,16,16) 0 1 2 3 4 5 6 7 8 9 1 2 7 4 5 6 9 8 0 3 2 7 8 5 6 9 3 0 1 4 3 4 5 2 7 8 0 6 9 1 4 5 6 7 8 0 1 9 3 2 5 6 9 8 0 1 2 3 4 7 6 9 3 0 1 2 7 4 5 8 7 8 0 6 9 3 4 1 2 5 8 0 1 9 3 4 5 2 7 6 9 3 4 1 2 7 8 5 6 0 (16,31,31) 0 1 8 9 4 7 5 2 3 6 1 8 9 4 0 5 2 3 6 7 8 9 4 0 1 2 3 6 7 5 9 4 0 1 8 3 6 7 5 2 4 0 1 8 9 6 7 5 2 3 6 7 5 2 3 0 1 8 9 4 7 5 2 3 6 1 8 9 4 0 5 2 3 6 7 8 9 4 0 1 2 3 6 7 5 9 4 0 1 8 3 6 7 5 2 4 0 1 8 9 (21,21,21) 8 0 6 2 5 9 1 3 7 4 5 1 7 3 8 4 0 2 6 9 9 3 1 5 4 6 2 8 0 7 0 4 8 6 1 3 9 7 5 2 7 5 3 9 6 0 8 4 2 1 3 7 9 1 2 8 6 0 4 5 1 9 5 7 0 2 4 6 8 3 6 8 2 4 7 1 5 9 3 0 2 6 4 0 3 5 7 1 9 8 4 2 0 8 9 7 3 5 1 6 (21,36,36) 0 7 2 4 8 1 3 9 6 5 8 3 6 9 0 5 7 4 2 1 3 1 9 8 7 2 5 0 4 6 2 4 7 5 6 8 9 1 3 0 1 6 8 3 5 4 2 7 0 9 9 8 1 6 4 7 0 2 5 3 6 9 3 1 2 0 4 5 7 8 5 2 0 7 1 9 6 3 8 4 4 0 5 2 9 3 8 6 1 7 7 5 4 0 3 6 1 8 9 2 (31,41,42) 0 5 1 6 2 7 3 8 4 9 5 0 6 1 7 2 8 3 9 4 1 6 2 7 3 8 4 9 0 5 6 1 7 2 8 3 9 4 5 0 2 7 3 8 4 9 0 5 1 6 7 2 8 3 9 4 5 0 6 1 3 8 4 9 0 5 1 6 2 7 8 3 9 4 5 0 6 1 7 2 4 9 0 5 1 6 2 7 3 8 9 4 5 0 6 1 7 2 8 3 (41,41,41) 0 8 1 4 2 5 3 6 9 7 2 5 3 6 0 8 1 4 7 9 8 1 4 7 5 3 6 9 2 0 7 0 8 1 9 2 5 3 6 4 1 4 7 0 3 6 9 2 5 8 3 6 9 2 1 4 7 0 8 5 4 7 0 8 6 9 2 5 3 1 6 9 2 5 4 7 0 8 1 3 5 3 6 9 8 1 4 7 0 2 9 2 5 3 7 0 8 1 4 6 (41,42,42) 0 4 8 7 5 9 3 2 6 1 3 2 6 5 8 7 1 0 4 9 1 0 4 8 6 5 9 3 2 7 4 8 7 1 9 3 2 6 5 0 7 1 0 4 2 6 5 9 3 8 5 9 3 2 0 4 8 7 1 6 8 7 1 0 3 2 6 5 9 4 6 5 9 3 1 0 4 8 7 2 9 3 2 6 4 8 7 1 0 5 2 6 5 9 7 1 0 4 8 3 Для симметрии (1,31,31) две очевидные симметрии, так и должно быть. Для симметрии (1,41,41) аж три очевидные симметрии. Это правильно? Почему их три? Для симметрий (16,31,31) и (16,16,16) полагаю, что всё правильно. На все остальные очевидные симметрии лучше не смотреть, это мои добавления и они могут быть неправильные. В общем, пока ёжик в тумане :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Опа! Удалила из файла standart.txt последний дописанный автоморфизм для симметрии (1,41,41). И теперь очевидных симметрий вывелось только две (1,41,41) 0 4 3 2 1 5 9 8 7 6 2 1 0 4 3 7 6 5 9 8 4 3 2 1 0 9 8 7 6 5 1 0 4 3 2 6 5 9 8 7 3 2 1 0 4 8 7 6 5 9 5 9 8 7 6 0 4 3 2 1 7 6 5 9 8 2 1 0 4 3 9 8 7 6 5 4 3 2 1 0 6 5 9 8 7 1 0 4 3 2 8 7 6 5 9 3 2 1 0 4 0 5 1 6 2 7 3 8 4 9 3 8 4 9 0 5 1 6 2 7 1 6 2 7 3 8 4 9 0 5 4 9 0 5 1 6 2 7 3 8 2 7 3 8 4 9 0 5 1 6 5 0 6 1 7 2 8 3 9 4 8 3 9 4 5 0 6 1 7 2 6 1 7 2 8 3 9 4 5 0 9 4 5 0 6 1 7 2 8 3 7 2 8 3 9 4 5 0 6 1 Такие вот чудеса! С утра весело поиграть :) Как я понимаю, вот эта очевидная симметрия 0 1 2 3 4 5 6 7 8 9 3 4 0 1 2 8 9 5 6 7 1 2 3 4 0 6 7 8 9 5 4 0 1 2 3 9 5 6 7 8 2 3 4 0 1 7 8 9 5 6 5 6 7 8 9 0 1 2 3 4 8 9 5 6 7 3 4 0 1 2 6 7 8 9 5 1 2 3 4 0 9 5 6 7 8 4 0 1 2 3 7 8 9 5 6 2 3 4 0 1как раз и соответствует последнему записанному в файл standart.txt автоморфизму ** 0123456789 1234067895 4012395678 Удалила этот автоморфизм и... исчезла соответствующая ему очевидная симметрия. Но ещё две остались. Почему две? Это правильно? Кстати, в этой очевидной симметрии 0 5 1 6 2 7 3 8 4 9 3 8 4 9 0 5 1 6 2 7 1 6 2 7 3 8 4 9 0 5 4 9 0 5 1 6 2 7 3 8 2 7 3 8 4 9 0 5 1 6 5 0 6 1 7 2 8 3 9 4 8 3 9 4 5 0 6 1 7 2 6 1 7 2 8 3 9 4 5 0 9 4 5 0 6 1 7 2 8 3 7 2 8 3 9 4 5 0 6 1 блочная структура не видна. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очередная проверка части БД ручного проекта на симметрии, в программу введены КФ ОДЛК - 69338 штук. Определитель симметрий Введено ЛК : 69338 51839 Из них симметричных : 13687 Найдено различных симметрий: 8 Время работы : 6.926 сек Список симметрий (1,1,1) (1,31,31) (2,31,31) (4,31,31) (8,31,31) (16,16,16) (16,31,31) (27,27,27) Пока не густо в этом списке. Это, собственно, те симметрии, поиском которых я так или иначе занималась. Вот об этих симметриях кое-что знаю :) Только кое-что! Ну, есть ещё несколько симметрий, у которых коды с плюсом; выше я их показывала. В поиске симметрии (4,31,31) мне помогал Demis. Сейчас поиск этой симметрии (специальный) остановлен. Но решения с этой симметрией стабильно появляются в двух экспериментах, которые я сейчас выполняю. Сейчас распишу по каждой симметрии отдельно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Готово Поиск чистых симметрий Введено ЛК: 69338 Введите код симметрии: (1,31,31) Квадратов с симметрией (1,31,31) найдено: 9 они записаны в файл symm_1_31_31.txt Время поиска: 4.587 сек Продолжить? (Y/N): y Введите код симметрии: (2,31,31) Квадратов с симметрией (2,31,31) найдено: 8 они записаны в файл symm_2_31_31.txt Время поиска: 4.57 сек Продолжить? (Y/N): y Введите код симметрии: (4,31,31) Квадратов с симметрией (4,31,31) найдено: 13385 они записаны в файл symm_4_31_31.txt Время поиска: 4.618 сек Продолжить? (Y/N): y Введите код симметрии: (8,31,31) Квадратов с симметрией (8,31,31) найдено: 42 они записаны в файл symm_8_31_31.txt Время поиска: 4.587 сек Продолжить? (Y/N): y Введите код симметрии: (16,16,16) Квадратов с симметрией (16,16,16) найдено: 10 они записаны в файл symm_16_16_16.txt Время поиска: 4.571 сек Продолжить? (Y/N): y Введите код симметрии: (16,31,31) Квадратов с симметрией (16,31,31) найдено: 150 они записаны в файл symm_16_31_31.txt Время поиска: 4.587 сек Продолжить? (Y/N): y Введите код симметрии: (27,27,27) Квадратов с симметрией (27,27,27) найдено: 25 они записаны в файл symm_27_27_27.txt Время поиска: 4.57 сек Поиск решений с симметрией (27,27,27) я завершила. Очень может быть, что нашла я не все решения с данной симметрией, но у меня больше не находится. Решения с остальными симметриями ищутся, и в эксперименте мультисимметрия, и в эксперименте с псевдоассоциативными ДЛК. Реже всех появляется симметрия (2,31,31). В двух указанных экспериментах появление этой симметрии вообще не припомню. Немного занималась поиском данной симметрии специально (от ассоциативных ЛК искала). Видимо, только эти решения и были найдены. Чаще всех других появляются симметрии (4,31,31) и (16,31,31), эти симметрии появляются в обоих экспериментах стабильно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Взяла один генератор для мультисимметричных ЛК, написала скрипт для выделения только трёх чистых симметрий: (8,8,8) (15,15,15) (16,16,16) Начала генерировать с помощью этого скрипта. Этот генератор генерирует не только мультисимметричные ЛК, но и просто "симметричные", к тому же, ещё и не "симметричные". Вот, например, порция нагенерированных с помощью скрипта ЛК Определитель симметрий Введено ЛК : 21191 Из них симметричных : 849 Найдено различных симметрий: 4 Время работы : 2.074 сек "Симметричных" ЛК 849, остальные не "симметричные". Среди этих 849 "симметричных" ЛК с указанными выше симметриями всего чуть-чуть. Вот Поиск чистых симметрий Введено ЛК: 21191 Введите код симметрии: (8,8,8) Квадратов с симметрией (8,8,8) найдено: 74 они записаны в файл symm_8_8_8.txt Время поиска: 1.856 сек Продолжить? (Y/N): y Введите код симметрии: (15,15,15) Квадратов с симметрией (15,15,15) найдено: 3 они записаны в файл symm_15_15_15.txt Время поиска: 1.903 сек Продолжить? (Y/N): y Введите код симметрии: (16,16,16) Квадратов с симметрией (16,16,16) найдено: 181 они записаны в файл symm_16_16_16.txt Время поиска: 1.934 сек Следовательно, остальные ЛК "симметричные" только с кодами симметрии с плюсом. Пока не знаю, что даст мне эта целенаправленная генерация ЛК с тремя указанными симметриями. Хочу попробовать накопить таких ЛК побольше, затем проверить на ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверила несколько ЛК из тех, что обладают какой-то из симметрий: (8,8,8), (15,15,15) и (16,16,16), программой avtoizor. Очень часто прицепляются симметрии с кодом с плюсом. Симметрии (8,8,8) и (16,16,16) могут быть совместными (смотрите самый первый ЛК из показанных ниже). Покажу несколько интересных ЛК с кодами их симметрий 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 0 1 7 9 8 4 6 5 3 2 4 9 6 1 5 0 7 8 4 8 5 6 9 7 3 2 1 0 5 6 9 2 8 0 4 1 3 7 6 7 8 5 3 4 0 9 2 1 7 4 1 0 2 8 9 3 5 6 8 9 6 7 1 3 2 5 0 4 9 5 7 8 0 2 1 6 4 3 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0529716483 0529716483 0529716483 -> (8,8,8) ** 6124350987 6124350987 0783546129 -> (8,8,8) ** 6527910384 6527910384 0489176523 -> (16,16,16) 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 6 7 8 9 4 2 3 0 1 6 9 8 5 4 7 3 2 1 0 8 7 4 9 6 5 4 5 6 8 2 0 9 3 7 1 5 9 7 4 1 8 2 6 3 0 6 8 4 7 9 3 1 0 5 2 7 6 5 9 0 1 3 4 2 8 8 7 9 5 3 4 0 2 1 6 9 4 8 6 7 2 5 1 0 3 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0132865947 1023789456 1023789456 -> (16,16,16) R* 0123548967 1032498765 1032498765 -> (8,16,16)+ R* 0132684759 0132765498 0132765498 -> (8,16,16)+ 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 4 6 8 7 5 9 0 1 3 7 1 2 9 8 0 6 5 4 4 5 0 1 6 9 8 2 7 3 5 8 9 7 1 2 4 0 3 6 6 2 7 5 0 1 9 3 4 8 7 4 8 9 2 3 1 5 6 0 8 9 6 0 7 4 3 1 2 5 9 6 5 8 3 0 2 4 1 7 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 7183694025 0625831947 7183694025 -> (16,16,16) R* 0143298765 1032987654 1032987654 -> (8,31,31)+ R* 7163852049 1738520496 1738520496 -> (8,42,42)+ 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 5 1 0 8 9 6 7 4 3 5 6 0 8 1 4 9 2 7 4 7 0 2 3 9 8 1 6 5 5 8 9 7 6 2 1 0 4 3 6 4 1 9 7 0 3 2 5 8 7 6 8 5 9 4 2 3 1 0 8 9 4 6 2 7 0 5 3 1 9 2 7 8 1 3 5 4 0 6 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0213479586 3140258769 3140258769 -> (8,8,8) C* 7681943250 2904356781 7681943250 -> (8,39,39)+ C* 7861920453 4932058761 7861920453 -> (16,42,42)+ 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 6 8 7 9 0 4 1 5 3 7 9 5 6 0 4 1 2 8 4 9 7 1 8 2 3 5 0 6 5 2 8 0 1 4 9 6 3 7 6 4 0 7 9 8 2 3 5 1 7 5 4 2 3 1 8 9 6 0 8 6 5 9 0 7 1 2 4 3 9 8 1 6 2 3 5 0 7 4 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 8197465302 8351429706 4976053281 -> (16,16,16) R* 0167492385 0129876543 0129876543 -> (8,8,8)+ R* 8153429706 4971823506 4971823506 -> (8,38,38)+ 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 8 7 6 9 0 5 4 1 3 9 6 5 0 7 4 2 1 8 4 8 5 1 3 2 9 0 7 6 5 7 4 9 2 8 1 6 0 3 6 2 9 8 7 1 5 4 3 0 7 4 1 0 8 3 2 9 6 5 8 6 7 2 9 0 3 1 5 4 9 5 0 6 1 4 8 3 2 7 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 5197406382 5729406183 8643251709 -> (8,8,8) R* 0179654283 0132987654 0132987654 -> (8,16,16)+ R* 5132604987 8634907152 8634907152 -> (16,38,38)+ 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 6 7 8 9 3 2 0 1 6 7 8 9 3 4 5 3 4 6 9 8 7 2 5 1 0 4 5 7 0 3 9 8 2 6 1 5 6 8 1 0 4 3 9 2 7 6 7 9 8 1 0 5 4 3 2 7 8 3 2 9 1 0 6 5 4 8 9 4 5 2 3 1 0 7 6 9 3 5 7 6 2 4 1 0 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0124567893 0124567893 0129345678 -> (15,15,15) ** 0125678934 0125678934 0128934567 -> (15,15,15) ** 0126789345 0126789345 0127893456 -> (15,15,15) ** 0127893456 0127893456 0126789345 -> (15,15,15) ** 0128934567 0128934567 0125678934 -> (15,15,15) ** 0129345678 0129345678 0124567893 -> (15,15,15) 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 6 7 8 9 3 2 0 1 6 7 8 9 3 4 5 3 6 4 9 8 7 1 5 0 2 4 7 5 2 3 9 8 1 6 0 5 8 6 0 2 4 3 9 1 7 6 9 7 8 0 2 5 4 3 1 7 3 8 1 9 0 2 6 5 4 8 4 9 5 1 3 0 2 7 6 9 5 3 7 6 1 4 0 2 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0124567893 0124567893 0129345678 -> (15,15,15) ** 0125678934 0125678934 0128934567 -> (15,15,15) ** 0126789345 0126789345 0127893456 -> (15,15,15) ** 0127893456 0127893456 0126789345 -> (15,15,15) ** 0128934567 0128934567 0125678934 -> (15,15,15) ** 0129345678 0129345678 0124567893 -> (15,15,15) R* 0123987654 2109876543 2109876543 -> (8,16,16)+ R* 0124398765 2103987654 2103987654 -> (8,16,16)+ R* 0125439876 2104398765 2104398765 -> (8,16,16)+ R* 0126543987 2105439876 2105439876 -> (8,16,16)+ R* 0127654398 2106543987 2106543987 -> (8,16,16)+ R* 0128765439 2107654398 2107654398 -> (8,16,16)+ R* 0129876543 2108765439 2108765439 -> (8,16,16)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 8 9 5 2 0 1 5 6 3 4 9 7 8 3 6 4 8 2 7 9 5 0 1 4 7 8 1 3 9 5 0 6 2 5 3 6 7 9 0 8 1 2 4 6 4 0 9 1 8 2 3 5 7 7 5 9 2 8 1 0 6 4 3 8 9 5 0 7 2 1 4 3 6 9 8 7 6 5 4 3 2 1 0 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0458126739 3170459286 3170459286 -> (8,8,8) R* 0123456789 9876543210 9876543210 -> (1,31,31)+ R* 0458126739 6829540713 6829540713 -> (8,16,16)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 5 3 4 8 9 6 7 3 4 5 0 1 2 9 6 7 8 4 5 7 8 6 9 0 2 3 1 5 7 0 9 8 3 2 1 4 6 6 9 8 7 0 1 4 3 2 5 7 3 4 6 9 8 1 0 5 2 8 6 9 1 2 7 3 5 0 4 9 8 6 2 7 0 5 4 1 3 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 7543216089 7693451082 0126983754 -> (8,8,8) R* 0123456789 5432109876 5432109876 -> (1,31,31)+ R* 7543216089 8962104573 8962104573 -> (8,40,40)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 5 3 4 8 9 6 7 3 7 5 8 6 9 4 1 0 2 4 5 0 1 2 8 9 6 7 3 5 4 8 7 9 0 2 3 1 6 6 8 7 9 0 1 3 5 2 4 7 9 6 2 1 3 5 0 4 8 8 6 9 0 7 2 1 4 3 5 9 3 4 6 8 7 0 2 5 1 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 2109458763 1024358769 0213546987 -> (8,8,8) R* 6589410723 7901235648 7901235648 -> (16,42,42)+ R* 8563412709 9702134658 9702134658 -> (8,40,40)+ Интересны ЛК с шестикратной симметрией (15,15,15). Суть данной симметрии я не знаю, очевидная симметрия выводится, но, возможно, неправильная, потому что я сама добавила эту симметрию. Суть симметрии (8,8,8) тоже не знаю (очень хотелось бы узнать!). Очевидная симметрия для данной симметрии выводится на основании автоморфизма, записанного в файл standart.txt Белышевым. Полагаю, что это правильная очевидная симметрия. Пример для ЛК 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 0 1 7 9 8 4 6 5 3 2 4 9 6 1 5 0 7 8 4 8 5 6 9 7 3 2 1 0 5 6 9 2 8 0 4 1 3 7 6 7 8 5 3 4 0 9 2 1 7 4 1 0 2 8 9 3 5 6 8 9 6 7 1 3 2 5 0 4 9 5 7 8 0 2 1 6 4 3 Программа get_standard выдаёт такие очевидные симметрии (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 4 7 6 9 8 2 3 0 4 7 9 1 8 5 6 3 4 1 6 8 0 9 2 7 5 4 7 9 8 6 1 0 5 3 2 5 2 4 0 1 3 8 9 6 7 6 5 7 9 0 8 3 1 2 4 7 6 8 1 9 2 5 0 4 3 8 9 5 7 3 6 2 4 0 1 9 8 6 5 2 7 4 3 1 0 (16,16,16) 0 2 3 1 5 4 8 6 7 9 2 0 1 3 8 6 5 4 9 7 3 1 0 8 4 2 7 9 5 6 8 3 2 6 9 7 0 1 4 5 4 8 7 9 6 0 2 5 3 1 5 6 4 7 0 3 9 2 1 8 1 5 8 0 2 9 3 7 6 4 6 4 9 2 7 5 1 0 8 3 7 9 5 4 3 1 6 8 0 2 9 7 6 5 1 8 4 3 2 0 Что должны видеть очи в очевидной симметрии для (8,8,8), я не знаю. Белышев знает, но не скажет :) Мои очи видят только: вроде бы, как и в симметрии (16,16,16), в первой и последней строках, в первом и последнем столбцах суммы симметрично расположенных чисел равны 9. Какими свойствами обладает квадрат 8х8 внутри рамки - никак не разгляжу! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
О-о-о!!! Кажется, вижу нечто в этой очевидной симметрии (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 4 7 6 9 8 2 3 0 4 7 9 1 8 5 6 3 4 1 6 8 0 9 2 7 5 4 7 9 8 6 1 0 5 3 2 5 2 4 0 1 3 8 9 6 7 6 5 7 9 0 8 3 1 2 4 7 6 8 1 9 2 5 0 4 3 8 9 5 7 3 6 2 4 0 1 9 8 6 5 2 7 4 3 1 0 О внешней рамке уже написала выше. Точно такая же рамка (с таким же свойством) в квадрате 8х8, который внутри рамки. А внутри этой рамки ассоциативный ЛК 6х6 0 4 7 9 1 8 1 6 8 0 9 2 9 8 6 1 0 5 4 0 1 3 8 9 7 9 0 8 3 1 8 1 9 2 5 0 Угадала? :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Взяла другой ЛК с симметрией (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 5 1 0 8 9 6 7 4 3 5 6 0 8 1 4 9 2 7 4 7 0 2 3 9 8 1 6 5 5 8 9 7 6 2 1 0 4 3 6 4 1 9 7 0 3 2 5 8 7 6 8 5 9 4 2 3 1 0 8 9 4 6 2 7 0 5 3 1 9 2 7 8 1 3 5 4 0 6 Очевидную симметрию программа get_standard выдала такую (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 0 7 4 6 3 5 2 9 8 2 4 0 7 8 9 1 6 5 3 5 3 1 9 0 6 4 8 2 7 6 2 4 0 7 1 8 9 3 5 3 7 9 8 1 2 0 5 6 4 4 6 8 5 3 0 9 1 7 2 7 5 3 1 9 8 2 0 4 6 8 9 6 2 5 4 7 3 0 1 9 8 5 6 2 7 3 4 1 0 Покажу иллюстрацию этой очевидной симметрии 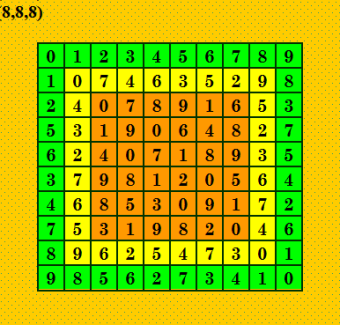 Возможно, моя догадка правильная. А если и неправильная, всё равно красиво получилось :) PS. При этом ассоциативность ЛК 6х6, наверное, не абы какая, а с некоторыми специальными свойствами. Предполагаю! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Пока не знаю, что даст мне эта целенаправленная генерация ЛК с тремя указанными симметриями. Эксперимент не удался. Мультисимметричный генератор очень быстро выдохся, в том смысле, что начал гнать одни изоморфы. Удалось сгенерировать всего 21453 уникальных ЛК. Симметрии оказались следующие: (1,1,1) (8,8,8) (10,10,10) (15,15,15) (16,16,16) (19,19,19) Много не "симметричных" ЛК Определитель симметрий Введено ЛК : 21453 Из них симметричных : 990 Найдено различных симметрий: 6 Время работы : 2.589 сек И конечно, все эти ЛК оказались "пустышками" (не дали ни одного ОДЛК). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Заинтересовала симметрия (8,8,8), хотя даже не знаю пока, в чём её суть. Есть только догадка (см. выше). Прям как в афоризме: "Всё знать нельзя, но обо всём можно догадываться" :) В науке тоже можно догадываться. Итак, перекопала свой банк КФ ЛК с различными симметриями. Нашла всего 102 стандарта для симметрии (8,8,8), из них 20 ЛК обладают совместной симметрией с (16,16,16). Все 102 стандарта "пустышки". В части БД ручного проекта нет ни одного решения с симметрией (8,8,8). Насколько помню, нет таких решений и в остальной части БД. Проверила программой Белышева avtoizor 20 ЛК, которые обладают совместной симметрией. Результаты очень интересные. Покажу их все, это ценная эмпирика, может пригодиться для исследований. Первые 10 ЛК (для некоторых ЛК показаны не все автоморфизмы, так как их много) 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 6 4 8 9 7 2 3 0 1 6 4 5 9 7 8 3 2 1 0 7 9 8 4 6 5 4 5 7 6 1 8 9 3 0 2 5 6 9 4 8 1 7 0 2 3 6 4 8 5 9 7 1 2 3 0 7 8 4 9 3 0 2 1 5 6 8 9 6 7 0 2 3 5 1 4 9 7 5 8 2 3 0 6 4 1 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0123564978 0123564978 0123645897 -> (10,10,10) ** 0123645897 0123645897 0123564978 -> (10,10,10) ** 0123789456 0123789456 0123789456 -> (8,8,8) ** 0123897645 0123897645 0123897645 -> (8,8,8) ** 0123978564 0123978564 0123978564 -> (8,8,8) ** 1023465987 1023465987 0132546798 -> (8,8,8) ** 1023546879 1023546879 0132654987 -> (8,8,8) ** 1023654798 1023654798 0132465879 -> (8,8,8) ** 1023798654 1023798654 0132798546 -> (19,19,19) . . . R* 1023798654 2310456897 2310564789 -> (14,14,19)+ R* 1023879546 2310645978 2310645978 -> (16,38,38)+ R* 1023987465 2310564789 2310456897 -> (14,14,19)+ 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 6 7 8 9 4 2 3 0 1 6 4 8 9 7 5 3 2 1 0 8 7 9 5 4 6 4 5 7 9 3 1 0 2 6 8 5 6 9 4 7 8 1 0 3 2 6 7 5 8 9 2 4 1 0 3 7 8 4 6 2 9 5 3 1 0 8 9 6 7 0 3 2 4 5 1 9 4 8 5 1 0 3 6 2 7 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0123789456 0123789456 0123789456 -> (8,8,8) ** 0213684957 3120879546 3120879546 -> (16,16,16) ** 0213957684 3120546879 3120546879 -> (8,8,8) ** 0463192875 5127604398 5127604398 -> (16,16,16) ** 0463875192 5127398604 8124907365 -> (22,22,22) ** 0583614729 6129470583 6129470583 -> (8,8,8) ** 0583729614 6129583470 9126740853 -> (21,21,21) ** 0643271598 7125938064 7125938064 -> (16,16,16) ** 0643598271 7125064938 4128635097 -> (22,22,22) ** 0793162548 8124907365 5127398604 -> (22,22,22) ** 0793548162 8124365907 8124365907 -> (16,16,16) ** 0853426917 9126853740 9126853740 -> (8,8,8) ** 0853917426 9126740853 6129583470 -> (21,21,21) ** 0973241865 4128635097 7125064938 -> (22,22,22) ** 0973865241 4128097635 4128097635 -> (16,16,16) *T 1032498765 1032498765 0123549876 -> (8,16,16)+ . . . RT 1752649380 6034159827 4128635097 -> (22,30,30)++ RT 1842073659 7039816254 5127398604 -> (22,30,30)++ RT 1842659073 7039254816 8124365907 -> (16,29,29)++ RT 1962408537 8035691742 6129583470 -> (21,29,29)++ RT 1962537408 8035742691 9126853740 -> (8,40,40)++ 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 0 1 6 8 4 9 5 7 3 2 1 9 7 4 8 5 6 0 4 5 7 8 0 1 9 2 3 6 5 4 9 0 1 2 3 6 7 8 6 9 4 2 8 7 5 3 0 1 7 8 6 5 9 3 2 0 1 4 8 7 5 6 2 9 0 1 4 3 9 6 8 7 3 0 1 4 2 5 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0529418763 4163052987 4163052987 -> (8,8,8) ** 0649281753 9165732480 9165732480 -> (16,16,16) ** 0843265719 7125936084 7125936084 -> (8,8,8) C* 1032549876 0123456789 1032549876 -> (1,31,31)+ C* 1436507892 4163052987 1436507892 -> (8,40,40)+ C* 1752394806 7125936084 1752394806 -> (8,40,40)+ C* 1956370842 9165732480 1956370842 -> (16,42,42)+ 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 0 1 7 9 8 4 6 5 3 2 1 0 9 7 5 6 4 8 4 8 7 9 0 1 3 2 5 6 5 6 9 2 8 0 4 1 3 7 6 7 8 5 3 4 0 9 2 1 7 5 4 6 2 8 9 0 1 3 8 9 6 7 1 3 2 5 0 4 9 4 5 8 6 2 1 3 7 0 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0529716483 0529716483 0529716483 -> (8,8,8) ** 6124350987 6124350987 0783546129 -> (8,8,8) ** 6527910384 6527910384 0489176523 -> (16,16,16) 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 0 1 7 9 8 4 6 5 3 2 4 9 6 1 5 0 7 8 4 8 5 6 9 7 3 2 1 0 5 6 9 2 8 0 4 1 3 7 6 7 8 5 3 4 0 9 2 1 7 4 1 0 2 8 9 3 5 6 8 9 6 7 1 3 2 5 0 4 9 5 7 8 0 2 1 6 4 3 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0529716483 0529716483 0529716483 -> (8,8,8) ** 6124350987 6124350987 0783546129 -> (8,8,8) ** 6527910384 6527910384 0489176523 -> (16,16,16) 0 1 2 3 4 5 6 7 8 9 1 0 3 4 5 6 7 8 9 2 2 3 0 1 9 7 8 6 4 5 3 2 1 7 6 8 4 9 5 0 4 8 5 9 7 2 3 0 1 6 5 7 9 2 8 3 0 1 6 4 6 9 7 8 3 4 5 2 0 1 7 5 8 6 0 1 9 4 2 3 8 4 6 0 1 9 2 5 3 7 9 6 4 5 2 0 1 3 7 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0563712489 7129486053 7129486053 -> (8,8,8) ** 8423176509 0168492735 8423176509 -> (8,8,8) ** 8763542109 7165432098 5429106873 -> (16,16,16) C* 1032879546 0123456789 1032879546 -> (1,31,31)+ C* 1792503846 7129486053 1792503846 -> (8,40,40)+ C* 4592783016 7165432098 4592783016 -> (16,38,38)+ C* 4832059716 0168492735 4832059716 -> (8,16,16)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 0 5 6 7 8 9 4 2 3 0 1 6 8 4 9 5 7 3 0 1 2 9 7 8 6 4 5 4 7 6 5 2 9 0 3 1 8 5 6 8 7 1 2 9 4 0 3 6 8 4 9 0 3 2 5 7 1 7 4 9 8 3 1 5 2 6 0 8 9 5 4 7 0 3 1 2 6 9 5 7 6 8 4 1 0 3 2 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0123789456 0123789456 0123789456 -> (8,8,8) ** 0321684957 0321684957 0321684957 -> (16,16,16) ** 0321957684 0321957684 0321957684 -> (8,8,8) ** 0426173598 0426173598 0426173598 -> (16,16,16) ** 0426598173 0426598173 0729143865 -> (22,22,22) ** 0528416937 0528416937 0528416937 -> (8,8,8) ** 0528937416 0528937416 0825719634 -> (21,21,21) ** 0624391875 0624391875 0624391875 -> (16,16,16) ** 0624875391 0624875391 0927361548 -> (22,22,22) ** 0729143865 0729143865 0426598173 -> (22,22,22) ** 0729865143 0729865143 0729865143 -> (16,16,16) ** 0825634719 0825634719 0825634719 -> (8,8,8) ** 0825719634 0825719634 0528937416 -> (21,21,21) ** 0927361548 0927361548 0624875391 -> (22,22,22) ** 0927548361 0927548361 0927548361 -> (16,16,16) . . . RT 0729865143 2709865143 2907548361 -> (16,31,31)++ RT 0825634719 2805634719 2508416937 -> (8,16,16)++ RT 0825719634 2805719634 2805719634 -> (21,36,36)++ RT 0927361548 2907361548 2406598173 -> (22,37,37)++ RT 0927548361 2907548361 2709865143 -> (16,31,31)++ 0 1 2 3 4 5 6 7 8 9 1 2 3 0 5 6 7 8 9 4 2 3 0 1 7 8 9 4 5 6 3 0 1 2 9 4 5 6 7 8 4 5 8 6 2 7 0 9 3 1 5 4 9 7 1 0 8 3 6 2 6 9 4 8 0 1 3 5 2 7 7 8 5 9 6 3 1 2 4 0 8 7 6 4 3 9 2 1 0 5 9 6 7 5 8 2 4 0 1 3 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0123789456 0123789456 0123789456 -> (8,8,8) ** 0321654987 2103498765 2103498765 -> (8,8,8) ** 0321987654 2103765498 2103765498 -> (16,16,16) ** 0486153927 9157428360 9157428360 -> (16,16,16) ** 0486927153 9157360428 6184725390 -> (28,28,28) ** 0684351729 5197406382 5197406382 -> (8,8,8) ** 0684729351 5197382406 8164709352 -> (27,27,27) ** 0759183624 6184725390 9157360428 -> (28,28,28) ** 0759624183 6184390725 6184390725 -> (16,16,16) ** 0957381426 8164709352 5197382406 -> (27,27,27) ** 0957426381 8164352709 8164352709 -> (8,8,8) R* 0123456789 2103498765 2103498765 -> (1,8,8)+ . . . R* 0957381426 6184725390 9157360428 -> (27,28,28)+ R* 0957426381 6184390725 6184390725 -> (8,16,16)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 5 6 3 8 9 4 7 3 5 6 8 9 4 0 1 7 2 4 6 8 9 0 7 1 5 2 3 5 3 4 6 7 8 9 2 0 1 6 4 0 7 8 9 2 3 1 5 7 8 9 0 1 2 5 6 3 4 8 9 7 1 2 0 3 4 5 6 9 7 5 2 3 1 4 0 6 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0361482957 2603871549 2603871549 -> (16,16,16) ** 0769452183 4183076529 4183076529 -> (8,8,8) ** 0927486351 8643251709 8643251709 -> (8,8,8) ** 2105436879 1025438769 0213654987 -> (8,8,8) ** 2561470938 2815670349 2063178945 -> (28,28,28) ** 2869430175 4065178329 4813670925 -> (27,27,27) ** 2908476531 6845230719 8463152907 -> (16,16,16) ** 6308412597 6207834519 1403892567 -> (28,28,28) ** 6527410398 8217654309 1043298765 -> (16,16,16) ** 6705492813 1487032569 6283094517 -> (27,27,27) ** 6823490715 0467152389 6823490715 -> (8,8,8) *T 3072965418 1830765294 4183076529 -> (8,37,37)+ . . . RT 9072315468 3510928674 4689071523 -> (31,33,40)++ RT 9250367814 1830765294 8149256703 -> (8,37,40)++ RT 9458317062 9570368214 0629451783 -> (4,36,42)++ RT 9874365210 7890125634 2109876543 -> (16,31,42)++ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 5 8 3 4 9 6 7 3 5 6 8 9 4 0 1 7 2 4 9 5 1 7 8 3 0 2 6 5 7 9 0 6 1 8 2 3 4 6 8 0 7 1 9 2 3 4 5 7 3 8 6 0 2 9 4 5 1 8 6 4 9 2 7 1 5 0 3 9 4 7 2 3 0 5 6 1 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0361792485 2603871549 2603871549 -> (16,16,16) ** 0529716483 4683051729 4683051729 -> (8,8,8) ** 0965432781 8143276509 8143276509 -> (8,8,8) R* 0123456789 2109876543 2109876543 -> (1,16,16)+ R* 0361792485 0629451783 0629451783 -> (4,4,16)+ R* 0529716483 8649271503 8649271503 -> (8,31,31)+ R* 0965432781 4189056723 4189056723 -> (8,8,8)+ Интересно: у всех показанных ЛК симметрия (8,8,8) 2n-кратная (n>=1). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё 10 ЛК, здесь без пропусков 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 7 3 9 8 6 4 5 3 4 5 6 1 8 0 9 2 7 4 8 7 1 2 0 9 5 3 6 5 6 9 8 0 1 4 3 7 2 6 7 8 0 9 2 3 1 5 4 7 5 0 9 8 4 1 2 6 3 8 9 6 5 7 3 2 4 0 1 9 3 4 2 6 7 5 0 1 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0943276581 8132465709 8132465709 -> (8,8,8) ** 3210976584 2408165739 5132408967 -> (16,16,16) ** 3490156782 3480156729 6123480957 -> (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 7 6 9 8 3 4 5 3 5 6 8 9 4 0 1 7 2 4 6 8 9 0 7 1 5 2 3 5 3 4 6 7 8 9 2 0 1 6 4 0 5 8 3 2 9 1 7 7 8 9 0 1 2 5 6 3 4 8 9 7 1 2 0 3 4 5 6 9 7 5 2 3 1 4 0 6 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0361482957 2603871549 2603871549 -> (16,16,16) ** 0769452183 4183076529 4183076529 -> (8,8,8) ** 0927486351 8643251709 8643251709 -> (8,8,8) R* 0123456789 2109876543 2109876543 -> (1,16,16)+ R* 0361482957 0629451783 0629451783 -> (4,4,16)+ R* 0769452183 8149256703 8149256703 -> (8,8,8)+ R* 0927486351 4689071523 4689071523 -> (8,31,31)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 1 7 8 9 4 3 6 5 3 5 6 8 9 4 0 1 7 2 4 9 5 1 7 8 3 0 2 6 5 7 9 0 6 1 8 2 3 4 6 8 0 5 1 3 2 9 4 7 7 3 8 6 0 2 9 4 5 1 8 6 4 9 2 7 1 5 0 3 9 4 7 2 3 0 5 6 1 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0361792485 2603871549 2603871549 -> (16,16,16) ** 0529716483 4683051729 4683051729 -> (8,8,8) ** 0965432781 8143276509 8143276509 -> (8,8,8) R* 0123456789 2109876543 2109876543 -> (1,16,16)+ R* 0361792485 0629451783 0629451783 -> (4,4,16)+ R* 0529716483 8649271503 8649271503 -> (8,31,31)+ R* 0965432781 4189056723 4189056723 -> (8,8,8)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 4 5 3 8 9 6 7 1 3 4 5 0 1 2 8 9 6 7 4 3 9 6 8 7 1 5 0 2 5 9 1 7 6 4 0 3 2 8 6 8 7 1 0 9 4 2 3 5 7 6 8 2 9 1 3 0 5 4 8 7 6 9 2 0 5 1 4 3 9 5 0 8 7 3 2 4 1 6 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0213496875 1024358769 1024358769 -> (8,8,8) ** 4593016872 6894350712 1028674539 -> (16,16,16) ** 4953026781 8693451702 0126873549 -> (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 5 8 3 4 9 6 7 1 3 9 0 2 6 7 4 5 1 8 4 7 6 5 0 9 8 1 2 3 5 3 4 6 2 8 1 9 0 7 6 8 9 0 7 1 5 2 3 4 7 4 8 9 1 3 2 0 6 5 8 6 7 1 9 0 3 4 5 2 9 5 1 7 8 2 0 3 4 6 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0219756483 1025438769 1025438769 -> (8,8,8) ** 5127906384 5321406987 8643251709 -> (8,8,8) ** 5214306987 3520418967 6845230719 -> (16,16,16) R* 0123456789 1098765432 1098765432 -> (1,31,31)+ R* 0219756483 0196783452 0196783452 -> (8,16,16)+ R* 5127906384 6890715234 6890715234 -> (8,40,40)+ R* 5214306987 8691703254 8691703254 -> (16,38,38)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 0 8 9 6 7 5 3 4 1 3 4 5 0 1 2 8 9 6 7 4 9 6 7 8 0 1 5 2 3 5 6 1 2 3 4 9 0 7 8 6 5 9 8 7 1 0 4 3 2 7 8 0 1 9 3 4 2 5 6 8 7 4 6 2 9 3 1 0 5 9 3 7 5 0 8 2 6 1 4 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0218546937 6573910284 6573910284 -> (16,16,16) ** 0458126739 6193750482 6193750482 -> (8,8,8) ** 0543216987 0543216987 0543216987 -> (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 0 1 7 9 8 4 6 5 3 7 8 5 6 2 4 9 0 1 4 8 7 9 0 1 3 2 5 6 5 9 6 2 8 3 0 1 4 7 6 4 1 7 9 0 5 3 2 8 7 5 4 6 2 8 9 0 1 3 8 6 9 0 1 7 2 5 3 4 9 0 5 8 3 4 1 6 7 2 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0925438761 0925438761 0925438761 -> (8,8,8) ** 7321498065 7625431098 0948265731 -> (16,16,16) ** 7529416083 7823459016 0146283759 -> (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 0 6 9 8 1 4 5 7 3 7 6 9 8 1 2 0 4 5 4 8 9 5 1 7 0 2 3 6 5 9 8 7 6 0 4 3 2 1 6 4 1 2 0 3 9 5 7 8 7 5 4 0 2 9 8 1 6 3 8 6 5 1 7 2 3 9 0 4 9 0 7 8 3 4 5 6 1 2 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0487159326 5729604183 5729604183 -> (16,16,16) ** 0683951724 5321406987 5321406987 -> (8,8,8) ** 0927654381 0927654381 0927654381 -> (8,8,8) R* 0183456729 0987654321 0987654321 -> (2,16,16)+ R* 0427159386 5381406927 5381406927 -> (8,16,16)+ R* 0623951784 5789604123 5789604123 -> (4,31,31)+ R* 0987654321 0183456729 0183456729 -> (2,2,16)+ 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 0 9 1 7 8 4 6 5 3 5 4 7 2 8 9 0 1 6 4 0 5 6 8 9 1 2 7 3 5 6 7 8 0 2 3 9 4 1 6 9 8 1 3 4 0 5 2 7 7 8 9 0 6 1 4 3 5 2 8 7 6 5 9 3 2 1 0 4 9 4 1 2 7 0 5 6 3 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0467192385 8725936104 8725936104 -> (16,16,16) ** 0527916384 0527916384 0527916384 -> (8,8,8) ** 0963542781 8321476509 8321476509 -> (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 4 0 1 7 9 8 5 6 3 3 8 9 7 6 1 4 0 5 2 4 9 1 2 8 0 5 6 3 7 5 6 7 8 0 2 3 9 4 1 6 3 8 9 1 7 0 4 2 5 7 5 4 0 2 8 9 3 1 6 8 7 6 5 9 3 2 1 0 4 9 0 5 6 3 4 1 2 7 8 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0467192385 8321976504 8321976504 -> (16,16,16) ** 0527916384 0527916384 0527916384 -> (8,8,8) ** 0963542781 8725436109 8725436109 -> (8,8,8) R* 0127456389 8765432109 8765432109 -> (2,16,16)+ R* 0463192785 0567912384 0567912384 -> (8,16,16)+ R* 0523916784 8361972504 8361972504 -> (4,31,31)+ R* 0967542381 0163452789 0163452789 -> (2,2,16)+ У всех этих ЛК симметрия (8,8,8) двукратная. Жаль, что стандартов с данной симметрией очень мало мне пока попалось, да ещё все "пустышки". |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Однако симметрия (8,8,8) не всегда 2n-кратная. Например 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 8 9 5 2 0 1 5 6 3 4 9 7 8 3 6 4 8 2 7 9 5 0 1 4 7 8 1 3 9 5 0 6 2 5 3 6 7 9 0 8 1 2 4 6 4 0 9 1 8 2 3 5 7 7 5 9 2 8 1 0 6 4 3 8 9 5 0 7 2 1 4 3 6 9 8 7 6 5 4 3 2 1 0 ** 0123456789 0123456789 0123456789 -> (1,1,1) ** 0458126739 3170459286 3170459286 -> (8,8,8) R* 0123456789 9876543210 9876543210 -> (1,31,31)+ R* 0458126739 6829540713 6829540713 -> (8,16,16)+ |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу очевидную симметрию для ЛК с шестикратной симметрией (8,8,8) (см. ЛК выше, самый первый в показанных); заодно и очевидная симметрия для совместной симметрии (16,16,16) (8,8,8) 0 1 2 3 4 5 6 7 8 9 1 0 3 4 2 7 5 6 9 8 2 3 1 5 7 0 9 8 6 4 3 4 5 1 6 8 0 9 7 2 4 2 7 6 1 9 8 0 5 3 5 7 0 8 9 1 3 2 4 6 6 5 9 0 8 3 1 4 2 7 7 6 8 9 0 2 4 1 3 5 8 9 4 2 3 6 7 5 0 1 9 8 6 7 5 4 2 3 1 0 (16,16,16) 0 1 4 2 3 6 7 5 8 9 1 0 2 3 4 7 5 6 9 8 5 2 9 6 7 1 8 0 3 4 7 3 6 9 5 8 0 1 4 2 6 4 7 5 9 0 1 8 2 3 3 7 1 8 0 9 4 2 5 6 2 5 8 0 1 4 9 3 6 7 4 6 0 1 8 2 3 9 7 5 8 9 3 4 2 5 6 7 0 1 9 8 5 7 6 3 2 4 1 0 Очевидные симметрии для симметрий (10,10,10) и (19,19,19) у меня выводятся, но я не уверена, что правильно (эти симметрии я сама добавила). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Банк КФ ЛК с различными симметриями у меня уже солидный. Вот только один файл с КФ ЛК проверила на симметрии, получилось 18 симметрий, кроме тождественной (1,1,1) (1,31,31) (1,41,41) (1,42,42) (4,31,31) (7,41,41) (7,42,42) (8,8,8) (10,10,10) (10,34,34) (16,16,16) (16,31,31) (21,21,21) (21,36,36) (27,27,27) (28,28,28) (31,41,42) (41,41,41) (41,42,42) Весьма экзотическая симметрия (31,41,42), найден всего один ЛК с такой симметрией, вот он 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 0 2 3 4 5 6 7 8 9 0 1 3 4 5 6 7 8 9 0 1 2 4 5 6 7 8 9 0 1 2 3 5 6 7 8 9 0 1 2 3 4 6 7 8 9 0 1 2 3 4 5 7 8 9 0 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 9 0 1 2 3 4 5 6 7 8 Выше, кажется, уже показывала этот ЛК (см. PS). Программа avtoizor выводит 2400 автоморфизмов для данного ЛК. А симметрии у него вот какие (1,1,1) (1,31,31) (1,41,41) (1,42,42) (16,16,16) (16,31,31) (21,21,21) (21,36,36) (31,41,42) (41,41,41) (41,42,42) Один этот ЛК подтверждает сразу 10 симметрий, кроме тождественной. У ЛК Агриппы 13 симметрий, не считая тождественную. PS. Вот нашла этот замечательный квадратик с экзотической симметрией (31,41,42), причём симметрия эта у него 24-кратная! 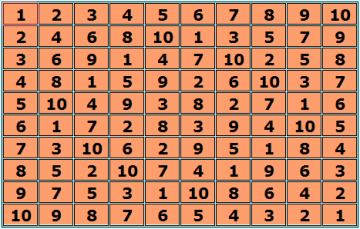 тут https://boinc.progger.info/odlk/forum_thread.php?id=81&postid=2026#2026 |

©2026 (C) Progger