О симметрии (1,31,31) я уже писала выше, ОДЛК с такой симметрией 9 штук в БД ручного проекта.

По другим симметриям расклад такой

Поиск чистых симметрий

Введено ЛК: 68224
Введите код симметрии:
(2,31,31)
Квадратов с симметрией (2,31,31) найдено: 8
они записаны в файл symm_2_31_31.txt
Время поиска: 4.54 сек

Продолжить? (Y/N): y

Введите код симметрии:
(4,31,31)
Квадратов с симметрией (4,31,31) найдено: 13381
они записаны в файл symm_4_31_31.txt
Время поиска: 4.586 сек

Продолжить? (Y/N): y

Введите код симметрии:
(8,31,31)
Квадратов с симметрией (8,31,31) найдено: 41
они записаны в файл symm_8_31_31.txt
Время поиска: 4.555 сек

Продолжить? (Y/N): y

Введите код симметрии:
(16,31,31)
Квадратов с симметрией (16,31,31) найдено: 94
они записаны в файл symm_16_31_31.txt
Время поиска: 4.524 сек

Продолжить? (Y/N): y

Введите код симметрии:
(16,16,16)
Квадратов с симметрией (16,16,16) найдено: 8
они записаны в файл symm_16_16_16.txt
Время поиска: 4.556 сек

Однако... по количеству "симметричных" решений опять непонятки.
Всего найдено "симметричных" решений 13599, а если просуммировать "чистые" симметрии, получается 13541.
Тут ещё надо прибавить те симметрии, коды которых с плюсом.
Но... я знаю эти симметрии далеко не все, только те, что нашла в своём эксперименте мультисимметрия.
Можно предположить, что таких симметрий значительно больше.
Но выудить решения с такими симметриями проблематично.
Кроме того, здесь ещё, вроде бы, играет роль канонизация (ДЛК как ЛК).

В любом случае, на совсем хорошо, что программа "Определитель симметрий" и программа "Поиск чистых симметрий" дают не совпадающие количества "симметричных" решений.
Вот и приходится ломать голову: почему не совпадают количества.

Канонизировала и проверила "Определителем симметрий".

Канонизатор ЛК10

Введено ЛК   : 68224
Найдено КФ ЛК: 66310
Время работы : 4.009 сек

КФ ЛК имеем 66310.

Определитель симметрий

Введено ЛК                 : 66310
Из них симметричных        : 13557

Найдено различных симметрий: 7
Время работы               : 4.477 сек

Да, количество "симметричных" решений сильно изменилось: было 13599, стало 13557.
Однако... 13557 опять же не совпадает с количеством "чистых" симметрий, которых программа нашла всего 13541.
Но теперь разница только 16.
Так что: эти 16 "симметричных" решений имеют коды симметрий с плюсом???

Поиск "чистых" симметрий после канонизации совершенно не изменился

Поиск чистых симметрий

Введено ЛК: 66310
Введите код симметрии:
(1,31,31)
Квадратов с симметрией (1,31,31) найдено: 9
они записаны в файл symm_1_31_31.txt
Время поиска: 4.446 сек

Продолжить? (Y/N): y

Введите код симметрии:
(2,31,31)
Квадратов с симметрией (2,31,31) найдено: 8
они записаны в файл symm_2_31_31.txt
Время поиска: 4.399 сек

Продолжить? (Y/N): y

Введите код симметрии:
(4,31,31)
Квадратов с симметрией (4,31,31) найдено: 13381
они записаны в файл symm_4_31_31.txt
Время поиска: 4.446 сек

Продолжить? (Y/N): y

Введите код симметрии:
(8,31,31)
Квадратов с симметрией (8,31,31) найдено: 41
они записаны в файл symm_8_31_31.txt
Время поиска: 4.415 сек

Продолжить? (Y/N): y

Введите код симметрии:
(16,31,31)
Квадратов с симметрией (16,31,31) найдено: 94
они записаны в файл symm_16_31_31.txt
Время поиска: 4.4 сек

Продолжить? (Y/N): y

Введите код симметрии:
(16,16,16)
Квадратов с симметрией (16,16,16) найдено: 8
они записаны в файл symm_16_16_16.txt
Время поиска: 4.415 сек

Всего 13541 "чистых" симметрий.
Значит, остальные 16 "симметричных" решений имеют коды симметрий с плюсом.
Другой версии у меня нет.

Алгоритм мультисимметрия по-прежнему отлично даёт решения.
Сегодня найдено 62 уникальные КФ ОДЛК, в том числе 11 "симметричных" [(симметрия (16,31,31)].

Кстати, сюда же плюс 3 КФ ОДЛК, найденные от нового генератора - для ЛК с симметрией (27,27,27).
Таким образом, мой новый алгоритм мультисимметрия получил уже третий генератор!
У меня нет возможности запустить поиск сразу от трёх генераторов.
Увы и ах! Пока постоянно работает самый первый генератор.
Генератор для симметрии (27,27,27) сегодня обкатывался, программа написана мной.
Первые марьяжные ДЛК найдены, вот они

0 2 4 8 7 3 9 6 5 1
9 1 6 4 2 7 8 5 0 3
8 0 2 1 6 9 5 3 4 7
6 5 1 3 9 8 4 0 7 2
2 3 5 0 4 6 7 1 9 8
1 6 7 9 8 5 2 4 3 0
7 9 3 2 5 0 6 8 1 4
3 8 9 6 0 4 1 7 2 5
4 7 0 5 1 2 3 9 8 6
5 4 8 7 3 1 0 2 6 9

0 2 5 4 7 8 9 6 3 1
3 1 6 7 9 2 4 5 0 8
1 9 2 8 6 0 5 3 4 7
8 0 9 3 5 7 2 1 6 4
9 3 7 5 4 6 0 8 1 2
4 6 1 0 8 5 7 9 2 3
7 4 8 9 3 1 6 2 5 0
2 5 4 1 0 3 8 7 9 6
6 7 0 2 1 9 3 4 8 5
5 8 3 6 2 4 1 0 7 9

Надо продолжать поиск.

Цитата

Сегодня алгоритм мультисимметрия дал 62 уникальные КФ ОДЛК.
Проверяю на симметрии

Определитель симметрий

Введено ЛК                 : 62
Из них симметричных        : 5

Найдено различных симметрий: 4
Время работы               : 0.015 сек

Список симметрий

(1,1,1)
(4,31,31)
(16,31,31)
(27,27,27)

Да, мультисимметрия подтверждается!
Это работали два генератора - первый и третий. Второй генератор, который даёт симметрии с кодами с плюсом, пока отдыхает: негде запустить.
Первый генератор у меня уже давно работает и стабильно даёт решения с симметриями (4,31,31) и (16,31,31). С другими симметриями пока не было ОДЛК.
Хотя ЛК этим генератором генерируются с разными симметриями, больше двух видов.
А больше всего симметрий у ЛК, генерируемых вторым генератором, однако, как ни странно, ОДЛК от этих ЛК получаются с кодами симметрий с плюсом.

В черновике второй части статьи "Новый алгоритм поиска ОДЛК" есть проверка порции ЛК от первого генератора на симметрии (проверяются КФ ЛК, полученные из миллиона ЛК)

Определитель симметрий

Введено ЛК                 : 141006
43674
85737
128349
Из них симметричных        : 106392

Найдено различных симметрий: 7
Время работы               : 16.754 сек

Список симметрий:

(1,1,1)
(1,31,31)
(4,31,31)
(16,16,16)
(16,31,31)
(21,21,21)
(21,36,36)

ОДЛК с симметриями (4,31,31) и (16,31,31) от ЛК, генерируемых первым генератором, как отмечено в цитате, находятся постоянно.
В цитате не сказано о симметрии (1,31,31), забыла. С симметрией (1,31,31) тоже ОДЛК попадаются, причём это не симметричные по Гергели/Брауну ОДЛК, о чём рассказано выше.
Хотя... и симметричные по Гергели/Брауну тоже встречались.
В черновике статьи написано:

ЛК с симметрией (1,31,31) проверила, найдены две двушки, но они в БД уже есть.

Значит, эти двушки симметричные по Гергели/Брауну.

Кстати, ЛК с симметрией (1,31,31) проверяю отдельно, потому что я пользуюсь программой family_mar, которая не ищет симметричные по Гергели/Брауну марьяжные ДЛК.
Ну, если считать, что все такие решения уже были найдены ранее в специальном эксперименте, то их, конечно, и искать не надо.
Однако... проверять ЛК с симметрией (1,31,31) надо!
Причину см. выше (находятся ОДЛК не симметричные по Гергели/Брауну).

Такие интересные намёки в программе Белышева "Определитель симметрий" :)
Вот проверяю 253 КФ ЛК на симметрии

Определитель симметрий

Введено ЛК                 : 253
Из них симметричных        : 16

Найдено различных симметрий: 2
Время работы               : 0.031 сек

Список симметрий

(1,1,1)
(27,27,27)

Программа говорит, что найдено 16 "симметричных" решений, симметрия найдена только одна (помимо тождественной): (27,27,27).
Теперь ищу все симметрии с кодом (27,27,27) среди тех же 253 КФ ЛК

Поиск чистых симметрий

Введено ЛК: 253
Введите код симметрии:
(27,27,27)
Квадратов с симметрией (27,27,27) найдено: 1
они записаны в файл symm_27_27_27.txt
Время поиска: 0.016 сек

Квадрат с симметрией (27,27,27) найден всего один!
Значит, с чистой симметрией только один ЛК.
Все остальные симметрии имеют коды с плюсом.

Проверила эту порцию КФ ЛК программой avtoizor.
Показываю различные коды найденных симметрий:

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  1  5  8  7  3  9  6  4 
 3  7  9  2  6  1  5  4  0  8 
 4  5  0  1  2  8  9  6  7  3 
 5  3  4  9  7  2  8  0  1  6 
 6  9  5  8  0  4  2  1  3  7 
 7  8  6  0  1  9  4  3  5  2 
 8  4  7  6  9  3  0  5  2  1 
 9  6  8  7  3  0  1  2  4  5 
** 0123456789 0123456789 0123456789 -> (1,1,1)
R* 2108476539 1204589673 1204589673 -> (8,39,39)+

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  5  6  7  8  9  4  1  3 
 3  6  7  8  2  9  1  5  0  4 
 4  7  0  9  8  2  3  1  5  6 
 5  8  6  7  9  0  2  3  4  1 
 6  5  8  1  3  4  0  9  2  7 
 7  4  9  5  1  3  8  0  6  2 
 8  9  1  0  6  7  4  2  3  5 
 9  3  4  2  0  1  5  6  7  8 
** 0123456789 0123456789 0123456789 -> (1,1,1)
R* 0948256731 0423156789 0423156789 -> (2,2,8)+

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  6  9  3  7  8  5  1  4 
 3  7  4  0  9  2  5  1  6  8 
 4  3  9  7  8  1  0  6  2  5 
 5  9  7  8  6  0  4  2  3  1 
 6  4  0  1  2  8  3  9  5  7 
 7  8  5  6  1  9  2  0  4  3 
 8  6  1  5  7  3  9  4  0  2 
 9  5  8  2  0  4  1  3  7  6 
** 0123456789 0123456789 0123456789 -> (1,1,1)
R* 0476153289 5928406731 5928406731 -> (8,8,8)+

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  9  5  6  3  8  1  4  7 
 3  7  4  8  2  1  9  5  0  6 
 4  6  0  2  8  7  1  9  3  5 
 5  9  8  6  0  4  3  2  7  1 
 6  8  5  0  7  9  4  3  1  2 
 7  3  6  1  9  8  2  0  5  4 
 8  5  7  9  1  2  0  4  6  3 
 9  4  1  7  3  0  5  6  2  8 
** 0123456789 0123456789 0123456789 -> (1,1,1)
R* 0963852741 7341289056 7341289056 -> (8,31,31)+

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  9  5  6  3  8  1  4  7 
 3  7  6  8  9  1  2  5  0  4 
 4  6  0  2  8  7  1  9  3  5 
 5  9  8  6  0  4  3  2  7  1 
 6  8  5  0  7  9  4  3  1  2 
 7  3  4  1  2  8  9  0  5  6 
 8  5  7  9  1  2  0  4  6  3 
 9  4  1  7  3  0  5  6  2  8 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 3415209768 7436512809 7438906521 -> (27,27,27)
** 5240138796 8562143079 5982176034 -> (27,27,27)
R* 0963852741 7341289056 7341289056 -> (8,31,31)+
R* 3895601724 0219834576 5894321706 -> (26,26,28)+
R* 5680934712 5894321706 0219834576 -> (26,26,28)+

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  9  7  8  3  1  6  4  5 
 3  6  1  2  9  0  8  4  5  7 
 4  8  6  9  0  2  3  5  7  1 
 5  4  8  6  3  7  9  0  1  2 
 6  3  5  1  7  8  2  9  0  4 
 7  9  4  5  2  1  0  3  6  8 
 8  5  7  0  6  9  4  1  2  3 
 9  7  0  8  1  4  5  2  3  6 
** 0123456789 0123456789 0123456789 -> (1,1,1)
C* 4589017623 0165432987 4589017623 -> (8,31,31)+

Интересный мульти-симметричный ЛК, предпоследний.
Он обладает симметрией (27,27,27) дважды!
Таким образом, симметрия (27,27,27) может быть кратной.
Симметрия с кодом

R* 3895601724 0219834576 5894321706 -> (26,26,28)+

у этого ЛК тоже кратная (дважды).

Цитата

Вчера проверила БД ручного проекта на симметрии

Определитель симметрий

Введено ЛК                 : 68100
Из них симметричных        : 13586

Найдено различных симметрий: 7
Время работы               : 4.633 сек

Список симметрий

(1,1,1)
(1,31,31)
(2,31,31)
(4,31,31)
(8,31,31)
(16,16,16)
(16,31,31)

Обратила внимание на симметрию с кодом (1,31,31).

Насколько я поняла из сообщений Белышева, симметрия с кодом (1,31,31) соответствует симметричным по Гергели/Брауну решениям.
Такие решения были ранее найдены по алгоритму, разработанному Белышевым. Этот эксперимент выполнялся и в нашем BOINC-проекте.

Возникает вопрос: откуда у меня в ручном проекте появились уникальные ОДЛК с симметрией (1,31,31)???
Выше у меня этот вопрос уже возникал и я его озвучивала [это было при поиске симметрии с кодом (4,31,31)].
В своё время Белышев выкладывал на форуме boinc.ru все решения (ОДЛК) симметричные по Гергели/Брауну.
Эти данные у меня сохранились.
Там были решения из линеек №1 и №6. И всего ОДЛК приведено 2749 штук.

Так вот, я сейчас выудила все ОДЛК с симметрией (1,31,31) в БД ручного проекта, их 9 штук, и... этих ОДЛК нет в наборе, приведённом Белышевым.

Ещё одна подробность о решениях с симметрией (1,31,31), выложенных давно Белышевым.
Как сказано в приведённой цитате, ОДЛК с симметрией (1,31,31) было выложено 2749 штук.
Выше я показала ещё 9 ОДЛК с симметрией (1,31,31), которых нет в приведённом списке Белышева (файл symm_odls10_all_2749.txt в архиве symm_odls10; данные от 22.01.2018).

А сейчас хочу показать, сколько ещё симметрий имеется у решений с симметрией (1,31,31); ввожу 2749 ОДЛК в программу Белышева "Определитель симметрий", вот что программа выводит

Определитель симметрий

Введено ЛК                 : 2749
Из них симметричных        : 2749

Найдено различных симметрий: 9
Время работы               : 3.073 сек

Список симметрий

(1,1,1)
(1,31,31)
(4,31,31)
(16,16,16)
(16,31,31)
(21,21,21)
(21,36,36)
(41,41,41)
(41,42,42)

Такая мульти-симметрия!
А вот найденные мной ещё 9 ОДЛК с симметрией (1,31,31) только этой симметрией обладают.

Подумалось с утречка :)
а ещё ведь, наверное, у решений с симметрией (1,31,31) есть симметрии с кодом с плюсом и/или с двумя плюсами.
Надо проверить программой avtoizor.

Сначала покажу расклад по симметриям

Поиск чистых симметрий

Введено ЛК: 2749
Введите код симметрии:
(1,31,31)
Квадратов с симметрией (1,31,31) найдено: 778
они записаны в файл symm_1_31_31.txt
Время поиска: 2.995 сек

Продолжить? (Y/N): y

Введите код симметрии:
(4,31,31)
Квадратов с симметрией (4,31,31) найдено: 2
они записаны в файл symm_4_31_31.txt
Время поиска: 3.011 сек

Продолжить? (Y/N): y

Введите код симметрии:
(16,16,16)
Квадратов с симметрией (16,16,16) найдено: 8
они записаны в файл symm_16_16_16.txt
Время поиска: 3.011 сек

Продолжить? (Y/N): y

Введите код симметрии:
(16,31,31)
Квадратов с симметрией (16,31,31) найдено: 8
они записаны в файл symm_16_31_31.txt
Время поиска: 3.011 сек

Продолжить? (Y/N): y

Введите код симметрии:
(21,21,21)
Квадратов с симметрией (21,21,21) найдено: 1
они записаны в файл symm_21_21_21.txt
Время поиска: 3.027 сек

Продолжить? (Y/N): y

Введите код симметрии:
(21,36,36)
Квадратов с симметрией (21,36,36) найдено: 1
они записаны в файл symm_21_36_36.txt
Время поиска: 3.011 сек

Продолжить? (Y/N): y

Введите код симметрии:
(41,41,41)
Квадратов с симметрией (41,41,41) найдено: 1
они записаны в файл symm_41_41_41.txt
Время поиска: 3.011 сек

Продолжить? (Y/N): y

Введите код симметрии:
(41,42,42)
Квадратов с симметрией (41,42,42) найдено: 1
они записаны в файл symm_41_42_42.txt
Время поиска: 3.027 сек

Как я понимаю, все решения обладают симметрией (1,31,31), а остальные симметрии к ней дополнительные, совместные.

Итак, начала проверку программой Белышева avtoizor 2749 ОДЛК с симметрией (1,31,31).
Проверяю своим скриптом, порциями по 10 штук.
Вот дошла до появления мульти-симметричных решений, дальше не буду проверять, очень долго.

 0  2  4  5  9  8  7  6  3  1 
 5  1  3  9  6  4  8  2  0  7 
 9  6  2  1  5  7  0  3  4  8 
 4  8  7  3  1  0  2  5  9  6 
 7  0  8  2  4  6  3  9  1  5 
 2  4  9  0  7  5  1  8  6  3 
 3  5  0  4  8  9  6  1  7  2 
 6  3  5  8  0  1  9  7  2  4 
 1  9  6  7  2  3  5  4  8  0 
 8  7  1  6  3  2  4  0  5  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032674598 -> (1,31,31)
** 8457129306 0123456789 1098674532 -> (1,31,31)
** 8457129306 9876543210 0189456723 -> (4,31,31)

 0  2  4  5  9  8  7  6  3  1 
 6  1  7  8  3  2  9  5  0  4 
 9  6  2  1  5  7  0  3  4  8 
 5  4  9  3  0  1  2  8  6  7 
 7  0  8  2  4  6  3  9  1  5 
 3  8  0  6  7  5  4  1  9  2 
 2  7  1  4  8  9  6  0  5  3 
 4  3  5  9  1  0  8  7  2  6 
 1  9  6  7  2  3  5  4  8  0 
 8  5  3  0  6  4  1  2  7  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032674598 -> (1,31,31)
** 8794365102 0523816749 1032674598 -> (4,31,31)
** 8794365102 9476183250 0123456789 -> (1,31,31)

 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  2  3  8  9  0  6 
 5  9  2  0  6  4  1  3  7  8 
 9  6  8  3  0  1  2  5  4  7 
 8  7  3  1  4  6  0  2  9  5 
 1  3  6  9  8  5  7  4  2  0 
 3  8  0  4  9  7  6  1  5  2 
 6  0  9  8  3  2  5  7  1  4 
 2  5  1  6  7  9  4  0  8  3 
 7  4  5  2  1  0  3  8  6  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 3180694725 1053726498 6497150382 -> (16,16,16)
** 3180694725 8946273501 4679081253 -> (16,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
** 9765832140 1053726498 4679081253 -> (16,31,31)
** 9765832140 8946273501 6497150382 -> (16,31,31)
R* 2138945706 2968105473 9208465137 -> (21,24,40)+
R* 2138945706 3745018692 7315648029 -> (21,26,42)+
R* 4796320158 2968105473 7315648029 -> (26,36,40)+
R* 4796320158 3745018692 9208465137 -> (24,36,42)+
R* 6754083192 7315648029 2968105473 -> (26,36,40)+
R* 6754083192 9208465137 3745018692 -> (24,36,42)+
R* 8102569734 7315648029 3745018692 -> (21,26,42)+
R* 8102569734 9208465137 2968105473 -> (21,24,40)+
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  2  3  8  9  0  6 
 5  9  2  1  6  4  0  3  7  8 
 9  4  5  3  0  1  2  8  6  7 
 8  7  3  0  4  6  1  2  9  5 
 1  3  6  9  8  5  7  4  2  0 
 2  8  1  4  7  9  6  0  5  3 
 6  0  9  8  3  2  5  7  1  4 
 3  5  0  6  9  7  4  1  8  2 
 7  6  8  2  1  0  3  5  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 3180694725 4167092385 0146293875 -> (16,16,16)
** 3180694725 5832907614 1064372598 -> (16,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
** 9765832140 4167092385 1064372598 -> (16,31,31)
** 9765832140 5832907614 0146293875 -> (16,31,31)
R* 0123456789 2057469813 2057469813 -> (1,30,30)+
R* 0123456789 3189647502 3189647502 -> (1,29,29)+
R* 3180694725 4098235716 4098235716 -> (16,30,30)+
R* 3180694725 6175328904 6175328904 -> (16,28,28)+
R* 5749208163 2057469813 3189647502 -> (29,30,31)+
R* 5749208163 3189647502 2057469813 -> (29,30,31)+
R* 9765832140 4098235716 6175328904 -> (28,30,31)+
R* 9765832140 6175328904 4098235716 -> (28,30,31)+
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  2  3  8  9  0  6 
 8  7  2  0  6  4  1  3  9  5 
 9  4  8  3  0  1  2  5  6  7 
 5  9  3  1  4  6  0  2  7  8 
 1  3  6  9  8  5  7  4  2  0 
 3  8  0  4  9  7  6  1  5  2 
 6  0  9  8  3  2  5  7  1  4 
 2  5  1  6  7  9  4  0  8  3 
 7  6  5  2  1  0  3  8  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
*T 2951476038 1956248037 7958624031 -> (21,31,38)+
*T 2951476038 7308426591 9785436120 -> (16,21,21)+
*T 7048523961 1956248037 9785436120 -> (16,38,38)+
*T 7048523961 7308426591 7958624031 -> (21,31,38)+
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  2  3  8  9  0  6 
 8  7  2  0  6  4  1  3  9  5 
 9  4  8  3  1  0  2  5  6  7 
 5  9  3  1  4  6  0  2  7  8 
 1  3  6  9  8  5  7  4  2  0 
 3  8  1  4  9  7  6  0  5  2 
 6  0  9  8  3  2  5  7  1  4 
 2  5  0  6  7  9  4  1  8  3 
 7  6  5  2  0  1  3  8  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
C* 0659813427 0214365879 0659813427 -> (16,30,30)+
C* 0659813427 9785634120 1487502639 -> (29,30,31)+
C* 1487502639 0214365879 1487502639 -> (16,29,29)+
C* 1487502639 9785634120 0659813427 -> (29,30,31)+
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  2  3  8  9  0  6 
 8  9  2  1  6  4  0  3  7  5 
 9  4  5  3  1  0  2  8  6  7 
 5  7  3  0  4  6  1  2  9  8 
 1  3  6  9  8  5  7  4  2  0 
 2  8  0  4  9  7  6  1  5  3 
 6  0  9  8  3  2  5  7  1  4 
 3  5  1  6  7  9  4  0  8  2 
 7  6  8  2  0  1  3  5  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
*T 0134692875 0162394875 0146293875 -> (16,17,17)+
*T 0134692875 5784932610 1064372598 -> (17,31,41)+
*T 9865307124 0162394875 1064372598 -> (17,31,41)+
*T 9865307124 5784932610 0146293875 -> (16,41,41)+
C* 2176938054 4867092315 3094725186 -> (25,29,31)+
C* 2176938054 5132907684 2176938054 -> (16,25,25)+
C* 3094725186 4867092315 2176938054 -> (25,29,31)+
C* 3094725186 5132907684 3094725186 -> (16,29,29)+
CT 4870256139 2187649503 6052849173 -> (15,28,42)++
CT 4870256139 3059467812 4183567092 -> (15,20,30)++
CT 5129743860 2187649503 4183567092 -> (20,22,28)++
CT 5129743860 3059467812 6052849173 -> (22,30,42)++
R* 3780694125 4178325906 6095238714 -> (25,29,31)+
R* 3780694125 6095238714 4178325906 -> (25,29,31)+
R* 9165832740 4178325906 4178325906 -> (16,29,29)+
R* 9165832740 6095238714 6095238714 -> (16,25,25)+
RT 4183567092 3748056219 3059467812 -> (15,20,30)++
RT 4183567092 9126508473 2187649503 -> (20,22,28)++
RT 6052849173 3748056219 2187649503 -> (15,28,42)++
RT 6052849173 9126508473 3059467812 -> (22,30,42)++
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  2  3  8  9  0  6 
 8  9  2  1  6  4  0  3  7  5 
 9  6  8  3  1  0  2  5  4  7 
 5  7  3  0  4  6  1  2  9  8 
 1  3  6  9  8  5  7  4  2  0 
 2  8  0  4  9  7  6  1  5  3 
 6  0  9  8  3  2  5  7  1  4 
 3  5  1  6  7  9  4  0  8  2 
 7  4  5  2  0  1  3  8  6  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 1046273598 0785634129 4697081352 -> (16,31,31)
** 1046273598 9214365870 6479150283 -> (16,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
** 7528419036 0785634129 6479150283 -> (16,16,16)
** 7528419036 9214365870 4697081352 -> (16,31,31)
C* 2951836740 0561278349 7354890216 -> (19,21,40)+
C* 2951836740 9438721650 9286571304 -> (19,36,42)+
C* 3780524961 0561278349 9286571304 -> (21,35,42)+
C* 3780524961 9438721650 7354890216 -> (35,36,40)+
C* 7354890216 0347812569 2951836740 -> (19,21,40)+
C* 7354890216 9652187430 3780524961 -> (35,36,40)+
C* 9286571304 0347812569 3780524961 -> (21,35,42)+
C* 9286571304 9652187430 2951836740 -> (19,36,42)+
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  3  2  8  9  0  6 
 5  7  2  0  6  4  1  3  9  8 
 9  4  5  3  1  0  2  8  6  7 
 8  9  3  1  4  6  0  2  7  5 
 1  3  6  9  8  5  7  4  2  0 
 2  8  1  4  7  9  6  0  5  3 
 6  0  9  8  2  3  5  7  1  4 
 3  5  0  6  9  7  4  1  8  2 
 7  6  8  2  0  1  3  5  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 1028479536 3520819746 5823709416 -> (16,16,16)
** 1028479536 6479180253 8532917604 -> (16,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
** 7546213098 3520819746 8532917604 -> (16,31,31)
** 7546213098 6479180253 5823709416 -> (16,31,31)
*T 1523789406 6549173208 8532917604 -> (17,31,41)+
*T 1523789406 8023719456 5823709416 -> (16,17,17)+
*T 4879253160 3128506479 1032684957 -> (11,30,31)+
*T 4879253160 9746058213 0123456789 -> (1,30,30)+
*T 5120746839 3128506479 0123456789 -> (1,11,11)+
*T 5120746839 9746058213 1032684957 -> (11,30,31)+
*T 8476210593 6549173208 5823709416 -> (16,41,41)+
*T 8476210593 8023719456 8532917604 -> (17,31,41)+
C* 4728360915 3520819746 4728360915 -> (16,30,30)+
C* 4728360915 6479180253 6935241708 -> (29,30,31)+
C* 6935241708 3520819746 6935241708 -> (16,29,29)+
C* 6935241708 6479180253 4728360915 -> (29,30,31)+
C* 7421395680 0123456789 7421395680 -> (1,20,20)+
C* 7421395680 9876543210 9630278451 -> (20,31,42)+
C* 9630278451 0123456789 9630278451 -> (1,42,42)+
C* 9630278451 9876543210 7421395680 -> (20,31,42)+
CT 1523789406 5930461278 6935241708 -> (17,29,30)++
CT 1523789406 8721640395 4728360915 -> (17,28,30)++
CT 4879253160 0635798241 7421395680 -> (20,30,30)++
CT 4879253160 1428975360 9630278451 -> (29,30,42)++
CT 5120746839 0635798241 9630278451 -> (11,30,42)++
CT 5120746839 1428975360 7421395680 -> (11,20,29)++
CT 8476210593 5930461278 4728360915 -> (30,30,41)++
CT 8476210593 8721640395 6935241708 -> (28,29,41)++
R* 0123456789 0635798241 0635798241 -> (1,30,30)+
R* 0123456789 1428975360 1428975360 -> (1,29,29)+
R* 1028479536 5930461278 5930461278 -> (16,30,30)+
R* 1028479536 8721640395 8721640395 -> (16,28,28)+
R* 5749208163 0635798241 1428975360 -> (29,30,31)+
R* 5749208163 1428975360 0635798241 -> (29,30,31)+
R* 7546213098 5930461278 8721640395 -> (28,30,31)+
R* 7546213098 8721640395 5930461278 -> (28,30,31)+
RT 4728360915 6549173208 5930461278 -> (30,30,41)++
RT 4728360915 8023719456 8721640395 -> (17,28,30)++
RT 6935241708 6549173208 8721640395 -> (28,29,41)++
RT 6935241708 8023719456 5930461278 -> (17,29,30)++
RT 7421395680 3128506479 1428975360 -> (11,20,29)++
RT 7421395680 9746058213 0635798241 -> (20,30,30)++
RT 9630278451 3128506479 0635798241 -> (11,30,42)++
RT 9630278451 9746058213 1428975360 -> (29,30,42)++
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  3  2  8  9  0  6 
 5  7  2  0  6  4  1  3  9  8 
 9  4  8  3  0  1  2  5  6  7 
 8  9  3  1  4  6  0  2  7  5 
 1  3  6  9  8  5  7  4  2  0 
 3  8  0  4  9  7  6  1  5  2 
 6  0  9  8  2  3  5  7  1  4 
 2  5  1  6  7  9  4  0  8  3 
 7  6  5  2  1  0  3  8  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
*T 2951476038 1956248037 7958624031 -> (21,31,38)+
*T 2951476038 7308426591 9785436120 -> (16,21,21)+
*T 7048523961 1956248037 9785436120 -> (16,38,38)+
*T 7048523961 7308426591 7958624031 -> (21,31,38)+
C* 2076935184 4867092315 3194728056 -> (25,29,31)+
C* 2076935184 5132907684 2076935184 -> (16,25,25)+
C* 3194728056 4867092315 2076935184 -> (25,29,31)+
C* 3194728056 5132907684 3194728056 -> (16,29,29)+
CT 3401967528 0435798261 5704182936 -> (26,39,42)++
CT 3401967528 1628975340 8916053724 -> (19,30,39)++
CT 6598032471 0435798261 8916053724 -> (19,26,42)++
CT 6598032471 1628975340 5704182936 -> (30,42,42)++
R* 6219780453 7682013549 9453102867 -> (26,30,31)+
R* 6219780453 9453102867 7682013549 -> (26,30,31)+
R* 8473165209 7682013549 7682013549 -> (16,30,30)+
R* 8473165209 9453102867 9453102867 -> (16,26,26)+
RT 5704182936 2380175694 0435798261 -> (26,39,42)++
RT 5704182936 4965710832 1628975340 -> (30,42,42)++
RT 8916053724 2380175694 1628975340 -> (19,30,39)++
RT 8916053724 4965710832 0435798261 -> (19,26,42)++
 0  2  4  7  5  8  9  6  3  1 
 4  1  7  5  3  2  8  9  0  6 
 5  7  2  1  6  4  0  3  9  8 
 9  4  5  3  1  0  2  8  6  7 
 8  9  3  0  4  6  1  2  7  5 
 1  3  6  9  8  5  7  4  2  0 
 2  8  1  4  7  9  6  0  5  3 
 6  0  9  8  2  3  5  7  1  4 
 3  5  0  6  9  7  4  1  8  2 
 7  6  8  2  0  1  3  5  4  9 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 9876543210 1032684957 -> (1,31,31)
** 5749208163 0123456789 1032684957 -> (1,31,31)
** 5749208163 9876543210 0123456789 -> (1,31,31)
R* 1028479536 5930461278 5930461278 -> (16,30,30)+
R* 1028479536 8721640395 8721640395 -> (16,28,28)+
R* 7546213098 5930461278 8721640395 -> (28,30,31)+
R* 7546213098 8721640395 5930461278 -> (28,30,31)+

Интересные мульти-симметричные решения!
Есть коды симметрий и с плюсом, и с двумя плюсами; есть кратные симметрии.
Я проверила всего 30 порций по 10 штук.
Помнится, Белышев делал программу avtoizor для массовой проверки, но что-то в ней перемудрил (на мой взгляд), и потому я этой программой не пользуюсь.
Написала свой пакетный файл и проверяю с его помощью по 10 штук.

Эксперимент "мультисимметрия" продолжается и стабильно даёт результаты.
Это притом, что сейчас эксперимент работает на одном генераторе.
Генератор ЛК с симметрией (27,27,27) что-то у меня очень быстро выдохся. Ну не даёт новых ЛК, хоть застрелись.
Всего нашла 143264 КФ ЛК с этой симметрией.
Надо подключить третий генератор; пока не было времени, возилась с генератором для симметрии (27,27,27).
Всё, прекращаю заниматься этим генератором. И на псевдотройки все имеющиеся ЛК с симметрией (27,27,27) проверила.
Только один личный рекорд - псевдотройка с х. о. 88.

Сейчас от работающего генератора стабильно идут решения с двумя симметриями: (4,31,31) и (16,31,31).
Завтра подключу третий генератор. Этот генератор у меня даёт решения с кодами симметрии с плюсом. Не густо даёт решений.
Может быть, ещё сделаю какой-нибудь генератор. Надо подумать.

Солидные группы пар ОДЛК в эксперименте "мультисимметрия" редко появляются. Но вот сегодня нашлась четвёрка

0 1 2 3 4 5 6 7 8 9
1 2 0 4 7 9 8 5 6 3
9 4 7 6 8 1 5 3 0 2
2 7 9 8 6 0 4 1 3 5
6 8 3 1 5 2 0 9 4 7
8 6 5 2 1 3 9 0 7 4
4 9 6 7 3 8 1 2 5 0
7 5 8 9 0 6 3 4 2 1
3 0 1 5 2 4 7 6 9 8
5 3 4 0 9 7 2 8 1 6

Это, кажется, вторая четвёрка в данном эксперименте.
И 440-ая четвёрка в нашей БД.
Четвёрка без симметрий, полновесная.

В программе перечисления семейств ЛК_4_31_31 был баг из-за которого 30 семейств были пропущены. В этих семействах содержится ровно 400000 ЛК. Из них д-марьяжных — два, соответствующих марьяжных ДЛК тоже два. Таким образом, число существенно различных д-марьяжных ЛК с симметрией (4,31,31) равно 19589, а соответствующих им марьяжных ДЛК — 19650.

отсюда
http://forum.boinc.ru/default.aspx?g=posts&m=91794#post91794

Белышев устал :)
Надо ему отдохнуть немного.

Новый термин появился

...число существенно различных д-марьяжных ЛК с симметрией (4,31,31) равно 19589...

(выделено мной)

Вот это самое у меня называется стандарты. Это короче, мне так больше нравится.
И по выложенным ранее Белышевым данным по симметрии (4,31,31) стандартов было 19587, а теперь их стало 19589.

По симметрии (27,27,27), например, в нашей БД на данный момент имеется 44 стандарта. 19 из них я выложила в теме "Симметрия (27,27,27)".

Эксперимент мультисимметрия продолжается!
Подключила к эксперименту ещё один генератор - для ЛК с симметрией (16,16,16).
Но пока этот генератор решений не дал. Обкатываю, посмотрю, что будет давать. Написала скрипт для борьбы с изоморфизмом. Изоморфных ЛК много.

Вот новая порция решений от эксперимента мультисимметрия (введены КФ ОДЛК)

Определитель симметрий

Введено ЛК                 : 70
Из них симметричных        : 6

Найдено различных симметрий: 3
Время работы               : 0.015 сек

6 "симметричных" решений, 2 симметрии, кроме тождественной.

Список симметрий

(1,1,1)
(8,31,31)
(16,31,31)

Конечно, в найденных ОДЛК список симметрий гораздо меньше, чем в сгенерированных ЛК, ОДЛК особой мультисимметрией не отличаются.
Солидных пар ОДЛК в этой порции нет.
Замыкание

. . . . . 
Проверено ДЛК           : 26097
Найдено КФ марьяжных ДЛК: 70
Время работы в сек      : 5.491

Найдено марьяжных КФ:
count[1] = 66
count[2] = 4
Всего: 70
Найдено соквадратов: 74
КФ соквадратов: 70

Скромно, всего 4 двушечки.

Цитата

Среди ЛК, выданных генератором для симметрии (16,16,16), увидела ещё такие симметрии

(7,41,41)
(7,42,42)
(10,34,34)

Такие симметрии мне ещё не встречались от первых трёх генераторов в эксперименте мультисимметрия.
Может быть, просто не видела, я же не проверяю абсолютно все сгенерированные ЛК на симметрии.

Показываю ЛК, который обладает симметриями (7,41,41) и (7,42,42)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 8 5 1 9 7 3 0 6 4
3 9 7 5 1 8 4 2 0 6
4 5 6 7 8 9 0 1 2 3
5 3 9 6 2 0 8 4 1 7
6 7 8 9 0 1 2 3 4 5
7 4 0 8 6 2 9 5 3 1
8 6 4 0 7 3 1 9 5 2
9 0 1 2 3 4 5 6 7 8

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123456789 5678901234 5678901234 -> (1,31,31)
** 0135476829 3456789012 7890123456 -> (7,42,42)
** 0135476829 8901234567 2345678901 -> (7,41,41)
** 0157486239 1234567890 9012345678 -> (7,42,42)
** 0157486239 6789012345 4567890123 -> (7,41,41)
** 0178426359 4567890123 6789012345 -> (7,41,41)
** 0178426359 9012345678 1234567890 -> (7,42,42)
** 0182436579 2345678901 8901234567 -> (7,41,41)
** 0182436579 7890123456 3456789012 -> (7,42,42)
** 0928674531 3210987654 3210987654 -> (16,31,31)
** 0928674531 8765432109 8765432109 -> (16,16,16)
** 0932684751 1098765432 1098765432 -> (16,31,31)
** 0932684751 6543210987 6543210987 -> (16,16,16)
** 0953624871 4321098765 4321098765 -> (16,16,16)
** 0953624871 9876543210 9876543210 -> (16,31,31)
** 0975634281 2109876543 2109876543 -> (16,16,16)
** 0975634281 7654321098 7654321098 -> (16,31,31)
** 0987654321 0987654321 0987654321 -> (16,16,16)
** 0987654321 5432109876 5432109876 -> (16,31,31)

Добавила в файл standart.txt автоморфизмы для данных симметрий, теперь программа get_standard выводит для них очевидные симметрии

(7,41,41)
0 1 2 3 4 5 6 7 8 9
1 8 3 0 5 2 7 4 9 6
8 2 4 6 9 0 3 5 7 1
2 4 7 8 1 3 5 9 6 0
6 7 8 9 0 1 2 3 4 5
5 6 9 1 3 7 4 8 0 2
4 5 6 7 8 9 0 1 2 3
7 9 1 5 2 6 8 0 3 4
9 3 0 4 6 8 1 2 5 7
3 0 5 2 7 4 9 6 1 8

(7,42,42)
0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 0 1 2
6 0 7 4 8 1 5 2 9 3
5 2 6 9 3 0 7 1 4 8
2 3 4 5 6 7 8 9 0 1
4 7 1 8 5 9 2 6 3 0
8 9 0 1 2 3 4 5 6 7
9 6 3 7 0 4 1 8 2 5
1 5 8 2 9 6 0 3 7 4
7 8 9 0 1 2 3 4 5 6

Правильно ли добавила?
Узнать бы ещё, что сии очевидные симметрии означают :)

ЛК с симметрией (10,34,34) у меня аж 9 штук

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 6 7 8 9 4
2 3 0 1 6 7 8 9 4 5
3 0 1 2 8 9 4 5 6 7
4 5 7 8 0 3 9 2 1 6
5 6 8 9 3 4 2 1 7 0
6 7 9 4 1 8 0 3 5 2
7 8 4 5 9 0 3 6 2 1
8 9 5 6 7 2 1 4 0 3
9 4 6 7 2 1 5 0 3 8

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 6 7 8 9 4
2 3 0 1 7 8 9 4 5 6
3 0 1 2 9 4 5 6 7 8
4 5 7 8 0 9 3 2 6 1
5 6 8 9 2 7 1 0 4 3
6 7 9 4 8 1 0 5 3 2
7 8 4 5 6 3 2 9 1 0
8 9 5 6 3 2 4 1 0 7
9 4 6 7 1 0 8 3 2 5

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 6 7 8 9 4
2 3 0 1 7 8 9 4 5 6
3 0 1 2 9 4 5 6 7 8
4 5 7 8 1 9 2 3 6 0
5 6 8 9 3 7 0 1 4 2
6 7 9 4 8 0 1 5 2 3
7 8 4 5 6 2 3 9 0 1
8 9 5 6 2 3 4 0 1 7
9 4 6 7 0 1 8 2 3 5

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 6 7 8 9 4
2 3 0 1 7 8 9 4 5 6
3 0 1 2 9 4 5 6 7 8
4 5 7 8 3 9 0 1 6 2
5 6 8 9 1 7 2 3 4 0
6 7 9 4 8 2 3 5 0 1
7 8 4 5 6 0 1 9 2 3
8 9 5 6 0 1 4 2 3 7
9 4 6 7 2 3 8 0 1 5

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 6 7 8 9 4
2 3 0 1 7 8 9 4 5 6
3 0 1 2 9 4 5 6 7 8
4 8 7 5 1 9 0 3 6 2
5 9 8 6 3 7 2 1 4 0
6 4 9 7 8 2 1 5 0 3
7 5 4 8 6 0 3 9 2 1
8 6 5 9 0 3 4 2 1 7
9 7 6 4 2 1 8 0 3 5

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 6 7 8 9 4
2 3 0 1 7 8 9 4 5 6
3 0 1 2 9 4 5 6 7 8
4 8 7 5 3 9 2 1 6 0
5 9 8 6 1 7 0 3 4 2
6 4 9 7 8 0 3 5 2 1
7 5 4 8 6 2 1 9 0 3
8 6 5 9 2 1 4 0 3 7
9 7 6 4 0 3 8 2 1 5

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 0 4 1 8 7 5 9 6 3
3 6 0 2 9 8 1 5 7 4
4 3 1 0 7 9 8 6 5 2
5 9 7 8 6 0 4 2 3 1
6 7 8 9 0 1 2 3 4 5
7 5 9 6 3 2 0 4 1 8
8 4 5 7 1 3 9 0 2 6
9 8 6 5 2 4 3 1 0 7

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 0 4 1 8 7 5 9 6 3
3 6 0 2 9 8 1 5 7 4
4 3 1 0 7 9 8 6 5 2
5 9 7 8 6 0 4 2 3 1
6 7 9 5 3 1 2 4 0 8
7 8 6 9 0 2 3 1 4 5
8 4 5 7 1 3 9 0 2 6
9 5 8 6 2 4 0 3 1 7

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 0 6 8 9 7 5 1 3 4
3 9 7 0 6 8 4 2 5 1
4 7 8 1 0 9 2 3 6 5
5 6 9 7 8 0 1 4 2 3
6 3 5 9 2 1 8 0 4 7
7 4 1 5 3 2 9 6 0 8
8 5 4 2 1 3 0 9 7 6
9 8 0 6 7 4 3 5 1 2

Для какого ЛК добавлять автоморфизм?
Помнится, вроде Белышев писал, что добавлять надо наименьший автоморфизм.
Сейчас поищу наименьший.

Добавила этот автоморфизм, он у меня наименьший

** 0123678945 2301945678 2301567894 -> (10,34,34)

Для этого ЛК, например

 0  1  2  3  4  5  6  7  8  9 
 1  2  3  4  5  6  7  8  9  0 
 2  0  6  8  9  7  5  1  3  4 
 3  9  7  0  6  8  4  2  5  1 
 4  7  8  1  0  9  2  3  6  5 
 5  6  9  7  8  0  1  4  2  3 
 6  3  5  9  2  1  8  0  4  7 
 7  4  1  5  3  2  9  6  0  8 
 8  5  4  2  1  3  0  9  7  6 
 9  8  0  6  7  4  3  5  1  2 

очевидная симметрия выводится такая

(10,34,34)
0 1 2 3 5 6 7 8 9 4
1 0 3 2 8 9 4 5 6 7
2 3 0 1 9 4 5 6 7 8
3 2 1 0 6 7 8 9 4 5
4 9 7 6 0 8 1 2 5 3
5 6 8 9 4 0 3 7 2 1
6 5 9 8 7 3 0 4 1 2
7 8 4 5 2 1 6 0 3 9
8 7 5 4 1 2 9 3 0 6
9 4 6 7 3 5 2 1 8 0

Это правильно?
Что ваши очи видят в этой очевидной симметрии? :)

Цитата

Всего через третий этап проходят следующие 46 кодов симметрии:

(1,1,1)
(1,31,31)
(1,41,41)
(1,42,42)
(2,31,31)
(2,42,42)
(4,31,31)
(4,42,42)
(7,7,7)
(7,41,41)
(7,42,42)
(8,8,8)
(8,31,31)
(8,42,42)
(10,10,10)
(10,34,34)
(11,11,11)
(11,34,34)
(13,42,42)
(15,15,15)
(16,16,16)
(16,31,31)
(16,42,42)
(17,36,36)
(18,34,34)
(19,19,19)
(19,34,34)
(21,21,21)
(21,36,36)
(22,22,22)
(22,37,37)
(24,42,42)
(27,27,27)
(28,28,28)
(30,30,30)
(31,31,31)
(31,41,42)
(31,42,42)
(32,36,36)
(33,34,34)
(34,34,34)
(36,36,36)
(37,37,37)
(41,41,41)
(41,42,42)
(42,42,42)

Осталось ещё проверить существование ЛК с соответствующими автотопиями.

отсюда
http://forum.boinc.ru/default.aspx?g=posts&m=91003#post91003

Как отметил Белышев, ЛК Агриппы подтверждает 14 симметрий из приведённого списка.

У меня в файле standart.txt на данный момент записаны автоморфизмы для 28 симметрий.
Не хватает подтверждений для 18 симметрий.

Напомню: ЛК Агриппы подтверждает следующие 14 симметрий

(1,1,1)
(1,31,31)
(1,41,41)
(7,7,7)
(7,41,41)
(7,42,42)
(16,16,16)
(16,31,31)
(16,42,42)
(21,21,21)
(21,36,36)
(31,41,42)
(41,41,41)
(41,42,42)

Выписала коды симметрий, которых у меня нет; вроде не встречались ЛК с такими симметриями

(1,42,42)
(2,42,42)
(4,42,42)
(8,42,42)
(11,11,11)
(11,34,34)
(13,42,42)
(17,36,36)
(18,34,34)
(19,34,34)
(24,42,42)
-(31,31,31)
(31,42,42)
(32,36,36)
(33,34,34)
(34,34,34)
(36,36,36)
(37,37,37)

ЛК с симметрией (31,31,31), по-моему, не существуют.
По крайней мере, среди ассоциативных ЛК я не нашла ЛК с такой симметрией (искала по типу соответствия элементов).
Осталось подтвердить 17 симметрий.

Надо посмотреть примеры различных мультисимметричных ЛК, которые я приводила в теме "Обобщённые симметрии".
Может быть, там ещё что-то есть.

Вот нашла в этой теме квадратик очень симпатичный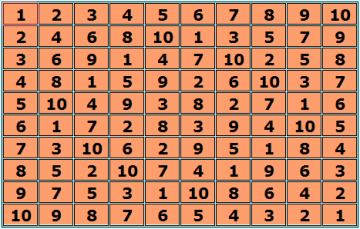



Этот ЛК обладает симметрией (1,42,42) причём 12-кратно.
Список всех симметрий этого ЛК

(1,1,1)
(1,31,31)
(1,41,41)
(1,42,42)
(16,16,16)
(16,31,31)
(21,21,21)
(21,36,36)
(31,41,42)
(41,41,41)
(41,42,42)

Т-э-к-с, одну симметрию подтвердила. Сейчас добавлю её и выведу очевидную симметрию.

Автоморфизмы (12 штук)

** 0123456789 1357902468 5061728394 -> (1,42,42)
** 0123456789 5061728394 1357902468 -> (1,42,42)
** 0123456789 6295184073 7419630852 -> (1,42,42)
** 0123456789 7419630852 6295184073 -> (1,42,42)
** 1357902468 0123456789 5061728394 -> (1,42,42)
** 1357902468 5061728394 0123456789 -> (1,42,42)
** 5061728394 0123456789 1357902468 -> (1,42,42)
** 5061728394 1357902468 0123456789 -> (1,42,42)
** 6295184073 0123456789 7419630852 -> (1,42,42)
** 6295184073 7419630852 0123456789 -> (1,42,42)
** 7419630852 0123456789 6295184073 -> (1,42,42)
** 7419630852 6295184073 0123456789 -> (1,42,42)

Записываю в файл standart.txt самый первый автоморфизм.
Получаю такую очевидную симметрию, аж два экземпляра

(1,42,42)
0 5 1 6 2 7 3 8 4 9
9 4 5 0 6 1 7 2 8 3
2 7 3 8 4 9 0 5 1 6
3 8 4 9 0 5 1 6 2 7
1 6 2 7 3 8 4 9 0 5
6 1 7 2 8 3 9 4 5 0
8 3 9 4 5 0 6 1 7 2
7 2 8 3 9 4 5 0 6 1
4 9 0 5 1 6 2 7 3 8
5 0 6 1 7 2 8 3 9 4

0 1 2 3 4 5 6 7 8 9
5 0 6 1 7 2 8 3 9 4
3 7 0 4 8 1 5 9 2 6
2 5 8 0 3 6 9 1 4 7
8 6 4 2 0 9 7 5 3 1
1 3 5 7 9 0 2 4 6 8
7 4 1 9 6 3 0 8 5 2
6 2 9 5 1 8 4 0 7 3
4 9 3 8 2 7 1 6 0 5
9 8 7 6 5 4 3 2 1 0

Исходный ЛК на иллюстрации в предыдущем посте.
На всякий случай покажу его (иллюстрации иногда пропадают)

0 1 2 3 4 5 6 7 8 9
1 3 5 7 9 0 2 4 6 8
2 5 8 0 3 6 9 1 4 7
3 7 0 4 8 1 5 9 2 6
4 9 3 8 2 7 1 6 0 5
5 0 6 1 7 2 8 3 9 4
6 2 9 5 1 8 4 0 7 3
7 4 1 9 6 3 0 8 5 2
8 6 4 2 0 9 7 5 3 1
9 8 7 6 5 4 3 2 1 0

Ещё ссылка на мою статью, из которой взят этот симпатичный квадратик
http://www.natalimak1.narod.ru/metod3.htm

PS. Переделываю. Нашла другой автоморфизм, меньший

** 0123456789 1234567890 9012345678 -> (1,42,42)

Сейчас его добавлю в файл standart.txt, а прежний автоморфизм удалю.
И теперь выводятся такие очевидные симметрии (тоже два экземпляра)

(1,42,42)
0 5 1 6 2 7 3 8 4 9
9 4 5 0 6 1 7 2 8 3
2 7 3 8 4 9 0 5 1 6
3 8 4 9 0 5 1 6 2 7
1 6 2 7 3 8 4 9 0 5
6 1 7 2 8 3 9 4 5 0
8 3 9 4 5 0 6 1 7 2
7 2 8 3 9 4 5 0 6 1
4 9 0 5 1 6 2 7 3 8
5 0 6 1 7 2 8 3 9 4

0 1 2 3 4 5 6 7 8 9
9 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 0 1
8 9 0 1 2 3 4 5 6 7
6 7 8 9 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 0
3 4 5 6 7 8 9 0 1 2
7 8 9 0 1 2 3 4 5 6
4 5 6 7 8 9 0 1 2 3
5 6 7 8 9 0 1 2 3 4

И какой вариант правильный??? ХЗ :)
Замечу, что первые экземпляры очевидной симметрии совпадают, а вторые экземпляры изоморфны.

А вот здесь
https://boinc.progger.info/odlk/forum_thread.php?id=81&postid=2053#2053
какой интересный ЛК показан

 0  1  2  3  4  5  6  7  8  9 
 1  0  3  2  5  6  7  8  9  4 
 2  3  0  1  8  9  4  5  6  7 
 3  4  7  0  9  8  2  6  5  1 
 4  9  8  6  0  7  3  2  1  5 
 5  6  9  8  7  0  1  4  3  2 
 6  2  5  4  3  1  0  9  7  8 
 7  8  1  9  6  4  5  0  2  3 
 8  7  4  5  2  3  9  1  0  6 
 9  5  6  7  1  2  8  3  4  0 
** 0123456789 0123456789 0123456789 -> (1,1,1)
** 0123957684 3210789456 3210789456 -> (4,31,31)
** 0463152789 3640281957 3640281957 -> (4,31,31)
** 0463957281 0463957281 0973152684 -> (10,10,10)
** 0973152684 0973152684 0463957281 -> (10,10,10)
** 0973456281 3790684152 3790684152 -> (4,31,31)
** 3120486759 5748209136 8695731402 -> (4,31,31)
** 3120987654 8475136209 5968402731 -> (16,16,16)
** 3460182759 8925437601 5178906234 -> (16,16,16)
** 3460987251 5298601437 8245639107 -> (33,34,34)
** 3970182654 5618704932 8715234906 -> (33,34,34)
** 3970486251 8165932704 5428107639 -> (16,16,16)
** 5218604937 8125436709 3690781452 -> (4,31,31)
** 5218709436 5218709436 0963452781 -> (4,31,31)
** 5648201937 5648201937 0173956284 -> (4,31,31)
** 5648709132 8465937201 3240689157 -> (33,34,34)
** 5798201436 8975132604 3710284956 -> (33,34,34)
** 5798604132 5798604132 0423157689 -> (4,31,31)
** 8215634907 3740289156 5128406739 -> (4,31,31)
** 8215739406 0473156289 8215739406 -> (4,31,31)
** 8645231907 0923457681 8645231907 -> (4,31,31)
** 8645739102 3290681457 5978102634 -> (33,34,34)
** 8795231406 3610784952 5468907231 -> (33,34,34)
** 8795634102 0163952784 8795634102 -> (4,31,31)
. . . . 

И ещё одна симметрия подтверждается: (33,34,34).
Думаю, что надо записать в файл standart.txt этот автоморфизм

** 3460987251 5298601437 8245639107 -> (33,34,34)

Сейчас попробую получить очевидную симметрию.

Вот очевидная симметрия

(33,34,34)
0 1 2 8 4 5 6 7 3 9
1 0 3 9 5 6 7 8 2 4
7 8 1 2 6 4 5 0 9 3
3 4 7 5 9 8 2 6 0 1
4 9 8 1 0 7 3 2 6 5
8 7 4 0 2 3 9 1 5 6
2 3 0 6 8 9 4 5 1 7
6 2 5 7 3 1 0 9 4 8
5 6 9 3 7 0 1 4 8 2
9 5 6 4 1 2 8 3 7 0

Выводится :) Правильно ли?