Первые группы из восьми пар ортогональных ДЛК (кратко называемые "восьмёрка") были найдены в нашем с Белышевым эксперименте с семейством ЛК блочной структуры №1. Их было всего две, вот они (КФ основного ДЛК в первом формате)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 9 8 7 2 1 0 5 6
8 7 6 5 9 0 4 3 2 1
7 3 4 0 8 1 9 5 6 2
5 0 8 7 3 6 2 1 9 4
4 9 1 2 6 3 7 8 0 5
2 6 5 9 1 8 0 4 3 7
9 8 7 6 5 4 3 2 1 0
6 5 0 1 2 7 8 9 4 3

0 1 2 3 4 5 6 7 8 9
1 2 3 4 9 0 5 6 7 8
8 7 6 5 0 9 4 3 2 1
4 0 1 7 6 3 2 8 9 5
7 6 4 9 8 1 0 5 3 2
9 8 7 6 5 4 3 2 1 0
2 3 5 0 1 8 9 4 6 7
5 9 8 2 3 6 7 1 0 4
3 4 0 1 2 7 8 9 5 6
6 5 9 8 7 2 1 0 4 3

Основные ДЛК этих восьмёрок симметричны по Гергели/Брауну. Более того, они являются "браунами".
КФ основных ДЛК этих восьмёрок во втором формате принадлежат линейке № 6.
Восьмёрки эти не полновесные, каждая даёт только 5 уникальных КФ ОДЛК. То есть среди ортогональных соквадратов каждой восьмёрки есть 4 не уникальных ДЛК.

Вот такие были наши первые восьмёрки.
О двух следующих восьмёрках далее.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Две следующие восьмёрки были найдены в эксперименте по поиску симметричных по Гергели/Брауну решений, который выполнялся в проекте ODLK в августе 2017 г.
Алгоритм поиска и ПО для этого эксперимента были разработаны Белышевым.
Вот эти восьмёрки (КФ основных ДЛК в первом формате):

0 1 2 3 4 5 6 7 8 9 
1 2 3 0 5 4 9 6 7 8 
4 9 6 8 2 7 1 3 0 5 
6 8 7 4 9 0 5 2 1 3 
7 3 5 9 1 8 0 4 6 2 
9 4 8 7 6 3 2 1 5 0 
3 5 9 1 7 2 8 0 4 6 
8 7 4 6 0 9 3 5 2 1 
5 0 1 2 3 6 7 8 9 4 
2 6 0 5 8 1 4 9 3 7

0 1 2 3 4 5 6 7 8 9 
1 2 3 4 9 0 5 6 7 8 
8 6 7 0 5 4 9 2 3 1 
5 8 9 6 2 7 3 0 1 4 
9 5 8 7 3 6 2 1 4 0 
3 7 4 9 1 8 0 5 2 6 
7 4 6 8 0 9 1 3 5 2 
6 9 5 2 8 1 7 4 0 3 
2 0 1 5 6 3 4 8 9 7 
4 3 0 1 7 2 8 9 6 5 

Основные ДЛК этих восьмёрок симметричны по Гергели/Брауну, однако не являются "браунами".
Основные ДЛК восьмёрок тоже из семейства ЛК блочной структуры, но уже другого - вида 10х5 (первые две восьмёрки из семейства БС вида 5х5).
КФ основных ДЛК восьмёрок во втором формате принадлежат линейке № 1.
Эти две восьмёрки тоже не полновесные, дают по 5 уникальных КФ ОДЛК.

Теперь в нашей БД стало 4 восьмёрки.
Читайте далее...

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

5 апреля с. г. мной была найдена пятая восьмёрка, в эксперименте с псевдоассоциативными ДЛК.
КФ основного ДЛК восьмёрки в первом формате

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 7 3 9 6 8
5 7 3 2 1 9 4 8 0 6
3 0 1 8 9 4 5 6 7 2
8 9 4 6 7 1 0 2 5 3
4 8 5 1 3 6 2 0 9 7
7 5 6 0 8 2 9 1 3 4
9 3 7 5 6 0 8 4 2 1
6 4 8 9 2 3 7 5 1 0
2 6 9 7 0 8 1 3 4 5

Эта восьмёрка полновесная, то есть даёт 9 уникальных КФ ОДЛК.
Ещё есть интересная особенность у этой восьмёрки: она происходит от ЛК блочной структуры рикошетом.
Я об этом уже где-то рассказывала. Два ортогональных соквадрата этой восьмёрки - блочные структуры, принадлежат одному семейству БС вида 10х10. Основной же ДЛК восьмёрки блочной структурой не является.

Конфигурацию, порождаемую этой восьмёркой, можно изобразить так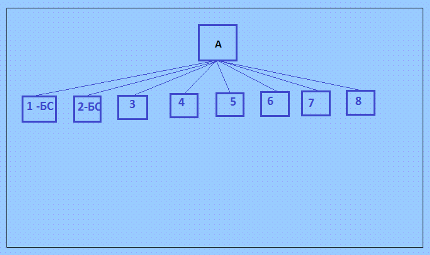



Основной ДЛК восьмёрки - квадрат А. Ортогональные соквадраты: 1, 2, 3, ..., 8. Среди ортогональных соквадратов есть две БС.

Читайте далее о нашей шестой восьмёрке...

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

6 июня с. г. тоже в эксперименте с псевдоассоциативными ДЛК Demis нашёл шестую восьмёрку

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 9 8 3 6 7
5 9 7 6 0 1 3 8 2 4
4 7 3 8 1 0 2 6 9 5
3 6 5 1 9 4 7 2 0 8
9 4 8 2 3 6 5 0 7 1
2 3 4 0 7 8 1 9 5 6
6 0 1 9 8 7 4 5 3 2
8 5 6 7 2 3 9 1 4 0
7 8 9 5 6 2 0 4 1 3

Восьмёрка не полновесная, даёт 5 уникальных КФ ОДЛК.
Ни основной ДЛК восьмёрки, ни ортогональные соквадраты блочными структурами не являются.
Ничего примечательного в этой восьмёрке не увидела.

Это пока все восьмёрки, имеющиеся в нашей БД КФ ОДЛК на данный момент.
Правда, не обработаны решения с проекта ODLK1, начиная с 1 мая с. г. Может быть, там есть интересные группы пар ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

У-р-р-р-а-а-а!

В эксперименте с псевдоассоциативными ДЛК только что найдена новая восьмёрка

0 1 2 3 4 5 6 7 8 9
1 2 0 6 7 9 8 3 4 5
4 6 1 9 5 7 2 8 0 3
7 4 5 8 6 0 3 1 9 2
2 7 3 0 9 6 4 5 1 8
6 8 9 5 2 3 0 4 7 1
9 5 4 1 8 2 7 0 3 6
3 9 7 4 1 8 5 6 2 0
8 0 6 2 3 4 1 9 5 7
5 3 8 7 0 1 9 2 6 4

Восьмёрка полновесная, даёт 9 уникальных КФ ОДЛК.
Это седьмая восьмёрка в нашей БД.
Я продолжаю обрабатывать псевдоассоциативные ДЛК в линейке № 51.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это цитата

6 июня с. г. тоже в эксперименте с псевдоассоциативными ДЛК Demis нашёл шестую восьмёрку

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 9 8 3 6 7
5 9 7 6 0 1 3 8 2 4
4 7 3 8 1 0 2 6 9 5
3 6 5 1 9 4 7 2 0 8
9 4 8 2 3 6 5 0 7 1
2 3 4 0 7 8 1 9 5 6
6 0 1 9 8 7 4 5 3 2
8 5 6 7 2 3 9 1 4 0
7 8 9 5 6 2 0 4 1 3

Восьмёрка не полновесная, даёт 5 уникальных КФ ОДЛК.
Ни основной ДЛК восьмёрки, ни ортогональные соквадраты блочными структурами не являются.
Ничего примечательного в этой восьмёрке не увидела.

Оказалось, что примечательное в этой восьмёрке есть.
По недавно разработанной классификации Белышева основной ДЛК этой восьмёрки принадлежит семейству симметрии с кодом (4,31,31)

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 9867542310 0132457689 7859624013 -> (4,31,31)

Отсюда и 5 уникальных КФ.

Данное семейство симметрии с кодом (4,31,31) дают ассоциативные ЛК с определённым соответствием элементов, а именно: 6 элементов переходят сами в себя, остальные 4 элемента дают две пары взаимно соответствующих элементов.
Пример такого ассоциативного ЛК

0 1 2 3 4 5 6 7 8 9
1 0 3 2 6 7 4 8 9 5
3 2 0 5 8 1 9 4 7 6
4 5 8 9 3 2 1 0 6 7
9 4 6 7 1 8 0 5 3 2
2 3 5 1 9 0 7 6 4 8
7 6 1 0 2 3 8 9 5 4
6 7 4 8 0 9 5 1 2 3
5 8 9 4 7 6 2 3 1 0
8 9 7 6 5 4 3 2 0 1

Соответствие элементов в этом ЛК следующее:

0 <--> 1
2 <--> 2
3 <--> 3
4 <--> 4
5 <--> 5
6 <--> 6
7 <--> 7
8 <--> 9

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Сегодня у нас отличная новость: Demis нашёл в эксперименте по поиску решений с симметрией (4,31,31) две восьмёрки, обладающие данной симметрией.
Вот они голубушки - "симметричные" красавицы

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 3 9 8 6 7
 4 9 8 5 6 2 3 1 7 0
 2 6 1 7 9 8 0 4 5 3
 6 8 5 9 1 7 4 3 0 2
 3 5 4 1 8 9 7 0 2 6
 7 3 6 2 0 1 5 9 4 8
 9 7 3 0 2 4 8 6 1 5
 8 4 9 6 7 0 2 5 3 1
 5 0 7 8 3 6 1 2 9 4

 0 1 2 3 4 5 6 7 8 9
 1 2 0 6 8 9 7 3 5 4
 5 6 4 1 0 2 3 8 9 7
 8 9 7 5 6 3 4 0 1 2
 6 8 5 9 7 1 0 2 4 3
 9 4 1 8 3 6 2 5 7 0
 4 7 3 2 9 0 8 1 6 5
 3 5 6 4 2 7 1 9 0 8
 2 0 9 7 1 8 5 4 3 6
 7 3 8 0 5 4 9 6 2 1

Это 8-ая - 9-ая восьмёрки в нашей БД.
Ах, на очереди юбилейная :)

А с симметрией (4,31,31) у нас теперь три восьмёрки, первая такая восьмёрка найдена давно в эксперименте с псевдоассоциативными ДЛК.
Кстати, эта восьмёрка в предыдущем посте показана.

По данным Белышева восьмёрок с симметрией (4,31,31) всего пять. Значит, нам осталось найти две таких "симметричных" восьмёрки.
Ещё десяточка "симметричная" где-то спряталась :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

О юбилейной восьмёрочке не рассказала :)
Эта восьмёрка с симметрией (4,31,31), найдена Demis в поиске по схеме Белышева, 3 октября с. г.

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 8 9 3 6 7
 6 5 3 9 8 2 7 0 4 1
 2 4 6 8 1 0 5 9 7 3
 5 3 9 2 7 4 1 6 0 8
 7 8 4 6 2 9 3 5 1 0
 8 0 7 1 9 6 4 2 3 5
 4 6 8 5 3 7 0 1 9 2
 9 7 1 0 6 3 2 8 5 4
 3 9 5 7 0 1 8 4 2 6

Итак, в нашей БД на данный момент имеется 10 уникальных восьмёрок. При этом 6 из них найдены в ручном проекте.
Покажу-ка их все вместе, КФ основных ДЛК в первом формате

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 3 9 8 6 7
4 9 8 5 6 2 3 1 7 0
2 6 1 7 9 8 0 4 5 3
6 8 5 9 1 7 4 3 0 2
3 5 4 1 8 9 7 0 2 6
7 3 6 2 0 1 5 9 4 8
9 7 3 0 2 4 8 6 1 5
8 4 9 6 7 0 2 5 3 1
5 0 7 8 3 6 1 2 9 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 7 3 9 6 8
5 7 3 2 1 9 4 8 0 6
3 0 1 8 9 4 5 6 7 2
8 9 4 6 7 1 0 2 5 3
4 8 5 1 3 6 2 0 9 7
7 5 6 0 8 2 9 1 3 4
9 3 7 5 6 0 8 4 2 1
6 4 8 9 2 3 7 5 1 0
2 6 9 7 0 8 1 3 4 5

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 3 6 7
6 5 3 9 8 2 7 0 4 1
2 4 6 8 1 0 5 9 7 3
5 3 9 2 7 4 1 6 0 8
7 8 4 6 2 9 3 5 1 0
8 0 7 1 9 6 4 2 3 5
4 6 8 5 3 7 0 1 9 2
9 7 1 0 6 3 2 8 5 4
3 9 5 7 0 1 8 4 2 6

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 9 8 3 6 7
5 9 7 6 0 1 3 8 2 4
4 7 3 8 1 0 2 6 9 5
3 6 5 1 9 4 7 2 0 8
9 4 8 2 3 6 5 0 7 1
2 3 4 0 7 8 1 9 5 6
6 0 1 9 8 7 4 5 3 2
8 5 6 7 2 3 9 1 4 0
7 8 9 5 6 2 0 4 1 3

0 1 2 3 4 5 6 7 8 9
1 2 0 6 7 9 8 3 4 5
4 6 1 9 5 7 2 8 0 3
7 4 5 8 6 0 3 1 9 2
2 7 3 0 9 6 4 5 1 8
6 8 9 5 2 3 0 4 7 1
9 5 4 1 8 2 7 0 3 6
3 9 7 4 1 8 5 6 2 0
8 0 6 2 3 4 1 9 5 7
5 3 8 7 0 1 9 2 6 4

0 1 2 3 4 5 6 7 8 9
1 2 0 6 8 9 7 3 5 4
5 6 4 1 0 2 3 8 9 7
8 9 7 5 6 3 4 0 1 2
6 8 5 9 7 1 0 2 4 3
9 4 1 8 3 6 2 5 7 0
4 7 3 2 9 0 8 1 6 5
3 5 6 4 2 7 1 9 0 8
2 0 9 7 1 8 5 4 3 6
7 3 8 0 5 4 9 6 2 1

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 4 9 6 7 8
4 9 6 8 2 7 1 3 0 5
6 8 7 4 9 0 5 2 1 3
7 3 5 9 1 8 0 4 6 2
9 4 8 7 6 3 2 1 5 0
3 5 9 1 7 2 8 0 4 6
8 7 4 6 0 9 3 5 2 1
5 0 1 2 3 6 7 8 9 4
2 6 0 5 8 1 4 9 3 7

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 9 8 7 2 1 0 5 6
8 7 6 5 9 0 4 3 2 1
7 3 4 0 8 1 9 5 6 2
5 0 8 7 3 6 2 1 9 4
4 9 1 2 6 3 7 8 0 5
2 6 5 9 1 8 0 4 3 7
9 8 7 6 5 4 3 2 1 0
6 5 0 1 2 7 8 9 4 3

0 1 2 3 4 5 6 7 8 9
1 2 3 4 9 0 5 6 7 8
8 6 7 0 5 4 9 2 3 1
5 8 9 6 2 7 3 0 1 4
9 5 8 7 3 6 2 1 4 0
3 7 4 9 1 8 0 5 2 6
7 4 6 8 0 9 1 3 5 2
6 9 5 2 8 1 7 4 0 3
2 0 1 5 6 3 4 8 9 7
4 3 0 1 7 2 8 9 6 5

0 1 2 3 4 5 6 7 8 9
1 2 3 4 9 0 5 6 7 8
8 7 6 5 0 9 4 3 2 1
4 0 1 7 6 3 2 8 9 5
7 6 4 9 8 1 0 5 3 2
9 8 7 6 5 4 3 2 1 0
2 3 5 0 1 8 9 4 6 7
5 9 8 2 3 6 7 1 0 4
3 4 0 1 2 7 8 9 5 6
6 5 9 8 7 2 1 0 4 3

Здесь лексикографический порядок, видим минимальную и максимальную восьмёрки.

Можно посмотреть на КФ основных ДЛК восьмёрок во втором формате

0 2 4 7 8 9 5 6 3 1
5 1 9 6 3 2 4 8 0 7
6 7 2 9 1 0 8 3 5 4
9 4 0 3 5 7 2 1 6 8
7 0 3 8 4 6 9 2 1 5
2 8 6 0 7 5 1 4 9 3
1 5 8 4 2 3 6 9 7 0
4 3 5 1 9 8 0 7 2 6
3 9 1 5 6 4 7 0 8 2
8 6 7 2 0 1 3 5 4 9

0 2 6 5 8 9 7 4 3 1
3 1 7 8 6 4 9 5 0 2
4 8 2 7 1 0 5 3 9 6
9 6 1 3 5 7 2 0 4 8
5 0 3 9 4 6 8 2 1 7
2 4 8 1 7 5 0 9 6 3
1 7 9 4 2 3 6 8 5 0
6 3 5 0 9 8 1 7 2 4
7 9 4 2 0 1 3 6 8 5
8 5 0 6 3 2 4 1 7 9

0 2 6 9 5 7 8 4 3 1
8 1 5 6 3 2 4 9 0 7
4 5 2 0 8 9 1 3 7 6
7 0 4 3 9 1 2 6 5 8
3 8 9 7 4 6 0 5 1 2
2 4 1 8 7 5 9 0 6 3
1 7 0 4 2 3 6 8 9 5
9 3 8 1 6 4 5 7 2 0
6 9 3 5 1 0 7 2 8 4
5 6 7 2 0 8 3 1 4 9

0 2 8 7 6 4 9 5 3 1
9 1 6 8 2 3 5 4 0 7
8 7 2 6 1 0 4 3 9 5
4 8 1 3 9 7 2 0 5 6
1 3 5 9 4 6 7 8 2 0
2 6 7 0 8 5 1 9 4 3
5 9 3 4 0 1 6 2 7 8
3 4 9 1 5 8 0 7 6 2
6 5 0 2 7 9 3 1 8 4
7 0 4 5 3 2 8 6 1 9

0 3 7 9 6 8 5 2 4 1
7 1 6 5 3 2 9 4 0 8
4 6 2 8 9 7 1 3 5 0
2 8 5 3 1 9 4 0 7 6
1 9 8 0 4 6 7 5 2 3
6 2 3 4 8 5 0 9 1 7
3 5 1 2 7 0 6 8 9 4
8 0 9 1 5 4 3 7 6 2
9 7 4 6 0 3 2 1 8 5
5 4 0 7 2 1 8 6 3 9

0 4 8 2 9 6 7 5 3 1
6 1 3 5 7 4 9 2 0 8
4 9 2 6 1 8 5 3 7 0
2 8 0 3 5 1 4 9 6 7
1 2 6 9 4 7 8 0 5 3
7 3 1 4 2 5 0 8 9 6
3 7 5 8 0 9 6 1 2 4
8 5 9 1 6 0 3 7 4 2
9 6 7 0 3 2 1 4 8 5
5 0 4 7 8 3 2 6 1 9

0 5 7 2 6 9 3 8 4 1
5 1 8 4 3 7 9 0 2 6
4 9 2 8 1 0 7 3 6 5
9 7 6 3 0 8 4 5 1 2
7 2 5 1 4 6 8 9 3 0
2 4 3 6 7 5 0 1 9 8
1 8 0 5 9 2 6 4 7 3
6 3 9 0 8 1 2 7 5 4
3 0 1 9 2 4 5 6 8 7
8 6 4 7 5 3 1 2 0 9

0 6 7 5 3 8 9 4 2 1
9 1 3 6 7 4 2 8 0 5
7 0 2 9 6 1 8 3 5 4
6 5 8 3 1 7 4 0 9 2
3 9 0 7 4 6 5 2 1 8
1 2 6 0 8 5 3 9 4 7
4 8 5 2 0 9 6 1 7 3
8 3 9 4 5 2 1 7 6 0
2 7 4 1 9 3 0 5 8 6
5 4 1 8 2 0 7 6 3 9

0 6 8 4 5 7 3 9 2 1
9 1 6 8 3 2 7 4 0 5
1 8 2 6 9 0 5 3 4 7
6 5 0 3 7 1 4 8 9 2
8 3 1 9 4 6 2 5 7 0
4 2 3 7 8 5 9 0 1 6
7 9 4 2 0 3 6 1 5 8
2 0 9 5 1 4 8 7 6 3
3 7 5 1 2 9 0 6 8 4
5 4 7 0 6 8 1 2 3 9

0 7 5 6 3 2 4 8 9 1
5 1 6 2 9 7 3 4 0 8
4 8 2 7 0 1 9 3 5 6
8 0 4 3 7 9 2 6 1 5
9 2 1 5 4 6 8 0 3 7
3 4 7 1 8 5 0 9 6 2
1 9 8 4 2 3 6 5 7 0
2 6 9 0 5 8 1 7 4 3
6 5 3 9 1 0 7 2 8 4
7 3 0 8 6 4 5 1 2 9

Здесь видно, из каких линеек основные ДЛК восьмёрок.

Вот какими симметриями обладают наши восьмёрочки (программа Белышева avtoizor_2.00)

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 3 9 8 6 7
4 9 8 5 6 2 3 1 7 0
2 6 1 7 9 8 0 4 5 3
6 8 5 9 1 7 4 3 0 2
3 5 4 1 8 9 7 0 2 6
7 3 6 2 0 1 5 9 4 8
9 7 3 0 2 4 8 6 1 5
8 4 9 6 7 0 2 5 3 1
5 0 7 8 3 6 1 2 9 4
(1,1,1): 	1
(4,31,31): 	1

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 7 3 9 6 8
5 7 3 2 1 9 4 8 0 6
3 0 1 8 9 4 5 6 7 2
8 9 4 6 7 1 0 2 5 3
4 8 5 1 3 6 2 0 9 7
7 5 6 0 8 2 9 1 3 4
9 3 7 5 6 0 8 4 2 1
6 4 8 9 2 3 7 5 1 0
2 6 9 7 0 8 1 3 4 5
(1,1,1): 	1

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 3 6 7
6 5 3 9 8 2 7 0 4 1
2 4 6 8 1 0 5 9 7 3
5 3 9 2 7 4 1 6 0 8
7 8 4 6 2 9 3 5 1 0
8 0 7 1 9 6 4 2 3 5
4 6 8 5 3 7 0 1 9 2
9 7 1 0 6 3 2 8 5 4
3 9 5 7 0 1 8 4 2 6
(1,1,1): 	1
(4,31,31): 	1

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 9 8 3 6 7
5 9 7 6 0 1 3 8 2 4
4 7 3 8 1 0 2 6 9 5
3 6 5 1 9 4 7 2 0 8
9 4 8 2 3 6 5 0 7 1
2 3 4 0 7 8 1 9 5 6
6 0 1 9 8 7 4 5 3 2
8 5 6 7 2 3 9 1 4 0
7 8 9 5 6 2 0 4 1 3
(1,1,1): 	1
(4,31,31): 	1

0 1 2 3 4 5 6 7 8 9
1 2 0 6 7 9 8 3 4 5
4 6 1 9 5 7 2 8 0 3
7 4 5 8 6 0 3 1 9 2
2 7 3 0 9 6 4 5 1 8
6 8 9 5 2 3 0 4 7 1
9 5 4 1 8 2 7 0 3 6
3 9 7 4 1 8 5 6 2 0
8 0 6 2 3 4 1 9 5 7
5 3 8 7 0 1 9 2 6 4
(1,1,1): 	1

0 1 2 3 4 5 6 7 8 9
1 2 0 6 8 9 7 3 5 4
5 6 4 1 0 2 3 8 9 7
8 9 7 5 6 3 4 0 1 2
6 8 5 9 7 1 0 2 4 3
9 4 1 8 3 6 2 5 7 0
4 7 3 2 9 0 8 1 6 5
3 5 6 4 2 7 1 9 0 8
2 0 9 7 1 8 5 4 3 6
7 3 8 0 5 4 9 6 2 1
(1,1,1): 	1
(4,31,31): 	1

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 4 9 6 7 8
4 9 6 8 2 7 1 3 0 5
6 8 7 4 9 0 5 2 1 3
7 3 5 9 1 8 0 4 6 2
9 4 8 7 6 3 2 1 5 0
3 5 9 1 7 2 8 0 4 6
8 7 4 6 0 9 3 5 2 1
5 0 1 2 3 6 7 8 9 4
2 6 0 5 8 1 4 9 3 7
(1,1,1): 	1
(1,31,31): 	1

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 9 8 7 2 1 0 5 6
8 7 6 5 9 0 4 3 2 1
7 3 4 0 8 1 9 5 6 2
5 0 8 7 3 6 2 1 9 4
4 9 1 2 6 3 7 8 0 5
2 6 5 9 1 8 0 4 3 7
9 8 7 6 5 4 3 2 1 0
6 5 0 1 2 7 8 9 4 3
(1,1,1): 	1
(1,31,31): 	3
(16,41,41)R: 	1
(16,42,42)R: 	1
(31,41,42)R: 	2
(16,26,26)C: 	1
(16,39,39)C: 	1
(26,31,39)C: 	2
(16,26,26)T: 	1
(16,30,30)T: 	1
(26,30,31)T: 	2
(17,18,24)RT: 	1
(17,28,39)RT: 	1
(18,28,32)RT: 	1
(24,32,39)RT: 	1
(17,18,24)CT: 	1
(17,28,39)CT: 	1
(18,28,32)CT: 	1
(24,32,39)CT: 	1

0 1 2 3 4 5 6 7 8 9
1 2 3 4 9 0 5 6 7 8
8 6 7 0 5 4 9 2 3 1
5 8 9 6 2 7 3 0 1 4
9 5 8 7 3 6 2 1 4 0
3 7 4 9 1 8 0 5 2 6
7 4 6 8 0 9 1 3 5 2
6 9 5 2 8 1 7 4 0 3
2 0 1 5 6 3 4 8 9 7
4 3 0 1 7 2 8 9 6 5
(1,1,1): 	1
(1,31,31): 	1

0 1 2 3 4 5 6 7 8 9
1 2 3 4 9 0 5 6 7 8
8 7 6 5 0 9 4 3 2 1
4 0 1 7 6 3 2 8 9 5
7 6 4 9 8 1 0 5 3 2
9 8 7 6 5 4 3 2 1 0
2 3 5 0 1 8 9 4 6 7
5 9 8 2 3 6 7 1 0 4
3 4 0 1 2 7 8 9 5 6
6 5 9 8 7 2 1 0 4 3
(1,1,1): 	1
(1,31,31): 	3
(16,41,41)R: 	1
(16,42,42)R: 	1
(31,41,42)R: 	2

Замыкание покажу от 6 восьмёрок [без восьмёрок с симметрией (1,31,31), потому что для этих восьмёрок очень долго будет строиться Замыкание]

Найдено марьяжных КФ:
count[1] = 66
count[2] = 3
count[8] = 6
Всего: 75
Найдено соквадратов: 120
КФ соквадратов: 75

Ждём новых восьмёрок! Они не часто появляются, крупные жемчужины. Крупнее пока есть в нашей БД только две десятки.

Вот и прибыла новая восьмёрочка!
Найдена в автономном подпроекте, в эксперименте по поиску решений с симметрией (4,31,31) по алгоритму Белышева.
Нашёл Tomas Brada.
Смотрите сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=57&postid=606#606

0 5 4 9 8 3 7 2 6 1
8 1 9 4 6 7 3 5 0 2
4 0 2 8 7 1 5 3 9 6
9 6 1 3 2 0 4 8 5 7
5 7 0 6 4 8 2 9 1 3
6 4 3 7 9 5 1 0 2 8
1 9 8 5 3 2 6 4 7 0
2 8 6 0 1 4 9 7 3 5
3 2 7 1 5 9 0 6 8 4
7 3 5 2 0 6 8 1 4 9

Это 11-ая восьмёрка в нашей БД.

Кстати, эта восьмёрка порождает интересную конфигурацию. Позже нарисую.

Изобразила конфигурацию, порождаемую этой восьмёркой



Восьмёрка с аппендиксом! Только восьмёрка не полновесная, так как "симметричная". Не уникальные ОДЛК на иллюстрации отмечены.
Аппендикс - квадрат В.
Кажется, таких восьмёрок в нашей БД ещё не было.

С этой конфигурацией я сделала ошибки.

1. переставила названия квадратов sq1 и sq3 и забыла переставить сами квадраты;
2. не увидела сразу четвёрку, происходящую от квадрата В.

Всё по пословице: поспешишь - людей насмешишь :)

Новая иллюстрация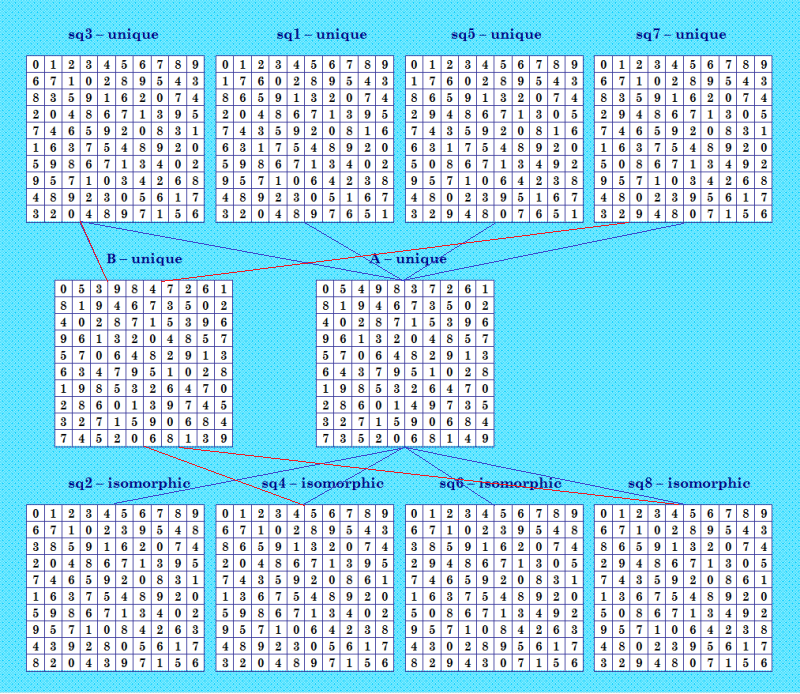



Теперь вроде всё на месте.
И уже нет восьмёрки с аппендиксом, а есть другая конфигурация - без названия.
В любом случае, Tomas Brada нашёл уникальную конфигурацию с восьмёркой и четвёркой. Да ещё с "симметричной" восьмёркой.

Хе-е, а четвёрка тоже "симметричная" - с симметрией (4,31,31), как и восьмёрка

Поиск чистых симметрий

Введено ЛК: 1
Введите код симметрии:
all
Квадратов с симметрией (4,31,31) найдено: 1 они записаны в файл symm_4_31_31.txt

Время поиска: 0.015 сек