Первые группы из шести пар ортогональных ДЛК (кратко называемые "шестёрки") были найдены более двух лет назад в нашем с Белышевым эксперименте с семейством ЛК блочной структуры №1.
Этот эксперимент подробно описан Белышевым на форуме Math Help Planet
http://mathhelpplanet.com/viewtopic.php?p=276832#p276832
http://mathhelpplanet.com/viewtopic.php?p=276863#p276863
http://mathhelpplanet.com/viewtopic.php?p=277544#p277544

Было найдено в этом эксперименте 6 шестёрок, вот они (КФ основного ДЛК в первом формате)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
2 3 4 0 8 1 9 5 6 7
9 8 7 6 5 4 3 2 1 0
8 7 6 5 9 0 4 3 2 1
6 4 9 1 2 7 8 0 5 3
3 5 0 8 7 2 1 9 4 6
5 0 1 7 6 3 2 8 9 4
7 6 5 9 1 8 0 4 3 2
4 9 8 2 3 6 7 1 0 5

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 9 1 7 2 8 0 5 6
6 5 0 8 2 7 1 9 4 3
7 6 5 0 1 8 9 4 3 2
9 8 7 6 5 4 3 2 1 0
5 9 1 2 6 3 7 8 0 4
8 7 6 5 9 0 4 3 2 1
2 3 4 9 8 1 0 5 6 7
4 0 8 7 3 6 2 1 9 5

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 9 1 7 2 8 0 5 6
6 5 0 8 2 7 1 9 4 3
9 8 7 6 5 4 3 2 1 0
5 0 1 7 6 3 2 8 9 4
8 7 6 5 9 0 4 3 2 1
4 9 8 2 3 6 7 1 0 5
7 3 5 9 8 1 0 4 6 2
2 6 4 0 1 8 9 5 3 7

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 9 8 2 7 1 0 5 6
6 5 0 1 7 2 8 9 4 3
9 8 7 6 5 4 3 2 1 0
4 0 8 2 6 3 7 1 9 5
8 7 6 5 9 0 4 3 2 1
5 9 1 7 3 6 2 8 0 4
7 3 4 9 1 8 0 5 6 2
2 6 5 0 8 1 9 4 3 7

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
4 0 8 2 3 6 7 1 9 5
9 8 7 6 5 4 3 2 1 0
3 5 9 8 7 2 1 0 4 6
2 3 5 9 8 1 0 4 6 7
7 6 4 0 1 8 9 5 3 2
8 7 6 5 9 0 4 3 2 1
6 4 0 1 2 7 8 9 5 3
5 9 1 7 6 3 2 8 0 4

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
5 0 1 2 6 3 7 8 9 4
7 6 5 9 1 8 0 4 3 2
3 5 0 8 7 2 1 9 4 6
9 8 7 6 5 4 3 2 1 0
6 4 9 1 2 7 8 0 5 3
8 7 6 5 9 0 4 3 2 1
2 3 4 0 8 1 9 5 6 7
4 9 8 7 3 6 2 1 0 5

Все 6 основных ДЛК этих шестёрок симметричные по Гергели/Брауну. Более того, они являются "браунами".
КФ основных ДЛК этих шестёрок во втором формате принадлежат линейке № 6.
Все эти шестёрки не полновесные, каждая шестёрка даёт только 4 уникальные КФ ОДЛК. То есть среди шести ортогональных соквадратов каждой шестёрки есть три не уникальных (изоморфных).
Вот такие шесть шестёрок мы имели в БД. Прошло два года, поиски продолжались, а новые шестёрки не появлялись.
Наконец, 9 апреля с. г. я нашла в своём эксперименте с псевдоассоциативными ДЛК, выполняемом в ручном режиме, седьмую шестёрку

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 6 8 9 7 5
2 6 9 5 3 8 4 0 1 7
6 4 8 7 5 3 1 2 9 0
7 9 5 0 8 4 2 1 3 6
4 0 7 6 2 1 9 8 5 3
3 7 1 8 6 9 5 4 0 2
9 5 6 1 7 2 0 3 4 8
8 3 4 2 9 0 7 5 6 1
5 8 0 9 1 7 3 6 2 4

Эта шестёрка полновесная, она даёт 7 уникальных КФ ОДЛК.
КФ основного ДЛК второго формата принадлежит линейке № 18

0 3 5 2 8 6 7 9 4 1
3 1 7 6 5 9 2 8 0 4
9 4 2 0 6 1 5 3 7 8
2 8 6 3 9 7 4 0 1 5
6 7 8 9 4 2 1 5 3 0
8 2 1 4 7 5 0 6 9 3
7 9 0 8 3 4 6 1 5 2
4 5 9 1 0 3 8 7 2 6
1 6 3 5 2 0 9 4 8 7
5 0 4 7 1 8 3 2 6 9

Это пока все шестёрки, имеющиеся в нашей БД. Будут ли ещё? Думаю, что будут.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Как насчёт шестёрок-близняшек?

Программа Harry White поворот блоков, применённая к основному ДЛК моей шестёрки, не дала новых решений.
Значит, надо пробовать более сложные перестановки, как, например, здесь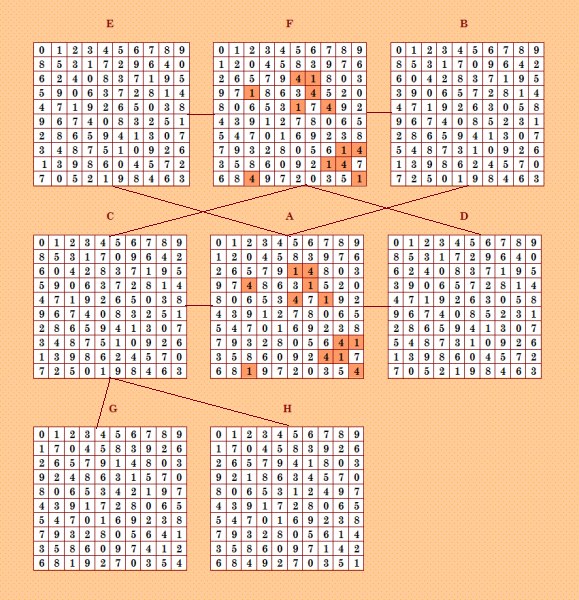



Кстати, у Беляева есть новая программа lat05, которая делает такие перестановки.
Я пробовала её покрутить для основного ДЛК моей шестёрки, но... у меня почему-то программа быстро зациклилась, то есть она начала повторять одни и те же квадраты. Поэтому прервала программу.

А подобные перестановки весьма интересные! Как видим на примере, показанном на иллюстрации, в реальности такие перестановки встречаются.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Изобразила свою шестёрку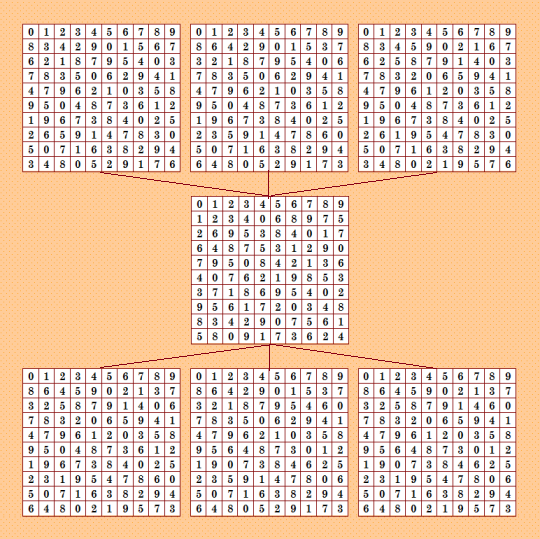



Такая простенькая конфигурация.
Все шесть ортогональных соквадратов несмотря на свою похожесть уникальны.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это цитата

Наконец, 9 апреля с. г. я нашла в своём эксперименте с псевдоассоциативными ДЛК, выполняемом в ручном режиме, седьмую шестёрку

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 6 8 9 7 5
2 6 9 5 3 8 4 0 1 7
6 4 8 7 5 3 1 2 9 0
7 9 5 0 8 4 2 1 3 6
4 0 7 6 2 1 9 8 5 3
3 7 1 8 6 9 5 4 0 2
9 5 6 1 7 2 0 3 4 8
8 3 4 2 9 0 7 5 6 1
5 8 0 9 1 7 3 6 2 4

Эта шестёрка полновесная, она даёт 7 уникальных КФ ОДЛК.

Долго шла я до восьмой шестёрочки, больше трёх месяцев.
Но вот она попалась, голубушка :) в том же самом эксперименте

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 9 8 3 6 7
 7 6 3 5 9 0 1 8 4 2
 2 3 8 1 0 4 7 9 5 6
 5 0 1 8 7 2 9 6 3 4
 8 4 9 7 1 6 5 0 2 3
 9 8 6 0 3 1 4 2 7 5
 6 7 4 9 8 3 2 5 0 1
 4 5 7 2 6 8 3 1 9 0
 3 9 5 6 2 7 0 4 1 8

Эта шестёрка не полновесная, даёт 4 уникальные КФ ОДЛК.
И основной ДЛК шестёрки имеет код симметрии (4,31,31)! Супер!
Семейство симметрии с кодом (4,31,31) пополнилось шестёркой.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нарисовала нашу восьмую шестёрку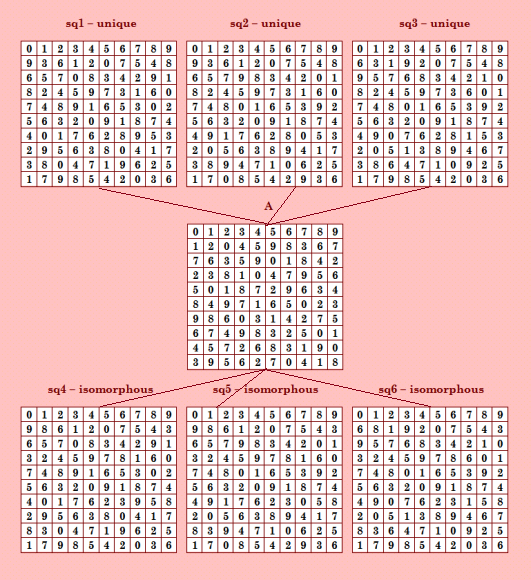



Простенькая конфигурация. Среди ортогональных соквадратов sqi три уникальных и три изоморфных.

Более двух лет прошло с эксперимента, в котором были найдены шесть первых шестёрок. И вот пока только две новые шестёрки найдены.
При этом обе они найдены в ручном проекте, в эксперименте с псевдоассоциативными ДЛК.
В BOINC-проектах шестёрок пока не найдено.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот и "симметричная" шестёрочка попалась в эксперименте по поиску решений с симметрией (4,31,31) (нашёл Demis)

0 2 3 9 6 7 5 8 4 1
6 1 5 8 9 3 7 4 0 2
9 6 2 7 1 8 0 3 5 4
7 0 8 3 2 9 4 6 1 5
3 5 0 6 4 2 1 9 7 8
1 4 9 2 7 5 8 0 3 6
2 8 7 5 0 4 6 1 9 3
5 3 6 4 8 1 9 7 2 0
4 9 1 0 3 6 2 5 8 7
8 7 4 1 5 0 3 2 6 9

Девятая шестёрочка в нашей БД!
Впереди юбилейная :)

Предыдущая шестёрка тоже с симметрией (4,31,31), но найдена она в другом эксперименте - с псевдоассоциативными ДЛК.
В эксперименте по поиску решений с симметрией (4,31,31) эта шестёрка тоже уже найдена Demis, не далее как вчера.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Юбилейная шестёрка запаздывает :)

Сейчас пристально рассматриваю 9 шестёрок, имеющихся в нашей БД.
Не только рассматриваю, выполняется у меня эксперимент вокруг крупных жемчужин.
Может быть, позже расскажу о результатах этого эксперимента.

Итак, 6 шестёрок-браунов были найдены в нашем с Белышевым эксперименте очень давно. Все эти шестёрки из линейки №6.
Три новые шестёрки найдены в ручном проекте.
Первая - полновесная, не "симметричная" - найдена мной в эксперименте с псевдоассоциативными ДЛК.
Две другие - с симметрией (4,31,31) - найдены мной и Demis (по одной).
Из 9 шестёрок только одна не "симметричная".

Крупные и очень редкие жемчужины - шестёрки!

Покажу три шестёрки, найденные в ручном проекте, и Замыкание от них (Замыкание от шестёрок-браунов строится очень долго).

0 3 5 2 8 6 7 9 4 1
3 1 7 6 5 9 2 8 0 4
9 4 2 0 6 1 5 3 7 8
2 8 6 3 9 7 4 0 1 5
6 7 8 9 4 2 1 5 3 0
8 2 1 4 7 5 0 6 9 3
7 9 0 8 3 4 6 1 5 2
4 5 9 1 0 3 8 7 2 6
1 6 3 5 2 0 9 4 8 7
5 0 4 7 1 8 3 2 6 9

0 2 3 8 9 4 7 5 6 1
9 1 7 6 3 8 2 4 0 5
8 6 2 7 5 1 9 3 4 0
7 0 5 3 6 9 4 2 1 8
1 3 0 5 4 6 8 9 2 7
3 9 1 4 8 5 0 6 7 2
4 5 8 2 1 7 6 0 9 3
6 8 9 1 2 0 3 7 5 4
2 7 4 9 0 3 5 1 8 6
5 4 6 0 7 2 1 8 3 9
 
0 2 3 9 6 7 5 8 4 1
6 1 5 8 9 3 7 4 0 2
9 6 2 7 1 8 0 3 5 4
7 0 8 3 2 9 4 6 1 5
3 5 0 6 4 2 1 9 7 8
1 4 9 2 7 5 8 0 3 6
2 8 7 5 0 4 6 1 9 3
5 3 6 4 8 1 9 7 2 0
4 9 1 0 3 6 2 5 8 7
8 7 4 1 5 0 3 2 6 9

Замыкание

Найдено марьяжных КФ:
count[1] = 22
count[2] = 1
count[6] = 3
Всего: 26
Найдено соквадратов: 42
КФ соквадратов: 26

Посмотрим на ортогональные соквадраты шестёрки с точки зрения узорчатости.

Цитата

Изобразила свою шестёрку



Такая простенькая конфигурация.
Все шесть ортогональных соквадратов несмотря на свою похожесть уникальны.

Здесь основной ДЛК шестёрки (он в центре) в первом формате. Шестёрка полновесная, порождает конфигурацию из 7 уникальных ОДЛК.
Ортогональные соквадраты узорчатые!
Сейчас сделаю эту же конфигурацию, но от основного ДЛК во втором формате.

Новая иллюстрация готова



Узорчатость ортогональных соквадратов очень интересная! Перестановки элементов совершенно одинаковые, но на основе разных ДЛК.
Эти разные ДЛК тоже по-своему узорчатые. Узорчатость в квадрате :)

Юбилейная, 10-ая шестёрка была найдена XAVER в одном из мини-экспериментов мультисимметрия 3 августа 2020 г. и хранится у него.

11-ая шестёрка найдена XAVER в одном из мини-экспериментов мультисимметрия 17 августа 2020 г. и хранится у него.

У меня тоже, конечно, хранятся эти шестёрки.

Сейчас проверяла БД ручного проекта с помощью программы сортировки, сделанной форумчанином на форуме Math Help Planet.
Ревизия, так сказать :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Показываю 10-ю и 11-ю шестёрки, найденные XAVER в эксперименте мультисимметрия в августе 2020 г.

№10

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 9 8 6 3 7
 6 7 9 0 3 1 5 8 4 2
 4 6 7 5 0 3 1 2 9 8
 8 5 1 9 6 0 2 4 7 3
 3 9 4 2 7 8 0 1 5 6
 5 3 8 6 1 4 7 9 2 0
 9 8 5 7 2 6 4 3 0 1
 7 4 6 8 9 2 3 0 1 5
 2 0 3 1 8 7 9 5 6 4

№11

0 1 2 3 4 5 6 7 8 9
1 2 3 0 6 9 4 8 7 5
3 5 6 9 8 7 1 2 4 0
7 8 1 5 2 4 3 0 9 6
2 3 7 1 9 8 0 6 5 4
9 6 4 8 1 3 7 5 0 2
4 7 5 6 0 2 8 9 3 1
8 9 0 7 5 1 2 4 6 3
6 4 9 2 7 0 5 3 1 8
5 0 8 4 3 6 9 1 2 7

Обе шестёрки полновесные, дают 7 уникальных КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg