Статьи о латинских квадратах
Message boards :
Science :
Статьи о латинских квадратах
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Здесь я попытаюсь собрать статьи о латинских квадратах, которые разбросаны по всем темам Статьи коллеги Алексея Чернова 1. "Метод Гергели построения диагональных латинских квадратов" http://alex-black.ru/article.php?content=123 2. Совершенные латинские квадраты http://alex-black.ru/article.php?content=122 3. ОДЛК. Метод Пелегрино-Ланселотти http://alex-black.ru/article.php?content=124 4. ОДЛК. Метод Линдера http://alex-black.ru/article.php?content=125 5. ОДЛК. Метод Ли Жу http://alex-black.ru/article.php?content=126 Статьи очень ценные, так как к ним приложены программные реализации описанных алгоритмов. Очень рекомендую! Статьи, на которые ссылается Чернов 1. Ervin Gergely. A Simple Method for Constructing Doubly Diagonalized Latin Squares. 1972. https://yadi.sk/i/reXszmOC3RFUQC (Яндекс.Диск) 2. L.Zhu. Orthogonal Diagonal Latin Squares of order fourteen. 1982 https://yadi.sk/i/vXQhLKYY3RFUYi (Яндекс.Диск) 3. K.Heinrich, K.Kim and V.K.Prasanna Kumar, Perfect latin squares, Discrete Applied Mathematics 37138 (1992) 281-286. 4. Consolato Pellegrino and Paola Lancellotti. A New Construction Of Doubly Diagonal Orthogonal Latin Squares. 5. Charles C.Linder. Construction Of Doubly Diagonalized Orthogonal Latin Squares. 1972 Первые две статьи загрузила на Яндекс.Диск. На статью Гергели я тоже часто ссылалась. Не помню, выкладывала ли её раньше. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Эту статью представлю скриншотом, ссылку не нашла  My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё англоязычные статьи 1. "Mutually Orthogonal Latin Squares (MOLS)", авторы R. Julian R. Abel, Charles J. Colbourn, Jeffrey H. Dinitz. https://yadi.sk/i/x1w4tkQx3MsvHw (Яндекс.Диск) 2. Ian M. Wanless. "Transversals in Latin squares". http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.244.6006&rank=17&q=Ian Wanless&osm=&ossid= 3. Miguel Angel Amela. "Franklinian Diagonal Latin Squares" https://yadi.sk/i/4yQLEKfB3Qsjg2 (Яндекс.Диск) 4. “Completion of the Spectrum of Orthogonal Diagonal Latin Squares” (J. W. Brown и другие). 5. B. D. McKay, A. Meynert and W. Myrvold (2007), Small latin squares, quasigroups and loops, Journal of Combinatorial Designs, 15, 2, 98–119. Буду добавлять, как вспомню другие статьи. Добавлено 6. D. T. Todorov. “Three Mutually Orthogonal Latin Squares of Order 14” (Ars Combinatoria, 20 (1985), pp. 45-48) Статья выложена на моём сайте http://www.natalimak1.narod.ru/mk/mols14.pdf My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Алексей Белышев нашёл статью со всеми классами SOLS 10-го порядка Вот здесь перечислены все 121642 представителя классов RC-paratopism SOLS10 (осторожно, почти 12 МБ). Из этого массива решений он получил 30534 SODLS, из них существенно различных 30502. Смотрите сообщение об этом здесь http://forum.boinc.ru/default.aspx?g=posts&m=87090#post87090 PS. К сожалению, эта ссылка сейчас недействительна. Я где-то цитировала данное сообщение Белышева. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Мои статьи 1. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin squares (MOLS) http://www.natalimak1.narod.ru/grolk.htm 2. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin Squares (MOLS) Часть II http://www.natalimak1.narod.ru/grolk1.htm 3. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin Squares (MOLS) Часть III http://www.natalimak1.narod.ru/grolk2.htm 4. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ НЕЧЁТНОГО ПОРЯДКА или НОВЫЕ АСПЕКТЫ МЕТОДА ЛАТИНСКИХ КВАДРАТОВ Часть VII http://www.natalimak1.narod.ru/grolk3.htm 5. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ НЕЧЁТНОГО ПОРЯДКА или НОВЫЕ АСПЕКТЫ МЕТОДА ЛАТИНСКИХ КВАДРАТОВ Часть VIII http://www.natalimak1.narod.ru/grolk4.htm 6. ОРТОГОНАЛЬНЫЕ ЛАТИНСКИЕ КВАДРАТЫ ДЕСЯТОГО ПОРЯДКА http://www.natalimak1.narod.ru/aspekty7.htm 7. МЕТОДЫ ПОСТРОЕНИЯ ЛАТИНСКИХ КВАДРАТОВ http://www.natalimak1.narod.ru/metod2.htm 8. ЕЩЁ ДВА МЕТОДА ПОСТРОЕНИЯ ЛАТИНСКИХ КВАДРАТОВ http://www.natalimak1.narod.ru/metod3.htm 9. ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ http://www.natalimak1.narod.ru/dlk.htm 10. ПОСТРОЕНИЕ ПАР ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ МЕТОДОМ СОСТАВНЫХ КВАДРАТОВ http://www.natalimak1.narod.ru/olk.htm 11. ПОСТРОЕНИЕ ПАР ОРТОГОНАЛЬНЫХ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ МЕТОДОМ СОСТАВНЫХ КВАДРАТОВ http://www.natalimak1.narod.ru/aspekty5.htm 12. МЕТОД ПОСТРОЕНИЯ ПАР ОЛК ПОРЯДКА n = 6k + 4 http://www.natalimak1.narod.ru/metod.htm 13. ГРУППЫ MOLS ПЯТНАДЦАТОГО ПОРЯДКА http://www.natalimak1.narod.ru/mols15.htm 14. О ГРУППАХ MOLS ВОСЕМНАДЦАТОГО ПОРЯДКА http://www.natalimak1.narod.ru/mols18.htm Буду добавлять в этот список. Но отмечу, что мои статьи можно посмотреть на сайте; список статей на странице http://www.klassikpoez.narod.ru/glavnaja.htm My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Недавно мне прислал свои "Записки о латинских квадратах" коллега Сергей Беляев. Я только немножко пока почитала, мало времени. Сергей разрешил выложить "Записки" для всех. Это он сам загрузил на Яндекс.Диск и прислал мне ссылку https://yadi.sk/d/ZmFQ-Vcw3RDX2k Правда, он предупредил, что "Записки" черновые, будут дорабатываться и соответственно изменяться. Но и с черновым вариантом интересно познакомиться. Особо ценным считаю в "Записках" наличие кодов процедур по различным задачам, связанным с ЛК. PS. Ссылка на статью Беляева изменилась https://yadi.sk/i/gdiclXCZgPH-ug (изменено 3 августа 2019 г.) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сначала первоисточник: D. T. Todorov.Three Mutually Orthogonal Latin Squares of Order 14 (Ars Combinatoria, 20 (1985), pp. 45-48). Статья была выложена ещё в то время, когда я пыталась в ней разобраться (проверила, статья там лежит) http://www.natalimak1.narod.ru/mk/mols14.pdf Теперь моя статья, написанная по данной статье Тодорова: ЗАДАЧА О СОСТАВЛЕНИИ ТРЁХ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ ЧЕТЫРНАДЦАТОГО ПОРЯДКА http://www.natalimak1.narod.ru/zadacha.htm Эта статья написана в 2009 году. Тогда я так и не поняла метод построения этой группы ортогональных пар ЛК 14-го порядка. Уже позже узнала, что метод основан на квази-разностных матрицах. Суть этого метода мне объяснили на форуме dxdy.ru После я написала несколько статей о квази-разностных матрицах и применении их к построению групп ортогональных пар ЛК. Интересно в статье описаны мои попытки найти хотя бы пару ортогональных ЛК 14-го порядка. Как только я ни сочиняла ЛК 14-го порядка: и по схеме Агриппы, и по придуманной мной схеме. На рис. 6 изображён ЛК 10-го порядка, построенный по моей схеме 0 2 4 6 8 9 3 5 7 1 8 1 3 5 7 0 9 4 6 2 7 0 2 4 6 8 1 9 5 3 6 8 1 3 5 7 0 2 9 4 9 7 0 2 4 6 8 1 3 5 4 9 8 1 3 5 7 0 2 6 3 5 9 0 2 4 6 8 1 7 2 4 6 9 1 3 5 7 0 8 1 3 5 7 9 2 4 6 8 0 5 6 7 8 0 1 2 3 4 9 К этому ЛК я тоже не нашла ортогональный соквадрат. Ну, сейчас программа Беляева с этим справляется элементарно, протокол работы программы Name:a.txt 1 - only the diagonal Max=1000 1 192 192 212 192 192 116 192 192 212 116 :1808 sq=324 67 69 71 73 cm=73 cmm=73 END Не хилый квадратик, 1808 трансверсалей! И 324 ортогональных соквадрата. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот одна из статей о построении по квази-разностной матрице ГРУППЫ MOLS ПЯТНАДЦАТОГО ПОРЯДКА http://www.natalimak1.narod.ru/mols15.htm В статье я ссылаюсь на книгу “Handbook of Combinatorial Designs” (издание 2007 г.), из которой взята квази-разностная матрица для группы MOLS из 4-х ЛК 15-го порядка. Квази-разностная матрица показана в статье на рис. 4, а на рис. 5 - 8 показаны 4 взаимно ортогональных ЛК 15-го порядка, построенные по данной квази-разностной матрице. Копирую эту интересную группу MOLS 1 7 12 10 9 3 15 6 5 13 4 11 14 2 8 3 2 8 13 11 10 4 15 7 6 14 5 12 1 9 2 4 3 9 14 12 11 5 15 8 7 1 6 13 10 14 3 5 4 10 1 13 12 6 15 9 8 2 7 11 8 1 4 6 5 11 2 14 13 7 15 10 9 3 12 4 9 2 5 7 6 12 3 1 14 8 15 11 10 13 11 5 10 3 6 8 7 13 4 2 1 9 15 12 14 13 12 6 11 4 7 9 8 14 5 3 2 10 15 1 15 14 13 7 12 5 8 10 9 1 6 4 3 11 2 12 15 1 14 8 13 6 9 11 10 2 7 5 4 3 5 13 15 2 1 9 14 7 10 12 11 3 8 6 4 7 6 14 15 3 2 10 1 8 11 13 12 4 9 5 10 8 7 1 15 4 3 11 2 9 12 14 13 5 6 6 11 9 8 2 15 5 4 12 3 10 13 1 14 7 9 10 11 12 13 14 1 2 3 4 5 6 7 8 15 1 11 8 3 6 12 9 4 13 15 5 10 2 7 14 8 2 12 9 4 7 13 10 5 14 15 6 11 3 1 4 9 3 13 10 5 8 14 11 6 1 15 7 12 2 13 5 10 4 14 11 6 9 1 12 7 2 15 8 3 9 14 6 11 5 1 12 7 10 2 13 8 3 15 4 15 10 1 7 12 6 2 13 8 11 3 14 9 4 5 5 15 11 2 8 13 7 3 14 9 12 4 1 10 6 11 6 15 12 3 9 14 8 4 1 10 13 5 2 7 3 12 7 15 13 4 10 1 9 5 2 11 14 6 8 7 4 13 8 15 14 5 11 2 10 6 3 12 1 9 2 8 5 14 9 15 1 6 12 3 11 7 4 13 10 14 3 9 6 1 10 15 2 7 13 4 12 8 5 11 6 1 4 10 7 2 11 15 3 8 14 5 13 9 12 10 7 2 5 11 8 3 12 15 4 9 1 6 14 13 12 13 14 1 2 3 4 5 6 7 8 9 10 11 15 1 9 7 13 3 2 12 10 6 11 14 4 15 8 5 9 2 10 8 14 4 3 13 11 7 12 1 5 15 6 15 10 3 11 9 1 5 4 14 12 8 13 2 6 7 7 15 11 4 12 10 2 6 5 1 13 9 14 3 8 4 8 15 12 5 13 11 3 7 6 2 14 10 1 9 2 5 9 15 13 6 14 12 4 8 7 3 1 11 10 12 3 6 10 15 14 7 1 13 5 9 8 4 2 11 3 13 4 7 11 15 1 8 2 14 6 10 9 5 12 6 4 14 5 8 12 15 2 9 3 1 7 11 10 13 11 7 5 1 6 9 13 15 3 10 4 2 8 12 14 13 12 8 6 2 7 10 14 15 4 11 5 3 9 1 10 14 13 9 7 3 8 11 1 15 5 12 6 4 2 5 11 1 14 10 8 4 9 12 2 15 6 13 7 3 8 6 12 2 1 11 9 5 10 13 3 15 7 14 4 14 1 2 3 4 5 6 7 8 9 10 11 12 13 15 1 6 13 7 12 5 8 14 11 4 2 15 10 9 3 10 2 7 14 8 13 6 9 1 12 5 3 15 11 4 12 11 3 8 1 9 14 7 10 2 13 6 4 15 5 15 13 12 4 9 2 10 1 8 11 3 14 7 5 6 6 15 14 13 5 10 3 11 2 9 12 4 1 8 7 9 7 15 1 14 6 11 4 12 3 10 13 5 2 8 3 10 8 15 2 1 7 12 5 13 4 11 14 6 9 7 4 11 9 15 3 2 8 13 6 14 5 12 1 10 2 8 5 12 10 15 4 3 9 14 7 1 6 13 11 14 3 9 6 13 11 15 5 4 10 1 8 2 7 12 8 1 4 10 7 14 12 15 6 5 11 2 9 3 13 4 9 2 5 11 8 1 13 15 7 6 12 3 10 14 11 5 10 3 6 12 9 2 14 15 8 7 13 4 1 5 12 6 11 4 7 13 10 3 1 15 9 8 14 2 13 14 1 2 3 4 5 6 7 8 9 10 11 12 15 Замечание: ЛК записаны в нетрадиционной форме, для перехода в традиционную форму надо уменьшить все элементы ЛК на единицу. У этой статьи есть интересное продолжение, где я превращаю эту группу MOLS 15-го порядка в группу MODLS, используя один известный алгоритм. Далее представлю эту статью. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ОРТОГОНАЛЬНЫЕ ДИАГОНАЛЬНЫЕ ЛАТИНСКИЕ КВАДРАТЫ http://www.natalimak1.narod.ru/diagon.htm В этой статье сначала строится пара ОДЛК 14-го порядка по статье ORTOGONAL DIAGONAL LATIN SQUARES OF ORDER FOURTEEN (L. Zhu, 1982 г.) (статья выложена на Яндекс.Диск выше) В этом построении тоже используется квази-разностная матрица. Затем смотрите пункт ПОСТРОЕНИЕ ГРУППЫ ПОПАРНО ОРТОГОНАЛЬНЫХ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ 15-го ПОРЯДКА Основываясь на методе построения ортогональной пары ДЛК 14-го порядка из статьи L. Zhu, я превращаю известную группу MOLS из 4-х ЛК 15-го порядка в группу MODLS. На рис. 22 - 25 показана полученная группа MODLS. Копирую её 1 7 12 10 9 3 15 8 2 14 11 4 13 5 6 3 2 8 13 11 10 4 9 1 12 5 14 6 7 15 2 4 3 9 14 12 11 10 13 6 1 7 8 15 5 14 3 5 4 10 1 13 11 7 2 8 9 15 6 12 8 1 4 6 5 11 2 12 3 9 10 15 7 13 14 4 9 2 5 7 6 12 13 10 11 15 8 14 1 3 11 5 10 3 6 8 7 14 12 15 9 1 2 4 13 9 10 11 12 13 14 1 15 8 7 6 5 4 3 2 6 11 9 8 2 15 5 7 14 1 13 10 3 12 4 10 8 7 1 15 4 3 6 5 13 14 12 9 2 11 7 6 14 15 3 2 10 5 9 4 12 13 11 8 1 5 13 15 2 1 9 14 4 6 8 3 11 12 10 7 12 15 1 14 8 13 6 3 4 5 7 2 10 11 9 15 14 13 7 12 5 8 2 11 3 4 6 1 9 10 13 12 6 11 4 7 9 1 15 10 2 3 5 14 8 1 11 8 3 6 12 9 14 7 2 10 5 15 13 4 8 2 12 9 4 7 13 1 3 11 6 15 14 5 10 4 9 3 13 10 5 8 2 12 7 15 1 6 11 14 13 5 10 4 14 11 6 3 8 15 2 7 12 1 9 9 14 6 11 5 1 12 4 15 3 8 13 2 10 7 15 10 1 7 12 6 2 5 4 9 14 3 11 8 13 5 15 11 2 8 13 7 6 10 1 4 12 9 14 3 12 13 14 1 2 3 4 15 11 10 9 8 7 6 5 10 7 2 5 11 8 3 13 14 6 1 9 4 15 12 6 1 4 10 7 2 11 12 9 13 5 14 8 3 15 14 3 9 6 1 10 15 11 5 8 12 4 13 7 2 2 8 5 14 9 15 1 10 13 4 7 11 3 12 6 7 4 13 8 15 14 5 9 1 12 3 6 10 2 11 3 12 7 15 13 4 10 8 6 14 11 2 5 9 1 11 6 15 12 3 9 14 7 2 5 13 10 1 4 8 1 9 7 13 3 2 12 5 8 15 4 14 11 6 10 9 2 10 8 14 4 3 6 15 5 1 12 7 11 13 15 10 3 11 9 1 5 7 6 2 13 8 12 14 4 7 15 11 4 12 10 2 8 3 14 9 13 1 5 6 4 8 15 12 5 13 11 9 1 10 14 2 6 7 3 2 5 9 15 13 6 14 10 11 1 3 7 8 4 12 12 3 6 10 15 14 7 11 2 4 8 9 5 13 1 14 1 2 3 4 5 6 15 13 12 11 10 9 8 7 8 6 12 2 1 11 9 4 14 7 15 3 13 10 5 5 11 1 14 10 8 4 3 7 13 6 15 2 12 9 10 14 13 9 7 3 8 2 4 6 12 5 15 1 11 13 12 8 6 2 7 10 1 9 3 5 11 4 15 14 11 7 5 1 6 9 13 14 12 8 2 4 10 3 15 6 4 14 5 8 12 15 13 10 11 7 1 3 9 2 3 13 4 7 11 15 1 12 5 9 10 6 14 2 8 1 6 13 7 12 5 8 3 9 10 15 2 4 11 14 10 2 7 14 8 13 6 4 11 15 3 5 12 1 9 12 11 3 8 1 9 14 5 15 4 6 13 2 10 7 15 13 12 4 9 2 10 6 5 7 14 3 11 8 1 6 15 14 13 5 10 3 7 8 1 4 12 9 2 11 9 7 15 1 14 6 11 8 2 5 13 10 3 12 4 3 10 8 15 2 1 7 9 6 14 11 4 13 5 12 13 14 1 2 3 4 5 15 12 11 10 9 8 7 6 5 12 6 11 4 7 13 2 14 8 9 15 1 3 10 11 5 10 3 6 12 9 1 4 13 7 8 15 14 2 4 9 2 5 11 8 1 14 10 3 12 6 7 15 13 8 1 4 10 7 14 12 13 3 9 2 11 5 6 15 14 3 9 6 13 11 15 12 7 2 8 1 10 4 5 2 8 5 12 10 15 4 11 13 6 1 7 14 9 3 7 4 11 9 15 3 2 10 1 12 5 14 6 13 8 Замечание: ДЛК записаны в нетрадиционной форме, для перехода в традиционную форму надо уменьшить все элементы ДЛК на единицу. Думаю, что ортогональность ДЛК я в момент написания статьи проверила. Можно проверить и сейчас, но для этого надо немного модифицировать программу проверки ортогональности двух заданных ДЛК (у меня сейчас эта программа работает для порядков 9 и 10). А вот с поиском ортогональных ДЛК к приведённым ДЛК 15-го порядка по программе Белышева Ортогон_У меня постигла неудача. Нет, количество диагональных трансверсалей у этих ДЛК не запредельное, но решения долго не находятся. Я вводила каждый из 4-х ДЛК в программу, крутила примерно час, но решений так и не нашла. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот, например, для первого ДЛК группы MODLS 15-го порядка 1 7 12 10 9 3 15 8 2 14 11 4 13 5 6 3 2 8 13 11 10 4 9 1 12 5 14 6 7 15 2 4 3 9 14 12 11 10 13 6 1 7 8 15 5 14 3 5 4 10 1 13 11 7 2 8 9 15 6 12 8 1 4 6 5 11 2 12 3 9 10 15 7 13 14 4 9 2 5 7 6 12 13 10 11 15 8 14 1 3 11 5 10 3 6 8 7 14 12 15 9 1 2 4 13 9 10 11 12 13 14 1 15 8 7 6 5 4 3 2 6 11 9 8 2 15 5 7 14 1 13 10 3 12 4 10 8 7 1 15 4 3 6 5 13 14 12 9 2 11 7 6 14 15 3 2 10 5 9 4 12 13 11 8 1 5 13 15 2 1 9 14 4 6 8 3 11 12 10 7 12 15 1 14 8 13 6 3 4 5 7 2 10 11 9 15 14 13 7 12 5 8 2 11 3 4 6 1 9 10 13 12 6 11 4 7 9 1 15 10 2 3 5 14 8 традиционная форма записи ДЛК 0 6 11 9 8 2 14 7 1 13 10 3 12 4 5 2 1 7 12 10 9 3 8 0 11 4 13 5 6 14 1 3 2 8 13 11 10 9 12 5 0 6 7 14 4 13 2 4 3 9 0 12 10 6 1 7 8 14 5 11 7 0 3 5 4 10 1 11 2 8 9 14 6 12 13 3 8 1 4 6 5 11 12 9 10 14 7 13 0 2 10 4 9 2 5 7 6 13 11 14 8 0 1 3 12 8 9 10 11 12 13 0 14 7 6 5 4 3 2 1 5 10 8 7 1 14 4 6 13 0 12 9 2 11 3 9 7 6 0 14 3 2 5 4 12 13 11 8 1 10 6 5 13 14 2 1 9 4 8 3 11 12 10 7 0 4 12 14 1 0 8 13 3 5 7 2 10 11 9 6 11 14 0 13 7 12 5 2 3 4 6 1 9 10 8 14 13 12 6 11 4 7 1 10 2 3 5 0 8 9 12 11 5 10 3 6 8 0 14 9 1 2 4 13 7 перекодировано в 15-ричную систему 0 6 B 9 8 2 E 7 1 D A 3 C 4 5 2 1 7 C A 9 3 8 0 B 4 D 5 6 E 1 3 2 8 D B A 9 C 5 0 6 7 E 4 D 2 4 3 9 0 C A 6 1 7 8 E 5 B 7 0 3 5 4 A 1 B 2 8 9 E 6 C D 3 8 1 4 6 5 B C 9 A E 7 D 0 2 A 4 9 2 5 7 6 D B E 8 0 1 3 C 8 9 A B C D 0 E 7 6 5 4 3 2 1 5 A 8 7 1 E 4 6 D 0 C 9 2 B 3 9 7 6 0 E 3 2 5 4 C D B 8 1 A 6 5 D E 2 1 9 4 8 3 B C A 7 0 4 C E 1 0 8 D 3 5 7 2 A B 9 6 B E 0 D 7 C 5 2 3 4 6 1 9 A 8 E D C 6 B 4 7 1 A 2 3 5 0 8 9 C B 5 A 3 6 8 0 E 9 1 2 4 D 7 Запустила программу Белышева Ортогон_У Проверка ДЛК15 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 306605 Соквадратов: 0 Время в сек: 30 20174 8165 3125 1091 202 89 19 Диагональных трансверсалей много - 306605. Но есть ли другие ортогональные ДЛК, кроме трёх известных? Интересный вопрос, но найти ответ сложно. PS. Покрутила 4 часа, бесполезно... Проверка ДЛК15 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 306605 Соквадратов: 0 Время в сек: 14705 20174 8165 3125 899 6 56 1 4 1 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сергей Беляев написал на форуме boinc.ru После длительного перерыва опять вернулся к квадратам. Возможно и не в тему - решайте сами. Как я понимаю, выложена статья "Латинские квадраты" (выше я давала ссылку на предварительный вариант этой статьи) и программа Lat05. Я пока ничего не смотрела. Ссылки в цитируемом сообщении. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Выкладываю первую часть своей статьи "Новый алгоритм поиска ОДЛК" https://cloud.mail.ru/public/6iPV/mAXRhFuEs В первой части статьи подводятся итоги большого пути. Показывается предыстория возникновения нового алгоритма. Статья не претендует на научные исследования, потому что есть много моментов в теории Белышева, которые я не понимаю. Показывается осмысление этой теории и применение её в поиске ОДЛК, а также пересечение этой теории с разработанным мной ранее алгоритмом, основанным на применении псевдоассоциативных ДЛК. На основе всего описанного в первой части и появилась идея нового алгоритма, названного мной "мультисимметрия". Об этом собираюсь написать во второй части статьи. Критика по существу приветствуется. Очень хотелось бы увидеть замечания создателя теории о "обобщённых симметриях" Белышева. Статья пока в формате doc, не стала переводить в формат pdf, потому что статья не завершена. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Отправила ссылку на статью коллегам. Жду отзывов :) Просмотрела статью ещё раз; кроме двух малозначительных опечаток ошибок не заметила. Вторая часть статьи дозревает в голове :) Как дозреет, начну писать. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
https://link.springer.com/chapter/10.1007%2F978-3-030-05807-4_49 Enumeration of Isotopy Classes of Diagonal Latin Squares of Small Order Using Volunteer Computing Eduard Vatutin, Alexey Belyshev, Stepan Kochemazov, Oleg Zaikin, Natalia Nikitina Abstract В этой работе, кажется, впервые появился термин каноническая форма ДЛК. Термин принадлежит Алексею Белышеву. Он же разработал алгоритм получения канонической формы ДЛК и реализовал его программно для порядков n<=10. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
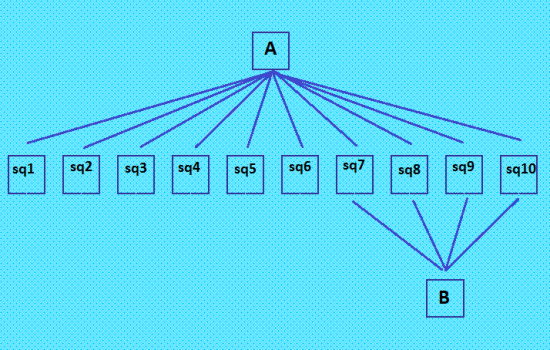
http://evatutin.narod.ru/evatutin_ls_all_structs_rus.pdf Ватутин Э.И., Манзюк М.О., Заикин О.С., Кочемазов С.Е., Белышев А.Д., Никитина Н.Н., Цитерров И.И. СПИСОК КОМБИНАТОРНЫХ СТРУКТУР ИЗ ДЛК ПОРЯДКА 10 НА МНОЖЕСТВЕ ОТНОШЕНИЯ ОРТОГОНАЛЬНОСТИ 07.11.2018 – 07.08.2019 Занятно. Кажется, тут бабушка ситерра тоже выступила; может, ошибаюсь, но слишком уж фамилия похожа. Растёт бабушка ситерра, вот уже статьи пишет :) Не буду писать много замечаний по статье, но одно всё же напишу. Вот об этой комбинаторной структуре 22. Дедал-10 Напомню господину Ватутину его статью в OEIS Maximum number of orthogonal diagonal Latin squares for one diagonal Latin square of order n. https://oeis.org/A287695 AUTHOR Eduard I. Vatutin, May 30 2017 В этой статье присутствует ссылка N. Makarova, Diagonal Latin square with 10 orthogonal squares которая показывает, что решение a(10)=10 найдено мной. Решение было найдено на моём ПК (25 апреля 2018 г.) по разработанному мной алгоритму "поиск от псевдоассоциативных ДЛК" (декабрь 2017 г.). Программа генерации псевдоассоциативных ДЛК тоже написана мной. В алгоритме используется программа Белышева проверки ДЛК на ОДЛК (family_mar). И вот она - конфигурация, порождаемая этой десяткой (следующий за ссылкой пост) Изучаю десяточку с разных сторон. Вместо термина комбинаторная структура я использую термин конфигурация, он кажется мне более соответствующим данным объектам (группам пар ОДЛК). Считаю, что авторам статьи "СПИСОК КОМБИНАТОРНЫХ СТРУКТУР ИЗ ДЛК ПОРЯДКА 10 НА МНОЖЕСТВЕ ОТНОШЕНИЯ ОРТОГОНАЛЬНОСТИ" необходимо исправить это противоречие со статьёй OEIS. По их статье получается, что данное решение принадлежит им, потому что никаких ссылок на автора решения не указано. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Статья в OEIS https://oeis.org/A329685 Цитирую EXTENSIONS a(9) from Eduard I. Vatutin, Mar 12 2020 Вот только вчера Э. Ватутин нашёл число главных классов SODLS 9-го порядка. И оперативно обновил статью в OEIS, как он пишет на форуме boinc.ru. Я не буду это КОММЕНТИРОВАТЬ, потому что у меня нет слов. Опубликую письмо француза Francis Gaspalou от 5 декабря 2017 г. Self Orthogonal Diagonal Latin Squares of order 9 Пожалуйста, читайте внимательно. В письме сообщается, что "Alex Belyshev found recently the same number". И это происходило на форуме boinc.ru в 2017 году! И Ватутин не мог этого не знать! Всё, дальше не буду комментировать. Я за один подобный комментарий вылетела из OEIS (тогда дело было связано с содранной Ватутиным на сайте Harry White последовательностью). Если бы могла, обязательно выступила бы в OEIS по поводу последовательности https://oeis.org/A329685, но, увы, не могу: блокировку с меня до сих пор не сняли. PS. Письмо Francis Gaspalou адресовано сообществу исследователей магических и латинских квадратов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Francis Gaspalou написал: Please note also that all SODLS of order 4, 5, 7 and 8 are doubly SODLS and it is only for the order 9 that we can make the difference between singly SODLS and doubly SODLS. Далее, я спросила у него: доказано ли, что doubly SODLS 10-го порядка не существует? Он ответил: Yes it is proven. See Abstract Как я поняла, это из следующей книги Principles and Practice of Constraint Programming – CP 2011 https://link.springer.com/book/10.1007/978-3-642-23786-7 Для порядка 9 doubly SODLS мне давно прислал Francis Gaspalou. Таких ДЛК 88 штук, они у меня есть. Если кому интересны эти ДЛК, пишите, я выложу. Не помню, занимался ли Белышев doubly SODLS 9-го порядка. И на форуме boinc.ru это теперь не посмотришь, потому что старый форум сдох, а на новом этого уже нет. Последовательность для doubly SODLS (до порядка 10 включительно) 1, 0, 0, 1, 1, 0, 2, 8, 88, 0 Напоминаю: все результаты, кроме последнего, получены Francis Gaspalou. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Относительно следующего члена в этой последовательности OEIS https://oeis.org/A329685... Как известно, Белышев нашёл 30502 КФ SODLS 10-го порядка. Он выложил их на форуме boinc.ru, но сейчас там этого уже нет. У меня эти ДЛК есть, если кому надо, пишите, выложу (смотрите ссылку на файл Белышева на Яндекс.Диске в следующем посте). Вопрос: это все SODLS 10-го порядка (существенно различные)? Я думаю, что ответ на этот вопрос положительный. Francis Gaspalou ответ на этот вопрос не знает. Он ответил на него так I don't know ; it is the first time I see this Belyshev's result. Да, конечно, результат Белышева - компьютерный результат, но алгоритм совершенно особенный. Интересно бы узнать мнение Белышева по данному вопросу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитирую сообщение из темы SOLS(10) и SODLS(10) И здесь Ссылка на Яндекс.Диск сохранилась, где Белышев выложил 30502 КФ SODLS 10-го порядка! Вот она https://yadi.sk/d/OiKwfw2b3Gan9x Да, это действительно был потрясающий результат! Гениальный! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пишу статью о SOLS и SODLS. Цитирую Теперь посмотрим последовательность в OEIS https://oeis.org/A287761 Может быть, я просто не вижу эти SODLS (?) Интересно бы проверить. PS. Статья пока ещё пишется, до конца далеко. |

©2026 (C) Progger