Изменю тактику поиска симметричных семёрок: не буду проверять длиннющий хвост последовательности A035795 (начиная с минимальной симметричной семёрки), в котором вероятность появления симметричной семёрки очень мала.
Начну с последнего решения этой последовательности

4608 1998071757535967

Буду ловить сразу двух зайцев - симметричных и кривых :)
Конечно, в хвосте всё равно придётся проверять, но отложу пока до лучших времён.

Цитата

Буду ловить сразу двух зайцев - симметричных и кривых :)

Забыла про третьего зайца!
Попутно можно искать шестёрки для последовательности A035794.
Для этой последовательности у нас уже кое-что найдено.
Мы с XAVER нашли следующие члены этой последовательности

a(1994) - 9000597877631
a(1995) - 9000786859409
a(1996) - 9001459196687
a(1997) - 9002289715577
a(1998) – 9014182820387
a(1999) – 9014409858827
a(2000) – 9024312077327
a(2001) – 9026230199837
a(2002) – 9046585520309
a(2003) – 9050076599567
a(2004) – 9060347329601
a(2005) – 9067633991231
a(2006) – 9075031461917
a(2007) – 9090736899707
a(2008) – 9093877464941
a(2009) – 9094692200681
a(2010) – 9107881171577
a(2011) – 9108173336369
a(2012) – 9135643909289
a(2013) – 9143150272889
a(2014) – 9143256816509
a(2015) – 9153467051777
a(2016) – 9153772563839
a(2017) – 9162394240541
a(2018) - 9175036784687
a(2019) - 9180237862769
a(2020) - 9188760984449
a(2021) - 9188827397537
a(2022) - 9190234978997
a(2023) - 9200542557881
a(2024) - 9208021925147

Дальше идёт большой пропуск и ещё несколько решений в крупном интервале, найденные мной

a(k) - 1987862319759551
a(k+1) - 1987873308378257
a(k+2) - 1987905779430167
a(k+3) - 1987939601647187
a(k+4) - 1987999792956641
a(k+5) - 1988019478996667
a(k+6) - 1988030840476661
a(k+7) – 1988051502946121
a(k+8) – 1988111047060529

Нет стыковки с интервалом, в котором я начала искать семёрки для последовательности A035795, но состыковать потом можно будет.

Изменила программку, чтобы она шестёрки из близнецов выводила при поиске семёрок из близнецов.
Вчера два интервала просчитала без вывода шестёрок, ну их, может, в этих интервалах и нет.
Сегодня с утра изменила программу, теперь шестёрки будут выводиться.
Ждём новых шестёрок и семёрок!

Ползёт моя черепашка

? \r a14.txt
1998086495234939
? \r a14.txt
? \r a14.txt

Проверяю порциями по 7 млрд.
В первой порции найдена шестёрка.

Итак, после этого крупного интервала, в котором я нашла несколько решений (шестёрок из близнецов)

a(k) - 1987862319759551
a(k+1) - 1987873308378257
a(k+2) - 1987905779430167
a(k+3) - 1987939601647187
a(k+4) - 1987999792956641
a(k+5) - 1988019478996667
a(k+6) - 1988030840476661
a(k+7) – 1988051502946121
a(k+8) – 1988111047060529

появляется следующий крупный интервал (тоже с пропуском); в этом интервале буду записывать решения так

a(k+m) - 1998086495234939

У-р-р-р-а-а-а!!!
Я нашла программу!
Вот хорошо помню, что была программа Белышева, которая искала симметричные кортежи, начиная с k=12.
Но забыла имя программы!
Очень долго искала, у меня сотни программ.
И помогло мне это сообщение на форуме Math Help Planet
http://mathhelpplanet.com/viewtopic.php?p=256565#p256565

В сообщении скриншот работы этой программы и на скриншоте имя программы!
Как хорошо, что я тогда сделала этот скриншот и выложила его на форуме.
В сообщении говорится о поиске второй симметричной семёрки из близнецов.
Как раз этот поиск у меня сейчас идёт.
Всё, PARI/GP в топку :)
Запустила программу Белышева, работает в разы быстрее, чем программа на PARI/GP



Итак, тут будут найдены симметричные кортежи, начиная с k=12.
Ну, а кортежи из близнецов уже надо будет среди них найти потом. Но это ерунда, проверим мгновенно программкой.
Тут не только семёрки, тут и шестёрки, и восьмёрки, и девятки, и т. д. ищутся.
Отличная программа! Здорово, что она у меня сохранилась.

Программа находит очень много симметричных кортежей для k=12, поменьше для k=14.
О симметричных кортежах длины 16 мы уже знаем, они ищутся в действующем варианте программы.

Цитата

Изменю тактику поиска симметричных семёрок: не буду проверять длиннющий хвост последовательности A035795 (начиная с минимальной симметричной семёрки), в котором вероятность появления симметричной семёрки очень мала.
Начну с последнего решения этой последовательности

4608 1998071757535967

Буду ловить сразу двух зайцев - симметричных и кривых :)
Конечно, в хвосте всё равно придётся проверять, но отложу пока до лучших времён.

Теперь проверю пропущенный хвост, начиная с минимальной семёрки.
По программе Белышева это проверится быстро.
И тогда никаких пропусков не будет в этом поиске.
Напомню минимальную симметричную семёрку, найденную Петуховым

1855418882807417: 0, 2, 12, 14, 30, 32, 72, 74, 114, 116, 132, 134, 144, 146

Вот с этой точки и надо начать проверку.
А я начала подальше - с последнего решения в последовательности A035795.
Вероятно того, что в хвосте есть симметричные семёрки, очень мала, но проверить всё равно надо.

Ой, как шпарит программа Белышева, прямо орлом летит на крыльях моей радости :)
Найдено уже более 7000 12-ок, 366 14-ок; будут среди них и из близнецов, из 12-ок побольше, из 14-ок, понятно, поменьше.
Появилась надежда найти вторую и третью симметричные семёрки из близнецов.

Смотрим последовательность в OEIS
https://oeis.org/A274792
A274792 a(n) = smallest prime p(1) in a symmetrical constellation of n consecutive twin primes: p(1), p(1)+2, ..., p(n), p(n)+2.

3, 5, 5, 663569, 3031329797, 17479880417, 1855418882807417, 2640138520272677

Это минимальные симметричные кортежи из последовательных пар простых чисел близнецов.
Минимальные семёрку и восьмёрку Петухов нашёл в июле 2016 г.
И на этом закруглился. Мог бы и девятку поискать.
Таким образом, симметричная девятка из последовательных простых чисел близнецов пока не найдена.
18-tuples ищутся в BOINC-проекте TBEG, в Stop@home они тоже искались.
Но сообщений о найденной симметричной девятке не появилось нигде, значит, она не была найдена.
Семёрочка единственная на данный момент.
Пытаюсь найти вторую семёрку. Может быть, повезёт.
По программе Белышева искать х-о-р-о-ш-о!

Тему "Симметричные композиции из последовательных близнецов" на форуме Math Help Planet всю прочитала.
Вот нашла интересное о связи восьмёрки и девятки
http://mathhelpplanet.com/viewtopic.php?p=256950#p256950

Посмотрите

(паттерн "девяточки") 0  2  12  14  30  32  54  56  72  74  90  92  114  116  132  134  144  146 
("восьмёрочка") 2640138520272677: 0, 2, 12, 14, 30, 32, 54, 56, 90, 92, 114, 116, 132, 134, 144, 146

Очень интересно! Паттерны почти совпадают! Только в паттерне девятки есть ещё одна пара близнецов (72, 74).
Таким образом, мы имеем почти девятку

2640138520272677: 0, 2, 12, 14, 30, 32, 54, 56, 72*, 74*, 90, 92, 114, 116, 132, 134, 144, 146

Крутое приближение! Всего одна пара элементов неправильная, это даже не простые числа.

Итак, поиск девяточки в будущем планируется, ну, если она не найдётся естественным образом в проекте TBEG (да если ещё этот проект снова будет работать, пока он остановился).
А пока у нас в поиске симметричные шестёрки и семёрки.
Поиск не симметричных кортежей останавливаю, ибо программа Белышева ищет только симметричные кортежи.

В том же сообщении выложены паттерны для симметричных девяток из близнецов (проверила до диаметра 200)

0  2  18  20  30  32  42  44  60  62  78  80  90  92  102  104  120  122
0  2  12  14  30  32  42  44  72  74  102  104  114  116  132  134  144  146 
0  2  12  14  30  32  54  56  72  74  90  92  114  116  132  134  144  146 
0  2  12  14  42  44  54  56  72  74  90  92  102  104  132  134  144  146 
0  2  30  32  42  44  54  56  72  74  90  92  102  104  114  116  144  146
0  2  12  14  42  44  48  50  90  92  132  134  138  140  168  170  180  182

Первый паттерн с минимальным диаметром 122.

В архиве нашла программу коллеги В. Чиркова для поиска симметричной девятки по паттерну с минимальным диаметром.
Ой, как много у меня в архиве разных программ!
Попробовала запустить программу Чиркова, работает, что-то там пишет на экране, только не понимаю, что пишет :)
Потом перестала писать и надолго задумалась. Прервала.
Ну, с минимальным диаметром может быть решение очень далеко (в смысле - с очень большими простыми числами).

Можно поискать девяточку и по паттернам, кто умеет. Вот Я. Врублевский очень хорошо это делает.

Запустила поиск симметричных семёрок (и не только семёрок!) по программе Белышева в два потока (две программы в разных папках).
Первый поток - начала поиск с минимальной семёрки.
Второй поток - продолжаю дальше с последнего решения последовательности A035795.
В первом потоке уже проверила найденные 12-tuples, интересно же :)
И вот первые симметричные шестёрочки из близнецов

1856270841368519: 0 2 30 32 42 44 90 92 102 104 132 134
1856513997898499: 0 2 90 92 120 122 210 212 240 242 330 332
1857050836177739: 0 2 12 14 42 44 138 140 168 170 180 182

Не проверяла, есть ли они в списке, представленном ранее.

Здорово! Симметричных 12-tuples программа находит огромное количество; конечно, и из близнецов среди них будет много встречаться.
А вот с семёрочками посложнее, симметричных 14-tuples намного меньше программа выдаёт, соответственно и ожидать быстрого появления семёрки из близнецов не приходится. Но когда-то она всё равно должна появиться!
В первом потоке найден 13-tuple, редкое явление :) Позже покажу его.

Во втором потоке пока ничего не проверяла, не буду прерывать, пусть до вечера считает.
12-tuples найдено 18854, 14-tuples - 905.
Ну прямо сердце радуется - как хорошо программы считают.

Цитата

В первом потоке уже проверила найденные 12-tuples, интересно же :)
И вот первые симметричные шестёрочки из близнецов

1856270841368519: 0 2 30 32 42 44 90 92 102 104 132 134
1856513997898499: 0 2 90 92 120 122 210 212 240 242 330 332
1857050836177739: 0 2 12 14 42 44 138 140 168 170 180 182

Не проверяла, есть ли они в списке, представленном ранее.

Проверила, да есть эти решения в архиве.
О них сообщала и на форуме Math Help Planet.
Я тогда искала немного вторую симметричную семёрку, попутно и шестёрки искала.
Семёрку вторую не нашла, а шестёрок несколько нашла, они выложены.
Ну, теперь уж не буду интервал разрывать, пусть проверяется по порядку; тогда я не так много проверила, что видно по выложенным шестёркам.
Вот они
http://mathhelpplanet.com/viewtopic.php?p=256591#p256591

1856270841368519: 0 2 30 32 42 44 90 92 102 104 132 134 
1856513997898499: 0 2 90 92 120 122 210 212 240 242 330 332
1857050836177739: 0 2 12 14 42 44 138 140 168 170 180 182
1863526348114127: 0 2 12 14 30 32 114 116 132 134 144 146 
1864570703056067: 0 2 12 14 42 44 180 182 210 212 222 224 
1865306547706409: 0 2 12 14 42 44 78 80 108 110 120 122 
1867320780974177: 0 2 12 14 42 44 60 62 90 92 102 104 
1867979944479191: 0 2 48 50 90 92 96 98 138 140 186 188

А в предыдущем посте скриншот, на котором хорошо видно просчитанный интервал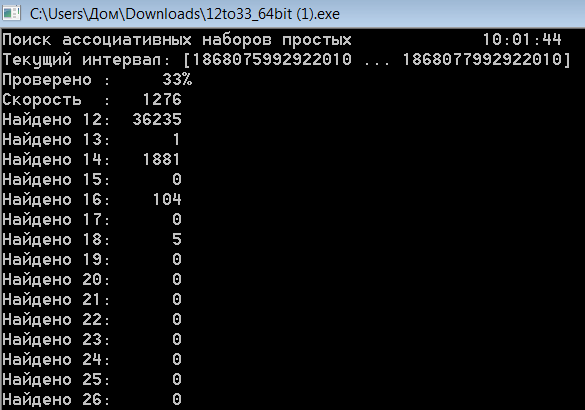



А сейчас считаю здесь

Поиск ассоциативных наборов простых              2:39:14
Текущий интервал: [1860496879954752 ... 1860498879954752]
Просеяно  :     15%
Скорость  :   1221
Найдено 12:   9465
Найдено 13:      1
Найдено 14:    466
Найдено 15:      0
Найдено 16:     29
Найдено 17:      0
Найдено 18:      0
Найдено 19:      0
Найдено 20:      0

Не так много осталось до конца просчитанного тогда интервала.

Сейчас буду прерывать программы.
Посмотрите на улов.
Первый поток

Поиск ассоциативных наборов простых              8:24:28
Текущий интервал: [1867724875895386 ... 1867726875895386]
Проверено :      2%
Скорость  :   1247
Найдено 12:  30158
Найдено 13:      1
Найдено 14:   1570
Найдено 15:      0
Найдено 16:     85
Найдено 17:      0
Найдено 18:      4
Найдено 19:      0
Найдено 20:      0

Второй поток

Поиск ассоциативных наборов простых             14:06:08
Текущий интервал: [2014849990601646 ... 2014851990601646]
Просеяно  :     18%
Скорость  :   1245
Найдено 12:  47022
Найдено 13:      0
Найдено 14:   2333
Найдено 15:      0
Найдено 16:    129
Найдено 17:      0
Найдено 18:      9
Найдено 19:      0
Найдено 20:      1

Сколько 12-tuples! И 14-tuples тоже немало. Завтра проверю на близнецов. Шестёрочки, конечно же, будут, семёрочка пока вряд ли.

А это экзотика :)

1857439592045431: 0 30 42 60 72 102 150 198 228 240 258 270 300

13-tuple, да красивый какой, диаметр 300. Ух!

Обратите внимание на скорость. Это в млрд./час. Офигенная скорость!

PS. Оба потока были запущены одновременно, но первый поток я прерывала, чтобы глянуть на решения, потом снова запустила.
И сегодня у меня не работали другие программы, только эти две. Скорость в обоих потоках почти одинаковая. Отлично!

Обработала полученные вчера решения.
В первом потоке найдены следующие симметричные шестёрки из близнецов

1863526348114127: 0 2 12 14 30 32 114 116 132 134 144 146
1864570703056067: 0 2 12 14 42 44 180 182 210 212 222 224
1865306547706409: 0 2 12 14 42 44 78 80 108 110 120 122
1867320780974177: 0 2 12 14 42 44 60 62 90 92 102 104

Все они были найдены мной давно, повторяю проверку этого интервала.
Ну ничего, перепроверка - это всегда хорошо.
Почти дошла до той точки, где тогда остановилась.
Ещё одной шестёрки, найденной тогда, нет пока.

Во втором потоке найдены следующие симметричные шестёрки из близнецов

2000808648526739: 0 2 30 32 60 62 102 104 132 134 162 164
2004579101477891: 0 2 66 68 78 80 168 170 180 182 246 248
2004732243966689: 0 2 30 32 72 74 108 110 150 152 180 182
2007804308738231: 0 2 90 92 108 110 150 152 168 170 258 260
2010830867747057: 0 2 12 14 24 26 30 32 42 44 54 56
2011158131247269: 0 2 30 32 42 44 90 92 102 104 132 134
2011493439603497: 0 2 12 14 42 44 90 92 120 122 132 134
2011855060374239: 0 2 12 14 42 44 78 80 108 110 120 122

Это уже все новые решения.
Интересное решение с минимальным диаметром!

2010830867747057: 0 2 12 14 24 26 30 32 42 44 54 56

Возможно, это второе такое решение, первое было найдено Петуховым, вот оно

5008751356547: 0 2 12 14 24 26 30 32 42 44 54 56

Очень редкий случай повторения решения с минимальным диаметром.
Где-то живёт третье простое число, которое припишется к этому паттерну, и не только третье. Интересное явление!
Кстати, этот паттерн единственный (с минимальным диаметром) для симметричных шестёрок из последовательных близнецов.

Симметричных семёрок из близнецов пока не найдено.
На восьмёрки и далее кортежи пока не проверяла, надо набрать их побольше, вероятность появления таких решений очень мала.
А симметричная девятка из близнецов пока вообще ни одна не найдена.
18-tuples не так много появляется и найти среди них из близнецов пока не удалось за всё время действия проекта по симметричным кортежам из последовательных простых чисел, если решение не было пропущено среди решений проекта Stop@home (следил ли Петухов за решениями из близнецов, ХЗ).

Я в восторге от работы программы Белышева. Так много вчера проверено! На PARI/GP и за месяц столько не проверить.

Моя черепашка побежала :)

Поиск ассоциативных наборов простых              0:41:54
Текущий интервал: [2016265989804462 ... 2016267989804462]
Проверено :      3%
Скорость  :   1258
Найдено 12:   2499
Найдено 13:      0
Найдено 14:    138
Найдено 15:      0
Найдено 16:      7
Найдено 17:      0
Найдено 18:      1
Найдено 19:      0
Найдено 20:      0

Ещё и часу не работала, а сколько уже результатов!
Это второй поток. Первый пока не запустила, работает программа по ОДЛК.

Господа!
Присоединяйтесь, пожалуйста, к поиску второй (а также третьей и т. д.) симметричной семёрочки из последовательных простых чисел близнецов.
Программу Белышева если надо - выложу.
Поиск кортежей в проекте TBEG пока стоит, неизвестно, что с ним случилось.
Кому нравится искать кортежи, добро пожаловать в мой автономный подпроект.

Проверила найденные 14-tuples на приближённое решение из близнецов.
Вот такое нашлось приближённое решение, только одна пара не близнецы (помечена символом *)

2010061600164659: 0 2 30 32 60 62 114* 140* 192 194 222 224 252 254

Всё не так безнадёжно :) вторая симметричная семёрочка найдётся! И не только вторая.

Ещё проверила все найденные 12-tuples на минимальный и максимальный диаметры и на максимальное первое смещение.
Минимальный диаметр равен 56, решение (тут близнецы, для решений из близнецов это самый минимальный диаметр)

2010830867747057: 0 2 12 14 24 26 30 32 42 44 54 56

Не помню сейчас, какой глобальный минимальный диаметр для симметричных 12-tuples (это можно посмотреть в соответствующей последовательности OEIS).
Текущий максимальный диаметр равен 758, решение

2014046756892293: 0 44 110 194 264 378 380 494 564 648 714 758

Толстенький 12-tuple :)
Текущее максимальное первое смещение равно 202, решение

2003518155983161: 0 202 210 226 262 292 396 426 462 478 486 688

Пока ищутся симметричные шестёрки и семёрки из близнецов, вспомним, что мы имеем по симметричным восьмёркам из близнецов.
Это минимальный симметричный 16-tuple из последовательных простых чисел близнецов

2640138520272677: 0, 2, 12, 14, 30, 32, 54, 56, 90, 92, 114, 116, 132, 134, 144, 146

Решение приведено в последовательности OEIS https://oeis.org/A274792
Очень симпатичная матрёшка из кортежей, состоящих из близнецов!

2640138520272731: 0 2 36 38
2640138520272707: 0 2 24 26 60 62 84 86 
2640138520272689: 0 2 18 20 42 44 78 80 102 104 120 122
2640138520272677: 0 2 12 14 30 32 54 56 90 92 114 116 132 134 144 146

К сожалению, этот кортеж не продолжается до симметричного 20-tuple
{2640138520272559, 2640138520272563, 2640138520272677, 2640138520272679, 2640138520272689, 2640138520272691, 2640138520272707, 2640138520272709, 2640138520272731, 2640138520272733, 2640138520272767, 2640138520272769, 2640138520272791, 2640138520272793, 2640138520272809, 2640138520272811,2640138520272821, 2640138520272823, 2640138520272859, 2640138520272901}
Получаем приближённое решение для симметричной десятки из близнецов, две пары неправильные.
Получаемое из этого кортежа приближённое решение для симметричной девятки из близнецов я уже показала выше.

Что у нас дальше с симметричными восьмёрками из близнецов, после минимального решения?
Не знаю, что следует сразу за минимальной восьмёркой.
Знаю решения Врублевского с очень большими простыми числами (они показаны выше).

И ещё имеем решения из проекта TBEG

517426190585100089: 0 2 18 20 60 62 72 74 138 140 150 152 192 194 210 212
519460320704755811: 0 2 6 8 78 80 96 98 120 122 138 140 210 212 216 218

Это пока всё, что у нас есть по симметричным восьмёркам близнецов.

Хорошая новость.
Макс Алексеев создал по моей просьбе последовательность в OEIS
https://oeis.org/A330278
A330278
Primes starting 12-tuples of consecutive primes that have symmetrical gaps about their mean and form 6 pairs of twin primes.
17479880417, 158074620437, 1071796554401, 1087779101699, 1153782400787, 1628444511389

Спасибо Максу!

Итак, начало последовательности симметричных шестёрок из близнецов положено, пока в последовательности всего 6 членов.
Желающие могут просчитать дальше.
По программе Белышева, которую я раскопала в своём архиве, симметричных шестёрочек из близнецов можно быстро нащёлкать много.

PS. Отмечу, что XAVER просчитал по программе на PARI/GP весь интервал, начиная с решения a(2) и до последнего решения a(6) включительно. Он прислал мне файл результатов, выданных программой.
Член a(2) подтверждён мной, смотрите сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=49&postid=4917#4917

И ещё хорошая новость!
В последовательности A330278 появились новые члены. Теперь уже 132 члена имеется.
Все решения, найденные мной в последовательности A035794 подтверждены.
Смотрите сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=49&postid=4918#4918
И дальше просчитано до 10^14.

Дальше у нас на подтверждение такие решения имеются

решения из архива
553710694696319: 0 2 12 14 30 32 222 224 240 242 252 254
1327784649892199: 0 2 30 32 42 44 78 80 90 92 120 122
1856270841368519: 0 2 30 32 42 44 90 92 102 104 132 134 
1856513997898499: 0 2 90 92 120 122 210 212 240 242 330 332
1857050836177739: 0 2 12 14 42 44 138 140 168 170 180 182
1863526348114127: 0 2 12 14 30 32 114 116 132 134 144 146 
1864570703056067: 0 2 12 14 42 44 180 182 210 212 222 224 
1865306547706409: 0 2 12 14 42 44 78 80 108 110 120 122 
1867320780974177: 0 2 12 14 42 44 60 62 90 92 102 104 
1867979944479191: 0 2 48 50 90 92 96 98 138 140 186 188
2000808648526739: 0 2 30 32 60 62 102 104 132 134 162 164
2004579101477891: 0 2 66 68 78 80 168 170 180 182 246 248
2004732243966689: 0 2 30 32 72 74 108 110 150 152 180 182
2007804308738231: 0 2 90 92 108 110 150 152 168 170 258 260
2010830867747057: 0 2 12 14 24 26 30 32 42 44 54 56
2011158131247269: 0 2 30 32 42 44 90 92 102 104 132 134
2011493439603497: 0 2 12 14 42 44 90 92 120 122 132 134
2011855060374239: 0 2 12 14 42 44 78 80 108 110 120 122
2640138520272689: 0 2 18 20 42 44 78 80 102 104 120 122
3280895246297399: 0 2 42 44 90 92 120 122 168 170 210 212
30767216828606387: 0 2 24 26 42 44 132 134 150 152 174 176
51477335518549079: 0 2 42 44 72 74 198 200 228 230 270 272
57789199456995449: 0 2 18 20 42 44 78 80 102 104 120 122
59642707519096391: 0 2 30 32 48 50 138 140 156 158 186 188
61111185001490597: 0 2 54 56 80 82 120 122 150 152 204 206
61496572337804837: 0 2 30 32 60 62 102 104 132 134 162 164
72249747916090559: 0 2 12 14 42 44 48 50 78 80 90 92
74441008149832937: 0 2 42 44 54 56 60 62 72 74 114 116 
74645028004901609: 0 2 12 14 48 50 132 134 168 170 180 182
119890755200640041: 0 2 36 38 48 50 78 80 90 92 126 128 (Врублевский)
500423295288129527: 0 2 14 16 32 34 54 56 72 74 84 86 (XAVER)

решения с проекта Tomas Brada
503982480704545937: 0 2 42 44 54 56 150 152 162 164 204 206
512504969296035731: 0 2 36 38 120 122 156 158 240 242 276 278
517426190585100107: 0 2 42 44 54 56 120 122 132 134 174 176
519460320704755817: 0 2 72 74 90 92 114 116 132 134 204 206
519992015770104089: 0 2 18 20 42 44 78 80 102 104 120 122

решения Врублевского 
1025519173619653121: 0 2 36 38 48 50 78 80 90 92 126 128
1709642327471063831: 0 2 30 32 60 62 66 68 96 98 126 128
1759943151645258959: 0 2 30 32 42 44 108 110 120 122 150 152
1960984050584219189: 0 2 12 14 18 20 42 44 48 50 60 62
3808061696393625131: 0 2 30 32 60 62 108 110 138 140 168 170
4018288550284158089: 0 2 30 32 42 44 78 80 90 92 120 122
5512467165717387047: 0 2 12 14 42 44 102 104 132 134 144 146
6118066623221589809: 0 2 12 14  42 44 48 50 78 80 90 92
6868687010299798949: 0 2 42 44 102 104 108 110 168 170 210 212
7214261446565240447: 0 2 72 74 84 86 120 122 132 134 204 206

Тут есть нюанс.
Включать ли в эту последовательность решения, которые получены из симметричных восьмёрок близнецов?
Решения Врублевского, например, все такие.

Ах, а какая ещё есть новость!
Смотрим сюда
https://oeis.org/A035794/b035794.txt

Эти решения

a(1994) - 9000597877631
a(1995) - 9000786859409
a(1996) - 9001459196687
a(1997) - 9002289715577
a(1998) – 9014182820387
a(1999) – 9014409858827
a(2000) – 9024312077327
a(2001) – 9026230199837
a(2002) – 9046585520309
a(2003) – 9050076599567
a(2004) – 9060347329601
a(2005) – 9067633991231
a(2006) – 9075031461917
a(2007) – 9090736899707
a(2008) – 9093877464941
a(2009) – 9094692200681
a(2010) – 9107881171577
a(2011) – 9108173336369
a(2012) – 9135643909289
a(2013) – 9143150272889
a(2014) – 9143256816509
a(2015) – 9153467051777
a(2016) – 9153772563839
a(2017) – 9162394240541
a(2018) - 9175036784687
a(2019) - 9180237862769
a(2020) - 9188760984449
a(2021) - 9188827397537
a(2022) - 9190234978997
a(2023) - 9200542557881
a(2024) - 9208021925147

найденные мной и XAVER, в последовательность A035794 уже внесены.
И не только эти, там теперь 10000 членов. Во как!
Это последний член последовательности на данный момент

a(10000) - 75753198352289

Однако этих решений, найденных мной

a(k) - 1987862319759551
a(k+1) - 1987873308378257
a(k+2) - 1987905779430167
a(k+3) - 1987939601647187
a(k+4) - 1987999792956641
a(k+5) - 1988019478996667
a(k+6) - 1988030840476661
a(k+7) – 1988051502946121
a(k+8) – 1988111047060529
. . . . . . 
a(k+m) - 1998086495234939

в последовательности пока нет.
Смотрите сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=49&postid=4944#4944

PS. Посмотрела историю редактирования последовательности
https://oeis.org/history?seq=A035794
и ничего не поняла!
Кем добавлены решения? Даниловым или Петуховым?
Добавлен новый прикреплённый файл, но кем добавлен?

У меня улов сегодня
первый поток

Поиск ассоциативных наборов простых             13:37:28
Текущий интервал: [1884656866378570 ... 1884658866378570]
Просеяно  :     34%
Скорость  :   1245
Найдено 12:  48192
Найдено 13:      1
Найдено 14:   2361
Найдено 15:      0
Найдено 16:    116
Найдено 17:      0
Найдено 18:      6
Найдено 19:      0
Найдено 20:      0

Второй поток

Поиск ассоциативных наборов простых             16:47:30
Текущий интервал: [2035681978902112 ... 2035683978902112]
Просеяно  :     36%
Скорость  :   1213
Найдено 12:  57142
Найдено 13:      2
Найдено 14:   2871
Найдено 15:      0
Найдено 16:    173
Найдено 17:      0
Найдено 18:      7
Найдено 19:      0
Найдено 20:      0

Колоссально!
Обрабатывать буду завтра.
Три 13-tuples найдено. Экзотика :) Завтра покажу их.

Прервала программы.
13-tuples показываю сегодняшние

1875536652154691: 0 30 36 78 96 108 138 168 180 198 240 246 276
2018006550302833: 0 6 18 60 90 126 138 150 186 216 258 270 276
2033313379581371: 0 6 42 72 90 132 156 180 222 240 270 306 312

Симметричные кортежи нечётных длин появляются очень редко, поэтому говорю "экзотика".
Хоть посмотреть на них :)
А вот 15-tuple пока ни одного у меня не найдено, даже посмотреть не на что.

Обработала вчерашние результаты.
Это все симметричные шестёрочки из близнецов

1867979944479191: 0 2 48 50 90 92 96 98 138 140 186 188
1870626409411517: 0 2 30 32 60 62 102 104 132 134 162 164
1871971770130127: 0 2 24 26 84 86 120 122 180 182 204 206
1872170908055417: 0 2 12 14 30 32 114 116 132 134 144 146
1872898471234277: 0 2 42 44 54 56 90 92 102 104 144 146
1873315498719317: 0 2 30 32 72 74 90 92 132 134 162 164
1873839863922071: 0 2 36 38 48 50 78 80 90 92 126 128
1880877967906277: 0 2 60 62 84 86 90 92 114 116 174 176
1881469781667557: 0 2 12 14 30 32 72 74 90 92 102 104
1881620312752109: 0 2 12 14 72 74 138 140 198 200 210 212
1882672640481497: 0 2 12 14 42 44 102 104 132 134 144 146
2022268433267471: 0 2 30 32 48 50 138 140 156 158 186 188
2023578707527841: 0 2 6 8 48 50 78 80 120 122 126 128
2031220905630149: 0 2 30 32 60 62 72 74 102 104 132 134

Это текущий максимальный диаметр у 12-tuples

1871598143307923: 0 24 66 104 336 374 420 458 690 728 770 794

Симметричной семёрочки из близнецов пока нет.
Приближённые решения - одна пара не близнецы (помечена символом *)

1871665735327907: 0 2 24 26 30 32 44* 192* 204 206 210 212 234 236
1873381067651369: 0 2 42 44 78 80 90* 122* 132 134 168 170 210 212

Интересная вторая семёрочка с разностями

2 2 2 2^5 2 2 2 

Больше нет ничего интересного, на мой взгляд.
Буду считать дальше.