В 49-й партии появился 22-tuple

510412231691005099: 0 58 88 100 108 144 150 180 184 190 208 210 228 234 238 268 274 310 318 330 360 418

Пока это самый длинный.

Ой, какую хорошую игрушку сочинила :)
Не просчитаю весь интервал, так хоть поиграю.

Новая программа на PARI/GP

{v= vector(14); 
w= vector(7); 
forprime(p=1987861000000000, 1987862000000000, 
v[1]=p; v[2]=nextprime(v[1]+1);v[3]=nextprime(v[2]+1);v[4]=nextprime(v[3]+1);
v[5]=nextprime(v[4]+1);v[6]=nextprime(v[5]+1);v[7]=nextprime(v[6]+1);
v[8]=nextprime(v[7]+1);v[9]=nextprime(v[8]+1); v[10]=nextprime(v[9]+1);
v[11]=nextprime(v[10]+1); v[12]=nextprime(v[11]+1); 
v[13]=nextprime(v[12]+1); v[14]=nextprime(v[13]+1);
w[1]=v[2]-v[1];w[2]=v[4]-v[3];w[3]=v[6]-v[5];w[4]=v[8]-v[7];
w[5]=v[10]-v[9];w[6]=v[12]-v[11];w[7]=v[14]-v[13];
if(w[1]==2,if(w[2]==2,if(w[3]==2,if(w[4]==2,print(v[1]);print1(w); ))))) 
}

Во-первых, теперь проверяю кортежи длины 14.
Логика такая: если нет 7 пар последовательных близнецов, 8 пар последовательных близнецов не будет и подавно.
Во-вторых, проверяю в программе только 4 первые пары кортежа на близнецов, но разности вывожу для всех 7 пар.
Ожидала, что эти модификации хоть немного ускорят выполнение программы, но ни фига! Никакого убыстрения не заметила.
Зато заодно проверю и кортежи из 7 последовательных пар близнецов, эта последовательность в OEIS https://oeis.org/A035795, может быть, новые найду.
Запустила программу в два потока и наблюдаю, очень интересно :)



По 5 пар последовательных близнецов много попадается, 6 и 7 последовательных пар близнецов пока не видела.
В консоли справа последнее решение интересное, надо его потом проверить отдельно.

Это проверка по программке известного кортежа из 7 пар последовательных близнецов

? \r a5.txt
1997651049274289
[2, 2, 2, 2, 2, 2, 2]1997651049274301
[2, 2, 2, 2, 2, 2, 22]1997651049274337
[2, 2, 2, 2, 2, 22, 24]1997651049274379
[2, 2, 2, 2, 22, 24, 6]1997651059223009
[2, 2, 2, 2, 12, 54, 48]

Программа кортеж находит, можно надеяться, что она мне не наврёт :)

Ого, Петухов настрогал в этой последовательности аж 4608 решений!

Table of n, a(n) for n = 1..4608

Это последние в списке

. . . . . . . 
4591 1986462499067411
4592 1986496053243929
4593 1986498121286741
4594 1987825700460569
4595 1988204822189447
4596 1988583442223471
4597 1989164431967957
4598 1989263201895647
4599 1989677936219339
4600 1992104877546731
4601 1992163038268769
4602 1994317754546081
4603 1994342841531827
4604 1994785882031027
4605 1995022824101687
4606 1997307567853109
4607 1997651049274289
4608 1998071757535967

Дальше тут очень даже можно поискать по предложенной выше программке. Может, что-то и найдётся.
Но меня интересуют кортежи из 8 пар последовательных близнецов, и не все, а находящиеся в интервале [1987799923250861,2640138520272677].

А теперь посмотрите на эту последовательность OEIS
https://oeis.org/A035794
Это кортежи из 6 пар последовательных близнецов.
Как мы с Даниловым эту последовательность заполняли, посмотрите дискуссию
https://oeis.org/history?seq=A035794
обхохочетесь :)
Ну вот, я ушла, и он быстренько закруглился, нашёл всего 1993 решения. Успокоился на этом, хватит и так :)
Последние решения в списке

. . . . . . . 
1979 8886888860909
1980 8903022369221
1981 8906159050289
1982 8908368781601
1983 8908837206107
1984 8909142290777
1985 8916042445727
1986 8916436096661
1987 8942757287159
1988 8953662379679
1989 8954139920177
1990 8962813705607
1991 8975318857007
1992 8994256560647
1993 8999536696751

Маленькие значения-то! Можно бы и дальше посчитать. А не попробовать ли, пока Данилов отдыхает :)

У меня вот сейчас шесть пар близнецов подряд попались

[2, 2, 2, 2, 12, 126, 6]1987862319759551
[2, 2, 2, 2, 2, 2, 12]1987862319759707
[2, 2, 2, 2, 2, 12, 2]1987862319759749
[2, 2, 2, 2, 12, 2, 6]1987862325454277
[2, 2, 2, 2, 8, 18, 50]

А такого кортежа и нет у Данилова, он намного дальше его списка. Непорядок :)

Не нашла в OEIS последовательности из минимальных симметричных кортежей из последовательных пар близнецов.
Поискала поиском, нету. Может, плохо искала.
Надо создать такую последовательность, если её нет.
Вот по моей головоломке, например
http://www.primepuzzles.net/puzzles/puzz_813.htm

PS. Такая последовательность есть - A274792.
Кстати, создана была мной в 2016 г. как раз на основе моей головоломки, указанной выше.
Забылось! :)

Здесь Данилов постарался :)
https://oeis.org/A035793
10000 решений!
Однако таких решений, которые мне попались при поиске кортежей из 6 пар последовательных близнецов, в OEIS пока нет

8999780265029: [2, 2, 2, 2, 2, 50]
8999695551359: [2, 2, 2, 2, 2, 38]

Плохо всё-таки постарался :)

Тэк-с, а с шестью парами близнецов подряд пока ничего не нашла, до 9*10^12 проверила.
Наверное, Данилов не просто так остановился, дальше, видимо, долго нет решений.

Поиск "7-8" продолжаю, пока ничего не нашла: ни 7 пар, ни 8 пар близнецов подряд

? \r a4.txt
1987865026357697
[2, 2, 2, 2, 2, 10, 12]1987865026357709
[2, 2, 2, 2, 10, 12, 48]1987865047991969
[2, 2, 2, 2, 18, 88, 16]1987865079392849
[2, 2, 2, 2, 18, 84, 262]1987865107289387
[2, 2, 2, 2, 22, 14, 68]1987865114849987
[2, 2, 2, 2, 6, 10, 28]1987865125444529
[2, 2, 2, 2, 10, 68, 22]1987865147511431
[2, 2, 2, 2, 26, 224, 22]1987865150795267
[2, 2, 2, 2, 28, 66, 50]1987865177040857
[2, 2, 2, 2, 14, 94, 10]1987865219748437
[2, 2, 2, 2, 56, 38, 34]1987865259944561
[2, 2, 2, 2, 20, 22, 6]1987865261855279
[2, 2, 2, 2, 2, 40, 50]1987865261855321
[2, 2, 2, 2, 40, 50, 46]1987865269057277
[2, 2, 2, 2, 96, 4, 40]1987865279779889
[2, 2, 2, 2, 6, 2, 74]1987865296139741
[2, 2, 2, 2, 28, 12, 24]
. . . . . . 

Попался довольно крупный промежуток между простыми (262), 5 пар близнецов подряд - мало интересно.

Зато есть первые решения с 6 парами близнецов подряд!
Вот они красавчики

9000597877631: [2, 2, 2, 2, 2, 2]
9001459196687: [2, 2, 2, 2, 2, 2]
9000786859409: [2, 2, 2, 2, 2, 2]

Ура! Ура! Ура!
Не зря игралась :)
Ну, вносить эти решения в OEIS пока не буду, а то Данилов опять придёт :)
И не для OEIS я их ищу, мне просто очень интересно искать, перемещаться по поиску: "5-6", "6-7", "7-8", программки писать.
Сам процесс наблюдаю и наслаждаюсь поиском.
Имея мощную технику, всё это можно за час найти, можно 10000 решений настрогать за полчаса, но суть не в этом!

PS. Посмотрите, как в последовательности OEIS развивались события

EXTENSIONS
a(11)-a(17) from Jud McCranie, Sep 16 2003
Offset corrected by Arkadiusz Wesolowski, May 06 2012
Data corrected from Sebastian Petzelberger, May 04 2015
a(27)-a(41) added by Natalia Makarova, Oct 05 2015
a(42)-a(111) added by Vasily Danilov, Oct 10 2015
a(112) added by Natalia Makarova, Oct 10 2015
a(113)-a(311) added by Vasily Danilov, Oct 10 2015, Oct 14 2015
a(227)-a(253) added by Natalia Makarova, Oct 14 2015
a(312)-a(1993) added by Vasily Danilov, Oct 14 2015, Oct 15 2015

Было очень весело :)
Редактор OEIS спросил: "У вас что конкурс?" :)
Заметьте: я начинала добавлять решения

a(27)-a(41) added by Natalia Makarova, Oct 05 2015

И вот наш "конкурс" закончился и 4 года Данилов отдыхает.
А я могу и продолжить :)
У меня уже есть a(1994) - a(1996).

Кстати, в статье OEIS есть даже программка для поиска кортежей

MATHEMATICA  
fQ[n_] := Block[{k = 6}, And[NextPrime[n, -1] - NextPrime[n, -2] != 2, NextPrime[n, 2 k + 1] - NextPrime[n, 2 k] != 2, AllTrue[NextPrime[n, # + 1] - NextPrime[n, #] & /@ (Range[0, 2 k - 1, 2]), # == 2 &]]]; Select[Prime@ Range[10^9], fQ] (* 

У кого есть пакет MATHEMATICA, можете попробовать эту программку.
Буду очень рада, если кто-нибудь дополнит эту последовательность OEIS хотя бы до 3000 членов.
Я столько на своём ПК просчитать не смогу, моя программка очень медленно работает.
Вот она

{v= vector(12); 
w= vector(6); 
forprime(p=8999999999000, 9002000000000, 
v[1]=p; v[2]=nextprime(v[1]+1);v[3]=nextprime(v[2]+1);v[4]=nextprime(v[3]+1);
v[5]=nextprime(v[4]+1);v[6]=nextprime(v[5]+1);v[7]=nextprime(v[6]+1);
v[8]=nextprime(v[7]+1);v[9]=nextprime(v[8]+1); v[10]=nextprime(v[9]+1);
v[11]=nextprime(v[10]+1); v[12]=nextprime(v[11]+1); 
w[1]=v[2]-v[1];w[2]=v[4]-v[3];w[3]=v[6]-v[5];w[4]=v[8]-v[7];
w[5]=v[10]-v[9];w[6]=v[12]-v[11];
if(w[1]==2,if(w[2]==2,if(w[3]==2,if(w[4]==2,print(v[1]);print1(w); ))))) 
}

Можете попробовать, это для среды программирования PARI/GP.
В программке вы видите последний проверенный интервал [8999999999000, 9002000000000].
В этом интервале и найдены три решения.

А черепашка моя пыхтит :) (поиск "7-8").
Ещё один крупный промежуток между простыми попался - 270

. . . . . .
[2, 2, 2, 2, 26, 30, 4]1987865505499799
[2, 2, 2, 2, 34, 30, 40]1987865506867661
[2, 2, 2, 2, 16, 270, 36]1987865517953171
[2, 2, 2, 2, 4, 38, 96]1987865557385021
[2, 2, 2, 2, 4, 8, 6]1987865573199059
[2, 2, 2, 2, 10, 20, 80]1987865601185417
[2, 2, 2, 2, 50, 18, 18]1987865606839787
[2, 2, 2, 2, 26, 30, 30]1987865621818409
[2, 2, 2, 2, 18, 40, 82]1987865639275277
[2, 2, 2, 2, 6, 98, 4]1987865646133091
[2, 2, 2, 2, 120, 4, 14]1987865655393461
[2, 2, 2, 2, 58, 70, 16]1987865659622387
[2, 2, 2, 2, 22, 6, 108]1987865662642841
[2, 2, 2, 2, 48, 10, 30]
. . . . . . . . . .

Поиск "7-8" важен: эту дыру [1987799923250861,2640138520272677] в OEIS надо заделать, очень некрасивая дыра.
Но мне этот поиск не осилить по программе на PARI/GP.
Нужна другая программа, типа программы Белышева для симметричных кортежей.

У мня новая модификация программы, и теперь ускорение есть, хотя и не очень сильное.
Придумала: перевела поиск в плоскость "5-6-7-8".
Логика та же: без 5 не будет 6, без 6 не будет 7, без 7 не будет 8.
Новая программка на PARI/GP

{v= vector(12); 
forprime(p=1987872999990000, 1987876000000000, v[1]=p; v[2]=nextprime(v[1]+1); a=v[2]-v[1]; 
if(a==2, v[3]=nextprime(v[2]+1); 
v[4]=nextprime(v[3]+1); a=v[4]-v[3]; if(a==2, v[5]=nextprime(v[4]+1); 
v[6]=nextprime(v[5]+1); a=v[6]-v[5]; 
if(a==2, v[7]=nextprime(v[6]+1); v[8]=nextprime(v[7]+1); a=v[8]-v[7]; 
if(a==2, v[9]=nextprime(v[8]+1); v[10]=nextprime(v[9]+1); a=v[10]-v[9]; 
if(a==2, v[11]=nextprime(v[10]+1); v[12]=nextprime(v[11]+1); a=v[12]-v[11]; print(v[1]);
if(a==2,  print(v); )))))))
}

Массив (вектор) стал меньше, проверок стало меньше, и всё замечательно работает!
Запустила две копии и с интересом наблюдаю.
В первой копии найдено только по 5 пар последовательных близнецов

? \r a3.txt
1987870087529057
1987870645644251
1987870771170287
1987870861795277
1987870941168767
1987871257693271
1987872074784569
?

Во второй копии найдено уже 6 пар последовательных близнецов

? \r a3.txt
1987873308378257
[1987873308378257, 1987873308378259, 1987873308378281, 1987873308378283, 1987873
308378311, 1987873308378313, 1987873308378317, 1987873308378319, 198787330837834
1, 1987873308378343, 1987873308378359, 1987873308378361]
1987873308378281
1987873649562257
1987874159680247
1987875309318671
?

По 7 и 8 пар пока не найдено.
В каждой копии просчитано по 3*10^9, довольно быстро такая порция просчитана моей черепашкой. Хорошая моя черепашка! Трудится.
Главное, что программа выводит на консоль всё, что нужно: и пятёрочки, и шестёрочки, и семёрочки, и восьмёрочки.
Ой, как в ОДЛК :)
Кстати, можно сделать вывод результатов и в файл, забыла, как это записать, можно подсмотреть в шпаргалке (в теме Алексеева).
Помню точно, что раньше я выводила результаты в файл.

Господа!
Это уже можно попробовать.
Как там с PARI/GP? Может быть, платным стал? Я не в курсе, потому что пользуюсь давно загруженной версией (тогда это было бесплатно).
Конечно, программа по-прежнему медленная, до программы Белышева далеко.
Но всё-таки уже побыстрее немножко.

Выше я показала три кортежа по 6 пар последовательных близнецов

9000597877631: [2, 2, 2, 2, 2, 2]
9001459196687: [2, 2, 2, 2, 2, 2]
9000786859409: [2, 2, 2, 2, 2, 2]

Сейчас найден новый кортеж из 6 пар последовательных близнецов

[1987873308378257, 1987873308378259, 1987873308378281, 1987873308378283, 1987873308378311, 1987873308378313, 1987873308378317, 1987873308378319, 1987873308378341, 1987873308378343, 1987873308378359, 1987873308378361]

И теперь в последовательности OEIS образовалась огромная дыра, эту дыру тоже надо заделать.
Но пока буду продолжать поиск "5-6-7-8", он мне очень нравится :)

А раньше была найдена ещё одна шестёрочка в проверяемом интервале

У меня вот сейчас шесть пар близнецов подряд попались

[2, 2, 2, 2, 12, 126, 6]1987862319759551
[2, 2, 2, 2, 2, 2, 12]1987862319759707
[2, 2, 2, 2, 2, 12, 2]1987862319759749
[2, 2, 2, 2, 12, 2, 6]1987862325454277
[2, 2, 2, 2, 8, 18, 50]

Вот она

1987862319759551: [2, 2, 2, 2, 2, 2]

В этом сообщении
https://dxdy.ru/post255964.html#p255964
М. Алексеев рассказал о выводе результатов в файл.
Всё очень просто.
Команда
\1 result.txt

Продолжаю поиск (5-6-7-8)

? \r a3.txt
1987885339381061
1987886222546597
1987886525571641
1987887508344707
1987887688669919
1987887794148899
? \r a3.txt
1987888059157337
1987888072568267
1987888557064169
1987888685524037
1987888981948367
1987889023839377
1987890058612571
1987890377092259
1987890649368707
1987890804576431
? \r a3.txt
1987895595263057
1987896254386109
?

Вот засомневалась: стоит ли собирать пятёрочки?
В последовательности OEIS с пятёрочками 10000 решений, Данилов постарался :)
Больше уж, наверное, никому не нужно.
Не буду их собирать.
А шестёрочек мало попадается, пока две в проверяемом интервале нашла.
Это последние решения из списка с пятёрочками

. . . . . . .
9985 1252309437077
9986 1252359048377
9987 1252436056139
9988 1252488417989
9989 1252631790647
9990 1252932886781
9991 1252947693131
9992 1252960474061
9993 1253128880249
9994 1253146714661
9995 1253219777477
9996 1253323503431
9997 1253473826387
9998 1253603016737
9999 1253683163111
10000 1253685867479

По значениям посмотрите: до проверяемого мной интервала очень далеко. Тут можно ещё много тысяч решений настрогать.

Новая шестёрочка найдена!

[1987905779430167, 1987905779430169, 1987905779430251, 1987905779430253, 1987905779430269, 1987905779430271, 1987905779430281, 1987905779430283, 1987905779430341, 1987905779430343, 1987905779430377, 1987905779430379]

Поиск продолжается.
Медленно, да. Но быстрой программы у меня нет.
Ну и пусть медленно, мне торопиться некуда.

Этот интервал [1987799923250861, 2640138520272677] (от последней не симметричной восьмёрки до первой симметричной восьмёрки) был проверен мной по программе Белышева полностью.
Смотрите отчёт об этой проверке в сообщении на форуме Math Help Planet
http://mathhelpplanet.com/viewtopic.php?p=259466#p259466
На всю проверку ушло меньше месяца.
Но это был поиск симметричных кортежей, я проверяла минимальность найденного Петуховым симметричного кортежа из 8 последовательных пар близнецов.
При этом начинала проверку от найденного им же не симметричного кортежа из 8 пар последовательных близнецов.
Вот как быстро была выполнена проверка по программе Белышева!

Теперь снова этот интервал проверяется, ищем не симметричные восьмёрки (симметричных восьмёрок в этом интервале нет), попутно ищем шестёрки и семёрки (всякие - как симметричные, так и не симметричные, какие попадутся).
Но проверка сейчас по другой программе, которая раз в 50 работает медленнее программы Белышева.
Что надо сделать? Надо просто чуть модифицировать программу Белышева, чтобы она искала кортежи из последовательных близнецов не только симметричные.

Дорогая моя черепашка, ползи,
ты доползёшь до всех концов всех интервалов!

Новую шестёрочку черепашка нашла

? \r a3.txt
1987938201162959
1987938478250339
1987939295824577
1987939601647187
[1987939601647187, 1987939601647189, 1987939601647199, 1987939601647201, 1987939601647247, 1987939601647249, 1987939601647271, 1987939601647273, 1987939601647289, 1987939601647291, 1987939601647331, 1987939601647333]
1987939601647199
1987941447163349
1987941712066151
1987941926236961
?

Ой, а пятёрок как же много! Куда их девать, посолить что ли :)
Черепашка дальше поползла.

Табличку вот сделала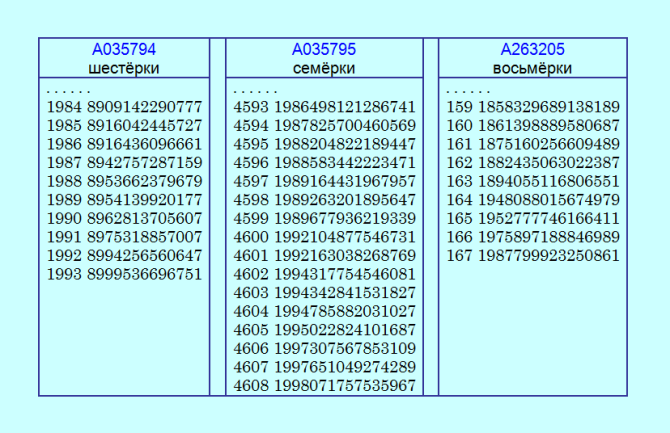



Это из последовательностей OEIS - шестёрки, семёрки и восьмёрки последовательных пар близнецов.
В шапке указаны номера последовательностей OEIS, в таблице приведены последние решения из каждой последовательности.

Ссылки на последовательности:
https://oeis.org/A035794
https://oeis.org/A035795
https://oeis.org/A263205

Главная цель у меня сейчас: просчитать интервал [1987799923250861, 2640138520272677] в последовательности A263205.
Но этот интервал для меня очень большой, по моей медленной программе я его и за 3 года не просчитаю.
Ну, попутно у меня ищутся шестёрки и семёрки. Первая семёрочка, которая должна попасться на пути моей черепашки: 1988204822189447.
Это будет просто подтверждение известного решения из последовательности A035795.
В последовательности A035794 (шестёрки) образовалась огромная дыра, которую надо, конечно, заделать.
Данилову весточку надо послать, он мигом заделает дыру :)

После последнего решения Данилова я нашла три шестёрочки, а потом перешла в большой интервал, и вот она - дыра

9000597877631
9000786859409
9001459196687
. . . . . . .  (большой пропуск!)
1987873308378257
1987905779430167
1987939601647187

Сейчас у меня шестёрочки ищутся в большом интервале.

Проверила последний выпуск БД, решения 16-tuples в проекте Tomas Brada.
Он исправил ошибки, удалил дубликаты, теперь вроде всё в порядке с БД.
16-tuples на данный момент в БД имеется 32250 шт.
Проверила на ассоциативные квадраты Стенли, новых не найдено.
Максимальный диаметр подрос

513134406491736319: 0 70 94 118 142 180 442 450 622 630 892 930 954 978 1002 1072

но текущий максимум диаметра (1162) не превышен пока.
Кортежей из близнецов не найдено.

В проекте начата новая партия WUs (16000).
Пожалуйста, подключайтесь к проекту!

А у меня новая модификация!
Очевидно же вроде бы, но не сразу пришло в голову: можно ещё на 2 координаты уменьшить длину вектора.
Сейчас ищу пятёрочки, всё остальное (шестёрки, семёрки, восьмёрки) по продолжению находится.
Новая версия программы

{v= vector(10); 
forprime(p=1987966999900000, 1987974000000000, v[1]=p; v[2]=nextprime(v[1]+1); a=v[2]-v[1]; 
if(a==2, v[3]=nextprime(v[2]+1); 
v[4]=nextprime(v[3]+1); a=v[4]-v[3]; if(a==2, v[5]=nextprime(v[4]+1); 
v[6]=nextprime(v[5]+1); a=v[6]-v[5]; 
if(a==2, v[7]=nextprime(v[6]+1); v[8]=nextprime(v[7]+1); a=v[8]-v[7]; 
if(a==2, v[9]=nextprime(v[8]+1); v[10]=nextprime(v[9]+1); a=v[10]-v[9]; 
if(a==2,  print(v); ))))))
}

Возможно потерять продолжения (они не будут выведены), если только пятёрочка на самом конце интервала находится, что маловероятно.
Ну, а чтобы всё-таки такую возможность исключить, надо последнюю пятёрочку в проверяемом интервале проверить на продолжение, это делается мгновенно.
Вот и все дела.
Ускорение снова получено, хотя, конечно, очень незначительное.
Так, черепашка моя ползёт дальше, путь у неё очень длинный, но она неутомима :)

PS. Если хорошо подумать, то никакой оптимизации не получилось, и соответственно никакого ускорения.
Вектор стал короче, но зато в интервале укладывается больше таких коротких векторов, следовательно, количество проверок не уменьшится.
Поскольку вывод решений в этой версии хуже и есть возможность потерять решения на конце интервала, возвращаюсь к предыдущей версии (ищу шестёрки и попутно семёрки с восьмёрками).

Цитата

Табличку вот сделала



Это из последовательностей OEIS - шестёрки, семёрки и восьмёрки последовательных пар близнецов.
В шапке указаны номера последовательностей OEIS, в таблице приведены последние решения из каждой последовательности.

Буду называть интервал [8999536696751, ...] мелким, имея в виду маленькие значения входящих в него чисел, а интервал [1987799923250861, ...] буду называть крупным, имея в виду большие значения входящих в него чисел.

Сейчас нашла ещё одну шестёрочку в мелком интервале, всего их у меня теперь 4, я приписала к ним очередные члены последовательности OEIS A035794

a(1994) - 9000597877631
a(1995) - 9000786859409
a(1996) - 9001459196687
a(1997) - 9002289715577

Заметила, что в мелком интервале считается малость побыстрее, нежели в крупном интервале, ну, и шестёрок вроде побольше попадается.

В крупном интервале тоже нашлась новая шестёрочка, их стало 4 штуки

1987873308378257
1987905779430167
1987939601647187
1987999792956641

В крупном интервале я ищу постоянно, в мелком интервале эпизодически, когда возникает пауза.