О трансверсалях латинских квадратов
Message boards :
Science :
О трансверсалях латинских квадратов
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Нашла статью Ian M. Wanless "Transversals in Latin squares". http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.244.6006&rank=17&q=Ian Wanless&osm=&ossid= Abstract PS. Ссылка странная, не берётся тегом. Но она работает. Скопируйте и введите в адресную строку браузера. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Что такое трансверсали и почему они так важны при исследовании ЛК? Читаем в Википедии https://ru.wikipedia.org/wiki/Латинский_квадрат Латинский квадрат L n-го порядка имеет ортогональный ему квадрат тогда и только тогда, когда в L существует n непересекающихся трансверсалей. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А вот определение трансверсали в Википедии какое-то заумное, по крайней мере, для меня. Смотрим выше из абстракта статьи Ian M. Wanless: A latin square of order n is an n×n array of n symbols in which each symbol occurs exactly once in each row and column. A transversal of such a square is a set of n entries such that no two entries share the same row, column or symbol. Здесь вполне понятно определена трансверсаль ЛК. По-русски будет так: трансверсаль ЛК порядка n - это набор из n различных элементов, в котором нет двух элементов из одной строки и также нет двух элементов из одного столбца. Другими словами: n элементов должны быть выбраны из всех n строк и из всех n столбцов ЛК, и все эти n элементов должны быть различны. Пример на иллюстрации изображён ЛК 9-го порядка и окрашены три трансверсали в этом ЛК 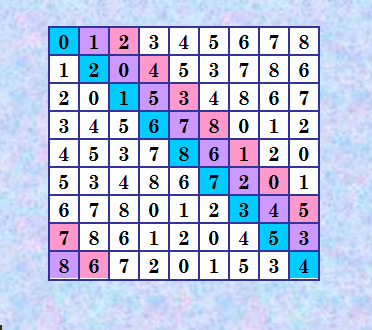 Конечно, элементы трансверсали не обязательно должны располагаться на диагонали ЛК (главной или разломанной). Просто в этом примере такое расположение. Кстати, на всех диагоналях данного направления (главной и разломанных) в этом ЛК мы получим трансверсали. Их будет ровно 9 и они будут неперсекающимися. И мы имеем из этого набора трансверсалей готовый ортогональный соквадрат к приведённому ЛК: 0 2 1 6 8 7 3 5 4 1 0 5 7 6 2 4 3 8 2 4 3 8 1 0 5 7 6 3 5 4 0 2 1 6 8 7 4 3 8 1 0 5 7 6 2 5 7 6 2 4 3 8 1 0 6 8 7 3 5 4 0 2 1 7 6 2 4 3 8 1 0 5 8 1 0 5 7 6 2 4 3 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
При поиске ортогональных диагональных соквадратов к ЛК используются диагональные трансверсали. Определение: диагональной трансверсалью ЛК называется трансверсаль, которая содержит точно по одному элементу из каждой диагонали ЛК (главной и побочной). Пример  На иллюстрации показан ДЛК 10-го порядка и в нём раскрашены три диагональные трансверсали. Как сообщает программа Белышева Ортогон_У, всего в этом ДЛК имеется 866 диагональных трансверсалей и у него есть 4 ортогональных ДЛК Проверка ДЛК10 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 866 Соквадратов: 4 Время в сек: 5 А общих трансверсалей у этого ДЛК 5504, как сообщает программа Беляева Name:a.txt 1 - only the diagonal Max=100 1 480 480 608 576 608 608 576 608 480 480 :5504 sq=100 44 46 48 50 52 53 54 55 cm=55 cmm=55 END И кроме четырёх ортогональных ДЛК он имеет ещё кучу ортогональных ЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А вот этот ассоциативный ДЛК 9-го порядка 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 имеет 323 диагональные трансверсали (как сообщает программа Белышева Ортогон_У) и 516 ортогональных диагональных соквадратов. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Колдую с трансверсалями :) Давно не занималась трансверсалями, позабылось малость. Да и остановилась я на самом начальном этапе знакомства с ними - на уровне определения. Сергей Беляев очень быстро реализовал трансверсальный поиск ОЛК, и не пришлось особо вникать в этот алгоритм. Вот иллюстрация задумки 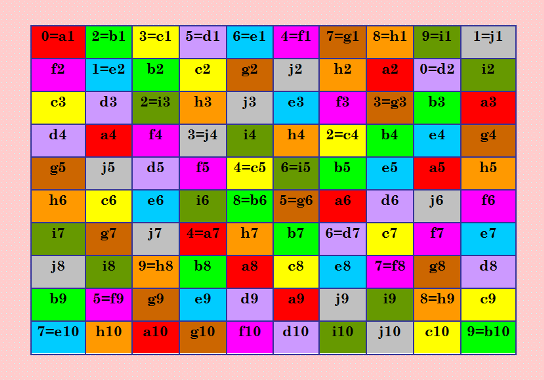 Ещё не знаю, что даст эта задумка. В любом случае интересно поколдовать с трансверсалями. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пожалуй, поясню, что изображено на иллюстрации. В ДЛК заданы главная и побочная диагонали, соответствующие СН ДЛК из линейки №6. Задана также первая строка. Далее, раскрашены диагональные трансверсали, дающие один из типов наборов непересекающихся трансверсалей. Каждая трансверсаль окрашена в свой цвет и обозначена своей буквой, первая трансверсаль - {ai}, вторая трансверсаль - {bi} и т. д. Вроде всё правильно, на мой взгляд. Дальше хочу поиграться с этим ДЛК, надо написать программу. Мучает один вопрос, хочу его решить. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Посмотрела на свежий взгляд и нашла ошибку. Трансверсаль {hi} содержит два одинаковых элемента - 8. Просмотрела вчера. Надо попробовать изменить первую строку ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Получилось с 9-м вариантом первой строки 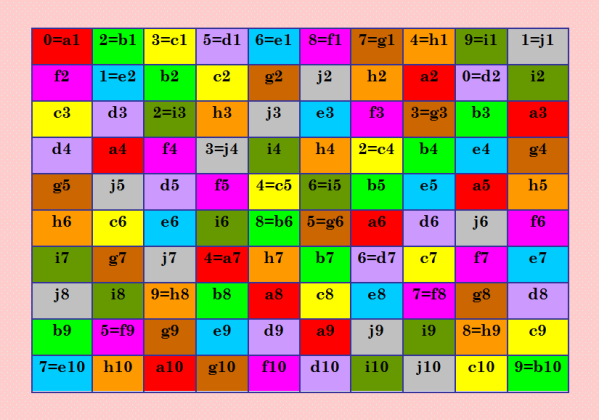 Теперь, кажется, всё правильно :) Можно писать программу по этому шаблону. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программу написала. Поскольку программа длинная, пришлось пока изменить начальные данные, чтобы сразу получилось известное решение. Известное решение программа построила, это самый-самый знаменитый "браун", давший первую четвёрку (начало которой было положено Брауном с компанией, а конец доработал О. Заикин). А начальные данные, как уже говорилось выше, это обе диагонали и первая строка ДЛК. Сейчас покажу на иллюстрации, что даёт тест. При этом программа делает полный перебор и решение выдаёт единственное! (если, конечно, я не наврала в программе). Тэк-с, поигралась с трансверсалями :) Вопрос, который мучает, до конца не решила пока. Теперь надо задать другие начальные данные в программе и снова поиграться. Понятно, что варьироваться будут побочная диагональ и первая строка ДЛК, главная диагональ остаётся неизменной. При заданных диагоналях не любой вариант первой строки подойдёт, как показал пример выше. Заданные трансверсали (раскраской) жёстко регламентируют расположение элементов в ДЛК. Надо заложить в программу предварительную проверку допустимости выбранного варианта первой строки. Вот иллюстрация 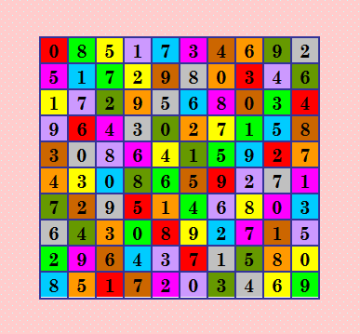 Самый-самый знаменитый "браун" "посажен" на набор из 10 не пересекающихся диагональных трансверсалей. Смотрите раскраску: каждая трансверсаль окрашена в свой цвет. Эта "посадка", как уже написала выше, оказалась единственная. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Показанное на иллюстрации представление будем называть трансверсальным представлением ДЛК. По трансверсальному представлению ДЛК очень легко получить ортогональный соквадрат  По первой трансверсали (красной) записываем в ячейки число 0, по второй трансверсали (зелёной) записываем в ячейки число 1 и т. д. по всем 10 трансверсалям. Нахожу по программе С. Беляева четвёрку от ДЛК (Square), трансверсальное представление которого показано на иллюстрации 0 1 2 3 4 5 6 7 8 9 1 6 9 2 0 3 7 8 5 4 9 8 3 4 5 0 2 1 6 7 3 5 8 7 2 1 0 4 9 6 2 9 5 8 1 7 4 6 0 3 4 0 6 9 3 8 1 5 7 2 5 4 7 6 8 2 9 0 3 1 6 3 4 5 7 9 8 2 1 0 7 2 1 0 9 6 5 3 4 8 8 7 0 1 6 4 3 9 2 5 sq1 0 1 2 3 4 5 6 7 8 9 3 9 1 8 6 4 5 0 7 2 7 3 5 2 9 6 8 4 1 0 4 0 9 6 8 3 2 1 5 7 2 7 0 5 3 8 1 9 4 6 8 4 6 9 1 7 3 2 0 5 5 6 7 0 2 1 4 3 9 8 9 2 3 1 5 0 7 8 6 4 1 5 8 4 7 9 0 6 2 3 6 8 4 7 0 2 9 5 3 1 sq2 0 1 2 3 4 5 6 7 8 9 5 4 1 2 6 9 7 0 3 8 2 3 8 7 9 4 5 6 1 0 3 0 5 9 8 7 2 1 4 6 6 9 3 5 2 8 1 4 0 7 7 2 4 8 1 6 0 3 9 5 8 6 9 0 7 1 3 2 5 4 9 8 7 1 0 2 4 5 6 3 1 5 6 4 3 0 9 8 7 2 4 7 0 6 5 3 8 9 2 1 sq3 0 1 2 3 4 5 6 7 8 9 7 2 9 4 5 3 1 8 0 6 9 8 5 1 3 0 7 4 6 2 2 4 8 7 6 1 3 0 9 5 3 5 0 8 1 6 4 9 2 7 4 9 7 6 2 8 0 3 5 1 1 0 6 5 8 7 9 2 3 4 5 3 1 2 9 4 8 6 7 0 6 7 3 9 0 2 5 1 4 8 8 6 4 0 7 9 2 5 1 3 sq4 Square: 0 8 5 1 7 3 4 6 9 2 5 1 7 2 9 8 0 3 4 6 1 7 2 9 5 6 8 0 3 4 9 6 4 3 0 2 7 1 5 8 3 0 8 6 4 1 5 9 2 7 4 3 0 8 6 5 9 2 7 1 7 2 9 5 1 4 6 8 0 3 6 4 3 0 8 9 2 7 1 5 2 9 6 4 3 7 1 5 8 0 8 5 1 7 2 0 3 4 6 9 Всё верно: найденный по трансверсальному представлению ортогональный соквадрат здесь sq3. А теперь по sq1, например, найдём другое трансверсальное представление исходного ДЛК (самого-самого знаменитого "брауна"). Ушла искать :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот оно - трансверсальное представление самого-самого знаменитого "брауна", соответствующее ортогональному соквадрату sq1  Точно так же можно сделать трансверсальные представления этого ДЛК, соответствующие ортогональным соквадратам sq2 и sq4, технология понятна. Таким образом, этот "браун" имеет 4 различных трансверсальных представления, которые и дают 4 ортогональных соквадрата. Как уже сообщалось здесь https://boinc.progger.info/odlk/forum_thread.php?id=47&postid=1196#1196 у этого "брауна" имеется 866 диагональных трансверсалей Проверка ДЛК10 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 866 Соквадратов: 4 Время в сек: 5 Это сообщила программа Белышева. То же самое сообщает программа Беляева Name:a.txt 1 - only the diagonal 1 Max=100 1 93 63 102 88 87 87 88 102 63 93 :866 sq=4 50 60 cm=60 cmm=60 END Вот, значит, так: из 866 диагональных трансверсалей нашлись 4 различных набора по 10 не пересекающихся трансверсалей, которые и дали 4 ортогональных диагональных соквадрата. И первый вопрос, который постоянно крутится в голове (может быть, и глупый): сколько всего существует различных типов трансверсальных представлений нормализованного по главной диагонали ДЛК? Замечание: нормализованным по главной диагонали ДЛК будем называть ДЛК, содержащий в главной диагонали естественную перестановку 0, 1, 2, ..., n-1. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё одно важное замечание: поскольку мы занимаемся поиском ортогональных пар ДЛК, рассматривать будем трансверсальные представления ДЛК, состоящие только из диагональных трансверсалей. В дальнейшем будет использоваться для указанных трансверсальных представлений аббревиатура ТП-Д. Теперь рассмотрим этот ДЛК из линейки №1 0 2 4 7 8 9 5 6 3 1 5 1 9 6 3 2 4 8 0 7 6 7 2 9 1 0 8 3 5 4 9 4 0 3 5 7 2 1 6 8 7 0 3 8 4 6 9 2 1 5 2 8 6 0 7 5 1 4 9 3 1 5 8 4 2 3 6 9 7 0 4 3 5 1 9 8 0 7 2 6 3 9 1 5 6 4 7 0 8 2 8 6 7 2 0 1 3 5 4 9 Этот СН ДЛК (который является КФ) даёт восьмёрку 0 1 2 3 4 5 6 7 8 9 9 7 4 1 3 0 8 5 2 6 2 5 8 9 6 7 0 1 4 3 8 4 3 6 2 9 7 0 5 1 7 6 9 8 5 4 1 2 3 0 3 2 6 4 8 1 5 9 0 7 4 8 7 0 9 2 3 6 1 5 1 0 5 2 7 3 9 4 6 8 5 3 1 7 0 6 2 8 9 4 6 9 0 5 1 8 4 3 7 2 sq1 0 1 2 3 4 5 6 7 8 9 9 7 4 1 3 0 8 5 2 6 2 5 8 9 6 7 0 1 4 3 8 4 3 6 2 9 7 0 5 1 7 6 9 8 5 4 1 2 3 0 3 2 6 5 8 1 4 9 0 7 5 8 7 0 9 2 3 6 1 4 1 0 5 2 7 3 9 4 6 8 4 3 1 7 0 6 2 8 9 5 6 9 0 4 1 8 5 3 7 2 sq2 0 1 2 3 4 5 6 7 8 9 9 7 4 8 3 0 1 5 2 6 2 5 8 9 6 7 0 1 4 3 1 4 3 6 2 9 7 0 5 8 7 6 9 1 5 4 8 2 3 0 3 2 6 4 8 1 5 9 0 7 4 8 7 0 9 2 3 6 1 5 8 0 5 2 7 3 9 4 6 1 5 3 1 7 0 6 2 8 9 4 6 9 0 5 1 8 4 3 7 2 sq3 0 1 2 3 4 5 6 7 8 9 9 7 4 8 3 0 1 5 2 6 2 5 8 9 6 7 0 1 4 3 1 4 3 6 2 9 7 0 5 8 7 6 9 1 5 4 8 2 3 0 3 2 6 5 8 1 4 9 0 7 5 8 7 0 9 2 3 6 1 4 8 0 5 2 7 3 9 4 6 1 4 3 1 7 0 6 2 8 9 5 6 9 0 4 1 8 5 3 7 2 sq4 0 1 2 3 4 5 6 7 8 9 3 7 4 1 9 6 8 5 2 0 6 5 8 9 2 3 0 1 4 7 8 4 9 2 0 7 3 6 5 1 9 6 7 8 5 4 1 0 3 2 2 9 0 4 8 1 5 3 7 6 4 8 3 6 7 0 9 2 1 5 1 3 5 0 6 2 7 4 9 8 5 0 1 7 3 9 2 8 6 4 7 2 6 5 1 8 4 9 0 3 sq5 0 1 2 3 4 5 6 7 8 9 3 7 4 1 9 6 8 5 2 0 6 5 8 9 2 3 0 1 4 7 8 4 9 2 0 7 3 6 5 1 9 6 7 8 5 4 1 0 3 2 2 9 0 5 8 1 4 3 7 6 5 8 3 6 7 0 9 2 1 4 1 3 5 0 6 2 7 4 9 8 4 0 1 7 3 9 2 8 6 5 7 2 6 4 1 8 5 9 0 3 sq6 0 1 2 3 4 5 6 7 8 9 3 7 4 8 9 6 1 5 2 0 6 5 8 9 2 3 0 1 4 7 1 4 9 2 0 7 3 6 5 8 9 6 7 1 5 4 8 0 3 2 2 9 0 4 8 1 5 3 7 6 4 8 3 6 7 0 9 2 1 5 8 3 5 0 6 2 7 4 9 1 5 0 1 7 3 9 2 8 6 4 7 2 6 5 1 8 4 9 0 3 sq7 0 1 2 3 4 5 6 7 8 9 3 7 4 8 9 6 1 5 2 0 6 5 8 9 2 3 0 1 4 7 1 4 9 2 0 7 3 6 5 8 9 6 7 1 5 4 8 0 3 2 2 9 0 5 8 1 4 3 7 6 5 8 3 6 7 0 9 2 1 4 8 3 5 0 6 2 7 4 9 1 4 0 1 7 3 9 2 8 6 5 7 2 6 4 1 8 5 9 0 3 sq8 Square: 0 2 4 7 8 9 5 6 3 1 5 1 9 6 3 2 4 8 0 7 6 7 2 9 1 0 8 3 5 4 9 4 0 3 5 7 2 1 6 8 7 0 3 8 4 6 9 2 1 5 2 8 6 0 7 5 1 4 9 3 1 5 8 4 2 3 6 9 7 0 4 3 5 1 9 8 0 7 2 6 3 9 1 5 6 4 7 0 8 2 8 6 7 2 0 1 3 5 4 9 Точно так же, как показано выше, мы можем сделать восемь ТП-Д исходного ДЛК, соответствующих восьми его ортогональным соквадратам sq1, sq2, ..., sq8. Это ТП-Д, соответствующее ортогональному соквадрату sq1  Выводы из этого примера (могу ошибаться!): 1. Исходный СН ДЛК имеет только 8 различных ТП-Д; 2. Ни один другой СН ДЛК не имеет таких же ТП-Д; 3. Для всего множества СН ДЛК существует ровно столько различных ТП-Д, сколько существует уникальных ортогональных пар СН ДЛК. PS. Я так подробно рассматриваю примеры ТП-Д, пытаясь уложить в стройную логичную цепочку свои представления о ТП-Д. Может быть, для кого-то всё это очевидные вещи. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот тут нашла вопрос о трансверсалях https://math.stackexchange.com/questions/1743064/transversals-of-latin-squares/2597339#2597339 Я там о наших проектах написала :) Если не удалят, как рекламу. Посмотрим. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ответ со ссылками на проекты им не понравился :) Сейчас написала новый ответ, привела пример, который в предыдущем посте. Интересно: обнаружила при написании ответа, что исходный ДЛК имеет всего 104 диагональные трансверсали. И восьмёрочка! Вот протокол работы программы С. Беляева Name:a.txt 1 - only the diagonal 1 Max=100 1 11 13 3 13 12 12 13 3 13 11 :104 sq=8 38 cm=38 cmm=38 END Классный квадратик! Ну конечно же - он симметричный по Гергели/Брауну. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, мне понравилась там форма записи трансверсалей t1 ={(1,1,1),(2,4,5),(3,3,4),(4,5,2),(5,2,3)}
t2 ={(1,4,4),(2,1,2),(3,5,1),(4,3,5),(5,2,3)}
t3 ={(1,5,5),(2,3,1),(3,4,2),(4,1,4),(5,2,3)}
Всё просто: первые два числа - номер строки и номер столбца, третье число - элемент в данной ячейке. Применительно к нашей картинке  первая трансверсаль (красная) запишется так: t1={(1,1,0),(2,6,2),(3,7,8),(4,8,1),(5,10,5),(6,9,9),(7,4,4),(8,2,3),(9,5,6),(10,3,7)}Аналогично остальные девять трансверсалей. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Здесь https://boinc.progger.info/odlk/forum_thread.php?id=54&postid=1339#1339 я показала группу MODLS 15-го порядка, состоящую из 4-х ДЛК. Интересная группа! Попробовала построить ТП-Д первого ДЛК группы в соответствии со вторым ДЛК, ортогональным ему. Вот что получилось 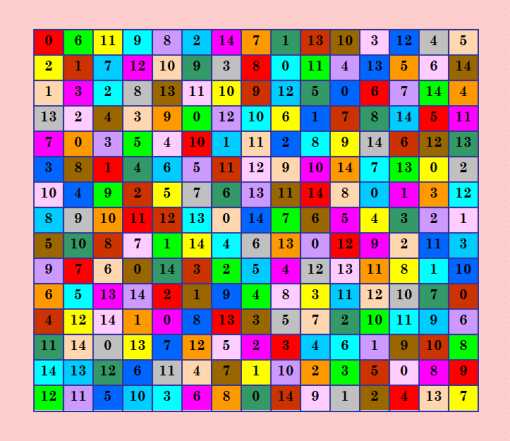 Вроде правильное ТП-Д, все диагональные трансверсали в порядке. Посмотрела я на синюю трансверсаль и подумалось, что ДЛК этот обладает какой-то симметрией. Присмотрелась получше. Точно, он ассоциативный. Сейчас нормализую главную диагональ в этом ДЛК, чтобы лучше увидеть ассоциативность. Готово! 0 6 10 12 13 2 7 14 1 8 11 3 9 4 5 2 1 14 9 11 12 3 13 0 10 4 8 5 6 7 1 3 2 13 8 10 11 12 9 5 0 6 14 7 4 8 2 4 3 12 0 9 11 6 1 14 13 7 5 10 14 0 3 5 4 11 1 10 2 13 12 7 6 9 8 3 13 1 4 6 5 10 9 12 11 7 14 8 0 2 11 4 12 2 5 14 6 8 10 7 13 0 1 3 9 13 12 11 10 9 8 0 7 14 6 5 4 3 2 1 5 11 13 14 1 7 4 6 8 0 9 12 2 10 3 12 14 6 0 7 3 2 5 4 9 8 10 13 1 11 6 5 8 7 2 1 12 4 13 3 10 9 11 14 0 4 9 7 1 0 13 8 3 5 14 2 11 10 12 6 10 7 0 8 14 9 5 2 3 4 6 1 12 11 13 7 8 9 6 10 4 14 1 11 2 3 5 0 13 12 9 10 5 11 3 6 13 0 7 12 1 2 4 8 14 Да, этот ДЛК ассоциативный. Думаю, что у него должна быть куча ортогональных диагональных соквадратов. Но найти их все проблематично. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Используя свойство ассоциативности данного ДЛК, составила новое ТП-Д 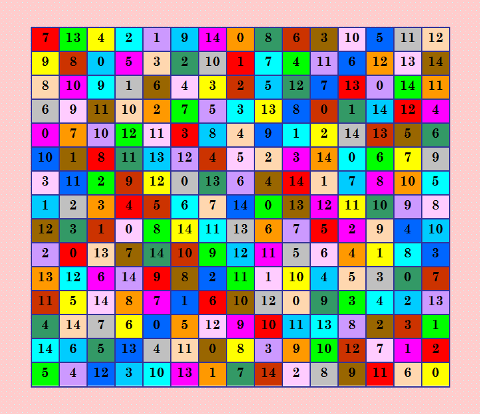 Весьма интересно! Полученный таким образом ДЛК тоже ортогонален второму ДЛК группы MODLS 15-го порядка, вот этому 0 10 7 2 5 11 8 13 6 1 9 4 14 12 3 7 1 11 8 3 6 12 0 2 10 5 14 13 4 9 3 8 2 12 9 4 7 1 11 6 14 0 5 10 13 12 4 9 3 13 10 5 2 7 14 1 6 11 0 8 8 13 5 10 4 0 11 3 14 2 7 12 1 9 6 14 9 0 6 11 5 1 4 3 8 13 2 10 7 12 4 14 10 1 7 12 6 5 9 0 3 11 8 13 2 11 12 13 0 1 2 3 14 10 9 8 7 6 5 4 9 6 1 4 10 7 2 12 13 5 0 8 3 14 11 5 0 3 9 6 1 10 11 8 12 4 13 7 2 14 13 2 8 5 0 9 14 10 4 7 11 3 12 6 1 1 7 4 13 8 14 0 9 12 3 6 10 2 11 5 6 3 12 7 14 13 4 8 0 11 2 5 9 1 10 2 11 6 14 12 3 9 7 5 13 10 1 4 8 0 10 5 14 11 2 8 13 6 1 4 12 9 0 3 7 Понятно, что ДЛК, представленные первым ТП-Д и вторым ТП-Д, изоморфны, так как они получаются друг из друга переобозначением элементов. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вчера ещё покрутила программу Белышева Ортогон_У для первого ДЛК группы MODLS 15-го порядка Проверка ДЛК15 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 306605 Соквадратов: 0 Время в сек: 38935 20174 8165 3125 581 203 47 10 Больше 10 часов. Увы! Эх, как же к этим ортогональкам подобраться? Очень хочется, но не получается. А они ведь есть наверняка. Не может быть, чтобы у такого хорошего квадратика (ассоциативного!) были только три ортогональных ДЛК. Я бы и ещё покрутила, но... непрерывно не могу, так как ночью у меня компьютер не работает. А после прерывания всё начинаю с самого начала. Так ведь никогда не дойти до решения - хоть какого-нибудь. Если кому интересно и есть возможность покрутить непрерывно, возьмите задачку :) Программа Белышева Ортогон_У выложена на форуме boinc.ru, ссылку я выше давала. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это ассоциативный классический магический квадрат 15-го порядка, построенный методом террас (нетрадиционная форма записи; для перехода к традиционной форме записи надо все элементы квадрата увеличить на единицу) 7 120 23 136 39 152 55 168 71 184 87 200 103 216 119 134 22 135 38 151 54 167 70 183 86 199 102 215 118 6 21 149 37 150 53 166 69 182 85 198 101 214 117 5 133 148 36 164 52 165 68 181 84 197 100 213 116 4 132 20 35 163 51 179 67 180 83 196 99 212 115 3 131 19 147 162 50 178 66 194 82 195 98 211 114 2 130 18 146 34 49 177 65 193 81 209 97 210 113 1 129 17 145 33 161 176 64 192 80 208 96 224 112 0 128 16 144 32 160 48 63 191 79 207 95 223 111 14 127 15 143 31 159 47 175 190 78 206 94 222 110 13 126 29 142 30 158 46 174 62 77 205 93 221 109 12 125 28 141 44 157 45 173 61 189 204 92 220 108 11 124 27 140 43 156 59 172 60 188 76 91 219 107 10 123 26 139 42 155 58 171 74 187 75 203 218 106 9 122 25 138 41 154 57 170 73 186 89 202 90 105 8 121 24 137 40 153 56 169 72 185 88 201 104 217 Разложила его на два ортогональных ЛК, к моему удивлению ЛК оказались не диагональными: 7 0 8 1 9 2 10 3 11 4 12 5 13 6 14 14 7 0 8 1 9 2 10 3 11 4 12 5 13 6 6 14 7 0 8 1 9 2 10 3 11 4 12 5 13 13 6 14 7 0 8 1 9 2 10 3 11 4 12 5 5 13 6 14 7 0 8 1 9 2 10 3 11 4 12 12 5 13 6 14 7 0 8 1 9 2 10 3 11 4 4 12 5 13 6 14 7 0 8 1 9 2 10 3 11 11 4 12 5 13 6 14 7 0 8 1 9 2 10 3 3 11 4 12 5 13 6 14 7 0 8 1 9 2 10 10 3 11 4 12 5 13 6 14 7 0 8 1 9 2 2 10 3 11 4 12 5 13 6 14 7 0 8 1 9 9 2 10 3 11 4 12 5 13 6 14 7 0 8 1 1 9 2 10 3 11 4 12 5 13 6 14 7 0 8 8 1 9 2 10 3 11 4 12 5 13 6 14 7 0 0 8 1 9 2 10 3 11 4 12 5 13 6 14 7 0 8 1 9 2 10 3 11 4 12 5 13 6 14 7 8 1 9 2 10 3 11 4 12 5 13 6 14 7 0 1 9 2 10 3 11 4 12 5 13 6 14 7 0 8 9 2 10 3 11 4 12 5 13 6 14 7 0 8 1 2 10 3 11 4 12 5 13 6 14 7 0 8 1 9 10 3 11 4 12 5 13 6 14 7 0 8 1 9 2 3 11 4 12 5 13 6 14 7 0 8 1 9 2 10 11 4 12 5 13 6 14 7 0 8 1 9 2 10 3 4 12 5 13 6 14 7 0 8 1 9 2 10 3 11 12 5 13 6 14 7 0 8 1 9 2 10 3 11 4 5 13 6 14 7 0 8 1 9 2 10 3 11 4 12 13 6 14 7 0 8 1 9 2 10 3 11 4 12 5 6 14 7 0 8 1 9 2 10 3 11 4 12 5 13 14 7 0 8 1 9 2 10 3 11 4 12 5 13 6 7 0 8 1 9 2 10 3 11 4 12 5 13 6 14 Оригинальные квадратики. Построила ТП (не ТП-Д!) первого ЛК по второму, ортогональному. Вот что получилось  Красивые трансверсали! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger