Различные группы пар ОДЛК10
Message boards :
Science :
Различные группы пар ОДЛК10
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У Ватутина со товарищи новое открытие http://forum.boinc.ru/default.aspx?g=posts&m=89697#post89697 Цитирую: ...применяемая нами классификация комбинаторных структур на пустышки, двушки, трешки и пр. (буквы б-ж на рисунке) неполна и ее можно расширить дополнительными комбинаторными структурами (см. картинку). Некоторые из них встречаются более менее часто, другие являются совсем редкими. Из новых структур в ней представлены: О группах ортогональных пар ДЛК 10-го порядка Белышев писал на форуме Math Help Planet больше года назад, причём не только о двушках, тройках и т. д. в чистом виде, то есть когда одному исходному ДЛК ортогональны несколько ДЛК. Вот такая, например, показана Ватутиным группа пар ОДЛК  Не знаю, как эта группа интерпретируется автором. Я понимаю это так: квадраты А и В образуют одиночную ортогональную пару (однушку), а у квадрата В есть ещё два ортогональных диагональных соквадрата: C и D, то есть от квадрата В происходит тройка. Я изобразила бы тройку иначе: от квадрата А три ортогональных соквадрата: B, C, D. Вот тройка, найденная Белышевым  В нашем BOINC- проекте были получены аналогичные конфигурации, только у квадрата В есть а) три своих ортогональных соквадрата; б) четыре своих ортогональных соквадрата. Вариантов а) найдено два. Вариант б) найден в проекте вчера. Дальше покажу иллюстрации этих конфигураций. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Начну с варианта б), недавно найденное в проекте ODLK решение, уникальная четвёрка. Смотрим иллюстрацию  От квадрата А происходит однушка А<-->B. Хорошая однушка, она найдена непосредственно от решения, полученного в проекте (квадрат А - КФ СН ДЛК из линейки №66). Далее, у квадрата В есть четыре ортогональных диагональных соквадрата: квадраты С, D, E, F. Это великолепная четвёрка! От квадрата В происходят 5 ортогональных пар. Но... это не пятёрка! Такая вот вкусная изюминка тут, оставляю изюминку в булочке :) Таким образом, имеем группу из 5 ортогональных пар: однушка и четвёрка. Об этой четвёрке сообщалось тут https://boinc.progger.info/odlk/forum_thread.php?id=39&postid=1021#1021 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Интересно: показанная выше группа ортогональных пар ДЛК может быть дополнена, только не ДЛК, а ЛК. У квадрата В есть два ортогональных ЛК, один из них: 0 1 2 3 4 5 6 7 8 9 8 2 1 0 7 3 5 4 9 6 5 9 8 2 0 4 3 6 1 7 7 4 3 8 5 0 9 1 6 2 1 7 9 4 6 2 8 0 3 5 4 3 7 1 9 6 2 5 0 8 2 6 5 7 8 1 0 9 4 3 9 0 6 5 1 8 7 3 2 4 6 8 0 9 3 7 4 2 5 1 3 5 4 6 2 9 1 8 7 0 У квадрата С есть один ортогональный ЛК: 0 1 2 3 4 5 6 7 8 9 6 8 1 5 3 0 7 9 4 2 9 7 5 4 8 2 3 0 6 1 7 3 6 2 9 1 5 8 0 4 2 0 9 7 6 3 1 4 5 8 8 5 7 1 2 4 0 3 9 6 5 6 4 9 0 8 2 1 3 7 1 4 0 8 5 7 9 6 2 3 4 2 3 6 1 9 8 5 7 0 3 9 8 0 7 6 4 2 1 5 У квадрата D нет ортогональных ЛК; у квадрата E есть два ортогональных ЛК, один из них: 0 1 2 3 4 5 6 7 8 9 5 0 4 8 7 9 2 1 6 3 2 4 9 6 8 7 1 3 0 5 1 5 3 7 2 0 4 6 9 8 8 9 6 2 3 1 0 5 4 7 6 2 7 5 0 3 9 8 1 4 3 8 1 4 6 2 5 9 7 0 9 7 0 1 5 8 3 4 2 6 7 6 5 9 1 4 8 0 3 2 4 3 8 0 9 6 7 2 5 1 И у квадрата F есть три ортогональных ЛК, один из них: 0 1 2 3 4 5 6 7 8 9 4 7 0 5 2 6 3 1 9 8 8 2 3 6 7 0 5 9 1 4 3 6 7 2 1 8 9 0 4 5 5 8 6 1 3 9 0 4 2 7 7 5 8 0 9 3 4 2 6 1 2 0 1 9 8 4 7 3 5 6 6 4 9 7 5 1 2 8 0 3 1 9 5 4 0 7 8 6 3 2 9 3 4 8 6 2 1 5 7 0 И это ещё не всё! У ЛК, ортогонального квадрату С, есть свой ортогональный ЛК: 0 1 2 3 4 5 6 7 8 9 5 4 8 7 9 6 3 1 2 0 7 9 1 0 2 4 5 8 3 6 4 6 0 1 8 9 2 3 5 7 6 2 3 8 1 7 0 9 4 5 1 8 5 2 7 3 9 0 6 4 9 7 6 5 3 0 8 4 1 2 3 5 7 6 0 1 4 2 9 8 8 3 4 9 5 2 7 6 0 1 2 0 9 4 6 8 1 5 7 3 И так далее, дальше не проверяла. Всё-таки нам интересны группы ортогональных пар ДЛК. Жаль только, что все эти ортогональные пары ЛК (и ДЛК) расходятся веером и нигде не замыкаются, чтобы образовать тройку MOLS. Вот в чём проблема! До сих пор открытая проблема. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Теперь показываю вариант а) 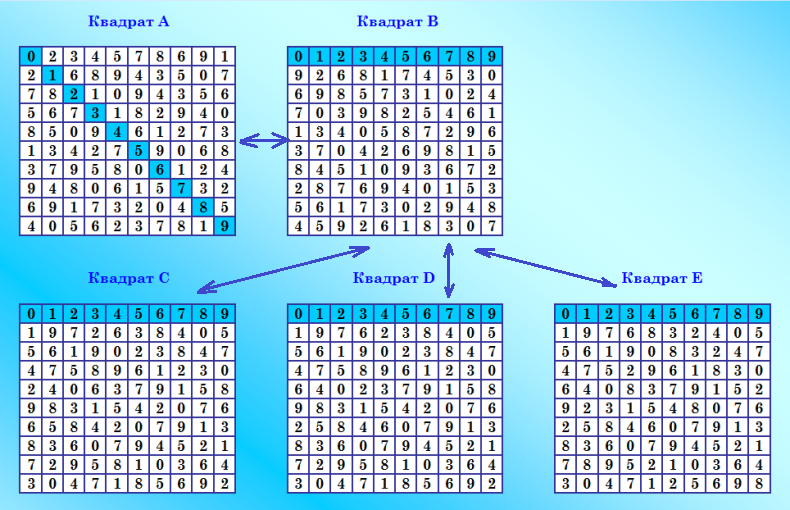 Всё совершенно аналогично показанному выше варианту б), только у квадрата В четыре ортогональных диагональных соквадрата. Но... это не четвёрка! Та же самая изюминка :) От квадрата В происходит великолепная тройка, недавно найденная в филиале проекта ODLK1. Об этой тройке сообщение тут https://boinc.progger.info/odlk/forum_thread.php?id=1&postid=979#979 Квадрат А, породивший эту группу пар ОДЛК, найден в проекте, это КФ СН ДЛК из линейки №57. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А от симметричных ДЛК вообще такие группы получаются - голову сломаешь :) Вот, например, двушка: 0 1 2 3 4 5 6 7 8 9 2 7 5 9 1 8 0 4 3 6 4 0 1 7 3 6 2 8 9 5 3 5 8 6 9 0 7 1 4 2 9 2 3 4 8 1 5 0 6 7 6 9 4 8 2 3 1 5 7 0 8 6 7 0 5 4 9 3 2 1 7 8 6 5 0 9 4 2 1 3 1 4 0 2 6 7 3 9 5 8 5 3 9 1 7 2 8 6 0 4 sq1 0 1 2 3 4 5 6 7 8 9 3 6 5 9 1 8 0 4 2 7 4 0 1 7 3 6 2 8 9 5 7 5 8 2 9 0 3 1 4 6 2 3 9 4 8 1 5 6 7 0 9 2 4 8 6 7 1 5 0 3 8 7 6 0 5 4 9 2 3 1 6 8 7 5 0 9 4 3 1 2 1 4 0 6 2 3 7 9 5 8 5 9 3 1 7 2 8 0 6 4 sq2 Square: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 3 9 8 5 2 7 4 1 0 6 4 3 9 1 7 2 8 0 6 5 8 7 6 0 5 4 9 3 2 1 5 6 1 2 0 9 7 8 3 4 7 0 4 6 1 8 3 5 9 2 9 4 3 7 8 1 2 6 5 0 6 5 7 8 9 0 1 2 4 3 2 8 5 9 6 3 0 4 1 7 Оба ортогональных соквадрата этой двушки sq1 и sq2 дают четвёрки, причём одинаковые! Обозначим в двушке квадрат Square - A, ортогональные ему квадраты: sq1 - B, sq2 - C. Конфигурация такая получается 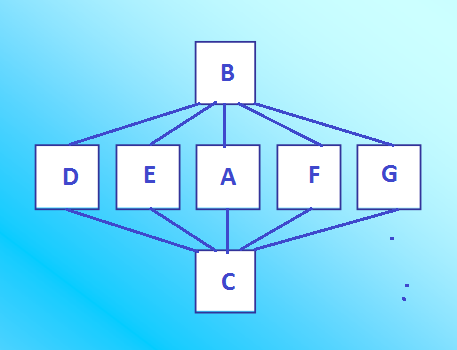 D, E, F, G - ортогональные соквадраты четвёрки, вот они: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 3 9 8 5 2 7 4 1 0 6 4 3 9 1 7 2 8 0 6 5 8 7 6 0 5 4 9 3 2 1 5 6 1 2 0 9 7 8 3 4 7 0 4 6 1 8 3 5 9 2 9 4 3 7 8 1 2 6 5 0 6 5 7 8 9 0 1 2 4 3 2 8 5 9 6 3 0 4 1 7 sq1 - D 0 1 2 3 4 5 6 7 8 9 1 2 0 5 3 6 4 9 7 8 3 9 8 4 2 7 5 1 0 6 5 3 9 1 7 2 8 0 6 4 8 7 6 0 5 4 9 3 2 1 4 6 1 2 0 9 7 8 3 5 7 0 5 6 1 8 3 4 9 2 9 4 3 7 8 1 2 6 5 0 6 5 7 8 9 0 1 2 4 3 2 8 4 9 6 3 0 5 1 7 sq2 - E 0 1 2 3 4 5 6 7 8 9 1 2 9 4 3 6 5 0 7 8 3 9 8 5 2 7 4 1 0 6 4 3 0 1 7 2 8 9 6 5 8 7 6 9 5 4 0 3 2 1 5 6 1 2 0 9 7 8 3 4 7 0 4 6 1 8 3 5 9 2 9 4 3 7 8 1 2 6 5 0 6 5 7 8 9 0 1 2 4 3 2 8 5 0 6 3 9 4 1 7 sq3 - F 0 1 2 3 4 5 6 7 8 9 1 2 9 5 3 6 4 0 7 8 3 9 8 4 2 7 5 1 0 6 5 3 0 1 7 2 8 9 6 4 8 7 6 9 5 4 0 3 2 1 4 6 1 2 0 9 7 8 3 5 7 0 5 6 1 8 3 4 9 2 9 4 3 7 8 1 2 6 5 0 6 5 7 8 9 0 1 2 4 3 2 8 4 0 6 3 9 5 1 7 sq4 - G На самом деле квадрат А можно выбросить из конфигурации, так как он совпадает с квадратом D. Но этот квадрат дал двушку, от которой потом получилась четвёрка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Посмотрела одну конфигурацию у Ватутина здесь http://forum.boinc.ru/default.aspx?g=posts&m=91251#post91251 Цитирую. ДЛК конфигурации DLS 0: 0123456789120478963573856014925916837204365291804790785423164590273168846719052368413259702739064851 DLS 1: 0123456789589621734030485691271672098435876012359442593716082437905816730168495295847320616915840273 DLS 2: 0123456789589621734039485601271672908435876912350442503716982437095816730168495295847320616015849273 DLS 3: 0123456789120476983573658014925918237064385691024790725483164590673128648719250386413259702739084651 DLS 4: 0123456789859621734030485691271672095438576012389442893716052437908516730168495298547320616915840273 DLS 5: 0123456789859621734039485601271672905438576912380442803716952437098516730168495298547320616015849273 DLS 6: 0123456789127406983573658014925918237064385691024797025483164590673128648719250386413259702039784651 DLS 7: 0123456789120476983578653014925918237064835691024790725483164590673128648719250336418259702739084651 Уникальные ДЛК конфигурации Unique CFs for combinatorial structure: DLS 0: 0123456789120478963573856014925916837204365291804790785423164590273168846719052368413259702739064851 DLS 1: 0123456789120459863730578194269546327801591870236446701832956495231078836107495278329651402789640513 DLS 2: 0123456789120476983573658014925918237064385691024790725483164590673128648719250386413259702739084651 DLS 3: 0123456789120459863730678194259645327801691870235445701832965496231078835107496278329651402789640513 DLS 4: 0123456789120476983578653014925918237064835691024790725483164590673128648719250336418259702739084651 Конфигурация показана из всех 8 ОДЛК, включая изоморфные, и названа Венера. Я изобразила эту конфигурацию в реальных квадратах, немного она у меня не уместилась в экран, но понять всё можно, все ОДЛК я обозначила в соответствии с обозначениями в первом списке ОДЛК (8 штук).  На мой взгляд, Венера слегка трухлявая из-за изоморфных ОДЛК. Истинная Венера была бы при всех 8 уникальных ОДЛК в конфигурации, и конечно, при соответствующих парах ОДЛК. Истинной Венеры я не нашла в нашей БД; конечно, проверила мало решений из БД, проверяла четвёрки да и то не все. В нашей БД есть конфигурация с 8 уникальными ОДЛК, но это не Венера. Данная конфигурация была показана, ниже повторю её. Вообще же, по-моему, конфигурации со всеми ОДЛК, включая изоморфные, мало интересны. Если начать изображать все конфигурации с изоморфными ОДЛК, их столько будет! Для меня интерес представляют конфигурации, состоящие из уникальных ОДЛК. Если уж необходимо показать конфигурацию с изоморфными ОДЛК, надо указывать изоморфные ОДЛК и/или отмечать их на иллюстрации. Так что, ищем подлинную Венеру :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот конфигурация из 8 уникальных ОДЛК; четвёрку, порождающую данную конфигурацию, нашёл Demis, помогая мне выполнять эксперимент с псевдоассоциативными ДЛК 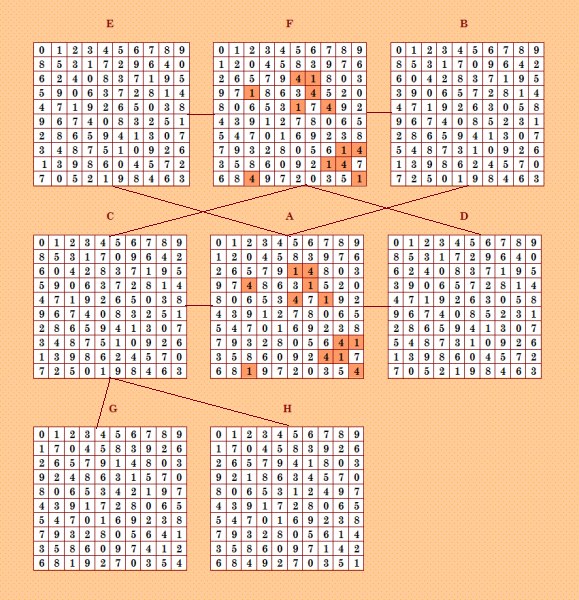 Супер! Конфигурация содержит две четвёрки-близняшки и ещё одну, третью, четвёрку, ну и двушки, само собой. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Четвёрки обычно дают либо 3 уникальных КФ ОДЛК (не полновесные), либо 5 уникальных КФ ОДЛК (полновесные), но встречаются такие четвёрки, которые дают 4 уникальные КФ ОДЛК. Есть и такие четвёрки, которые дают больше 5 уникальных КФ ОДЛК, выше были рассмотрены такие четвёрки, они порождают интересные конфигурации. Пример четвёрки, дающей 4 уникальные КФ ОДЛК 0 2 4 5 7 9 8 6 3 1 9 1 6 8 2 3 5 4 0 7 4 0 2 9 5 8 7 3 1 6 5 9 0 3 6 4 2 1 7 8 3 8 7 0 4 6 1 9 5 2 1 6 3 7 8 5 9 2 4 0 2 7 5 4 0 1 6 8 9 3 8 3 9 6 1 0 4 7 2 5 6 5 1 2 9 7 3 0 8 4 7 4 8 1 3 2 0 5 6 9 Интересно посмотреть на конфигурацию, порождаемую этой четвёркой. Вижу в решениях, происходящих от данной четвёрки, двушки и две четвёрки. Четвёрки не могут быть полновесными и, наверное, близняшки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Нарисовала конфигурацию, порождаемую четвёркой, показанной в предыдущем сообщении 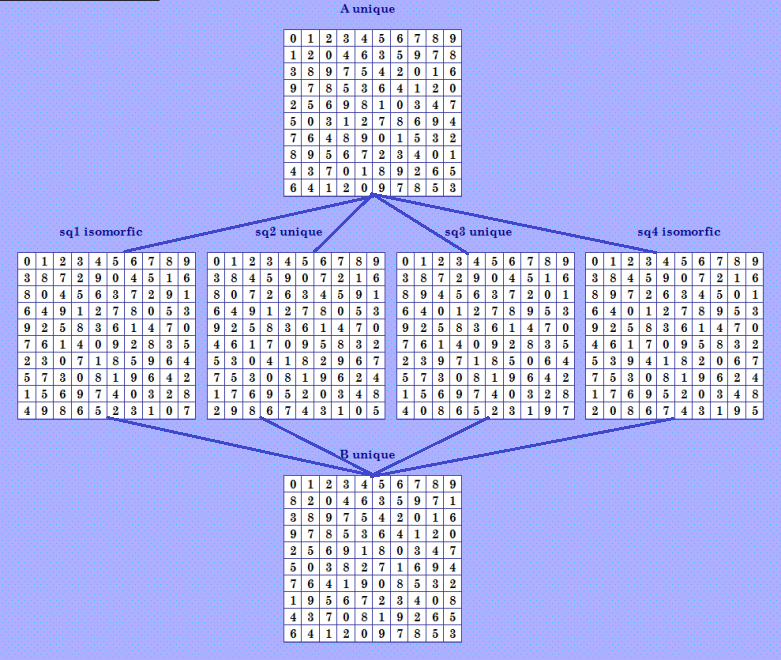 Как и предполагала, это не полновесные четвёрки-близняшки. Подобную конфигурацию я уже показывала раньше. Бывают и полновесные четвёрки-близняшки; такая конфигурация состоит из 6 уникальных КФ ОДЛК. Тоже раньше была показана такая конфигурация. Посмотрю на четвёрки ещё; их много, может быть, ещё что-то интересное обнаружится в смысле оригинальной конфигурации, порождаемой четвёркой. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Бегло посмотрела все четвёрки, имеющиеся в нашей БД КФ ОДЛК (299 штук). Максимальное количество уникальных КФ ОДЛК, порождаемых четвёркой, пока равно 12. Такая конфигурация в нашей БД на данный момент всего одна. Основной ДЛК четвёрки, порождающей эту конфигурацию, во втором формате 0 2 6 9 5 7 8 4 3 1 8 1 5 6 3 2 4 9 0 7 4 5 2 1 8 9 0 3 7 6 7 6 4 3 9 8 2 5 1 0 3 0 9 7 4 6 5 1 2 8 2 4 1 8 7 5 9 0 6 3 1 7 0 4 2 3 6 8 9 5 9 3 8 0 6 4 1 7 5 2 6 9 3 5 0 1 7 2 8 4 5 8 7 2 1 0 3 6 4 9 Я уже много раз показывала эту конфигурацию, конфигурация содержит уникальную десяточку (она пока всего одна известна в нашей БД). Покажу ещё раз. Это в моём изображении 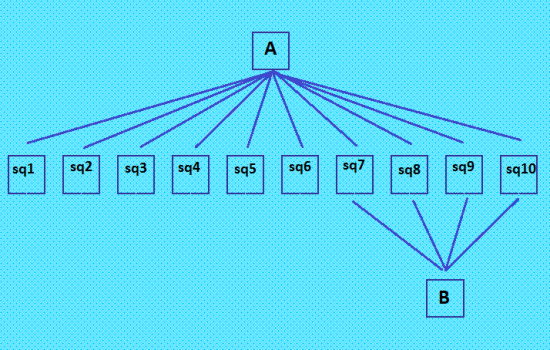 Это художественное изображение Demis, он же дал и название Кубок Грааля 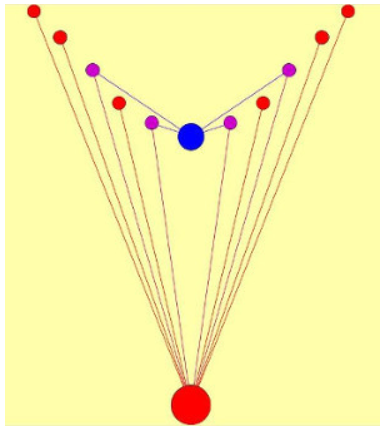 Красивый кубок! Подчеркну: все ОДЛК в данной конфигурации уникальные. В конфигурации 12 уникальных ОДЛК и 14 пар ОДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Следующая интересная конфигурация, порождаемая четвёркой, содержит 8 уникальных ОДЛК. Данная конфигурация порождается любой из трёх следующих четвёрок (основные ДЛК четвёрок во втором формате) 0 3 6 9 8 4 7 5 2 1 9 1 3 7 5 8 4 2 0 6 7 0 2 5 6 9 8 3 1 4 4 6 0 3 9 7 2 1 5 8 8 5 7 2 4 6 1 0 9 3 3 2 8 1 7 5 9 6 4 0 1 9 5 8 0 3 6 4 7 2 6 8 9 4 2 1 0 7 3 5 2 4 1 6 3 0 5 9 8 7 5 7 4 0 1 2 3 8 6 9 0 4 7 5 2 3 9 8 6 1 5 1 9 4 3 2 7 6 0 8 7 6 2 8 0 1 5 3 9 4 9 8 6 3 1 0 2 4 7 5 3 5 1 0 4 6 8 9 2 7 2 9 4 7 8 5 1 0 3 6 8 3 0 9 7 4 6 1 5 2 6 2 5 1 9 8 0 7 4 3 1 7 3 6 5 9 4 2 8 0 4 0 8 2 6 7 3 5 1 9 0 4 7 5 3 2 9 8 6 1 5 1 9 4 2 3 7 6 0 8 7 6 2 8 1 0 5 3 9 4 9 8 6 3 0 1 2 4 7 5 3 5 1 0 4 6 8 9 2 7 2 9 4 7 8 5 1 0 3 6 8 3 0 9 7 4 6 1 5 2 6 2 5 1 9 8 0 7 4 3 1 7 3 6 5 9 4 2 8 0 4 0 8 2 6 7 3 5 1 9 Все эти четвёрки входят в данную конфигурацию. Конфигурация была показана выше https://boinc.progger.info/odlk/forum_thread.php?id=46&postid=2311#2311 Других конфигураций с 8 уникальными ОДЛК, порождаемых четвёрками, в нашей БД пока нет. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Конфигурация была показана выше Кстати, Demis вам задание :) изобразить эту конфигурацию художественно и придумать ей название. Вы и автор конфигурации (четвёрки найдены вами). My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Далее идут конфигурации из 6 уникальных ОДЛК, порождаемые четвёрками. Таких конфигураций я насчитала 11 штук в нашей БД. Эти конфигурации встречаются двух видов (пока), я назвала их так: 1. полновесные четвёрки-близняшки; 2. четвёрка с аппендиксом. Оба вида конфигураций показаны выше. Покажу ещё раз по одной конфигурации каждого вида. Полновесные четвёрки-близняшки 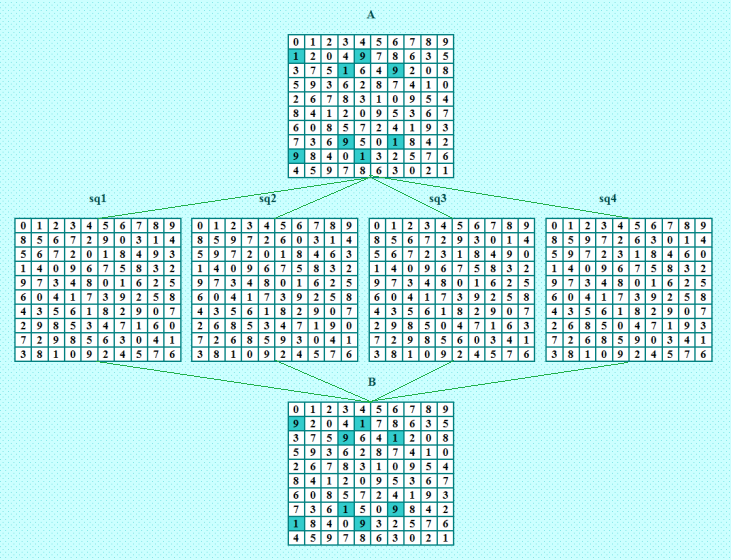 Четвёрка с аппендиксом 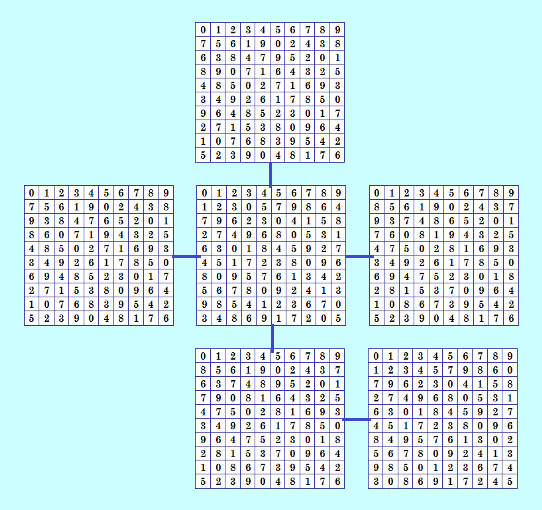 Я исследовала в теме о четвёрках конфигурации с 6 уникальными ОДЛК, порождаемые четвёрками, и обнаружила их только двух указанных видов. Но не уверена, что я проверила все 11 таких конфигураций. И снова подчёркиваю: все представленные конфигурации состоят исключительно из уникальных ОДЛК. PS. Кажется, у Ватутина четвёрка с аппендиксом называется крестом. Ну да, если аппендикс (нижний правый квадрат) развернуть, то получится крест. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
О четвёрках-близняшках смотрите тему https://boinc.progger.info/odlk/forum_thread.php?id=80 Мне кажется, что вполне можно организовать поиск четвёрок-близняшек с помощью узорчатых ДЛК. Я даже писала программы для поиска узорчатых ДЛК (и ЛК), но глубоко тему не исследовала, не хватает времени на все темы. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Далее следуют стандартные полновесные четвёрки, которые состоят из 5 уникальных КФ ОДЛК и порождают простенькую конфигурацию: основной ДЛК и 4 ортогональных соквадрата. Таких четвёрок я насчитала в нашей БД 40 штук. Пример 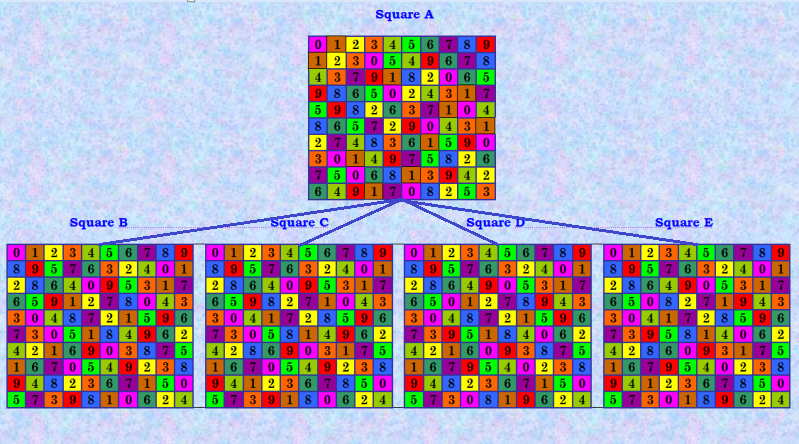 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Далее идут конфигурации, происходящие от четвёрок и состоящие из 4 уникальных КФ ОДЛК. Таких конфигураций в нашей БД сейчас 10 штук. Это не полновесные четвёрки-близняшки. Пример показан тут https://boinc.progger.info/odlk/forum_thread.php?id=46&postid=2316#2316 Не проверила 10 конфигураций; думаю, что они все подобные, ничего другого не дают. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Наконец, последняя и самая многочисленная группа четвёрок порождает конфигурацию, состоящую всего из 3 уникальных КФ ОДЛК. В эту группу входят "симметричные" четвёрки. Ранее всего были найдены четвёрки "симметричные" по Гергели/Брауну (что соответствует коду симметрии (1,31,31) по классификации Белышева); затем найдены четвёрки с симметрией (4,31,31) по классификации Белышева. Возможно есть четвёрки и с другими видами обобщённых симметрий, которые мы ещё не нашли. Пример покажу классический - самую первую из известных четвёрок; эта четвёрка "симметричная" по Гергели/Брауну, начало этой четвёрки было найдено в 1992 г. самим Брауном с компанией. Цитата Начнём с самого первого - исторического - вида четвёрок. Вот такая интересная четвёрка. Я назвала такие четвёрки не полновесными, так как они дают всего 3 уникальных КФ ОДЛК, то есть из четырёх ортогональных соквадратов четвёрки два уникальные и два изоморфные. Интересно, что большинство четвёрок, найденных на сегодня, "симметричные". My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Подведу итоги по конфигурациям, порождаемым четвёрками, имеющимися в нашей БД на данный момент. 1. 12 уникальных КФ ОДЛК Кубок Грааля. 2. 8 уникальных КФ ОДЛК без названия. 3. 6 уникальных КФ ОДЛК: а) полновесные четвёрки-близняшки; б) четвёрка с аппендиксом. 4. 5 уникальных КФ ОДЛК полновесная четвёрка. 5. 4 уникальные КФ ОДЛК не полновесные четвёрки-близняшки. 6. 3 уникальных КФ ОДЛК не полновесная четвёрка. Наверняка со временем будут найдены новые конфигурации, порождаемые четвёрками. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вспомним Венеру Ватутина. Цитата Посмотрела одну конфигурацию у Ватутина здесь Данная конфигурация порождается четвёркой и содержит 5 уникальных ОДЛК, но это не полновесная четвёрка, как у нас. Это некая другая конфигурация. Если 3 изоморфных OДЛК выбросить из конфигурации, то Венера будет с дырками. Существует ли подлинная Венера - без дырок? Для этого конфигурация должна содержать 8 уникальных ОДЛК, ну и, конечно, соответствующие пары ОДЛК. Кстати, надо внимательно просмотреть 40 конфигураций, порождаемых четвёрками нашей БД и состоящих из 5 уникальных ОДЛК. Вдруг среди них есть не только полновесные четвёрки... Надо заняться этим на досуге. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Кстати, надо внимательно просмотреть 40 конфигураций, порождаемых четвёрками нашей БД и состоящих из 5 уникальных ОДЛК. Просмотрела, никаких новых конфигураций не обнаружила. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger
