Закончилась генерация новой порции ОДЛК.
В этой порции максимальная группа из 18 ортогональных пар

[DLK(18)]
0 1 2 3 4 5 6 7 8
7 8 1 4 6 2 0 5 3
8 3 5 6 2 7 1 0 4
4 6 7 1 5 0 3 8 2
5 0 6 8 3 4 7 2 1
3 4 0 2 7 6 8 1 5
1 5 4 7 8 3 2 6 0
2 7 3 0 1 8 5 4 6
6 2 8 5 0 1 4 3 7
[mate#1]
7 1 0 5 2 3 4 8 6
0 5 3 6 7 4 1 2 8
8 2 6 1 5 7 0 3 4
3 0 5 4 1 8 6 7 2
4 6 8 0 3 5 2 1 7
1 8 4 7 6 2 3 5 0
2 7 1 3 4 0 8 6 5
6 4 7 2 8 1 5 0 3
5 3 2 8 0 6 7 4 1
[mate#2]
7 1 0 5 2 3 4 8 6
0 5 3 6 8 4 1 2 7
8 2 6 1 5 7 0 3 4
3 0 5 4 1 8 6 7 2
4 6 7 0 3 5 2 1 8
1 8 4 7 6 2 3 5 0
2 7 1 3 4 0 8 6 5
6 4 8 2 7 1 5 0 3
5 3 2 8 0 6 7 4 1
[mate#3]
7 5 3 4 6 0 2 8 1
0 3 2 1 7 4 6 5 8
8 1 6 5 0 7 4 2 3
2 4 1 0 3 8 5 7 6
4 0 8 6 2 5 3 1 7
6 8 5 7 4 1 0 3 2
1 7 0 2 5 3 8 6 4
5 6 7 3 8 2 1 4 0
3 2 4 8 1 6 7 0 5
. . . . . . . 
[mate#17]
5 3 1 2 4 7 0 6 8
0 1 7 8 6 2 4 3 5
6 0 4 3 8 5 2 7 1
7 2 8 0 1 6 3 5 4
2 8 5 4 7 3 1 0 6
4 6 3 5 2 8 7 1 0
8 5 0 7 3 1 6 4 2
3 4 6 1 5 0 8 2 7
1 7 2 6 0 4 5 8 3
[mate#18]
5 3 1 2 4 7 0 6 8
0 1 8 7 6 2 4 3 5
6 0 4 3 8 5 2 7 1
8 2 7 0 1 6 3 5 4
2 8 5 4 7 3 1 0 6
4 6 3 5 2 8 7 1 0
7 5 0 8 3 1 6 4 2
3 4 6 1 5 0 8 2 7
1 7 2 6 0 4 5 8 3

Обработала порцию программой Белышева Ортогон_У.
Эффект снежного кома работает потрясающе! Пришлось повторить обработку раз 7, пока не прекратилось появление новых ОДЛК.

Найдено 234 КФ, но увы - ни одна из них не уникальная

Канонизатор ДЛК9

Введено ДЛК:            5526
Найдено КФ:             5292
КФ записаны в файл:     output.txt
Общее время работы:     0.078 сек

В БД по-прежнему содержится 5292 уникальные КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Отличная новость!
Harry White прислал генератор СН ДЛК 9-го порядка аналогичный генератору СН ДЛК 10-го порядка - по линейкам.
Линейки я ему послала, которые нашла в имеющейся у меня БД, он прямо так и заложил их в программу, как я ему послала:

The variants of diagonal

 .  .  .  .  .  .  .  . y1
 .  .  .  .  .  .  . y2  .
 .  .  .  .  .  . y3  .  .
 .  .  .  .  . y4  .  .  .
 .  .  .  . y5  .  .  .  .
 .  .  . y6  .  .  .  .  .
 .  . y7  .  .  .  .  .  .
 . y8  .  .  .  .  .  .  .
y9  .  .  .  .  .  .  .  .


y1 y2 y3 y4 y5 y6 y7 y8 y9

 1  0  3  2  4  6  5  8  7
 1  2  3  8  4  0  5  6  7
 1  2  3  0  4  8  5  6  7
 1  2  0  6  4  7  8  3  5
 1  8  3  6  4  2  5  0  7
 1  0  3  6  4  2  5  8  7
 1  0  3  2  4  7  8  6  5
 1  0  3  7  4  6  8  5  2
 1  0  3  2  4  7  8  5  6
 1  0  3  6  4  7  8  5  2
 1  2  3  6  4  0  8  5  7
 1  2  3  6  4  8  5  0  7
 1  0  3  2  4  6  7  8  5
 1  2  7  6  4  8  5  0  3
 1  2  3  6  4  7  8  0  5
 1  0  3  6  4  2  7  8  5
 1  0  3  7  4  8  5  6  2
 1  0  3  6  4  7  8  2  5
 1  0  3  7  4  6  8  2  5
 1  0  3  7  4  8  5  2  6

Ну вот в таком порядке пусть и будут они у нас, неважно, что не в лексикографическом порядке.
Подчеркну: я не уверена, что это все линейки. БД у меня маленькая пока.

Немножко тестировала программу.
Всё замечательно работает в пакетном файле: миллион СН ДЛК генератор Harry генерирует, этот миллион проверяется программой Белышева Ортогон_У и так в цикле.
Взяла первую линейку, побочная диагональ

1  0  3  2  4  6  5  8  7

Должны быть ассоциативные ДЛК в этой линейке.
Вариантов первой строки в этой линейке программа Harry выдаёт 920.
Взяла первую строку и запустила программу.
Вот первая найденная двушка

[DLK(2)]
0 2 3 4 5 6 7 8 1
2 1 4 5 6 7 8 0 3
6 4 2 7 1 8 3 5 0
4 5 6 3 8 2 0 1 7
3 6 7 8 4 0 1 2 5
1 7 8 6 0 5 2 3 4
8 3 5 0 7 1 6 4 2
5 8 0 1 2 3 4 7 6
7 0 1 2 3 4 5 6 8
[mate#1]
2 1 3 4 5 0 6 7 8
5 3 1 8 7 2 0 6 4
4 2 7 3 6 8 5 0 1
8 7 5 6 1 3 4 2 0
1 6 8 2 0 5 7 4 3
0 5 6 1 3 4 2 8 7
3 0 2 7 4 1 8 5 6
6 4 0 5 8 7 3 1 2
7 8 4 0 2 6 1 3 5
[mate#2]
1 2 3 4 5 6 0 7 8
5 0 6 8 7 1 4 3 2
4 1 7 2 3 8 5 0 6
8 7 5 6 0 4 2 1 3
0 3 8 1 2 5 7 6 4
6 5 2 0 4 3 1 8 7
3 4 1 7 6 2 8 5 0
2 6 0 5 8 7 3 4 1
7 8 4 3 1 0 6 2 5

Ну, наверное, в БД уже есть такие ортогональки. Сейчас проверю.

Да, конечно, есть. От ассоциативных ДЛК, наверное, все КФ ОДЛК в БД есть.
Хотя что-то их не шибко много пока. Я Harry послала имеющуюся у меня БД, он насчитал в ней всего 80 ассоциативных КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Интересный момент -
для ДЛК 10-го порядка существуют симметричные по Гергели/Брауну и не существует ассоциативных.
А для ДЛК 9-го порядка наоборот: не существуют симметричные по Гергели/Брауну, но существуют ассоциативные.

Как симметричные по Гергели/Брауну ДЛК 10-го порядка, так и ассоциативные ДЛК 9-го порядка дают много ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Интересно!
Скармливаю Канонизатору Белышева 516 ортогональных соквадратов вместе с исходным ДЛК. Программа выдаёт:

Канонизатор ДЛК9

Введено ДЛК:            517
Найдено КФ:             74
КФ записаны в файл:     output.txt
Общее время работы:     0.013 сек

Для выхода нажмите любую клавишу . . .

От всех 517 ОДЛК получилось всего 74 КФ!

Это тоже надо проверить по исправленной программе Белышева Канонизатор_ДЛК9.
Может быть, число КФ от данного массива изменится.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверила.
Протокол работы Канонизатора

Канонизатор ДЛК9

Введено ДЛК:            517
Найдено КФ:             54
КФ записаны в файл:     output.txt
Общее время работы:     0.013 сек

Итак, рекордный на данный момент ДЛК 9-го порядка вместе со своими 516 ОДЛК даёт 54 уникальные КФ ОДЛК.
Напомню: этот ДЛК является ассоциативным. Вот его КФ

0 4 7 8 3 6 2 5 1
5 1 4 6 8 3 0 2 7
8 0 2 4 7 1 3 6 5
2 7 1 3 6 8 5 0 4
6 5 0 1 4 7 8 3 2
4 8 3 0 2 5 7 1 6
3 2 5 7 1 4 6 8 0
1 6 8 5 0 2 4 7 3
7 3 6 2 5 0 1 4 8

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

У-р-р-р-а!!!

Но всё по порядку. Продолжаю проверку первой линейки, первой группы, то есть с первым вариантом первой строки.
Связка программ Harry White --> whitefox (о которой писала выше) работает замечательно!

[А кстати, весьма интересная связка - по авторам :) Заметили?]

Итак, продолжаю проверку...



Найдена однушечка

[DLK(1)]
0 2 3 4 5 6 7 8 1
2 1 4 8 7 3 5 0 6
5 4 2 7 8 1 3 6 0
4 6 8 3 1 2 0 5 7
3 7 6 0 4 8 2 1 5
1 3 7 6 0 5 8 2 4
8 0 5 1 2 7 6 4 3
6 8 1 5 3 0 4 7 2
7 5 0 2 6 4 1 3 8
[mate#1]
1 5 4 2 3 0 6 7 8
3 7 8 4 5 1 0 6 2
7 4 2 0 1 6 3 8 5
6 3 0 5 4 7 8 2 1
2 8 6 7 0 3 1 5 4
0 6 7 1 2 8 5 4 3
8 0 5 3 6 2 4 1 7
5 2 1 6 8 4 7 3 0
4 1 3 8 7 5 2 0 6

Интересно, что исходный ДЛК этой однушки не ассоциативный. Это значит, что в данной линейке имеются не только ассоциативные ДЛК, что не удивительно.
Ну и вот нашлась уникальная однушка. От однушки 2 уникальные КФ ОДЛК, которые добавились в БД:

Канонизатор ДЛК9

Введено ДЛК:            5294
Найдено КФ:             5294
КФ записаны в файл:     output.txt
Общее время работы:     0.078 сек

По этому поводу и у-р-р-р-а :)

Теперь в составляемой БД содержится 5294 уникальных КФ ОДЛК.

Пока не проверила, будут ли от ортогонального соквадрата другие ОДЛК. Сейчас проверю.

Проверила, кроме исходного ДЛК, у ортогонального соквадрата нет ОДЛК.
Чистая однушка!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И ещё отличная новость!

Вот и генератор КФ ОДЛК 9-го порядка от Белышева готов
http://forum.boinc.ru/default.aspx?g=posts&m=89784#post89784

Алексей, большое спасибо!

В файл config.txt запишите номер линейки (число из интервала [1..20])...

Ага, значит линеек 20 и есть. Я нашла все. Ура!
Линейки показаны выше.

Отлично! Можно и по этой программе теперь искать ОДЛК.
У меня пока работает связка программ от Harry White и whitefox (Белышева). В этой связке используется генератор Harry White и программа проверки на ОДЛК Ортогон_У Белышева.

Ну, всего 20 линеечек, мелочи. Для BOINC-проекта семечки, на один зуб :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Поехали! :)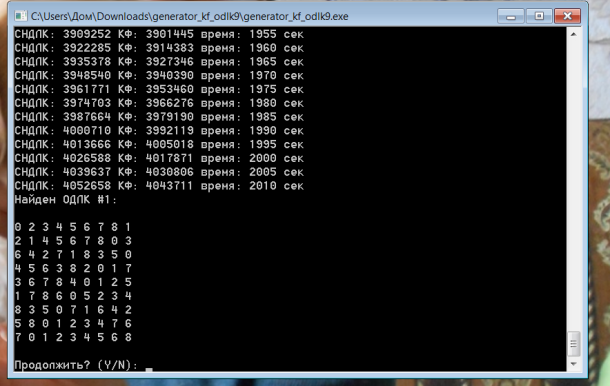



Линейка первая, КФ ОДЛК первая. Всё замечательно!
Интересно: почти на старте КФ начали таять, то есть не каждый СН ДЛК является КФ.

Сравните ---

Немножко тестировала программу.
Всё замечательно работает в пакетном файле: миллион СН ДЛК генератор Harry генерирует, этот миллион проверяется программой Белышева Ортогон_У и так в цикле.
Взяла первую линейку, побочная диагональ

1  0  3  2  4  6  5  8  7

Должны быть ассоциативные ДЛК в этой линейке.
Вариантов первой строки в этой линейке программа Harry выдаёт 920.
Взяла первую строку и запустила программу.
Вот первая найденная двушка

[DLK(2)]
0 2 3 4 5 6 7 8 1
2 1 4 5 6 7 8 0 3
6 4 2 7 1 8 3 5 0
4 5 6 3 8 2 0 1 7
3 6 7 8 4 0 1 2 5
1 7 8 6 0 5 2 3 4
8 3 5 0 7 1 6 4 2
5 8 0 1 2 3 4 7 6
7 0 1 2 3 4 5 6 8
[mate#1]
2 1 3 4 5 0 6 7 8
5 3 1 8 7 2 0 6 4
4 2 7 3 6 8 5 0 1
8 7 5 6 1 3 4 2 0
1 6 8 2 0 5 7 4 3
0 5 6 1 3 4 2 8 7
3 0 2 7 4 1 8 5 6
6 4 0 5 8 7 3 1 2
7 8 4 0 2 6 1 3 5
[mate#2]
1 2 3 4 5 6 0 7 8
5 0 6 8 7 1 4 3 2
4 1 7 2 3 8 5 0 6
8 7 5 6 0 4 2 1 3
0 3 8 1 2 5 7 6 4
6 5 2 0 4 3 1 8 7
3 4 1 7 6 2 8 5 0
2 6 0 5 8 7 3 4 1
7 8 4 3 1 0 6 2 5

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А вот и вторая КФ ОДЛК



Сейчас сравним с найденной недавно уникальной однушкой (по двум программам).

[DLK(1)]
0 2 3 4 5 6 7 8 1
2 1 4 8 7 3 5 0 6
5 4 2 7 8 1 3 6 0
4 6 8 3 1 2 0 5 7
3 7 6 0 4 8 2 1 5
1 3 7 6 0 5 8 2 4
8 0 5 1 2 7 6 4 3
6 8 1 5 3 0 4 7 2
7 5 0 2 6 4 1 3 8
[mate#1]
1 5 4 2 3 0 6 7 8
3 7 8 4 5 1 0 6 2
7 4 2 0 1 6 3 8 5
6 3 0 5 4 7 8 2 1
2 8 6 7 0 3 1 5 4
0 6 7 1 2 8 5 4 3
8 0 5 3 6 2 4 1 7
5 2 1 6 8 4 7 3 0
4 1 3 8 7 5 2 0 6

Да, она самая.

Всё замечательно! Тест прошли. Можно продолжать.
Лучше бы, конечно, в BOINC-проекте продолжать :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И ещё одна чистая однушка найдена - КФ ОДЛК №3

. . . . . . . 
СНДЛК: 15304698 КФ: 15193165 время: 5989 сек
СНДЛК: 15317884 КФ: 15206216 время: 5994 сек
СНДЛК: 15330959 КФ: 15219123 время: 5999 сек
СНДЛК: 15343792 КФ: 15231915 время: 6004 сек
Найден ОДЛК #1:

0 2 3 4 5 6 7 8 1
2 1 6 7 8 3 4 0 5
5 6 2 1 7 8 3 4 0
8 4 7 3 1 2 0 5 6
3 5 8 0 4 7 1 6 2
1 7 0 6 3 5 8 2 4
4 3 5 8 2 0 6 1 7
6 8 1 5 0 4 2 7 3
7 0 4 2 6 1 5 3 8

Продолжить? (Y/N):

Продолжаю...

В БД теперь содержится 5296 уникальных КФ ОДЛК.
А интересная картина прорисовывается: кажется, большинство решений и тут - однушки. А группы пар ОДЛК в основном от ассоциативных ДЛК происходят. Всё аналогично ДЛК 10-го порядка, только симметрия другая.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

КФ ОДЛК №4

. . . . . . . .
СНДЛК: 27250412 КФ: 27014671 время: 10786 сек
СНДЛК: 27263447 КФ: 27027613 время: 10791 сек
СНДЛК: 27276582 КФ: 27040549 время: 10796 сек
СНДЛК: 27289977 КФ: 27053653 время: 10801 сек
СНДЛК: 27303311 КФ: 27066724 время: 10806 сек
Найден ОДЛК #2:

0 2 3 4 5 6 7 8 1
2 1 7 5 3 4 8 0 6
1 4 2 7 0 8 3 6 5
6 5 1 3 8 2 0 4 7
3 6 8 0 4 7 1 5 2
8 3 0 6 7 5 2 1 4
4 7 5 8 1 3 6 2 0
5 8 6 1 2 0 4 7 3
7 0 4 2 6 1 5 3 8

Продолжить? (Y/N): Время работы:        10809.4 сек

И опять чистая однушка!
Обратите внимание, насколько растаяли КФ:

СНДЛК: 27303311 КФ: 27066724 время: 10806 сек

В БД теперь содержится 5298 уникальных КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

В общем, однушки посыпались, ещё одна найдена. Жду, что будет дальше, программа работает.
Скорость очень хорошая, миллион СН ДЛК генерируется и проверяется за 7-8 минут.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А вот чистая двушка не от ассоциативной КФ

[DLK(2)]
0 2 3 4 5 6 7 8 1
3 1 4 2 6 8 5 0 7
4 5 2 8 7 1 3 6 0
6 4 7 3 8 2 0 1 5
2 3 1 0 4 7 8 5 6
1 7 8 6 0 5 2 3 4
8 0 5 7 1 3 6 4 2
5 8 6 1 2 0 4 7 3
7 6 0 5 3 4 1 2 8
[mate#1]
2 0 3 4 5 6 7 8 1
5 8 1 6 0 7 3 4 2
3 7 4 0 1 5 8 2 6
7 6 5 1 4 2 0 3 8
8 2 0 5 7 3 6 1 4
6 4 2 3 8 0 1 7 5
1 3 6 8 2 4 5 0 7
4 5 8 7 3 1 2 6 0
0 1 7 2 6 8 4 5 3
[mate#2]
3 2 4 5 6 0 1 7 8
6 7 8 1 2 4 0 5 3
2 4 5 0 8 6 7 3 1
1 6 0 8 5 3 2 4 7
7 3 1 4 0 2 6 8 5
0 5 3 6 7 1 8 2 4
8 0 2 7 3 5 4 1 6
5 1 7 2 4 8 3 6 0
4 8 6 3 1 7 5 0 2

Двушка даёт 3 уникальные КФ ОДЛК.
Найдено две ассоциативные КФ, которые не добавили в БД уникальных КФ ОДЛК.
И ещё найдено несколько однушек, некоторые из них разветвились.

БД на данный момент содержит 5317 уникальных КФ ОДЛК.
Программа продолжает работать.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А сегодня ортогональки 9-го порядка пропали...
Вчера не успевала их собирать, а сегодня за целый день ни одного решения!

. . . . . . . . 
СНДЛК: 74983123 КФ: 72072105 время: 28997 сек
СНДЛК: 74996015 КФ: 72084743 время: 29002 сек
СНДЛК: 75008591 КФ: 72096974 время: 29007 сек
СНДЛК: 75020972 КФ: 72109228 время: 29012 сек
СНДЛК: 75033957 КФ: 72121719 время: 29017 сек
СНДЛК: 75047072 КФ: 72134543 время: 29022 сек
СНДЛК: 75060541 КФ: 72147450 время: 29027 сек
СНДЛК: 75074582 КФ: 72160413 время: 29032 сек
СНДЛК: 75088453 КФ: 72173392 время: 29037 сек
СНДЛК: 75101762 КФ: 72186336 время: 29042 сек
СНДЛК: 75115468 КФ: 72199338 время: 29047 сек
СНДЛК: 75128603 КФ: 72212317 время: 29052 сек
СНДЛК: 75142258 КФ: 72225387 время: 29057 сек
СНДЛК: 75155749 КФ: 72238423 время: 29062 сек
. . . . . . 

А я думала, что решения так и будут сыпаться, как вчера. Увы и ах! Попалась грибная поляна в самом начале линейки, а теперь вот пусто.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это побочные диагонали в линейках, как они были отправлены мной Harry White

The variants of diagonal

 .  .  .  .  .  .  .  . y1
 .  .  .  .  .  .  . y2  .
 .  .  .  .  .  . y3  .  .
 .  .  .  .  . y4  .  .  .
 .  .  .  . y5  .  .  .  .
 .  .  . y6  .  .  .  .  .
 .  . y7  .  .  .  .  .  .
 . y8  .  .  .  .  .  .  .
y9  .  .  .  .  .  .  .  .


y1 y2 y3 y4 y5 y6 y7 y8 y9

№1: 1  0  3  2  4  6  5  8  7
№2: 1  2  3  8  4  0  5  6  7
№3: 1  2  3  0  4  8  5  6  7
№4: 1  2  0  6  4  7  8  3  5
№5: 1  8  3  6  4  2  5  0  7
№6: 1  0  3  6  4  2  5  8  7
№7: 1  0  3  2  4  7  8  6  5
№8: 1  0  3  7  4  6  8  5  2
№9: 1  0  3  2  4  7  8  5  6
№10: 1  0  3  6  4  7  8  5  2
№11: 1  2  3  6  4  0  8  5  7
№12: 1  2  3  6  4  8  5  0  7
№13: 1  0  3  2  4  6  7  8  5
№14: 1  2  7  6  4  8  5  0  3
№15: 1  2  3  6  4  7  8  0  5
№16: 1  0  3  6  4  2  7  8  5
№17: 1  0  3  7  4  8  5  6  2
№18: 1  0  3  6  4  7  8  2  5
№19: 1  0  3  7  4  6  8  2  5
№20: 1  0  3  7  4  8  5  2  6

Как я уже писала, Harry в таком порядке и заложил линейки в свою программу.
Я перенумеровала линейки в лексикографическом порядке.
Не знаю, каков порядок линеек у Белышева, но, по крайней мере, линейка №1 совпадает.
Кроме того, нашла для каждой линейки минимальную КФ и количество вариантов первой строки, используя программу Harry.
Вот что у меня получилось

Линейка №1 (1)
1 0 3 2 4 6 5 8 7

содержит ассоциативные ДЛК
вариантов первой строки 920
минимальная КФ
0 2 3 4 5 6 7 8 1
2 1 4 5 3 7 8 0 6
1 0 2 7 6 8 3 4 5
4 5 0 3 8 2 1 6 7
5 6 7 8 4 0 2 1 3
3 7 8 6 1 5 4 2 0
8 4 5 0 7 1 6 3 2
6 8 1 2 0 3 5 7 4
7 3 6 1 2 4 0 5 8

Линейка №2 (13)
1 0 3 2 4 6 7 8 5

вариантов первой строки 924
минимальная КФ
0 2 3 4 5 6 7 8 1
2 1 4 5 3 7 8 0 6
1 0 2 7 6 8 3 4 5
4 5 0 3 8 2 1 6 7
3 7 6 8 4 0 5 1 2
7 3 8 6 1 5 0 2 4
8 4 7 1 2 3 6 5 0
6 8 5 2 0 1 4 7 3
5 6 1 0 7 4 2 3 8

Линейка №3 (9)
1 0 3 2 4 7 8 5 6

вариантов первой строки 928
минимальная КФ
0 2 3 4 5 6 7 8 1
2 1 4 5 3 7 8 0 6
1 0 2 6 7 8 3 4 5
4 6 0 3 8 2 1 5 7
7 3 5 8 4 1 0 6 2
3 8 1 7 6 5 4 2 0
5 7 8 0 2 3 6 1 4
8 5 6 1 0 4 2 7 3
6 4 7 2 1 0 5 3 8

Линейка №4 (7)
1 0 3 2 4 7 8 6 5

вариантов первой строки 928
минимальная КФ
0 2 3 4 5 6 7 8 1
2 1 4 5 3 7 8 0 6
1 0 2 6 7 8 3 4 5
4 5 0 3 8 2 1 6 7
3 7 6 8 4 0 5 1 2
6 8 1 7 0 5 2 3 4
7 3 8 2 1 4 6 5 0
8 6 5 0 2 1 4 7 3
5 4 7 1 6 3 0 2 8

Линейка №5 (6)
1 0 3 6 4 2 5 8 7

содержит ассоциативные ДЛК
вариантов первой строки 916
минимальная КФ
0 2 3 4 5 7 8 6 1
2 1 4 5 3 8 7 0 6
1 0 2 6 7 4 3 8 5
4 5 0 3 8 6 1 2 7
3 6 7 8 4 0 5 1 2
6 7 8 2 1 5 0 3 4
8 3 5 7 2 1 6 4 0
5 8 1 0 6 2 4 7 3
7 4 6 1 0 3 2 5 8

Линейка №6 (16)
1 0 3 6 4 2 7 8 5

вариантов первой строки 922
минимальная КФ
0 2 3 4 5 7 8 6 1
2 1 4 5 3 8 7 0 6
1 0 2 6 7 4 3 8 5
4 5 0 3 8 6 1 2 7
3 7 6 8 4 0 5 1 2
7 6 8 2 1 5 4 3 0
8 4 7 0 2 1 6 5 3
6 8 5 1 0 3 2 7 4
5 3 1 7 6 2 0 4 8

Линейка №7 (18)
1 0 3 6 4 7 8 2 5

вариантов первой строки 927
минимальная КФ
0 3 4 2 5 7 8 6 1
2 1 3 4 6 8 5 0 7
1 0 2 5 7 4 3 8 6
4 5 0 3 8 6 7 1 2
3 6 7 8 4 0 1 2 5
6 8 1 7 0 5 2 3 4
7 4 8 0 1 2 6 5 3
8 2 5 6 3 1 4 7 0
5 7 6 1 2 3 0 4 8

Линейка №8 (10)
1 0 3 6 4 7 8 5 2

вариантов первой строки 926
минимальная КФ
0 2 3 4 5 7 8 6 1
3 1 4 2 6 8 5 0 7
1 0 2 5 7 4 3 8 6
4 7 0 3 8 6 1 2 5
5 6 7 8 4 0 2 1 3
6 8 1 7 2 5 0 3 4
7 4 8 0 1 3 6 5 2
8 5 6 1 3 2 4 7 0
2 3 5 6 0 1 7 4 8

Линейка №9 (19)
1 0 3 7 4 6 8 2 5

вариантов первой строки 928
минимальная КФ
0 3 4 2 5 6 7 8 1
2 1 3 4 6 8 5 0 7
1 0 2 7 8 4 3 5 6
4 5 0 3 1 7 8 6 2
6 7 5 8 4 0 1 2 3
3 8 1 6 7 5 2 4 0
7 4 8 0 2 3 6 1 5
8 2 6 5 3 1 0 7 4
5 6 7 1 0 2 4 3 8

Линейка №10 (8)
1 0 3 7 4 6 8 5 2

вариантов первой строки 928
минимальная КФ
0 2 3 4 5 6 7 8 1
3 1 4 2 6 8 5 0 7
1 0 2 7 8 4 3 5 6
4 6 0 3 1 7 8 2 5
6 7 5 8 4 0 1 3 2
7 8 1 6 0 5 2 4 3
5 3 8 0 7 2 6 1 4
8 5 6 1 2 3 4 7 0
2 4 7 5 3 1 0 6 8

Линейка №11 (20)
1 0 3 7 4 8 5 2 6

вариантов первой строки 928
минимальная КФ
0 3 4 2 5 6 7 8 1
2 1 3 4 6 8 5 0 7
1 0 2 7 8 4 3 5 6
4 5 0 3 1 7 8 6 2
5 7 8 6 4 0 1 2 3
3 6 1 8 7 5 2 4 0
7 8 5 0 2 1 6 3 4
8 2 6 1 0 3 4 7 5
6 4 7 5 3 2 0 1 8

Линейка №12 (17)
1 0 3 7 4 8 5 6 2

вариантов первой строки 928
минимальная КФ
0 2 3 4 5 6 7 8 1
3 1 4 2 6 8 5 0 7
1 0 2 7 8 4 3 5 6
4 5 0 3 1 7 8 6 2
5 7 8 6 4 0 1 2 3
6 3 7 8 0 5 2 1 4
7 8 5 1 2 3 6 4 0
8 6 1 0 3 2 4 7 5
2 4 6 5 7 1 0 3 8

Линейка №13 (4)
1 2 0 6 4 7 8 3 5

вариантов первой строки 927
минимальная КФ
0 2 3 4 5 7 8 6 1
3 1 0 5 6 8 4 2 7
1 4 2 6 7 3 0 8 5
2 0 1 3 8 6 7 5 4
6 7 5 8 4 0 1 3 2
4 8 6 7 0 5 2 1 3
7 5 8 1 3 2 6 4 0
8 3 4 0 2 1 5 7 6
5 6 7 2 1 4 3 0 8

Линейка №14 (3)
1 2 3 0 4 8 5 6 7

содержит ассоциативные ДЛК
вариантов первой строки 928
минимальная КФ
0 2 3 4 5 6 7 8 1
3 1 0 5 6 4 8 2 7
1 0 2 6 7 8 3 4 5
2 4 7 3 8 0 1 5 6
5 3 8 1 4 7 0 6 2
6 7 1 8 0 5 2 3 4
4 8 5 7 1 2 6 0 3
8 6 4 2 3 1 5 7 0
7 5 6 0 2 3 4 1 8

Линейка №15 (11)
1 2 3 6 4 0 8 5 7

вариантов первой строки 928
минимальная КФ
0 2 3 4 5 7 8 6 1
3 1 0 5 6 8 4 2 7
1 0 2 6 7 4 3 8 5
2 4 1 3 8 6 7 5 0
6 7 5 8 4 0 2 1 3
4 8 7 0 2 5 1 3 6
5 3 8 7 0 1 6 4 2
8 5 6 1 3 2 0 7 4
7 6 4 2 1 3 5 0 8

Линейка №16 (15)
1 2 3 6 4 7 8 0 5

вариантов первой строки 902
минимальная КФ
0 2 3 4 5 7 8 6 1
3 1 0 5 6 8 4 2 7
1 4 2 6 7 0 3 8 5
2 5 1 3 8 6 7 0 4
6 7 5 8 4 1 0 3 2
4 8 6 7 0 5 2 1 3
7 3 8 1 2 4 6 5 0
8 0 4 2 1 3 5 7 6
5 6 7 0 3 2 1 4 8

Линейка №17 (12)
1 2 3 6 4 8 5 0 7

вариантов первой строки 902
минимальная КФ
0 2 3 4 5 7 8 6 1
3 1 0 5 6 8 4 2 7
1 4 2 6 7 0 3 8 5
2 5 1 3 8 6 7 0 4
5 7 8 0 4 1 2 3 6
6 3 7 8 0 5 1 4 2
4 8 5 7 2 3 6 1 0
8 0 6 2 1 4 5 7 3
7 6 4 1 3 2 0 5 8

Линейка №18 (2)
1 2 3 8 4 0 5 6 7

содержит ассоциативные ДЛК
вариантов первой строки 928
минимальная КФ
0 2 3 4 5 6 7 8 1
3 1 0 5 6 4 8 2 7
1 0 2 6 8 7 3 4 5
2 4 1 3 7 8 0 5 6
5 3 7 8 4 0 1 6 2
6 7 8 0 1 5 2 3 4
4 8 5 7 0 2 6 1 3
8 6 4 1 2 3 5 7 0
7 5 6 2 3 1 4 0 8

Линейка №19 (14)
1 2 7 6 4 8 5 0 3

вариантов первой строки 900
минимальная КФ
0 2 3 4 5 7 8 6 1
4 1 0 5 6 8 3 2 7
1 3 2 0 8 4 7 5 6
2 4 1 3 7 6 0 8 5
5 6 8 7 4 0 1 3 2
6 7 4 8 0 5 2 1 3
7 8 5 1 2 3 6 4 0
8 0 6 2 3 1 5 7 4
3 5 7 6 1 2 4 0 8

Линейка №20 (5)
1 8 3 6 4 2 5 0 7

содержит ассоциативные ДЛК
вариантов первой строки 900
минимальная КФ
0 2 3 4 5 7 8 6 1
2 1 0 5 3 4 7 8 6
1 4 2 0 6 8 3 5 7
4 5 7 3 8 6 0 1 2
3 6 8 7 4 0 1 2 5
6 8 1 2 7 5 4 3 0
8 7 5 1 0 2 6 4 3
5 0 6 8 1 3 2 7 4
7 3 4 6 2 1 5 0 8

[В скобках старые номера линеек, мне нужна эта информация, чтобы правильно пользоваться программой Harry; не стала её тут выбрасывать.]
Могла, конечно, ошибиться.
А вот интересный вопрос: есть ли линейки со стопроцентным содержанием КФ?
Линейка №1, которую сейчас проверяю, этим свойством не обладает.
Интересно: минимальные КФ во всех линейках являются самым первым ДЛК в линейке.

Текущая минимальная КФ ОДЛК в БД на данный момент

0 2 3 4 5 6 7 8 1
2 1 4 5 6 7 8 0 3
6 4 2 7 1 8 3 5 0
4 5 6 3 8 2 0 1 7
3 6 7 8 4 0 1 2 5
1 7 8 6 0 5 2 3 4
8 3 5 0 7 1 6 4 2
5 8 0 1 2 3 4 7 6
7 0 1 2 3 4 5 6 8

Эта КФ принадлежит линейке №1, является ассоциативной.
Пока не знаю, есть ли это глобальный минимум БД КФ ОДЛК 9-го порядка, надо проверить.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И происходит от текущей минимальной КФ ОДЛК двушечка

[DLK(2)]
0 2 3 4 5 6 7 8 1
2 1 4 5 6 7 8 0 3
6 4 2 7 1 8 3 5 0
4 5 6 3 8 2 0 1 7
3 6 7 8 4 0 1 2 5
1 7 8 6 0 5 2 3 4
8 3 5 0 7 1 6 4 2
5 8 0 1 2 3 4 7 6
7 0 1 2 3 4 5 6 8
[mate#1]
2 1 3 4 5 0 6 7 8
5 3 1 8 7 2 0 6 4
4 2 7 3 6 8 5 0 1
8 7 5 6 1 3 4 2 0
1 6 8 2 0 5 7 4 3
0 5 6 1 3 4 2 8 7
3 0 2 7 4 1 8 5 6
6 4 0 5 8 7 3 1 2
7 8 4 0 2 6 1 3 5
[mate#2]
1 2 3 4 5 6 0 7 8
5 0 6 8 7 1 4 3 2
4 1 7 2 3 8 5 0 6
8 7 5 6 0 4 2 1 3
0 3 8 1 2 5 7 6 4
6 5 2 0 4 3 1 8 7
3 4 1 7 6 2 8 5 0
2 6 0 5 8 7 3 4 1
7 8 4 3 1 0 6 2 5

причём чистая двушечка, то есть ортогональные соквадраты двушки не дают новых ОДЛК (нет ветвления).
И даёт эта двушка 3 уникальные КФ ОДЛК

0 2 3 4 5 6 7 8 1
2 1 4 5 6 7 8 0 3
6 4 2 7 1 8 3 5 0
4 5 6 3 8 2 0 1 7
3 6 7 8 4 0 1 2 5
1 7 8 6 0 5 2 3 4
8 3 5 0 7 1 6 4 2
5 8 0 1 2 3 4 7 6
7 0 1 2 3 4 5 6 8

0 2 3 4 7 6 8 5 1
6 1 4 8 3 7 2 0 5
1 5 2 7 6 8 3 4 0
5 6 8 3 0 2 7 1 4
2 0 7 5 4 3 1 8 6
4 7 1 6 8 5 0 2 3
8 4 5 0 2 1 6 3 7
3 8 6 1 5 0 4 7 2
7 3 0 2 1 4 5 6 8

0 2 3 4 7 6 8 5 1
6 1 7 8 2 3 4 0 5
1 5 2 7 0 8 3 4 6
4 6 8 3 5 2 7 1 0
5 0 6 1 4 7 2 8 3
8 7 1 6 3 5 0 2 4
2 4 5 0 8 1 6 3 7
3 8 4 5 6 0 1 7 2
7 3 0 2 1 4 5 6 8

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А тем временем программа нашла, наконец-то, очередную КФ ОДЛК в линейке №1

. . . . . . . . . . 
СНДЛК: 59544160 КФ: 55842878 время: 21654 сек
СНДЛК: 59557661 КФ: 55855769 время: 21659 сек
СНДЛК: 59571931 КФ: 55868471 время: 21664 сек
СНДЛК: 59585680 КФ: 55881297 время: 21669 сек
СНДЛК: 59599278 КФ: 55894234 время: 21674 сек
Найден ОДЛК #1:

0 2 3 4 5 6 7 8 1
5 1 6 7 3 4 8 0 2
6 0 2 8 7 1 3 4 5
1 6 7 3 8 2 4 5 0
2 5 8 1 4 7 0 6 3
8 7 0 6 1 5 2 3 4
3 4 5 0 2 8 6 1 7
4 8 1 2 0 3 5 7 6
7 3 4 5 6 0 1 2 8

Продолжить? (Y/N):

Конечно, продолжить :)
Вчера за день проверила 97 миллионов СН ДЛК и ни одного решения! И сегодня решение нашлось на 60-м миллионе.

Кстати, обратите внимание на вторую строку в найденном решении.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Покажу свои последние находки в линейке №1. Пять уникальных однушек, все чистые, каждая даёт 2 уникальные КФ.

0 2 3 4 5 6 7 8 1
3 1 6 5 2 8 4 0 7
5 6 2 7 8 1 3 4 0
6 4 8 3 7 2 0 1 5
2 5 1 0 4 7 8 6 3
8 3 7 6 0 5 1 2 4
4 7 5 8 1 0 6 3 2
1 8 0 2 3 4 5 7 6
7 0 4 1 6 3 2 5 8

0 2 3 4 5 6 7 8 1
3 1 6 7 2 4 8 0 5
4 5 2 0 1 8 3 6 7
5 0 7 3 8 2 1 4 6
6 3 8 1 4 7 0 5 2
8 7 1 6 0 5 2 3 4
2 4 5 8 7 3 6 1 0
1 8 4 2 6 0 5 7 3
7 6 0 5 3 1 4 2 8

0 2 3 4 5 6 7 8 1
5 1 6 7 3 4 8 0 2
6 0 2 8 7 1 3 4 5
1 6 7 3 8 2 4 5 0
2 5 8 1 4 7 0 6 3
8 7 0 6 1 5 2 3 4
3 4 5 0 2 8 6 1 7
4 8 1 2 0 3 5 7 6
7 3 4 5 6 0 1 2 8

0 2 3 4 5 6 7 8 1
5 1 6 8 2 3 4 0 7
4 6 2 7 1 8 3 5 0
8 5 1 3 7 2 0 6 4
6 3 8 0 4 7 1 2 5
2 4 7 6 0 5 8 1 3
3 7 5 1 8 0 6 4 2
1 8 0 2 3 4 5 7 6
7 0 4 5 6 1 2 3 8

0 2 3 4 5 6 7 8 1
5 1 6 8 3 4 2 0 7
6 5 2 1 8 7 3 4 0
4 7 8 3 1 2 0 5 6
3 6 0 7 4 8 1 2 5
2 3 7 6 0 5 8 1 4
8 4 5 0 7 1 6 3 2
1 8 4 2 6 0 5 7 3
7 0 1 5 2 3 4 6 8

В составляемой БД теперь содержится 5327 уникальных КФ ОДЛК.
Продолжаю проверять линейку №1.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И под занавес сегодняшних поисков уникальная четвёрка!

[DLK(4)]
0 2 3 4 5 6 7 8 1
5 1 8 7 6 3 4 0 2
1 7 2 5 8 0 3 4 6
4 0 1 3 7 2 8 6 5
2 6 0 8 4 7 1 5 3
8 3 7 6 0 5 2 1 4
3 4 5 0 1 8 6 2 7
6 8 4 2 3 1 5 7 0
7 5 6 1 2 4 0 3 8
[mate#1]
2 4 0 6 1 7 3 8 5
0 7 5 8 4 6 1 3 2
8 0 3 7 2 1 4 5 6
4 6 2 1 5 8 7 0 3
1 5 7 3 0 2 6 4 8
6 3 4 2 8 5 0 1 7
5 2 6 4 3 0 8 7 1
3 1 8 5 7 4 2 6 0
7 8 1 0 6 3 5 2 4
[mate#2]
2 4 0 6 1 7 3 8 5
0 7 5 8 4 6 1 3 2
8 0 3 7 2 1 4 5 6
4 6 2 1 5 8 7 0 3
1 5 8 3 0 2 6 4 7
6 3 4 2 7 5 0 1 8
5 2 6 4 3 0 8 7 1
3 1 7 5 8 4 2 6 0
7 8 1 0 6 3 5 2 4
[mate#3]
4 1 0 6 3 7 2 8 5
8 7 5 0 1 6 3 2 4
0 8 2 7 4 3 1 5 6
1 6 4 3 5 8 7 0 2
3 5 7 2 0 4 6 1 8
6 2 1 4 8 5 0 3 7
5 4 6 1 2 0 8 7 3
2 3 8 5 7 1 4 6 0
7 0 3 8 6 2 5 4 1
[mate#4]
4 1 0 6 3 7 2 8 5
8 7 5 0 1 6 3 2 4
0 8 2 7 4 3 1 5 6
1 6 4 3 5 8 7 0 2
3 5 8 2 0 4 6 1 7
6 2 1 4 7 5 0 3 8
5 4 6 1 2 0 8 7 3
2 3 7 5 8 1 4 6 0
7 0 3 8 6 2 5 4 1

Чистая четвёрка, нет ветвлений. Четвёрка даёт 5 уникальных КФ - полновесная.

И в БД стало 5332 уникальные КФ ОДЛК.
Завтра продолжу поиск решений в линейке №1.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Поиск идёт хорошо.
Посмотрите на два последних решения

0 2 3 4 5 6 7 8 1
6 1 8 5 3 4 2 0 7
4 5 2 8 1 7 3 6 0
5 7 1 3 8 2 0 4 6
2 6 7 0 4 1 8 3 5
8 3 0 6 7 5 1 2 4
3 4 5 7 0 8 6 1 2
1 8 4 2 6 0 5 7 3
7 0 6 1 2 3 4 5 8

0 2 3 4 5 7 8 6 1
2 1 4 5 3 8 7 0 6
5 6 2 7 8 1 3 4 0
6 5 7 3 0 2 1 8 4
8 0 6 2 4 3 5 1 7
4 7 8 6 1 5 0 2 3
1 4 5 8 7 0 6 3 2
3 8 0 1 2 6 4 7 5
7 3 1 0 6 4 2 5 8

Предпоследнее решение было ещё в первой группе (см. первую строку), а последнее решение уже во второй группе (изменилась первая строка).
Довольно быстро проверена целая группа (тотально!).
Напомню: в линейке №1 имеется 920 вариантов первой строки, то есть 920 групп.
Считаем: на одном ПК в один поток одна группа проверялась примерно 4-5 дней (по 10-12 часов в день).
На 920 групп многовато надо времени, ПК не потянет. И это только одна линейка. А всего у нас 20 линеек.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg