Немного исследуем группы из четырёх ортогональных пар ДЛК, кратко называемые "четвёрками".
Как уже давно известно, четвёрки происходят от разных ДЛК и бывают полновесные (дают 5 уникальных КФ) и не полновесные (дают 3 уникальные КФ).
Некоторые четвёрки имеют парные, то есть при обработке четвёрки программой Белышева Канонизатор ЛК по ДЛК появляется новая четвёрка.

Начнём с самого первого - исторического - вида четвёрок.
1. Четвёрки, происходящие от "браунов".

Первая, классическая, четвёрка такого вида была опубликована в 1992 г. в статье
“Completion of the Spectrum of Orthogonal Diagonal Latin Squares” (J. W. Brown и другие).
Фактически была опубликована только двушка, смотрите две первые (сверху) ортогональные пары на иллюстрации



В 2016 г. О. Заикин нашёл ещё две пары ортогональных ДЛК в этой группе, и двушка превратилась в четвёрку. Смотрите
Pairs of diagonal orthogonal Latin squares of order 10 based on the turn square from Brown et al, 1992.
http://sat.isa.ru/pdsat/additional_solutions.php
Интересный момент в том, что два найденных Заикиным ортогональных диагональных соквадрата оказались изоморфными двум известным ортогональным диагональным соквадратам.

Покажу эту классическую четвёрку

0 1 2 3 4 5 6 7 8 9
1 6 9 2 0 3 7 8 5 4
9 8 3 4 5 0 2 1 6 7
3 5 8 7 2 1 0 4 9 6
2 9 5 8 1 7 4 6 0 3
4 0 6 9 3 8 1 5 7 2
5 4 7 6 8 2 9 0 3 1
6 3 4 5 7 9 8 2 1 0
7 2 1 0 9 6 5 3 4 8
8 7 0 1 6 4 3 9 2 5
sq1

0 1 2 3 4 5 6 7 8 9
3 9 1 8 6 4 5 0 7 2
7 3 5 2 9 6 8 4 1 0
4 0 9 6 8 3 2 1 5 7
2 7 0 5 3 8 1 9 4 6
8 4 6 9 1 7 3 2 0 5
5 6 7 0 2 1 4 3 9 8
9 2 3 1 5 0 7 8 6 4
1 5 8 4 7 9 0 6 2 3
6 8 4 7 0 2 9 5 3 1
sq2

0 1 2 3 4 5 6 7 8 9
5 4 1 2 6 9 7 0 3 8
2 3 8 7 9 4 5 6 1 0
3 0 5 9 8 7 2 1 4 6
6 9 3 5 2 8 1 4 0 7
7 2 4 8 1 6 0 3 9 5
8 6 9 0 7 1 3 2 5 4
9 8 7 1 0 2 4 5 6 3
1 5 6 4 3 0 9 8 7 2
4 7 0 6 5 3 8 9 2 1
sq3

0 1 2 3 4 5 6 7 8 9
7 2 9 4 5 3 1 8 0 6
9 8 5 1 3 0 7 4 6 2
2 4 8 7 6 1 3 0 9 5
3 5 0 8 1 6 4 9 2 7
4 9 7 6 2 8 0 3 5 1
1 0 6 5 8 7 9 2 3 4
5 3 1 2 9 4 8 6 7 0
6 7 3 9 0 2 5 1 4 8
8 6 4 0 7 9 2 5 1 3
sq4

Square:
0 1 2 3 4 5 6 7 8 9
2 3 4 9 8 1 0 5 6 7
3 4 9 8 2 7 1 0 5 6
8 7 6 5 0 9 4 3 2 1
5 0 1 7 6 3 2 8 9 4
6 5 0 1 7 2 8 9 4 3
4 9 8 2 3 6 7 1 0 5
7 6 5 0 1 8 9 4 3 2
9 8 7 6 5 4 3 2 1 0
1 2 3 4 9 0 5 6 7 8

Вследствие изоморфности ортогональных соквадратов данная четвёрка даёт только 3 уникальные КФ, то есть является не полновесной, как и все четвёрки. присходящие от "браунов".
А много ли таких четвёрок?
Можно посчитать, они все были найдены в нашем с Белышевым эксперименте. В этом эксперименте всего было найдено 95 четвёрок, среди них и все, происхдящие от "браунов".

Все КФ второго формата основных ДЛК четвёрок, происходящих от "браунов", принадлежат линейке №6.
Для классической четвёрки, происходящей от "брауна", КФ второго формата:

0 3 5 7 6 4 9 8 2 1
9 1 6 8 3 2 5 4 0 7
5 7 2 6 1 0 4 3 9 8
6 8 1 3 7 9 2 0 5 4
1 2 8 9 4 6 7 5 3 0
3 4 7 0 8 5 1 9 6 2
8 9 3 4 0 1 6 2 7 5
2 6 9 1 5 8 0 7 4 3
4 5 0 2 9 7 3 1 8 6
7 0 4 5 2 3 8 6 1 9

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посчитала четвёрки, происходящие от "браунов". Из 95 четвёрок таких оказалось 92, и только три четвёрки происходят не от "браунов", вот эти:

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 6 9 8 5 7
7 8 5 6 9 0 1 3 4 2
6 9 7 8 1 3 4 5 2 0
3 4 0 5 6 7 8 2 9 1
9 7 8 1 2 4 0 6 3 5
2 3 4 0 5 9 7 1 6 8
4 0 1 2 3 8 5 9 7 6
5 6 9 7 8 2 3 0 1 4
8 5 6 9 7 1 2 4 0 3

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 8 5 9 7 6
3 9 6 5 2 4 7 1 0 8
9 0 5 8 7 6 4 2 1 3
8 7 9 6 1 3 2 0 4 5
2 3 4 0 5 7 8 6 9 1
4 6 1 2 3 0 9 8 5 7
7 4 0 1 8 9 3 5 6 2
5 8 7 9 6 2 1 4 3 0
6 5 8 7 9 1 0 3 2 4

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 8 5 9 7 6
7 9 6 1 8 4 3 5 0 2
9 0 5 8 3 6 4 2 1 7
8 7 4 0 5 3 2 6 9 1
2 3 9 6 1 7 8 0 4 5
4 6 1 2 7 0 9 8 5 3
3 4 0 5 2 9 7 1 6 8
5 8 7 9 6 2 1 4 3 0
6 5 8 7 9 1 0 3 2 4

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посмотрела на эти 3 оставшиеся ДЛК, которые дают четвёрки. Эти ДЛК являются ЛК блочной структуры.
Показываю результат работы программы Белышева Интеркалятор для этих ДЛК по порядку (как они приведены в предыдущем посте), показываю только один срез.

для первого ДЛК:

срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 6 9 8 5 7
2 3 4 0 5 9 7 1 6 8
3 4 0 5 6 7 8 2 9 1
4 0 1 2 3 8 5 9 7 6
5 6 9 7 8 2 3 0 1 4
6 9 7 8 1 3 4 5 2 0
7 8 5 6 9 0 1 3 4 2
8 5 6 9 7 1 2 4 0 3
9 7 8 1 2 4 0 6 3 5

{0,8} = 5 : (0,8,0,8) (1,5,4,7) (2,6,3,9) (3,9,2,6) (4,7,1,5) 
{1,5} = 5 : (0,8,1,5) (1,5,0,8) (2,6,4,7) (3,9,3,9) (4,7,2,6) 
{2,6} = 5 : (0,8,2,6) (1,5,1,5) (2,6,0,8) (3,9,4,7) (4,7,3,9) 
{3,9} = 5 : (0,8,3,9) (1,5,2,6) (2,6,1,5) (3,9,0,8) (4,7,4,7) 
{4,7} = 5 : (0,8,4,7) (1,5,3,9) (2,6,2,6) (3,9,1,5) (4,7,0,8)

для второго ДЛК:

срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 8 5 9 7 6
2 3 4 0 5 7 8 6 9 1
3 9 6 5 2 4 7 1 0 8
4 6 1 2 3 0 9 8 5 7
5 8 7 9 6 2 1 4 3 0
6 5 8 7 9 1 0 3 2 4
7 4 0 1 8 9 3 5 6 2
8 7 9 6 1 3 2 0 4 5
9 0 5 8 7 6 4 2 1 3

{0,6} = 5 : (0,6,0,6) (1,5,4,9) (2,8,3,7) (3,7,2,8) (4,9,1,5) 
{1,5} = 5 : (0,6,1,5) (1,5,0,6) (2,8,4,9) (3,7,3,7) (4,9,2,8) 
{2,8} = 5 : (0,6,2,8) (1,5,1,5) (2,8,0,6) (3,7,4,9) (4,9,3,7) 
{3,7} = 5 : (0,6,3,7) (1,5,2,8) (2,8,1,5) (3,7,0,6) (4,9,4,9) 
{4,9} = 5 : (0,6,4,9) (1,5,3,7) (2,8,2,8) (3,7,1,5) (4,9,0,6)

для третьего ДЛК:

срез #1
0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 8 5 9 7 6
2 3 9 6 1 7 8 0 4 5
3 4 0 5 2 9 7 1 6 8
4 6 1 2 7 0 9 8 5 3
5 8 7 9 6 2 1 4 3 0
6 5 8 7 9 1 0 3 2 4
7 9 6 1 8 4 3 5 0 2
8 7 4 0 5 3 2 6 9 1
9 0 5 8 3 6 4 2 1 7

{0,6} = 5 : (0,6,0,6) (1,5,4,9) (2,8,3,7) (3,7,2,8) (4,9,1,5) 
{1,5} = 5 : (0,6,1,5) (1,5,0,6) (2,8,4,9) (3,7,3,7) (4,9,2,8) 
{2,8} = 5 : (0,6,2,8) (1,5,1,5) (2,8,0,6) (3,7,4,9) (4,9,3,7) 
{3,7} = 5 : (0,6,3,7) (1,5,2,8) (2,8,1,5) (3,7,0,6) (4,9,4,9) 
{4,9} = 5 : (0,6,4,9) (1,5,3,7) (2,8,2,8) (3,7,1,5) (4,9,0,6)

Все данные четвёрки тоже не полновесные.

Вроде бы новый вид четвёрок эти 3 четвёрки представляют, но! "Брауны" тоже являются ЛК блочной структуры.
Тогда надо бы назвать первый вид четвёрок - происходящие от ЛК блочной структуры, но пусть останется так, как есть.

Итак, 95 четвёрок, найденных в нашем с Белышевым эксперименте, проверены.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

2. Четвёрки от симметричных ДЛК, но не "браунов"

Здесь https://boinc.progger.info/odlk/forum_thread.php?id=18&postid=148#148 я сообщила о первой четвёрке, найденной в нашем BOINC-проекте ODLK в Приложении odlksym (поиск решений от симметричных ДЛК).
Вот эта симметричная КФ ОДЛК, дающая четвёрку:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
2 9 3 1 5 4 8 6 0 7
9 6 7 5 1 8 4 2 3 0
7 5 9 8 6 3 1 0 4 2
8 7 4 6 0 9 3 5 2 1
4 0 6 2 8 1 7 3 9 5
6 4 1 9 2 7 0 8 5 3
3 8 5 7 9 0 2 4 1 6
5 3 8 0 7 2 9 1 6 4

Этот ДЛК тоже является ЛК блочной структуры, что хорошо видно на иллюстрации



Программа Белышева Интеркалятор показывает для данного ДЛК (привожу один срез):

срез #1
0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
2 9 3 1 5 4 8 6 0 7
3 8 5 7 9 0 2 4 1 6
4 0 6 2 8 1 7 3 9 5
5 3 8 0 7 2 9 1 6 4
6 4 1 9 2 7 0 8 5 3
7 5 9 8 6 3 1 0 4 2
8 7 4 6 0 9 3 5 2 1
9 6 7 5 1 8 4 2 3 0

{0,1} = 1 : (8,9,4,9) 
{0,2} = 1 : (7,9,7,9) 
{0,6} = 1 : (0,6,0,6) 
{0,7} = 1 : (0,7,0,7) 
{2,4} = 1 : (3,9,6,7) 
{2,9} = 1 : (0,7,2,9) 
{3,9} = 1 : (0,6,3,9) 
{5,7} = 1 : (3,9,2,3) 
{7,9} = 1 : (7,9,0,2) 
{8,9} = 1 : (8,9,0,5) 
{1,5} = 2 : (2,9,3,4) (3,6,2,8) 
{4,8} = 2 : (2,9,5,6) (3,6,1,7) 
{3,4} = 3 : (0,1,3,4) (3,4,0,7) (5,6,1,9) 
{5,6} = 3 : (0,1,5,6) (3,4,2,9) (5,6,0,8) 
{0,9} = 5 : (0,9,0,9) (1,7,2,7) (2,4,1,8) (3,8,4,5) (5,6,3,6) 
{1,8} = 5 : (0,3,1,8) (1,8,0,9) (2,7,3,6) (4,9,4,5) (5,6,2,7) 
{2,7} = 5 : (0,9,2,7) (1,8,1,8) (2,7,0,9) (3,4,3,6) (5,6,4,5) 
{3,6} = 5 : (0,8,3,6) (1,7,4,5) (2,4,2,7) (3,6,0,9) (5,9,1,8) 
{4,5} = 5 : (0,2,4,5) (1,9,3,6) (3,8,2,7) (4,5,0,9) (6,7,1,8)

Данная четвёрка тоже не полновесная.

А вот и КФ основного ДЛК парной четвёрки, как видим, она тоже симметричная

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
3 4 7 1 9 0 8 2 5 6
9 8 6 5 2 7 4 3 1 0
8 9 4 2 6 3 7 5 0 1
7 0 5 6 8 1 3 4 9 2
5 3 8 0 7 2 9 1 6 4
4 6 1 7 0 9 2 8 3 5
2 5 3 9 1 8 0 6 4 7
6 7 9 8 5 4 1 0 2 3

Феномен парности четвёрок (и двушек), происходящих от симметричных ДЛК, мне до сих пор не понятен. Я открыла этот феномен опытным путём и не знаю теоретического обоснования.

КФ ОДЛК второго формата, соответствующие симметричным КФ ОДЛК, находятся в линейках №1 и №6.
Для рассмотренных четвёрок КФ второго формата принадлежат линейке №6, вот они:

0 2 5 6 7 9 4 8 3 1 
5 1 4 2 9 7 3 6 0 8 
4 9 2 5 1 0 8 3 7 6 
1 7 8 3 6 4 2 5 9 0 
3 8 7 0 4 6 1 9 5 2 
2 0 6 7 8 5 9 4 1 3 
9 3 0 4 5 8 6 1 2 7 
8 6 9 1 2 3 0 7 4 5 
6 5 3 9 0 1 7 2 8 4 
7 4 1 8 3 2 5 0 6 9

0 2 5 6 7 9 4 8 3 1 
8 1 6 9 3 2 7 4 0 5 
9 6 2 8 1 0 5 3 4 7 
4 8 7 3 0 1 2 9 5 6 
1 7 8 2 4 6 3 5 9 0 
2 9 4 0 8 5 1 6 7 3 
5 0 3 4 9 7 6 2 1 8 
3 4 9 1 5 8 0 7 6 2 
6 5 1 7 2 3 9 0 8 4 
7 3 0 5 6 4 8 1 2 9

PS. Согласно теории Белышева все блочные структуры (БС), соответствующие симметричным ДЛК, находятся в линейках №1 и №6.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

В текущем варианте БД имеется 80 четвёрок второго вида (происходящих от симметричных ДЛК, но не "браунов").
Надеюсь, что не ошиблась, завтра перепроверю.

Итак, имеем 95+80 =175 четвёрок, происходящих от ЛК блочной структуры.

Далее посмотрим на оставшиеся четвёрки. Это четвёрки, происходящие от не симметричных (по Брауну) ДЛК. Они, как уже было показано в соседней теме, полновесные, то есть дают 5 уникальных КФ.
Может быть, и не только такие четвёрки есть среди оставшихся. Надо проверять.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посмотрела на эти 3 оставшиеся ДЛК, которые дают четвёрки. Эти ДЛК являются ЛК блочной структуры.

И ещё информация: КФ второго формата основных ДЛК этих четвёрок принадлежат линейке №6:

0 2 5 7 6 4 9 8 3 1
8 1 6 2 7 9 3 4 0 5
9 4 2 5 0 1 8 3 6 7
5 0 4 3 9 7 2 6 1 8
1 3 8 9 4 6 7 5 2 0
3 7 1 6 8 5 4 0 9 2
2 9 0 4 5 8 6 1 7 3
6 8 9 1 2 3 0 7 5 4
4 5 7 0 3 2 1 9 8 6
7 6 3 8 1 0 5 2 4 9

0 2 5 7 6 4 9 8 3 1
8 1 6 2 9 7 3 4 0 5
9 4 2 8 1 0 5 3 6 7
5 0 4 3 7 9 2 6 1 8
1 3 8 9 4 6 7 5 2 0
2 9 1 6 8 5 4 0 7 3
3 7 0 4 5 8 6 1 9 2
6 8 9 1 2 3 0 7 5 4
4 5 7 0 3 2 1 9 8 6
7 6 3 5 0 1 8 2 4 9

0 2 5 9 6 4 7 8 3 1
9 1 6 8 3 2 5 4 0 7
8 7 2 6 1 0 4 3 9 5
6 8 1 3 7 9 2 0 5 4
1 3 8 7 4 6 9 5 2 0
3 4 7 0 8 5 1 9 6 2
5 9 3 4 0 1 6 2 7 8
2 6 9 1 5 8 0 7 4 3
4 5 0 2 9 7 3 1 8 6
7 0 4 5 2 3 8 6 1 9

PS. Это о четвёрках, рассмотренных здесь https://boinc.progger.info/odlk/forum_thread.php?id=40&postid=744#744

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посчитала все четвёрки в текущем варианте БД (содержит 247838 уникальных КФ ОДЛК), их оказалось 213.
Вычитаем 175 четвёрок, рассмотренных выше (происходящих от ЛК блочной структуры), остаётся 38 четвёрок.
Выудила эти 38 четвёрок из БД. Теперь надо их проверить. Все они происходят от не симметричных (по Брауну) ДЛК.
А от каких ДЛК они происходят, надо выяснить. Много ли среди них полновесных четвёрок? Есть ли ещё четвёрки, происходящие от ЛК блочной структуры?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

3. Четвёрки, происходящие не от ЛК блочной структуры

Прежде чем начать проверять все оставшиеся 38 четвёрок, отмечу данный вид четвёрок.
Вот пример такого вида четвёрок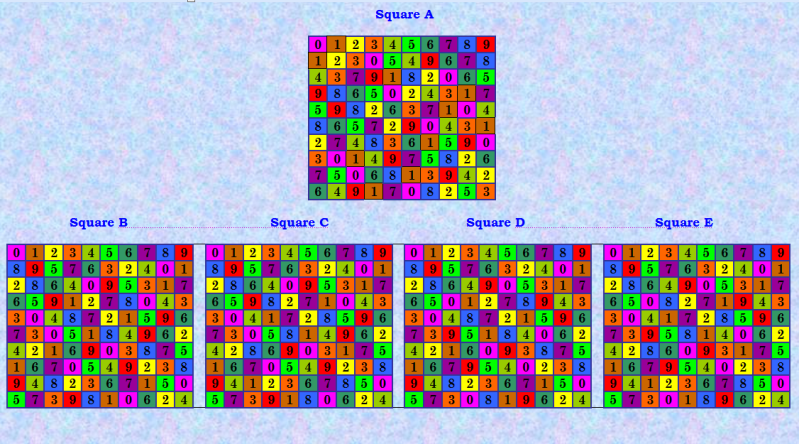



Эта четвёрка происходит от ДЛК (Square A), не являющегося ЛК блочной структуры. Четвёрка полновесная, даёт 5 уникальных КФ.
У этой четвёрки нет парной.
Осталось выяснить, сколько в нашей БД четвёрок такого вида.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверила 38 четвёрок. Не от ЛК блочной структуры происходят всего 4 четвёрки из этих 38. Одна показана в предыдущем посте, вот ещё три:

0 1 2 3 4 5 6 7 8 9
1 2 0 6 5 4 7 9 3 8
8 4 3 7 0 9 5 2 6 1
3 8 7 5 9 0 4 6 1 2
4 6 9 2 1 8 3 0 5 7
9 3 5 8 6 7 1 4 2 0
6 5 8 0 2 3 9 1 7 4
7 0 1 4 3 6 2 8 9 5
2 7 6 9 8 1 0 5 4 3
5 9 4 1 7 2 8 3 0 6

0 1 2 3 4 5 6 7 8 9
1 2 0 6 5 4 8 9 7 3
4 7 6 9 8 1 0 3 2 5
9 6 3 4 2 7 5 1 0 8
7 8 5 0 9 6 3 4 1 2
3 5 9 7 1 8 2 0 4 6
6 4 7 8 3 9 1 2 5 0
8 9 4 2 0 3 7 5 6 1
5 0 8 1 7 2 9 6 3 4
2 3 1 5 6 0 4 8 9 7

0 1 2 3 4 5 6 7 8 9
1 2 3 4 0 9 5 6 7 8
3 4 1 7 9 0 2 8 5 6
5 9 7 6 8 1 3 4 0 2
9 7 5 8 3 6 1 2 4 0
4 5 6 0 1 8 9 3 2 7
6 8 0 5 2 4 7 9 1 3
8 6 4 9 7 2 0 5 3 1
7 0 8 2 6 3 4 1 9 5
2 3 9 1 5 7 8 0 6 4

Остальные 34 четвёрки происходят от ЛК блочной структуры.
Проверяла программой Белышева Интеркалятор.

Как видим, пока четвёрки этого вида очень редкое явление. Может быть, они ещё будут и много, кто их знает. Не проверено в n раз больше ДЛК, чем проверено.
Все представленные четвёрки данного вида
а) полновесные;
б) не имеют парной.

Интересный момент: КФ второго формата основных ДЛК всех этих четвёрок принадлежат линейке №2.
Вот они:

0 2 4 7 9 8 3 6 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 0 4 5 2 6 1 3 7
2 0 8 9 6 4 5 7 1 3
3 9 6 5 1 0 7 4 8 2
5 6 1 2 3 7 8 0 4 9

0 2 6 7 9 8 3 4 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 1 4 5 2 6 0 3 7
2 0 8 9 6 4 5 7 1 3
3 9 4 5 1 0 7 6 8 2
5 6 0 2 3 7 8 1 4 9

0 4 3 7 8 9 5 2 6 1
7 1 5 2 6 4 3 9 0 8
9 0 2 6 5 8 4 3 1 7
1 8 6 3 9 7 2 4 5 0
2 5 9 1 4 6 0 8 7 3
6 2 0 9 7 5 8 1 3 4
8 7 1 4 3 2 6 0 9 5
3 6 8 5 0 1 9 7 4 2
4 9 7 0 2 3 1 5 8 6
5 3 4 8 1 0 7 6 2 9

0 5 3 6 9 8 4 2 7 1
3 1 9 7 6 4 8 5 0 2
7 6 2 1 5 9 0 3 4 8
9 8 4 3 1 0 2 6 5 7
1 7 5 2 4 6 3 8 9 0
2 4 1 8 7 5 9 0 6 3
8 0 7 4 3 2 6 9 1 5
6 3 8 9 0 1 5 7 2 4
4 9 0 5 2 3 7 1 8 6
5 2 6 0 8 7 1 4 3 9

Случайное совпадение? Или же линейка №2 богата такими четвёрками?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Четвёрки, происходящие от ЛК блочной структуры, часто дают 3 уникальные КФ.
Но вот неожиданно обнаружила четвёрку, происходящую от ЛК блочной структуры, которая даёт 4 уникальные КФ.
Основной ДЛК четвёрки:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 8 9 5 7
2 8 9 6 1 4 7 3 0 5
5 0 3 1 8 9 2 6 7 4
8 5 7 9 6 1 3 2 4 0
9 3 1 8 0 7 5 4 2 6
3 6 5 7 9 8 4 0 1 2
4 9 8 0 7 2 1 5 6 3
7 4 6 2 5 0 9 8 3 1
6 7 4 5 2 3 0 1 9 8

и 4 уникальные КФ от неё:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 8 9 5 7
2 8 9 6 1 4 7 3 0 5
5 0 3 1 8 9 2 6 7 4
8 5 7 9 6 1 3 2 4 0
9 3 1 8 0 7 5 4 2 6
3 6 5 7 9 8 4 0 1 2
4 9 8 0 7 2 1 5 6 3
7 4 6 2 5 0 9 8 3 1
6 7 4 5 2 3 0 1 9 8

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 8 9 5 7
4 8 9 6 1 2 7 3 0 5
5 0 3 1 8 9 2 6 7 4
8 5 7 9 6 1 3 4 2 0
9 3 1 8 0 7 5 2 4 6
3 6 5 7 9 8 4 0 1 2
2 9 8 0 7 4 1 5 6 3
7 4 6 2 5 0 9 8 3 1
6 7 4 5 2 3 0 1 9 8

0 1 2 3 4 5 6 7 8 9
1 2 3 4 6 9 5 0 7 8
9 7 5 8 3 0 1 4 2 6
7 5 0 9 8 1 3 6 4 2
5 3 8 6 7 2 0 1 9 4
2 4 9 1 0 6 8 3 5 7
3 8 6 5 2 7 4 9 1 0
6 9 1 2 5 4 7 8 0 3
4 6 7 0 1 8 9 2 3 5
8 0 4 7 9 3 2 5 6 1

0 1 2 3 4 5 6 7 8 9
1 2 3 4 8 6 7 9 5 0
2 6 5 8 7 9 0 3 4 1
5 7 9 6 0 3 8 4 1 2
8 9 4 5 3 0 1 6 2 7
9 8 6 7 1 4 3 2 0 5
7 5 8 2 6 1 9 0 3 4
4 0 7 9 5 8 2 1 6 3
3 4 1 0 9 2 5 8 7 6
6 3 0 1 2 7 4 5 9 8

А вот полновесные четвёрки, происходящие от ЛК блочной структуры, мне пока не встречались.
Все 34 четвёрки на набор уникальных КФ ещё не проверила.

Теперь проверила. Ещё несколько четвёрок (штук пять) дали 4 уникальные КФ, остальные - три. Полновесных нет.
Осталось выяснить, каким линейкам принадлежат эти 34 четвёрки.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

На линейки проверила 34 четвёрки, происходящие от ЛК блочной структуры.
Большинство принадлежат линейке №6. Только 5 четвёрок из линейки №1, вот эти:

0 2 4 5 9 8 7 6 3 1
5 1 9 2 6 4 3 8 0 7
7 4 2 9 1 0 8 3 6 5
6 5 8 3 0 1 2 9 7 4
2 7 0 8 4 6 9 1 5 3
3 8 6 1 7 5 0 4 9 2
1 3 7 4 8 9 6 5 2 0
9 6 5 0 2 3 1 7 4 8
4 9 1 7 3 2 5 0 8 6
8 0 3 6 5 7 4 2 1 9

0 2 4 5 9 8 7 6 3 1
6 1 9 7 2 3 5 8 0 4
4 5 2 1 8 9 0 3 7 6
9 0 6 3 5 7 2 4 1 8
5 3 8 0 4 6 1 9 2 7
3 4 0 9 7 5 8 1 6 2
1 8 7 4 3 2 6 5 9 0
2 6 5 8 1 0 9 7 4 3
7 9 3 6 0 1 4 2 8 5
8 7 1 2 6 4 3 0 5 9

0 2 4 5 9 8 7 6 3 1
7 1 9 2 6 4 3 8 0 5
1 4 2 8 5 7 9 3 6 0
6 7 0 3 8 9 2 1 5 4
3 5 8 0 4 6 1 9 7 2
2 6 1 9 7 5 8 0 4 3
9 0 7 4 3 2 6 5 1 8
4 8 5 1 2 3 0 7 9 6
5 9 3 6 0 1 4 2 8 7
8 3 6 7 1 0 5 4 2 9

0 2 4 7 8 9 5 6 3 1
2 1 8 5 6 4 7 9 0 3
6 7 2 1 9 8 0 3 5 4
1 6 9 3 5 7 2 8 4 0
7 8 3 0 4 6 1 2 9 5
3 0 6 8 7 5 9 4 1 2
9 5 0 4 3 2 6 1 7 8
4 3 5 9 0 1 8 7 2 6
5 9 1 6 2 3 4 0 8 7
8 4 7 2 1 0 3 5 6 9

0 2 4 9 5 7 8 6 3 1
2 1 8 5 6 4 7 9 0 3
6 7 2 1 9 8 0 3 5 4
5 6 0 3 8 9 2 1 4 7
1 5 3 8 4 6 9 2 7 0
9 3 6 0 7 5 1 4 2 8
7 0 9 4 3 2 6 8 1 5
3 8 5 6 0 1 4 7 9 2
4 9 1 7 2 3 5 0 8 6
8 4 7 2 1 0 3 5 6 9

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Может быть, не совсем удачно я классифицировала четвёрки.
Необходимо к видам 1-2 добавить ещё и все остальные четвёрки, происходящие от ЛК блочной структуры (хотя они происходят и не от "браунов", и не от симметричных ДЛК).
Таким образом, в этой большой группе будут все четвёрки, происходящие от ЛК блочной структуры.
Таких четвёрок в нашей БД имеется на данный момент 209.
И вторая группа - это четвёрки, происходящие не от ЛК блочной структуры, таких четвёрок в нашей БД всего 4 штуки.

Ну, какой-никакой анализ выполнен, все 213 четвёрок проверены.
Теперь дело за новыми четвёрками, чтобы продолжить анализ.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вывод по поводу линеек, которым принадлежат четвёрки, имеющиеся в нашей БД:

а) все четвёрки, происходящие от ЛК блочной структуры, принадлежат линейкам №1 и №6, причём от "браунов" - только линейке №6;
б) 4 четвёрки, происходящие не от ЛК блочной структуры, принадлежат линейке №2.

Больше пока нет у нас четвёрок.
Надо будет попытать линейку №2, может, в ней ещё есть четвёрки.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Пытаюсь дальше исследовать имеющиеся у нас четвёрки.
Есть такая программа В. Чиркова, которая делает в ДЛК перестановки элементов (и не только в ДЛК, может и в ЛК делать).
На выходе преобразованные такими перестановками элементов ДЛК.
Вот решила проверить 34 четвёрки, происходящие от ЛК блочной структуры, этой программой.

Первую четвёрку из списка проверила, преобразованных ДЛК около миллиона, не нашлось от этой кучи ДЛК ни одного решения (ОДЛК).
Проверила вторую четвёрку из списка, вот эту:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 8 9 5 7
2 8 9 6 1 4 7 3 0 5
5 0 3 1 8 9 2 6 7 4
8 5 7 9 6 1 3 2 4 0
9 3 1 8 0 7 5 4 2 6
3 6 5 7 9 8 4 0 1 2
4 9 8 0 7 2 1 5 6 3
7 4 6 2 5 0 9 8 3 1
6 7 4 5 2 3 0 1 9 8

Преобразованных ДЛК получилось миллион с хвостиком. При проверке на ОДЛК они дали три четвёрки.
Каждая четвёрка отдельно даёт 4 уникальные КФ, все вместе дают только 8 уникальных КФ.
Проверила основные ДЛК этих четвёрок программой Интеркалятор, результат (показываю только один срез):

 основной ДЛК первой четвёрки
 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 6 8 9 5 7
 4 8 9 6 1 2 7 3 0 5
 5 0 3 1 8 9 2 6 7 4
 8 5 7 9 6 1 3 4 2 0
 9 3 1 8 0 7 5 2 4 6
 3 6 5 7 9 8 4 0 1 2
 2 9 8 0 7 4 1 5 6 3
 7 4 6 2 5 0 9 8 3 1
 6 7 4 5 2 3 0 1 9 8
 
 срез #1
1 2 0 4 3 6 8 9 5 7
2 9 8 0 7 4 1 5 6 3
3 6 5 7 9 8 4 0 1 2
4 8 9 6 1 2 7 3 0 5
5 0 3 1 8 9 2 6 7 4
6 7 4 5 2 3 0 1 9 8
7 4 6 2 5 0 9 8 3 1
8 5 7 9 6 1 3 4 2 0
9 3 1 8 0 7 5 2 4 6

{0,1} = 1 : (7,8,5,9) 
{0,7} = 1 : (1,8,2,9) 
{0,8} = 1 : (3,7,5,7) 
{1,6} = 1 : (7,9,2,9) 
{1,8} = 1 : (6,7,7,9) 
{1,9} = 1 : (5,8,3,5) 
{2,3} = 1 : (2,3,0,9) 
{2,8} = 1 : (7,9,3,7) 
{4,5} = 1 : (4,5,0,9) 
{4,9} = 1 : (1,8,3,7) 
{6,7} = 1 : (1,9,5,9) 
{6,9} = 1 : (1,5,5,7) 
{7,8} = 1 : (3,9,3,5) 
{7,9} = 1 : (0,1,7,9) 
{1,5} = 2 : (0,8,1,5) (4,7,4,9) 
{2,5} = 2 : (1,8,1,8) (6,7,3,4) 
{3,4} = 2 : (0,1,3,4) (7,9,1,8) 
{3,7} = 2 : (1,2,4,9) (6,9,1,5) 
{0,6} = 5 : (0,6,0,6) (1,7,2,5) (2,4,3,8) (3,5,1,7) (8,9,4,9) 
{1,7} = 5 : (0,6,1,7) (1,7,0,9) (2,4,4,6) (3,5,3,8) (8,9,2,5) 
{2,4} = 5 : (0,6,2,4) (1,7,1,3) (2,4,0,5) (3,5,6,9) (8,9,7,8) 
{3,5} = 5 : (0,6,3,5) (1,7,4,8) (2,4,7,9) (3,5,0,2) (8,9,1,6) 
{8,9} = 5 : (0,6,8,9) (1,7,6,7) (2,4,1,2) (3,5,4,5) (8,9,0,3) 

 основной ДЛК второй четвёрки
 0 1 2 3 4 5 6 7 8 9
 1 2 6 4 3 0 8 9 5 7
 2 8 9 0 7 4 1 3 6 5
 3 0 5 1 8 9 2 6 7 4
 8 5 7 9 6 1 3 2 4 0
 9 3 1 8 0 7 5 4 2 6
 5 6 3 7 9 8 4 0 1 2
 4 9 8 6 1 2 7 5 0 3
 7 4 0 2 5 6 9 8 3 1
 6 7 4 5 2 3 0 1 9 8
 
 срез #1
0 1 2 3 4 5 6 7 8 9
1 2 6 4 3 0 8 9 5 7
2 8 9 0 7 4 1 3 6 5
3 0 5 1 8 9 2 6 7 4
4 9 8 6 1 2 7 5 0 3
5 6 3 7 9 8 4 0 1 2
6 7 4 5 2 3 0 1 9 8
7 4 0 2 5 6 9 8 3 1
8 5 7 9 6 1 3 2 4 0
9 3 1 8 0 7 5 4 2 6

{0,2} = 1 : (5,8,7,9) 
{0,4} = 1 : (1,2,3,5) 
{1,4} = 1 : (6,9,2,7) 
{1,8} = 1 : (6,7,7,9) 
{1,9} = 1 : (3,8,3,5) 
{2,6} = 1 : (4,7,3,5) 
{2,7} = 1 : (0,8,2,7) 
{4,6} = 1 : (3,9,7,9) 
{7,8} = 1 : (5,9,3,5) 
{7,9} = 1 : (0,1,7,9) 
{1,5} = 2 : (0,8,1,5) (1,5,0,8) 
{2,5} = 2 : (2,5,0,9) (6,7,3,4) 
{3,4} = 2 : (0,1,3,4) (3,4,0,9) 
{3,7} = 2 : (3,7,0,8) (6,9,1,5) 
{0,6} = 5 : (0,6,0,6) (1,7,2,5) (2,4,3,8) (3,5,1,7) (8,9,4,9) 
{1,7} = 5 : (0,6,1,7) (1,7,0,9) (2,4,4,6) (3,5,3,8) (8,9,2,5) 
{2,4} = 5 : (0,6,2,4) (1,7,1,3) (2,4,0,5) (3,5,6,9) (8,9,7,8) 
{3,5} = 5 : (0,6,3,5) (1,7,4,8) (2,4,7,9) (3,5,0,2) (8,9,1,6) 
{8,9} = 5 : (0,6,8,9) (1,7,6,7) (2,4,1,2) (3,5,4,5) (8,9,0,3) 

 основной ДЛК третьей четвёрки
 0 1 2 3 4 5 6 7 8 9
 1 2 6 4 3 0 8 9 5 7
 4 8 9 0 7 2 1 3 6 5
 3 0 5 1 8 9 2 6 7 4
 8 5 7 9 6 1 3 4 2 0
 9 3 1 8 0 7 5 2 4 6
 5 6 3 7 9 8 4 0 1 2
 2 9 8 6 1 4 7 5 0 3
 7 4 0 2 5 6 9 8 3 1
 6 7 4 5 2 3 0 1 9 8
 
 срез #1
0 1 2 3 4 5 6 7 8 9
1 2 6 4 3 0 8 9 5 7
2 9 8 6 1 4 7 5 0 3
3 0 5 1 8 9 2 6 7 4
4 8 9 0 7 2 1 3 6 5
5 6 3 7 9 8 4 0 1 2
6 7 4 5 2 3 0 1 9 8
7 4 0 2 5 6 9 8 3 1
8 5 7 9 6 1 3 4 2 0
9 3 1 8 0 7 5 2 4 6

{1,8} = 1 : (6,7,7,9) 
{1,9} = 1 : (3,8,3,5) 
{2,8} = 1 : (7,9,3,7) 
{4,9} = 1 : (1,8,3,7) 
{7,8} = 1 : (5,9,3,5) 
{7,9} = 1 : (0,1,7,9) 
{1,5} = 2 : (0,8,1,5) (1,5,0,8) 
{2,5} = 2 : (1,8,1,8) (6,7,3,4) 
{3,4} = 2 : (0,1,3,4) (7,9,1,8) 
{3,7} = 2 : (3,7,0,8) (6,9,1,5) 
{0,6} = 5 : (0,6,0,6) (1,7,2,5) (2,4,3,8) (3,5,1,7) (8,9,4,9) 
{1,7} = 5 : (0,6,1,7) (1,7,0,9) (2,4,4,6) (3,5,3,8) (8,9,2,5) 
{2,4} = 5 : (0,6,2,4) (1,7,1,3) (2,4,0,5) (3,5,6,9) (8,9,7,8) 
{3,5} = 5 : (0,6,3,5) (1,7,4,8) (2,4,7,9) (3,5,0,2) (8,9,1,6) 
{8,9} = 5 : (0,6,8,9) (1,7,6,7) (2,4,1,2) (3,5,4,5) (8,9,0,3) 

Обратите внимание на набор из 5 типов непересекающихся интеркалятов. Для всех четвёрок он одинаковый и даже все координаты интеркалятов одинаковые (координаты визуально сравнила, могла ошибиться). Это о чём-нибудь говорит, наверное. Срочно нужна экспертиза главного эксперта Белышева :)

Обработала полученные четвёрки программой Канонизатор ЛК по ДЛК; получается несколько четвёрок и двушек, 20 новых различных КФ, но все они не уникальные (то есть в нашей БД всё это уже есть).

Моя гипотеза: исходная четвёрка и все полученные в этом эксперименте двушки, четвёрки происходят от одного семейства ЛК блочной структуры. И это имеет обоснование: как я уже писала выше, преобразование перестановки элементов (простой перестановки 2х2 - 2 элемента в строках и 2 элемента в столбцах) эквивалентно преобразованию поворота блока. Фактически это одно и то же действие с четырьмя элементами блока.
А именно такие перестановки элементов и делает программа Чиркова и моя программа Карусель - тоже.

Но вот в чём вопрос: находит ли программа Чиркова все ДЛК, происходящие от данного семейства ЛК блочной структуры?
Очень сильно подозреваю, что не находит.
Это может сделать только программа Белышева Канонизатор ЛК по ДЛК.
А этой программе надо дать на обработку все не изоморфные ЛК семейства.
Круг опять замкнулся! Нету у меня всех не изоморфных ЛК семейства. И не знаю, как их получить.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Кстати, для исходной (проверяемой) четвёрки программа Интеркалятор выдаёт:

срез #1
0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 8 9 5 7
2 8 9 6 1 4 7 3 0 5
3 6 5 7 9 8 4 0 1 2
4 9 8 0 7 2 1 5 6 3
5 0 3 1 8 9 2 6 7 4
6 7 4 5 2 3 0 1 9 8
7 4 6 2 5 0 9 8 3 1
8 5 7 9 6 1 3 2 4 0
9 3 1 8 0 7 5 4 2 6

{0,1} = 1 : (7,8,5,9) 
{0,7} = 1 : (1,8,2,9) 
{0,8} = 1 : (3,7,5,7) 
{1,4} = 1 : (6,9,2,7) 
{1,6} = 1 : (7,9,2,9) 
{1,8} = 1 : (6,7,7,9) 
{1,9} = 1 : (5,8,3,5) 
{2,5} = 1 : (6,7,3,4) 
{2,7} = 1 : (0,8,2,7) 
{3,4} = 1 : (0,1,3,4) 
{6,7} = 1 : (1,9,5,9) 
{6,9} = 1 : (1,5,5,7) 
{7,8} = 1 : (3,9,3,5) 
{7,9} = 1 : (0,1,7,9) 
{0,2} = 2 : (3,8,7,9) (4,7,3,5) 
{1,5} = 2 : (0,8,1,5) (2,7,4,9) 
{3,7} = 2 : (1,4,4,9) (6,9,1,5) 
{4,6} = 2 : (1,2,3,5) (5,9,7,9) 
{0,6} = 5 : (0,6,0,6) (1,7,2,5) (2,4,3,8) (3,5,1,7) (8,9,4,9) 
{1,7} = 5 : (0,6,1,7) (1,7,0,9) (2,4,4,6) (3,5,3,8) (8,9,2,5) 
{2,4} = 5 : (0,6,2,4) (1,7,1,3) (2,4,0,5) (3,5,6,9) (8,9,7,8) 
{3,5} = 5 : (0,6,3,5) (1,7,4,8) (2,4,7,9) (3,5,0,2) (8,9,1,6) 
{8,9} = 5 : (0,6,8,9) (1,7,6,7) (2,4,1,2) (3,5,4,5) (8,9,0,3) 

Тот же самый набор 5 типов непересекающихся интеркалятов и те же самые координаты!
Всё это неспроста - не случайное совпадение.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверила полученные программой Чиркова преобразованные ДЛК программой Белышева kanonizator_dlk.
Протокол работы программы:

Загружена хеш-таблица
Время загрузки:         0.01 сек

Введено ДЛК:            1021483
Время загрузки:         50.491 сек

Найдено КФ:             958995
Время поиска:           4.078 сек

КФ записаны в файл output.txt
Время записи:           95.129 сек

Общее время работы:     149.717 сек

Для выхода нажмите ENTER:

КФ (в формате СН ДЛК) среди найденных ДЛК много.
Но сомнения меня терзают: не все ДЛК от данного семейства ЛК блочной структуры найдены!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

24 ноября в Приложении odlkmax найдена уникальная четвёрка

 0 1 2 3 4 5 6 7 8 9
 4 5 9 6 1 8 7 0 3 2
 6 0 3 7 5 4 9 8 2 1
 9 3 5 8 7 2 1 6 4 0
 3 6 0 2 9 7 4 1 5 8
 1 7 8 5 2 6 3 9 0 4
 7 8 4 0 6 1 2 3 9 5
 8 2 6 1 0 9 5 4 7 3
 2 4 7 9 8 3 0 5 1 6
 5 9 1 4 3 0 8 2 6 7
sq1

 0 1 2 3 4 5 6 7 8 9
 9 5 4 6 1 8 7 0 3 2
 6 0 3 7 5 4 9 8 2 1
 4 3 5 8 7 2 1 6 9 0
 3 6 0 2 9 7 4 1 5 8
 1 7 8 5 2 6 3 9 0 4
 7 8 9 0 6 1 2 3 4 5
 8 2 6 1 0 9 5 4 7 3
 2 4 7 9 8 3 0 5 1 6
 5 9 1 4 3 0 8 2 6 7
sq2

 0 1 2 3 4 5 6 7 8 9
 4 5 9 6 2 8 7 0 3 1
 6 0 3 7 5 4 9 8 1 2
 9 3 5 8 7 1 2 6 4 0
 3 6 0 2 9 7 4 1 5 8
 2 7 8 5 1 6 3 9 0 4
 7 8 4 0 6 2 1 3 9 5
 8 2 6 1 0 9 5 4 7 3
 1 4 7 9 8 3 0 5 2 6
 5 9 1 4 3 0 8 2 6 7
sq3

 0 1 2 3 4 5 6 7 8 9
 9 5 4 6 2 8 7 0 3 1
 6 0 3 7 5 4 9 8 1 2
 4 3 5 8 7 1 2 6 9 0
 3 6 0 2 9 7 4 1 5 8
 2 7 8 5 1 6 3 9 0 4
 7 8 9 0 6 2 1 3 4 5
 8 2 6 1 0 9 5 4 7 3
 1 4 7 9 8 3 0 5 2 6
 5 9 1 4 3 0 8 2 6 7
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 7 9 5 6 8
 3 4 8 5 0 9 2 1 7 6
 5 7 3 9 2 6 4 8 0 1
 9 5 6 1 7 0 8 2 4 3
 7 8 4 6 5 1 0 3 9 2
 6 0 5 2 9 8 3 4 1 7
 2 9 7 0 8 4 1 6 3 5
 4 3 1 8 6 2 7 9 5 0
 8 6 9 7 1 3 5 0 2 4

Программа Белышева Интеркалятор говорит, что эта четвёрка происходит не от ЛК блочной структуры.
Это у нас пятая такая четвёрка в БД.
Четвёрка полновесная, то есть даёт 5 уникальных КФ:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 7 9 5 6 8
3 4 8 5 0 9 2 1 7 6
5 7 3 9 2 6 4 8 0 1
9 5 6 1 7 0 8 2 4 3
7 8 4 6 5 1 0 3 9 2
6 0 5 2 9 8 3 4 1 7
2 9 7 0 8 4 1 6 3 5
4 3 1 8 6 2 7 9 5 0
8 6 9 7 1 3 5 0 2 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 3 7 9 6 8
4 6 8 7 2 9 3 5 0 1
9 8 1 5 6 7 2 4 3 0
6 0 9 2 3 1 5 8 4 7
8 5 7 1 0 6 4 2 9 3
5 4 3 8 7 0 9 6 1 2
3 7 4 6 9 8 0 1 2 5
2 3 5 9 1 4 8 0 7 6
7 9 6 0 8 2 1 3 5 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 3 8 9 6 7
2 7 5 8 6 9 0 3 4 1
9 6 8 7 2 1 4 5 3 0
6 4 3 5 1 7 9 8 0 2
3 9 4 6 0 8 7 2 1 5
4 8 9 2 7 0 3 1 5 6
5 0 1 9 8 4 2 6 7 3
7 5 6 0 3 2 1 4 9 8
8 3 7 1 9 6 5 0 2 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 3 8 9 6 7
2 7 5 8 6 9 0 3 4 1
9 8 6 7 2 1 4 5 3 0
6 4 3 5 1 7 9 8 0 2
3 9 4 6 0 8 7 2 1 5
4 6 9 2 7 0 3 1 5 8
5 0 1 9 8 4 2 6 7 3
7 5 8 0 3 2 1 4 9 6
8 3 7 1 9 6 5 0 2 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 7 9 6 3
4 6 8 7 2 9 3 5 0 1
9 8 1 5 6 7 2 4 3 0
6 0 9 2 3 1 5 8 4 7
3 5 7 1 0 6 4 2 9 8
5 4 3 8 7 0 9 6 1 2
8 7 4 6 9 3 0 1 2 5
2 3 5 9 1 4 8 0 7 6
7 9 6 0 8 2 1 3 5 4

КФ основного ДЛК четвёрки во втором формате принадлежит линейке №52

0 5 4 6 3 7 8 2 9 1
8 1 5 7 6 3 0 9 2 4
6 0 2 5 9 8 1 3 4 7
9 2 6 3 7 1 4 8 5 0
7 3 1 2 4 6 9 5 0 8
2 4 8 9 0 5 7 6 1 3
1 9 7 8 5 0 6 4 3 2
4 8 9 0 1 2 3 7 6 5
3 7 0 4 2 9 5 1 8 6
5 6 3 1 8 4 2 0 7 9

Теперь в нашей БД содержатся 214 уникальных четвёрок.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

В эксперименте по тотальной проверке всех БС, дающих симметричные по Гергели/Брауну ДЛК, найдены 6 уникальных четвёрок!

При этом пять четвёрок найдено при первичной обработке решений с проекта, а шестая четвёрка найдена при вторичной обработке.
Показываю все 6 четвёрок в полном виде (КФ основных ДЛК четвёрок в первом формате)

 0 1 2 3 4 5 6 7 8 9
 4 7 9 8 3 1 0 2 5 6
 5 4 1 6 8 2 9 0 3 7
 1 3 0 2 5 4 7 9 6 8
 2 5 7 9 6 3 8 1 0 4
 7 9 3 5 1 8 2 6 4 0
 6 0 8 4 9 7 3 5 1 2
 9 8 6 1 7 0 5 4 2 3
 3 2 5 7 0 6 4 8 9 1
 8 6 4 0 2 9 1 3 7 5
sq1

 0 1 2 3 4 5 6 7 8 9
 4 7 9 8 3 6 0 2 5 1
 5 4 1 6 8 2 9 0 3 7
 6 3 0 2 5 4 7 9 1 8
 2 5 7 9 6 3 8 1 0 4
 7 9 3 5 1 8 2 6 4 0
 1 0 8 4 9 7 3 5 6 2
 9 8 6 1 7 0 5 4 2 3
 3 2 5 7 0 1 4 8 9 6
 8 6 4 0 2 9 1 3 7 5
sq2

 0 1 2 3 4 5 6 7 8 9
 7 4 9 8 3 1 2 0 5 6
 5 0 1 6 8 3 9 2 4 7
 1 3 0 2 5 8 7 9 6 4
 8 5 7 9 6 0 4 1 2 3
 4 9 8 5 1 7 0 6 3 2
 6 7 3 4 9 2 8 5 1 0
 9 2 6 1 0 4 5 3 7 8
 2 8 5 0 7 6 3 4 9 1
 3 6 4 7 2 9 1 8 0 5
sq3

 0 1 2 3 4 5 6 7 8 9
 7 4 9 8 3 6 2 0 5 1
 5 0 1 6 8 3 9 2 4 7
 6 3 0 2 5 8 7 9 1 4
 8 5 7 9 6 0 4 1 2 3
 4 9 8 5 1 7 0 6 3 2
 1 7 3 4 9 2 8 5 6 0
 9 2 6 1 0 4 5 3 7 8
 2 8 5 0 7 1 3 4 9 6
 3 6 4 7 2 9 1 8 0 5
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 9 7 8 6 3
 9 6 8 0 2 1 3 4 7 5
 3 4 5 6 1 7 8 2 9 0
 5 0 4 1 7 2 9 6 3 8
 6 7 9 8 0 3 4 5 2 1
 2 9 6 5 8 0 1 3 4 7
 4 5 1 7 3 8 2 9 0 6
 8 3 7 9 6 4 0 1 5 2
 7 8 3 2 9 6 5 0 1 4
---------------------

 0 1 2 3 4 5 6 7 8 9
 4 6 1 2 9 0 7 3 5 8
 8 7 3 0 2 9 5 1 4 6
 5 3 6 9 1 7 0 8 2 4
 9 2 7 5 8 3 4 6 0 1
 6 0 8 1 7 4 3 2 9 5
 1 4 0 6 5 8 2 9 7 3
 7 9 4 8 6 2 1 5 3 0
 3 8 5 7 0 6 9 4 1 2
 2 5 9 4 3 1 8 0 6 7
sq1

 0 1 2 3 4 5 6 7 8 9
 4 6 5 2 9 0 7 3 1 8
 8 7 3 0 2 9 1 5 4 6
 1 3 6 9 5 7 0 8 2 4
 9 2 7 5 8 3 4 6 0 1
 6 0 8 1 7 4 3 2 9 5
 5 4 0 6 1 8 2 9 7 3
 7 9 4 8 6 2 5 1 3 0
 3 8 1 7 0 6 9 4 5 2
 2 5 9 4 3 1 8 0 6 7
sq2

 0 1 2 3 4 5 6 7 8 9
 4 6 1 9 7 8 2 3 5 0
 9 2 3 6 8 0 5 1 4 7
 5 3 7 8 1 6 0 2 9 4
 8 7 6 5 9 3 4 0 2 1
 2 0 9 1 6 4 3 8 7 5
 1 4 8 2 5 9 7 6 0 3
 6 9 4 7 0 2 1 5 3 8
 3 8 5 0 2 7 9 4 1 6
 7 5 0 4 3 1 8 9 6 2
sq3

 0 1 2 3 4 5 6 7 8 9
 4 6 5 9 7 8 2 3 1 0
 9 2 3 6 8 0 1 5 4 7
 1 3 7 8 5 6 0 2 9 4
 8 7 6 5 9 3 4 0 2 1
 2 0 9 1 6 4 3 8 7 5
 5 4 8 2 1 9 7 6 0 3
 6 9 4 7 0 2 5 1 3 8
 3 8 1 0 2 7 9 4 5 6
 7 5 0 4 3 1 8 9 6 2
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 9 8 6 7 3
 6 0 5 8 1 7 3 2 9 4
 2 7 3 6 8 4 1 9 5 0
 3 6 9 1 7 0 2 8 4 5
 7 5 1 9 3 8 4 0 2 6
 4 3 7 5 0 2 9 1 6 8
 5 8 6 0 9 3 7 4 1 2
 9 4 8 2 6 1 0 5 3 7
 8 9 4 7 2 6 5 3 0 1
---------------------
 0 1 2 3 4 5 6 7 8 9
 7 3 1 5 9 0 4 6 2 8
 2 6 5 0 8 7 9 3 1 4
 4 8 0 7 3 9 5 2 6 1
 5 9 4 2 6 1 7 8 0 3
 8 2 7 9 0 4 1 5 3 6
 3 5 6 4 1 2 8 9 7 0
 9 0 8 6 5 3 2 1 4 7
 1 7 3 8 2 6 0 4 9 5
 6 4 9 1 7 8 3 0 5 2
sq1

 0 1 2 3 4 5 6 7 8 9
 7 3 1 5 9 0 4 6 2 8
 2 6 8 0 5 7 9 3 1 4
 4 5 0 7 3 9 8 2 6 1
 5 9 4 2 6 1 7 8 0 3
 8 2 7 9 0 4 1 5 3 6
 3 8 6 4 1 2 5 9 7 0
 9 0 5 6 8 3 2 1 4 7
 1 7 3 8 2 6 0 4 9 5
 6 4 9 1 7 8 3 0 5 2
sq2

 0 1 2 3 4 5 6 7 8 9
 3 4 6 5 9 0 7 1 2 8
 2 7 5 0 8 6 9 3 1 4
 6 8 0 1 3 9 5 2 4 7
 5 9 4 2 7 1 3 8 6 0
 8 2 1 9 0 3 4 5 7 6
 1 5 7 4 6 2 8 9 0 3
 9 0 8 7 5 4 2 6 3 1
 4 6 3 8 2 7 1 0 9 5
 7 3 9 6 1 8 0 4 5 2
sq3

 0 1 2 3 4 5 6 7 8 9
 3 4 6 5 9 0 7 1 2 8
 2 7 8 0 5 6 9 3 1 4
 6 5 0 1 3 9 8 2 4 7
 5 9 4 2 7 1 3 8 6 0
 8 2 1 9 0 3 4 5 7 6
 1 8 7 4 6 2 5 9 0 3
 9 0 5 7 8 4 2 6 3 1
 4 6 3 8 2 7 1 0 9 5
 7 3 9 6 1 8 0 4 5 2
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 6 7 8 3 9 4 5
 7 4 3 5 1 9 0 6 2 8
 2 3 9 8 0 4 1 5 7 6
 4 8 6 9 5 3 2 0 1 7
 6 0 4 1 2 7 5 8 9 3
 5 7 1 0 8 6 9 2 3 4
 3 6 7 2 9 1 8 4 5 0
 9 5 8 4 3 0 7 1 6 2
 8 9 5 7 6 2 4 3 0 1
---------------------
 0 1 2 3 4 5 6 7 8 9
 3 9 5 4 6 1 0 8 7 2
 5 0 4 1 2 3 8 6 9 7
 8 4 6 2 7 9 3 1 0 5
 9 7 3 6 1 4 5 0 2 8
 6 3 7 9 0 8 1 2 5 4
 4 8 1 5 3 2 7 9 6 0
 2 6 8 0 9 7 4 5 1 3
 7 2 0 8 5 6 9 4 3 1
 1 5 9 7 8 0 2 3 4 6
sq1

 0 1 2 3 4 5 6 7 8 9
 7 9 5 4 6 1 0 8 3 2
 5 0 4 1 2 3 8 6 9 7
 8 4 6 2 3 9 7 1 0 5
 9 3 7 6 1 4 5 0 2 8
 6 7 3 9 0 8 1 2 5 4
 4 8 1 5 7 2 3 9 6 0
 2 6 8 0 9 7 4 5 1 3
 3 2 0 8 5 6 9 4 7 1
 1 5 9 7 8 0 2 3 4 6
sq2

 0 1 2 3 4 5 6 7 8 9
 3 6 5 4 1 9 2 8 7 0
 6 9 4 5 2 3 8 1 0 7
 8 4 0 1 7 6 3 2 9 5
 9 7 3 2 5 4 0 6 1 8
 2 3 7 9 0 8 1 5 6 4
 4 8 9 6 3 2 7 0 5 1
 1 5 8 0 6 7 4 9 2 3
 7 2 1 8 9 0 5 4 3 6
 5 0 6 7 8 1 9 3 4 2
sq3

 0 1 2 3 4 5 6 7 8 9
 7 6 5 4 1 9 2 8 3 0
 6 9 4 5 2 3 8 1 0 7
 8 4 0 1 3 6 7 2 9 5
 9 3 7 2 5 4 0 6 1 8
 2 7 3 9 0 8 1 5 6 4
 4 8 9 6 7 2 3 0 5 1
 1 5 8 0 6 7 4 9 2 3
 3 2 1 8 9 0 5 4 7 6
 5 0 6 7 8 1 9 3 4 2
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 6 7 8 9 3 5 4
 3 5 8 7 1 9 4 0 6 2
 2 3 9 5 6 0 8 4 7 1
 4 0 5 8 9 2 7 1 3 6
 5 6 4 1 3 7 2 8 9 0
 7 9 3 4 0 6 1 5 2 8
 9 4 1 2 8 3 5 6 0 7
 8 7 6 0 2 1 3 9 4 5
 6 8 7 9 5 4 0 2 1 3
---------------------
 0 1 2 3 4 5 6 7 8 9
 8 4 5 7 6 3 0 9 2 1
 9 5 7 1 8 0 3 6 4 2
 6 9 3 2 5 4 1 8 0 7
 2 6 1 5 9 8 7 0 3 4
 7 0 8 6 3 1 4 2 9 5
 4 3 9 0 7 2 8 1 5 6
 3 2 4 8 1 6 9 5 7 0
 1 7 0 4 2 9 5 3 6 8
 5 8 6 9 0 7 2 4 1 3
sq1

 0 1 2 3 4 5 6 7 8 9
 8 4 5 7 6 3 0 9 2 1
 9 5 7 1 8 0 3 6 4 2
 6 9 3 2 5 4 8 1 0 7
 2 6 8 5 9 1 7 0 3 4
 7 0 1 6 3 8 4 2 9 5
 4 3 9 0 7 2 1 8 5 6
 3 2 4 8 1 6 9 5 7 0
 1 7 0 4 2 9 5 3 6 8
 5 8 6 9 0 7 2 4 1 3
sq2

 0 1 2 3 4 5 6 7 8 9
 8 5 4 7 6 3 0 9 2 1
 9 6 7 1 8 2 3 0 5 4
 7 9 3 4 5 6 1 8 0 2
 5 4 1 2 9 8 7 6 3 0
 6 2 8 0 3 1 5 4 9 7
 2 3 9 6 0 7 8 1 4 5
 3 0 5 8 1 4 9 2 7 6
 1 7 0 5 2 9 4 3 6 8
 4 8 6 9 7 0 2 5 1 3
sq3

 0 1 2 3 4 5 6 7 8 9
 8 5 4 7 6 3 0 9 2 1
 9 6 7 1 8 2 3 0 5 4
 7 9 3 4 5 6 8 1 0 2
 5 4 8 2 9 1 7 6 3 0
 6 2 1 0 3 8 5 4 9 7
 2 3 9 6 0 7 1 8 4 5
 3 0 5 8 1 4 9 2 7 6
 1 7 0 5 2 9 4 3 6 8
 4 8 6 9 7 0 2 5 1 3
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 3 8 0 7 9 6 4 5
 3 4 1 2 9 6 5 8 7 0
 2 7 9 6 1 8 0 4 5 3
 8 9 7 0 5 3 4 2 6 1
 9 8 0 7 2 4 3 5 1 6
 5 0 8 1 6 9 7 3 2 4
 4 3 6 5 8 1 2 9 0 7
 6 5 4 9 7 0 8 1 3 2
 7 6 5 4 3 2 1 0 9 8
---------------------
 0 1 2 3 4 5 6 7 8 9
 9 7 1 2 0 8 3 5 6 4
 8 2 5 9 3 7 0 4 1 6
 2 0 3 4 7 6 1 8 9 5
 1 9 4 5 6 3 7 2 0 8
 4 3 8 0 2 1 9 6 5 7
 6 5 9 7 1 2 8 3 4 0
 7 6 0 1 8 4 5 9 3 2
 3 8 7 6 5 9 4 0 2 1
 5 4 6 8 9 0 2 1 7 3
sq1

 0 1 2 3 4 5 6 7 8 9
 9 7 1 6 0 8 3 5 2 4
 8 6 5 9 3 7 0 4 1 2
 2 0 3 4 7 6 1 8 9 5
 1 9 4 5 2 3 7 6 0 8
 4 3 8 0 6 1 9 2 5 7
 6 5 9 7 1 2 8 3 4 0
 7 2 0 1 8 4 5 9 3 6
 3 8 7 2 5 9 4 0 6 1
 5 4 6 8 9 0 2 1 7 3
sq2

 0 1 2 3 4 5 6 7 8 9
 9 3 8 2 0 4 1 5 6 7
 8 2 5 7 3 1 0 4 9 6
 2 0 4 8 7 6 3 9 1 5
 1 9 3 5 6 7 4 2 0 8
 7 4 1 0 2 9 8 6 5 3
 6 5 9 1 8 2 7 3 4 0
 3 6 0 4 9 8 5 1 7 2
 4 8 7 6 5 3 9 0 2 1
 5 7 6 9 1 0 2 8 3 4
sq3

 0 1 2 3 4 5 6 7 8 9
 9 3 8 6 0 4 1 5 2 7
 8 6 5 7 3 1 0 4 9 2
 2 0 4 8 7 6 3 9 1 5
 1 9 3 5 2 7 4 6 0 8
 7 4 1 0 6 9 8 2 5 3
 6 5 9 1 8 2 7 3 4 0
 3 2 0 4 9 8 5 1 7 6
 4 8 7 2 5 3 9 0 6 1
 5 7 6 9 1 0 2 8 3 4
sq4

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 7 9 8 5 6
 9 0 6 5 7 8 4 2 3 1
 6 5 1 7 9 2 8 0 4 3
 2 7 9 1 8 0 3 5 6 4
 3 6 5 8 1 4 2 9 7 0
 7 9 8 6 5 3 1 4 0 2
 5 4 7 9 6 1 0 3 2 8
 8 3 4 0 2 6 5 1 9 7
 4 8 3 2 0 9 7 6 1 5

Вот такое у нас замечательное прибавление по группам из 4-х ортогональных пар ДЛК.
Теперь в нашей БД содержится 220 уникальных четвёрок.

Данный эксперимент запущен в проекте ODLK1
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=24

PS. Все эти четвёрки происходят от ДЛК блочной структуры.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Множество четвёрок пополнено, в эксперименте с псевдоассоциативными ДЛК только что найдена ещё одна уникальная четвёрка, 221-ая.
Смотрите её здесь
https://boinc.progger.info/odlk/forum_thread.php?id=51&postid=1440#1440

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Сделала ревизию четвёркам; оказалось, что одну четвёрку я тут пропустила (об одной четвёрке из двух, найденных в эксперименте с псевдоассоциативными ДЛК, здесь не сообщила).
Всего в нашей БД на данный момент 222 четвёрки.
Среди них только 7 четвёрок, которые происходят не от ДЛК блочной структуры, вот они:

0 2 4 7 9 8 3 6 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 0 4 5 2 6 1 3 7
2 0 8 9 6 4 5 7 1 3
3 9 6 5 1 0 7 4 8 2
5 6 1 2 3 7 8 0 4 9

0 2 6 7 9 8 3 4 5 1
8 1 7 6 2 3 4 9 0 5
4 5 2 0 8 9 1 3 7 6
6 7 5 3 0 1 2 8 9 4
7 3 9 1 4 6 0 5 2 8
1 4 3 8 7 5 9 2 6 0
9 8 1 4 5 2 6 0 3 7
2 0 8 9 6 4 5 7 1 3
3 9 4 5 1 0 7 6 8 2
5 6 0 2 3 7 8 1 4 9

0 4 3 7 8 9 5 2 6 1
7 1 5 2 6 4 3 9 0 8
9 0 2 6 5 8 4 3 1 7
1 8 6 3 9 7 2 4 5 0
2 5 9 1 4 6 0 8 7 3
6 2 0 9 7 5 8 1 3 4
8 7 1 4 3 2 6 0 9 5
3 6 8 5 0 1 9 7 4 2
4 9 7 0 2 3 1 5 8 6
5 3 4 8 1 0 7 6 2 9

0 5 3 6 9 8 4 2 7 1
3 1 9 7 6 4 8 5 0 2
7 6 2 1 5 9 0 3 4 8
9 8 4 3 1 0 2 6 5 7
1 7 5 2 4 6 3 8 9 0
2 4 1 8 7 5 9 0 6 3
8 0 7 4 3 2 6 9 1 5
6 3 8 9 0 1 5 7 2 4
4 9 0 5 2 3 7 1 8 6
5 2 6 0 8 7 1 4 3 9

0 5 4 6 3 7 8 2 9 1
8 1 5 7 6 3 0 9 2 4
6 0 2 5 9 8 1 3 4 7
9 2 6 3 7 1 4 8 5 0
7 3 1 2 4 6 9 5 0 8
2 4 8 9 0 5 7 6 1 3
1 9 7 8 5 0 6 4 3 2
4 8 9 0 1 2 3 7 6 5
3 7 0 4 2 9 5 1 8 6
5 6 3 1 8 4 2 0 7 9

0 2 3 7 5 9 8 4 6 1
4 1 8 6 9 7 3 5 0 2
6 5 2 9 1 0 4 3 7 8
5 8 6 3 0 1 2 9 4 7
2 7 9 8 4 6 0 1 3 5
3 6 0 1 7 5 9 8 2 4
1 4 7 5 8 3 6 2 9 0
9 0 4 2 3 8 5 7 1 6
7 9 5 0 2 4 1 6 8 3
8 3 1 4 6 2 7 0 5 9

0 3 4 2 7 8 5 9 6 1
3 1 7 9 2 4 8 5 0 6
6 4 2 7 8 9 1 3 5 0
5 2 1 3 9 0 4 6 7 8
9 8 0 6 4 2 7 1 3 5
1 7 3 4 6 5 0 8 9 2
2 9 5 8 1 7 6 0 4 3
8 0 9 1 5 6 3 7 2 4
4 5 6 0 3 1 9 2 8 7
7 6 8 5 0 3 2 4 1 9

Две четвёрки, найденные мной в эксперименте с псевдоассоциативными ДЛК, находятся в этой группе.

Как я уже отмечала выше, характерной особенностью четвёрок, происходящих не от ДЛК блочной структуры, является их полновесность, то есть они дают пять уникальных КФ - максимально возможное для четвёрки количество уникальных КФ.
А вот четвёрки, происходящие от ДЛК блочной структуры не полновесные, они дают 3 или 4 уникальные КФ.
Полновесные четвёрки, происходящие от ДЛК блочной структуры, мне не встречались.

PS. Оказывается, есть исключения из правила.
Последняя из показанных четвёрок, происходящих не от ДЛК блочной структуры, даёт только 3 уникальные КФ. Остальные 6 четвёрок дают 5 уникальных КФ.
Наверное, в основном ДЛК последней четвёрки есть какая-то симметрия.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg