В эксперименте с псевдоассоциативными ДЛК найдена 223-я четвёрка в нашей БД.

Смотрите сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=51&postid=1700#1700
Список (в предыдущем посте) из 7 четвёрок, происходящих не от ЛК блочной структуры, пополнился ещё одной четвёркой

0 2 3 7 6 8 5 4 9 1
2 1 5 4 8 6 3 9 0 7
1 4 2 6 9 0 7 3 5 8
5 7 9 3 0 1 4 8 2 6
7 0 8 9 4 2 1 6 3 5
4 3 1 8 7 5 9 0 6 2
3 8 0 5 1 9 6 2 7 4
9 5 6 1 2 3 8 7 4 0
6 9 4 0 5 7 2 1 8 3
8 6 7 2 3 4 0 5 1 9

Кстати, выяснилось, что 4 четвёрки из этого списка происходят от ЛК блочной структуры косвенным образом.
Остаются "приблудными" три найденных мной четвёрки (от псевдоассоциативных ДЛК) и ещё какая-то одна.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

На данный момент в нашей БД КФ ОДЛК содержится 270 четвёрок.
Здесь все четвёрки:
1. 95 четвёрок, найденных в нашем с Белышевым эксперименте с семейством БС вида 5х5;
2. четвёрки, найденные в BOINC-проектах ODLK и ODLK1;
3. четвёрки, найденные в моём эксперименте с псевдоассоциативными ДЛК (выполняемом в ручном режиме) мной и Demis.

Показываю три первые и три последние четвёрки (КФ основного ДЛК во втором формате)

0 2 3 7 5 9 8 4 6 1
4 1 8 6 9 7 3 5 0 2
6 5 2 9 1 0 4 3 7 8
5 8 6 3 0 1 2 9 4 7
2 7 9 8 4 6 0 1 3 5
3 6 0 1 7 5 9 8 2 4
1 4 7 5 8 3 6 2 9 0
9 0 4 2 3 8 5 7 1 6
7 9 5 0 2 4 1 6 8 3
8 3 1 4 6 2 7 0 5 9

0 2 3 7 6 8 5 4 9 1
2 1 5 4 8 6 3 9 0 7
1 4 2 6 9 0 7 3 5 8
5 7 9 3 0 1 4 8 2 6
7 0 8 9 4 2 1 6 3 5
4 3 1 8 7 5 9 0 6 2
3 8 0 5 1 9 6 2 7 4
9 5 6 1 2 3 8 7 4 0
6 9 4 0 5 7 2 1 8 3
8 6 7 2 3 4 0 5 1 9

0 2 3 8 6 7 5 9 4 1
3 1 7 6 9 4 8 5 0 2
6 8 2 9 5 0 1 3 7 4
5 0 1 3 2 9 4 8 6 7
7 3 0 1 4 2 9 6 5 8
2 6 8 4 7 5 0 1 9 3
4 7 9 5 8 1 6 2 3 0
9 4 6 0 1 8 3 7 2 5
1 9 5 2 0 3 7 4 8 6
8 5 4 7 3 6 2 0 1 9

. . . . . . . 

0 8 4 7 3 2 9 5 6 1
2 1 6 9 8 3 7 4 0 5
4 7 2 5 9 8 0 3 1 6
9 5 0 3 6 1 2 8 7 4
1 2 5 0 4 6 8 9 3 7
8 4 9 6 7 5 3 1 2 0
7 3 1 4 5 0 6 2 9 8
6 0 8 2 1 9 4 7 5 3
3 9 7 1 0 4 5 6 8 2
5 6 3 8 2 7 1 0 4 9

0 9 3 5 6 2 7 8 4 1
6 1 8 4 5 7 9 0 2 3
4 7 2 8 1 9 5 3 0 6
5 8 6 3 2 0 4 9 1 7
3 5 9 1 4 6 8 2 7 0
9 6 7 0 8 5 1 4 3 2
2 3 0 9 7 4 6 1 5 8
8 2 5 6 0 1 3 7 9 4
1 0 4 7 9 3 2 6 8 5
7 4 1 2 3 8 0 5 6 9

0 9 8 7 6 4 5 2 3 1
6 1 5 9 2 3 7 4 0 8
1 0 2 8 5 7 9 3 4 6
9 8 7 3 0 2 4 6 1 5
8 2 3 1 4 6 0 5 9 7
3 6 1 4 8 5 2 9 7 0
7 4 0 5 1 9 6 8 2 3
4 5 9 0 3 8 1 7 6 2
5 7 6 2 9 1 3 0 8 4
2 3 4 6 7 0 8 1 5 9

Некоторые четвёрки, найденные мной и Demis в данном эксперименте, я выкладывала на форуме Math Help Planet в теме "Ортогональные латинские квадраты 10-го порядка".

Последняя четвёрка, найденная Demis 13 июня с. г. (КФ основного ДЛК в первом формате)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 7 9 8 5 6 0
3 8 9 2 6 1 5 4 0 7
9 4 0 6 5 8 7 3 1 2
5 7 8 9 1 2 0 6 3 4
2 6 1 5 3 7 9 0 4 8
7 3 6 1 8 0 4 9 2 5
6 9 5 0 2 4 3 8 7 1
4 0 7 8 9 3 1 2 5 6
8 5 4 7 0 6 2 1 9 3

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

В эксперименте с псевдоассоциативными ДЛК найдены весьма интересные четвёрки.
Вот, например, конфигурация - четвёрки-близняшки, найденная мной



А это конфигурация, порождаемая четвёркой, найденной Demis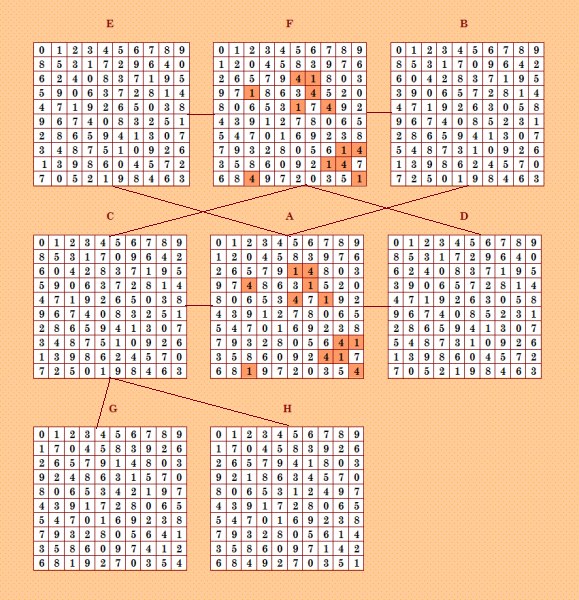



В этой конфигурации три четвёрки (!) и три двушки.

Наконец, конфигурация из четвёрки и десятки (найдена мной)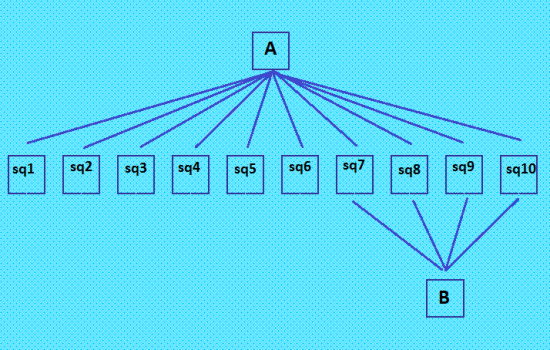



Четвёрка, происходящая от квадрата В, порождает десятку! В этой конфигурации можно ещё четыре двушки засчитать.

Может быть, есть и другие интересные конфигурации, порождаемые четвёрками; я особо не исследую конфигурации.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Только что найдена в эксперименте с псевдоассоциативными ДЛК 271-ая четвёрка

0 1 2 3 4 5 6 7 8 9
1 2 0 4 9 8 7 5 3 6
6 3 8 5 1 7 0 4 9 2
3 9 5 6 8 0 2 1 7 4
2 7 4 9 5 1 8 0 6 3
4 6 7 2 0 9 3 8 1 5
8 5 9 7 3 4 1 6 2 0
9 0 6 1 7 2 4 3 5 8
7 8 3 0 2 6 5 9 4 1
5 4 1 8 6 3 9 2 0 7

Четвёрка даёт положенные по штату 5 уникальных КФ ОДЛК.
Решение найдено при обработке псевдоассоциативных ДЛК в линейке № 51.

Эксперимент продолжается!
Трудно даже предположить, сколько было бы найдено различных групп пар ОДЛК в данном эксперименте, если бы запустить его в BOINC-проекте.
Какую часть всего объёма обрабатывает один мой ПК? Это же мизерная часть!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вспомнила интересную конфигурацию, порождаемую четвёркой, найденной в эксперименте с псевдоассоциативными ДЛК.
На форуме Math Help Planet выкладывала эту конфигурацию.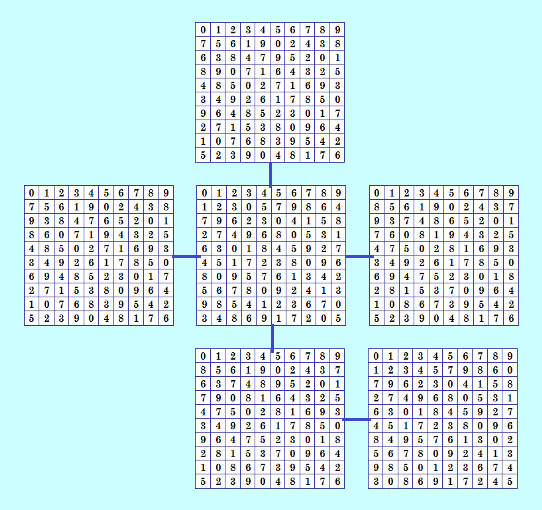



Можно назвать конфигурацию "четвёрка с аппендиксом" :)
В конфигурации содержатся четвёрка и двушка.

Данная четвёрка даёт 6 уникальных КФ ОДЛК.
Подобных четвёрок (дающих 6 уникальных КФ ОДЛК) было найдено несколько в эксперименте с псевдоассоциативными ДЛК. Надо рассмотреть их повнимательнее, может, есть и другие конфигурации, кроме четвёрки с аппендиксом.

Вот при беглом просмотре нашла четвёрки, дающие 6 уникальных КФ ОДЛК (все найдены в эксперименте с псевдоассоциативными ДЛК)

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 6 8 9 3 5 7
 3 7 5 1 2 4 8 0 9 6
 2 9 6 7 0 3 1 8 4 5
 5 3 4 9 8 7 0 6 1 2
 4 0 1 6 3 9 7 5 2 8
 8 5 7 2 1 6 3 9 0 4
 9 6 8 0 5 1 2 4 7 3
 7 4 3 8 9 2 5 1 6 0
 6 8 9 5 7 0 4 2 3 1

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 9 7 8 6 3 5
 3 7 5 1 6 4 9 2 0 8
 5 9 3 6 2 8 7 4 1 0
 2 6 7 8 3 1 0 9 5 4
 8 4 1 2 0 9 5 3 6 7
 6 0 8 5 7 2 4 1 9 3
 7 3 6 9 5 0 1 8 4 2
 9 8 4 0 1 3 2 5 7 6
 4 5 9 7 8 6 3 0 2 1

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 9 7 6 3 8
 9 7 8 6 1 3 0 2 4 5
 5 9 3 7 6 8 1 4 2 0
 8 6 5 2 9 0 4 1 7 3
 4 8 9 5 7 6 2 3 0 1
 2 4 1 8 0 7 3 9 5 6
 7 3 4 0 8 1 9 5 6 2
 3 5 6 9 2 4 8 0 1 7
 6 0 7 1 3 2 5 8 9 4

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 6 8 9 5 7
 9 4 1 8 2 7 5 3 6 0
 2 3 5 7 9 8 0 4 1 6
 8 9 6 0 5 2 7 1 3 4
 5 8 4 6 7 9 1 2 0 3
 6 0 7 1 8 4 3 5 9 2
 3 7 8 9 1 0 4 6 2 5
 7 6 9 5 0 3 2 8 4 1
 4 5 3 2 6 1 9 0 7 8

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 6 8 9 3 7
 9 4 1 8 2 7 3 5 6 0
 2 3 5 7 9 8 0 4 1 6
 8 9 6 0 3 2 7 1 5 4
 3 8 4 6 7 9 1 2 0 5
 6 0 7 1 8 4 5 3 9 2
 5 7 8 9 1 0 4 6 2 3
 7 6 9 5 0 3 2 8 4 1
 4 5 3 2 6 1 9 0 7 8

Завтра рассмотрю конфигурации, порождаемые этими четвёрками.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Просматривала проанализированные выше четвёрки.
Заинтересовала четвёрка, дающая 4 уникальные КФ ОДЛК.
Нарисовала конфигурацию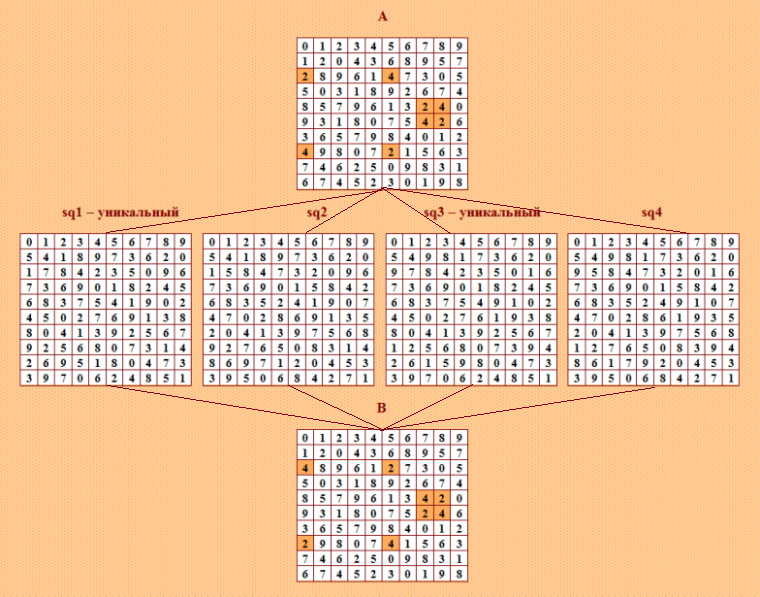



Основной ДЛК четвёрки - квадрат А. Это симметричный по Гергели/Брауну ДЛК.
Среди ортогональных соквадратов четвёрки только два уникальных.
Вторая четвёрка та же самая, но происходит от квадрата В.
Получились не полновесные четвёрки-близняшки. На две четвёрки всего 4 уникальные КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Начала обработку результатов с проекта ODLK1 за июнь.
Найдена в этой порции результатов 272-ая четвёрка

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 9 7 8 3 6
8 5 9 0 3 6 2 1 7 4
3 6 5 7 1 4 0 2 9 8
7 0 6 9 8 2 1 5 4 3
2 3 7 8 6 1 9 4 5 0
6 8 3 5 9 7 4 0 2 1
9 4 8 6 2 0 5 3 1 7
5 7 4 1 0 3 8 9 6 2
4 9 1 2 7 8 3 6 0 5

Четвёрка даёт 5 уникальных КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Это цитата

Вот при беглом просмотре нашла четвёрки, дающие 6 уникальных КФ ОДЛК (все найдены в эксперименте с псевдоассоциативными ДЛК)

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 6 8 9 3 5 7
 3 7 5 1 2 4 8 0 9 6
 2 9 6 7 0 3 1 8 4 5
 5 3 4 9 8 7 0 6 1 2
 4 0 1 6 3 9 7 5 2 8
 8 5 7 2 1 6 3 9 0 4
 9 6 8 0 5 1 2 4 7 3
 7 4 3 8 9 2 5 1 6 0
 6 8 9 5 7 0 4 2 3 1

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 9 7 8 6 3 5
 3 7 5 1 6 4 9 2 0 8
 5 9 3 6 2 8 7 4 1 0
 2 6 7 8 3 1 0 9 5 4
 8 4 1 2 0 9 5 3 6 7
 6 0 8 5 7 2 4 1 9 3
 7 3 6 9 5 0 1 8 4 2
 9 8 4 0 1 3 2 5 7 6
 4 5 9 7 8 6 3 0 2 1

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 9 7 6 3 8
 9 7 8 6 1 3 0 2 4 5
 5 9 3 7 6 8 1 4 2 0
 8 6 5 2 9 0 4 1 7 3
 4 8 9 5 7 6 2 3 0 1
 2 4 1 8 0 7 3 9 5 6
 7 3 4 0 8 1 9 5 6 2
 3 5 6 9 2 4 8 0 1 7
 6 0 7 1 3 2 5 8 9 4

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 6 8 9 5 7
 9 4 1 8 2 7 5 3 6 0
 2 3 5 7 9 8 0 4 1 6
 8 9 6 0 5 2 7 1 3 4
 5 8 4 6 7 9 1 2 0 3
 6 0 7 1 8 4 3 5 9 2
 3 7 8 9 1 0 4 6 2 5
 7 6 9 5 0 3 2 8 4 1
 4 5 3 2 6 1 9 0 7 8

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 5 6 8 9 3 7
 9 4 1 8 2 7 3 5 6 0
 2 3 5 7 9 8 0 4 1 6
 8 9 6 0 3 2 7 1 5 4
 3 8 4 6 7 9 1 2 0 5
 6 0 7 1 8 4 5 3 9 2
 5 7 8 9 1 0 4 6 2 3
 7 6 9 5 0 3 2 8 4 1
 4 5 3 2 6 1 9 0 7 8

Завтра рассмотрю конфигурации, порождаемые этими четвёрками.

Только дошли руки до исследования конфигураций, порождаемых этими четвёрками.
Первая четвёрка дала четвёрку с аппендиксом.
Вторая четвёрка дала полновесные четвёрки-близняшки. Выше я показывала такую конфигурацию, но без конкретных квадратов.
А теперь с конкретными квадратами покажу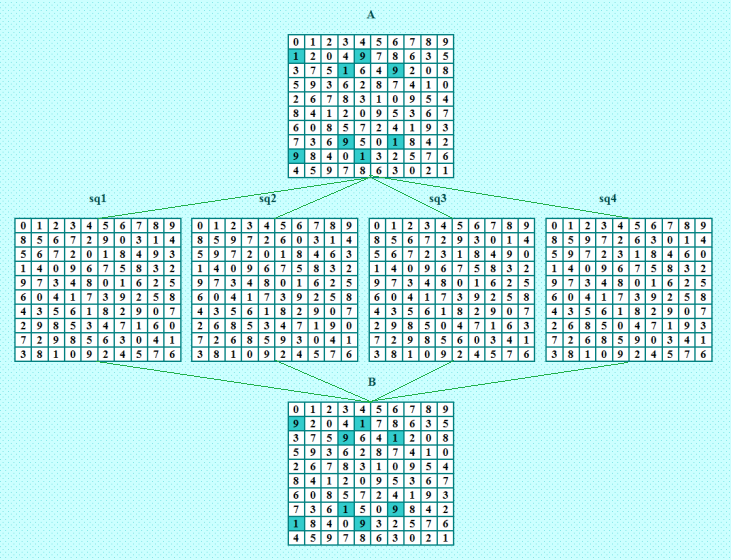



Пока ничего нового не обнаружила. Продолжу проверку оставшихся четвёрок.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Следующую четвёрку проверила в быстром темпе. Если не ошиблась, она тоже даёт четвёрок-близняшек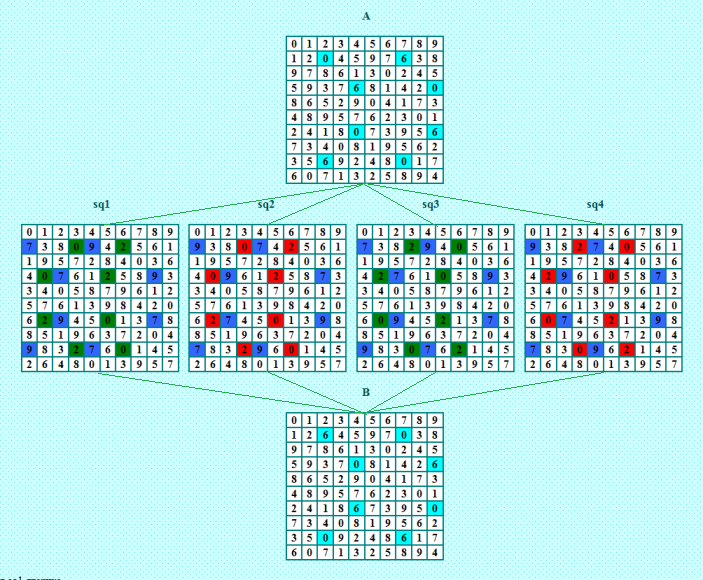



Здесь я раскрасила повёрнутые блоки не только в основных ДЛК четвёрок, но и в ортогональных соквадратах.
Гармония потрясающая! Посмотрите на предыдущий пример, там точно такая же гармония.
Если включить теоретический ум Белышева, можно вывести алгоритм получения всех четвёрок-близняшек.
Ну не может такая гармония не иметь красивого алгоритма!
Надо набрать побольше примеров, вдуматься в эту гармонию.

Немножко неправильно я раскрасила голубые ячейки в ортогональках, надо тоже два разных цвета для этих ячеек.

Ну, а у меня ещё две четвёрки остались для проверки.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Оставшиеся две четвёрки дали точно такую же конфигурацию - четвёрки-близняшки.
Вроде все четвёрки, дающие 6 уникальных КФ ОДЛК, проверила.
Два вида конфигураций у меня получилось: четвёрка с аппендиксом и четвёрки-близняшки.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Покажу ещё одну иллюстрацию, тоже четвёрки-близняшки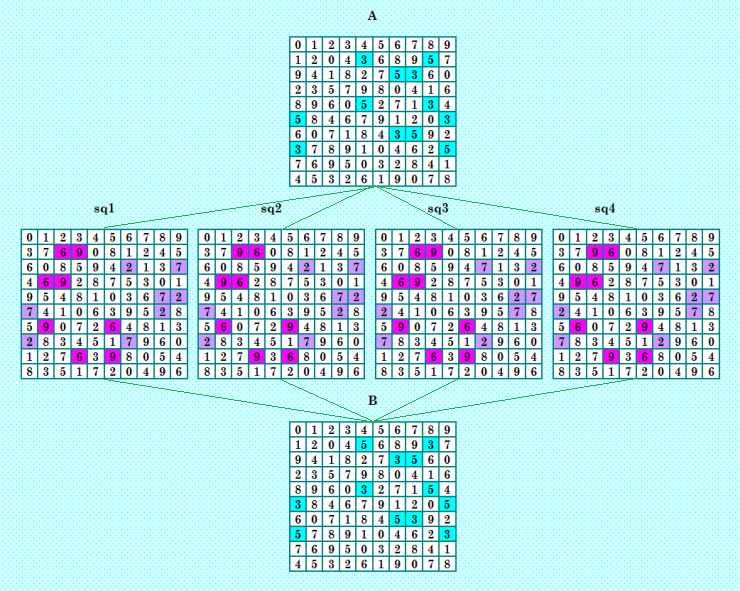



В основных ДЛК четвёрок (квадраты А и В) имеется поворот блоков.
А вот в ортогональных соквадратах перестановки элементов посложнее. Но гармония изумительная! Залюбуешься.

Много ли существует четвёрок-близняшек?
Как было показано выше, четвёрки-близняшки могут быть и не полновесные, то есть каждая четвёрка даёт 3 уникальные КФ ОДЛК, а две вместе дают 4 уникальные КФ ОДЛК.
В последних примерах все четвёрки полновесные, то есть каждая даёт 5 уникальных КФ ОДЛК, а две вместе дают 6 уникальных КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А тем временем мой эксперимент с псевдоассоциативными ДЛК выдаёт группы пар ОДЛК, пока только тройки и четвёрки.
Ну и им я очень рада, побольше бы выдавал :)

273-ая в нашей БД четвёрка только что найдена в этом эксперименте

0 1 2 3 4 5 6 7 8 9
1 2 3 8 0 4 9 5 6 7
7 9 5 2 3 0 8 1 4 6
9 7 8 6 5 1 4 2 3 0
2 8 6 1 9 7 5 4 0 3
4 6 7 0 2 8 3 9 5 1
3 0 4 5 7 9 1 6 2 8
6 4 0 9 8 2 7 3 1 5
5 3 9 4 1 6 0 8 7 2
8 5 1 7 6 3 2 0 9 4

Эта четвёрка даёт только 3 уникальные КФ ОДЛК, не полновесная.

Я продолжаю обрабатывать псевдоассоциативные ДЛК в линейке № 51.
При этом у меня работает новый генератор псевдоассоциативных ДЛК; прежним генератором Demis эту линейку проверил, правда, не полностью, а выборочно.
Пришлось выбирать, как я уже писала выше, из-за очень большого количества повторов. Очень вероятно, что пропуская некоторые области, мы пропустили и целый ряд решений в этих областях.
Разумеется, эксперимент требует тотальной проверки, без пропусков.
Но для ручного эксперимента это нереально.

Кстати, линейки №№ 15, 38, 51, которые могут содержать псевдоассоциативные ДЛК, у нас находятся в проверке в проекте ODLK.
Но! пользы от этого мало, потому что сами псевдоассоциативные ДЛК решений не дают, их надо обрабатывать Канонизатором ЛК по ДЛК.
Это значит: для этих трёх линеек надо изменить алгоритм поиска, чтобы достигнуть максимальной эффективности.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Эксперимент с псевдоассоциативными ДЛК стабильно продолжает давать неплохие результаты: не только однушки и двушки, но и группы пар ОДЛК посолиднее. Недавно найдена новая восьмёрка (о ней сообщалось в теме о восьмёрках).
А сейчас найдены две новые четвёрки

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 7 9 5 6 8
 5 6 8 7 9 1 3 2 0 4
 6 7 5 9 8 2 1 4 3 0
 7 9 4 6 1 8 5 0 2 3
 9 5 3 1 0 6 7 8 4 2
 3 8 9 5 2 0 4 6 1 7
 8 4 7 0 6 9 2 3 5 1
 2 3 1 8 5 4 0 9 7 6
 4 0 6 2 7 3 8 1 9 5

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 7 9 5 6 8
 5 6 1 7 9 8 3 2 0 4
 6 7 5 9 1 2 8 4 3 0
 7 9 4 6 8 1 5 0 2 3
 9 5 3 8 0 6 7 1 4 2
 3 8 9 5 2 0 4 6 1 7
 8 4 7 0 6 9 2 3 5 1
 2 3 8 1 5 4 0 9 7 6
 4 0 6 2 7 3 1 8 9 5

Это 274-ая и 275-ая четвёрки в нашей БД.
Количество четвёрок приближается к 300. И это наверняка не предел.

Кажется, это четвёрки-близняшки. Каждая четвёрка даёт 6 уникальных КФ ОДЛК и обе вместе тоже дают 6 уникальных КФ ОДЛК.
Нарисую попозже конфигурацию.
В линейке № 51 я уже обработала больше половины псевдоассоциативных ДЛК с помощью нового генератора (второго).
Думаю о новом генераторе (третьем) псевдоассоциативных ДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот конфигурация с новыми четвёрками-близняшками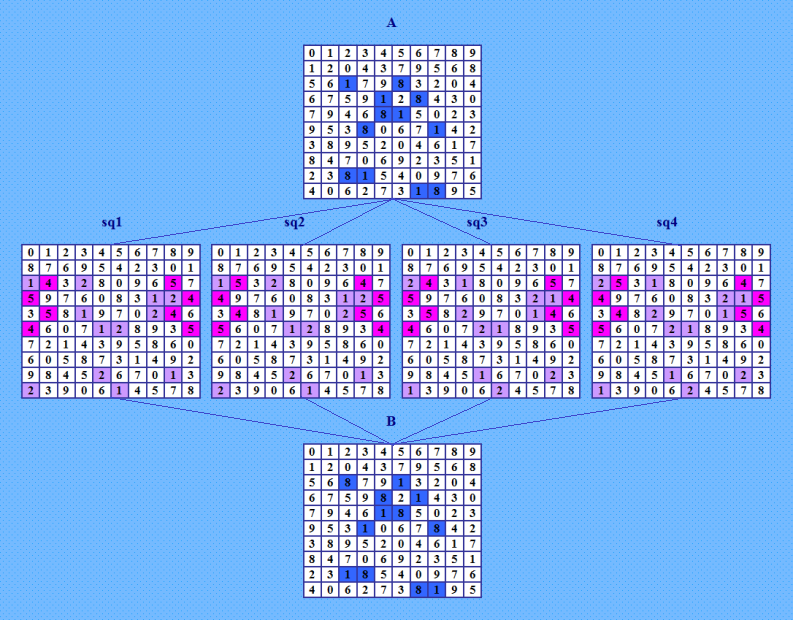



И узорчатые ДЛК налицо. И узоры в этих узорчатых ДЛК уже другие, но принцип тот же: две группы узоров в разных комбинациях, итого 4 варианта ДЛК.
Весьма устойчивая закономерность. Как мне кажется, все четвёрки-близняшки (или, по крайней мере, большинство из них) можно выловить с помощью узорчатых ДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Сделала ревизию четвёркам, имеющимся в нашей БД.
Всё правильно: 275 уникальных четвёрок в БД имеется.

Покажу пять самых маленьких четвёрок (они находятся в начале БД) и пять самых больших (они находятся в конце БД); формат основного ДЛК четвёрок первый.

Пять самых маленьких:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
2 3 5 1 0 9 8 4 6 7
8 5 9 6 7 2 3 0 4 1
3 7 4 9 1 8 0 5 2 6
4 0 6 8 2 7 1 3 9 5
7 4 8 0 6 3 9 1 5 2
6 9 1 2 5 4 7 8 0 3
9 6 7 5 8 1 4 2 3 0
5 8 3 7 9 0 2 6 1 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
2 9 3 1 5 4 8 6 0 7
9 6 7 5 1 8 4 2 3 0
7 5 9 8 6 3 1 0 4 2
8 7 4 6 0 9 3 5 2 1
4 0 6 2 8 1 7 3 9 5
6 4 1 9 2 7 0 8 5 3
3 8 5 7 9 0 2 4 1 6
5 3 8 0 7 2 9 1 6 4

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
3 4 7 1 2 9 8 0 5 6
4 8 3 9 7 0 2 5 6 1
8 7 5 2 6 4 9 3 1 0
9 5 6 7 1 8 0 4 2 3
7 6 1 5 9 2 3 8 0 4
2 0 8 6 5 3 4 1 9 7
5 3 9 8 0 1 7 6 4 2
6 9 4 0 8 7 1 2 3 5

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
3 4 7 1 9 0 8 2 5 6
9 8 6 5 2 7 4 3 1 0
8 9 4 2 6 3 7 5 0 1
7 0 5 6 8 1 3 4 9 2
5 3 8 0 7 2 9 1 6 4
4 6 1 7 0 9 2 8 3 5
2 5 3 9 1 8 0 6 4 7
6 7 9 8 5 4 1 0 2 3

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
3 7 5 2 1 4 9 8 0 6
6 0 8 7 9 2 3 4 1 5
8 4 1 9 6 0 2 5 3 7
4 9 7 6 5 8 0 3 2 1
9 8 6 1 7 3 4 0 5 2
7 3 4 5 2 9 8 1 6 0
5 6 3 8 0 7 1 2 9 4
2 5 9 0 8 1 7 6 4 3

Пять самых больших:

0 1 2 3 4 5 6 7 8 9
1 2 3 8 0 7 9 6 4 5
3 4 1 2 9 6 5 8 7 0
2 7 9 6 1 8 0 4 5 3
8 9 7 0 5 3 4 2 6 1
9 8 0 7 2 4 3 5 1 6
5 0 8 1 6 9 7 3 2 4
4 3 6 5 8 1 2 9 0 7
6 5 4 9 7 0 8 1 3 2
7 6 5 4 3 2 1 0 9 8

0 1 2 3 4 5 6 7 8 9
1 2 8 6 5 7 9 4 3 0
7 0 9 4 2 3 1 6 5 8
9 8 1 5 6 4 2 0 7 3
6 9 5 2 3 8 0 1 4 7
8 4 0 7 1 6 5 3 9 2
4 6 3 0 8 9 7 5 2 1
2 5 4 9 7 1 3 8 0 6
3 7 6 8 0 2 4 9 1 5
5 3 7 1 9 0 8 2 6 4

0 1 2 3 4 5 6 7 8 9
1 2 9 6 5 4 3 0 7 8
3 4 8 2 0 9 7 1 5 6
6 5 1 9 2 7 0 8 4 3
9 8 3 5 7 2 4 6 1 0
7 6 5 0 8 1 9 4 3 2
8 7 0 4 3 6 5 9 2 1
4 9 6 7 1 8 2 3 0 5
2 3 4 8 9 0 1 5 6 7
5 0 7 1 6 3 8 2 9 4

0 1 2 3 4 5 6 7 8 9
2 3 0 4 1 8 5 9 6 7
7 5 8 0 3 6 9 1 4 2
5 2 6 1 9 0 8 3 7 4
1 9 7 6 5 4 3 2 0 8
8 4 3 7 0 9 2 6 5 1
4 0 1 2 6 3 7 8 9 5
9 6 5 8 7 2 1 4 3 0
6 7 9 5 8 1 4 0 2 3
3 8 4 9 2 7 0 5 1 6

0 1 2 3 4 5 6 7 8 9
2 3 1 4 0 9 5 8 6 7
1 5 6 9 2 7 0 3 4 8
6 0 4 7 1 8 2 5 9 3
7 6 8 5 9 0 4 1 3 2
8 4 3 0 7 2 9 6 5 1
5 7 9 1 3 6 8 0 2 4
3 9 5 2 8 1 7 4 0 6
9 8 7 6 5 4 3 2 1 0
4 2 0 8 6 3 1 9 7 5

Интересно: большинство четвёрок происходит от семейств БС.
Вот статистика для всех четвёрок в нашей БД:

Определитель семейств блочных ЛК

Введено ЛК       : 275
Из них блочных   : 215

Найдено семейств блочных ЛК

5x5              : 1
9x5              : 4
10x5             : 31

Время работы     : 0.202 сек

215 четвёрок из 275 в семействах БС!

Ещё известны четвёрки, которые происходят от семейства БС косвенным образом.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Четвёрочка новенькая, 276-ая в нашей БД (эксперимент с псевдоассоциативными ДЛК, новая ветвь алгоритма)

0 1 2 3 4 5 6 7 8 9
1 2 3 4 8 0 7 9 5 6
2 8 4 9 5 3 0 1 6 7
5 6 9 1 7 4 2 3 0 8
6 3 0 7 9 8 4 5 2 1
4 5 6 2 0 7 9 8 1 3
9 7 5 6 3 1 8 0 4 2
8 0 7 5 1 2 3 6 9 4
7 4 1 8 6 9 5 2 3 0
3 9 8 0 2 6 1 4 7 5

Четвёрка не полновесная, всего 3 уникальные КФ ОДЛК даёт.

Эксперимент продолжаю - в двух вариантах алгоритма. Оба варианта дают отличные решения.
Удивительно богатое семейство - псевдоассоциативные ДЛК! Ещё ни одно из проверенных ранее семейств не дало столько интересных решений.
И ресурсы у этого семейства ещё очень и очень велики, проверена мизерная часть.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

О-о-о!
Проверила основной ДЛК новой четвёрки программой Белышева avtoizor; что-нибудь есть в этом ДЛК? - думаю себе.
И вот

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 9476183250 0523816749 3680791425 -> (4,31,31)

Код (4,31,31)!
Какая сия симметрия есть? :)

И главный вопрос: как её расплодить?

А недаром эта четвёрка даёт только 3 уникальные КФ ОДЛК.
Посмотрите на уникальные ортогональки этой четвёрки

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 7 9 3 6
5 4 7 1 3 6 2 0 9 8
4 5 8 9 6 2 1 3 7 0
6 3 9 0 1 7 5 8 4 2
3 0 5 6 8 4 9 1 2 7
9 7 1 5 0 3 8 2 6 4
7 9 4 8 2 0 3 6 1 5
8 6 3 2 7 9 0 4 5 1
2 8 6 7 9 1 4 5 0 3

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 7 9 3 6
5 7 4 1 3 6 2 0 9 8
7 5 8 9 6 2 1 3 4 0
6 3 9 0 1 4 5 8 7 2
3 0 5 6 8 7 9 1 2 4
9 4 1 5 0 3 8 2 6 7
4 9 7 8 2 0 3 6 1 5
8 6 3 2 7 9 0 4 5 1
2 8 6 7 9 1 4 5 0 3

Похожи, правда? А две остальные ортогональки вообще изоморфы этих уникальных ортогоналек.
Явно здесь присутствует какая-то загадочная симметрия, которая имеет код (4,31,31).

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А вот и 277-ая четвёрка в нашей БД, найдена только что в эксперименте с псевдоассоциативными ДЛК

 0 1 2 3 4 5 6 7 8 9
 1 2 7 4 5 8 9 0 3 6
 6 9 8 7 3 2 4 5 1 0
 4 5 0 1 8 6 7 3 9 2
 5 3 9 0 6 4 8 1 2 7
 7 4 3 5 1 9 0 2 6 8
 9 6 1 2 7 3 5 8 0 4
 3 8 6 9 0 7 2 4 5 1
 2 0 4 8 9 1 3 6 7 5
 8 7 5 6 2 0 1 9 4 3

Четвёрка тоже из семейства симметрии с кодом (4,31,31). Здорово!

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 3120459786 6879540213 7932684051 -> (4,31,31)

Три уникальные КФ ОДЛК даёт.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И ещё одна четвёрка найдена! Это 278-ая четвёрка в нашей БД.

И эта четвёрка тоже из семейства симметрии с кодом (4,31,31)

 0 1 2 3 4 5 6 7 8 9
 1 2 3 4 0 6 7 9 5 8
 2 7 4 8 5 0 1 6 9 3
 5 3 1 9 6 4 2 8 0 7
 8 6 9 5 7 3 0 2 1 4
 6 5 7 2 8 1 9 3 4 0
 3 0 6 1 9 2 8 4 7 5
 4 9 0 7 1 8 3 5 6 2
 9 4 8 6 2 7 5 0 3 1
 7 8 5 0 3 9 4 1 2 6

** 0123456789 0123456789 0123456789 -> (1,1,1)
** 1023456798 8976543201 5897604312 -> (4,31,31)

Вот это семейство!! Восьмёрка, шестёрка, уже 16 четвёрок, двушки...
Раскрутить бы это семейство по полной программе.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Только что в семействе симметрии (4,31,31) нашла новую четвёрку

 0 1 2 3 4 5 6 7 8 9
 1 2 0 4 3 6 5 9 7 8
 3 7 8 6 5 9 0 1 2 4
 7 6 1 5 8 2 3 4 9 0
 6 3 7 2 9 8 4 5 0 1
 9 0 3 1 6 4 7 8 5 2
 8 9 6 0 7 3 1 2 4 5
 4 8 5 9 0 7 2 6 1 3
 5 4 9 7 2 1 8 0 3 6
 2 5 4 8 1 0 9 3 6 7

Это 279-ая четвёрка в нашей БД.

Четвёрка не полновесная, даёт 3 уникальные КФ, как и положено "симметричному" решению.

Выше приведены четвёрки, найденные в эксперименте с псевдоассоциативными ДЛК, которые тоже оказались из семейства симметрии (4,31,31).
А сейчас я выполняю ещё один эксперимент - ищу решения непосредственно в семействе симметрии (4,31,31).
Последняя четвёрка найдена в этом эксперименте.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg