Центральной 15-й мы называем симметричный кортеж длины 15 из последовательных простых чисел со следующим паттерном

0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228

Центральная 15-ка расположена в центре ключевой 17-ки, 19-ки с минимальным диаметром, а также симметричных k-tuplet длины больше 19 с преемственным паттерном.
Например, в центре симметричного 21-tuplet со следующим преемственным паттерном

0, 54, 60, 66, 84, 96, 126, 144, 150, 174, 180, 186, 210, 216, 234, 264, 276, 294, 300, 306, 360

Самые первые центральные 15-ки были найдены в BOINC-проекте Tomas Brada Experimental Grid

2079914861571286679: 0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228
3665619319531504883: 0, 18, 30, 60, 78, 84, 108, 114, 120, 144, 150, 168, 198, 210, 228

Далее буду приводить только начальные элементы кортежей, без паттерна, так как паттерн всегда один и тот же.

Следующие центральные 15-ки (6 штук) были найдены Ярославом Врублевским в конкурсе по кортежам, они содержатся в найденных им ключевых 17-х, то есть являются матрёшечными.

Вот они

1006882292528806742273,
3954328349097827424403,
4896552110116770789779,
6751407944109046348069,
7768326730875185894813,
19252814175273852997763,

Далее присоединяю ещё 7 матрёшечных 15-к из ключевых 17-к, найденных командой г. Петухова.

154787380396512840656513,
187749702383119068641843,
901985248981556228168773,
4246610002636339828954843,
9425346484752129657862229,
9701757886114895320879553,
14451615724941305041645453

Все известные ключевые 17-ки опубликованы здесь
https://dxdy.ru/post1674162.html#p1674162

Наконец все перечисленные кортежи объединяю с центральными 15-ми, найденными Ядряррой (Антон Никонов).
Он выложил эти центральные 15-ки здесь
https://dxdy.ru/post1692623.html#p1692623

В результате получаю БД из 170 кортежей

2079914861571286679, 3665619319531504883, 214946236533755076289, 271541128585758431779, 356824342193987437163, 944273532072632171243, 1006882292528806742273, 2022711875770842846529, 2162149531729604295103, 2225037046903483907473, 2321104522630063134343, 2619820297764034190219, 2865889199912908889659, 2938616605475118382193, 3536266327242777212023, 3730861010539166369959, 3731183113236698329043, 3954328349097827424403, 4010322518824084606823, 4385038454541770260783, 4896552110116770789779, 5424443345599274902999, 5550244178896033210273, 5563684279615769106739, 6137356084057875005723, 6751407944109046348069, 6822640902781117403669, 6961394541011197172279, 7768326730875185894813, 8140616600819764641413, 8232485038811356957313, 8247840611942752240513, 8749161465060085980289, 8790344504647482496553, 9100228069582396220699, 9369566116899129925723, 9750634398553127404873, 10326968803949363609983, 10671796931507693781739, 11303999667139928672603, 11562084795586986305023, 11644034428493619141929, 12419328750104774994043, 12480848738857754155279, 12744508017243603506299, 12967362495788256980803, 14832445430292682412599, 15636034351630168471829, 16257917584261857368243, 17716330748916274931003, 18164396263690092225203, 18742586057174230251379, 18826403258369198671859, 19138427715111031577083, 19252814175273852997763, 19536294443804410516183, 19832606831753483622233, 20897856447156043589173, 21287941491290623223299, 21426089952025093895393, 21488607476073832073659, 22544235579330598703663, 23868792350514616905493, 24556642668231947322989, 24715153027336908055313, 24859382344782684063913, 26082913722886576565843, 26913993896984416720723, 27297597458437704698239, 27479373083803560368843, 29579059173365490432583, 29674090145515624849133, 30718149799825764081199, 30851792637019107009089, 31009930868332327847329, 31167395346004527024809, 31715036252267904940343, 34106328260995613527283, 34166808184761843016519, 34835558850415981958239, 37367256014233652901619, 38099366441650179970243, 39216955475536658705279, 39361383755151849280283, 39842748138202357199399, 40531790348980239064589, 41571851018171428160039, 44761079941336435616333, 44983394322579412629323, 46605568368689126923219, 47154869430452973042533, 47304080109955215170563, 52264855622295011930173, 55387608544709590254499, 57719793361407278115239, 58699110641240596200353, 59420623555803628802623, 62188637790255951955073, 63226570023969085287779, 63759453481474995309899, 63782109938986060927699, 66028664267510812801873, 67573133790751305436813, 67848565105721445324673, 68590100635528913186579, 69560459768252700493079, 70606494541667514405809, 71148528607852127772433, 71843954888597214127183, 71886191622880324824359, 73747183773847416132679, 73766760615158048158099, 74045741561841469990663, 74414461590007232037283, 74760856231911720860929, 75276528825104016990673, 75638264185684530139643, 77167667313721912547713, 78011968236472724757983, 78177137860469750814259, 82271491566840819212363, 83184839632177306358729, 84033052786999568221649, 84387934001117621785003, 84822854688108109313119, 84949079966606930488639, 85369375842841727813269, 87067612907202519977779, 87281038039521657164513, 88034157597305900444843, 88517765275434034287973, 91185245883302581564933, 92366725594191458390359, 93481186216018797526163, 93739605702138425379443, 94556056426114059781229, 96881461860437484320029, 97412412419565768558713, 97570972106536058625889, 97621863230890879951009, 98526220101384954128629, 99493156211464035650569, 99640983528107766668863, 99669093522863952747053, 100111954792639831080433, 100650851799425508064709, 100985323593521985253469, 102093924044096143334569, 102110199709522918633813, 106161181043449521118523, 106716682191731618526353, 106873384318882314032579, 108005058102095804880169, 108201961535370666827543, 109414309195407294698999, 111127758316689619731059, 111220039058734980013319, 112110792462260879407499, 112863712827167421979253, 114180755793664174725049, 115305596346681043106483, 115772734261787152058903, 116980545753429433155019, 154787380396512840656513, 187749702383119068641843, 901985248981556228168773, 4246610002636339828954843, 9425346484752129657862229, 9701757886114895320879553, 14451615724941305041645453

Ядряра выполнял поиск центральных 15-к в диапазоне 0 - 61#.
Последний найденный им кортеж в этом диапазоне
116980545753429433155019.

Как утверждает Ядряра, в указанном диапазоне существует около 1100 центральных 15-к. согласно его прогнозу. основанному на первой гипотезе Харди-Литлвуда.

Я не верю этому прогнозу: слишком большое количество центральных 15-к прогнозируется.
Однако проверить это о-ч-е-н-ь проблематично.
Диапазон. конечно, большой, может, и действительно столько центральных 15-к в нём существует.
Интересно бы найти их все!

В BOINC-проекте ODLK2025 несколько дней назад запущено Приложение 4, которое ищет центральные 15-ки в диапазоне
[2079914861571286679, 117288381359406970983270).

То есть поиск начинается с минимальной центральной 15-ки.

Все центральный 15-ки, приведённые в БД, кроме 7 последних, должны быть найдены в Приложении 4.
А ещё должны быть найдены все дополнительно до "около 1100" центральных 15-к, согласно прогнозу Ядряры.

Алгоритм поиска - распараллеливание поиска в нулевом периоде для периода 61#.

Попутно в Приложении 4 ищутся центральные кортежи длин 9, 11 и 13.

Центральных 9-к находится море.
Центральных 11-к - небольшое озеро :)
И центральных 13-к - единицы.

И ещё попутно ищутся приближения к центральной 15-ке с valids>9.
Цель - заполнить весь спектр приближений к центральной 15-ке.

Центральная 15-ка пока ни одна не найдена.

Чем ценны центральные 15-ки?

Если будут найдены все центральные 15-ки в указанном диапазоне 0 - 61#, это закроет все вопросы по ключевым 17-м в этом диапазоне.

Ну, о 19-ке с минимальным диаметром не говорю.
Если верить г. Петухову, 19-к с минимальным диаметром в этом диапазоне не существует.
Однако независимую проверку этого факта никто не выполнял.
Все могут ошибаться, в том числе и г. Петухов.

Так вот, вопрос по 19-ке с минимальным диаметром в указанном диапазоне тоже будет закрыт.

На данный момент нам известны всего 6 ключевых 17-к в указанном диапазоне, все они найдены Врублевским

1006882292528806742267
3954328349097827424397
4896552110116770789773
6751407944109046348063
7768326730875185894807
19252814175273852997757

Очень сильно подозреваю, что это не все ключевые 17-ки, существующие в данном диапазоне.
Из "почти 1100" центральных 15-к только 6 матрёшечных?
И все они собрались в очень небольшом интервале
[1006882292528806742273, 19252814175273852997763].

А в остальном огромном диапазоне ничего нет?
Это весьма сомнительно.

Вот тут они собрались - шесть матрёшечных центральных 15-к, остальные не матрёшечные

1006882292528806742273, 2022711875770842846529, 2162149531729604295103, 2225037046903483907473, 2321104522630063134343, 2619820297764034190219, 2865889199912908889659, 2938616605475118382193, 3536266327242777212023, 3730861010539166369959, 3731183113236698329043, 3954328349097827424403, 4010322518824084606823, 4385038454541770260783, 4896552110116770789779, 5424443345599274902999, 5550244178896033210273, 5563684279615769106739, 6137356084057875005723, 6751407944109046348069, 6822640902781117403669, 6961394541011197172279, 7768326730875185894813, 8140616600819764641413, 8232485038811356957313, 8247840611942752240513, 8749161465060085980289, 8790344504647482496553, 9100228069582396220699, 9369566116899129925723, 9750634398553127404873, 10326968803949363609983, 10671796931507693781739, 11303999667139928672603, 11562084795586986305023, 11644034428493619141929, 12419328750104774994043, 12480848738857754155279, 12744508017243603506299, 12967362495788256980803, 14832445430292682412599, 15636034351630168471829, 16257917584261857368243, 17716330748916274931003, 18164396263690092225203, 18742586057174230251379, 18826403258369198671859, 19138427715111031577083, 19252814175273852997763

Понятно, что в приведённых 170 центральных 15-х сидят центральные 13-ки.

Можно проверить, все ли эти центральные 13-ки есть у нас в БД центральных 13-к.

БД центральных 13-к мы уже начали чуть-чуть пополнять.
Мне даже в ручном проекте удалось найти две центральные 13-ки.

Смотрите о центральных 13-х темы на этом форуме
https://boinc.progger.info/odlk/forum_thread.php?id=317
https://boinc.progger.info/odlk/forum_thread.php?id=282

и тему на форуме проекта ODLK2025
https://boinc.mak.termit.me/odlk2025/forum_thread.php?id=51

Проверила 170 показанных центральных 15-к на продолжение до приближения к 19-ке с минимальным диамтером.

Выдалось только одно продолжение, это дважды матрёшечная центральная 15-ка продолжилась, не до приближения, а до самой 19-ки с минимальным диамтером

(18:54) gp > \rprod15-19.txt
   logfile = "prod15-19_res.txt"
170
[9425346484752129657862229, 9425346484752129657862247, 9425346484752129657862259, 9425346484752129657862289, 9425346484752129657862307, 9425346484752129657862313, 9425346484752129657862337, 9425346484752129657862343, 9425346484752129657862349, 9425346484752129657862373, 9425346484752129657862379, 9425346484752129657862397, 9425346484752129657862427, 9425346484752129657862439, 9425346484752129657862457]

[9425346484752129657862217, 9425346484752129657862223, 9425346484752129657862229, 9425346484752129657862247, 9425346484752129657862259, 9425346484752129657862289, 9425346484752129657862307, 9425346484752129657862313, 9425346484752129657862337, 9425346484752129657862343, 9425346484752129657862349, 9425346484752129657862373, 9425346484752129657862379, 9425346484752129657862397, 9425346484752129657862427, 9425346484752129657862439, 9425346484752129657862457, 9425346484752129657862463, 9425346484752129657862469]
PRODOLJENO!

9425346484752129657862217: [0, 6, 12, 30, 42, 72, 90, 96, 120, 126, 132, 156, 162, 180, 210, 222, 240, 246, 252]
9425346484752129657862217: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
9425346484752129657862217: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=19
code=131071

Больше продолжений моя утилита не обнаружила.

Цитата

Понятно, что в приведённых 170 центральных 15-х сидят центральные 13-ки.

Можно проверить, все ли эти центральные 13-ки есть у нас в БД центральных 13-к.

А вот тут интересно получилось.

Взяла 170 центральных 13-к из показанных центральных 15-к и объединила их с имеющейся у меня БД центральных 13-к (247 штук), получилось 417 штук.

После сортировки с удалением дубликатов получила новую БД центральных 13-к из 402 кортежей.

Показываю эту БД

2479672831189511, 14532269076393311, 18243592974347137, 19841272539468077, 28522877055638377, 30490730621120881, 31253201754308491, 38282996618836381, 49709746203086381, 80367014131763771, 83438316647980691, 85836761919895097, 94424620755941587, 112152555556206731, 127300190958286457, 141573325723293161, 190482508374758557, 209626115330591917, 324871384687349611, 359200217773681241, 377360542797737911, 471562489911768821, 507060265610887231, 508915645637755207, 513703914377659417, 565872074218044991, 591077243357392357, 615687149309852731, 719352790533795661, 724441950436884637, 737022973022892407, 756339821775119147, 866333070522198977, 1106546274252479017, 1117671752456935241, 1172721864197147221, 1179253269821020091, 1300163787652263931, 1329646489109438611, 1418270815389299437, 1423610902748910287, 1452170623713349651, 1519868669534901797, 1547774749949068037, 1585171697800866587, 1595789926324317421, 1598652316382625901, 1598910494136939941, 1693757605510957097, 1734666951919567231, 1877578187722687301, 1923347213715058697, 1928712975761020861, 2005516910277736267, 2026800755699304997, 2062897943302958327, 2079914861571286697, 2141953556478461137, 2162340821309048231, 2211981473498456357, 2287480654647217441, 2340719042583491527, 2352939510668616721, 2352964120516043431, 2395881037604209567, 2471987077466546051, 2484326920901485357, 2515493075987457131, 2541747186116223497, 2550131387381397671, 2674974492601947101, 2677743243160459871, 2695625376192494311, 2894485774484624431, 2936602930622426477, 3031999351885804411, 3079616503897177201, 3096444749446298647, 3162966145385182247, 3186415899409788611, 3222219486998896081, 3241648437603927917, 3336305588836446337, 3369321533573605021, 3407866161686156281, 3444356540727417881, 3519431297683595537, 3547548469412787251, 3603907153349082977, 3607780647540700027, 3665619319531504901, 3691209032300115437, 3694354730530744237, 3703374309709930267, 3708255663747484261, 3720413147141906627, 3745555989870014431, 3767557397733559387, 3789170069190319771, 3798968086852634107, 3891084247157576881, 3901526069826829841, 3927943343304714691, 3986146508940089891, 4072248798829199231, 4142123207730122011, 4153179876729803617, 4172681114134608487, 4219902427094580337, 4244451916898989907, 4259678964460405337, 4273219938795882317, 4333643948938217611, 4431963500323803841, 4433540325487853537, 4510041409664625077, 4562395882350129521, 4620361398866869507, 4627598729361597401, 4695861047917389307, 4800295914170340827, 4801915213940184737, 4887254764886530147, 4908582056043581767, 5081754393702091957, 5177865449056250347, 5272061120090938871, 5274459076607520497, 5295461415259491587, 5298397695164187857, 5323054178356526177, 5446793225310501307, 5457300427330179671, 5489506938939158987, 5547566724498692591, 5628333974508845011, 5651655407449942001, 5651665747048195117, 5736050483438911487, 5774922180427595761, 5787666885543632501, 5848083324368204771, 5858876497317579587, 5945630520732837331, 5960874817022916187, 6055908245681868817, 6150520901591150041, 6170064225722536991, 6239897593258813181, 6310239031186385861, 6322902263969110777, 6324258749843480011, 6341013627099961661, 6362093275873170401, 6364333587724492231, 6372954494816114771, 6402252208683390911, 6517756993810041677, 6524637964487862631, 6572013008215924967, 6617463747108414311, 6625259351674447181, 6870466192359493967, 6884493860771648687, 6896093661996138011, 6931319014788808051, 6947087924504017141, 6966074684666833847, 7041490249810602151, 7059804246444819721, 7104201033213158117, 7113627041480844127, 7204544196923753377, 7210689261679233727, 7422049836115903231, 7438677298357028681, 7447957431670669871, 7542462099012324181, 7642046724351133337, 7741166999714278241, 7842599855066005441, 8203473252345436631, 8245423017819998407, 8296494844824485711, 8300219963306992117, 8421952759754289167, 8470429089744827617, 8533351897373793341, 8546323226694232831, 8560317076865713571, 8677404716190380281, 8854975042860577027, 9035209616091919217, 9047858012249718227, 9120158129331713861, 9153806495525111377, 9170747899837687861, 9172510963390759381, 9190378489555104407, 9263347979564458477, 9391346125970494097, 9412507796260543217, 9492565717618653367, 9526974418387614431, 9556820127521832731, 9599643914361807157, 9633607413909975061, 9687571205573180771, 9779213400414113221, 9920250559572037081, 9995348564889375931, 10013230717641471277, 10130392328070474157, 10153185061549088971, 10236355150921661327, 10246017460829141557, 10304613318488232701, 10326541662008009681, 10371425130288542017, 10383682450304082877, 10408168773472119061, 10499493692947708861, 10540143033014354611, 10560397483948992091, 10567963099523203771, 10607521634695145011, 10716366929681877161, 10717708445691097247, 10723236960793555441, 10732242437627290537, 10861110627532434967, 10960719362282020897, 10962757032949087217, 10965448136607379981, 214946236533755076307, 271541128585758431797, 356824342193987437181, 944273532072632171261, 1006882292528806742291, 2022711875770842846547, 2162149531729604295121, 2225037046903483907491, 2321104522630063134361, 2619820297764034190237, 2865889199912908889677, 2938616605475118382211, 3536266327242777212041, 3730861010539166369977, 3731183113236698329061, 3954328349097827424421, 4010322518824084606841, 4385038454541770260801, 4896552110116770789797, 5424443345599274903017, 5550244178896033210291, 5563684279615769106757, 6137356084057875005741, 6751407944109046348087, 6822640902781117403687, 6961394541011197172297, 7768326730875185894831, 8140616600819764641431, 8232485038811356957331, 8247840611942752240531, 8749161465060085980307, 8790344504647482496571, 9100228069582396220717, 9369566116899129925741, 9750634398553127404891, 10326968803949363610001, 10671796931507693781757, 11303999667139928672621, 11562084795586986305041, 11644034428493619141947, 12419328750104774994061, 12480848738857754155297, 12744508017243603506317, 12967362495788256980821, 14832445430292682412617, 15636034351630168471847, 16257917584261857368261, 17716330748916274931021, 18164396263690092225221, 18742586057174230251397, 18826403258369198671877, 19138427715111031577101, 19252814175273852997781, 19536294443804410516201, 19832606831753483622251, 20897856447156043589191, 21287941491290623223317, 21426089952025093895411, 21488607476073832073677, 22544235579330598703681, 23868792350514616905511, 24556642668231947323007, 24715153027336908055331, 24859382344782684063931, 26082913722886576565861, 26913993896984416720741, 27297597458437704698257, 27479373083803560368861, 29579059173365490432601, 29674090145515624849151, 30718149799825764081217, 30851792637019107009107, 31009930868332327847347, 31167395346004527024827, 31715036252267904940361, 34106328260995613527301, 34166808184761843016537, 34835558850415981958257, 37367256014233652901637, 38099366441650179970261, 39216955475536658705297, 39361383755151849280301, 39842748138202357199417, 40531790348980239064607, 41571851018171428160057, 44761079941336435616351, 44983394322579412629341, 46605568368689126923237, 47154869430452973042551, 47304080109955215170581, 52264855622295011930191, 55387608544709590254517, 57719793361407278115257, 58699110641240596200371, 59420623555803628802641, 62188637790255951955091, 63226570023969085287797, 63759453481474995309917, 63782109938986060927717, 66028664267510812801891, 67573133790751305436831, 67848565105721445324691, 68590100635528913186597, 69560459768252700493097, 70606494541667514405827, 71148528607852127772451, 71843954888597214127201, 71886191622880324824377, 73747183773847416132697, 73766760615158048158117, 74045741561841469990681, 74414461590007232037301, 74760856231911720860947, 75276528825104016990691, 75638264185684530139661, 77167667313721912547731, 78011968236472724758001, 78177137860469750814277, 82271491566840819212381, 83184839632177306358747, 84033052786999568221667, 84387934001117621785021, 84822854688108109313137, 84949079966606930488657, 85369375842841727813287, 87067612907202519977797, 87281038039521657164531, 88034157597305900444861, 88517765275434034287991, 91185245883302581564951, 92366725594191458390377, 93481186216018797526181, 93739605702138425379461, 94556056426114059781247, 96881461860437484320047, 97412412419565768558731, 97570972106536058625907, 97621863230890879951027, 98526220101384954128647, 99493156211464035650587, 99640983528107766668881, 99669093522863952747071, 100111954792639831080451, 100650851799425508064727, 100985323593521985253487, 102093924044096143334587, 102110199709522918633831, 106161181043449521118541, 106716682191731618526371, 106873384318882314032597, 108005058102095804880187, 108201961535370666827561, 109414309195407294699017, 111127758316689619731077, 111220039058734980013337, 112110792462260879407517, 112863712827167421979271, 114180755793664174725067, 115305596346681043106501, 115772734261787152058921, 116980545753429433155037, 154787380396512840656531, 187749702383119068641861, 901985248981556228168791, 4246610002636339828954861, 9425346484752129657862247, 9701757886114895320879571, 14451615724941305041645471

Надеюсь, не напортачила.

Это хорошая БД центральных 13-к!
Сейчас я её проверю утилитой.

Утилита говорит, что центральные 13-ки вполне правильные.

Покажу частично вывод утилиты

> \rappr13.txt
   logfile = "appr13_res.txt"
402
2479672831189511: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
2479672831189511: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
2479672831189511: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

14532269076393311: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
14532269076393311: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
14532269076393311: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

18243592974347137: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
18243592974347137: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
18243592974347137: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

19841272539468077: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
19841272539468077: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
19841272539468077: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

28522877055638377: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
28522877055638377: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
28522877055638377: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047
. . . . . . . 
901985248981556228168791: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
901985248981556228168791: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
901985248981556228168791: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

4246610002636339828954861: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
4246610002636339828954861: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4246610002636339828954861: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

9425346484752129657862247: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
9425346484752129657862247: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
9425346484752129657862247: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

9701757886114895320879571: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
9701757886114895320879571: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
9701757886114895320879571: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

14451615724941305041645471: [0, 12, 42, 60, 66, 90, 96, 102, 126, 132, 150, 180, 192]
14451615724941305041645471: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
14451615724941305041645471: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
valids=13
code=2047

Вот теперь можно и пополнять БД центральных 13-к.

Пока их очень мало у нас найдено, но будет и больше.

Ядряра писал в сообщении
https://dxdy.ru/post1694670.html#p1694670

Статистика по центральным 15-кам по диапазонам:

0-53# 0-59# 0-61#
Посчитано 35% 13% 13%
Прогноз по HL1 2 49 1133
Найдено 2 7 180

Итак, "около 1100" приобрело более точное значение - 1133.
Такое количество центральных 15-к Ядряра спрогнозировал в диапазоне 0 - 61#.

Непонятно, почему в диапазонах 0-59# и 0-61# посчитано одинаковое количество процентов.

Итак. в диапазоне (0, 32589158477190044730) найдено 2 центральные 15-ки, по прогнозу их тоже 2.
Вот они

2079914861571286679, 
3665619319531504883

Найдены они были очень давно в BOINC-проекте TBEG.
В этом проекте работал алгоритм брутфорс, программно реализованный Алексеем Белышевым.
Так что, здесь ничего не могло быть пропущено.

Смотрим дальше, в диапазоне (0, 1922760350154212639070)
найдено 7 центральных 15-к, по прогнозу должно быть 49.

Наконец, в диапазоне (0, 117288381359406970983270)
найдено 180 центральных 15-к, по прогнозу должно быть найдено 1133.

Таким образом, на данный момент во всём диапазоне (0, 117288381359406970983270) найдено 15,89% центральных 15-к от прогнозируемого количества.

Ещё искать и искать!

P.S. Кажется, поняла о процентах.
Проценты - это не абсолютное выражение посчитанных количеств, это сколько посчитано "на каждые сто".

Вот идейка возникла: распараллелю сейчас поиск центральных 15-к в нулевом периоде для периода 59#.

По прогнозу Ядряры в этом диапазоне болжно быть найдено 49 центральных 15-к, найдено всего 7.

Таблица данных для распараллеливания готова

v2=[1];
v3=[1, 2]; \\2
v5=[3, 4]; \\2
v7=[1, 2]; \\2
v11=[5, 9]; \\2
v13=[2, 4]; \\2
v17=[12, 13, 14, 15]; \\4
v19=[4, 5, 7, 9, 10, 12, 14, 15]; \\8
v23=[3, 4, 6, 10, 12, 13, 15, 19, 21, 22]; \\10
v29=[7, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 23, 26]; \\14
v31=[3, 6, 8, 12, 14, 17, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]; \\16
v37=[1, 2, 5, 6, 8, 9, 10, 11, 13, 15, 16, 18, 20, 21, 22, 23, 25, 26, 29, 30, 32, 36]; \\22
v41=[1, 2, 5, 6, 8, 10, 12, 13, 16, 17, 19, 21, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 38, 40]; \\26
v43=[1, 3, 6, 7, 10, 11, 12, 14, 16, 18, 19, 20, 23, 24, 27, 29, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42]; \\28
v47=[1, 2, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 15, 18, 19, 22, 23, 24, 26, 28, 30, 31, 32, 35, 36, 39, 40, 41, 42, 43, 45, 46]; \\32
v53=[1, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 16, 17, 18, 19, 20, 21, 24, 25, 26, 27, 29, 30, 31, 32, 33, 34, 36, 38, 40, 41, 42, 43, 47, 48, 49, 50, 52]; \\38
v59=[1, 2, 3, 5, 6, 7, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 28, 30, 31, 32, 35, 36, 37, 39, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
52, 53, 54, 55, 56]; \\44

1965568966000640 formulae expected

Распараллеливать буду так:

16*22*26*28*32*38*44 = 13710721024 добавок в одной программе;
140 программ в серии;
1024 всех серий;
140*1024 = 143360 всех программ;
143360*13710721024 = 1965568966000640 всех добавок.

Программы, конечно, будут долгие.
Это хорошо, реже перезапускать.
Серий мало, программ в одной серии тоже мало.

Ещё одна идейка осенила, опробую её в этом поиске.

Пойду генерировать вушки.

Их всего будет 140 штук.

Потом надо написать программу.
Ахиллесы ждут работу :)
А у меня застой; слава Богу, чуть-чуть похолодало.
Можно немножко поработать.

Готово!

Вушки сгенерировала.

Сейчас буду сочинять программу.

Новый ресурс дистанционного управления скурвился!

Внезапно узнаю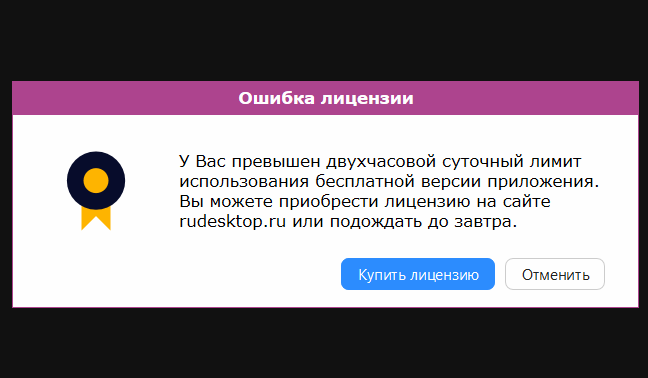



Очень интересно!
Бесплатно я могу пользоваться ресурсом только два часа в сутки.

Ну все хотят денег!
Весь мир помешался на деньгах.

Я понимаю: разработчики ПО хотят плату за свой труд.
Но продавайте вы лицензии организациям, предприятиям, крупным пользователям!

Что же вы хотите обдирать пенсионерку, которая работает скромно над своими личными вычислениями, никуда, никому их не продаёт.
Откуда же у пенсионерки деньги?!
Едва на хлеб хватает.
При этом ведь ещё плачу за электричество и за Интернет.

Нет мозгов ни у кого!

Только хотела запустить новую программу, как всё закончилось, туши свет и сливай воду!!

Интересно, а когда у них начинается "завтра"?
По какому времени???
По московскому или по мухосранскому?

- Россия, сынок!

Ах, у них даже служба поддержки имеется!

Написала им такое послание

Читайте сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=323&postid=17134

Когда у вас начинается "завтра"?
Сколько стоит лицензия для физических лиц?
Есть ли скидка для пенсионеров?

Посмотрим, что ответят.

Ого!
Уже ответ пришёл!

Спасибо за обращение в RuDesktop!

Ваша заявка зарегистрирована под #10086

Ха-ха-ха!
И когда же они доберутся до моей "заявки"?
Лет через 5-6?

Может, в Мухосранске уже наступило "завтра", у нас в Саратове ещё сегодня.
Поэтому придётся идти спать, работать на Ахиллесах не дают :(

Хотела на черепашке попробовать, а программа-то у меня на Ахиллесе-3, я её там писала, а к себе на черепашку не скопировала.

Тьфу, пропасть!
И какой дурак придумал сервисы, которые не работают??????
Или работают два часа в сутки!

Почему есть сервисы, которые всегда работают, причём бесплатно, например, Гугло-переводчик???????
Они вот как же без денег-то обходятся?

Ну, вот, здравствуйте, господа!

У нас в Саратове "завтра" уже наступило.
А в Мухосранске, где сидят разработчики сервиса rudesktop.ru, конечно, ещё не наступило.

Очень сильно подозреваю, что картинку эту



они не снимут ни завтра, ни послезавтра, никогда.
Пока не получат деньги.

Придётся заново генерировать вушки и писать программу на черепашке, и тестировать на ней же.

Хотя... программу может взять на Ахиллесе-3 Corporal и прислать мне.
Ну, а вушки сгенерировать не проблема.

Corporal вчера уже написала о новом фокусе сервиса.
Он пока не ответил.

Это, кажется, из "Крокодила", из раздела "Нарочно не придумаешь".

Раньше говорили: "Пошёл вон!", а теперь вежливо говорят: "Приходите завтра."

"Завтра" в Мухосранске всё ещё не наступило!

Сейчас написала им второе сообщение.
Ответ точно такой же, как был вчера:

Спасибо за обращение в RuDesktop!

Ваша заявка зарегистрирована под #10089

Только номер другой, вчера был #10086.
Как я понимаю, обращение в службу поддержки абсолютно бесполезно.

Картинка продолжает висеть, как я и предположила.

Corporal пока не ответил.
Наверное, думает, что делать с этим идиотизмом.

А что тут думать: они не дадут доступ к компьютерам, пока не получат деньги.
Это очевидно.

Попросила Corporal хоть программу мне прислать, которую вчера написала, она на Ахиллесе-3 лежит.

Ну, слава Богу, Ахиллесы подключились.

То ли в Мухосранске наступило "завтра", то ли Corporal что-то сделал.

Новый эксперимент поехал!
Запущено 27 программ, 20 на Ахиллесе-3 и 7 на Ахиллесе.

Напомню: в серии всего 140 программ. но они долгие - на несколько суток.
Зато редко перезапускать.

А серий всего 1024.
Конечно, для Ахиллесов нереально выполнить все серии.
Но поэкспериментируем с этим вариантом распараллеливания.

Центральные 9-ки уже кое-где выскочили.

Итак, в этом эксперименте ожидаются 49 спрогнозированных Ядрярой центральных 15-к (7 из них уже известны).
И не только!
Я ещё кое-что добавила в программу.
Посмотрю, как это будет работать.

Ну, а также центральные кортежи длин 9, 11 и 13. как и прежде, и приближения к центральной 15-ке с valids>9.