Дважды симметричные ДЛК
Message boards :
Science :
Дважды симметричные ДЛК
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · 7 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Нашла интересную статью  Насколько я понимаю, свежая статья - 2017 г. В статье рассматриваются симметричные ЛК, метод их составления, причём весьма интересное определение этих ЛК. Вот  Здесь в ЛК A опечатка, в последней строке должно быть 4 1 2 3 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А вот и метод составления симметричных ЛК  Ба, старый знакомый квадратик 9-го порядка! :) Сравните с самым первым ЛК в этой полной системе MOLS 9-го порядка  ЛК блочной структуры? Блоки хорошо показаны. Только здесь они 3х3. Поворачивать их на 90 градусов тоже можно. Что это даст? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Я составила данным методом симметричный ЛК 10-го порядка (в смысле определения, данного в рассматриваемой статье) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 6 7 8 9 5 2 3 4 0 1 7 8 9 5 6 3 4 0 1 2 8 9 5 6 7 4 0 1 2 3 9 5 6 7 8 5 6 7 8 9 0 1 2 3 4 6 7 8 9 5 1 2 3 4 0 7 8 9 5 6 2 3 4 0 1 8 9 5 6 7 3 4 0 1 2 9 5 6 7 8 4 0 1 2 3 Кажется, нечто подобное мне встречалось при исследовании ЛК 10-го порядка. Интересно, что этот ЛК блочной структуры. 5 типов непересекающихся интеркалятов (как показывает программа Белышева Интеркалятор): {0,5}, {1,6},{2,7}, {3,8}, {4,9}. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё интереснее! Составила этим методом симметричный ЛК 10-го порядка (в смысле определения в статье), только используя блоки 2х2, а не 5х5: 0 1 2 3 4 5 6 7 8 9 1 0 3 2 5 4 7 6 9 8 2 3 4 5 6 7 8 9 0 1 3 2 5 4 7 6 9 8 1 0 4 5 6 7 8 9 0 1 2 3 5 4 7 6 9 8 1 0 3 2 6 7 8 9 0 1 2 3 4 5 7 6 9 8 1 0 3 2 5 4 8 9 0 1 2 3 4 5 6 7 9 8 1 0 3 2 5 4 7 6Ну, так это уж точно известный нам давно ЛК блочной структуры :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
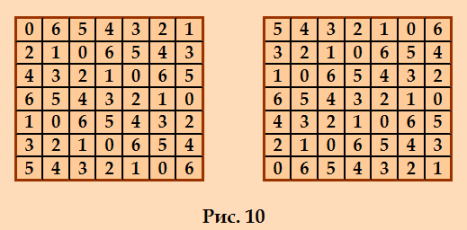
Кстати, методом составных квадратов можно строить не только дважды симметричные ДЛК. И ещё продолжу построение. На первой иллюстрации показана пара ОДЛК 7-го порядка. Методом составных квадратов можно строить и пары ортогональных ЛК и ДЛК. Этот метод описан в моей статье Построение пар ортогональных латинских квадратов методом составных квадратов. К идеальному ДЛК 5-го порядка, показанному на второй иллюстрации, ортогональным будет следующий ДЛК: 3 2 1 0 4 1 0 4 3 2 4 3 2 1 0 2 1 0 4 3 0 4 3 2 1 Ну, теперь используем программу Harry, введя в неё два ортогональных соквадрата к ДЛК, используемым при построении первого ДЛК 35-го порядка, и получим ДЛК ортогональный построенному ранее ДЛК 35-го порядка  Этот ДЛК тоже идеальный. А дальше из построенной ортогональной пары идеальных ДЛК 35-го порядка легко построить магический квадрат 35-го порядка, который тоже будет идеальный. Это один из основных методов построения магических квадратов - метод латинских квадратов. С этого метода и началось моё знакомство с латинскими квадратами. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Я составила данным методом симметричный ЛК 10-го порядка (в смысле определения, данного в рассматриваемой статье) Конечно, встречалось :) Вот ЛК блочной структуры, сочинённый мной по образцу ЛК Паркера  Смотрим на верхний вариант ЛК. Этот ЛК симметричный (в смысле определения в рассматриваемой статье). Впрочем, и нижний вариант ЛК тоже! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Хорошая новость! Белышев выложил новую версию программы для проверки всех симметричных ДЛК. Цитирую: Программа написана с учётом облегчения создания boinc-проекта. Если будут вопросы, обращайтесь в ЛС. отсюда http://forum.boinc.ru/default.aspx?g=posts&m=89617#post89617 Скачала программу и немножко тестирую. Да, скорость проверки хорошая. Однако... КФ ОДЛК и нету, одни нули :) Будут ли ещё решения от симметричных ДЛК? Или найденные 2207 решений - это уже всё? Ну, для ответа на этот вопрос надо выполнить предложенную программу. Конечно, на одном ПК выполнить её проблематично. В BOINC-проекте просто, в чём и Белышев уверен. Progger запускаем? :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Засветилась одна КФ ОДЛК!!! . . . . . . . 1189822 5632 0 7 1189823 4864 0 5 1189824 14336 0 15 1189825 9216 1 10 1189826 7168 0 7 1189827 6656 0 7 1189828 12288 0 13 1189829 5632 0 5 1189830 8960 0 9 1189831 7168 0 7 1189832 8192 0 8 1189833 14336 0 14 . . . . . . . Не посмотрела пока - уникальная или нет. Пусть до конца программа отработает. Задала 500 БС проверить в линейке №6. Скорее всего, не уникальная. Но... а вдруг и попалась в сети рыбка :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Найдена двушка 0 1 2 3 4 5 6 7 8 9 4 7 3 9 0 8 1 2 5 6 8 3 5 1 9 4 0 6 2 7 5 9 8 4 2 6 7 1 3 0 7 2 0 8 6 1 9 3 4 5 6 4 7 5 8 3 2 0 9 1 1 6 9 2 3 0 8 5 7 4 2 8 4 0 1 7 5 9 6 3 9 0 6 7 5 2 3 4 1 8 3 5 1 6 7 9 4 8 0 2 sq1 0 1 2 3 4 5 6 7 8 9 3 4 7 8 1 9 0 6 2 5 2 7 3 9 5 0 8 4 6 1 9 6 8 2 3 7 5 1 0 4 4 5 6 0 8 3 1 9 7 2 8 0 9 7 6 1 4 2 5 3 5 2 4 1 9 6 7 0 3 8 6 3 0 4 2 8 9 5 1 7 1 8 5 6 7 4 2 3 9 0 7 9 1 5 0 2 3 8 4 6 sq2 Square: 0 2 8 9 6 4 7 5 3 1 8 1 3 6 7 9 4 2 0 5 4 8 2 7 0 1 9 3 5 6 5 4 7 3 1 0 2 9 6 8 9 3 1 5 4 6 8 0 2 7 2 7 4 1 8 5 0 6 9 3 1 9 5 4 2 3 6 8 7 0 6 0 9 2 5 8 3 7 1 4 3 5 6 0 9 7 1 4 8 2 7 6 0 8 3 2 5 1 4 9 Увы, не уникальная. Так-то решения разбросаны по БС: 500 БС проверила, одно решение нашла. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё хорошая новость. Harry White прислал doubly SODLS (далее сокращение: DSODLS) 9-го порядка, их 28608 штук. Интересные ДЛК. В массиве всех SODLS, который прислал мне Francis Gaspalou, конечно, есть и все DSODLS, но интересно посмотреть эти ДЛК отдельно. Обработала эти ДЛК Канонизатором Белышева, получилось 120 КФ (в формате СН ДЛК). А от всех SODLS получилось 620 КФ. Покажу первые три КФ, полученные от DSODLS 0 2 3 5 6 7 8 4 1 4 1 6 0 3 2 7 8 5 1 8 2 4 7 0 3 5 6 8 5 7 3 0 6 4 1 2 5 6 8 7 4 1 0 2 3 6 7 4 2 8 5 1 3 0 2 3 5 8 1 4 6 0 7 3 0 1 6 5 8 2 7 4 7 4 0 1 2 3 5 6 8 0 2 3 5 6 7 8 4 1 4 1 6 0 3 2 7 8 5 1 8 2 7 0 4 3 5 6 8 5 4 3 7 6 0 1 2 5 6 7 8 4 0 1 2 3 6 7 8 2 1 5 4 3 0 2 3 5 4 8 1 6 0 7 3 0 1 6 5 8 2 7 4 7 4 0 1 2 3 5 6 8 0 2 3 5 6 7 8 4 1 4 1 6 0 5 2 7 8 3 1 8 2 4 7 0 3 5 6 8 5 7 3 0 6 4 1 2 3 6 8 7 4 1 0 2 5 6 7 4 2 8 5 1 3 0 2 3 5 8 1 4 6 0 7 5 0 1 6 3 8 2 7 4 7 4 0 1 2 3 5 6 8 Все DSODLS дают двушки, то есть у каждого из них два ортогональных соквадрата; но КФ ОДЛК от этих двушек получается только одна, потому что оба ортогональных соквадрата изоморфны основному ДЛК двушки. Мне интересен такой вопрос: есть ли у каких-то DSODLS другие ортогональные соквадраты, кроме транспонированного и антитранспонированного? Выложила на Яндекс.Диск массив решений от Harry White и добавила массив КФ для этих DSODLS. Ссылка для скачивания https://yadi.sk/d/Ivt1XlKr3PVCnn А вот DSODLS 10-го порядка не существует. SODLS есть много, более 30 тысяч. Все их нашёл Белышев. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Здесь http://stop.inferia.ru/forum_thread.php?id=16&postid=102 я писала: Dear colleagues! I received a very interesting letter. A self-orthogonal diagonal Latin square of order 10 (SODLS(10)) was found by Bennett, Du, and Zhang by an exhaustive search using a computer [1]. Здесь представлен SODLS 10-го порядка и транспонированный ДЛК, который ортогонален исходному. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И далее в этом посте http://stop.inferia.ru/forum_thread.php?id=16&postid=120 я сообщила о найденных Белышевым SODLS 10-го порядка в количестве 30534, которые он нашёл из массива 121642 SOLS. Это интереснейший результат! Цитирую сообщение: I have interesting news. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё раз перечитываю выводы, сделанные здесь http://forum.boinc.ru/default.aspx?g=posts&m=89489#post89489 1. Ассоциативные ДЛК есть, они являются подмножеством центрально симметричных ДЛК (справедливости ради, весьма небольшим по мощности). О выводе (1) я уже писала выше. Да, ассоциативные ДЛК есть и! они тоже являются центрально-симметричными, именно в смысле определения Ватутина, то есть центрально-симметричные элементы в ассоциативных ДЛК взаимно-однозначно соответствуют друг другу. Только в ассоциативных ДЛК есть дополнительное условие - постоянная сумма центрально-симметричных элементов. А вот вывод (3) меня повергает в глубокое непонимание: что утверждается автором этого вывода (?) Любой ассоциативный ДЛК является центрально-симметричным!, что автор сказал в выводе (1). Это значит то самое, что следует в выводе (3) за словами "в то время как". Наверное, тут какая-то супернаучная логика, недоступная моему пониманию. То же самое с выводом (2). Любой ДЛК (хоть ассоциативный, хоть не ассоциативный) имеет КФ. А ОДЛК мы можем искать только для КФ (собственно, так и следует искать). При чём тут не инвариантность ассоциативного ДЛК относительно М-преобразований? Но даже если с этой позиции смотреть. Пусть исчезнет постоянная сумма центрально-симметричных элементов, но центральная симметрия при М-преобразованиях ассоциативного ДЛК никуда не исчезнет. И после нормализации ассоциативного ДЛК, кстати говоря, постоянная сумма центрально-симметричных элементов пропадает, но центральная симметрия остаётся. Это и на картинке сам Ватутин показал. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу интересный пример - две ассоциативные КФ 9-го порядка. Отсюда https://boinc.progger.info/odlk/forum_thread.php?id=31&postid=783#783 Здесь Действительно, чудесные квадратики. И подозреваю, что у этих ассоциативных ДЛК очень много ОДЛК. Проверьте! А теперь нормализую первую КФ. Да, постоянная сумма центрально-симметричных элементов пропала, но центральная симметрия никуда не делась! 0 1 2 3 4 5 6 7 8 7 8 4 0 6 1 2 3 5 4 3 1 2 8 7 5 6 0 1 6 7 5 3 4 0 8 2 5 4 0 8 7 2 3 1 6 8 2 3 1 0 6 7 5 4 3 5 6 7 2 8 4 0 1 6 0 8 4 5 3 1 2 7 2 7 5 6 1 0 8 4 3 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу интересный пример - две ассоциативные КФ 9-го порядка. Я уже проверила :) Ватутин выкладывал ДЛК 9-го порядка, у которого 516 ОДЛК Source square: 0 1 2 3 4 5 6 7 8 2 4 3 0 7 6 8 1 5 4 6 7 1 8 2 3 5 0 8 3 5 6 0 7 1 2 4 7 8 1 4 5 3 0 6 2 3 7 0 2 1 8 5 4 6 1 5 4 7 6 0 2 8 3 5 0 6 8 2 1 4 3 7 6 2 8 5 3 4 7 0 1 Так вот, этот ДЛК как раз имеет ассоциативную КФ, показанную выше, вот эту 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 Оказывается, ассоциативность очень даже не бесполезна при поиске ОДЛК! Наглядный пример показан. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё раз цитирую (Ватутин): 1. Ассоциативные ДЛК есть, они являются подмножеством центрально симметричных ДЛК (справедливости ради, весьма небольшим по мощности). Интересно, как мощность измерял? :) У меня есть прекрасная гипотеза, которая родилась из примера, рассмотренного выше; вот она. Гипотеза: ассоциативные ДЛК дают всё множество центрально-симметричных ДЛК. То есть мощность множества ассоциативных ДЛК и мощность центрально-симметричных ДЛК по Ватутину как раз точно совпадают, потому что это одно множество. Рассмотрим аналогичный пример с симметричными ДЛК по Брауну (конкретнее: вертикально-симметричными). Если симметричный ДЛК не нормализованный, то нет постоянной суммы симметричных элементов. Но как только мы его нормализуем, постоянная сумма симметричных элементов имеет место. Это, однако, не означает, что есть отдельно симметричные ДЛК с постоянной суммой симметричных элементов и отдельно симметричные ДЛК, в которых нет постоянной суммы симметричных элементов. Есть одно множество симметричных ДЛК! Всё точно так же и для центрально-симметричных ДЛК. Ватутин рассматривает нормализованные центрально-симметричные ДЛК и говорит: а вот эти ДЛК не ассоциативные, потому что в них нет постоянной суммы центрально-симметричных элементов. А вот теперь возьмите такой нормализованный центрально-симметричный ДЛК и сделайте его сильно нормализованным (по определению Белышева), то есть естественная перестановка чисел расположится в главной диагонали ДЛК. И всё - ДЛК стал ассоциативным! Приведу пример. Беру самый первый нормализованный центрально-симметричный ДЛК 9-го порядка из файла, выложенного Ватутиным: Source square: 0 1 2 3 4 5 6 7 8 2 3 0 7 6 8 1 4 5 3 6 1 2 8 7 0 5 4 7 8 6 5 0 3 4 2 1 6 7 4 8 2 1 5 0 3 8 2 5 6 7 4 3 1 0 5 4 7 0 1 2 8 3 6 4 5 8 1 3 0 7 6 2 1 0 3 4 5 6 2 8 7 Пропускаю его через Канонизатор Белышева. Эта программа превращает данный ДЛК в сильно нормализованный, и... ДЛК получился ассоциативный! 0 2 6 7 3 8 5 4 1 3 1 4 5 0 2 7 8 6 1 6 2 8 7 4 3 5 0 5 8 7 3 2 6 0 1 4 6 5 0 1 4 7 8 3 2 4 7 8 2 6 5 1 0 3 8 3 5 4 1 0 6 2 7 2 0 1 6 8 3 4 7 5 7 4 3 0 5 1 2 6 8 Вот такой фокус! :) Желающие могут строго доказать или опровергнуть мою гипотезу. Думаю, опровергнуть не получится. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Тестирую программу Белышева для проверки на ОДЛК, выложенную тут http://forum.boinc.ru/default.aspx?g=posts&m=89712#post89712 Проверяю первую ассоциативную КФ, показанную выше: 0 2 7 8 6 3 5 4 1 4 1 6 0 5 2 7 8 3 6 8 2 7 1 4 3 5 0 2 5 4 3 8 6 0 1 7 3 6 0 1 4 7 8 2 5 1 7 8 2 0 5 4 3 6 8 3 5 4 7 1 6 0 2 5 0 1 6 3 8 2 7 4 7 4 3 5 2 0 1 6 8 Программа сообщает: Проверка ДЛК9 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 1 Время работы: 0.01 сек Для выхода нажмите любую клавишу: Я думала, что у введённого ДЛК есть только один ОДЛК. Открываю выходной файл, а там аж 308 ОДЛК :) [DLK(308)] 0 2 7 8 6 3 5 4 1 4 1 6 0 5 2 7 8 3 6 8 2 7 1 4 3 5 0 2 5 4 3 8 6 0 1 7 3 6 0 1 4 7 8 2 5 1 7 8 2 0 5 4 3 6 8 3 5 4 7 1 6 0 2 5 0 1 6 3 8 2 7 4 7 4 3 5 2 0 1 6 8 [mate#1] 1 0 5 7 8 2 3 6 4 7 2 3 5 6 4 8 1 0 4 6 7 0 1 3 5 2 8 3 1 4 8 2 7 0 5 6 6 5 2 3 0 1 4 8 7 8 7 0 6 4 5 1 3 2 5 4 8 2 3 0 6 7 1 0 3 6 1 7 8 2 4 5 2 8 1 4 5 6 7 0 3 [mate#2] 1 0 5 7 8 2 3 6 4 8 2 3 5 6 4 7 1 0 4 6 7 0 1 3 5 2 8 3 1 4 8 2 7 0 5 6 6 5 2 3 0 1 4 8 7 7 8 0 6 4 5 1 3 2 5 4 8 2 3 0 6 7 1 0 3 6 1 7 8 2 4 5 2 7 1 4 5 6 8 0 3 [mate#3] 1 0 5 7 6 2 3 8 4 7 2 3 8 5 4 6 1 0 4 6 7 0 1 3 8 2 5 3 1 4 6 2 7 0 5 8 5 8 2 3 0 1 4 6 7 6 7 0 5 4 8 1 3 2 8 4 6 2 3 0 5 7 1 0 3 8 1 7 5 2 4 6 2 5 1 4 8 6 7 0 3 . . . . . . . . [mate#306] 5 2 3 1 6 4 0 7 8 8 3 4 2 5 0 7 6 1 2 0 7 6 4 1 5 8 3 6 1 5 8 7 3 4 2 0 7 8 6 5 0 2 3 1 4 0 5 8 4 1 6 2 3 7 4 6 2 3 8 7 1 0 5 3 7 1 0 2 5 8 4 6 1 4 0 7 3 8 6 5 2 [mate#307] 5 2 3 1 4 6 0 7 8 3 7 6 2 5 0 8 4 1 2 0 8 4 6 1 5 3 7 4 1 5 3 8 7 6 2 0 7 8 4 5 0 2 3 1 6 0 5 7 6 1 4 2 8 3 6 4 2 8 7 3 1 0 5 8 3 1 0 2 5 7 6 4 1 6 0 7 3 8 4 5 2 [mate#308] 4 3 5 1 2 6 0 7 8 6 7 1 8 3 0 4 2 5 5 0 8 7 4 2 1 6 3 1 8 3 2 7 4 6 5 0 7 6 2 3 0 8 5 4 1 0 2 4 6 1 5 8 3 7 8 4 7 5 6 1 3 0 2 2 5 6 0 8 3 7 1 4 3 1 0 4 5 7 2 8 6 Запускаю на проверку эти 308 ОДЛК (исходную КФ выбрасываю). Программа сообщает: Проверка ДЛК9 на марьяжность (ОДЛК) Введено ДЛК: 308 Найдено ОДЛК: 308 Время работы: 0.318 сек Для выхода нажмите любую клавишу: Тут тоже не поняла. Введено 308 ДЛК, это понятно. Но насчёт найденных ОДЛК - не совсем понятно. Открываю выходной файл, показываю начало и конец этого файла: [DLK(40)] 1 0 5 6 7 2 3 8 4 5 2 3 7 6 4 8 1 0 4 5 6 0 1 3 7 2 8 3 1 4 8 2 6 0 5 7 6 8 2 3 0 1 4 7 5 8 6 0 5 4 7 1 3 2 7 4 8 2 3 0 5 6 1 0 3 7 1 5 8 2 4 6 2 7 1 4 8 5 6 0 3 [mate#1] 5 2 6 7 1 3 4 0 8 0 8 2 6 3 1 5 7 4 2 7 1 5 8 0 3 4 6 1 4 0 3 7 2 6 8 5 4 1 5 8 0 6 7 2 3 7 6 8 1 5 4 0 3 2 8 3 4 0 6 7 2 5 1 3 5 7 2 4 8 1 6 0 6 0 3 4 2 5 8 1 7 [mate#2] 5 2 6 7 1 3 4 0 8 0 8 2 6 3 1 5 7 4 2 7 1 5 8 0 3 4 6 1 4 0 3 7 2 6 8 5 4 1 5 8 0 6 7 2 3 8 6 7 1 5 4 0 3 2 7 3 4 0 6 8 2 5 1 3 5 8 2 4 7 1 6 0 6 0 3 4 2 5 8 1 7 [mate#3] 5 2 7 6 1 3 4 0 8 0 8 2 5 3 1 7 6 4 2 6 1 8 7 0 3 4 5 1 4 0 3 5 2 6 8 7 4 1 6 7 0 8 5 2 3 8 7 5 1 6 4 0 3 2 6 3 4 0 8 7 2 5 1 3 5 8 2 4 6 1 7 0 7 0 3 4 2 5 8 1 6 . . . . . . . . [DLK(2)] 7 5 6 0 8 1 3 4 2 2 4 3 1 6 8 0 5 7 5 7 2 4 1 6 8 0 3 0 1 8 6 3 4 2 7 5 3 2 5 8 0 7 6 1 4 6 8 1 3 4 5 7 2 0 4 0 7 5 2 3 1 8 6 8 6 0 7 5 2 4 3 1 1 3 4 2 7 0 5 6 8 [mate#1] 0 4 2 5 3 6 7 1 8 1 8 4 3 6 5 0 7 2 8 5 6 7 0 1 4 2 3 3 7 1 4 8 2 5 6 0 2 3 5 0 1 7 8 4 6 7 2 8 6 5 3 1 0 4 4 6 3 1 7 0 2 8 5 6 0 7 8 2 4 3 5 1 5 1 0 2 4 8 6 3 7 [mate#2] 0 3 7 1 2 4 5 6 8 6 8 2 0 5 3 7 1 4 2 1 3 7 8 6 4 5 0 3 5 6 4 1 2 0 8 7 4 2 0 8 6 7 1 3 5 8 7 1 3 0 5 6 4 2 1 4 5 6 7 8 2 0 3 5 0 8 2 4 1 3 7 6 7 6 4 5 3 0 8 2 1 Как я понимаю, у самого первого ДЛК в выходном файле 40 ОДЛК, а у самого последнего - 2 ОДЛК. А сколько найдено всего ОДЛК у введённых 308 ДЛК - не понятно. Может быть, их и 308 оказалось в итоге (случайно совпало с исходным количеством введённых ДЛК). Но подозреваю, что это не так. Дальше не стала проверять (искать ОДЛК от полученных на втором шаге ДЛК). PS. Подумала ещё так: из введённых ДЛК - столько-то найдено марьяжных ДЛК. Но с 308 введёнными ДЛК всё равно не совсем понятно: там вроде бы не самый первый ДЛК марьяжный, то есть не все 308 ДЛК марьяжные. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверяю вторую ассоциативную КФ из показанных выше 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 Программа также сообщает, что найден 1 ОДЛК. А в выходном файле 516 ОДЛК: [DLK(516)] 0 4 7 8 3 6 2 5 1 5 1 4 6 8 3 0 2 7 8 0 2 4 7 1 3 6 5 2 7 1 3 6 8 5 0 4 6 5 0 1 4 7 8 3 2 4 8 3 0 2 5 7 1 6 3 2 5 7 1 4 6 8 0 1 6 8 5 0 2 4 7 3 7 3 6 2 5 0 1 4 8 [mate#1] 0 2 1 4 3 5 6 7 8 8 1 4 3 5 6 7 0 2 2 8 3 0 4 7 1 6 5 7 6 2 5 8 3 0 4 1 1 3 5 6 7 0 8 2 4 6 7 8 2 1 4 3 5 0 4 5 6 7 0 8 2 1 3 3 4 0 1 6 2 5 8 7 5 0 7 8 2 1 4 3 6 [mate#2] 0 2 1 4 3 5 7 8 6 7 1 6 3 5 4 8 0 2 2 4 3 0 8 7 1 6 5 8 6 2 5 4 3 0 7 1 1 3 5 8 7 0 6 2 4 4 7 8 2 1 6 3 5 0 6 5 4 7 0 8 2 1 3 3 8 0 1 6 2 5 4 7 5 0 7 6 2 1 4 3 8 . . . . . . . . My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
PS. Подумала ещё так: из введённых ДЛК - столько-то найдено марьяжных ДЛК. Правильно подумала. Да, именно так: программа сообщает, сколько среди введённых ДЛК найдено марьяжных ДЛК. Ещё раз проверила 308 ДЛК, все они марьяжные. Всё стало понятно. Вторичная обработка 308 ДЛК новых КФ ОДЛК не дала. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Белышев выложил новую версию программы проверки на ОДЛК. Исправил ошибки и, кроме того, добавил перекодирование ДЛК порядков больше 10 в N-ричное представление. Проверила для ДЛК 12-го порядка, в качестве исходного ДЛК взяла дважды симметричный ДЛК, построенный моей программой (самый первый): 0 1 2 3 4 5 6 7 8 9 10 11 2 3 0 1 6 7 4 5 10 11 8 9 4 8 5 9 0 1 10 11 2 6 3 7 6 10 8 4 2 11 0 9 7 3 1 5 8 4 6 10 11 2 9 0 1 5 7 3 10 6 11 7 9 8 3 2 4 0 5 1 11 7 10 6 8 9 2 3 5 1 4 0 9 5 7 11 10 3 8 1 0 4 6 2 7 11 9 5 3 10 1 8 6 2 0 4 5 9 4 8 1 0 11 10 3 7 2 6 3 2 1 0 7 6 5 4 11 10 9 8 1 0 3 2 5 4 7 6 9 8 11 10 Программа выдала для этого ДЛК аж 373 ортогональных диагональных соквадрата [DLK(373)] 0 1 2 3 4 5 6 7 8 9 A B 2 3 0 1 6 7 4 5 A B 8 9 4 8 5 9 0 1 A B 2 6 3 7 6 A 8 4 2 B 0 9 7 3 1 5 8 4 6 A B 2 9 0 1 5 7 3 A 6 B 7 9 8 3 2 4 0 5 1 B 7 A 6 8 9 2 3 5 1 4 0 9 5 7 B A 3 8 1 0 4 6 2 7 B 9 5 3 A 1 8 6 2 0 4 5 9 4 8 1 0 B A 3 7 2 6 3 2 1 0 7 6 5 4 B A 9 8 1 0 3 2 5 4 7 6 9 8 B A [mate#1] 4 0 5 2 6 3 7 8 9 A B 1 0 7 A 6 3 4 2 B 1 9 5 8 B 2 0 4 1 7 5 A 3 6 8 9 2 A B 3 9 0 8 5 7 4 1 6 A 4 1 7 8 6 9 0 5 2 3 B 6 5 4 0 B 1 3 2 8 7 9 A 5 6 8 9 7 2 A 1 4 B 0 3 3 8 2 B 4 5 0 9 6 1 A 7 1 3 7 A 0 9 4 6 B 8 2 5 7 1 9 8 2 B 6 3 A 5 4 0 9 B 3 5 A 8 1 7 2 0 6 4 8 9 6 1 5 A B 4 0 3 7 2 [mate#2] 2 0 8 4 3 1 9 A 6 7 B 5 0 9 7 A 1 3 4 B 5 6 8 2 B 4 6 3 5 9 8 2 7 A 1 0 4 7 B 1 A 8 0 6 9 2 5 3 A 8 5 9 0 6 1 3 2 4 7 B 3 2 1 6 B 5 7 4 A 9 0 8 7 1 2 0 9 4 3 5 8 B 6 A 8 A 4 B 6 0 2 7 1 5 3 9 5 3 9 2 8 A 6 0 B 1 4 7 9 5 0 7 4 B A 1 3 8 2 6 6 B 3 8 2 7 5 9 4 0 A 1 1 6 A 5 7 2 B 8 0 3 9 4 . . . . . . . [mate#373] 4 7 8 9 3 2 1 5 A 6 B 0 0 5 6 8 4 B 7 1 9 A 3 2 2 6 B 3 1 A 4 7 5 9 0 8 8 0 1 6 9 4 B A 7 3 2 5 B A 7 5 8 3 9 2 1 0 4 6 7 2 9 1 B 0 8 6 4 5 A 3 3 9 2 0 5 1 A 4 6 B 8 7 5 8 3 B A 7 2 9 0 1 6 4 A 1 0 4 2 6 5 8 3 7 9 B 9 4 5 7 0 8 6 3 B 2 1 A 1 B 4 A 6 5 3 0 2 8 7 9 6 3 A 2 7 9 0 B 8 4 5 1 Интересно! Плодовиты, похоже, дважды симметричные ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger