Ватутин пишет на форуме boinc.ru

Напомню, что до этого четверки были только от горизонтально симметричных, эти две получены от новой симметрии, которая работает!

А эта четвёрка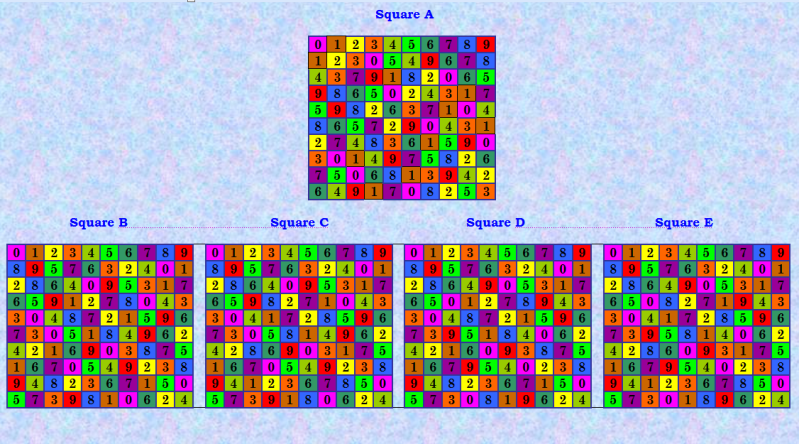



Или в альтернативной БД citerra таких нет, которые от не симметричных ДЛК???
Не думаю.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

В указанном выше посте Ватутин выложил два ДЛК, дающие четвёрки по новой симметрии.

0 1 2 3 4 5 6 7 8 9 
1 2 3 0 6 9 7 8 5 4 
4 3 9 8 0 7 5 1 6 2 
5 7 4 1 9 3 2 6 0 8 
8 9 6 7 5 0 3 2 4 1 
2 8 5 4 7 6 0 9 1 3 
7 5 1 6 2 4 8 3 9 0 
6 0 8 2 3 1 9 4 7 5 
9 4 7 5 8 2 1 0 3 6 
3 6 0 9 1 8 4 5 2 7 

0 1 2 3 4 5 6 7 8 9 
1 2 3 4 5 7 0 9 6 8 
4 7 8 6 9 2 3 5 1 0 
8 9 6 7 2 0 4 3 5 1 
3 0 5 9 6 8 1 4 2 7 
9 5 4 8 1 3 7 2 0 6 
6 4 9 0 7 1 5 8 3 2 
5 8 7 2 0 6 9 1 4 3 
7 3 0 1 8 4 2 6 9 5 
2 6 1 5 3 9 8 0 7 4

Заметила интересную особенность: обе эти четвёрки дают только три уникальные КФ.
Четвёрка от первого ДЛК даёт следующие три уникальные КФ:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 8 9 5 7
6 3 4 5 2 0 7 1 9 8
3 6 9 7 8 1 0 5 4 2
4 7 6 9 5 8 2 0 3 1
8 5 1 2 7 9 3 4 0 6
5 0 8 6 9 7 1 3 2 4
7 9 3 0 6 2 4 8 1 5
9 4 7 8 1 3 5 2 6 0
2 8 5 1 0 4 9 6 7 3

0 1 2 3 4 5 6 7 8 9
1 2 0 4 6 3 8 9 5 7
7 0 3 5 2 6 4 8 9 1
6 5 8 9 1 2 7 4 0 3
5 6 9 8 7 0 1 3 2 4
8 7 5 1 3 4 9 2 6 0
9 8 4 6 0 7 5 1 3 2
4 3 1 0 9 8 2 6 7 5
3 4 7 2 8 9 0 5 1 6
2 9 6 7 5 1 3 0 4 8

0 1 2 3 4 5 6 7 8 9
1 2 3 0 6 9 7 8 5 4
4 3 9 8 0 7 5 1 6 2
5 7 4 1 9 3 2 6 0 8
8 9 6 7 5 0 3 2 4 1
2 8 5 4 7 6 0 9 1 3
7 5 1 6 2 4 8 3 9 0
6 0 8 2 3 1 9 4 7 5
9 4 7 5 8 2 1 0 3 6
3 6 0 9 1 8 4 5 2 7

Четвёрка от второго ДЛК даёт следующие три уникальные КФ:

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 7 9 8 4 6
2 4 7 6 0 3 8 1 9 5
8 6 9 1 7 2 0 3 5 4
9 8 0 4 3 6 7 5 1 2
7 0 8 5 2 9 4 6 3 1
4 3 1 8 6 0 5 9 2 7
6 9 5 7 8 1 2 4 0 3
5 7 4 9 1 8 3 2 6 0
3 5 6 2 9 4 1 0 7 8

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 7 0 9 6 8
4 7 8 6 9 2 3 5 1 0
8 9 6 7 2 0 4 3 5 1
3 0 5 9 6 8 1 4 2 7
9 5 4 8 1 3 7 2 0 6
6 4 9 0 7 1 5 8 3 2
5 8 7 2 0 6 9 1 4 3
7 3 0 1 8 4 2 6 9 5
2 6 1 5 3 9 8 0 7 4

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 7 9 8 6 0
2 6 7 9 0 3 4 1 5 8
7 9 8 5 6 2 3 0 1 4
9 3 1 7 8 4 5 2 0 6
6 4 0 1 2 9 8 5 3 7
3 8 4 0 7 6 1 9 2 5
4 0 5 2 3 8 7 6 9 1
5 7 6 8 9 1 0 3 4 2
8 5 9 6 1 0 2 4 7 3

А показанная выше (найденная мной) четвёрка даёт 5 уникальных КФ (максимально возможное для четвёрки количество):

0 1 2 3 4 5 6 7 8 9
1 2 0 4 3 6 5 9 7 8
2 3 4 9 8 1 0 5 6 7
7 9 3 1 5 4 8 6 0 2
5 7 6 8 9 0 1 3 2 4
8 0 5 7 6 3 2 4 9 1
4 6 9 2 1 8 7 0 3 5
9 5 1 6 2 7 3 8 4 0
6 4 8 0 7 2 9 1 5 3
3 8 7 5 0 9 4 2 1 6

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 3 8 9 6 7
3 8 7 0 1 6 5 4 9 2
4 3 9 5 0 1 7 8 2 6
5 6 4 1 9 0 3 2 7 8
2 4 6 7 3 8 9 5 1 0
6 9 3 2 8 7 1 0 5 4
9 0 1 8 7 4 2 6 3 5
7 5 8 6 2 9 0 3 4 1
8 7 5 9 6 2 4 1 0 3

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 6 3 7
9 7 5 0 3 1 2 4 6 8
2 9 4 7 0 3 1 8 5 6
7 6 3 2 8 0 5 9 1 4
5 0 9 8 2 6 7 3 4 1
8 3 1 5 6 9 4 2 7 0
3 5 7 6 9 4 8 1 0 2
4 8 6 1 7 2 3 0 9 5
6 4 8 9 1 7 0 5 2 3

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 6 3 7
9 7 5 0 3 4 2 1 6 8
2 9 1 7 0 3 4 8 5 6
7 6 3 2 8 0 5 9 1 4
5 0 9 8 2 6 7 3 4 1
8 3 4 5 6 9 1 2 7 0
3 5 7 6 9 1 8 4 0 2
4 8 6 1 7 2 3 0 9 5
6 4 8 9 1 7 0 5 2 3

0 1 2 3 4 5 6 7 8 9
1 2 3 0 5 4 9 6 7 8
4 3 7 9 1 8 2 0 6 5
9 8 6 5 0 2 4 3 1 7
5 9 8 2 6 3 7 1 0 4
8 6 5 7 2 9 0 4 3 1
2 7 4 8 3 6 1 5 9 0
3 0 1 4 9 7 5 8 2 6
7 5 0 6 8 1 3 9 4 2
6 4 9 1 7 0 8 2 5 3

Такие четвёрки (и двушки соответственно) я называю полновесными, так как они дают максимально возможное количество уникальных КФ.

Можно предположить, что данная полновесная четвёрка происходит от ни каким образом не симметричного ДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверила двушку, выложенную здесь
http://forum.boinc.ru/default.aspx?g=posts&m=89500#post89500

0 1 2 3 4 5 6 7 8 9 
1 3 8 7 2 4 5 9 6 0 
9 7 1 5 6 2 0 4 3 8 
2 8 7 4 5 6 3 0 9 1 
6 0 4 8 9 7 1 3 5 2 
5 2 3 0 1 8 9 6 7 4 
3 6 9 2 0 1 7 8 4 5 
7 4 0 6 8 9 2 5 1 3 
4 5 6 9 3 0 8 1 2 7 
8 9 5 1 7 3 4 2 0 6 

2 ODLSs 

Orthogonal square 1: 
2 8 6 9 4 1 3 5 7 0 
9 0 2 4 8 5 7 6 1 3 
4 7 5 6 0 2 1 9 3 8 
1 4 9 7 3 6 5 0 8 2 
7 6 3 0 1 8 4 2 9 5 
5 9 1 8 7 3 2 4 0 6 
8 5 7 3 9 0 6 1 2 4 
3 1 4 2 5 9 0 8 6 7 
0 2 8 5 6 7 9 3 4 1 
6 3 0 1 2 4 8 7 5 9 

Orthogonal square 2: 
2 8 6 9 4 1 3 5 7 0 
9 0 2 4 8 5 7 6 1 3 
4 7 5 6 0 2 1 8 3 9 
1 4 8 7 3 6 5 0 9 2 
7 6 3 0 1 9 4 2 8 5 
5 9 1 8 7 3 2 4 0 6 
8 5 7 3 9 0 6 1 2 4 
3 1 4 2 5 8 0 9 6 7 
0 2 9 5 6 7 8 3 4 1 
6 3 0 1 2 4 9 7 5 8

Она тоже не полновесная! Даёт только две уникальные КФ

0 1 2 3 4 5 6 7 8 9
1 2 0 4 6 9 7 3 5 8
8 5 4 7 9 2 0 1 6 3
3 6 7 9 1 8 4 5 0 2
7 4 9 6 8 3 5 2 1 0
9 8 6 5 7 1 2 0 3 4
5 9 1 2 0 6 3 8 4 7
4 3 8 0 5 7 9 6 2 1
2 0 5 8 3 4 1 9 7 6
6 7 3 1 2 0 8 4 9 5

0 1 2 3 4 5 6 7 8 9
1 2 3 0 6 7 4 9 5 8
9 4 8 5 3 0 7 1 2 6
4 5 0 7 1 9 2 8 6 3
6 7 1 2 9 3 8 5 4 0
5 9 6 8 0 4 3 2 1 7
8 3 9 6 7 1 5 4 0 2
3 0 4 9 8 2 1 6 7 5
2 8 7 1 5 6 9 0 3 4
7 6 5 4 2 8 0 3 9 1

Тогда как известно много полновесных двушек (дающих три уникальные КФ), которые происходят от не симметричных ДЛК (в смысле известной ранее симметрии по Брауну).

Вот пример полновесной двушки, эта двушка - первая найденная в нашем BOINC-проекте ODLK



Двушка даёт три уникальные КФ:

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 6 3 7
8 6 9 7 2 1 4 5 0 3
5 0 7 8 1 3 2 9 4 6
6 3 4 9 7 0 1 2 5 8
7 9 5 6 8 4 0 3 2 1
9 5 8 1 0 6 3 4 7 2
2 4 6 5 3 7 8 1 9 0
3 7 1 0 9 2 5 8 6 4
4 8 3 2 6 9 7 0 1 5

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 6 7 3
6 9 3 5 1 4 7 2 0 8
9 7 4 1 8 3 5 0 2 6
7 5 8 6 9 0 1 3 4 2
8 4 7 0 3 6 2 5 9 1
2 3 6 8 0 7 4 9 1 5
5 0 1 2 7 9 3 8 6 4
3 6 9 7 2 1 8 4 5 0
4 8 5 9 6 2 0 1 3 7

0 1 2 3 4 5 6 7 8 9
1 2 0 4 5 8 9 6 7 3
6 9 3 5 1 4 7 2 0 8
9 7 4 1 8 3 5 0 6 2
7 5 8 2 9 0 1 3 4 6
8 4 7 0 3 6 2 5 9 1
2 3 6 8 0 7 4 9 1 5
5 0 1 6 7 9 3 8 2 4
3 6 9 7 2 1 8 4 5 0
4 8 5 9 6 2 0 1 3 7

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И из того же поста, откуда скопирована двушка, полученная Ватутиным.
Цитирую:

Теперь я знаю кун фу (с)
В смысле, как получаются вроде бы несимметричные двушки, которые мы периодически находим в проекте в приблизительном соотношении 1000 однушек : 1 двушка.

Очень сильно подозреваю, что эти "вроде бы несимметричные двушки", которые мы находим в BOINC-проекте (и они находят в своём BOINC-проекте), совсем не такие двушки, которые Ватутин получил по новой симметрии.
Потому что первые двушки полновесные, а вторые (от Ватутина) не полновесные.
Хотя, разумеется, среди первых двушек могут встретиться и такие, как нашёл Ватутин по новой симметрии.
А вот наоборот... это надо подтвердить конкретным примером.
То есть чтобы двушка, найденная по новой симметрии, была полновесной.

Цитирую

Опробовал новую симметрию на своей машине: за сутки в 4 потока найдено + канонизировано citerra'ой:

93 новых пар ОДЛК
40 новых двушек
2 новых четверки

отсюда
http://forum.boinc.ru/default.aspx?g=posts&m=89505#post89505

Ну вот тут и надо искать пример полновесной двушки.
Предположу, что такой двушки нет.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Или в альтернативной БД citerra таких нет, которые от не симметричных ДЛК???
Не думаю.

Конечно же, в БД citerra есть четвёрки от не симметричных (по Брауну) ДЛК.
Вот эту он давно выкладывал на форуме boinc.ru

0 1 2 3 4 5 6 7 8 9 
1 2 3 4 0 9 5 6 7 8 
3 4 1 7 9 0 2 8 5 6 
5 9 7 6 8 1 3 4 0 2 
9 7 5 8 3 6 1 2 4 0 
4 5 6 0 1 8 9 3 2 7 
6 8 0 5 2 4 7 9 1 3 
8 6 4 9 7 2 0 5 3 1 
7 0 8 2 6 3 4 1 9 5 
2 3 9 1 5 7 8 0 6 4

Эта четвёрка полновесная (даёт 5 уникальных КФ).

Так что, утверждение Ватутина

Напомню, что до этого четверки были только от горизонтально симметричных ...

не соответствует действительности.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Немножко отдохнула от ОДЛК 10-го порядка :)
Построила вручную нормализованный дважды симметричный ДЛК 16-го порядка методом составных квадратов (4*4).
Вот этот дважды симметричный ДЛК 4-го порядка взят в качестве и базового, и основного квадратов:

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

Кстати, этот ДЛК ещё и "браун". И ДЛК 16-го порядка тоже получился "браун". Вот он - красавец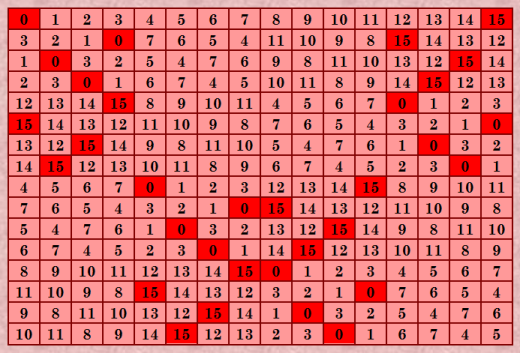



Теперь хочу построить нормализованный дважды симметричный ДЛК 64-го порядка на основе полученного ДЛК 16-го порядка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И из того же поста, откуда скопирована двушка, полученная Ватутиным.
Цитирую:

Теперь я знаю кун фу (с)
В смысле, как получаются вроде бы несимметричные двушки, которые мы периодически находим в проекте в приблизительном соотношении 1000 однушек : 1 двушка.

Очень сильно подозреваю, что эти "вроде бы несимметричные двушки", которые мы находим в BOINC-проекте (и они находят в своём BOINC-проекте), совсем не такие двушки, которые Ватутин получил по новой симметрии.
Потому что первые двушки полновесные, а вторые (от Ватутина) не полновесные.

Вот и свежий пример. За 21 октября в нашем BOINC-проекте ODLK найдены 2 двушки (на 938 уникальных КФ ОДЛК).

0 1 2 3 4 5 6 7 8 9
8 9 4 2 5 6 1 0 7 3
7 5 3 6 2 4 0 8 9 1
6 8 9 7 1 3 4 5 0 2
3 0 6 9 8 1 7 2 4 5
5 4 0 8 6 2 9 1 3 7
1 6 8 0 3 7 5 9 2 4
9 2 5 1 7 8 3 4 6 0
4 3 7 5 9 0 2 6 1 8
2 7 1 4 0 9 8 3 5 6
sq1

 0 1 2 3 4 5 6 7 8 9
 8 9 4 7 5 6 1 0 2 3
 2 5 3 6 7 4 0 8 9 1
 6 8 9 2 1 3 4 5 0 7
 3 0 6 9 8 1 7 2 4 5
 5 4 0 8 6 7 9 1 3 2
 1 6 8 0 3 2 5 9 7 4
 9 7 5 1 2 8 3 4 6 0
 4 3 7 5 9 0 2 6 1 8
 7 2 1 4 0 9 8 3 5 6
sq2

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 3 0 6 9 4 8 5 7
 4 0 6 7 9 2 5 3 1 8
 3 6 0 9 2 1 8 4 7 5
 5 9 8 4 7 0 2 1 6 3
 2 7 4 5 1 8 3 9 0 6
 7 5 9 2 8 3 1 6 4 0
 8 3 7 6 0 4 9 5 2 1
 9 4 1 8 5 6 7 0 3 2
 6 8 5 1 3 7 0 2 9 4
 ------------------

 0 1 2 3 4 5 6 7 8 9
 4 8 5 9 7 0 3 2 1 6
 2 0 9 6 1 3 7 4 5 8
 7 5 6 2 9 1 0 8 3 4
 5 9 0 4 6 2 8 1 7 3
 8 6 3 1 5 7 4 9 0 2
 3 4 1 8 0 9 5 6 2 7
 1 2 7 0 8 4 9 3 6 5
 9 3 8 7 2 6 1 5 4 0
 6 7 4 5 3 8 2 0 9 1
sq1

 0 1 2 3 4 5 6 7 8 9
 4 8 5 9 7 0 3 2 1 6
 2 0 9 6 1 3 7 4 5 8
 7 5 6 2 9 1 0 8 3 4
 5 9 0 4 6 2 8 1 7 3
 8 6 3 1 5 7 4 9 2 0
 3 4 1 8 2 9 5 6 0 7
 1 2 7 0 8 4 9 3 6 5
 9 3 8 7 0 6 1 5 4 2
 6 7 4 5 3 8 2 0 9 1
sq2

Square:
 0 1 2 3 4 5 6 7 8 9
 1 2 3 6 5 9 8 0 4 7
 5 7 8 0 9 6 1 3 2 4
 9 8 4 1 0 3 2 6 7 5
 6 4 5 2 3 7 9 8 0 1
 3 5 9 7 1 4 0 2 6 8
 4 6 0 5 8 1 7 9 3 2
 2 9 6 4 7 8 3 5 1 0
 7 0 1 8 6 2 5 4 9 3
 8 3 7 9 2 0 4 1 5 6

Обе эти двушки полновесные.

Гипотеза у меня такая: двушки и четвёрки, найденные Ватутиным по новой симметрии, сосредоточены в каких-то других линейках, которые в нашем BOINC-проекте не проверяются.
Проверила выложенные Ватутиным двушку и две четвёрки, они принадлежат линейкам №49 и №51.
Кстати, в линейке №51 интересная побочная диагональ

1 2 3 4 0 9 5 6 7 8

Центрально-симметричная диагональ!
А поскольку главная диагональ тоже центрально-симметричная, получается, что обе диагонали в СН ДЛК линейки №51 центрально-симметричные.

Вот основной ДЛК одной из четвёрок, выложенных Ватутиным (из линейки №51):

0 3 8 4 6 2 7 5 9 1
4 1 5 7 8 9 3 0 2 6
7 5 2 9 0 4 1 3 6 8
1 9 0 3 2 6 4 8 7 5
6 2 3 8 4 0 9 1 5 7
3 0 7 2 9 5 8 6 1 4
2 8 9 5 7 1 6 4 3 0
9 4 6 1 5 8 2 7 0 3
5 7 4 6 1 3 0 9 8 2
8 6 1 0 3 7 5 2 4 9

Может быть, это и не играет никакой роли, но... вдруг играет.
Тут Белышеву надо поразмыслить :)

PS. Линейка, в которой в СН ДЛК обе диагонали центрально-симметричные, не единственная.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Теперь хочу построить нормализованный дважды симметричный ДЛК 64-го порядка на основе полученного ДЛК 16-го порядка.

В качестве базового ДЛК взяла тот же самый нормализованный дважды симметричный ДЛК 4-го порядка, который ещё и "браун"

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

Вот левый верхний квадрант нормализованного дважды симметричного ДЛК 64-го порядка, построен, конечно, вручную



Ну, это всё очень просто - метод составных квадратов работает!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Новое сообщение Белышева о дважды симметричных ДЛК
http://forum.boinc.ru/default.aspx?g=posts&m=89547#post89547

Очень интересно!
Оказывается, считать нормализованные дважды симметричные ДЛК порядка 12 не надо :)
Достаточно посчитать количество ЛК порядка 6 с главной диагональю вида (0,0,1,1,2,2).
В формуле это количество обозначено L.

Цитирую:

Утверждение 4. Число нормализованных дважды симметричных ДЛК порядка N = 4n определяется формулой:

L * 16^{n(n-1)} * (2n)! / n!

где L означает число ЛК порядка 2n, указанного в Утверждении 1 вида.

Приведён пример для N=8, то есть n=2. Количество ЛК порядка 4 с нужной главной диагональю L=4.
Эти ЛК показаны. Далее элементарное вычисление по приведённой формуле.
Всё! Никаких подсчётов не надо.

Осталось выяснить, сколько будет ЛК 6-го порядка с главной диагональю вида (0,0,1,1,2,2).
Если, конечно, я всё правильно поняла :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И ещё интересная новость: заинтересовала Harry White задачей подсчёта нормализованных дважды симметричных ДЛК 12-го порядка.
Он работает ещё над этой задачей. Но покажу предварительный результат.
Например, для комбинации 3-х строк {первая строка фиксированная, как в нормализованном ДЛК; первый вариант 12-й строки; первый вариант 2-й строки} его программа выдала:
Number of double symmetric DLS 57147392

Первый ДЛК в этой группе такой:

0 1 2 3 4 5 6 7 8 9 10 11
2 3 0 1 6 7 4 5 10 11 8 9
4 8 5 9 0 1 10 11 2 6 3 7
6 10 8 4 2 11 0 9 7 3 1 5
8 4 6 10 11 2 9 0 1 5 7 3
10 6 11 7 9 8 3 2 4 0 5 1
11 7 10 6 8 9 2 3 5 1 4 0
9 5 7 11 10 3 8 1 0 4 6 2
7 11 9 5 3 10 1 8 6 2 0 4
5 9 4 8 1 0 11 10 3 7 2 6
3 2 1 0 7 6 5 4 11 10 9 8
1 0 3 2 5 4 7 6 9 8 11 10

Считалось на моём компьютере 2 мин. 34 сек. Квадраты не записываются, только считаются.
Конечно, вариантов 12-й строки и вариантов 2-й строки много. И подсчитать всё для всех комбинаций вариантов 12-й и 2-й строк на одном ПК проблематично. Однако интересен сам алгоритм. Harry удалось определить число вариантов 12-й строки и число вариантов 2-й строки.
Но он пишет, что испытания ещё не закончились.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Итак, сколько существует ЛК 6-го порядка с главной диагональю вида (0,0,1,1,2,2)?
Моя программка (на скорую руку сварганила) нашла таких ЛК 400 штук, но! нормализованных.
Если не напортачила (вполне могла), вот первые три и последние три ЛК:

0  1  2  3  4  5 
1  0  3  2  5  4 
2  4  1  5  0  3 
4  2  5  1  3  0 
3  5  0  4  2  1 
5  3  4  0  1  2 

 0  1  2  3  4  5 
 1  0  3  2  5  4 
 2  4  1  5  0  3 
 4  2  5  1  3  0 
 3  5  4  0  2  1 
 5  3  0  4  1  2 

 0  1  2  3  4  5 
 1  0  3  2  5  4 
 2  4  1  5  0  3 
 4  2  5  1  3  0 
 5  3  0  4  2  1 
 3  5  4  0  1  2 
. . . . . . . . 

 0  1  2  3  4  5 
 5  0  4  2  3  1 
 4  2  1  0  5  3 
 2  5  3  1  0  4 
 1  3  5  4  2  0 
 3  4  0  5  1  2 

 0  1  2  3  4  5 
 5  0  4  2  3  1 
 4  2  1  5  0  3 
 2  3  0  1  5  4 
 1  5  3  4  2  0 
 3  4  5  0  1  2 

 0  1  2  3  4  5 
 5  0  4  2  3  1 
 4  2  1  5  0  3 
 2  4  3  1  5  0 
 1  3  5  0  2  4 
 3  5  0  4  1  2

Дальше рассуждаю так: элементы 0, 1, 2 переобозначать нельзя. Значит, можно переобозначать только три элемента: 3, 4, 5. Это даст 6 перестановок. Тогда общих ЛК нужного вида будет 400*6=2400.
Это правильно я рассуждаю? Вполне возможно, что неправильно.
Ну, допустим, что какая-то доля истины имеется :)

Подставив в формулу Белышева все данные, нахожу, что нормализованных дважды симметричных ДЛК 12-го порядка будет
4831838208000.
Ой! Наверняка наврала :)
Просто было интересно по-быстрому посчитать :)
Кто-нибудь посчитает правильно.

PS. Это ж надо такую формулу придумать! На грани фантастики :)
А ЛК 8-го порядка с главной диагональю вида (0,0,1,1,2,2,3,3), наверное, м-н-о-г-о будет. Но не запредельно много; во всяком случае, их посчитать легче, чем нормализованные дважды симметричные ДЛК 16-го порядка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Белышев изменил значение параметра L в формуле для количества нормализованных дважды симметричных ДЛК порядка N = 4n

Утверждение 4. Число нормализованных дважды симметричных ДЛК порядка N = 4n определяется формулой:

L * 16^{n(n-1)} * (2n)! / n!

где L означает число квази-ЛК порядка 2n, указанного в Утверждении 1 вида.

Например, для N = 8 число нормализованных дважды симметричных ДЛК равно
4 * 16^{2(2-1)} * 4! / 2! = 4 * 256 * 24 / 2 = 12288.

отсюда
http://forum.boinc.ru/default.aspx?g=posts&m=89547#post89547

Тогда наверняка мои вчерашние расчёты для N = 12 неправильные.
Хотя я не знаю, как связано количество квази-ЛК 6-го порядка с количеством ЛК данного порядка (при одной и той же главной диагонали).
Но думаю, что эти количества разные.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Harry White прислал нормализованный дважды симметричный ДЛК 20-го порядка

Thursday 2017-10-26 09:06:02 Newfoundland Daylight Time
Which row 20 choice, (1 .. 106866)? 49999
Which row 2 choice, (1 .. 1181020320)? 22222222
.. writing DSDLS to file 20DSDLS_2.txt
First DSDLS:

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 1  6 19 15  8 10  7  5 16 17  2  3 14 12  9 11  4  0 13 18
 2  0  1  4  3  6  5  8  9  7 12 10 11 14 13 16 15 18 19 17
 3  2  0  5  1  4  8  6 10 12  7  9 13 11 15 18 14 19 17 16
 4  3  5  0  7  1  2  9  6  8 11 13 10 17 18 12 19 14 16 15
 5  4  3  1  0  9 11  2 12  6 13  7 17  8 10 19 18 16 15 14
 6  5  4  2 10  3 12  1 11 19  0  8 18  7 16  9 17 15 14 13
 7  8 16 10  2 18  0 13  4 14  5 15  6 19  1 17  9  3 11 12
 8  7  6 18  5 16 10 19 17  4 15  2  0  9  3 14  1 13 12 11
10 19 18  7  6  2  4  3 14 11  8  5 16 15 17 13 12  1  0  9
19 10  8 16 15 14 13 12  2  1 18 17  7  6  5  4  3 11  9  0
18 16 15  8 17  7 19 10  5 13  6 14  9  0 12  2 11  4  3  1
16 18  7 19 14  8  9  4 13  2 17  6 15 10 11  5  0 12  1  3
15 17 13 14 19 12  3 11  1 10  9 18  8 16  7  0  5  6  2  4
17 13 12 11  9  0  1 14  3 15  4 16  5 18 19 10  8  7  6  2
13 12 17  9 16 11 14  0 15 18  1  4 19  5  8  3 10  2  7  6
12 14  9 17 11 13 18 15 19  3 16  0  4  1  6  8  2 10  5  7
14  9 11 13 12 15 17 18  0 16  3 19  1  2  4  7  6  8 10  5
11 15 10  6 18 19 16 17  7  5 14 12  2  3  0  1 13  9  4  8
 9 11 14 12 13 17 15 16 18  0 19  1  3  4  2  6  7  5  8 10

Здесь точно так же, как для порядка 12: вводится вариант 20-й строки и вариант 2-й строки. В скобках указано количество этих вариантов.
Как видно из протокола, Harry ввёл 49999-й вариант 20-й строки и 22222222-й вариант 2-й строки.

Класс! Раскрашу этот квадратик на досуге :)

На основе дважды симметричных ДЛК 20-го порядка легко строить дважды симметричные ДЛК 80-го порядка даже вручную - методом составных квадратов (80=20*4). И не только 80-го порядка, конечно, а любого порядка N=20*k, если для порядка k существует дважды симметричный ДЛК.
Разумеется, для больших порядков процедуру (метод составных квадратов) лучше запрограммировать.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Harry прислал ещё ряд вариантов нормализованных дважды симметричных ДЛК 20-го порядка.
Для раскраски выбрала этот вариант

Thursday 2017-10-26 16:53:47 Newfoundland Daylight Time
Which row 20 choice, (1 .. 106866)? 1
Which row 2 choice, (1 .. 1259545104)? 700000
.. writing DSDLS to file 20DSDLS_6.txt
First DSDLS:

Симпатичный квадратик :)
Спасибо Harry!

Мне нравится вариант 20-й строки, эта строка получается инверсией пар элементов первой строки - по порядку следования этих пар. Красивая строка!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нормализованный дважды симметричный ДЛК 24-го порядка от Harry White

Thursday 2017-10-26 17:38:46 Newfoundland Daylight Time
Which row 24 choice? 49999
Which row 2 choice? 22222222
.. writing DSDLS to file 24DSDLS_6.txt
First DSDLS: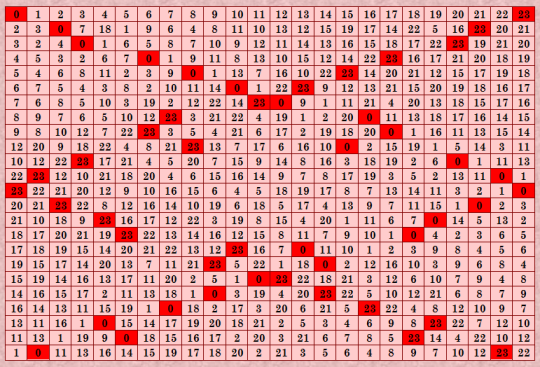

В этом ДЛК уже не первый вариант 24-й строки (который мне нравится), а 49999-й.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нормализованный дважды симметричный ДЛК 28-го порядка от Harry White

Thursday 2017-10-26 18:21:50 Newfoundland Daylight Time
Which row 28 choice? 1
Which row 2 choice? 1000000000
.. writing DSDLS to file 28DSDLS_2.txt
First DSDLS:

В этом ДЛК моя любимая последняя строка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нормализованный дважды симметричный ДЛК 32-го порядка от Harry White

Thursday 2017-10-26 19:19:51 Newfoundland Daylight Time
Which row 32 choice? 66666
Which row 2 choice? 66666
.. writing DSDLS to file 32DSDLS_1.txt
First DSDLS:

Очень красивый!
А варианты строк-то (32-й и 2-й), посмотрите, одни шестёрки :)
Сравните с моим нормализованным дважды симметричным ДЛК, построенным методом составных квадратов



Этот ДЛК ещё и "браун".
Итак, до порядка 32 включительно мы с Harry построили нормализованные дважды симметричные ДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ну вот Белышев и посчитал количество нормализованных дважды симметричных ДЛК 12-го порядка

Первые три числа L для формулы из Утверждения 4:

L(1) = 1
L(2) = 4
L(3) = 40341

Соответственно, последовательность A287650 становится:

2, 12288, 81217160478720

здесь указаны члены последовательности только для N кратных четырём.

отсюда
http://forum.boinc.ru/default.aspx?g=posts&m=89557#post89557

Правильно: так и надо указывать - только для N кратных четырём. А зачем указывать для тех N, для которых дважды симметричные ДЛК не существуют. Об этом я писала выше.
В общем, последовательность ждёт ещё одна правка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Разумеется, для больших порядков процедуру (метод составных квадратов) лучше запрограммировать.

Это сделал Harry White.
Он пишет сегодня:

I modified the CompositeSquares program for magic squares on my website
to also work for Latin squares.

http://budshaw.ca/Download.html

Go to Composite and click the Download Win32 zip button.

Отлично! Метод составных квадратов работает и для магических, и для латинских квадратов.
Спасибо, Harry!

Я попробовала по этой программе построить нормализованный дважды симметричный ДЛК 48-го порядка.
Ввела в программу два нормализованных дважды симметричных ДЛК: 4-го и 12-го порядков:

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

 0  1  2  3  4  5  6  7  8  9 10 11
 2  3  0  1  6  7  4  5 10 11  8  9
 4  8  5  9  0  1 10 11  2  6  3  7
 6 10  8  4  2 11  0  9  7  3  1  5
 8  4  6 10 11  2  9  0  1  5  7  3
10  6 11  7  9  8  3  2  4  0  5  1
11  7 10  6  8  9  2  3  5  1  4  0
 9  5  7 11 10  3  8  1  0  4  6  2
 7 11  9  5  3 10  1  8  6  2  0  4
 5  9  4  8  1  0 11 10  3  7  2  6
 3  2  1  0  7  6  5  4 11 10  9  8
 1  0  3  2  5  4  7  6  9  8 11 10

На выходе имеем нормализованный дважды симметричный ДЛК 48-го порядка.
Покажу верхнюю половину этого ДЛК



Выше я показывала нормализованный ДЛК 48-го порядка (фрагмент), построенный мной методом составных квадратов вручную.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Кстати, методом составных квадратов можно строить не только дважды симметричные ДЛК.
Покажу построение этим методом идеального ДЛК 35-го порядка (ultra).
Исходные идеальные ДЛК взяла отсюда: 7-го и 5-го порядков (7-го порядка взяла левый квадрат на иллюстрации)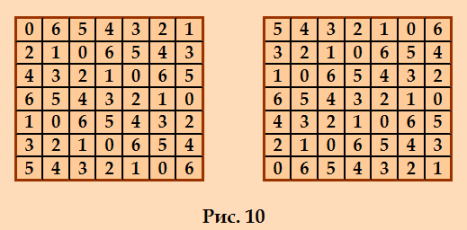





На выходе получила идеальный ДЛК 35-го порядка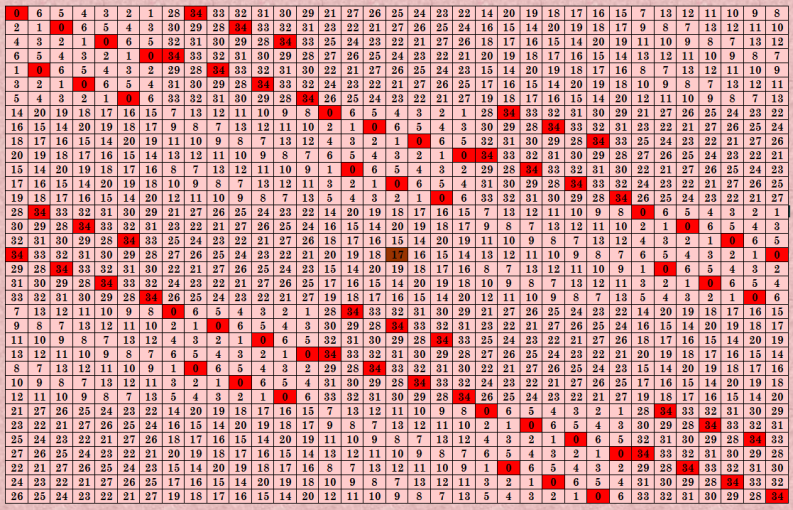



Красавец! Этот ДЛК и ассоциативный, и пандиагональный.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg