О применении первой гипотезы Харди_Литтлвуда

Я согласна с тем, что в этой гипотезе рассматриваются именно наборы из простых чисел; о том, что простые числа обязательно должны быть последовательными, ничего не сказано.

В теме "Магические квадраты" г. Петухов что-то промолвил насчёт того, что Ядряра разобрался в применении первой гипотезы Х-Л к паттернам для квадрата Стенли 5-го порядка.
Значит, как бы уже применили и вынесли вердикт: поиск по паттерну в этой задаче бессмысленный.

Помилуйте!
Для квадрата Стенли существуют тысячи теоретических (допустимых) паттернов!!
Все уже проверили гипотезой ???

Есть 4 паттерна с минимальным диаметром 156, которые были найдены ещё Andersen.
Он тогда же написал, что для этих паттернов решения не существует до 10^20.
Ну, на 10^20 и даже на 10^37 простые числа не заканчиваются!
Конечно, искать в таком диапазоне будет непросто и долго, но отнюдь не бессмысленно.

Я нашла уже более 10 тысяч теоретических паттернов для квадрата Стенли.
Не думаю, что поиск по всем этим паттернам бессмысленный.
Другое дело, что техника моя не тянет обработку всех этих паттернов.

Ядряра писал

Беру оттуда кортеж:

4666036648287026461: 0 108 120 150 180 186 228 270 276 306 336 348 456

Числа 4666036648287026461 и 4666036648287026569 простые?

Сколько простых чисел между ними?

Ответ желает получить только от Demis
Занялся просвещением Demis? :))

Demis вроде не первый день в проекте.
К тому же, BOINC-проект SPT полностью им управляется.

Ну и что тут Ядряра увидел?
Проверила своей утилитой

4666036648287026461, 4666036648287026569, 4666036648287026581, 46660366482870266
11, 4666036648287026641, 4666036648287026647, 4666036648287026689, 4666036648287
026731, 4666036648287026737, 4666036648287026767, 4666036648287026797, 466603664
8287026809, 4666036648287026917, 13

паттерн

0, 108, 120, 150, 180, 186, 228, 270, 276, 306, 336, 348, 456

Симметричный кортеж из 13 последовательных простых чисел.
Между последовательными простыми числами других простых чисел не бывает!

Ну, ликбез мне не интересен.
Снова прекращаю читать тему.
Когда увидела сообщение Demis в теме, не смогла удержаться, чтобы не прочитать.

Ядряра писал

В первую очередь для DemISdx, gris, vicvolf, ice00, Jarek ...

Вместо многоточия можно поставить: для глупой Макаровой.
Ну, Jarek сам может Ядряре всё написать, он кортежами занимается больше, чем существует мой проект по симметричным кортежам.
Глупая Макарова как-нибудь обойдётся без ликбеза.

Мне было интересно узнать применение первой гипотезы Х-Л к показанному мной паттерну.
А про "грязные" и "чистые" кортежи абсолютно не интересно.

Ещё раз об этом кортеже

41: [0, 2, 6, 12, 18, 20, 26, 30, 32, 38, 42, 48, 56, 60, 62, 66, 68, 72, 86, 90, 96, 98, 108, 110, 116, 122, 126, 132, 138, 140, 150, 152, 156, 158, 170, 182, 186, 188, 192, 198, 200, 210, 216, 222, 228, 230, 236, 240, 242, 252, 266, 270, 272, 276, 290, 296, 306, 308, 312, 318, 326, 332, 338, 342, 348, 356, 360, 368, 378, 380, 390, 392, 398, 402, 408, 416, 420, 422, 426, 438, 446, 450, 458, 462, 468, 480, 482, 500, 506, 516, 522, 528, 530, 536, 546, 552, 558, 560, 566, 572, 576, 578, 590, 600, 602, 606, 612, 618, 620, 632, 636, 642, 650, 660, 668, 678, 686, 692, 698, 702, 710, 716, 720, 728, 732, 746, 756, 768, 770, 780, 782, 786, 788, 798, 812, 816, 818, 822, 836, 840, 842, 846, 866, 870, 878, 888, 896, 900, 906, 912, 926, 930, 936, 942, 950, 956, 968, 972, 978, 980, 990, 992, 998, 1008, 1010,
1020, 1022, 1028, 1046, 1050, 1052, 1056, 1062, 1068, 1076, 1082, 1088, 1110, 1112,1122,1130, 1140, 1146, 1152, 1160, 1172, 1176, 1182,
1188, 1190, 1196, 1208, 1218, 1236, 1238, 1242, 1248, 1250, 1256, 1260, 1262, 1266, 1278, 1280, 1286, 1320]

Включаю утилиту, она выводит

41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127
, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211
, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307
, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401
, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499
, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607
, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709
, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823
, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937
, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 103
3, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117,
 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1
229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 130
7, 1319, 1321, 1327, 1361, 206

В этом кортеже 206 последовательных простых чисел!
И в нём есть все простые числа, соответствующие паттерну

0, 60, 72, 132, 210, 270, 348, 408, 420, 450, 480, 522, 660, 798, 840, 870, 900, 912, 972, 1050, 1110, 1188, 1248, 1260, 1320

Г. Петухов написал бы так:
len=206, valids=25
Я пишу так:
len=206, q=25

Когда будет найдено решение с len>25 и q=25, это будет второй идеальный квадрат 5-го порядка из простых чисел (не последовательных).

Когда будет найдено решение с len=25 и q=25, это будет идеальный (а значит, пандиагональный) квадрат 5-го порядка из последовательных простых чисел, а также симметричный кортеж длины 25 из последовательных простых чисел.

При len=25 и q<25 имеем приближения к симметричной 25-ке из последовательных простых чисел, а также к идеальному (а значит, пандиагональному) квадрату из последовательных простых чисел.

Кстати, я недавно нашла второй теоретический паттерн с диаметром 1320 для ассоциативного квадрата Стенли

0, 12, 60, 72, 210, 270, 408, 420, 450, 462, 468, 480, 660, 840, 852, 858, 870, 900, 912, 1050, 1110, 1248, 1260, 1308, 1320

Посмотрим, сколько в кортеже

41: [0, 2, 6, 12, 18, 20, 26, 30, 32, 38, 42, 48, 56, 60, 62, 66, 68, 72, 86, 90, 96, 98, 108, 110, 116, 122, 126, 132, 138, 140, 150, 152, 156, 158, 170, 182, 186, 188, 192, 198, 200, 210, 216, 222, 228, 230, 236, 240, 242, 252, 266, 270, 272, 276, 290, 296, 306, 308, 312, 318, 326, 332, 338, 342, 348, 356, 360, 368, 378, 380, 390, 392, 398, 402, 408, 416, 420, 422, 426, 438, 446, 450, 458, 462, 468, 480, 482, 500, 506, 516, 522, 528, 530, 536, 546, 552, 558, 560, 566, 572, 576, 578, 590, 600, 602, 606, 612, 618, 620, 632, 636, 642, 650, 660, 668, 678, 686, 692, 698, 702, 710, 716, 720, 728, 732, 746, 756, 768, 770, 780, 782, 786, 788, 798, 812, 816, 818, 822, 836, 840, 842, 846, 866, 870, 878, 888, 896, 900, 906, 912, 926, 930, 936, 942, 950, 956, 968, 972, 978, 980, 990, 992, 998, 1008, 1010,
1020, 1022, 1028, 1046, 1050, 1052, 1056, 1062, 1068, 1076, 1082, 1088, 1110, 1112,1122,1130, 1140, 1146, 1152, 1160, 1172, 1176, 1182,
1188, 1190, 1196, 1208, 1218, 1236, 1238, 1242, 1248, 1250, 1256, 1260, 1262, 1266, 1278, 1280, 1286, 1320]

содержится элементов этого паттерна.
Я насчитала 22 элемента, нет элементов 852, 858 и 1308.

Таким образом, для этого паттерна и показанного кортежа
len=206, q=22.

Имеем идеальный квадрат 5-го порядка с 3 "дырками".

Сейчас у меня программа работает с 32 теоретическими паттернами для ассоциативного квадрата Стенли.

Вот выдалось приближение

[0, 60, 78, 138, 270, 330, 420, 462, 498, 522, 540, 600, 690, 780, 840, 858, 882, 918, 960, 1050, 1110, 1242, 1302, 1320, 1380]
10693593092947113109: [0, 60, 78, 88, 120, 138, 178, 232, 258, 304, 330, 400, 420, 444, 454, 484, 510, 522, 528, 540, 574, 690, 720, 750, 780, 882, 892, 904, 918, 928, 948, 960, 972, 984, 1012, 1044, 1050, 1110, 1198, 1224, 1284, 1302, 1314, 1320, 1330, 1380]
q=18

Как видите, это уже другой паттерн - с диаметром 1380.

В кортеже, состоящем из 46 последовательных простых чисел, содержатся следующие 18 элементов паттерна

0, 60, 78, 138, 330, 420, 522, 540, 690, 780, 882, 918, 960, 1050, 1110, 1302, 1320, 1380

Собираюсь поискать новые теоретические (допустимые) паттерны для ассоциативного квадрата Стенли.
Надо с меньшими диаметрами поискать.

Господа!
А что вы думаете: трудно ли найти симметричный 25-tuplet?

Наверное, трудно.
На сегодня у нас только-только найдены три симметричные 19-tuplet.
Симметричные 21-tuplet и 23-tuplet пока не найдены.

Если вдруг найдётся симметричный 25-tuplet, в нём будут содержаться и симметричный 21-tuplet и симметричный 23-tuplet.
Матрёшки!

Я понятия не имею, в каком диапазоне можно ожидать симметричный 25-tuplet.

Вот посмотрите на симметричные 19-tuplet

6919940122097246303: 0 48 78 138 198 204 210 264 288 294 300 324 378 384 390 450 510 540 588
7325015925425379457: 0 6 30 90 126 132 150 162 216 246 276 330 342 360 366 402 462 486 492
9218260110780722411: 0 18 102 120 132 222 252 258 270 300 330 342 348 378 468 480 498 582 600

Диаметры, как видите, самые разные, максимальный кругленький такой - 600

Ну вот, а симметричный 19-tuplet с минимальным диаметром 252 не найден до сих пор.

Ищут учёные, ищут военные, ищет полиция... :))

И никак не могут найти.
Хорошо спрятался :)

У симметричного 25-tuplet, как уже сказано, минимальный диаметр 420.
Ну, я с минимальным диаметром здесь не ищу.
Это в другой теме
https://boinc.progger.info/odlk/forum_thread.php?id=275

Покажу приближение к ассоциативному квадрату Стенли с 7 "дырками" для этого паттерна

0, 60, 78, 138, 270, 330, 420, 462, 498, 522, 540, 600, 690, 780, 840, 858, 882, 918, 960, 1050, 1110, 1242, 1302, 1320, 1380

Это полный ассоциативный квадрат Стенли, построенный из элементов этого паттерна

0  60  420  780  840  
78  138  498  858  918 
270  330  690  1050  1110 
462  522  882  1242  1302 
540  600  960  1320  1380

это - с 7 "дырками"

0 60 420 780 □
78 138 □ □ 918
□ 330 690 1050 1110
□ 522 882 □ 1302
540 □ 960 1320 1380

"Дырки" отмечены квадратиками.

Лучшее приближение пока не найдено.

Удалось найти теоретический паттерн для ассоциативного квадрата Стенли с диаметром 924

0, 30, 42, 54, 84, 180, 210, 222, 234, 264, 420, 450, 462, 474, 504, 660, 690,,702, 714, 744, 840, 870, 882, 894, 924

Ассоциативный квадрат Стенли

0  30  42  54  84
180  210  222  234  264
420  450  462  474  504
660  690  702  714  744
840  870  882  894  924

Индекс квадрата S=2310.

Теперь теоретический паттерн с минимальным диаметром надо искать в интервале (420, 924).

PS. Обратите внимание: кажется, это уникальный случай, когда паттерн уложился в квадрат Стенли в естественном порядке.

Ещё одно приближение найдено к ассоциативному квадрату Стенли, паттерн с другим диаметром

[0, 60, 270, 330, 450, 534, 594, 720, 798, 840, 858, 900, 984, 1068, 1110, 1128, 1170, 1248, 1374, 1434, 1518, 1638, 1698, 1908, 1968]
10693760832797302423: [0, 28, 34, 60, 64, 70, 190, 220, 228, 234, 436, 520, 534, 594, 654, 688, 738, 748, 790, 798, 840, 858, 876, 928, 934, 954, 966, 988, 1068, 1078, 1108, 1128, 1170, 1206, 1210, 1248, 1264, 1266, 1368, 1374, 1404, 1428, 1434, 1446, 1494, 1518, 1530,
1536, 1600, 1638, 1656, 1660, 1686, 1698, 1704, 1714, 1750, 1756, 1758, 1830, 1908, 1926, 1948, 1968]
q=18

В кортеже из 64 последовательных простых чисел содержатся всего 18 чисел для построения квадрата Стенли, вот они

0, 60, 534, 594, 798, 840, 858, 1068, 1128, 1170, 1248, 1374, 1434, 1518, 1638, 1698, 1908, 1968

Опять 7 "дырок".
Лучше пока никак не находится.

Проверяю паттерн на построение ассоциативного квадрата Стенли

0  60  450  840  900
270  330  720  1110  1170
534  594  984  1374  1434
798  858  1248  1638  1698
1068  1128  1518  1908  1968

Всё правильно.

Вот нашла ещё 9 теоретических (допустимых) паттернов для ассоциативного квадрата Стенли

0, 60, 168, 180, 228, 300, 348, 360, 468, 528, 630, 690, 810, 930, 990, 1092, 1152, 1260, 1272, 1320, 1392, 1440, 1452, 1560, 1620;
0, 60, 180, 300, 336, 360, 396, 516, 630, 636, 690, 696, 810, 924, 930, 984, 990, 1104, 1224, 1260, 1284, 1320, 1440, 1560, 1620;
0, 60, 180, 300, 360, 462, 522, 546, 606, 630, 642, 690, 726, 762, 810, 822, 846, 906, 930, 990, 1092, 1152, 1272, 1392, 1452;
0, 42, 66, 90, 132, 210, 252, 276, 300, 342, 480, 522, 546, 570, 612, 750, 792, 816, 840, 882, 960, 1002, 1026, 1050, 1092;
0, 42, 66, 90, 132, 210, 252, 276, 300, 342, 780, 822, 846, 870, 912, 1350, 1392, 1416, 1440, 1482, 1560, 1602, 1626, 1650, 1692;
0, 42, 66, 90, 132, 300, 342, 366, 390, 432, 570, 612, 636, 660, 702, 840, 882, 906, 930, 972, 1140, 1182, 1206, 1230, 1272;
0, 42, 66, 90, 132, 360, 402, 426, 450, 492, 570, 612, 636, 660, 702, 780, 822, 846, 870, 912, 1140, 1182, 1206, 1230, 1272;
0, 42, 66, 90, 132, 570, 612, 636, 660, 702, 780, 822, 846, 870, 912, 990, 1032, 1056, 1080, 1122, 1560, 1602, 1626, 1650, 1692;
0, 30, 42, 54, 84, 180, 210, 222, 234, 264, 420, 450, 462, 474, 504, 660, 690, 702, 714, 744, 840, 870, 882, 894, 924;

Теперь программа обрабатывает 41 теоретический паттерн.

Здесь уже показанный выше паттерн с наименьшим диметром 924.
Вполне возможно, что это не минимальный диаметр.
Поищу дальше.

А знаете ли вы разницу между теоретическими паттернами для ассоциативного квадрата Стенли и для симметричной 25-ки?
Теоретический паттерн для ассоциативного квадрата Стенли всегда является теоретическим паттерном для симметричной 25-ки.
А вот обратное неверно.
Например, ни из одного теоретического паттерна с минимальным диаметром 420 для симметричной 25-ки ассоциативный квадрат Стенли не составляется.

И ещё одно приближение для паттерна с меньшим диаметром

[0, 60, 126, 186, 228, 288, 330, 390, 420, 456, 516, 546, 648, 750, 780, 840, 876, 906, 966, 1008, 1068, 1110, 1170, 1236, 1296]
10694203879858206163: [0, 4, 24, 70, 126, 144, 186, 228, 240, 276, 288, 304, 306, 330, 390, 408, 420, 444, 456, 466, 478, 484, 516,
546, 630, 736, 750, 780, 808, 826, 828, 840, 856, 1008, 1044, 1110, 1170, 1174, 1186, 1188, 1296]
q=18

В кортеже из 41 последовательного простого числа содержатся 18 чисел нужных для построения ассоциативного квадрата Стенли, вот они

0, 126, 186, 228, 288, 330, 390, 420, 456, 516, 546, 750, 780, 840, 1008, 1110, 1170, 1296

Никак не находятся менее дырявые квадраты.

Проверка построения квадрата Стенли для показанного паттерна

0  60  420  780  840
126  186  546  906  966
228  288  648  1008  1068
330  390  750  1110  1170
456  516  876  1236  1296

Всё верно.

Нашла ещё 65 теоретических паттернов для ассоциативного квадрата Стенли 5-го порядка.
Теперь у меня их стало 106 штук.

Показываю все, отсортированы по диамтеру

0, 36, 78, 120, 156, 240, 276, 318, 330, 360, 366, 396, 408, 420, 450, 456, 486, 498, 540, 576, 660, 696, 738, 780, 816
0, 12, 132, 210, 222, 252, 264, 300, 312, 342, 390, 402, 432, 462, 474, 522, 552, 564, 600, 612, 642, 654, 732, 852, 864
0, 42, 126, 210, 252, 270, 312, 330, 372, 390, 396, 432, 456, 480, 516, 522, 540, 582, 600, 642, 660, 702, 786, 870, 912
0, 30, 42, 54, 84, 180, 210, 222, 234, 264, 420, 450, 462, 474, 504, 660, 690, 702, 714, 744, 840, 870, 882, 894, 924
0, 30, 120, 210, 240, 264, 294, 342, 372, 384, 420, 450, 462, 474, 504, 540, 552, 582, 630, 660, 684, 714, 804, 894, 924
0, 36, 78, 120, 156, 330, 366, 408, 420, 450, 456, 486, 498, 510, 540, 546, 576, 588, 630, 666, 840, 876, 918, 960, 996
0, 30, 114, 150, 180, 198, 228, 264, 348, 378, 390, 420, 504, 588, 618, 630, 660, 744, 780, 810, 828, 858, 894, 978, 1008
0, 12, 90, 168, 180, 210, 222, 300, 378, 390, 420, 432, 510, 588, 600, 630, 642, 720, 798, 810, 840, 852, 930, 1008, 1020
0, 12, 90, 168, 180, 300, 312, 390, 420, 432, 468, 480, 510, 540, 552, 588, 600, 630, 708, 720, 840, 852, 930, 1008, 1020
0, 30, 90, 150, 180, 378, 408, 420, 450, 462, 468, 492, 510, 528, 552, 558, 570, 600, 612, 642, 840, 870, 930, 990, 1020
0, 30, 180, 210, 240, 330, 336, 360, 366, 390, 462, 492, 516, 540, 570, 642, 666, 672, 696, 702, 792, 822, 852, 1002, 1032
0, 42, 126, 210, 252, 330, 372, 390, 432, 450, 456, 492, 516, 540, 576, 582, 600, 642, 660, 702, 780, 822, 906, 990, 1032
0, 30, 108, 186, 210, 216, 240, 318, 396, 420, 426, 450, 528, 606, 630, 636, 660, 738, 816, 840, 846, 870, 948, 1026, 1056
0, 30, 114, 180, 198, 210, 228, 294, 378, 408, 420, 450, 534, 618, 648, 660, 690, 774, 840, 858, 870, 888, 954, 1038, 1068
0, 30, 204, 240, 270, 330, 360, 378, 408, 420, 444, 450, 534, 618, 624, 648, 660, 690, 708, 738, 798, 828, 864, 1038, 1068
0, 30, 120, 210, 240, 342, 372, 420, 450, 462, 498, 528, 540, 552, 582, 618, 630, 660, 708, 738, 840, 870, 960, 1050, 1080
0, 42, 120, 198, 240, 330, 372, 420, 450, 462, 510, 528, 540, 552, 570, 618, 630, 660, 708, 750, 840, 882, 960, 1038, 1080
0, 42, 66, 90, 132, 210, 252, 276, 300, 342, 480, 522, 546, 570, 612, 750, 792, 816, 840, 882, 960, 1002, 1026, 1050, 1092
0, 6, 66, 126, 132, 330, 336, 396, 456, 462, 480, 486, 546, 606, 612, 630, 636, 696, 756, 762, 960, 966, 1026, 1086, 1092
0, 30, 240, 252, 282, 306, 336, 360, 390, 450, 480, 492, 546, 600, 612, 642, 702, 732, 756, 786, 810, 840, 852, 1062, 1092
0, 30, 90, 150, 180, 294, 324, 384, 444, 462, 474, 492, 552, 612, 630, 642, 660, 720, 780, 810, 924, 954, 1014, 1074, 1104
0, 12, 132, 252, 264, 330, 342, 420, 432, 462, 510, 522, 552, 582, 594, 642, 672, 684, 762, 774, 840, 852, 972, 1092, 1104
0, 24, 132, 210, 234, 240, 264, 342, 420, 444, 450, 474, 552, 630, 654, 660, 684, 762, 840, 864, 870, 894, 972, 1080, 1104
0, 54, 132, 210, 264, 330, 384, 420, 462, 474, 510, 540, 552, 564, 594, 630, 642, 684, 720, 774, 840, 894, 972, 1050, 1104
0, 30, 156, 180, 210, 282, 312, 336, 420, 450, 462, 492, 576, 660, 690, 702, 732, 816, 840, 870, 942, 972, 996, 1122, 1152
0, 42, 156, 180, 222, 270, 312, 336, 420, 450, 462, 492, 576, 660, 690, 702, 732, 816, 840, 882, 930, 972, 996, 1110, 1152
0, 30, 78, 126, 156, 180, 210, 258, 306, 336, 510, 540, 588, 636, 666, 840, 870, 918, 966, 996, 1020, 1050, 1098, 1146, 1176
0, 48, 174, 300, 330, 348, 378, 420, 468, 504, 510, 558, 594, 630, 678, 684, 720, 768, 810, 840, 858, 888, 1014, 1140, 1188
0, 30, 180, 294, 324, 330, 360, 420, 450, 474, 546, 576, 600, 624, 654, 726, 750, 780, 840, 870, 876, 906, 1020, 1170, 1200
0, 60, 156, 240, 252, 300, 312, 396, 450, 492, 510, 552, 606, 660, 702, 720, 762, 816, 900, 912, 960, 972, 1056, 1152, 1212
0, 60, 144, 228, 288, 330, 390, 474, 480, 540, 558, 618, 624, 630, 690, 708, 768, 774, 858, 918, 960, 1020, 1104, 1188, 1248
0, 12, 90, 168, 180, 330, 342, 420, 498, 510, 540, 552, 630, 708, 720, 750, 762, 840, 918, 930, 1080, 1092, 1170, 1248, 1260
0, 42, 120, 180, 198, 222, 240, 300, 378, 420, 510, 552, 630, 708, 750, 840, 882, 960, 1020, 1038, 1062, 1080, 1140, 1218, 1260
0, 42, 180, 240, 282, 318, 360, 420, 450, 492, 558, 600, 630, 660, 702, 768, 810, 840, 900, 942, 978, 1020, 1080, 1218, 1260
0, 48, 90, 120, 132, 168, 180, 210, 252, 300, 540, 588, 630, 672, 720, 960, 1008, 1050, 1080, 1092, 1128, 1140, 1170, 1212, 1260
0, 42, 66, 90, 132, 300, 342, 366, 390, 432, 570, 612, 636, 660, 702, 840, 882, 906, 930, 972, 1140, 1182, 1206, 1230, 1272
0, 42, 66, 90, 132, 360, 402, 426, 450, 492, 570, 612, 636, 660, 702, 780, 822, 846, 870, 912, 1140, 1182, 1206, 1230, 1272
0, 12, 132, 180, 192, 252, 264, 312, 432, 444, 510, 522, 642, 762, 774, 840, 852, 972, 1020, 1032, 1092, 1104, 1152, 1272, 1284
0, 30, 180, 252, 282, 330, 360, 432, 462, 492, 582, 612, 642, 672, 702, 792, 822, 852, 924, 954, 1002, 1032, 1104, 1254, 1284
0, 30, 210, 234, 264, 390, 420, 432, 444, 462, 624, 630, 642, 654, 660, 822, 840, 852, 864, 894, 1020, 1050, 1074, 1254, 1284
0, 60, 126, 186, 228, 288, 330, 390, 420, 456, 516, 546, 648, 750, 780, 840, 876, 906, 966, 1008, 1068, 1110, 1170, 1236, 1296
0, 60, 168, 228, 234, 294, 300, 360, 420, 468, 528, 588, 654, 720, 780, 840, 888, 948, 1008, 1014, 1074, 1080, 1140, 1248, 1308
0, 60, 72, 132, 210, 270, 348, 408, 420, 450, 480, 522, 660, 798, 840, 870, 900, 912, 972, 1050, 1110, 1188, 1248, 1260, 1320
0, 12, 60, 72, 210, 270, 408, 420, 450, 462, 468, 480, 660, 840, 852, 858, 870, 900, 912, 1050, 1110, 1248, 1260, 1308, 1320
0, 30, 120, 198, 210, 228, 240, 318, 408, 438, 540, 570, 660, 750, 780, 882, 912, 1002, 1080, 1092, 1110, 1122, 1200, 1290, 1320
0, 42, 120, 198, 210, 240, 252, 330, 408, 450, 540, 582, 660, 738, 780, 870, 912, 990, 1068, 1080, 1110, 1122, 1200, 1278, 1320
0, 12, 132, 210, 222, 252, 264, 342, 462, 474, 540, 552, 672, 792, 804, 870, 882, 1002, 1080, 1092, 1122, 1134, 1212, 1332, 1344
0, 30, 120, 132, 162, 210, 240, 252, 342, 372, 552, 582, 672, 762, 792, 972, 1002, 1092, 1104, 1134, 1182, 1212, 1224, 1314, 1344
0, 30, 210, 324, 354, 390, 420, 462, 492, 534, 600, 630, 672, 714, 744, 810, 852, 882, 924, 954, 990, 1020, 1134, 1314, 1344
0, 6, 168, 330, 336, 390, 396, 510, 516, 558, 630, 636, 678, 720, 726, 798, 840, 846, 960, 966, 1020, 1026, 1188, 1350, 1356
0, 36, 168, 300, 336, 390, 426, 510, 546, 558, 630, 666, 678, 690, 726, 798, 810, 846, 930, 966, 1020, 1056, 1188, 1320, 1356
0, 30, 84, 138, 168, 210, 240, 294, 348, 378, 600, 630, 684, 738, 768, 990, 1020, 1074, 1128, 1158, 1200, 1230, 1284, 1338, 1368
0, 60, 78, 138, 270, 330, 420, 462, 498, 522, 540, 600, 690, 780, 840, 858, 882, 918, 960, 1050, 1110, 1242, 1302, 1320, 1380
0, 60, 210, 270, 276, 336, 342, 402, 420, 552, 612, 630, 696, 762, 780, 840, 972, 990, 1050, 1056, 1116, 1122, 1182, 1332, 1392
0, 30, 150, 270, 300, 462, 492, 546, 576, 612, 630, 660, 696, 732, 762, 780, 816, 846, 900, 930, 1092, 1122, 1242, 1362, 1392
0, 60, 180, 240, 252, 312, 324, 384, 450, 504, 564, 630, 702, 774, 840, 900, 954, 1020, 1080, 1092, 1152, 1164, 1224, 1344, 1404
0, 30, 162, 294, 324, 330, 360, 492, 540, 570, 624, 654, 702, 750, 780, 834, 864, 912, 1044, 1074, 1080, 1110, 1242, 1374, 1404
0, 30, 210, 294, 324, 390, 420, 492, 504, 522, 684, 690, 702, 714, 720, 882, 900, 912, 984, 1014, 1080, 1110, 1194, 1374, 1404
0, 30, 210, 324, 354, 390, 420, 492, 522, 534, 660, 690, 702, 714, 744, 870, 882, 912, 984, 1014, 1050, 1080, 1194, 1374, 1404
0, 30, 240, 318, 348, 450, 474, 480, 504, 558, 630, 660, 714, 768, 798, 870, 924, 948, 954, 978, 1080, 1110, 1188, 1398, 1428
0, 60, 180, 300, 360, 462, 522, 546, 606, 630, 642, 690, 726, 762, 810, 822, 846, 906, 930, 990, 1092, 1152, 1272, 1392, 1452
0, 30, 126, 210, 222, 240, 252, 336, 432, 462, 600, 630, 726, 822, 852, 990, 1020, 1116, 1200, 1212, 1230, 1242, 1326, 1422, 1452
0, 30, 180, 252, 282, 330, 360, 432, 546, 576, 582, 612, 726, 840, 870, 876, 906, 1020, 1092, 1122, 1170, 1200, 1272, 1422, 1452
0, 30, 210, 270, 300, 390, 420, 480, 534, 564, 660, 690, 744, 798, 828, 924, 954, 1008, 1068, 1098, 1188, 1218, 1278, 1458, 1488
0, 30, 210, 390, 408, 420, 438, 534, 564, 618, 660, 690, 744, 798, 828, 870, 924, 954, 1050, 1068, 1080, 1098, 1278, 1458, 1488
0, 60, 66, 126, 336, 396, 420, 486, 606, 666, 672, 732, 756, 780, 840, 846, 906, 1026, 1092, 1116, 1176, 1386, 1446, 1452, 1512
0, 60, 210, 270, 336, 396, 420, 462, 522, 630, 672, 732, 756, 780, 840, 882, 990, 1050, 1092, 1116, 1176, 1242, 1302, 1452, 1512
0, 30, 210, 390, 420, 432, 462, 546, 576, 642, 660, 690, 756, 822, 852, 870, 936, 966, 1050, 1080, 1092, 1122, 1302, 1482, 1512
0, 30, 210, 390, 420, 462, 492, 546, 576, 630, 660, 672, 756, 840, 852, 882, 936, 966, 1020, 1050, 1092, 1122, 1302, 1482, 1512
0, 30, 240, 252, 282, 450, 480, 492, 516, 546, 702, 732, 756, 780, 810, 966, 996, 1020, 1032, 1062, 1230, 1260, 1272, 1482, 1512
0, 30, 240, 360, 390, 450, 480, 516, 546, 600, 672, 702, 756, 810, 840, 912, 966, 996, 1032, 1062, 1122, 1152, 1272, 1482, 1512
0, 30, 240, 450, 462, 480, 492, 516, 546, 570, 600, 702, 756, 810, 912, 942, 966, 996, 1020, 1032, 1050, 1062, 1272, 1482, 1512
0, 30, 168, 210, 240, 306, 336, 378, 516, 546, 600, 630, 768, 906, 936, 990, 1020, 1158, 1200, 1230, 1296, 1326, 1368, 1506, 1536
0, 30, 198, 210, 240, 366, 396, 408, 576, 600, 606, 630, 798, 966, 990, 996, 1020, 1188, 1200, 1230, 1356, 1386, 1398, 1566, 1596
0, 60, 168, 180, 228, 300, 348, 360, 468, 528, 630, 690, 810, 930, 990, 1092, 1152, 1260, 1272, 1320, 1392, 1440, 1452, 1560, 1620
0, 60, 180, 300, 336, 360, 396, 516, 630, 636, 690, 696, 810, 924, 930, 984, 990, 1104, 1224, 1260, 1284, 1320, 1440, 1560, 1620
0, 30, 210, 276, 306, 390, 420, 486, 600, 630, 666, 696, 810, 924, 954, 990, 1020, 1134, 1200, 1230, 1314, 1344, 1410, 1590, 1620
0, 30, 210, 336, 366, 390, 420, 546, 600, 630, 726, 756, 810, 864, 894, 990, 1020, 1074, 1200, 1230, 1254, 1284, 1410, 1590, 1620
0, 30, 210, 390, 402, 420, 432, 600, 612, 630, 792, 798, 810, 822, 828, 990, 1008, 1020, 1188, 1200, 1218, 1230, 1410, 1590, 1620
0, 30, 210, 390, 420, 462, 492, 600, 630, 672, 738, 768, 810, 852, 882, 948, 990, 1020, 1128, 1158, 1200, 1230, 1410, 1590, 1620
0, 30, 210, 390, 420, 474, 504, 600, 630, 684, 726, 756, 810, 864, 894, 936, 990, 1020, 1116, 1146, 1200, 1230, 1410, 1590, 1620
0, 60, 120, 180, 396, 420, 456, 540, 672, 732, 780, 792, 816, 840, 852, 900, 960, 1092, 1176, 1212, 1236, 1452, 1512, 1572, 1632
0, 60, 126, 186, 396, 420, 456, 546, 666, 726, 780, 792, 816, 840, 852, 906, 966, 1086, 1176, 1212, 1236, 1446, 1506, 1572, 1632
0, 60, 162, 222, 396, 420, 456, 582, 630, 690, 780, 792, 816, 840, 852, 942, 1002, 1050, 1176, 1212, 1236, 1410, 1470, 1572, 1632
0, 60, 132, 192, 402, 420, 462, 552, 672, 732, 780, 804, 822, 840, 864, 912, 972, 1092, 1182, 1224, 1242, 1452, 1512, 1584, 1644
0, 60, 210, 270, 402, 420, 462, 594, 630, 654, 780, 804, 822, 840, 864, 990, 1014, 1050, 1182, 1224, 1242, 1374, 1434, 1584, 1644
0, 42, 66, 90, 132, 210, 252, 276, 300, 342, 780, 822, 846, 870, 912, 1350, 1392, 1416, 1440, 1482, 1560, 1602, 1626, 1650, 1692
0, 42, 66, 90, 132, 570, 612, 636, 660, 702, 780, 822, 846, 870, 912, 990, 1032, 1056, 1080, 1122, 1560, 1602, 1626, 1650, 1692
0, 60, 156, 216, 408, 450, 468, 606, 660, 720, 816, 840, 858, 876, 900, 996, 1056, 1110, 1248, 1266, 1308, 1500, 1560, 1656, 1716
0, 60, 198, 258, 408, 450, 468, 618, 648, 678, 816, 840, 858, 876, 900, 1038, 1068, 1098, 1248, 1266, 1308, 1458, 1518, 1656, 1716
0, 60, 210, 270, 408, 450, 468, 606, 660, 666, 816, 840, 858, 876, 900, 1050, 1056, 1110, 1248, 1266, 1308, 1446, 1506, 1656, 1716
0, 60, 270, 330, 408, 450, 468, 546, 606, 720, 816, 840, 858, 876, 900, 996, 1110, 1170, 1248, 1266, 1308, 1386, 1446, 1656, 1716
0, 60, 192, 252, 420, 462, 522, 612, 732, 780, 792, 840, 882, 924, 972, 984, 1032, 1152, 1242, 1302, 1344, 1512, 1572, 1704, 1764
0, 60, 234, 294, 420, 462, 522, 654, 690, 750, 780, 840, 882, 924, 984, 1014, 1074, 1110, 1242, 1302, 1344, 1470, 1530, 1704, 1764
0, 60, 270, 330, 420, 462, 522, 654, 690, 714, 780, 840, 882, 924, 984, 1050, 1074, 1110, 1242, 1302, 1344, 1434, 1494, 1704, 1764
0, 54, 60, 114, 450, 462, 504, 522, 840, 870, 894, 900, 912, 924, 930, 954, 984, 1302, 1320, 1362, 1374, 1710, 1764, 1770, 1824
0, 60, 210, 270, 450, 462, 522, 660, 714, 774, 840, 900, 912, 924, 984, 1050, 1110, 1164, 1302, 1362, 1374, 1554, 1614, 1764, 1824
0, 60, 150, 210, 450, 474, 534, 600, 798, 840, 858, 900, 924, 948, 990, 1008, 1050, 1248, 1314, 1374, 1398, 1638, 1698, 1788, 1848
0, 60, 210, 270, 450, 474, 534, 660, 738, 798, 840, 900, 924, 948, 1008, 1050, 1110, 1188, 1314, 1374, 1398, 1578, 1638, 1788, 1848
0, 60, 264, 324, 450, 474, 534, 684, 714, 744, 840, 900, 924, 948, 1008, 1104, 1134, 1164, 1314, 1374, 1398, 1524, 1584, 1788, 1848
0, 60, 126, 186, 420, 528, 546, 588, 780, 840, 906, 930, 948, 966, 990, 1056, 1116, 1308, 1350, 1368, 1476, 1710, 1770, 1836, 1896
0, 60, 258, 318, 420, 528, 588, 678, 780, 798, 840, 858, 948, 1038, 1056, 1098, 1116, 1218, 1308, 1368, 1476, 1578, 1638, 1836, 1896
0, 42, 60, 102, 450, 492, 516, 576, 840, 882, 900, 942, 966, 990, 1032, 1050, 1092, 1356, 1416, 1440, 1482, 1830, 1872, 1890, 1932
0, 18, 60, 78, 450, 468, 534, 594, 840, 858, 900, 918, 984, 1050, 1068, 1110, 1128, 1374, 1434, 1500, 1518, 1890, 1908, 1950, 1968
0, 60, 210, 270, 450, 534, 594, 660, 840, 858, 900, 918, 984, 1050, 1068, 1110, 1128, 1308, 1374, 1434, 1518, 1698, 1758, 1908, 1968
0, 60, 270, 330, 450, 534, 594, 720, 798, 840, 858, 900, 984, 1068, 1110, 1128, 1170, 1248, 1374, 1434, 1518, 1638, 1698, 1908, 1968

Наименьший диаметр на данный момент имеет паттерн

0, 36, 78, 120, 156, 240, 276, 318, 330, 360, 366, 396, 408, 420, 450, 456, 486, 498, 540, 576, 660, 696, 738, 780, 816

Вполне возможно, что это не минимальный диаметр.
Требуется подтверждение, а для этого надо продолжать поиск.

Сейчас проверю паттерн с наименьшим диаметром 816 на построение ассоциативного квадрата Стенли.

Вот ассоциативный квадрат Стенли

0  36  78  120  156
240  276  318  360  396
330  366  408  450  486
420  456  498  540  576
660  696  738  780  816

Индекс квадрата равен 2040.

Всё верно.

Теперь надо искать минимальный диаметр в интервале (420,816).

Только что программа выдала теоретический паттерн для ассоциативного квадрата Стенли 5-го порядка с диаметром 780

0, 30, 126, 156, 180, 210, 240, 294, 306, 324, 330, 360, 390, 420, 450, 456, 474, 486, 540, 570, 600, 624, 654, 750, 780

Теперь минимальный диаметр надо искать в интервале (420, 780).
Всё меньше остаётся кандидатов на минимальный диаметр, если учесть что диаметр здесь всегда кратен 12.

Сейчас проверю на построение ассоциативного квадрата Стенли этот паттерн.

Вот

0  30  180  330  360
126  156  306  456  486
210  240  390  540  570
294  324  474  624  654
420  450  600  750  780

Индекс квадрата S=1950.

Приближение для паттерна с большим диаметром

[0, 60, 270, 330, 408, 450, 468, 546, 606, 720, 816, 840, 858, 876, 900, 996, 1110, 1170, 1248, 1266, 1308, 1386, 1446, 1656, 1716]
10694234342360706013: [0, 6, 60, 84, 118, 270, 330, 340, 408, 444, 468, 486, 510, 526, 546, 606, 634, 664, 706, 756, 804, 816, 844, 858, 900, 940, 1018, 1110, 1120, 1134, 1170, 1200, 1210, 1218, 1248, 1276, 1308, 1386, 1428, 1446, 1486, 1516, 1564, 1590, 1668, 1716]
q=18
Тоже 7 "дырок".

Проверка построения ассоциативного квадрата Стенли

0  60  450  840  900
270  330  720  1110  1170
408  468  858  1248  1308
546  606  996  1386  1446
816  876  1266  1656  1716

Индекс квадрата s=4290.

Вчера нашла ещё 60 теоретических паттернов для ассоциативного квадрата Стенли.

Показываю все, не отсортированы по диаметру

0, 6, 48, 90, 96, 240, 246, 288, 330, 336, 750, 756, 798, 840, 846, 1260, 1266, 1308, 1350, 1356, 1500, 1506, 1548, 1590, 1596
0, 6, 66, 126, 132, 300, 306, 366, 426, 432, 780, 786, 846, 906, 912, 1260, 1266, 1326, 1386, 1392, 1560, 1566, 1626, 1686, 1692
0, 6, 108, 210, 216, 270, 276, 378, 480, 486, 630, 636, 738, 840, 846, 990, 996, 1098, 1200, 1206, 1260, 1266, 1368, 1470, 1476
0, 6, 126, 246, 252, 390, 396, 516, 636, 642, 720, 726, 846, 966, 972, 1050, 1056, 1176, 1296, 1302, 1440, 1446, 1566, 1686, 1692
0, 6, 138, 210, 216, 270, 276, 348, 480, 486, 630, 636, 768, 900, 906, 1050, 1056, 1188, 1260, 1266, 1320, 1326, 1398, 1530, 1536
0, 6, 168, 330, 336, 540, 546, 630, 636, 708, 720, 726, 798, 870, 876, 888, 960, 966, 1050, 1056, 1260, 1266, 1428, 1590, 1596
0, 6, 198, 210, 216, 390, 396, 408, 600, 606, 630, 636, 828, 1020, 1026, 1050, 1056, 1248, 1260, 1266, 1440, 1446, 1458, 1650, 1656
0, 6, 300, 330, 336, 540, 546, 594, 600, 630, 750, 756, 840, 924, 930, 1050, 1080, 1086, 1134, 1140, 1344, 1350, 1380, 1674, 1680
0, 6, 300, 390, 396, 510, 516, 594, 600, 630, 636, 690, 810, 930, 984, 990, 1020, 1026, 1104, 1110, 1224, 1230, 1320, 1614, 1620
0, 6, 300, 390, 396, 594, 600, 690, 720, 726, 984, 990, 1020, 1050, 1056, 1314, 1320, 1350, 1440, 1446, 1644, 1650, 1740, 2034, 2040
0, 6, 300, 540, 546, 594, 600, 630, 636, 720, 726, 840, 930, 1020, 1134, 1140, 1224, 1230, 1260, 1266, 1314, 1320, 1560, 1854, 1860
0, 12, 42, 72, 84, 270, 282, 312, 342, 354, 660, 672, 702, 732, 744, 1050, 1062, 1092, 1122, 1134, 1320, 1332, 1362, 1392, 1404
0, 12, 90, 168, 180, 330, 342, 420, 498, 510, 750, 762, 840, 918, 930, 1170, 1182, 1260, 1338, 1350, 1500, 1512, 1590, 1668, 1680
0, 12, 90, 168, 180, 420, 432, 510, 588, 600, 750, 762, 840, 918, 930, 1080, 1092, 1170, 1248, 1260, 1500, 1512, 1590, 1668, 1680
0, 12, 132, 210, 222, 252, 264, 342, 462, 474, 720, 732, 852, 972, 984, 1230, 1242, 1362, 1440, 1452, 1482, 1494, 1572, 1692, 1704
0, 12, 132, 252, 264, 330, 342, 462, 582, 594, 750, 762, 882, 1002, 1014, 1170, 1182, 1302, 1422, 1434, 1500, 1512, 1632, 1752, 1764
0, 12, 132, 252, 264, 450, 462, 582, 702, 714, 750, 762, 882, 1002, 1014, 1050, 1062, 1182, 1302, 1314, 1500, 1512, 1632, 1752, 1764
0, 12, 210, 270, 282, 408, 420, 480, 660, 672, 678, 690, 870, 1050, 1062, 1068, 1080, 1260, 1320, 1332, 1458, 1470, 1530, 1728, 1740
0, 12, 210, 390, 402, 408, 420, 600, 630, 642, 798, 810, 840, 870, 882, 1038, 1050, 1080, 1260, 1272, 1278, 1290, 1470, 1668, 1680
0, 12, 252, 450, 462, 492, 504, 660, 672, 702, 870, 882, 912, 942, 954, 1122, 1152, 1164, 1320, 1332, 1362, 1374, 1572, 1812, 1824
0, 18, 84, 150, 168, 300, 318, 384, 450, 468, 780, 798, 864, 930, 948, 1260, 1278, 1344, 1410, 1428, 1560, 1578, 1644, 1710, 1728
0, 18, 198, 210, 228, 378, 396, 408, 588, 606, 660, 678, 858, 1038, 1056, 1110, 1128, 1308, 1320, 1338, 1488, 1506, 1518, 1698, 1716
0, 18, 198, 270, 288, 378, 396, 468, 648, 660, 666, 678, 858, 1038, 1050, 1056, 1068, 1248, 1320, 1338, 1428, 1446, 1518, 1698, 1716
0, 12, 90, 102, 132, 222, 252, 264, 300, 312, 342, 354, 432, 510, 522, 552, 564, 600, 612, 642, 732, 762, 774, 852, 864
0, 18, 30, 48, 198, 228, 378, 396, 408, 420, 426, 438, 618, 798, 810, 816, 828, 840, 858, 1008, 1038, 1188, 1206, 1218, 1236
0, 18, 150, 168, 198, 348, 378, 390, 396, 408, 528, 546, 588, 630, 648, 768, 780, 786, 798, 828, 978, 1008, 1026, 1158, 1176
0, 24, 210, 222, 234, 390, 414, 420, 432, 444, 570, 594, 612, 630, 654, 780, 792, 804, 810, 834, 990, 1002, 1014, 1200, 1224
0, 30, 84, 90, 114, 150, 174, 180, 234, 264, 462, 492, 552, 612, 642, 840, 870, 924, 930, 954, 990, 1014, 1020, 1074, 1104
0, 30, 78, 108, 120, 198, 210, 240, 288, 318, 420, 450, 540, 630, 660, 762, 792, 840, 870, 882, 960, 972, 1002, 1050, 1080
0, 30, 126, 156, 180, 210, 240, 294, 306, 324, 330, 360, 390, 420, 450, 456, 474, 486, 540, 570, 600, 624, 654, 750, 780
0, 30, 126, 156, 180, 306, 330, 360, 378, 408, 456, 486, 558, 630, 660, 708, 738, 756, 786, 810, 936, 960, 990, 1086, 1116
0, 30, 90, 120, 204, 294, 378, 408, 420, 450, 468, 498, 624, 750, 780, 798, 828, 840, 870, 954, 1044, 1128, 1158, 1218, 1248
0, 30, 60, 90, 198, 210, 228, 270, 336, 366, 390, 396, 408, 420, 426, 450, 480, 546, 588, 606, 618, 726, 756, 786, 816
0, 30, 60, 90, 210, 270, 324, 354, 390, 420, 450, 480, 534, 588, 618, 648, 678, 714, 744, 798, 858, 978, 1008, 1038, 1068
0, 30, 72, 102, 210, 282, 366, 390, 396, 420, 462, 492, 576, 660, 690, 732, 756, 762, 786, 870, 942, 1050, 1080, 1122, 1152
0, 30, 96, 126, 210, 306, 378, 390, 408, 420, 486, 516, 588, 660, 690, 756, 768, 786, 798, 870, 966, 1050, 1080, 1146, 1176
0, 30, 198, 210, 228, 324, 354, 390, 408, 420, 450, 480, 534, 588, 618, 648, 660, 678, 714, 744, 840, 858, 870, 1038, 1068
0, 30, 150, 180, 240, 306, 336, 390, 450, 462, 480, 492, 546, 600, 612, 630, 642, 702, 756, 786, 852, 912, 942, 1062, 1092
0, 30, 168, 198, 240, 408, 450, 474, 480, 504, 618, 648, 714, 780, 810, 924, 948, 954, 978, 1020, 1188, 1230, 1260, 1398, 1428
0, 30, 186, 216, 240, 408, 426, 438, 450, 480, 630, 636, 648, 660, 666, 816, 846, 858, 870, 888, 1056, 1080, 1110, 1266, 1296
0, 36, 90, 126, 228, 318, 360, 396, 420, 456, 510, 546, 588, 630, 666, 720, 756, 780, 816, 858, 948, 1050, 1086, 1140, 1176
0, 30, 42, 72, 120, 150, 198, 228, 240, 270, 330, 372, 450, 528, 570, 630, 660, 672, 702, 750, 780, 828, 858, 870, 900
0, 42, 90, 120, 132, 198, 210, 240, 288, 300, 330, 342, 420, 498, 510, 540, 552, 600, 630, 642, 708, 720, 750, 798, 840
0, 42, 60, 102, 126, 186, 210, 252, 270, 312, 390, 432, 516, 600, 642, 720, 762, 780, 822, 846, 906, 930, 972, 990, 1032
0, 42, 120, 126, 162, 210, 246, 252, 330, 372, 390, 432, 516, 600, 642, 660, 702, 780, 786, 822, 870, 906, 912, 990, 1032
0, 42, 120, 126, 162, 210, 246, 252, 330, 372, 450, 492, 576, 660, 702, 780, 822, 900, 906, 942, 990, 1026, 1032, 1110, 1152
0, 42, 60, 102, 186, 246, 270, 312, 330, 372, 390, 432, 456, 480, 522, 540, 582, 600, 642, 666, 726, 810, 852, 870, 912
0, 42, 216, 330, 372, 390, 420, 432, 462, 510, 546, 552, 636, 720, 726, 762, 810, 840, 852, 882, 900, 942, 1056, 1230, 1272
0, 30, 42, 72, 240, 270, 420, 438, 462, 468, 480, 510, 660, 810, 840, 852, 858, 882, 900, 1050, 1080, 1248, 1278, 1290, 1320
0, 54, 120, 132, 174, 210, 252, 264, 330, 384, 420, 474, 552, 630, 684, 720, 774, 840, 852, 894, 930, 972, 984, 1050, 1104
0, 60, 198, 240, 300, 336, 396, 438, 450, 510, 576, 636, 648, 660, 720, 786, 846, 858, 900, 960, 996, 1056, 1098, 1236, 1296
0, 60, 102, 162, 210, 312, 360, 420, 462, 480, 522, 540, 690, 840, 858, 900, 918, 960, 1020, 1068, 1170, 1218, 1278, 1320, 1380
0, 60, 126, 186, 210, 228, 288, 330, 336, 360, 390, 420, 438, 456, 486, 516, 540, 546, 588, 648, 666, 690, 750, 816, 876
0, 60, 210, 234, 294, 360, 420, 444, 462, 522, 594, 654, 672, 690, 750, 822, 882, 900, 924, 984, 1050, 1110, 1134, 1284, 1344
0, 60, 228, 330, 390, 396, 456, 480, 540, 558, 630, 690, 708, 726, 786, 858, 876, 936, 960, 1020, 1026, 1086, 1188, 1356, 1416
0, 60, 150, 210, 240, 306, 366, 390, 420, 462, 480, 522, 546, 570, 612, 630, 672, 702, 726, 786, 852, 882, 942, 1032, 1092
0, 60, 222, 240, 282, 306, 366, 390, 420, 450, 462, 480, 546, 612, 630, 642, 672, 702, 726, 786, 810, 852, 870, 1032, 1092
0, 66, 150, 234, 270, 300, 336, 420, 480, 504, 546, 570, 630, 690, 714, 756, 780, 840, 924, 960, 990, 1026, 1110, 1194, 1260
0, 66, 156, 210, 246, 276, 312, 366, 420, 456, 486, 522, 576, 630, 666, 696, 732, 786, 840, 876, 906, 942, 996, 1086, 1152
0, 30, 66, 96, 180, 210, 294, 324, 360, 390, 420, 486, 600, 714, 780, 810, 840, 876, 906, 990, 1020, 1104, 1134, 1170, 1200

Последний паттерн нравится, диаметр кругленький такой.

Здесь уже показанный выше паттерн с диаметром 780.
Это у меня пока наименьший диаметр.

Меньший диаметр надо искать в интервале (420, 780).
Есть ли он?

Вчера на форуме Math Help Planet открыла тему
https://mathhelpplanet.com/viewtopic.php?f=48&t=83941

Н-и-ч-е-г-о!

tomtitsin(=gris), похоже, совсем на меня рассердился и не пишет в моих темах, может, даже и не читает их.
Ну, как говорит поговорка, на сердитых воду возят :)

Итак, господа, задача поиска теоретического (допустимого) паттерна с минимальным диаметром для ассоциативного квадрата Стенли 5-го порядка открытая.

Надо посмотреть тему на форуме dxdy.ru "Антимагические квадраты".
Я там искала для каких-то квадратов теоретические паттерны, сейчас не помню уже, очень давно это было.

Покажу картинку и формулы построения ассоциативного квадрата Стенли 5-го порядка (из сообщения на форуме MHP)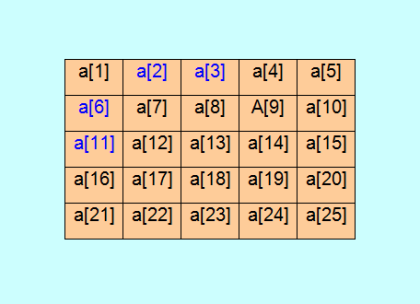

a[1]=0;
a[2] перебор от 6 до … с шагом 6;
a[3] перебор от a[2]+6 до … с шагом 6;
a[4]=2*a[3]-a[2];
a[5]=a[4]+a[2];
a[6] перебор от 6 до … с шагом 6;
a[11] перебор от a[6]+6 до … с шагом 6;
a[16]=2*a[11]-a[6];
a[21]=a[16]+a[6];
a[7]=a[6]+a[2]; a[8]=a[6]+a[3]; a[9]=a[6]+a[4]; a[10]=a[6]+a[5];
a[12]=a[11]+a[2]; a[13]=a[11]+a[3]; a[14]=a[11]+a[4]; a[15]=a[11]+a[5];
a[17]=a[16]+a[2]; a[18]=a[16]+a[3]; a[19]=a[16]+a[4]; a[20]=a[16]+a[5];
a[22]=a[21]+a[2]; a[23]=a[21]+a[3]; a[24]=a[21]+a[4]; a[25]=a[21]+a[5];

Это готовый алгоритм построения искомого квадрата.
Осталось закодировать; у меня, конечно, программа на PARI/GP.

Тут надо играться с зависимыми переменными, их всего четыре; на картинке они выделены синим цветом.
Написано "перебор от 6 до ... с шагом 6", вот от конечной точки перебора зависит, как долго будет работать программа.

Так вот, требуется построить ассоциативный квадрат Стенли 5-го порядка с минимальным элементом a[25].
Этот минимум, как уже сказано, находится в интервале (420, 780), а может быть, даже в интервале (420, 780].
То есть вполне возможно, что минимум равен 780.
Но требуется это подтвердить.
Или же опровергнуть, найдя меньший диаметр теоретического паттерна.
Элемент a[25] и есть диаметр теоретического паттерна квадрата Стенли, изображённого на картинке.

Для моего поиска теоретический паттерн с минимальным диаметром для ассоциативного квадрата Стенли 5-го порядка и не нужен; наверняка для этого паттерна решение надо искать в заоблачных высотах.

Просто интересно узнать теоретический паттерн с минимальным диаметром, для полноты теоретической картины.

У меня поиск сейчас идёт по 106 теоретическим паттернам, а новый проход запущу по 166 теоретическим паттернам.

Не забываем: любой теоретический паттерн для ассоциативного квадрата Стенли 5-го порядка - это теоретический паттерн симметричной 25-ки.
Таким образом, мы ищем не только ассоциативный квадрат Стенли 5-го порядка из последовательных простых чисел, но и симметричный 25-tuplet.

Ещё немного покрутила программу, нашла 131 новый теоретический паттерн для ассоциативного квадрата Стенли 5-го порядка.
Но меньшего диаметра не нашлось.

Теперь у меня 297 теоретических паттернов в базе.
Отсортировала их по диаметру.
Показываю несколько первых и последних

0, 30, 126, 156, 180, 210, 240, 294, 306, 324, 330, 360, 390, 420, 450, 456, 474, 486, 540, 570, 600, 624, 654, 750, 780
0, 36, 78, 120, 156, 240, 276, 318, 330, 360, 366, 396, 408, 420, 450, 456, 486, 498, 540, 576, 660, 696, 738, 780, 816
0, 30, 60, 90, 198, 210, 228, 270, 336, 366, 390, 396, 408, 420, 426, 450, 480, 546, 588, 606, 618, 726, 756, 786, 816
0, 42, 90, 120, 132, 198, 210, 240, 288, 300, 330, 342, 420, 498, 510, 540, 552, 600, 630, 642, 708, 720, 750, 798, 840
0, 30, 84, 90, 96, 114, 120, 126, 180, 210, 330, 414, 420, 426, 510, 630, 660, 714, 720, 726, 744, 750, 756, 810, 840
0, 12, 132, 210, 222, 252, 264, 300, 312, 342, 390, 402, 432, 462, 474, 522, 552, 564, 600, 612, 642, 654, 732, 852, 864
0, 12, 90, 102, 132, 222, 252, 264, 300, 312, 342, 354, 432, 510, 522, 552, 564, 600, 612, 642, 732, 762, 774, 852, 864
0, 60, 126, 186, 210, 228, 288, 330, 336, 360, 390, 420, 438, 456, 486, 516, 540, 546, 588, 648, 666, 690, 750, 816, 876
0, 30, 42, 72, 120, 150, 198, 228, 240, 270, 330, 372, 450, 528, 570, 630, 660, 672, 702, 750, 780, 828, 858, 870, 900
0, 30, 72, 102, 120, 150, 168, 198, 240, 270, 330, 402, 450, 498, 570, 630, 660, 702, 732, 750, 780, 798, 828, 870, 900
0, 42, 126, 210, 252, 270, 312, 330, 372, 390, 396, 432, 456, 480, 516, 522, 540, 582, 600, 642, 660, 702, 786, 870, 912
0, 42, 60, 102, 186, 246, 270, 312, 330, 372, 390, 432, 456, 480, 522, 540, 582, 600, 642, 666, 726, 810, 852, 870, 912
0, 42, 90, 132, 210, 246, 252, 330, 336, 372, 420, 450, 456, 462, 492, 540, 576, 582, 660, 666, 702, 780, 822, 870, 912
0, 30, 42, 54, 84, 180, 210, 222, 234, 264, 420, 450, 462, 474, 504, 660, 690, 702, 714, 744, 840, 870, 882, 894, 924
0, 30, 120, 210, 240, 264, 294, 342, 372, 384, 420, 450, 462, 474, 504, 540, 552, 582, 630, 660, 684, 714, 804, 894, 924
0, 66, 90, 150, 156, 210, 216, 276, 300, 318, 366, 408, 468, 528, 570, 618, 636, 660, 720, 726, 780, 786, 846, 870, 936
0, 30, 72, 102, 162, 192, 252, 282, 324, 330, 354, 402, 492, 582, 630, 654, 660, 702, 732, 792, 822, 882, 912, 954, 984
0, 36, 78, 120, 156, 330, 366, 408, 420, 450, 456, 486, 498, 510, 540, 546, 576, 588, 630, 666, 840, 876, 918, 960, 996
0, 30, 78, 108, 168, 198, 258, 288, 330, 336, 366, 408, 498, 588, 630, 660, 666, 708, 738, 798, 828, 888, 918, 966, 996
0, 30, 114, 150, 180, 198, 228, 264, 348, 378, 390, 420, 504, 588, 618, 630, 660, 744, 780, 810, 828, 858, 894, 978, 1008
. . . . . . . . .
0, 30, 36, 66, 330, 360, 540, 576, 624, 654, 660, 690, 870, 1050, 1080, 1086, 1116, 1164, 1200, 1380, 1410, 1674, 1704, 1710, 1740
0, 42, 120, 162, 330, 450, 540, 582, 618, 660, 738, 780, 870, 960, 1002, 1080, 1122, 1158, 1200, 1290, 1410, 1578, 1620, 1698, 1740
0, 60, 192, 252, 420, 462, 522, 612, 732, 780, 792, 840, 882, 924, 972, 984, 1032, 1152, 1242, 1302, 1344, 1512, 1572, 1704, 1764
0, 60, 234, 294, 420, 462, 522, 654, 690, 750, 780, 840, 882, 924, 984, 1014, 1074, 1110, 1242, 1302, 1344, 1470, 1530, 1704, 1764
0, 60, 270, 330, 420, 462, 522, 654, 690, 714, 780, 840, 882, 924, 984, 1050, 1074, 1110, 1242, 1302, 1344, 1434, 1494, 1704, 1764
0, 12, 132, 252, 264, 330, 342, 462, 582, 594, 750, 762, 882, 1002, 1014, 1170, 1182, 1302, 1422, 1434, 1500, 1512, 1632, 1752, 1764
0, 12, 132, 252, 264, 450, 462, 582, 702, 714, 750, 762, 882, 1002, 1014, 1050, 1062, 1182, 1302, 1314, 1500, 1512, 1632, 1752, 1764
0, 54, 120, 174, 342, 462, 540, 594, 630, 684, 750, 804, 882, 960, 1014, 1080, 1134, 1170, 1224, 1302, 1422, 1590, 1644, 1710, 1764
0, 54, 60, 114, 450, 462, 504, 522, 840, 870, 894, 900, 912, 924, 930, 954, 984, 1302, 1320, 1362, 1374, 1710, 1764, 1770, 1824
0, 60, 210, 270, 450, 462, 522, 660, 714, 774, 840, 900, 912, 924, 984, 1050, 1110, 1164, 1302, 1362, 1374, 1554, 1614, 1764, 1824
0, 12, 252, 450, 462, 492, 504, 660, 672, 702, 870, 882, 912, 942, 954, 1122, 1152, 1164, 1320, 1332, 1362, 1374, 1572, 1812, 1824
0, 60, 150, 210, 450, 474, 534, 600, 798, 840, 858, 900, 924, 948, 990, 1008, 1050, 1248, 1314, 1374, 1398, 1638, 1698, 1788, 1848
0, 60, 210, 270, 450, 474, 534, 660, 738, 798, 840, 900, 924, 948, 1008, 1050, 1110, 1188, 1314, 1374, 1398, 1578, 1638, 1788, 1848
0, 60, 264, 324, 450, 474, 534, 684, 714, 744, 840, 900, 924, 948, 1008, 1104, 1134, 1164, 1314, 1374, 1398, 1524, 1584, 1788, 1848
0, 6, 300, 540, 546, 594, 600, 630, 636, 720, 726, 840, 930, 1020, 1134, 1140, 1224, 1230, 1260, 1266, 1314, 1320, 1560, 1854, 1860
0, 60, 126, 186, 420, 528, 546, 588, 780, 840, 906, 930, 948, 966, 990, 1056, 1116, 1308, 1350, 1368, 1476, 1710, 1770, 1836, 1896
0, 60, 258, 318, 420, 528, 588, 678, 780, 798, 840, 858, 948, 1038, 1056, 1098, 1116, 1218, 1308, 1368, 1476, 1578, 1638, 1836, 1896
0, 42, 60, 102, 450, 492, 516, 576, 840, 882, 900, 942, 966, 990, 1032, 1050, 1092, 1356, 1416, 1440, 1482, 1830, 1872, 1890, 1932
0, 18, 60, 78, 450, 468, 534, 594, 840, 858, 900, 918, 984, 1050, 1068, 1110, 1128, 1374, 1434, 1500, 1518, 1890, 1908, 1950, 1968
0, 60, 210, 270, 450, 534, 594, 660, 840, 858, 900, 918, 984, 1050, 1068, 1110, 1128, 1308, 1374, 1434, 1518, 1698, 1758, 1908, 1968
0, 60, 270, 330, 450, 534, 594, 720, 798, 840, 858, 900, 984, 1068, 1110, 1128, 1170, 1248, 1374, 1434, 1518, 1638, 1698, 1908, 1968
0, 6, 300, 390, 396, 594, 600, 690, 720, 726, 984, 990, 1020, 1050, 1056, 1314, 1320, 1350, 1440, 1446, 1644, 1650, 1740, 2034, 2040

Всё, мне хватит теоретических паттернов для поиска.
Останавливаю эту программу.

Минимальный диаметр 780 требует подтверждения.

Наконец-то - прогресс!

Найдено приближение к ассоциативному квадрату Стенли 5-го порядка с 6 "дырками"

[0, 42, 66, 90, 132, 570, 612, 636, 660, 702, 780, 822, 846, 870, 912, 990, 1032, 1056, 1080, 1122, 1560, 1602, 1626, 1650, 1692]
10694212627299772357: [0, 12, 36, 52, 54, 66, 90, 106, 112, 132, 180, 226, 232, 282, 316, 420, 430, 502, 510, 556, 612, 624, 660, 666, 702, 780, 822, 826, 846, 870, 880, 882, 912, 922, 946, 954, 990, 1074, 1080, 1170, 1212, 1294, 1312, 1330, 1350, 1366, 1414, 1456, 1536, 1560, 1596, 1602, 1624, 1626, 1650, 1672, 1674, 1692]
q=19

Отлично!
В кортеже из 58 последовательных простых чисел содержатся 19 чисел нужных для построения квадрата, вот они

0, 66, 90, 132, 612, 660, 702, 780, 822, 846, 870, 912, 990, 1080, 1560, 1602, 1626, 1650, 1692

А 6 нужных чисел нет, это и есть 6 "дырок".

Полный ассоциативный квадрат Стенли, построенный из элементов эталонного паттерна

0  42  66  90  132
570  612  636  660  702
780  822  846  870  912
990  1032  1056  1080  1122
1560  1602  1626  1650  1692

Этот же квадрат с 6 "дырками", построенный из реальных простых чисел

10694212627299772357+

0 □ 66 90 132
□ 612 □ 660 702
780 822 846 870 912
990 □ □ 1080 □
1560 1602 1626 1650 1692

Из этого квадрата известным преобразованием получается идеальный квадрат 5-го порядка из простых чисел с 6 "дырками".