В верней части спектра повторяющихся элементов не так много, вот они

20480
(113606005040995458557503277, 182296896240610437979344523, 115425488755349926544942401, 116153282241091713768993923)
20928
(35177522975676261059455117, 35177522978707156770893257, 29160708297427537140420197, 29160708297927561014690117, 17490495362879648375327603)
20929
(17490495338610650964683617, 29160708296643285620492453, 17490495348429370139588543)
20936
(17490495316473328050997483, 35177522982585888405234667, 17490495360008256622612117)
20943
(29160708272256677576003917, 17490495313447144375597297)
25024
(31166313192908601903539717, 35177522977226676119563577, 39188732783437909144252453, 29160708300321013017987773)
25026
(17490495328400109170605277, 39188732784841368565334717)
25056
(39188732785809900150737813, 17490495338029902848916343)
29120
(35177522982446153187714923, 39188732782822878129230183, 17490495339574353706235167)
29121
(29160708291566123573506747, 17490495345750375550121347)
32767
(1006882292528806742267, 3954328349097827424397, 4896552110116770789773, 6751407944109046348063, 7768326730875185894807,
19252814175273852997757, 154787380396512840656507, 901985248981556228168767)

В нижней части спектра повторяющихся элементов очень много.

Вот как выглядит верхняя часть спектра на картинке, полученной программой Захара Пехтерева



Голубые квадратики - найденные элементы.
Как видим, заполненность в этой части спектра очень низкая.
Всего в этой части спектра 12769 элементов, найдено 203 элемента, то есть 1,6%.

Поигралась

(06:43) gp > i=32724; print(hammingweight(i))
11
(06:44) gp > i=32725; print(hammingweight(i))
12
(06:45) gp > i=32728; print(hammingweight(i))
11
(06:47) gp > i=32767; print(hammingweight(i))
15

Кажется, всё правильно, valids получается, если прибавить 2.

Это я для картинки gris для valids11 и valids12, вот этой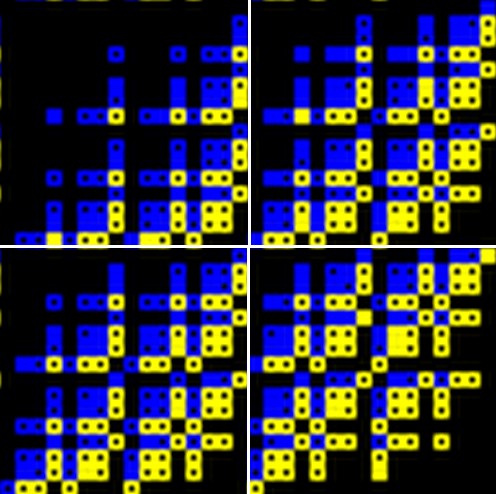



Меня интересуют два подквадрата 16х16: левый нижний и правый верхний.
В этих подквадратах спектр имеет совершенно одинаковую структуру.
Начну с левого нижнего подквадрата.

Если не ошиблась, элементы спектра в нижней строке этого подквадрата будут такие:
32704, 32705, 32706, ..., 32718, 32719.
Можно вычислить valids для этих элементов спектра и сравнить с тем, что есть на картинке.
Напомню: синие квадратики соответствуют valids11, а жёлтые - valids12.

Вот что мы имеем в нижней строке левого нижнего подквадрата 16х16 - это значения valids

(13:53) gp > \r hamming.txt
11
12
12
13
12
13
13
14
12
13
13
14
13
14
14
15

Всё совпадает с картинкой.

Обратите внимание: ни один из элементов, соответствующих valids11 и valids12, не найден, в том числе элемент 32704 с valids11 (самый первый элемент в строке).
Чёрные точки стоят в этих квадратиках.

А теперь посмотрим на верхний правый подквадрат 16х16.
Там соответствующий элемент в нижней строке найден!
Чудеса!

Ну, надо вычислить этот элемент и посмотреть на него.
Подозреваю, что при том же значении valids=11, у этого элемента расположение единичек менее сложное, чем у соответствующего элемента в нижнем левом подквадрате.

Цитата

Если не ошиблась, элементы спектра в нижней строке этого подквадрата будут такие:
32704, 32705, 32706, ..., 32718, 32719.

Смотрела, смотрела на подквадраты и засомневалась: кажется, я не в том подквадрате элементы вычислила :(

А если взять в том подквадрате элементы: 32736, 32737, ..., 32751, тогда valids не такие получаются

(13:55) gp > \r hamming.txt
12
13
13
14
13
14
14
15
13
14
14
15
14
15
15
16

Вот вычислила valids в последней строке правого нижнего подквадрата 16х16

(14:50) gp > \r hamming.txt
32752, 13
32753, 14
32754, 14
32755, 15
32756, 14
32757, 15
32758, 15
32759, 16
32760, 14
32761, 15
32762, 15
32763, 16
32764, 15
32765, 16
32766, 16
32767, 17

Там самый первый элемент в нижней строке жёлтый, но для него valids=13, а не 12.
А для последнего элемента в строке 32767 valids правильный, равен 17.
Может, valids и для первого элемента правильный?

Где я ошибаюсь?

Кажется, поняла.

gris,
вы мне какой фрагмент прислали в письме?
Похоже, это не правый нижний квадрат 32х32, а соседний с ним.
Тогда всё получается.
Вот так

(14:51) gp > \r hamming.txt
32704, 11
32705, 12
32706, 12
32707, 13
32708, 12
32709, 13
32710, 13
32711, 14
32712, 12
32713, 13
32714, 13
32715, 14
32716, 13
32717, 14
32718, 14
32719, 15

Новая порция приближений подоспела.
Две великолепные девяточки

33171918115595274250795493: [0, 6, 24, 36, 66, 86, 110, 114, 120, 126, 138, 140, 176, 216, 218, 224, 240]
33171918115595274250795493: [0, 0, 0, 0, 0, 2, 20, 0, 0, 0, -12, -16, 2, 12, 2, -10, 0]
9

Элемент спектра

31168
33171918115595274250795493

29160708312349982827599227: [0, 6, 24, 36, 66, 84, 90, 104, 120, 152, 156, 162, 192, 194, 222, 230, 240]
29160708312349982827599227: [0, 0, 0, 0, 0, 0, 0, -10, 0, 26, 6, 6, 18, -10, 6, -4, 0]
9

Элемент спектра

32384
29160708312349982827599227

В новой порции нашлись такие элементы в верхней части спектра (включая показанные выше)

27009
31166313213024034796114297
32384
29160708312349982827599227
21427
29160708312382889354060167
26817
31166313213694041217834387
28292
29160708312499077381078553
20880
29160708312511610135396923
22664
31166313214220834479891603
31168
33171918115595274250795493

Очень хорошо!
Немножко заполняется верхняя часть спектра.

Возвращаюсь к спектру.
Опять у меня нестыковка.

Если синий квадратик в начале нижней строки подквадрата 16х16 соответствует элементу 32704, тогда почему он отмечен как не найденный (с чёрной точкой в центре)?

Элемент 32704 в спектре г. Петухова имеется

196693822643: [0,6,24,36,66,84,90,114,120,126,128,146,156,180,204,224,240], num15=32704, valids=11

Он с valids=11, то есть как раз соответствует синему квадратику в начале нижней строки.

Вот всё про элемент 32704

(16:33) gp > i=32704;print(digits(i,2))
[1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0]

Полный вектор совпадений в приближении к ключевой 17-ке

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1

В общем, никак у меня ничего не получается с этим фрагментом спектра :(

Новое пополнение в верхней части спектра

21504
23636390722848944404513
29696
23742019073392601426063
21472
6996831518512829222308907
24640
8310934448149399127743037
20513
8374462415559198508805537
29360
17490495409209166614810913
25219
17490495409702483292390093
20680
17490495412142071216793437
22912
17490495412006785538646363
27328
17490495412598159168712883
28865
17490495412538243477897903
24771
17490495414628925668078927
26816
17490495415442712150289343
25284
17490495416010812664194813
24712
17490495415919426969454473

А вот всего пятёрочка

24534231702472585232093: [0, 6, 26, 36, 56, 78, 86, 114, 128, 146, 164, 174, 194, 206, 224, 230, 240]
24534231702472585232093: [0, 0, 2, 0, -10, -6, -4, 0, 8, 20, 14, 18, 20, 2, 8, -4, 0]
5

Приближение дало элемент в верхней части спектра

20736
24534231702472585232093

Отлично!

Это приближение найдено жадным алгоритмом в диапазоне, следующем за последней ключевой 17-й Врублевского

19252814175273852997757: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240

Жадный алгоритм бежит!
Пока ещё находимся в области 23-значных чисел.

Элементы спектра от10000 по 19999 включительно буду считать средней частью спектра.
Покажу частично эту часть спектра

10116
31166313210129284130193337
10178
6996831480423943761899123
10240
23477948197032819066097
10241
6611561319937268018830697
10257
7105888316344768821991597
10321
118024751204427738064939387
10368
29160708309664535699845423
10369
33171918106602081799500727
10377
17490495396561611110010257
10384
33171918111160134329813723
10416
31166313206882945036279267
10489
29160708307206237967080703
10496
152075089287347067317628127
10497
206856957718685950901638813
10624
29160708307066838574100247
10625
31166313205940055567039443
10688
17490495351821179225664213
10689
(17490495323565442810722023, 17490495360585559428396653)
10704
31166313205488963265859923
10705
31166313213572557384954417
10912
2048815063513005672595013
11222
33171918077387969736931007
11392
17490495374534998383397217
11394
29160708303253958520679523
11400
29160708309124648487801657
. . . . . . . 
19329
33171918109172232277452953
19392
(17490495330773818395446077, 29160708296679559895490737)
19394
6996831512412583443031517
19456
21312567010880122384273
19457
23900461599208670706943
19584
33171918113062823312307763
19589
17490495377591853590523923
19591
29160708311485617488241707
19649
33171918110197583665668653
19713
22949806444312873427927
19840
17490495377789334671840743
19841
17490495387810191611219897
19850
17490495408993233226593927
19904
35177522977608209142210353
19914
17490495389557692209463583
19960
29160708272918093039764423
19967
464754942522208950860461
19984
21999151289416153949917

Повторяющихся элементов фактически больше, просто я в последнее время повторяющиеся элементы приписываю к спектру, а не вставляю в спектр.
Всего в средней части спектра 10000 элементов.

Вот посмотрите на повторяемость элемента 16384 (это центральный элемент спектра)

16384
(6448770903449657375849351
6597664577066374487544493
6643325303642167673535713
6748543499664647895421673
6784277981332659817037221
6808100969111334536683993
6883540430410471252856143
6937142152912489356477383
7038389850971857035978401
7064198087732088000493891
7125740806160331109042661
7179342528662349253934081
7228973753201255029459027
7262722985887710925244371
7270663981813935865213013
7330221451260622560244141
7473159377932671102675271
7475144626914227209915271
7483085622840452156413223
7494997116729789442712633
111422624583770097016844063
112306373816456552944583441
116673134730907276063428137
117244972469704394520382141
122963349857675579717835451
123067320355638692047379357
123275261351564917142966833
128317830502775871200435611
133412384902968381555634271
135803706356119968040096421
139494659033810460140209931
139702600029736685010666307
173742268085325708792996781
178709471530329745084307447
189195789914227155088801391
195634757342936090916675143
198302329563401221721090971
209800485686095750077572357
210628352926929756087236141
221390627057771834818330711
227829594486480770847401887
228289520731388551907374151
281660564389191444550190023
288759517066881936731599703
296858322234387991185904021
312256050577547650361921087
315855519540883674620261311
317055342528662349350381393
321754649230795491897213253
321854634479777048180361751
333952849606545351774766901)

51 приближений найдено для этого элемента спектра!
Впечатляет.

При этом обратный элемент 16383 не найден.
Немудрено, посмотрите на вектор совпадений этого элемента

16383
[1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
16384
[1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]

Очень редкий элемент 16383, почти не встречается в природе :)

gris прислал новый фрагмент, который я рассматривала выше



Спасибо!
Очень красиво :)

Добавлены ещё оранжевые квадратики, которые соответствуют элементам спектра с valids>14.

Теперь буду разбираться.
Напомню: мне интересны два подквадрата 16х16 - правый верхний и левый нижний, назову эти квадраты А и В соответственно.

Нижняя строка в квадрате В содержит элементы спектра:
32704, 32705, 32706, ..., 32718, 32719.

Для этих элементов спектра имеем следующие valids

(14:51) gp > \r hamming.txt
32704, 11
32705, 12
32706, 12
32707, 13
32708, 12
32709, 13
32710, 13
32711, 14
32712, 12
32713, 13
32714, 13
32715, 14
32716, 13
32717, 14
32718, 14
32719, 15

Синие квадратики - элементы спектра с valids11, жёлтые квадратики - элементы спектра с valids12.
Если в квадратике стоит чёрная точка - соответствующий элемент спектра не найден.

Итак, в нижней строке квадрата B найден только элемент 32704 (среди синих, жёлтых и оранжевых элементов).
В нижней строке квадрата А полное совпадение.

Жадный алгоритм находит элемент спектра 16384 очень часто.
Вот например только что найден

161120522610137851164476587: [0, 6, 12, 22, 34, 36, 40, 60, 76, 84, 102, 106, 130, 142, 144, 172, 240]
161120522610137851164476587: [0, 0, -12, -14, -32, -48, -50, -54, -44, -42, -48, -50, -44, -62, -72, -62, 0]
3

Эх, нашёл бы этот алгоритм обратный элемент 16383 :)
А ещё лучше - элемент 32767 :))

Вот ещё один в другом диапазоне

24692674228288919286121: [0, 6, 10, 46, 48, 72, 108, 130, 150, 156, 190, 202, 210, 220, 226, 228, 240]
24692674228288919286121: [0, 0, -14, 10, -18, -12, 18, 16, 30, 30, 40, 46, 36, 16, 10, -6, 0]
3

Г. Петухов писал в сообщении
https://dxdy.ru/post1631796.html#p1631796

Забавно что это напрямую биномиальные коэффициенты:

Хи-хи-хи!

И чего же в этом забавного?
Что такое, например, количество элементов с valids1?
Очевидно, что это число сочетаний из 15 по 1.
Далее: количество элементов с valids2 – это число сочетаний из 15 по 2.
И так далее.

Ах, какая симпатичная десяточка только что найдена!

33171918116191392743166503: [0, 6, 24, 36, 66, 68, 90, 114, 120, 128, 150, 170,176, 188, 204, 224, 240]
33171918116191392743166503: [0, 0, 0, 0, 0, -16, 0, 0, 0, 2, 0, 14, 2, -16, -12, -10, 0]
10

Какой элемент спектра даёт?
Сейчас посчитаю.

Ого!
31648.
Такого элемента у меня ещё не было в спектре, самая верхушка.

Покажу самую верхушку спектра - элементы >30000

30143
492033133172934312048911
30180
31166313200166785765249513
30335
58240441875215114770637
30656
17490495352896582872805337
30720
19939398453808522071547
30860
29160708306359004343243663
30900
29160708308457625390286623
31168
33171918115595274250795493
31648
33171918116191392743166503
31737
714173405945839792853267
31743
548934853673670454695071
31995
628588812289345578755011
32190
447839391652547767407917
32243
346660334189390590675127
32254
87073837458351874240477
32384
29160708312349982827599227
32499
567059251329873879997787
32571
376586558667542501138227
32663
782299017592858073313541
32715
770821085331994725002341
32727
141707126033472669940351
32739
161341697637500999318521
32741
17490495325553024845924787
32753
53166202711423237425917
32761
347681709124158402217151
32767
(1006882292528806742267, 3954328349097827424397, 4896552110116770789773, 6751407944109046348063, 7768326730875185894807,
19252814175273852997757, 154787380396512840656507, 901985248981556228168767)

Добавления в верхнюю часть спектра из новой порции приближений к ключевой 17-ке

22469
31166313214661382163259527
22928
29160708313526431967719327
25536
33171918116116788060892927
24728
31166313215685054446434937
24992
33171918116965182552673063

Возвращаюсь к фрагменту



Вторая снизу строка в квадрате В имеет следующий вид

32448 32449 32450 32451 32452 32453 32454 32455 32456 32457 32458 32459 32460 32461 32462 32463

Сейчас посчитаю valids.

Вот

(20:13) gp > \r hamming.txt
32448, 10
32449, 11
32450, 11
32451, 12
32452, 11
32453, 12
32454, 12
32455, 13
32456, 11
32457, 12
32458, 12
32459, 13
32460, 12
32461, 13
32462, 13
32463, 14

Всё верно.

Теперь посмотрим на второй синий квадратик слева в этой строке, это элемент 32450, он найден.
Да, вот он в спектре г. Петухова

138130789249357: [0,6,24,36,66,84,90,100,120,126,132,154,186,214,216,220,240], num15=32450, valids=11

Посмотрим на вектор совпадений для этого элемента

1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1

А теперь переходим в квадрат А.
Вторая снизу строка в этом квадрате состоит из следующих элементов

28368 28369 28370 28371 28372 28373 28374 28375 28376 28377 28378 28379 28380 28381 28382 28383

Проверим valids

(20:20) gp > \r hamming.txt
28368, 10
28369, 11
28370, 11
28371, 12
28372, 11
28373, 12
28374, 12
28375, 13
28376, 11
28377, 12
28378, 12
28379, 13
28380, 12
28381, 13
28382, 13
28383, 14

Всё в точности совпадает со второй строкой снизу в квадрате В.

Теперь внимание на второй синий квадратик во второй строке снизу в квадрате А !
Элемент, соответствующий этому квадратику, 28370, и он не найден!
Чем же он отличается от соответствующего элемента 32450, который найден?
Ранее я предположила, что причина в разном расположении единичек в векторах совпадений.

Сравним вектора совпадений этих двух элементов

32450
[1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1]
28370
[1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0,1]

Да, конечно, единички (совпадающие элементы) расположены в векторах совпадений по-разному, что совершенно естественно.
Но почему-то вектор совпадений элемента 28370 оказался более сложным, нежели вектор совпадений элемента 32450.
Казалось бы, должно быть наоборот, ведь в векторе совпадений элемента 32450 семь единичек подряд (семь элементов подряд совпадают).

Однако если вы внимательно посмотрите на квадраты А и В, то заметите. что в большинстве случаев найденные и не найденные элементы совпадают (квадратики с точками и квадратики без точек).
И это хорошо!

Сравним ещё пару элементов - один найденный, другой не найденный.
Это второй жёлтенький квадратик во второй строке снизу в квадратах А и В.
В квадрате А этот элемент найден, а в квадрате В не найден.

В квадрате А это элемент 28373.
Да, в спектре г. Петухова этот элемент присутствует

299412336238073: [0,6,24,38,66,84,90,104,120,126,146,156,158,204,224,234,240], num15=28373, valids=12

В квадрате В это элемент 32453, он не найден.

Посмотрим на вектора совпадений этих элементов

28373
[1,1,1,0,1,1,1,0,1,1,0,1,0,1,0,1,1]
32453
[1,1,1,1,1,1,1,0,1,1,0,0,0,1,0,1,1]

Да, здесь можно согласиться, что вектор совпадений элемента 32453 сложнее, чем вектор совпадений элемента 28373.

Интересно: расстояние Хэмминга между элементами 28370 и 32450 равно 2.
Расстояние Хэмминга между элементами 28373 и 32453 тоже равно 2.
Случайность или закономерность?
Может быть, все элементы квадратов А и В связаны именно таким расстоянием Хэмминга между соответствующими элементами?
Это просто предположение.
Надо проверять.

Кстати, в PARI/GP есть функция определения расстояния Хэмминга между двумя заданными строками из нулей и единичек?

Например:
str1="11101110110101011"
str2="11111110110001011"

Я определила расстояние Хэмминга между этими строками визуально.
А можно в PARI/GP определить?

Ну, можно написать эту функцию, если её нет в PARI/GP.

PS. Поигралась

(21:07) gp > str1="01001"; str2="11011"; print(hamming(str1,str2))
  ***   at top-level: ...1001";str2="11011";print(hamming(str1,str2))
  ***                                             ^-------------------
  ***   not a function in function call
(21:48) gp > str1="01001"; print(hamming(str1))
  ***   at top-level: str1="01001";print(hamming(str1))
  ***                                    ^--------------
  ***   not a function in function call
(21:50) gp > i=28370; j=32450; print(hamming(i,j))
  ***   at top-level: i=28370;j=32450;print(hamming(i,j))
  ***                                       ^-------------
  ***   not a function in function call

Похоже, нет такой функции в PARI/GP.
Или просто я не знаю, как её правильно записывать.

Г. Петухов писал в сообщении
https://dxdy.ru/post1631837.html#p1631837

И последнее, отсутствие расстояний 2 и 4, как-то странно.

gris писал в сообщении
https://dxdy.ru/post1631839.html#p1631839

Из забавного: если в векторе совпадений заменить одну единичку на нолик, а один нолик на единичку, то valids не изменится! Помогает понять многое в визуализации оных

Ага, так вот почему в квадратах А и В расстояние Хэмминга между соответствующими элементами равно 2.

И видимо, по этой же причине у г. Петухова отсутствуют расстояния Хэмминга 2 и 4 (у него valids разные).

В том же сообщении г Петухов писал

Максимально нашлась одна цепочка с valids=15, ...

Насколько могу понимать, нашлась 19-ка с минимальным диаметром с 15 правильными элементами, с 4 "дырками".
Ну вот, можно уже поздравить г. Петухова :)
Может, скоро и 19-ка с минимальным диаметром найдётся - не дырявая :))
Если г. Петухов изменит диапазон и перестанет искать приближения там, где полной 19-ки с минимальным диаметром точно нету (по его утверждению!), то вполне вероятно, что и найдёт искомую 19-ку.

А, так он уже перестал искать приближения к 19-ке с минимальным диаметром в диапазоне малых чисел

Таблица num17 досчиталась до 1e15 (num15 до 7e14), 62774 элемента, на этом её остановил.

Ну, слава Богу!

О, хорошее приближение нашлось

17490495420191770142640407: [0, 6, 24, 62, 66, 84, 90, 114, 120, 134, 140, 156, 176, 206, 222, 234, 240]
17490495420191770142640407: [0, 0, 0, 26, 0, 0, 0, 0, 0, 8, -10, 0, 2, 2, 6, 0, 0]
11

Приближение дало уникальный элемент в верхней части спектра

28561
17490495420191770142640407