Ещё одна иллюстрация плотности заполнения спектра приближений к ключевой 17-ке, сделанная gris.
Здесь по 256 элементов в строке.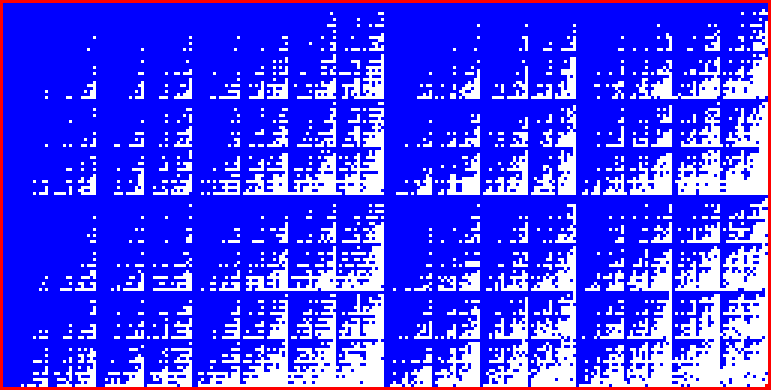



Интересное разделение на секции, такие одинаковые квадраты.
Магические квадраты! :)
Вряд ли такое разделение случайно.
Но проникнуть в эту закономерность непросто.

Белые квадратики - отсутствующие в спектре элементы (на данный момент).
При полном заполнении спектра вся картинка должна стать синей.

PS, Ещё заметила: правая половина картинки сильно похожа на левую половину по структуре заполнения спектра.
То же самое можно сказать про верхнюю и нижнюю половины картинки.

Ой, почитала дискуссию про num15.
Щупаю - мозги на месте ли? :)))

gris писал в сообщении
https://dxdy.ru/post1631342.html#p1631342

Посмотрим на все найденные в недалёком будущем num15. Это числа от 0 до 32767 каждое со своим valids. Количество каждого valids от 0 до 15 вот:
[1, 15, 105, 455, 1365, 3003, 5005, 6435, 6435, 5005, 3003, 1365, 455, 105, 15, 1]

Подчёркиваю:

Количество каждого valids от 0 до 15 вот:

То есть valids есть от 0 до 15.
Глупая шестиклассница (то бишь я) так поняла.

Г. Петухов писал в сообщении
https://dxdy.ru/post1631354.html#p1631354

Кстати для тех что найдено менее примерно половины просматривается "закон" падения количества в 10 раз на каждый valids. А значит valids=15 до 1e15 наверняка не найдётся, не говоря уж про более длинные.
Это например прямая польза от метрики valids, а вот пользы от метрики num15/17 так и не вижу, ни в чём.

Подчёркиваю:

... valids=15 до 1e15 наверняка не найдётся, не говоря уж про более длинные.

Какие такие "более длинные"???
valids=16, valids=17 что ли?
А такие у gris не заявлены.

Разобрались бы gris и г. Петухов с соответствием двух метрик, прежде чем дискутировать!

Цитата из письма gris (это когда г. Петухов выложил первую порцию num15)

Если честно, то я не совсем разбираюсь в обозначении приближений. П выложил таблицу для num17 до 5 е14. Это граница сплошного перебора (брутфорса). Причём фиксируется только первое появление приближения с определённым кодом. там заполненность по кодам меньше половины. А что он имел в виду под таблицей num15 я не знаю. Если двоичные коды для num15 и имеют вид 11***************11, то их можно получить из таблицы для num17 до 5е14, а если *1***************1*, то надо начинать новый расчёт.

Это был его ответ на сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13718

И далее gris продолжил (в следующем письме), цитирую

Вот я тоже посмотрел по его массиву, но там явно меньше половины. А тут да, заполненность будет больше, потому что кортежей больше, а в код края не входят.

Такая вот неразбериха :))

И зачем г, Петухову понадобилось num15?
Да и num17 ведь совершенно незачем, по его же словам.
Какого чёрта тогда считает?!

Я начала искать приближения к ключевой 17-ке задолго до того, как gris опубликовал тему со своей метрикой.
Мне эта метрика понравилась, и я её применяю к своим приближениям к ключевой 17-ке.
Никаких valids у меня нет, никаких num15 тоже нет.
Есть только то, что определил gris в своей метрике для приближений к 19-ке с минимальным диаметром.

Ну, и вот это

Это например прямая польза от метрики valids, а вот пользы от метрики num15/17 так и не вижу, ни в чём.

в комментариях не нуждается.
Только - ха-ха-ха или наоборот (читать справа налево).
Супермен вы наш :)))

А то что весь этот массив можно представить как 15-мерный единичный гиперкуб с расслоением на 15 плоскостей по valids>0 и в общем достаточно случайным (надеюсь) заполнением вершин каждого слоя - тоже откровение? В нём ведь вообще совсем наглядно видны и периоды, и остатки по модулям степеней двойки, и слоистость, и независимость (тоже надеюсь) заполнения вершин каждого слоя от предыдущих слоёв (что напрочь убивает идею предсказания лучших решений по предыдущим), и какие именно вершины считаются близкими и насколько именно (хинт: расстояние Хемминга, а не просто сравнение чисел num15 которое ничего в общем не даёт), и ещё чего-нибудь.

Ах-ах-ах! Про гиперкуб знает, про расстояние Хемминга.
Учитесь, господа!

Если про цепочки с дырками/ошибками, то - оценка вероятностей и по ней оценка когда ждать решение. Но для этого в общем достаточно метрики valids (ну или с добавлением отдельных метрик по каждому месту паттерна).

И где "оценка вероятностей"? И где оценка "когда ждать решение"?
Все прикидки и оценки г. Петухова по 19-ке с любым диаметром абсолютно ничего не дали (по его собственному признанию).
19-ка с минимальным диаметром по оценкам г. Петухова уже должна была найтись.
И где она???

Ядряра начинал считать кэфы, потом частотности.
Что-то всё заглохло.
Есть какие-то "грязные" количества и какие-то "чистые" количества.
Так вот "чистых" примерно в 30 раз меньше, чем "грязных".
Хи-хи-хи!
Очень научная оценка.
Потом Ядряра усомнился в этой оценке и решил посчитать valids18.
Но и это что-то заглохло.
Я очень рада, что всё заглохло: меньше мусору будет в теме о кортежах.

А то что весь этот массив можно представить как 15-мерный единичный гиперкуб с расслоением на 15 плоскостей по valids>0 и в общем достаточно случайным (надеюсь) заполнением вершин каждого слоя - тоже откровение? В нём ведь вообще совсем наглядно видны и периоды, и остатки по модулям степеней двойки, и слоистость, и независимость (тоже надеюсь) заполнения вершин каждого слоя от предыдущих слоёв (что напрочь убивает идею предсказания лучших решений по предыдущим), и какие именно вершины считаются близкими и насколько именно (хинт: расстояние Хемминга, а не просто сравнение чисел num15 которое ничего в общем не даёт), и ещё чего-нибудь.

А ну-ка, gris, представьте!
Чего это вы какие-то плоские глупые картинки рисуете (с подачи глупой шестиклассницы) :))
Вот в гиперкубе мы всё и увидим.
И расстояние Хемминга обязательно посчитайте!
Ибо говорит Супермен

Вот честно, лучше бы проверили что распределение valids=12(13) от valids=11(12) действительно случайно в смысле расстояния Хемминга, это хотя бы осмысленный критерий.

Неплохая десяточка найдена (десять правильных элементов)

17490495401124613011830513: [0, 6, 24, 44, 50, 84, 90, 114, 120, 126, 164, 168, 170, 176, 188, 234, 240]
17490495401124613011830513: [0, 0, 0, 8, -16, 0, 0, 0, 0, 0, 14, 12, -4, -28, -28, 0, 0]
10

Приближение дало оригинальный элемент в верхней части моего спектра

26561
17490495401124613011830513

Обратного элемента 6206 в моём спектре пока нет.

6206
[1,0,0,1,1,0,0,0,0,0,1,1,1,1,1,0,1]
26561
[1,1,1,0,0,1,1,1,1,1,0,0,0,0,0,1,1]

gris писал в сообщении
https://dxdy.ru/post1631393.html#p1631393

ой, я немного перепутал. начал изучать файл d252-num15.5e14valids и споткнулся на строке
822609101533: [0,18,24,36,58,64,90,114,120,126,150,156,186,190,216,234,240], num15=13299, valids=12
А я считаю val=vecsum(digits(13299,2))=10
То есть valids=val+2

Г. Петухов писал в сообщении
https://dxdy.ru/post1631433.html#p1631433

И да, я 2 добавляю чтобы valids отвечало исходному паттерну, а не его подвнутренностям. Все эти игрища с переназваниями укороченных цепочек раздражают.

Ну вот и разобрались :)

Интересно: а почему г. Петухов сразу не сказал gris, что у него что-то не так с valids?
Такой был страшный зуд начать свою убойную критику?
Ну, и начал - с места в карьер.

Кстати, о птичках...
Вы думаете, что г. Петухов только gris мозги промывает?
О! Вы глубоко ошибаетесь!
Почитайте, например, тему Батороева об интервалах между простыми числами.
Мне было очень стыдно, когда я это читала.
И была рада, что не принадлежу этому сообществу, в котором находится такой раздражительный господин.
"Счастье" общения с ним на dxdy.ru для меня давно закончилось.
Спасибо администрации форума!

... а не его подвнутренностям.

Хи-хи-хи!
Вот тут редактор подчеркнул слово "подвнутренностям" красной волнистой линией.
Нет такого слова!
Есть слово "внутренности".
А внутри паттернов находятся подпаттерны, между прочим.

Все эти игрища с переназваниями укороченных цепочек раздражают.

Слово "переназваниями" редактор тоже подчеркнул красной волнистой линией.
Сплошные перлы выдаёт г. Петухов!
Нет слова "переназвание", а есть слово "переименование".

Супермену не мешало бы русский язык подтянуть.
А то просто уши вянут от его перлов!

И пора уже кортежи называть кортежами, а не цепочками.

Г. Петухов писал в сообщении
[url]https://dxdy.ru/post1631433.html#p1631433

... и на hammingweight(i). А последнее это как раз расстояние Хемминга числа от нуля.

В Википедии пишут "Хэмминг"
https://ru.wikipedia.org/wiki/Расстояние_Хэмминга

Цитата из Википедии

Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей: в этом случае расстоянием Хэмминга
d(x,y) между двумя двоичными последовательностями (векторами) x и y длины n называется число позиций, в которых они различны.

Иллюстрация из Википедии


примеры расстояний в двоичном тессеракте: расстояние 1 0110 → 1110, расстояние 3 0100 → 1001

Г. Петухов писал в сообщении
https://dxdy.ru/post1631354.html#p1631354

Интересно посмотреть на картинку отдельно для valids=11 и для valids=12 (остальные или найдены или слишком мало для статистики), вдруг найденные или не найденные как-то кучкуются (и не по периодам, это тривиально).

Картинка для valids=11 и valids=12 показана



Как я понимаю, на картинке показаны все элементы спектра с valids=11 и valids=12 (одни жёлтые, другие синие).
Тогда при чём найденные и не найденные?
Показано для всех элементов спектра с указанными valids.

Г. Петухов писал в сообщении
https://dxdy.ru/post1631366.html#p1631366

Вот честно, лучше бы проверили что распределение valids=12(13) от valids=11(12) действительно случайно в смысле расстояния Хемминга, это хотя бы осмысленный критерий.

Ну, глупая шестиклассница не понимает, что г. Петухов желает проверить :)

gris,
а вы понимаете?

Вот "распределение valids=12 от valids=11" - это как?
Вы на картинке в предыдущем посте что показали?
Не распределение valids=12 от valids=11?

Хорошая восьмёрочка

29160708309723683850331393: [0, 6, 24, 36, 58, 66, 90, 118, 120, 126, 136, 150, 156, 178, 198, 204, 240]
29160708309723683850331393: [0, 0, 0, 0, -8, -18, 0, 4, 0, 0, -14, -6, -18, -26, -18, -30, 0]
8

Приближение дало оригинальный элемент в верхней части моего спектра

29376
29160708309723683850331393

Обратный элемент 3391 в моём спектре пока отсутствует.

3391
[1,0,0,0,1,1,0,1,0,0,1,1,1,1,1,1,1]
29376
[1,1,1,1,0,0,1,0,1,1,0,0,0,0,0,0,1]

Цитата из письма gris

Кстати, о картинке. Если её смотреть покрупнее, то можно увидеть

<изображение>

В этом фрагменте видны синие (11) и желтые(12) квадратики. Если квадратик без чёрной точки в середине, то соответствующий кортеж найден, а с точкой — ожидает боинка:)

Показываю фрагмент спектра по valids11 и valids12, который взяла из сообщения
https://dxdy.ru/post1631364.html#p1631364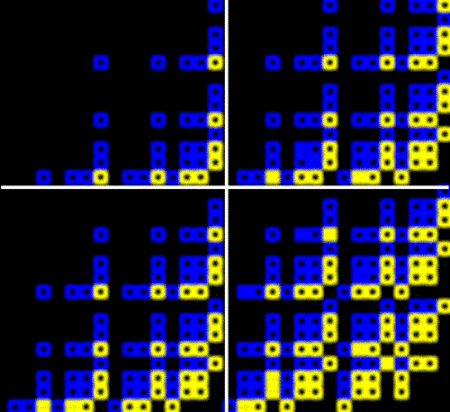



Я провела в этом фрагменте белые линии, которые разделили фрагмент на четыре квадрата 16х16.
К сожалению, сверху фрагмент чуть меньше (на три строки), чем должен быть для полных квадратов 16х16.

Сравните верхний правый подквадрат и левый нижний подквадрат.
Абсолютная похожесть структуры, то есть расположения элементов спектра, соответствующих valids11 и valids12.
Но вот точки в квадратиках (жёлтых и синих) стоят не во всех одинаково в этих двух подквадратах, есть несколько отличий.
И это очень интересно!

Если мне не врут глаза, есть два отличия в жёлтых квадратиках и два отличия в синих квадратиках.
Ну, и ещё не забудем, что верхний подквадрат на три строки укорочен сверху; не знаю, есть ли там отличия в двух синих квадратиках.

Интересно бы вычислить элементы спектра, которые соответствуют двум жёлтым и двум синим квадратикам с различным наличием в них точек.

Кроме того, один жёлтый квадратик без точки в обоих подквадратах.
Вот как: и там, и там найден соответствующий элемент спектра.

PS. Г. Петухов скажет, что нет ничего удивительного в этом факте.
И подведёт научную базу :)

Замечание: кажется, в сообщении https://dxdy.ru/post1631364.html#p1631364 приведена картинка для valids9 и valids10.
Но это описанного выше факта не меняет.

Для valids11 и valids12 показываю фрагмент спектра из письма gris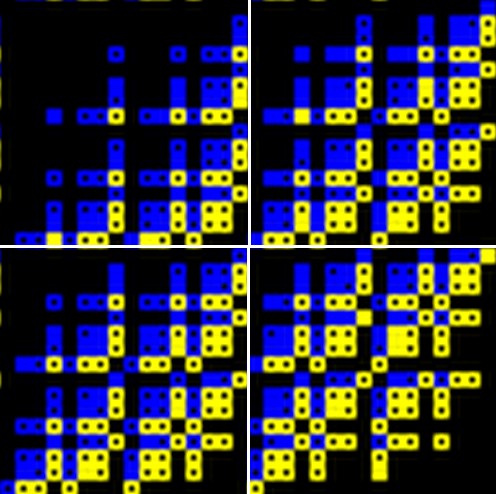



Всё совершенно аналогично для подквадратов 16х16 - правого верхнего и левого нижнего.

Интересно, что здесь жёлтых и синих квадратиков без точки побольше.
Получается, что элементов спектра, соответствующих valids11 и valids12, найдено больше, чем элементов спектра, соответствующих valids9 и valids10.
Ну, возможно, это только в рассматриваемых подквадратах, а во всём спектре не так.

А может быть, gris картинки перепутал?
Или я их перепутала :)

Я тут показала фрагмент из письма, а в письме gris писал

В этом фрагменте видны синие (11) и желтые(12) квадратики. Если квадратик без чёрной точки в середине, то соответствующий кортеж найден, а с точкой — ожидает боинка:)

Вроде как речь идёт о valids11 и valids12.

Если вы посмотрите на весь спектр для valids11 и valids12 в сообщении
https://dxdy.ru/post1631393.html#p1631393
то увидите, что описанная выше закономерность с подквадратами 16х16 имеет место во всём спектре.

Конечно, теоретическое объяснение этому факту может быть найдено (не только г. Петуховым!).
Но в любом случае закономерность интересная, даже если она совсем не удивительная.

Интересно бы вычислить все соответствующие элементы спектра в этих парах подквадратов и посмотреть, почему одни из них найдены одновременно, а другие не одновременно.

gris,
задачка для вас :)

А может быть, в спектре есть ещё пары подквадратов 16х16 с одинаковой структурой?

Вот картинка



Присмотритесь, господа!
Мне кажется, такие пары подквадратов есть.
Но трудно сравнивать, так как очень мелкие жёлтые и синие квадратики.
В увеличенном фрагменте легко было сравнить.

Увеличенный фрагмент - это квадрат 32х32 в правом нижнем углу.
Всего таких квадратов в спектре 32 шт.
И в каждом таком квадрате, кажется, есть аналогичная пара подквадратов 16х16 с одинаковой структурой.

Залетела в голову идея. как быстро добавлять в спектр новые элементы из найденных.
Добавила уже почти все элементы, которые раньше просто приписывала к спектру.

Нашлось несколько оригинальных элементов в верхней части моего спектра

26753
17490495372751298163956077
24708
17490495374138086704603587
24769
17490495376472005256274733
25217
17490495376039954038442213
22657
17490495376494220447919093
25029
17490495376887561751933037
24968
17490495376706664486850217
24816
17490495376576475923039043
25280
17490495378479390108711803
26272
17490495379337693999235337
24705
17490495379424209353582913
29123
29160708305029931259950147
25281
33171918107826401834765053

Очень хорошо.
Закончу вставлять элементы, выложу новый вариант моего спектра.

Самый большой элемент

29123
29160708305029931259950147

Сейчас я попробую его развернуть для проверки.

29160708305029931259950147:
    [  0,  6, 24, 36, 42, 80,104,114,120,126,156,174,176,210,216,234,240]
    [  0,  0,  0,  0,-24, -4, 14,  0,  0,  0,  6, 18,  2,  6,  0,  0,  0]
10

Отличная десяточка!

{29160708305029931259950147, 29160708305029931259950153, 29160708305029931259950171, 29160708305029931259950183,
*29160708305029931259950189, *29160708305029931259950227, *29160708305029931259950251, 29160708305029931259950261,
29160708305029931259950267, 29160708305029931259950273, *29160708305029931259950303, *29160708305029931259950321,
*29160708305029931259950323, *29160708305029931259950357, 29160708305029931259950363, 29160708305029931259950381,
29160708305029931259950387}

Симпатичное приближение с центральной тройкой и с 10 правильными элементами.

Вот ещё нашлись элементы в верхней части спектра

29057
33171918109431326148923387
24784
33171918109731300719840393
24816
17490495376576475923039043
21891
31166313209037508121177777
21184
29160708308780535774102203
20640
17490495393570292427239447
20104
17490495393785237136469243
24961
33171918111623783189381903
24707
31166313211412849561695537
28868
17490495394882377286194863
20868
17490495394659857275665893
20870
17490495395551536442938787
22680
17490495397146067062001777
24801
17490495398356110536055037
24706
17490495398249807976782413
25270
17490495400781791892545583
28808
17490495399290627123133943
20353
29160708310637230260487487

Прекрасно!
Ещё не всё элементы вставила.
Много накопилось приписыванием.

Вот ещё добавились элементы в верхней части спектра

24592
22685735567952239295193
28742
154934277981332659969587143
28850
17490495407539697434637287
20144
17490495407378917235111627
20944
17490495407218192945525613
20480
261312225115767237855130271
28096
17490495402934910075163377
24800
17490495403232650441777067
23680
17490495403902945733947857
20952
17490495403455879821836907
24776
17490495405074885347293967
24817
17490495405655291803633677
25256
17490495405358392067104827
25824
17490495406066797942309023
25232
17490495406392404310766393
26049
17490495406827800322801223
24583
8245421231758043766324733
24467
17490495415487196257707093

Кажется, всё добавила.

Покажу частично географию поиска приближений к ключевой 17-ке

19252814175273060003749
19252814175273117021197
19252814175273133347349
19252814175273144491743
19252814175273157178633
19252814175273225677017
19252814175273245433401
19252814175273319062619
19252814175273458062817
19252814175273859234693
19252814175273936580159
19252814175273936580177
19305628350544247208767
19305628350544371190793
19305628350544435727083
19305628350544516125643
19305628350544660027753
. . . . . . . 
364448350545920001358495567
365248232537772451159722527
365348217786754007290326001
367947834260274469296256643
368247790007219138139468439
368947686750090031662066631
368947686750090031662066641
370847406480739599833639381
370847406480739599833639443
370847406480739599927511423
370947391729721156056429631
371247347476665824867576537
371247347476665824959206899
371647288472592049775151169
371847258970555162289687063
372547155713426055816206869
372647140962407612069296751
373147067207315393230267067
374846816440001848965296537
374846816440001849042301199

Разброс от 23-значных до 27-значных чисел.
Это только для повторяющихся элементов спектра.

Где же на этом огромном поле сидит ключевая 17-ка?
Где-то же сидит!

Выложила на Яндекс.Диск новый вариант спектра приближений к ключевой 17-ке.

Ссылка та же
https://disk.yandex.ru/d/g2qh8m09lmUjMQ

В файле есть строка "Добавления", все элементы спектра, следующие за этой строкой, повторяются.
До этой строки элемента спектра уникальные.

Со спектром г. Петухова для num15 пока не объединяла.
Ранее были добавлены элементы спектра, полученные из массива г. Петухова для num17, и по некоторым другим его приближениям к 19-ке с минимальным диаметром.

Элементы >=20000 буду считать верхней частью спектра.

Показываю частично верхнюю часть спектра на данный момент

20096
29160708304993502476074923
20104
17490495393785237136469243
20144
17490495407378917235111627
20353
29160708310637230260487487
20400
17490495380670356432918203
20480
(113606005040995458557503277, 182296896240610437979344523, 115425488755349926544942401, 116153282241091713768993923)
20481
6931186405967820691854427
20482
6462667646320550987832703
20488
6607590821974155676434523
20544
207684824959519956772200011
20608
29160708303464566211126677
20609
33171918107929848299316637
20610
33171918109317091649785327
20611
29160708303696422616793303
20612
17490495389070882228400177
20613
7387793671725753192985703
20619
17490495379918861441751437
20628
31166313207809034020491267
20640
17490495393570292427239447
20642
17490495387690322986794347
20656
29160708306364404635457133
20657
17490495373936439406650317
20660
33171918112675475303716633
20672
29160708303375583292794523
20673
29160708308580805451655533
20676
33171918106084311936587593
20693
29160708309172627187756297
20712
31166313206641131277663277
20721
31166313206522505366569587
20864
31166313206761383124768667
20866
33171918109221322957229377
20868
17490495394659857275665893
20870
17490495395551536442938787
20872
33171918106266878180711857
20874
29160708303759642732852817
20881
31166313212293719367213393
20928
(35177522975676261059455117, 35177522978707156770893257, 29160708297427537140420197, 29160708297927561014690117, 17490495362879648375327603)
20929
(17490495338610650964683617, 29160708296643285620492453, 17490495348429370139588543)
20930
33171918099805391302714537
20933
35177522983157894282452897
20935
35177522973799712950574063
20936
(17490495316473328050997483, 35177522982585888405234667, 17490495360008256622612117)
20937
17490495336552190469921077
20941
35177522978737350892270523
20943
(29160708272256677576003917, 17490495313447144375597297)
20944
17490495407218192945525613
20952
17490495403455879821836907
20959
52944031235917
20960
17490495363023492304564457
20961
17490495321490927326875657
20965
6996831501471533670212483
20976
17490495329102358379581137
20994
329453513402375321498351431
21120
2569026525774694095205307
21121
33171918107766424756002907
21122
2305965047699181134699857
21129
17490495391879659722052307
21184
29160708308780535774102203
21441
17490495360854355097243813
21442
17490495345160352205396533
21476
29160708300383780600279473
21493
17490495348947836665261353
21697
17490495380976645243597923
21891
31166313209037508121177777
21952
33171918104474687637895883
21953
6996831477659004948266387
22334
10083190144121
22528
135595765360193743167351427
22657
17490495376494220447919093
22680
17490495397146067062001777
. . . . . . . .
27330
29160708306205449319367563
27352
2232102066624229011552853
28096
17490495402934910075163377
28605
961303358077526306301841
28608
39188732785711495079793373
28611
35208513528401
28637
311717602138792979434687
28659
177409982362777824724277
28665
972818417099805969903137
28670
583744157229748086506147
28742
154934277981332659969587143
28800
33171918107214944603287283
28801
17490495399641710247833573
28808
17490495399290627123133943
28816
33171918106828160623211467
28848
17490495378398555390397893
28850
17490495407539697434637287
28864
29160708307805104530393827
28868
17490495394882377286194863
29057
33171918109431326148923387
29073
17490495389692023350615897
29120
(35177522982446153187714923, 39188732782822878129230183, 17490495339574353706235167)
29121
(29160708291566123573506747, 17490495345750375550121347)
29123
29160708305029931259950147
29153
29160708308209725239456837
29158
33171918090410309876227217
29376
29160708309723683850331393
29568
17490495393037272628211863
29687
361025072688751200443641
30143
492033133172934312048911
30180
31166313200166785765249513
30335
58240441875215114770637
30656
17490495352896582872805337
30720
19939398453808522071547
30860
29160708306359004343243663
30900
29160708308457625390286623
31737
714173405945839792853267
31743
548934853673670454695071
31995
628588812289345578755011
32190
447839391652547767407917
32243
346660334189390590675127
32254
87073837458351874240477
32499
567059251329873879997787
32571
376586558667542501138227
32663
782299017592858073313541
32715
770821085331994725002341
32727
141707126033472669940351
32739
161341697637500999318521
32741
17490495325553024845924787
32753
53166202711423237425917
32761
347681709124158402217151
32767
(1006882292528806742267, 3954328349097827424397, 4896552110116770789773, 6751407944109046348063, 7768326730875185894807,
19252814175273852997757, 154787380396512840656507, 901985248981556228168767)

Полностью вы можете посмотреть на Яндекс.Диске по указанной выше ссылке.