Проект gris по кортежу 19-252
Message boards :
Cafe :
Проект gris по кортежу 19-252
Message board moderation
Previous · 1 . . . 9 · 10 · 11 · 12 · 13 · 14 · 15 . . . 54 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот с векторами совпадений 14447 [1,0,1,1,1,0,0,0,0,1,1,0,1,1,1,1,1] 14574 [1,0,1,1,1,0,0,0,1,1,1,0,1,1,1,0,1] 14701 [1,0,1,1,1,0,0,1,0,1,1,0,1,1,0,1,1] 14828 [1,0,1,1,1,0,0,1,1,1,1,0,1,1,0,0,1] 14955 [1,0,1,1,1,0,1,0,1,0,0,1,0,0,1,1,1] 15082 [1,0,1,1,1,0,1,0,1,1,1,0,1,0,1,0,1] 15209 [1,0,1,1,1,0,1,1,0,1,1,0,1,0,0,1,1] 15336 [1,0,1,1,1,0,1,1,1,1,1,0,1,0,0,0,1] 15463 [1,0,1,1,1,1,0,0,0,1,1,0,0,1,1,1,1] 15590 [1,0,1,1,1,1,0,0,1,1,1,0,0,1,1,0,1] 15717 [1,0,1,1,1,1,0,1,0,1,1,0,0,1,0,1,1] 15844 [1,0,1,1,1,1,0,1,1,1,1,0,0,1,0,0,1] 15971 [1,0,1,1,1,1,1,0,0,1,1,0,0,0,1,1,1] 16098 [1,0,1,1,1,1,1,0,1,1,1,0,0,0,1,0,1] 16225 [1,0,1,1,1,1,1,1,0,1,1,0,0,0,0,1,1] 16352 [1,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,1] Закономерность прослеживается. Расстояние Хэмминга между соседними элементами равно 2. Интересно, что найден элемент с самым сложным вектором совпадений, из спектра г. Петухова 14695184639767: [0,10,24,36,66,84,90,114,120,126,150,172,184,196,214,220,240], num15=16352, valids=11 Все остальные элементы в этом списке не найдены, если судить по точкам в соответствующих оранжевых квадратиках. PS. Можно ли как-то придумать прицельный поиск этих элементов? 15 элементов с valids=11 - это хорошее пополнение спектра будет. Может быть, в самом последнем варианте спектра г. Петухова некоторые из этих элементов найдены. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Да, ещё можно прихватить (в прицельный поиск) околодиагональные оранжевые квадратики - элементы 14573, 14702, 15081, 15210, 15589, 15718, 16097, 16226. Все эти элементы, кроме 16097, не найдены. А они очень близки к диагональным элементам, значит, в векторах совпадений есть какая-то закономерность (похожесть). Из спектра г. Петухова 35784076817393: [0,20,24,36,66,84,90,116,120,126,150,164,170,218,224,234,240], num15=16097, valids=11 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
vicvolf писал в сообщении https://dxdy.ru/post1632667.html#p1632667 Кстати, несимметричные цепочки кортежей нечетной длины могут располагаться на обеих последовательностях. О Боже! Теперь уже "цепочки кортежей". Скоро будут кортежи цепочек :))) Когда, наконец, эти "цепочки" выбросят из темы??? И про обозначения кортежей уже Ядряра написал. Я выше уже говорила, что vicvolf абсолютно не в теме. Простыми числами он занимался, но в теме "Симметричные кортежи из последовательных простых чисел" наверняка не прочитал ни одной страницы. А это ведь базовая тема. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
gris прекрасно поработал с моим спектром из двух частей, который я выложила на Яндекс.Диск https://disk.yandex.ru/d/CzIzf3xW2JORpA Спасибо! Оказывается, в моём спектре уже 1974 уникальных элемента. А по моей прикидке было примерно 1500 уникальных элементов. Выше я говорила, что использовала некоторые результаты г. Петухова из его приближений к 19-ке с минимальным диаметром и из массива с num17. Покажу начало и конец моего спектра 0 [112337, 117920780706464625549246043, 131800842184540138342950671, 131852827433521694579610917, 131852827433521694671056887, 132684591417226594325144629, 132840547164171263083109479, 133568340649913050209746653, 133828266894820831272082639, 135127898119359737041838111, 135595765360193742993030517, 135699735858156855600835351, 136947381833714205060799183, 137155322829640429976983721] 1 [6438844658541876221834339, 6444800405486544980686303, 6452741401412769747882097, 6482520136136113269682883, 6561930095398362292702117, 6571856340306143553368183, 6579797336232368326963649, 6591708830121705779313733, 6597664577066374546055309, 6605605572992599379577199, 112150418069511884169982577, 113294093547106121193195479, 113606005040995458557503283, 114541739522663470771649939, 118232692200353962851830629, 137051352331677317421544597, 171718592607731471730302489, 173742268085325708753339809, 176041899309864614431347869, 281760549638173000778235659, 283260328372896344201336179] 2 [6474579140209888283342003, 6508328372896344270938021, 6520239866785681492418113, 6593694079103262059987057, 110382919604138972499626081, 131488930690650801084920273, 297858174724203553461136607] 3 [6875599434484246479759007, 226725771498702096003550337] 4 [6424947915670982651511839, 6436859409560319965809033, 6484505385117669471629257, 114541739522663470779021283, 119532323424892868694198653, 182388881489591994151941367] 5 [6953024144764939279491049, 193887037612286522764616099] 6 [188551893171356261528386037, 296158425491517097605386293] 7 [20678796907616271070643, 26805241239168641267797] 8 [6464652895302107248307359, 6546048103545912438540293, 6669133540402398736173229, 131748856935558582130596553, 131956797931484807034523769, 281260623393265219597970887, 288659531817900380483981179] 9 [117037031473778169644135023, 137155322829640430013410053, 197382477073585659288550963] 10 [235924296396857718919472233, 255057228185021414403883127] 11 [23108248970128325207843] 12 [27899617, 6476564389191444499065467] 14 [9194870024476790075846167] 16 [6456711899375882184708163, 6502372625951675448505457, 291459118789383954843832061] 17 [1006882292528815387343] 18 [29287507476952246238623, 361848734072399539315640383] 20 [28336852322056393385993, 151711192544476173758544377] . . . . . . . . 31168 [33171918115595274250795493] 31648 [33171918116191392743166503] 31737 [714173405945839792853267] 31743 [548934853673670454695071] 31995 [628588812289345578755011] 32190 [447839391652547767407917] 32243 [346660334189390590675127] 32254 [87073837458351874240477] 32384 [29160708312349982827599227] 32499 [567059251329873879997787] 32571 [376586558667542501138227] 32663 [782299017592858073313541] 32715 [770821085331994725002341] 32727 [141707126033472669940351] 32739 [161341697637500999318521] 32741 [17490495325553024845924787] 32753 [53166202711423237425917] 32761 [347681709124158402217151] 32767 [1006882292528806742267, 3954328349097827424397, 4896552110116770789773, 6751407944109046348063, 7768326730875185894807, 19252814175273852997757, 154787380396512840656507, 901985248981556228168767] Начальные элементы приближений gris оформил в виде вектора. В настоящий момент я прекратила добавлять новые приближения, трудоёмкая ручная работа. Ой, а элемента 13 нету :) Вот чёртова дюжина! В спектре г. Петухова имеется 924793: [0,16,18,34,36,48,78,84,88,114,136,168,174,204,226,234,240], num15=13, valids=5 И не только 13 нет, ещё и 15, и 19. Ну, в моём спектре много чего нет :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата PS. Можно ли как-то придумать прицельный поиск этих элементов? Сочинила программу прицельного поиска. Запустила тестировать. Посмотрю, что получится. Это для оранжевых диаганальных и околодиагональных квадратиков, они с valids=11 и почти все не найдены. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вкусная десяточка нашлась (десять правильных элементов) 17490495467873743566565247: [0, 6, 24, 30, 42, 44, 86, 114, 120, 126, 134, 156, 194, 204, 212, 234, 240] 17490495467873743566565247: [0, 0, 0, -6, -24, -40, -4, 0, 0, 0, -16, 0, 20, 0, -4, 0, 0] 10 Для моего спектра уникальный элемент 25045 17490495467873743566565247 В спектре г. Петухова имеется 862497056123: [0,6,24,26,30,66,86,114,120,126,140,156,198,204,218,234,240], num15=25045, valids=10 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Да, ещё можно прихватить (в прицельный поиск) околодиагональные оранжевые квадратики - элементы _______________________________ конец цитаты Я повторила элемент 16097 ! 17490495466952735351514323: [0, 14, 24, 36, 66, 84, 90, 104, 120, 126, 150, 170, 206, 224, 230, 234, 240] 17490495466952735351514323: [0, 8, 0, 0, 0, 0, 0, -10, 0, 0, 0, 14, 32, 20, 14, 0, 0] 11 Теперь 16097 (35784076817393, 17490495466952735351514323) И да, вектор совпадений близок к векторам совпадений диагональных элементов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Добавление к верхней части спектра приближений к ключевой 17-ке 29066 17490495463803844627731413 [1,1,1,1,0,0,0,1,1,0,0,0,1,0,1,0,1] 29428 17490495465484129364027293 [1,1,1,1,0,0,1,0,1,1,1,1,0,1,0,0,1] 22148 17490495465284559350517257 [1,1,0,1,0,1,1,0,1,0,0,0,0,1,0,0,1] 20705 17490495464732295051520847 [1,1,0,1,0,0,0,0,1,1,1,0,0,0,0,1,1] 20649 17490495465736378618857697 [1,1,0,1,0,0,0,0,1,0,1,0,1,0,0,1,1] 25045 17490495467873743566565247 [1,1,1,0,0,0,0,1,1,1,0,1,0,1,0,1,1] 21664 17490495468548788856496413 [1,1,0,1,0,1,0,0,1,0,1,0,0,0,0,0,1] 24738 17490495461992000375077083 [1,1,1,0,0,0,0,0,1,0,1,0,0,0,1,0,1] 24713 33171918127195246296497273 [1,1,1,0,0,0,0,0,1,0,0,0,1,0,0,1,1] 29408 29160708324820984750828663 [1,1,1,1,0,0,1,0,1,1,1,0,0,0,0,0,1] 25736 33171918127794857788472483 [1,1,1,0,0,1,0,0,1,0,0,0,1,0,0,0,1] 29321 10039334444255081229413977 [1,1,1,1,0,0,1,0,1,0,0,0,1,0,0,1,1] Хорош элемент 29428 17490495465484129364027293 [1,1,1,1,0,0,1,0,1,1,1,1,0,1,0,0,1] с 11 правильными элементами (valids=11). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё немножко элементов в верхнюю часть спектра 20683 17490495468769030617024943 [1,1,0,1,0,0,0,0,1,1,0,0,1,0,1,1,1] 20865 17490495470606531215538237 [1,1,0,1,0,0,0,1,1,0,0,0,0,0,0,1,1] 25992 17490495470735637190420667 [1,1,1,0,0,1,0,1,1,0,0,0,1,0,0,0,1] 25504 17490495470045329512089983 [1,1,1,0,0,0,1,1,1,0,1,0,0,0,0,0,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Парадигмы поиска приближений к ключевой 17-ке Основа всех парадигм - поиск ключевой 17-ки (17-ки с заданным паттерном, содержащейся в 19-ке с минимальным диаметром) по паттерну. Сначала парадигма у меня была такая: а) правильные первый и последний элементы; б) наличие в приближении центральной тройки (как минимум). Эта парадигма у меня работала довольно долго. Было найдено много приближений, удовлетворяющих условиям этой парадигмы. Потом gris ввёл свою метрику. Это натолкнуло на мысль изменить парадигму поиска приближений к ключевой 17-ке. Парадигма 2 правильные первый и последний элементы. Всё остальное - как сложится. Эта парадигма дала очень много оригинальных приближений, которые не могли быть найдены первой парадигмой. Она работает до сих пор. Затем началась визуализация спектра приближений. Она началась с моей подачи. gris сделал очень хорошие визуализации - различные варианты. Я начала рассматривать фрагменты спектра на картинках. Так родилась парадигма 3. Это прицельный поиск диагональных и околодиагональных элементов спектра, которые имеют valids=11. Повторю иллюстрацию, чтобы было понятно, о каких элементах речь 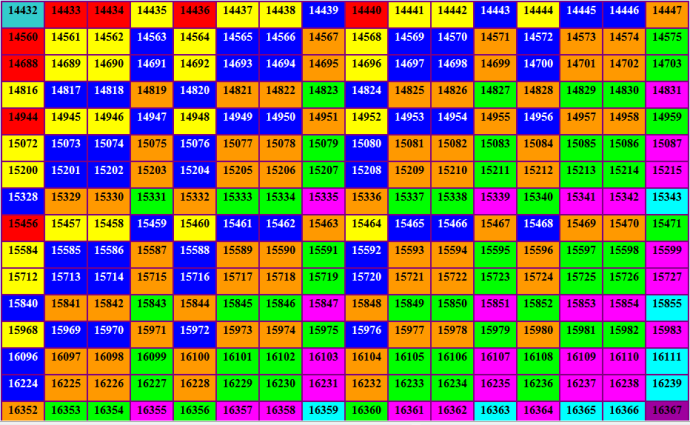 Это оранжевые элементы на диагонали квадрата и прилегающие к ним оранжевые элементы (околодиагональные). Если вы посмотрите на векторы совпадений этих элементов, то увидите большую похожесть. Этот факт и используется в парадигме 3. Основа парадигмы та же - поиск по паттерну. Первое условие парадигмы тоже сохраняется (правильные первый и последний элементы). А следующее условие изменяется. Сначала я запрограммировала такое условие (вектор совпадений) [1, 0, 1,1,1,0,0,0,0,1,1,0,0,0,0,0,1] то есть так if(pat1[3]==24 && pat1[4]==36 && pat1[5]==66 && pat1[10]==126 && pat1[11]==150, print(vmy[1],": ",pat1); res=pat1-pt; print(vmy[1],": ",res); print(vecsum(vector(#res,i,res[i]==0))); print(); Приближения при этом условии будут иметь минимум семь правильных элементов (valids=7). При появлении единичек в других позициях valids будет возрастать. За двое суток работы программа с таким условием не выдала ни одного приближения. Сейчас я изменила условие на менее жёсткое (минимальный valids снизился до 6) [1, 0, 1,1,1,0,0,0,0,1,0,0,0,0,0,0,1] Запустила новую версию программы. Жду результаты. PS. Про векторы совпадений диагональных элементов смотрите сообщение https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13874 Интересно: в парадигме 2 нашёлся один околодиагональный элемент, который был найден ранее г. Петуховым. Цитата Я повторила элемент 16097 ! Обратите внимание на вектор совпадений этого элемента [1,0,1,1,1,1,1,0,1,1,1,0,0,0,0,1,1] Замечание: в парадигме 2 минимум valids равен 2 [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1] а в парадигме 1 минимум valids равен 5 [1,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это приближение с 10 правильными элементами (valids=10) найдено жадным алгоритмом 41253696916057417847597: [0, 6, 26, 42, 54, 84, 92, 114, 120, 126, 150, 170, 192, 204, 216, 222, 240] 41253696916057417847597: [0, 0, 2, 6, -12, 0, 2, 0, 0, 0, 0, 14, 18, 0, 0, -12, 0] 10 Очень редко в жадном алгоритме находятся приближения с 10 правильными элементами. Элемент спектра не уникальный, уже было 17894 [29160708316457187405114853] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё раз покажу диагональные и околодиагональные элементы спектра с valids=11, которые ищет парадигма 3. Диагональные (16 шт.) 14447, 14574, 14701, 14828, 14955, 15082, 15209, 15336, 15463, 15590, 15717, 15844, 15971, 16098, 16225, 16352 околодиагональные (8 шт.) 14573, 14702, 15081, 15210, 15589, 15718, 16097, 16226 Из этих элементов найдены 16352 и 16097. Я не проверяла последний вариант спектра г. Петухова. Возможно, там есть ещё найденные элементы из этого списка. Попутно парадигмой 3 будут найдены некоторые элементы от valids=6 до valids=10 и от valids=12 до valids=16. Кроме того, с valids=11 могут быть найдены другие элементы, помимо перечисленных выше. Ну, и полная ключевая 17-ка (valids=17) тоже может быть найдена, как и предыдущими двумя парадигмами. На мой взгляд, парадигма 3 - очень перспективный поиск приближений к ключевой 17-ке. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Грызло сомнение, почему парадигма 3 до сих пор не нашла ни одного приближения. Думала, что ошибка в программу вкралась. Запустила программу в другом диапазоне (поменьше числа), и ... с ходу нашлись два приближения с valids=9 ! (08:10) gp > \r pricel.txt *** Warning: new maximum stack size = 1000000000 (953.674 Mbytes). log = 1 (on) [logfile is "pricel_res.txt"] 19214758 from number 19214759 to number [0,6,24,36,66,84,90,114,120,126,150,156,174,204,216,234,240] patterns length 17 prove by 37#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37] 7420738134810 period search in 142587687441745525980 - 142587702283221795600 32112640 formulae expected 142587701237468576917: [0, 6, 24, 36, 66, 70, 76, 102, 120, 126, 132, 150, 174, 190, 204, 226, 240] 142587701237468576917: [0, 0, 0, 0, 0, -14, -14, -12, 0, 0, -18, -6, 0, -14, -12, -8, 0] 9 142587690610115244427: [0, 6, 24, 36, 66, 70, 76, 96, 120, 126, 142, 156, 162, 1 90, 220, 226, 240] 142587690610115244427: [0, 0, 0, 0, 0, -14, -14, -18, 0, 0, -8, 0, -12, -14, 4, -8, 0] 9 time = 30min, 7,177 ms. Отлично! Первое приближение даёт элемент 30920, а второе даёт элемент 30928. Для моего спектра оба элемента уникальные. Итак, парадигма 3 нашла два элемента в верхней части спектра с valids=9 30920 142587701237468576917 30928 142587690610115244427 Ошибки в программе нет, можно продолжать поиск. У меня программа сейчас ищет в заоблачных высотах ? \r pricel.txt logfile = "pricel_res.txt" 1999921436788 from number 1999921436817 to number [0,6,24,36,66,84,90,114,120,126,150,156,174,204,216,234,240] patterns length 17 prove by 37#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37] 7420738134810 period search in 14840893272596718437390280 - 14840893272819340581434580 32112640 formulae expected Диапазон 26-значных чисел. Пока ничего не нашла. Почему такие большие числа? Потому что я хочу иметь шансы найти ключевую 17-ку, а не только приближения к ней. PS. Покажу векторы совпадений найденных элементов 30920 [1,1,1,1,1,0,0,0,1,1,0,0,1,0,0,0,1] 30928 [1,1,1,1,1,0,0,0,1,1,0,1,0,0,0,0,1] Красным цветом помечены элементы, правильность которых обеспечивается парадигмой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну вот, gris сделал пересечение моего спектра и спектра г. Петухова. Цитата из его письма in num15df 26954 найденные П коды Итак, есть 36 элементов, которые есть в моём спектре и которых нет в спектре г. Петухова. В спектре г. Петухова есть 26954 элемента. Следовательно, всего на данный момент найдено 26954 + 36 = 26990 элементов спектра приближений к ключевой 17-ке, что составляет 82,37% всего спектра (32768 элементов). Осталось найти 5778 элементов. Совсем чуть-чуть :) При этом г. Петухов писал, что элементы с valids=2 - valids=9 найдены все. Таким образом, остались не найдены элементы с valids=10 - valids=16. gris, большое спасибо за пересечение! Замечание: не все 36 уникальных элементов спектра приближений к ключевой 17-ке найдены мной, часть из них получена из результатов г. Петухова (приближения к 19-ке с минимальным диаметром). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Какое отличное приближение найдено! 17490495477730584175356163: [0, 6, 24, 36, 78, 84, 94, 114, 120, 126, 136, 150, 196, 204, 216, 238, 240] 17490495477730584175356163: [0, 0, 0, 0, 12, 0, 4, 0, 0, 0, -14, -6, 22, 0, 0, 4, 0] 11 Приближение дало уникальный для моего спектра элемент в верхней части 30150 17490495477730584175356163 Интересно: приближение найдено парадигмой 2; оно могло быть найдено и парадигмой 1, а вот парадигмой 3 не могло быть найдено. Вектор совпадений элемента [1,1,1,1,0,1,0,1,1,1,0,0,0,1,1,0,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Новое пополнение верхней части спектра 23744 31166313227059763538369803 [1,1,0,1,1,1,0,0,1,1,0,0,0,0,0,0,1] 24781 31166313227386059542277677 [1,1,1,0,0,0,0,0,1,1,0,0,1,1,0,1,1] 24717 31166313228058999569162257 [1,1,1,0,0,0,0,0,1,0,0,0,1,1,0,1,1] 20512 9783758676072764813937131 [1,1,0,1,0,0,0,0,0,0,1,0,0,0,0,0,1] 24780 17490495480131221915084937 [1,1,1,0,0,0,0,0,1,1,0,0,1,1,0,0,1] 24744 17490495480019365236096597 [1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,0,1] 25793 17490495479077497172047293 [1,1,1,0,0,1,0,0,1,1,0,0,0,0,0,1,1] 28880 17490495481491001715759947 [1,1,1,1,0,0,0,0,1,1,0,1,0,0,0,0,1] 24819 17490495481915873150109203 [1,1,1,0,0,0,0,0,1,1,1,1,0,0,1,1,1] 26838 17490495482612320130281993 [1,1,1,0,1,0,0,0,1,1,0,1,0,1,1,0,1] 27782 17490495482464772320222757 [1,1,1,0,1,1,0,0,1,0,0,0,0,1,1,0,1] Ну, и те, которые уже показаны выше 30920 142587701237468576917 [1,1,1,1,1,0,0,0,1,1,0,0,1,0,0,0,1] 30928 142587690610115244427 [1,1,1,1,1,0,0,0,1,1,0,1,0,0,0,0,1] 30150 17490495477730584175356163 [1,1,1,1,0,1,0,1,1,1,0,0,0,1,1,0,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И ещё добавление в верхнюю часть спектра 20614 17490495477143206846686577 [1,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,1] 24760 17490495477297131157979043 [1,1,1,0,0,0,0,0,1,0,1,1,1,0,0,0,1] 28672 377384097664584360659694773 [1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,1] 20697 33171918130014336547568627 [1,1,0,1,0,0,0,0,1,1,0,1,1,0,0,1,1] 20617 31166313229115341984865377 [1,1,0,1,0,0,0,0,1,0,0,0,1,0,0,1,1] 26833 31166313229418832137026027 [1,1,1,0,1,0,0,0,1,1,0,1,0,0,0,1,1] 28840 33171918130740512921347223 [1,1,1,1,0,0,0,0,1,0,1,0,1,0,0,0,1] 26760 25149498467110155329200943 [1,1,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1] 20492 451401829618470748165393633 [1,1,0,1,0,0,0,0,0,0,0,0,1,1,0,0,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
С парадигмой 3 всё глухо, до сих пор не найдено ни одного приближения. Цитата Сейчас я изменила условие на менее жёсткое (минимальный valids снизился до 6) Сделала и второй вариант парадигмы 3 [1, 0, 1,1,1,0,0,0,0,0,1,0,0,0,0,0,1] По-прежнему минимальный valids равен 6. Ни первый, ни второй вариант не дали пока ни одного приближения. Вот они - редкие элементы спектра! Остаётся ждать. Ну, можно попробовать искать приближения этой парадигмой в диапазоне малых чисел. А какой смысл? Только найти редкие элементы спектра. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот запускаю программу в диапазоне 17-значных чисел (06:42) gp > \r pricel1.txt logfile = "pricel1_res.txt" 1510 from number 1513 to number [0,6,24,36,66,84,90,114,120,126,150,156,174,204,216,234,240] patterns length 17 prove by 37#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37] 7420738134810 period search in 11205314583563100 - 11234997536102340 32112640 formulae expected 11222899950421987: [0, 16, 24, 36, 66, 70, 102, 106, 114, 126, 132, 142, 150, 19 2, 204, 234, 240] 11222899950421987: [0, 10, 0, 0, 0, -14, 12, -8, -6, 0, -18, -14, -24, -12, -12, 0, 0] 7 11216731634432257: [0, 10, 24, 36, 66, 72, 84, 90, 114, 126, 136, 174, 192, 220, 222, 226, 240] 11216731634432257: [0, 4, 0, 0, 0, -12, -6, -24, -6, 0, -14, 18, 18, 16, 6, -8, 0] 6 Приближения сразу пошли! Конечно, это попутные приближения, далеко не valids=11. Но всё-таки они есть! А в диапазоне 26-значных чисел вообще никаких пока нет. Первое приближение даёт уникальный для моего спектра элемент 14401 11222899950421987 [1,0,1,1,1,0,0,0,0,1,0,0,0,0,0,1,1] Теперь понятно, почему г. Петухов нашёл более 20000 элементов спектра, а я нашла всего чуть более 2000 элементов спектра. Это Ядряре на заметку. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А вот и valids=11 !! 11208062693747747: [0, 2, 24, 36, 66, 84, 86, 114, 120, 126, 150, 174, 192, 210, 216, 230, 240] 11208062693747747: [0, -4, 0, 0, 0, 0, -4, 0, 0, 0, 0, 18, 18, 6, 0, -4, 0] 11 15842 11208062693747747 [1,0,1,1,1,1,0,1,1,1,1,0,0,0,1,0,1] Кстати, Попутно парадигмой 3 будут найдены некоторые элементы от valids=6 до valids=10 и от valids=12 до valids=16. Элемент 15842 как раз не из списка диагональных и околодиагональных оранжевых элементов, он близко к одному из элементов этого списка - 15844. А вот элемент с valids=6, аж с двумя приближениями 14400 [11216731634432257, 11205909549508607] |

©2026 (C) Progger