Проект gris по кортежу 19-252
Message boards :
Cafe :
Проект gris по кортежу 19-252
Message board moderation
Previous · 1 . . . 7 · 8 · 9 · 10 · 11 · 12 · 13 . . . 54 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот полный спектр приближений к ключевой 17-ке, в котором раскрашены только элементы с valids: 13,14,15,16,17 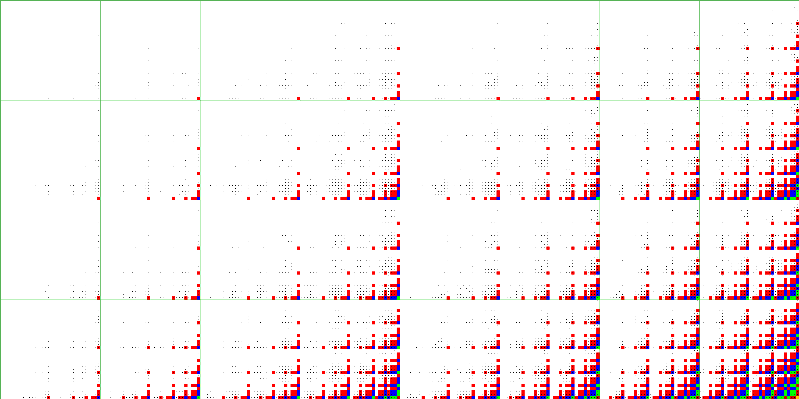 Все остальные элементы - белые квадратики. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Г. Петухов писал в сообщении https://dxdy.ru/post1631354.html#p1631354 Интереснее проверить равномерность найденных кортежей. Т.е. для каждого valids сколько в процентах найдено от всех возможных. Вот данные для 5e14 (файл в облаке обновил): Уточню valids=14 найдено >5 из 455; valids=15 найдено >4 из 105; valids=16 найдено 1 из 15; valids=17 найдено 1 из 1. В файле г. Петухова d252-num15.7e14sort.txt нашла 670762250362577: [0,20,24,60,66,84,90,114,116,126,150,156,174,204,216,234,240], num15=12159, valids=14 28031151913907: [0,6,32,36,72,74,90,114,120,126,150,156,174,204,216,234,240], num15=21503, valids=14 234534892099727: [0,6,24,60,66,84,90,114,120,140,150,156,174,212,216,234,240], num15=28603, valids=14 368729285519297: [0,6,24,36,72,84,110,114,120,126,150,156,174,204,212,234,240], num15=30205, valids=14 И ещё найденное мной приближение с valids=14 32741 17490495325553024845924787 На фрагменте gris, показанном в сообщении https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13816 видим 4 зелёных квадратика без точки, это найденные 4 элемента с valids=15. На этом же фрагменте видим довольно много синих квадратиков без точки, которые соответствуют приближениям с valids=14. Сколько точно найдено приближений с valids=14 и valids=15, не знаю. Надо спросить у gris, он наверное, знает, в спектре он закрашивал квадратики. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Векторы совпадений для элементов с valids=16 [1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1] - 16383 [1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1] - 24575 (+8192) [1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1] - 28671 (+4096) [1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1] - 30719 (+2048) [1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1] - 31743 (+1024) [1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1] - 32255 (+512) [1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1] - 32511 (+256) [1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1] - 32639 (+128) [1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1] - 32703 (+64) [1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1] - 32735 (+32) [1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1] - 32751 (+16) [1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1] - 32759 (+8) [1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1] - 32763 (+4) [1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1] - 32765 (+2) [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1] - 32766 (+1) Найденный элемент 31743 548934853673670454695071 (из приближения к 19-ке с минимальным диаметром, найденного г. Петуховым) Интересно: расстояние Хэмминга между любыми двумя элементами из этого списка равно 2. Даёт ли это что-нибудь для поиска? Найти оставшиеся 14 элементов сложно. Это приближения с одной "дыркой", то есть самые близкие. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Показываю элементы спектра >30000 с вектором совпадений 30143 492033133172934312048911 [1,1,1,1,0,1,0,1,1,0,1,1,1,1,1,1,1] - 14 30148 31166313217662307095971233 [1,1,1,1,0,1,0,1,1,1,0,0,0,1,0,0,1] - 10 30180 31166313200166785765249513 [1,1,1,1,0,1,0,1,1,1,1,0,0,1,0,0,1] - 11 30335 58240441875215114770637 [1,1,1,1,0,1,1,0,0,1,1,1,1,1,1,1,1] - 14 30656 17490495352896582872805337 [1,1,1,1,0,1,1,1,1,1,0,0,0,0,0,0,1] - 10 30720 19939398453808522071547 [1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1] - 6 30848 17490495419881128989159903 [1,1,1,1,1,0,0,0,1,0,0,0,0,0,0,0,1] - 7 30860 29160708306359004343243663 [1,1,1,1,1,0,0,0,1,0,0,0,1,1,0,0,1] - 9 30900 29160708308457625390286623 [1,1,1,1,1,0,0,0,1,0,1,1,0,1,0,0,1] - 10 30913 23143893564678849298916953 [1,1,1,1,1,0,0,0,1,1,0,0,0,0,0,1,1] - 9 31168 33171918115595274250795493 [1,1,1,1,1,0,0,1,1,1,0,0,0,0,0,0,1] - 9 31648 33171918116191392743166503 [1,1,1,1,1,0,1,1,1,0,1,0,0,0,0,0,1] - 10 31737 714173405945839792853267 [1,1,1,1,1,0,1,1,1,1,1,1,1,0,0,1,1] - 14 31743 548934853673670454695071 [1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1] - 16 31995 628588812289345578755011 [1,1,1,1,1,1,0,0,1,1,1,1,1,0,1,1,1] - 14 32190 447839391652547767407917 [1,1,1,1,1,1,0,1,1,0,1,1,1,1,1,0,1] - 14 32243 346660334189390590675127 [1,1,1,1,1,1,0,1,1,1,1,1,0,0,1,1,1] - 14 32254 87073837458351874240477 [1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,0,1] - 15 32384 29160708312349982827599227 [1,1,1,1,1,1,1,0,1,0,0,0,0,0,0,0,1] - 9 32499 567059251329873879997787 [1,1,1,1,1,1,1,0,1,1,1,1,0,0,1,1,1] - 14 32571 376586558667542501138227 [1,1,1,1,1,1,1,1,0,0,1,1,1,0,1,1,1] - 14 32663 782299017592858073313541 [1,1,1,1,1,1,1,1,1,0,0,1,0,1,1,1,1] - 14 32715 770821085331994725002341 [1,1,1,1,1,1,1,1,1,1,0,0,1,0,1,1,1] - 14 32727 141707126033472669940351 [1,1,1,1,1,1,1,1,1,1,0,1,0,1,1,1,1] - 15 32739 161341697637500999318521 [1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1] - 14 32741 17490495325553024845924787 [1,1,1,1,1,1,1,1,1,1,1,0,0,1,0,1,1] - 14 32753 53166202711423237425917 [1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1] - 14 32761 347681709124158402217151 [1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1] - 15 32767 (1006882292528806742267, 3954328349097827424397, 4896552110116770789773, 6751407944109046348063, 7768326730875185894807, 19252814175273852997757, 154787380396512840656507, 901985248981556228168767) [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1] - 17 После вектора совпадений указано количество правильных элементов, оно равно количеству единичек в векторе совпадений (это valids). Ну, а "дырки" - это нули в векторе совпадений; похожи на "дырки" :) Напомню: здесь объединённые результаты (найденные мной, г. Петуховым и Ярославом Врублевским). PS. Это из спектра г. Петухова, тоже для элементов >30000, с valids>=13 161530486193933: [0,6,24,36,38,84,96,114,120,146,150,164,174,204,216,234,240], num15=30127, valids=13 368729285519297: [0,6,24,36,72,84,110,114,120,126,150,156,174,204,212,234,240], num15=30205, valids=14 265407446586943: [0,6,24,36,64,84,90,96,100,138,150,156,174,204,216,234,240], num15=30271, valids=13 298456445875807: [0,6,24,36,70,84,90,94,120,126,150,156,174,186,226,234,240], num15=30457, valids=13 41384604493627: [0,6,24,36,70,84,90,114,120,136,150,156,174,180,184,234,240], num15=30649, valids=13 473911294021483: [0,6,24,36,58,84,90,114,120,126,136,168,190,204,216,234,240], num15=30663, valids=13 393905300885407: [0,6,24,36,54,84,90,114,120,126,150,180,202,204,216,226,240], num15=30694, valids=13 178143173981083: [0,6,24,36,76,84,90,114,120,126,150,156,160,180,220,234,240], num15=30705, valids=13 477258620012617: [0,6,24,36,66,70,84,114,120,126,150,160,172,204,216,234,240], num15=31207, valids=13 329805667939967: [0,6,24,36,66,92,102,114,120,126,150,156,162,192,216,234,240], num15=31219, valids=13 129532434451247: [0,6,24,36,66,84,92,114,120,122,150,156,174,192,200,234,240], num15=32185, valids=13 95393328164837: [0,6,24,36,66,84,104,114,120,126,134,156,170,204,216,222,240], num15=32214, valids=13 419033500525243: [0,6,24,36,66,84,94,114,120,126,148,156,174,184,190,234,240], num15=32217, valids=13 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пополнение верхней части спектра приближений к ключевой 17-ке вывела с вектором совпадений 24672 173441026618766677145674907 [1,1,1,0,0,0,0,0,0,1,1,0,0,0,0,0,1] 20992 174272790602471576716660801 [1,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,1] 20626 17490495431864522334586993 [1,1,0,1,0,0,0,0,1,0,0,1,0,0,1,0,1] 27264 17490495435572414914102117 [1,1,1,0,1,0,1,0,1,0,0,0,0,0,0,0,1] 27016 17490495434701198232857207 [1,1,1,0,1,0,0,1,1,0,0,0,1,0,0,0,1] 21128 17490495434817980417458157 [1,1,0,1,0,0,1,0,1,0,0,0,1,0,0,0,1] 20648 17490495436524969085426873 [1,1,0,1,0,0,0,0,1,0,1,0,1,0,0,0,1] 28832 17490495436281527644084187 [1,1,1,1,0,0,0,0,1,0,1,0,0,0,0,0,1] 30944 17490495436351397544704993 [1,1,1,1,1,0,0,0,1,1,1,0,0,0,0,0,1] 29312 17490495436953857695827277 [1,1,1,1,0,0,1,0,1,0,0,0,0,0,0,0,1] 24960 17490495437664753589930217 [1,1,1,0,0,0,0,1,1,0,0,0,0,0,0,0,1] 25008 29160708317451881849778773 [1,1,1,0,0,0,0,1,1,0,1,1,0,0,0,0,1] 20106 29160708317533003161226103 [1,1,0,0,1,1,1,0,1,0,0,0,1,0,1,0,1] 26848 31166313218899648733272717 [1,1,1,0,1,0,0,0,1,1,1,0,0,0,0,0,1] 24794 29160708317727287725013417 [1,1,1,0,0,0,0,0,1,1,0,1,1,0,1,0,1] 22912 29160708317760618696613057 [1,1,0,1,1,0,0,1,1,0,0,0,0,0,0,0,1] 20624 29160708318211911525728317 [1,1,0,1,0,0,0,0,1,0,0,1,0,0,0,0,1] 21185 29160708318555341779212503 [1,1,0,1,0,0,1,0,1,1,0,0,0,0,0,1,1] Все приближения сильно дырявые. Разверну для проверки самое хорошее приближение из этого списка 30944 17490495436351397544704993 [1,1,1,1,1,0,0,0,1,1,1,0,0,0,0,0,1] {17490495436351397544704993, 17490495436351397544704999, 17490495436351397544705017, 17490495436351397544705029, 17490495436351397544705059, *17490495436351397544705073, *17490495436351397544705107, *17490495436351397544705109, 17490495436351397544705113, 17490495436351397544705119, 17490495436351397544705143, *17490495436351397544705151, *17490495436351397544705157, *17490495436351397544705161, *17490495436351397544705163, *17490495436351397544705223, 17490495436351397544705233} Всё верно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё парочка элементов добавилась в верхнюю часть спектра 25600 28336852322056769208433 [1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,0,1] 21169 17490495432851364124753093 [1,1,0,1,0,0,1,0,1,0,1,1,0,0,0,1,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Репост Цитата _______________________________ конец репоста У-р-р-р-а-а-а! Идея сработала! Спасибо gris за помощь в написании программки. Итак. всё по порядку. В векторе совпадений [1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1] мы видим центральную 13-ку в ключевой 17-ке. Паттерн этой 13-ки такой 0,12,42,60,66,90,96,102,126,132,150,180,192 Выбрала вручную все 13-ки с таким паттерном, найденные в BOINC-проекте TBEG и в моём ручном проекте. Всего таких 13-ок нашлось 121 шт. Далее gris написал программу по заданному мной алгоритму. И вот оно - великолепное приближение к ключевой 17-ке 3241648437603927893: [0, 14, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 234, 240] [16] 3241648437603927893: [ 0, 14, 24, 36, 66, 84, 90,114,120,126,150,156,174,204,216,234,240] [ 0, 8, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Вектор совпадений [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] Элемент спектра 16383 3241648437603927893 16 правильных элементов, одна "дырка". Вот такой прицельный поиск! Хороший алгоритм. Можно ещё что-нибудь попробовать этим алгоритмом поискать. Кстати, в BOINC-проекте SPT найдено много 13-ок. Их тоже надо проверить. Приближение в развёрнутом виде {3241648437603927893, *3241648437603927907, 3241648437603927917, 3241648437603927929, 3241648437603927959, 3241648437603927977, 3241648437603927983, 3241648437603928007, 3241648437603928013, 3241648437603928019, 3241648437603928043, 3241648437603928049, 3241648437603928067, 3241648437603928097, 3241648437603928109, 3241648437603928127, 3241648437603928133} Лепота! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, статистика: в BOINC-проекте TBEG и в моём ручном проекте было найдено примерно 170000 13-ок. Из них всего 121 13-ка с паттерном 0,12,42,60,66,90,96,102,126,132,150,180,192 то есть центральная в ключевой 17-ке, а также в 19-ке с минимальным диаметром. В BOINC-проекте SPT на данный момент найдено 130450 13-ок, из них только 79 13-ок с паттерном 0,12,42,60,66,90,96,102,126,132,150,180,192 gris вчера проверил и эти 13-ки по описанному выше алгоритму. Увы! Решение не нашлось. Есть очень близко 5272061120090938871 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0] 6931319014788808051 [0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1] То один, то другой край подкачал. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё парочка элементов в верхнюю часть спектра добавилась 28812 28812179899504560913727 [1,1,1,1,0,0,0,0,1,0,0,0,1,1,0,0,1] 21508 29023436600592505229407 [1,1,0,1,0,1,0,0,0,0,0,0,0,1,0,0,1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, по описанному выше алгоритму мы с gris проверяли центральные 9-ки, содержащиеся в ключевой 17-ке, а также в 19-ке с минимальным диаметром. Цитата из сообщения https://boinc.progger.info/odlk/forum_thread.php?id=268&postid=13296 Г. Петухов выложил на форуме dxdy.ru симметричные 9-ки из последовательных простых чисел, найденные в BOINC-проекте Stop@home, смотрите ссылку в сообщении _____________________________ конец цитататы Очень интересные результаты! Часть этих приближений должна присутствовать в спектре г. Петухова. Таким образом, алгоритм-то давно работает. Но центральные 13-ки почему-то до сих пор были не проверены. Теперь проверили их. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Определила программкой gris, какие у этих приближений с центральной 9-ой количества правильных элементов (valids) (10:31) gp > \r spg_by_centre.gp
[11, 11, 12, 11, 13, 11, 12, 11, 12, 11, 11, 12, 11, 12, 11, 12, 12, 13, 11, 13,
11, 11, 12, 13, 12, 11, 11, 13, 11, 13, 13, 12, 12, 13]
5 61909098512627:
[ 0, 2, 6, 36, 66, 84, 90,114,120,126,150,156,174,204,212,230,240]
[ 0, -4,-18, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -4, -4, 0]
18 3692939714570017:
[ 0, 4, 36, 46, 66, 84, 90,114,120,126,150,156,174,192,216,234,240]
[ 0, -2, 12, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0,-12, 0, 0, 0]
20 4066905498223787:
[ 0, 14, 24, 60, 66, 84, 90,114,120,126,150,156,174,200,216,230,240]
[ 0, 8, 0, 24, 0, 0, 0, 0, 0, 0, 0, 0, 0, -4, 0, -4, 0]
24 4704032160866257:
[ 0, 22, 24, 42, 66, 84, 90,114,120,126,150,156,174,190,216,226,240]
[ 0, 16, 0, 6, 0, 0, 0, 0, 0, 0, 0, 0, 0,-14, 0, -8, 0]
28 7184298747301217:
[ 0, 6, 24, 62, 66, 84, 90,114,120,126,150,156,174,194,222,224,240]
[ 0, 0, 0, 26, 0, 0, 0, 0, 0, 0, 0, 0, 0,-10, 6,-10, 0]
30 7849758790696217:
[ 0, 6, 14, 42, 66, 84, 90,114,120,126,150,156,174,176,204,234,240]
[ 0, 0,-10, 6, 0, 0, 0, 0, 0, 0, 0, 0, 0,-28,-12, 0, 0]
31 8915277661475677:
[ 0, 16, 24, 60, 66, 84, 90,114,120,126,150,156,174,192,216,226,240]
[ 0, 10, 0, 24, 0, 0, 0, 0, 0, 0, 0, 0, 0,-12, 0, -8, 0]
34 9297384447350933:
[ 0, 14, 24, 26, 66, 84, 90,114,120,126,150,156,174,224,230,234,240]
[ 0, 8, 0,-10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 20, 14, 0, 0]Программа вывела приближения с максимальным в данной порции количеством правильных элементов - 13 (то есть valids=13). Это приближения с 4 "дырками". Остальные приближения имеют valids=11 и valids=12. PS. Вот, например, первое приближение с valids=13 из спектра г. Петухова 61909098512627: [0,2,6,36,66,84,90,114,120,126,150,156,174,204,212,230,240], num15=8188, valids=13 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
По тому же алгоритму мы проверили все центральные 13-ки на вхождение в 19-ку с минимальным диаметром. Увы! Решений не найдено. Есть очень близкие 6364333587724492231 [1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0] 591077243357392357 [1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0] Правый край подкачал. Второе приближение весьма интересное: три "дырки", центральная 13-ка; хотя и один крайний элемент неправильный. Разверну это приближение {591077243357392327, 591077243357392333, *591077243357392349, 591077243357392357, 591077243357392369, 591077243357392399, 591077243357392417, 591077243357392423, 591077243357392447, 591077243357392453, 591077243357392459, 591077243357392483, 591077243357392489, 591077243357392507, 591077243357392537, 591077243357392549, 591077243357392567, *591077243357392639, *591077243357392667} |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё одна визуализация спектра приближений к ключевой 17-ке  Раскрашены элементы с valids: 8, 9, 10, 11, 12, 13. Остальные элементы - белые квадратики (все элементы с valids: 2 - 7, 14 - 17). Картинку рисовал gris. Сейчас какой-нибудь фрагмент вырежу и покажу, будет покрупнее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сначала посмотрите на этот фрагмент 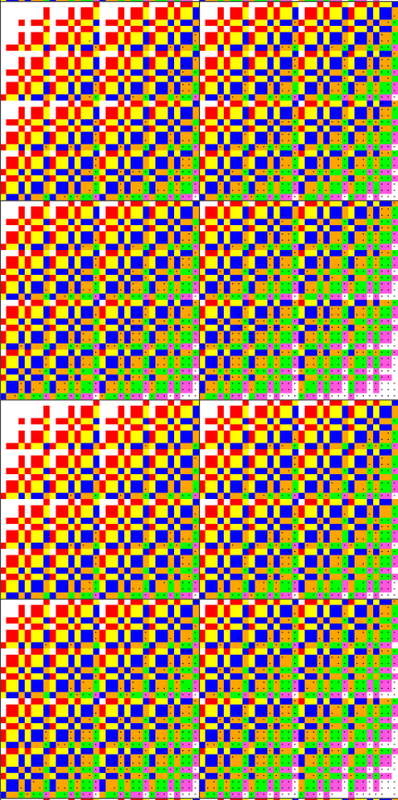 Он состоит из двух квадратов 64х64 совершенно одинаковой структуры. А поэтому я сейчас отрежу верхний квадрат 64х64 (или нижний квадрат 64х64, что то же самое). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Готово! 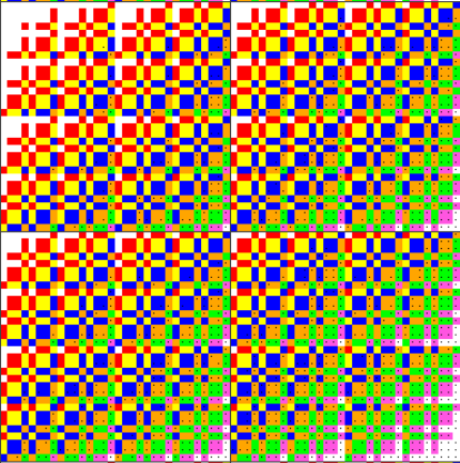 valids8 - красный; valids9 - жёлтый; valids10 - синий; valids11 - оранжевый; valids12 - зелёный; valids13 - розовый. По-прежнему точка в квадратике означает, что данный элемент не найден. Теперь исследуйте, господа. Может быть, найдёте какие-нибудь интересные закономерности. PS. В полном спектре это квадрат 64х64 непосредственно над угловым (справа снизу) квадратом 64х64. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Красных квадратиков (valids8) с точкой я не вижу, значит все такие элементы найдены. Жёлтый квадратик (valids9) вижу всего один с точкой. Ну, возможно, в других местах ещё есть. Синих квадратиков (valids10) мало с точками, я вижу примерно 5 - 7 (нечётко видны точки в синих квадратиках). Оранжевые, зелёные и розовые квадратики (valids11, valids12, valids13) - много с точками. Ещё можно заметить, что в этой визуализации очень мало белых квадратиков. Это значит, что элементы с valids8 - valids13 заполняют бОльшую часть спектра. Ну, это и по количествам valids видно. Вот valids2 - 1 valids3 - 15 valids4 - 105 valids5 - 455 valids6 - 1365 valids7 - 3003 valids8 - 5005 valids9 - 6435 valids10 - 6435 valids11 - 5005 valids12 - 3003 valids13 - 1365 valids14 - 455 valids15 - 105 valids16 - 15 valids17 - 1 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
vicvolf писал в сообщении https://dxdy.ru/post1632305.html#p1632305 Dmitriy40 в сообщении #1632256 писал(а): Ого! Вот это прогноз! Ну, точно на тысячу лет :) Г. Петухова не пугает тысяча лет? :) Надо ещё убыстрять программу в 1000 раз. Тогда, возможно, решение найдётся за год. Впрочем, г. Петухов обещал 19-ку с минимальным диаметром до 1е25. Слишком уж расходятся прогнозы. Обоснования прогнозов никто не даёт. "Я прикинул" - это не обоснование. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пополнение верхней части спектра приближений к ключевой 17-ке 27329 29160708318938851024875893 [1,1,1,0,1,0,1,0,1,1,0,0,0,0,0,1,1] 21152 29160708319105059654803387 [1,1,0,1,0,0,1,0,1,0,1,0,0,0,0,0,1] 24712 29160708319558933317860047 [1,1,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1] 20912 31166313220771233737442143 [1,1,0,1,0,0,0,1,1,0,1,1,0,0,0,0,1] 27010 29160708319947950252832713 [1,1,1,0,1,0,0,1,1,0,0,0,0,0,1,0,1] 20977 31166313221202587438220583 [1,1,0,1,0,0,0,1,1,1,1,1,0,0,0,1,1] 21009 8970037110026067077160797 [1,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,1] 26817 17490495439340740008686867 [1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,1] 24969 17490495441608999304334513 [1,1,1,0,0,0,0,1,1,0,0,0,1,0,0,1,1] 24778 17490495443294828576771977 [1,1,1,0,0,0,0,0,1,1,0,0,1,0,1,0,1] 25039 17490495441938268597777863 [1,1,1,0,0,0,0,1,1,1,0,0,1,1,1,1,1] 20660 17490495445516085287455533 [1,1,0,1,0,0,0,0,1,0,1,1,0,1,0,0,1] 28802 180563005729239880212891343 [1,1,1,1,0,0,0,0,1,0,0,0,0,0,1,0,1] Последнее приближение, по всей видимости, найдено жадным алгоритмом. 27-значное! Разверну его для проверки {180563005729239880212891343, 180563005729239880212891349, 180563005729239880212891367, 180563005729239880212891379, *180563005729239880212891389, *180563005729239880212891407, *180563005729239880212891409, *180563005729239880212891437, 180563005729239880212891463, *180563005729239880212891479, *180563005729239880212891497, *180563005729239880212891517, *180563005729239880212891527, *180563005729239880212891539, 180563005729239880212891559, *180563005729239880212891569, 180563005729239880212891583} Всё верно. Сильно дырявое приближение, но десятичный код большой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Возвращаюсь к фрагменту, показанному в сообщении https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13833 Меня интересует жёлтый квадратик с точкой в левом верхнем подквадрате 16х16. Это жёлтый квадратик, значит, соответствует элементу с valids9. Это элемент 9038 [1,0,1,0,0,0,1,1,0,1,0,0,1,1,1,0,1] И не такой уж сложный вектор совпадений. Почему до сих пор не найден? При этом соседний с ним элемент 9037 - тоже жёлтый квадратик, найден 9037 [1,0,1,0,0,0,1,1,0,1,0,0,1,1,0,1,1] векторы совпадений отличаются совсем немного (отличие помечено красный цветом). Из спектра г. Петухова 7437068757947: [0,12,24,56,80,86,90,114,122,126,134,170,174,204,206,234,240], num15=9037, valids=9 Посмотрите на начальный элемент приближения. Малюсенький! Элемента 9038 нет и в моём спектре - с большими числами. И куда запропастился? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Представляю ещё один интересный фрагмент, вырезанный из фрагмента, показанного в сообщении https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13833  В этом фрагменте два подквадрата 16х16 с совершенно одинаковой структурой. Назовём левый подквадрат 16х16 квадратом А, а правый подквадрат 16х16 квадратом В. Рассматривайте, господа, внимательно :) Наверняка есть много закономерностей. Розовые квадратики - это элементы с valids13. Я не вижу ни одного розового квадратика без точки. Дефицит найденных элементов с valids13. Зелёные квадратики - это элементы с valids12. Эти квадратики встречаются без точки, но очень мало. Вот в нижней строке квадрата А зелёный квадратик справа с точкой, а соответствующий ему зелёный квадратик в квадрате В без точки. Надо посмотреть на эти элементы. |

©2026 (C) Progger