Представляю квадрат Стенли с 8 "дырками"

Это 25-ка из последовательных простых чисел

{539792123400323, 539792123400331, 539792123400359, 539792123400371, 539792123400379, 539792123400407,
539792123400421, 539792123400469, 539792123400503, 539792123400511, 539792123400539, 539792123400557,
539792123400643, 539792123400671, 539792123400679, 539792123400737, 539792123400809, 539792123400869,
539792123400877, 539792123400947, 539792123400967, 539792123400979, 539792123400991, 539792123401073,
539792123401093}

это её паттерн

[0, 8, 36, 48, 56, 84, 98, 146, 180, 188, 216, 234, 320, 348, 356, 414, 486, 546, 554, 624, 644, 656, 668, 750, 770]

это кандидат

539792123400323, [0, 56, 216, 644, 770], [8, 48, 36, 180, 84, 188, 98, 546, 146, 554, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Кандидат достроен вручную до следующего квадрата Стенли ("дырки" помечены звёздочкой)

0 8 36 98 320
48 56 84 146 *368
180 188 216 *278 *500
546 554 *582 644 *866
*450 *458 486 *548 770

S=1686

В сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12822
показан квадрат Стенли с 9 "дырками".

Ждём квадрат с 7 "дырками".
Кандидатов всё меньше находится.
За ночь на Ахиллесе-3 нашёлся всего один кандидат.
Но! хорошо то, что они находятся.

В сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12805
показан вектор главной диагонали квадрата Стенли a.

Сейчас я покажу кандидат полностью, то есть ещё добавлю элементы вектора b.

Вот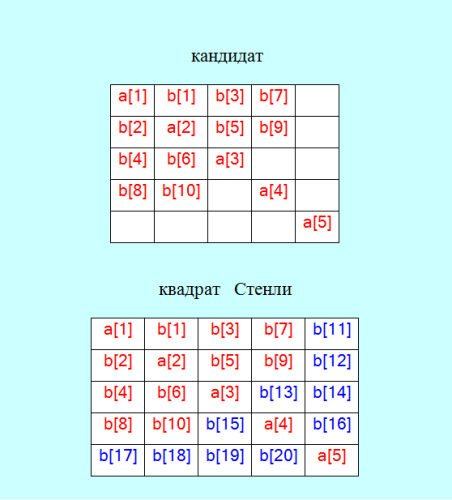



Программа выводит кандидата в виде

539792123400323, [0, 56, 216, 644, 770], [8, 48, 36, 180, 84, 188, 98, 546, 146, 554, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Сначала идёт первый элемент 25-ки, затем вектор a, далее вектор b, в котором известны 10 компонент.
Можно, конечно, вектор b выводить с 10 известными компонентами, но я специально вывожу его полностью: видны 10 "дырок" (нулевые компоненты).

Цитата

Программа выводит кандидата в виде

539792123400323, [0, 56, 216, 644, 770], [8, 48, 36, 180, 84, 188, 98, 546, 146, 554, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Интересный момент: некоторые кандидаты выводятся в двух вариантах.
Для показанного в цитате кандидата второй вариант такой

539792123400323, [0, 56, 216, 644, 770], [48, 8, 180, 36, 188, 84, 546, 98, 554, 146, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Диагональная симметрия квадрата Стенли!

Вот достроенный квадрат Стенли для этого варианта

0 48 180 546 *450
8 56 188 554 *458
36 84 216 *582 486
98 146 *278 644 *548
320 *368 *500 *866 770

Сравните с квадратом Стенли в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12844

0 8 36 98 320
48 56 84 146 *368
180 188 216 *278 *500
546 554 *582 644 *866
*450 *458 486 *548 770

Строки квадрата стали столбцами, а столбцы - строками.
Вектор главной диагонали квадрата остался неизменным.

Таких кандидатов с диагональной симметрией довольно много находится.
Квадраты Стенли в этих случаях получаются эквивалентные.

Следующие кандидаты найдены и проверены

539789527374421, [0, 178, 448, 582, 772], [70, 108, 220, 228, 328, 298, 372, 210, 480, 280, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
539789952795707, [0, 146, 182, 264, 444], [20, 126, 50, 132, 176, 152, 204, 60, 330, 80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539792123400323, [0, 56, 216, 644, 770], [8, 48, 36, 180, 84, 188, 98, 546, 146, 554, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539792123400323, [0, 56, 216, 644, 770], [48, 8, 180, 36, 188, 84, 546, 98, 554, 146, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]  
539793633959227, [0, 76, 294, 406, 550], [40, 36, 90, 204, 126, 244, 376, 30, 412, 70, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539793943933043, [0, 114, 230, 308, 524], [66, 48, 86, 144, 134, 210, 248, 60, 296, 126, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539796452848711, [0, 102, 388, 438, 808], [42, 60, 172, 216, 232, 258, 192, 246, 252, 288, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539796452848711, [0, 102, 388, 438, 808], [60, 42, 216, 172, 258, 232, 246, 192, 288, 252, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539797148920319, [0, 38, 350, 402, 660], [24, 14, 210, 140, 224, 164, 288, 114, 302, 138, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539799153372443, [0, 44, 170, 198, 516], [6, 38, 60, 110, 98, 116, 150, 48, 188, 54, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539799177459463, [0, 96, 286, 336, 558], [18, 78, 150, 136, 228, 154, 216, 120, 294, 138, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 
539799929836691, [0, 242, 258, 306, 590], [110, 132, 186, 72, 318, 182, 216, 90, 348, 200, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 

Ошибок в программе не обнаружено.

Проверяю кандидатов вручную.
Надо бы программу написать.

На Ахиллесе-3 найдено ещё несколько кандидатов.
Жду, когда закончится обработка интервала.

Уже совсем было собралась писать программу проверки кандидатов, но осенила идея.
Решила усилить предпроверку.
Идея-то давно была озвучена

PS. Можно добавить в программу вписывание в квадрат Стенли ещё двух правильных элементов.
Тогда кандидатов станет намного меньше, и они будут с 8 "дырками".

Вот кандидат и полный квадрат Стенли



Добавлю проверку возможности вписать в квадрат Стенли ещё два элемента: b[11] и
b[17].
После такой предпроверки кандидаты будут с 8 "дырками" и их будет гораздо меньше.

Программу предпроверки уже дописала и протестировала на квадрате от Andersen.
Можно запускать программу в работу и ждать новых кандидатов.

Вот у меня был такой кандидат

539799929836691, [0, 242, 258, 306, 590], [110, 132, 186, 72, 318, 182, 216, 90, 348, 200, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Этот кандидат проходит дополнительную проверку двух элементов: b[11] и b[17].
Замечательно!

При ручном достраивании я получила такой квадрат Стенли с 8 "дырками"

0 110 186 216 342
132 242 318 348 *474
72 182 258 *288 *414
90 200 *276 306 *432
248 *358 *434 *464 590

Элементы b[11] и b[17] на месте!

Квадрат строился из элементов паттерна

[0, 56, 72, 90, 110, 132, 182, 186, 200, 216, 242, 248, 258, 278, 306, 318, 342, 348, 396, 426, 446, 462, 506, 570, 590]

Итак, кандидаты с 8 "дырками" встречаются.
Из 25 элементов квадрата Стенли 17 удаётся вписать.

Нашёлся кандидат (это ещё с 10 "дырками"), который при достраивании дал квадрат Стенли с 7 "дырками"

539815777431211, [0, 120, 178, 270, 490], [12, 108, 78, 100, 186, 112, 102, 168, 210, 180, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Это достроенный вручную квадрат Стенли, в нём 7 "дырок"

0 12 78 102 172
108 120 186 210 *280
100 112 178 *202 *272
168 180 *246 270 340
318 *330 *396 *420 490

S = 1058

Квадрат строился из элементов паттерна

[0, 12, 78, 100, 102, 108, 112, 120, 156, 168, 172, 178, 180, 186, 190, 210, 232, 270, 318, 340, 348, 352, 432, 436, 490]

Вот такой прогресс.
Ждём квадрат Стенли с 6 "дырками".

На Ахиллесе-3 запустила новую программу предпроверки, которая вписывает в квадрат Стенли 17 элементов.

Ждём новых кандидатов - с 8 "дырками".

Вот и приплыли :)
Ни одного кандидата с 8 "дырками" пока не дождалась.
Ахиллес-3 считает вторые сутки.
Уже черепашку подключила.
И н-и-ч-е-г-о!

Выложу свою программу предпроверки

\l st3_res.txt
{start=540002999999251;
w=vector(25);v=vector(25);
a=vector(5);
b=vector(20);
a[1]=0;
v[1]=start;
for (i=2,25, v[i]=nextprime(v[i-1]+1); );
while(v[25]<5.40005*10^14,
for (i=1,24, v[i]=nextprime(v[i+1]+1); );
v[25]=nextprime(v[24]+1); 
for(i=1,25, w[i]=v[i]-v[1]; );
s1=w[2];
for(i=3,25, s1=s1+w[i]; );
if(type(s1/5)<>"t_INT", next);
s=s1/5;
a[5]=w[25];
for (i=2,24, a[2]=w[i];
for (j=i+1,24,
a[3]=w[j];
for (k=j+1,24,
a[4]=w[k];
if(a[2]+a[3]+a[4]+a[5]==s, 
for (l=2,24,
b[1]=w[l];
if(b[1]>a[2],next);
if(b[1]==a[2] || b[1]==a[3] || b[1]==a[4], next); 
b[2]=a[2]-b[1];
if(b[2]==b[1], next);
for (m=2,24,
if(b[2]<>w[m], next);
for (m=l+1,24, b[3]=w[m];
if(b[3]>a[3], next);
if(b[3]==a[2] || b[3]==a[3] || b[3]==a[4] || b[3]==b[2], next); 
b[4]=a[3]-b[3];
if(b[4]==a[2] || b[4]==a[4] || b[4]==b[1] || b[4]==b[2] || b[4]==b[3], next); 
for (n=2,24,
if(b[4]<>w[n], next);
b[5]=b[2]+b[3];
if(b[5]==a[2] || b[5]==a[3] || b[5]==a[4] || b[5]==b[1] || b[5]==b[4], next); 
for (n=2,24,
if(b[5]<>w[n], next);
b[6]=b[4]+b[1];
if(b[6]==a[2] || b[6]==a[3] || b[6]==a[4] || b[6]==b[2] || b[6]==b[3] || b[6]==b[5], next); 
for (n=2,24,
if(b[6]<>w[n], next);
for (n=m+1,24, b[7]=w[n];
if(b[7]>a[4], next);
if(b[7]==a[2] || b[7]==a[3] || b[7]==a[4] || b[7]==b[2] || b[7]==b[4] || b[7]==b[5] || b[7]==b[6], next); 
b[8]=a[4]-b[7];
if(b[8]==a[2] || b[8]==a[3] || b[8]==b[1] || b[8]==b[2] || b[8]==b[3] || b[8]==b[4] || b[8]==b[5] || b[8]==b[6] || b[8]==b[7], next); 
for (o=2,24,
if(b[8]<>w[o], next);
if(b[7]+b[5]+b[6]+b[8]+a[5]<>s, next);
b[9]=b[2]+b[7];
if(b[9]==a[2] || b[9]==a[3] || b[9]==a[4] || b[9]==b[1] || b[9]==b[3] || b[9]==b[4] || b[9]==b[5] || b[9]==b[6] || b[9]==b[8], next); 
for (o=2,24,
if(b[9]<>w[o], next);
b[10]=b[1]+b[8];
if(b[10]==a[2] || b[10]==a[3] || b[10]==a[4] || b[10]==b[2] || b[10]==b[3] || b[10]==b[4] || b[10]==b[5] || b[10]==b[6] || b[10]==b[7] || b[10]==b[9], next); 
for (o=2,24,
if(b[10]<>w[o], next);

for (o=n+1,24, b[11]=w[o];
if(b[11]==a[2] || b[11]==a[3] || b[11]==a[4] || b[11]==b[2] || b[11]==b[4] || b[11]==b[5] || b[11]==b[6] || b[11]==b[8] || b[11]==b[9] || b[11]==b[10], next); 
b[17]=s-a[3]-b[9]-b[10]-b[11];
if(b[17]==a[2] || b[17]==a[3] || b[17]==a[4] || b[17]==b[1] || b[17]==b[2] || b[17]==b[3] || b[17]==b[4] || b[17]==b[5] || b[17]==b[6] || b[17]==b[7] || b[17]==b[8] || b[17]==b[9] || b[17]==b[10] || b[17]==b[11], next); 
for (p=2,24,
if(b[17]<>w[p], next);
print1(v[1],", "); print1(a,", "); print1(b); print(); print(); ););););););););););););););););
);
print(v);
}

В программе задан интервал (540002999999251, 5.40005*10^14), в этом интервале сейчас черепашка считает.
Ни одного кандидата пока не нашла.
Уже сомнение закрадывается: не напортачила ли при дописывании программы - добавление проверки ещё двух элементов.
Но тестирование программы вроде бы прошло успешно.

Господа!
Прошу оптимизировать программу, чтобы побыстрее работала :)
Я пишу программы очень примитивно - в лоб, никаких оптимизаций.
Возможности языка PARI/GP плохо знаю.

Пишите мне, пожалуйста, если удастся оптимизировать
natalimak1@yandex.ru

Наконец-то, посмотрела алгоритм предпроверки Макса, описанный в сообщении
https://dxdy.ru/post896257.html#p896257

Помню, что и тогда я не поняла этот алгоритм.
И сейчас тоже не поняла.
Написать программу по этому алгоритму не смогу.

А кто-нибудь сможет?

Итак, пока у меня есть две программы: моя и Алексея Белышева.

К сожалению, программа Белышева не хочет работать на Ахиллесах.
Выдаётся сообщение, что нет программы MSVCP100.dll
А на черепашке работает.
Но на черепашке я прерываю программу на ночь.
Хотя в программе прерывание предусмотрено и конечная точка интервала сохраняется, но мало ли что, вдруг в какой-то момент не сработает.
А на Ахиллесе прерывать не надо.

Пока кручу свою программу.
Но она работает медленно.
Кстати, программа Белышева тоже не очень быстро работает.

Пока моя программа не выдала ни одного нового кандидата ни на черепашке, ни на Ахиллесе-3.

О! Что я вчера нашла!
Умница моя черепашка - она всё хранит для меня.
Залетела в голову мысль, что генератор primesieve я в своё время скачала и опрбовала.
Давно это было, но память - удивительная вещь.
Полезла в папку "Загрузки" поискать этот генератор.
И нашла!
Архив называется так: "primesieve-5.0-win64-console".
Да! Это как раз то, что нужно.
Задаю интервал, в котором надо сгенерировать простые числа, и мгновенно получаю массив простых чисел!

Вчера весь день колдовала с этим массивом.
Получилось читать его в программу на PARI/GP как вектор, но только при точном задании длины вектора.
Не знаю, как прочитать массив простых чисел в программу, не задавая длину вектора.
Возможно ли это?
Ну вот, пока работаю с указанием длины вектора. Это прекрасно работает.

Массив сгенерированных простых чисел primesieve выводит так

539840239999153
539840239999169
539840239999189
539840239999273
539840239999279
539840239999427
539840239999433
539840239999447
539840239999453
539840239999457
539840239999559
539840239999637
539840239999667
539840239999673
539840239999717
539840239999741
539840239999757
539840239999793
539840239999831
539840239999847

Если задать в программе длину этого вектора, то программа прекрасно его читает.

Можно ли прочитать в программу на PARI/GP этот вектор, не задавая в программе его длину?

Господа!
Пожалуйста, просветите в этом вопросе.
Как я уже говорила, возможности языка PARI/GP очень плохо знаю.
Ну, например, задать чтение массива в вектор до первой пустой строки.
Так ведь можно?
Но тогда длину вектора надо задавать заранее и с большим запасом.
А если не задавать длину вектора заранее?
Так можно прочитать вектор в программу?

Теперь я понимаю, как Белышев задействовал генератор primesieve в своей программе на С++.
Всё очень просто!

Сейчас экспериментирую.
В интервале длины 50.000.000 (натуральных чисел) генерируется около 1.500.000 простых чисел.
Такой вектор программа на PARI/GP берёт, конечно. с увеличением памяти.
Обработка этого массива моей программой предпроверки выполняется довольно быстро.
Всё тормозится именно генерацией простых чисел в PARI/GP.

Белышев в своей программе генерировал простые числа в интервале 2.000.000.000 натуральных чисел.
И этот массив простых чисел он хранил в программе и обрабатывал его.
Отсюда огромное использование ОЗУ в программе.

Вот, определила время работы программы предпроверки для интервала длины 50.000.000 натуральных чисел

? default(timer,1)
? \r st4.txt
   logfile = "st4_res.txt"
  ***   Warning: not enough memory, new PARI stack 2147483648
  ***   Warning: new stack size = 2147483648 (2048.000 Mbytes).
[539840369998967, 539840369999011, 539840369999027, 539840369999041, 53984036999
9053, 539840369999123, 539840369999141, 539840369999303, 539840369999323, 539840
369999369, 539840369999417, 539840369999453, 539840369999459, 539840369999573, 5
39840369999591, 539840369999611, 539840369999639, 539840369999743, 5398403699997
47, 539840369999759, 539840369999783, 539840369999851, 539840369999867, 53984036
9999893, 539840369999911]
time = 14min, 35,760 ms.

Неплохое время.
А генерация простых чисел генератором primesieve в таком интервале выполняется 2-3 секунды!

Если ещё оптимизировать программу предпроверки, вообще всё будет замечательно.

PS. Программа выводит последнюю проверенную 25-ку.
Кандидатов не найдено.
Пропали кандидаты :)

Всё утро экспериментировала с массивом простых чисел, пытаясь записать его в вектор наиболее приемлемым способом.
Да, метод тыка, конечно, не самый эффективный метод :)

Ну, кое-что придумала.
Для запуска сочинила вот такой пакетный файл

primesieve 539841669998000 539841719999000 --print >inp1.txt
primesieve 539841719998000 539841769999000 --print >inp2.txt
primesieve 539841769998000 539841819999000 --print >inp3.txt
primesieve 539841819998000 539841869999000 --print >inp4.txt
primesieve 539841869998000 539841919999000 --print >inp5.txt
gp st4_1.txt
gp st4_2.txt
gp st4_3.txt
gp st4_4.txt
gp st4_5.txt
pause

По-моему, тут всё понятно.
Сначала генерируются пять порций простых чисел в заданных интервалах генератором primesieve.
Затем эти порции простых чисел проверяются на возможность построения квадрата Стенли 5х5 из 25 последовательных простых чисел.
Вот и всё.
Такая простая рационализация дала хорошее убыстрение процесса.
Можно сделать пакетный файл и на большее количество порций.

Генерировать порции в бОльших интервалах я не рискую, потому что вектор получается длинный, PARI/GP может не потянуть.
И так уже увеличение памяти делаю.

Поехал скрипт из 10 порций!

Вот как это выглядит

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842169998000 5398422
19999000 --print  1>inp1.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842219998000 5398422
69999000 --print  1>inp2.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842269998000 5398423
19999000 --print  1>inp3.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842319998000 5398423
69999000 --print  1>inp4.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842369998000 5398424
19999000 --print  1>inp5.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842419998000 5398424
69999000 --print  1>inp6.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842469998000 5398425
19999000 --print  1>inp7.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842519998000 5398425
69999000 --print  1>inp8.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842569998000 5398426
19999000 --print  1>inp9.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>primesieve 539842619998000 5398426
69999000 --print  1>inp10.txt

E:\Pari64-2-13-4\primesieve-5.0-win64-console>gp st4_1.txt
                  GP/PARI CALCULATOR Version 2.13.4 (released)
          amd64 running mingw (x86-64/GMP-6.1.2 kernel) 64-bit version
          compiled: Mar 25 2022, gcc version 8.3-posix 20190406 (GCC)
                            threading engine: single
                 (readline v8.0 enabled, extended help enabled)

                     Copyright (C) 2000-2020 The PARI Group

PARI/GP is free software, covered by the GNU General Public License, and comes
WITHOUT ANY WARRANTY WHATSOEVER.

Type ? for help, \q to quit.
Type ?17 for how to get moral (and possibly technical) support.

parisize = 8000000, primelimit = 500000
   log = 1 (on)
   [logfile is "st4_res.txt"]
  ***   Warning: not enough memory, new PARI stack 2147483648
  ***   Warning: new stack size = 2147483648 (2048.000 Mbytes).
1474229
[539842219998371, 539842219998377, 539842219998421, 539842219998437, 53984221999
8443, 539842219998503, 539842219998517, 539842219998541, 539842219998553, 539842
219998619, 539842219998629, 539842219998691, 539842219998709, 539842219998727, 5
39842219998737, 539842219998773, 539842219998797, 539842219998871, 5398422199988
77, 539842219998901, 539842219998929, 539842219998959, 539842219998971, 53984221
9998973, 539842219998997]
Goodbye!

E:\Pari64-2-13-4\primesieve-5.0-win64-console>gp st4_2.txt

. . . . . . . . 

Сначала, понятно, идёт генерация простых чисел - в 10 интервалах.
Длина одного интервала 50.000.000, следовательно, 10 интервалов это уже 500.000.000.

Это запуск программы предпроверки в первом интервале

E:\Pari64-2-13-4\primesieve-5.0-win64-console>gp st4_1.txt

1474229 - это количество простых чисел в первом интервале.

[539842219998371, 539842219998377, 539842219998421, 539842219998437, 53984221999
8443, 539842219998503, 539842219998517, 539842219998541, 539842219998553, 539842
219998619, 539842219998629, 539842219998691, 539842219998709, 539842219998727, 5
39842219998737, 539842219998773, 539842219998797, 539842219998871, 5398422199988
77, 539842219998901, 539842219998929, 539842219998959, 539842219998971, 53984221
9998973, 539842219998997]

это последняя проверенная 25-ка.

И
Goodbye!
Это понятно, что такое :)

Это запуск программы предпроверки во втором интервале

E:\Pari64-2-13-4\primesieve-5.0-win64-console>gp st4_2.txt

Ну, и так далее.

Примитивно, но работает!

Итак, генерацию простых чисел оптимизировала: применила генератор primesieve.
Как давно я мечтала о такой оптимизации!
Мечты сбываются :)

Теперь надо оптимизировать программу предпроверки.
По сравнению с генерацией простых чисел предпроверка работает безобразно медленно.
Как я уже говорила, генерация простых чисел в одном интервале длины 50.000.000 выполняется 2-3 секунды.

Пока экспериментирую на черепашке.
Собираюсь попробовать на Ахиллесе-3.
Не знаю, будет ли там работать этот скрипт.

Да, забыла сказать...
Вставила в программу предпроверки вывод кандидата в квадрат Стенли с 10 "дырками".
Прямо началось нечто странное - кандидаты пропали!

Ну вот, за всё время экспериментирования по новой программе предпроверки (усиленной) нашёлся один кандидат с 10 "дырками", а с 8 "дырками" пока не нашлось ни одного.

Ждём-с...

Наконец-то!
У-р-р-р-а-а-а!
На Ахиллесе-3 найдены кандидаты с 8 "дырками"

539830704654083, [0, 156, 164, 260, 656], [30, 126, 108, 56, 234, 86, 170, 90, 296, 120, 248, 0, 0, 0, 0, 0, 408, 0, 0, 0]
539830704654083, [0, 156, 164, 260, 656], [30, 126, 108, 56, 234, 86, 170, 90, 296, 120, 408, 0, 0, 0, 0, 0, 248, 0, 0, 0]
539830704654083, [0, 156, 164, 260, 656], [30, 126, 108, 56, 234, 86, 170, 90, 296, 120, 618, 0, 0, 0, 0, 0, 38, 0, 0, 0]

Ну, в первых двух вариантах просто переставлены элементы b[11] и b[17].
А третий вариант другой!

Дострою кандидатов вручную, может быть, получится меньше 8 "дырок".

Теперь можно написать программу окончательной проверки кандидатов с 8 "дырками".
Дальше усиливать предпроверку не имеет смысла, кандидатов и так находится очень мало.
Конечно, в BOINC-проекте их побольше будет находиться, но BOINC-проект для задачи века пока только в планах.
Материализовать BOINC-проект ох как непросто!
Я сделала это уже шесть раз!
Три BOINC-проекта в настоящее время работают, а три остановлены.
Впереди седьмая попытка. Не знаю, хватит ли на неё сил.

Да!
Получился при достраивании квадрат Стенли с 7 "дырками".
Завтра покажу иллюстрацию.

Ну, с 7 "дырками" уже был квадрат Стенли; смотрите сообщение
https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12852

Надо бы поменьше "дырок", но пока нет.
Хорошо хоть с 8 "дырками" иногда программа находит решения, а то совсем было бы тоскливо.

Завтра попробую на Ахиллесе-3 запустить скрипт на 10 порций.
Черепашка пока не нашла кандидатов с 8 "дырками".

Вот он - квадрат Стенли с 7 "дырками"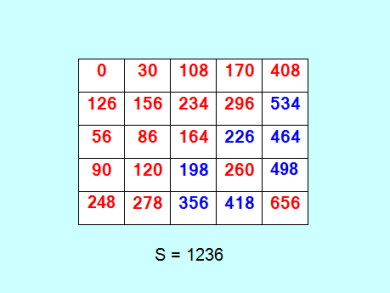



Красавец!

Квадрат строился из элементов следующей 25-ки из последовательных простых чисел

539830704654083: 0, 30, 38, 56, 86, 90, 108, 120, 126, 156, 164, 170, 204, 234, 248, 260, 278, 296, 350, 408, 468, 476, 540, 618, 656

Выданный программой предпроверки кандидат с 8 "дырками"

539830704654083, [0, 156, 164, 260, 656], [30, 126, 108, 56, 234, 86, 170, 90, 296, 120, 408, 0, 0, 0, 0, 0, 248, 0, 0, 0]

Квадрат на иллюстрации получен ручным достраиванием кандидата.

С 6 "дырками" (и менее) квадрат Стенли пока не найден.

Скрипт на Ахиллесе-3 запустился!
Ура!

Итак, скриптом проверяются 10 интервалов по 50.000.000.
Генерация простых чисел в заданных интервалах прошла успешно.
Началась предпроверка.
Наблюдаю.

Следующие 10 интервалов запустила на черепашке.
Посмотрим, кто быстрее справится.
У Ахиллеса-3 производительность не очень высокая.

Черепашка уже отстрелялась!
На Ахиллесе-3 проверятся седьмая порция.

Кандидатов на черепашке не найдено даже с 10 "дырками".