Задача века
Message boards :
Cafe :
Задача века
Message board moderation
Previous · 1 . . . 9 · 10 · 11 · 12 · 13 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Господа, вам интересна история задачи века? Я начала было рассказывать на форуме Math Help Planet, но там абсолютно никому не интересно. Вот репост https://mathhelpplanet.com/viewtopic.php?p=485896#p485896 "Nataly-Mak" wrote: У задачи века должна быть богатая история. ___________________________ конец репоста Это о минимальном магическом квадрате 3-го порядка из последовательных простых чисел. tomtitsin спросил: "Почему нужны симметричные кортежи?" Потому что все магические квадраты 3-го порядка ассоциативные (ассоциативность = симметричность). Кстати, вот тут и родился термин КПППЧ - Комплементарные Пары Последовательных Простых Чисел. Дальше стояла задача построения минимального пандиагонального квадрата 4-го порядка из последовательных простых чисел. Известный факт: между ассоциативными и пандиагональными квадратами 4-го порядка существует взаимно-однозначное соответствие. Следовательно, достаточно построить ассоциативный квадрат 4-го порядка из последовательных простых чисел. Для построения такого квадрата нужна КПППЧ-16, то есть симметричный кортеж длины 16 из последовательных простых чисел. Вот с поиска КПППЧ-16, собственно, и начался проект "Симметричные кортежи из последовательных простых чисел". Это было осенью 2014 года, то есть ровно 10 лет назад. И первым участником проекта был г. Петухов. Проект начинался ещё на форуме ПЕН (Портал Естественных Наук). Потом Макс Алексеев подключился, Бегемот ещё, Ярослав Врублевский и даже... Progger! Это уже было на форуме dxdy.ru. Максу повезло: он нашёл минимальный пандиагональный квадрат 4-го порядка из последовательных простых чисел. Почти одновременно с Максом квадрат нашли г. Петухов и Progger. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, ещё раз о минимальном пандиагональном квадрате 4-го порядка. Посмотрите, пожалуйста, сообщение https://boinc.progger.info/odlk/forum_thread.php?id=259&postid=12682 Макс посвятил найденному им квадрату отдельную последовательность в OEIS https://oeis.org/A245721 Вот он - красавец  Квадрат построен из чисел следующего симметричного кортежа длины 16 из последовательных простых чисел 170693941183817: 0 30 42 44 72 74 86 90 116 120 132 134 162 164 176 206 В конце этого года автор французской энциклопедии о магических квадратах Christian Boyer подвёл итоги за год. Я написала ему о находке Макса. От сразу же внёс этот квадрат в энциклопедию! Вот такая история минимального пандиагонального квадрата 4-го порядка из последовательных простых чисел. Для меня захватывающая история, всё очень живо помню. PS. Дата последовательности OEIS о квадрате Макса: Jul 30 2014. Это было даже не осенью, а летом 2014 г. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Забыла сказать, что ассоциативный квадраты 4-го порядка взаимно-однозначно связан с ассоциативным квадратом Стенли. Поэтому искался ассоциативный квадрат Стенли 4-го порядка из последовательных простых чисел, а дальше известным преобразованием получался ассоциативный квадрат 4-го порядка и из него пандиагональный квадрат. В последовательности OEIS Макс даже привёл соответствующий квадрат Стенли A Stanley antimagic square formed by these primes: Вот так выглядит соответствующий квадрат Стенли из элементов паттерна (моя программа немного по-другому построила квадрат - отразила относительно главной диагонали) 0 30 44 74 42 72 86 116 90 120 134 164 132 162 176 206 Здесь хорошо видна ассоциативность квадрата Стенли. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну, с квадратами 3-го и 4-го порядка теперь совсем всё понятно :) А дальше была поставлена задача: построить минимальный пандиагональный квадрат 5-го порядка из последовательных простых чисел. И до сих пор эта задача не решена! Не только минимальный - вообще никакой не найден. Поразительно, что минимальный пандиагональный квадрат 6-го порядка из последовательных простых чисел найден давным-давно. Посмотрите, пожалуйста, сообщение https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12729 Покажу ещё раз квадрат  Для построения квадрата использовался не симметричный кортеж длины 36 из последовательных простых чисел 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251 Крупно повезло квадрату 6-го порядка! Этому квадрату посвящена последовательность OEIS https://oeis.org/A073523 PS. Я очень долго искала второй пандиагональный квадрат 6-го порядка из последовательных простых чисел, но не нашла. Тогда я ещё не знала о поиске по паттерну. Можно попробовать. Теоретический паттерн у нас есть 0, 4, 6, 12, 16, 22, 30, 34, 36, 40, 42, 46, 60, 64, 70, 72, 82, 84, 90, 96, 100, 106, 112, 114, 124, 126, 130, 132, 144, 156, 160, 162, 166, 172, 174, 184 Скорее всего, и ещё есть; кажется, никто не искал теоретические паттерны для пандиагонального квадрата 6-го порядка. Но, думаю, поиск по паттерну для пандиагонального квадрата 6-го порядка будет не простым, так же, как и для квадрата Стенли 5-го порядка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Не надоела вам история, господа? Я могу ещё много рассказывать :) Пандиагональный квадрат 7-го порядка из последовательных простых чисел тоже искала и нашла с 4 "дырками". Сейчас найду иллюстрацию. Вот 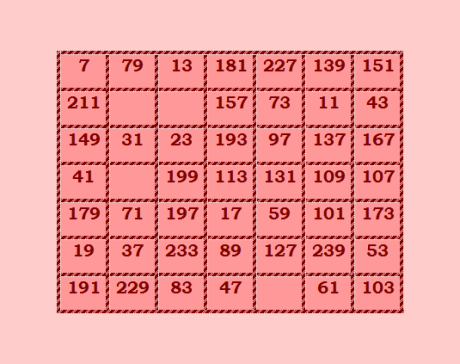 Всё это было давным-давно. Ну, история, одним словом :) Я искала и пандиагональный квадрат 8-го порядка из последовательных простых чисел. Не помню, сколько у меня "дырок" получилось в этом квадрате. Но что дальше искать, если пандиагональный квадрат 5-го порядка из последовательных простых чисел не найден! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
tomtitsin (=gris) писал https://mathhelpplanet.com/viewtopic.php?p=485905#p485905 "tomtitsin" wrote:
Ну, во-первых, не пандиагонализм, а пандиагональность, лучше звучит. А потом, есть термины и помудрёнее, например: "Пентадекагональные треугольники". Это тема на форуме dxdy.ru. Этот термин я вообще не выговариваю, особенно ежели спросонья или натощак :) А "пандиагональный" очень простой термин. Во-вторых, не все задачу забросили. Вот и г. Петухов недавно что-то вспомнил. Ностальгия! :)) Я задачей год назад занималась, и сейчас занимаюсь. ... надо подробно и со вкусом изучить эти ваши квадраты, поиграть с ними, поразмыслить над теорией, потом почитать то, что уже создано. Провести эксперименты. А что мешает? Изучите, поиграйте, поразмыслите, почитайте, проведите :) Квадраты не только мои, их много и коллеги построили, очень разных и вкусных! Прямо со вкусом эти квадратики надо бы изучить :) А потом надо двигаться вперёд! Ещё никто не опоздал, ибо задача не решена. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А ещё есть идеальные магические квадраты! Это когда квадрат одновременно пандиагональный и ассоциативный. Идеальные квадраты существуют для порядков n>=5. Построить идеальный квадрат 5-го порядка из простых чисел не проблема, и 6-го порядка тоже. Они давно построены. А вот из последовательных простых чисел - проблема! Для идеального квадрата 5-го прядка требуется симметричная 25-ка из последовательных простых чисел. А для идеального квадрата 6-го порядка - симметричная 36-ка из последовательных простых чисел. Ну, эти кортежи точно в этом веке не найдут :) Разве что квантовые компьютеры получат распространение или хотя бы суперкомпьютеры или кластеры. Не помню, кто нашёл минимальный идеальный квадрат 5-го порядка из простых чисел, а 6-го порядка нашёл Макс. Вот посмотрите, пожалуйста, об идеальных квадратах из простых чисел сообщение на форуме dxdy.ru https://dxdy.ru/post1002869.html#p1002869 А это последовательность в OEIS https://oeis.org/A257316 Идеальные магические квадраты по-английски называются ultramagic squares. Вот минимальный идеальный квадрат 6-го порядка из простых чисел, найденный Максом EXAMPLE Красивый квадратик! Он построен из симметричной 36-ки, но! не из последовательных простых чисел. А это найденный мной минимальный идеальный квадрат 5-го порядка из простых чисел 113 1151 1229 911 101 839 521 41 1013 1091 941 953 701 449 461 311 389 1361 881 563 1301 491 173 251 1289 Он построен из симметричной 25-ки, но! не из последовательных простых чисел. Кстати, вот кортеж, из чисел которого построен квадрат 41 101 113 173 251 311 389 449 461 491 521 563 701 839 881 911 941 953 1013 1091 1151 1229 1289 1301 1361 Это паттерн 0 60 72 132 210 270 348 408 420 450 480 522 660 798 840 870 900 912 972 1050 1110 1188 1248 1260 1320 Как видим, диаметр кортежа очень большой. А если из кортежей с минимальным диаметром строить идеальный квадрат 5-го порядка, то вот теоретические паттерны a(25) 0 6 24 36 60 66 84 120 126 150 186 204 210 216 234 270 294 300 336 354 360 384 396 414 420 0 6 24 36 66 84 120 126 144 150 186 204 210 216 234 270 276 294 300 336 354 384 396 414 420 0 6 24 60 66 84 90 120 126 144 186 204 210 216 234 276 294 300 330 336 354 360 396 414 420 0 6 30 84 90 96 114 126 156 174 180 204 210 216 240 246 264 294 306 324 330 336 390 414 420 0 12 30 42 48 78 120 132 162 168 180 198 210 222 240 252 258 288 300 342 372 378 390 408 420 0 12 30 48 78 90 120 132 162 168 180 198 210 222 240 252 258 288 300 330 342 372 390 408 420 0 24 30 54 60 66 84 96 126 144 156 186 210 234 264 276 294 324 336 354 360 366 390 396 420 0 24 30 54 60 66 84 126 144 150 156 186 210 234 264 270 276 294 336 354 360 366 390 396 420 0 24 30 54 60 66 114 126 144 156 180 186 210 234 240 264 276 294 306 354 360 366 390 396 420 0 24 30 60 66 84 114 126 144 150 156 180 210 240 264 270 276 294 306 336 354 360 390 396 420 https://oeis.org/A266512/a266512_1.txt PS. Проверила эти теоретические паттерны на построение квадрата Стенли 5-го порядка, ни из одного паттерна квадрат Стенли не построился. Надо искать теоретические паттерны с минимальным диаметром для идеального квадрата 5-го порядка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А ещё интересно: каждому пандиагональному квадрату 5-го порядка соответствует один и только один квадрат Стенли, а каждому идеальному квадрату 5-го порядка соответствует один и только один ассоциативный квадрат Стенли. Для показанного выше идеального квадрата 5-го порядка вот соответствующий ассоциативный квадрат Стенли 0 60 450 840 900 72 132 522 912 972 210 270 660 1050 1110 348 408 798 1188 1248 420 480 870 1260 1320 Очень симпатичный квадратик! А как вы думаете, господа, ассоциативный квадрат Стенли не проще ли искать? Конечно, сам ассоциативный квадрат Стенли искать проще. Однако реальный симметричный кортеж длины 25 из последовательных простых чисел искать очень сложно. Совсем недавно только 19-ку симметричную нашли из последовательных простых чисел. Почти 10 лет искали! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Утром сняла результаты с обоих Ахиллесов, все приближения только с q=17. Постобработка тоже ничего не дала лучшего. Решила подбросить теоретических паттернов. Нашла своей программой 182 новых теоретических паттерна для квадрата Стенли. Теперь у меня 794 теоретических паттерна. Запустила программу с новым списком теоретических паттернов. И вот нашлось приближение с q=19 ! [0, 6, 10, 16, 24, 30, 46, 52, 60, 70, 84, 90, 100, 106, 114, 136, 210, 220, 226, 232, 234, 256, 286, 316, 436] 39174919880420557: [0, 6, 10, 16, 22, 24, 30, 46, 70, 84, 100, 102, 114, 120, 136, 220, 226, 232, 256, 286, 316, 364, 366, 384, 436] q=19 Оно нашлось с новым паттерном. Постобработка, увы, этот результат не улучшила. Очевидно, что необходимо расширять базу теоретических паттернов. Их надо много, даже не одну тысячу, а несколько тысяч. Но тогда Ахиллесы не потянут поиск с такой базой. Нужна техника! А технику можно получить только в BOINC-проекте. С этим у нас пока всё глухо :( Залетела мыслишка: можно расширить базу теоретических паттернов пока только для постобработки. Эта программа потянет проверку по большой базе. Она у меня вообще на черепашке работает, это несколько секунд всего с теперешней базой в 794 паттерна. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В новой порции результатов только с q=18 найдены приближения [0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 130, 136, 190, 210, 214, 220, 226, 340, 466, 472, 526, 556, 676] 39069132645743797: [0, 4, 6, 10, 16, 22, 60, 94, 114, 130, 154, 174, 190, 210, 214, 220, 340, 354, 462, 466, 472, 480, 526, 610, 676] q=18 [0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 130, 136, 190, 210, 214, 220, 226, 276, 282, 336, 340, 366, 486] 39467510249276167: [0, 4, 10, 16, 22, 34, 60, 64, 106, 130, 136, 144, 210, 220, 232, 234, 276, 282, 336, 340, 366, 394, 450, 454, 486] q=18 [0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 148, 154, 208, 210, 214, 238, 258, 270, 276, 330, 358, 360, 480] 39502692400667053: [0, 4, 6, 10, 24, 34, 60, 70, 94, 96, 108, 138, 148, 208, 214, 238, 258, 276, 330, 358, 360, 376, 424, 444, 480] q=18 Постобработка приближения не улучшила. Расширила базу теоретических паттернов для постобработки до 7310 штук. Программа поиска пока работает с базой из 794 теоретических паттернов. Если для 7310 теоретических паттернов запустить программу, это будет очень долго считаться. Но смысл в этом, конечно, есть. Здесь очень пригодилась бы петуховская супер-пупер программа поиска по паттерну, которая в 1000 раз быстрее работает, чем программа на PARI/GP. Ну, г. Петухов считает, что поиск по паттерну в этой задаче бессмысленный. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Я убрала в программе вывод номеров паттернов. Покажу результаты одного прохода программы на Ахиллесе (10:31) gp > \r st_pat.txt logfile = "st_pat1_res.txt" [0, 4, 6, 10, 48, 54, 66, 70, 96, 100, 114, 144, 180, 184, 228, 270, 276, 336, 3 66, 450, 490, 496, 556, 586, 670] 39463078575570313: [0, 4, 54, 60, 66, 70, 96, 100, 144, 180, 184, 228, 244, 360, 366, 378, 390, 450, 490, 496, 520, 586, 598, 658, 670] q=17 [0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 130, 136, 186, 190, 192, 210, 214 , 220, 226, 246, 276, 340, 396] 39461167290453967: [0, 4, 6, 10, 22, 34, 64, 90, 94, 106, 130, 190, 192, 220, 24 6, 252, 276, 300, 304, 312, 340, 346, 366, 370, 396] q=17 [0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 130, 136, 190, 210, 214, 220, 226 , 276, 282, 336, 340, 366, 486] 39467510249276167: [0, 4, 10, 16, 22, 34, 60, 64, 106, 130, 136, 144, 210, 220, 232, 234, 276, 282, 336, 340, 366, 394, 450, 454, 486] q=18 [0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 210, 214, 220, 226, 228, 238, 244 , 280, 298, 310, 328, 430, 448] 39516670304544463: [0, 4, 10, 18, 24, 60, 64, 120, 210, 214, 220, 228, 244, 280, 294, 298, 310, 336, 358, 364, 378, 400, 408, 430, 448] q=17 [0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 118, 124, 138, 178, 208, 210, 214, 25 8, 294, 300, 328, 354, 384, 504] 39408719199982543: [0, 4, 6, 10, 48, 54, 60, 64, 108, 120, 124, 178, 180, 210, 2 70, 294, 300, 316, 336, 346, 354, 384, 400, 406, 504] q=17 [0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 148, 154, 208, 210, 214, 238, 25 8, 270, 276, 330, 358, 360, 480] 39502692400667053: [0, 4, 6, 10, 24, 34, 60, 70, 94, 96, 108, 138, 148, 208, 214 , 238, 258, 276, 330, 358, 360, 376, 424, 444, 480] q=18 [0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 174, 180, 210, 214, 234, 258, 26 4, 328, 334, 384, 388, 418, 538] 39618418191405793: [0, 48, 54, 60, 90, 108, 124, 138, 154, 160, 166, 168, 180, 2 14, 216, 234, 258, 328, 334, 358, 384, 388, 390, 418, 538] q=17 [0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 210, 214, 238, 244, 258, 270, 27 6, 298, 328, 330, 360, 448, 480] 39620202953456683: [0, 4, 6, 10, 48, 60, 88, 90, 94, 96, 108, 136, 210, 214, 244 , 270, 298, 328, 330, 354, 384, 400, 406, 460, 480] q=17 [0, 6, 10, 12, 16, 18, 60, 70, 72, 90, 100, 102, 112, 118, 172, 202, 210, 220, 2 22, 276, 282, 322, 336, 366, 486] 39491112473733241: [0, 6, 60, 70, 90, 100, 102, 112, 126, 202, 220, 222, 228, 27 6, 282, 318, 322, 336, 352, 366, 406, 448, 466, 480, 486] q=17 [0, 6, 10, 16, 24, 30, 60, 70, 84, 90, 100, 114, 154, 160, 210, 214, 220, 234, 2 44, 276, 282, 336, 364, 366, 486] 39595263340065127: [0, 6, 10, 16, 30, 36, 60, 70, 100, 112, 114, 154, 160, 186, 244, 276, 282, 300, 312, 364, 366, 412, 426, 454, 486] q=17 time = 14h, 7min, 32,099 ms. Приближения выводятся для q>=17. Потом эти приближения проходят постобработку. Иногда в результате постобработки получается улучшение приближения. Этот проход выполнялся для 794 теоретических паттернов. Если ввести базу из 7310 теоретических паттернов, время обработки увеличится почти пропорционально. Супер-пупер программа г. Петухова потянула бы. На PARI/GP это очень медленно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот проверка последнего приближения с q=19 [0, 6, 10, 16, 24, 30, 46, 52, 60, 70, 84, 90, 100, 106, 114, 136, 210, 220, 226, 232, 234, 256, 286, 316, 436] 39174919880420557: [0, 6, 10, 16, 22, 24, 30, 46, 70, 84, 100, 102, 114, 120, 136, 220, 226, 232, 256, 286, 316, 364, 366, 384, 436] q=19 Полный квадрат Стенли 0 6 60 90 210 10 16 70 100 220 24 30 84 114 234 46 52 106 136 256 226 232 286 316 436 Квадрат Стенли с 6 "дырками" 0 6 □ □ □ 10 16 70 100 220 24 30 84 114 □ 46 □ □ 136 256 226 232 286 316 436 Диаметр паттерна не очень большой. Симпатичный квадратик! С q=20 пока никак не найдётся приближение. Расширила базу теоретических паттернов до 9779 штук. Ах, число какое получилось - палиндромное :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это новые приближения [0, 6, 10, 16, 24, 30, 60, 70, 84, 90, 100, 114, 156, 162, 210, 216, 220, 226, 232, 234, 246, 286, 316, 366, 436] 40737920945886397: [0, 6, 10, 16, 22, 24, 30, 36, 70, 84, 90, 100, 106, 132, 136, 160, 162, 220, 226, 232, 234, 316, 366, 402, 436] q=18 и с q=17 40805200131689023: [0, 4, 6, 10, 60, 76, 88, 90, 94, 120, 156, 160, 210, 214, 238, 268, 280, 294, 316, 328, 354, 444, 450, 456, 478] 40744178978058883: [0, 4, 6, 10, 60, 64, 88, 118, 126, 160, 210, 214, 216, 220, 238, 246, 250, 274, 370, 376, 384, 438, 468, 480, 484] 40673478928545553: [0, 6, 10, 16, 24, 58, 60, 70, 84, 94, 100, 154, 178, 184, 214, 216, 220, 228, 238, 250, 256, 268, 270, 336, 388] 40803206404055647: [0, 4, 10, 24, 60, 70, 76, 84, 100, 114, 210, 214, 216, 234, 244, 276, 286, 292, 304, 336, 354, 364, 366, 432, 486] 40471069129917523: [0, 6, 10, 28, 48, 66, 76, 96, 100, 130, 174, 270, 276, 286, 336, 388, 396, 430, 490, 504, 534, 556, 564, 586, 616] 40435410971761363: [0, 4, 6, 10, 24, 46, 48, 70, 76, 78, 108, 130, 148, 150, 166, 174, 208, 210, 214, 238, 244, 246, 280, 306, 358] 40559268302151013: [0, 4, 6, 60, 64, 70, 94, 100, 108, 114, 120, 154, 174, 204, 210, 226, 228, 244, 298, 328, 364, 396, 400, 444, 448] 40568758665908503: [0, 4, 10, 18, 24, 30, 60, 64, 78, 94, 108, 148, 174, 198, 220, 228, 280, 310, 328, 370, 378, 394, 408, 448, 528] 40461547172203033: [0, 4, 10, 28, 34, 70, 78, 90, 94, 118, 174, 204, 210, 214, 238, 240, 244, 276, 298, 316, 324, 330, 364, 426, 480] 40479024391815193: [0, 6, 10, 16, 28, 34, 64, 88, 90, 94, 114, 210, 270, 276, 286, 316, 330, 406, 438, 444, 480, 538, 568, 624, 688] 40516957121956873: [0, 4, 18, 28, 54, 64, 94, 96, 108, 138, 154, 208, 210, 214, 238, 280, 294, 318, 336, 340, 346, 358, 370, 486, 490] 40607814450590263: [0, 4, 6, 16, 28, 34, 88, 90, 100, 114, 118, 130, 204, 210, 220, 238, 240, 244, 258, 298, 316, 318, 324, 346, 364] Плохо! Некоторые приближения с q=17 при постобработке дали приближения с q=18, но это уже мало интересно. Сейчас программа работает с 794 теоретическими паттернами. Теоретически каждый из этих паттернов может дать реальный кортеж X: [теоретический паттерн] но при каком X это случится??? Вот в чём вопрос! Расширила ещё базу теоретических паттернов - до 10616 штук. Но это только для постобработки. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот очередная порция результатов с Ахиллеса [0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 160, 166, 210, 214, 220, 228, 250, 370, 424, 430, 484, 514, 634] 41267664093956473: [0, 4, 6, 10, 60, 64, 66, 78, 90, 108, 166, 210, 220, 250, 276, 288, 306, 370, 390, 400, 418, 424, 430, 550, 634] q=17 [0, 4, 6, 10, 28, 34, 48, 54, 60, 64, 88, 90, 94, 108, 118, 138, 210, 214, 238, 258, 270, 276, 330, 360, 480] 41237258522423983: [0, 4, 28, 48, 54, 78, 90, 108, 118, 138, 148, 180, 210, 214, 238, 246, 270, 276, 328, 330, 336, 360, 444, 468, 480] q=17 [0, 6, 10, 16, 24, 30, 46, 52, 60, 70, 84, 90, 100, 106, 114, 136, 210, 220, 234, 256, 276, 282, 336, 366, 486] 41262228434401207: [0, 6, 10, 16, 22, 24, 30, 46, 52, 90, 114, 136, 160, 162, 210, 220, 226, 234, 282, 330, 336, 340, 354, 364, 486] q=17 [0, 6, 10, 16, 24, 30, 60, 70, 84, 90, 100, 114, 126, 132, 186, 210, 216, 220, 234, 336, 354, 360, 414, 444, 564] 41105030828145517: [0, 6, 10, 16, 24, 114, 126, 132, 186, 210, 216, 220, 270, 312, 316, 336, 340, 354, 360, 384, 414, 424, 436, 496, 564] q=17 [0, 6, 10, 16, 24, 30, 60, 70, 84, 90, 100, 114, 154, 160, 210, 214, 220, 234, 244, 276, 282, 336, 364, 366, 486] 41273628989518477: [0, 6, 10, 16, 24, 90, 100, 114, 142, 210, 214, 220, 244, 250, 252, 270, 276, 282, 300, 310, 336, 352, 364, 402, 486] q=17 [0, 4, 42, 46, 64, 66, 70, 106, 130, 144, 186, 210, 246, 250, 276, 280, 294, 310, 336, 340, 360, 390, 420, 540, 570] 40925846100133387: [0, 4, 42, 52, 64, 66, 70, 72, 84, 96, 106, 144, 162, 186, 250, 280, 294, 336, 376, 390, 420, 526, 540, 562, 570] q=17 [0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 130, 136, 190, 210, 214, 220, 226, 276, 282, 336, 340, 366, 486] 41013607494510247: [0, 4, 6, 10, 22, 60, 90, 130, 136, 142, 150, 156, 190, 210, 214, 220, 282, 312, 324, 330, 340, 366, 420, 454, 486] q=17 [0, 4, 6, 10, 18, 24, 60, 64, 70, 76, 78, 90, 94, 108, 130, 160, 210, 214, 228, 238, 244, 280, 298, 328, 448] 40919494929873733: [0, 4, 6, 10, 64, 70, 94, 96, 108, 130, 144, 160, 210, 214, 228, 238, 244, 246, 280, 286, 298, 364, 400, 424, 448] q=18 [0, 4, 6, 10, 18, 24, 60, 64, 70, 76, 78, 90, 94, 108, 130, 160, 210, 214, 228, 280, 304, 310, 364, 394, 514] 41017437873740743: [0, 4, 6, 10, 24, 34, 64, 70, 76, 78, 108, 130, 160, 214, 268, 280, 304, 316, 330, 358, 394, 396, 466, 496, 514] q=17 [0, 6, 10, 16, 24, 30, 60, 70, 84, 90, 100, 114, 154, 160, 210, 214, 220, 234, 244, 258, 264, 318, 348, 364, 468] 41028348949219183: [0, 4, 6, 16, 24, 30, 70, 90, 114, 160, 166, 186, 214, 220, 226, 244, 250, 258, 264, 318, 334, 336, 340, 364, 468] q=17 [0, 6, 10, 16, 28, 34, 60, 70, 88, 90, 100, 118, 138, 144, 198, 210, 220, 228, 238, 244, 250, 304, 334, 348, 454] 40965839869688593: [0, 4, 10, 16, 28, 34, 60, 70, 88, 100, 144, 198, 210, 226, 228, 244, 324, 334, 346, 348, 420, 424, 444, 450, 454] q=17 Ничего интересного. Сейчас пропущу через постобработку. Напомню: сначала выводится теоретический паттерн для квадрата Стенли, затем найденный кортеж-приближение; q - количество совпадающих элементов в теоретическом паттерне и в паттерне приближения. Ещё напомню, что здесь совпадающие элементы не обязательно должны находиться в одинаковых позициях. То есть мы находим пересечение двух паттернов. Из элементов пересечения и строится дырявый квадрат Стенли. PS. Постобработка не дала улучшений до q=19. Улучшения до q=18 уже не интересны. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Открыла тему на форуме Math Help Planet "Первая гипотеза Харди-Литтлвуда и квадрат Стенли" https://mathhelpplanet.com/viewtopic.php?f=48&t=83765 Господа! Если вы хотите принять участие в обсуждении проблемы, а здесь не можете писать, то на форуме Math Help Planet тема как раз для вас. gris, ау! Вы вернулись из страны коз и енотов? :) Пожалуйста, подключайтесь к обсуждению проблемы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот ещё порция результатов [0, 4, 36, 40, 64, 66, 70, 100, 130, 144, 180, 210, 252, 256, 270, 274, 294, 316, 330, 334, 360, 396, 414, 546, 564] 41898561342417907: [0, 36, 40, 54, 66, 70, 100, 114, 130, 136, 144, 186, 210, 252, 270, 274, 330, 334, 396, 414, 504, 514, 526, 546, 564] q=18 [0, 4, 6, 10, 36, 40, 48, 54, 84, 120, 124, 168, 186, 190, 234, 270, 276, 306, 390, 456, 490, 496, 526, 610, 676] 41860991406028303: [0, 10, 36, 48, 54, 106, 120, 124, 168, 186, 190, 234, 276, 306, 346, 364, 390, 490, 504, 526, 556, 564, 610, 640, 676] q=18 и с q=17 42168799280563513: [0, 10, 18, 24, 54, 60, 78, 94, 108, 160, 180, 210, 214, 264, 270, 294, 318, 348, 360, 384, 418, 448, 460, 468, 480; 42105556167941593: [0, 4, 6, 10, 18, 28, 34, 40, 48, 60, 64, 88, 90, 106, 126, 166, 210, 220, 250, 346, 400, 418, 460, 516, 550; 42008811248038507: [0, 4, 6, 12, 36, 42, 60, 64, 90, 130, 132, 136, 214, 220, 246, 292, 334, 384, 390, 412, 426, 432, 486, 526, 636; 42048722997766357: [0, 4, 36, 42, 64, 90, 96, 174, 192, 196, 202, 246, 256, 274, 280, 300, 306, 330, 334, 346, 364, 402, 406, 444, 484; 42078941396744947: [0, 4, 6, 10, 22, 24, 30, 36, 70, 84, 90, 94, 114, 126, 204, 220, 234, 246, 294, 336, 340, 354, 400, 430, 550; 42078948015939067: [0, 10, 30, 36, 70, 84, 90, 100, 106, 114, 142, 154, 160, 186, 220, 234, 244, 276, 282, 310, 330, 364, 366, 370, 396; 41898561342417907: [0, 36, 40, 54, 66, 70, 100, 114, 130, 136, 144, 186, 210, 252, 270, 274, 330, 334, 396, 414, 504, 514, 526, 546, 564; 41860991406028303: [0, 10, 36, 48, 54, 106, 120, 124, 168, 186, 190, 234, 276, 306, 346, 364, 390, 490, 504, 526, 556, 564, 610, 640, 676; 41785207188334783: [0, 4, 10, 18, 28, 34, 40, 60, 78, 90, 94, 108, 118, 148, 196, 210, 228, 238, 250, 276, 306, 420, 448, 460, 580; 41812359980847013: [0, 4, 6, 18, 24, 46, 60, 64, 90, 94, 214, 228, 238, 246, 250, 298, 306, 328, 420, 474, 540, 550, 556, 558, 678; 41897312780048773: [0, 4, 6, 28, 36, 48, 54, 60, 64, 108, 138, 144, 150, 210, 214, 234, 258, 298, 358, 388, 414, 438, 474, 526, 588; 42008054131428943: [0, 6, 10, 18, 34, 48, 54, 60, 64, 70, 90, 94, 210, 214, 238, 246, 270, 286, 330, 336, 340, 358, 360, 424, 490; По-прежнему ничего интересного, нет даже с q=19. Начала по чуть-чуть наращивать базу теоретических паттернов в программе поиска. На данный момент 959 теоретических паттернов в базе, было 794. Поиск превысил 4,2е16. Ну, это ведь не брутфорс. В программе Белышева с брутфорсом пока так Поиск антимага Стенли 5-го порядка 262:15:24 Текущий интервал: [1056313533444312 ... 1056315533444312] Проверено: 2112%% Скорость: 89 Всего: 57815845 Подходящих: 11559637 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Интересно: для диаметра 490 сгенерировалось 165 различных (допустимых) паттернов. Отлично! Все их добавила в базу поиска. Покажу немного этих паттернов 0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 114, 120, 174, 204, 210, 214, 226, 280, 286, 324, 340, 370, 490; 0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 126, 132, 186, 210, 214, 216, 226, 280, 286, 336, 340, 370, 490; 0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 186, 192, 210, 214, 226, 246, 276, 280, 286, 340, 370, 396, 490; 0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 210, 214, 226, 270, 276, 280, 286, 330, 340, 360, 370, 480, 490; 0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 114, 120, 174, 204, 210, 214, 228, 280, 286, 324, 340, 370, 490; 0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 148, 154, 208, 210, 214, 228, 238, 280, 286, 340, 358, 370, 490; 0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 198, 204, 210, 214, 228, 258, 280, 286, 288, 340, 370, 408, 490; 0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 210, 214, 228, 238, 244, 280, 286, 298, 328, 340, 370, 448, 490; 0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 210, 214, 228, 258, 264, 280, 286, 318, 340, 348, 370, 468, 490; 0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 210, 214, 228, 270, 276, 280, 286, 330, 340, 360, 370, 480, 490; 0, 4, 6, 10, 28, 34, 48, 54, 60, 64, 88, 90, 94, 108, 118, 138, 210, 214, 238, 258, 280, 286, 340, 370, 490; 0, 4, 6, 10, 28, 34, 60, 64, 88, 90, 94, 114, 118, 120, 174, 204, 210, 214, 238, 280, 286, 324, 340, 370, 490; . . . . . . . . . 0, 6, 24, 30, 34, 40, 60, 84, 90, 94, 114, 124, 178, 184, 210, 234, 238, 244, 268, 280, 286, 340, 370, 388, 490; 0, 6, 24, 30, 46, 52, 60, 66, 72, 84, 90, 106, 114, 126, 136, 156, 210, 234, 256, 276, 280, 286, 340, 370, 490; 0, 6, 24, 30, 46, 52, 60, 84, 90, 94, 100, 106, 114, 136, 154, 184, 210, 234, 256, 280, 286, 304, 340, 370, 490; 0, 6, 24, 30, 46, 52, 60, 84, 90, 106, 114, 126, 132, 136, 186, 210, 216, 234, 256, 280, 286, 336, 340, 370, 490; 0, 6, 24, 30, 46, 52, 60, 84, 90, 106, 114, 136, 154, 160, 210, 214, 234, 244, 256, 280, 286, 340, 364, 370, 490; 0, 6, 24, 30, 46, 52, 60, 84, 90, 106, 114, 136, 156, 162, 210, 216, 234, 246, 256, 280, 286, 340, 366, 370, 490; 0, 6, 24, 30, 60, 66, 72, 84, 90, 100, 106, 114, 126, 156, 160, 190, 210, 234, 276, 280, 286, 310, 340, 370, 490; 0, 6, 24, 30, 60, 66, 72, 84, 90, 114, 126, 154, 156, 160, 210, 214, 234, 244, 276, 280, 286, 340, 364, 370, 490; 0, 6, 28, 34, 40, 46, 48, 54, 60, 88, 90, 100, 108, 118, 130, 138, 210, 238, 250, 258, 280, 286, 340, 370, 490; 0, 6, 28, 34, 40, 46, 60, 78, 84, 88, 90, 100, 118, 130, 138, 168, 210, 238, 250, 280, 286, 288, 340, 370, 490; 0, 6, 28, 34, 40, 46, 60, 88, 90, 100, 114, 118, 120, 130, 174, 204, 210, 238, 250, 280, 286, 324, 340, 370, 490; 0, 6, 28, 34, 40, 46, 60, 88, 90, 100, 118, 130, 138, 144, 198, 210, 228, 238, 250, 280, 286, 340, 348, 370, 490; 0, 6, 28, 34, 40, 46, 60, 88, 90, 100, 118, 130, 154, 160, 210, 214, 238, 244, 250, 280, 286, 340, 364, 370, 490; 0, 6, 28, 34, 40, 46, 60, 88, 90, 100, 118, 130, 180, 186, 210, 238, 240, 250, 270, 280, 286, 340, 370, 390, 490; 0, 6, 28, 34, 48, 54, 60, 88, 90, 108, 118, 138, 154, 160, 210, 214, 238, 244, 258, 280, 286, 340, 364, 370, 490; 0, 6, 28, 34, 48, 54, 60, 88, 90, 108, 118, 138, 180, 186, 210, 238, 240, 258, 270, 280, 286, 340, 370, 390, 490; 0, 6, 28, 34, 60, 78, 84, 88, 90, 100, 106, 118, 138, 160, 168, 190, 210, 238, 280, 286, 288, 310, 340, 370, 490; 0, 6, 28, 34, 60, 78, 84, 88, 90, 118, 138, 144, 150, 168, 204, 210, 234, 238, 280, 286, 288, 340, 354, 370, 490; 0, 6, 28, 34, 60, 78, 84, 88, 90, 118, 138, 154, 160, 168, 210, 214, 238, 244, 280, 286, 288, 340, 364, 370, 490; Ну. позарез нужна массовость! Без этого тут ничего не получится. База теоретических паттернов огромная, всю её я никак не могу обрабатывать в поиске. На данный момент в базе 10667 теоретических паттернов (различных, допустимых). А я обрабатываю в программе поиска всего 959 паттернов. Это же мизер, меньше 10%. Эх, был бы тут один теоретический паттерн. как в задаче 19-252 !! Ну, с минимальным диаметром имеется 4 теоретических паттерна. Можно попробовать для этих паттернов искать, но диапазон надо менять до ... ??? Andersen утверждал, что до 10^20 нет решений для этих паттернов. А г. Петухов продвинулся значительно дальше, что-то вроде до 10^36 - 10^37. Это он по гипотезе Харди-Литтлвуда насчитал. Ну и что? На 10^37 простые числа не заканчиваются! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот как Ахиллес-3 трудится (всего один поток) ? \r st_pat1.txt logfile = "st_pat_res.txt" [0, 2, 12, 14, 30, 42, 60, 62, 90, 102, 104, 132, 134, 146, 194, 236, 260, 272, 320, 362, 480, 482, 510, 614, 740] 41632162877084147: [0, 2, 12, 60, 62, 90, 104, 134, 146, 194, 260, 272, 320, 404, 432, 456, 476, 480, 510, 524, 602, 614, 650, 734, 740] q=17 [0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 114, 120, 174, 204, 210, 214, 228, 280, 286, 324, 340, 370, 490] 41574307738491943: [0, 4, 6, 16, 18, 24, 60, 64, 76, 78, 90, 130, 150, 186, 204, 210, 214, 226, 246, 286, 324, 340, 370, 396, 490] q=17 [0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 114, 120, 174, 204, 210, 214, 228, 280, 286, 324, 340, 370, 490] 41623175476050583: [0, 10, 18, 24, 60, 64, 90, 94, 108, 114, 130, 136, 148, 156, 214, 228, 280, 286, 310, 340, 370, 384, 408, 484, 490] q=17 [0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 210, 214, 228, 238, 244, 298, 324, 328, 330, 384, 414, 448, 534] 41611578510715243: [0, 4, 6, 28, 60, 64, 78, 94, 154, 186, 210, 214, 228, 244, 258, 268, 298, 310, 324, 328, 330, 384, 430, 444, 534] q=17 [0, 4, 6, 10, 36, 42, 60, 64, 76, 82, 90, 94, 96, 126, 136, 166, 210, 214, 246, 286, 484, 490, 544, 574, 694] 41767092034962397: [0, 4, 10, 36, 42, 60, 90, 96, 124, 126, 166, 180, 210, 214, 246, 286, 316, 420, 442, 484, 490, 564, 574, 594, 694] q=18 [0, 4, 6, 10, 36, 42, 60, 64, 90, 94, 96, 126, 174, 180, 210, 214, 234, 246, 264, 384, 484, 490, 544, 574, 694] 41767092034962397: [0, 4, 10, 36, 42, 60, 90, 96, 124, 126, 166, 180, 210, 214, 246, 286, 316, 420, 442, 484, 490, 564, 574, 594, 694] q=17 [0, 6, 10, 16, 24, 30, 60, 70, 84, 90, 100, 114, 126, 132, 186, 210, 216, 220, 234, 336, 396, 402, 456, 486, 606] 41644062539311927: [0, 10, 24, 30, 60, 70, 112, 114, 126, 132, 210, 216, 220, 234, 300, 310, 346, 354, 366, 396, 402, 424, 486, 594, 606] q=17 Хорошо трудится! А теперь представьте, что теоретических паттернов обрабатывается в 10 раз больше. Или в 100 раз больше. Представили? Шансы-то возрастают тоже в разы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У - р - р - р - а - а - а!!! Только что на Ахиллесе-3 найдено приближение [0, 6, 12, 18, 22, 28, 60, 72, 82, 90, 102, 112, 156, 162, 210, 216, 222, 232, 246, 280, 286, 340, 366, 370, 490] 44537433465001831: [0, 6, 18, 22, 28, 58, 60, 72, 82, 90, 102, 112, 156, 162, 186, 222, 232, 280, 286, 292, 340, 366, 412, 450, 490] q=20 Недаром я сгенерировала 165 теоретических паттернов с диаметром 490. Вот оно - приближение с таким паттерном. 5 "дырок"! Этот квадрат достоин иллюстрации :) Сейчас нарисую. 20 правильных элементов - это уже очень неплохо. Конечно, до полного решения ещё далеко, но надежда есть. Через постобработку пропустила это приближение, увы, не улучшилось. Остальные результаты в этой порции ещё не проверила, сразу кинулась смотреть на квадрат с q=20. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, рисую квадрат Стенли по приближению [0, 6, 12, 18, 22, 28, 60, 72, 82, 90, 102, 112, 156, 162, 210, 216, 222, 232, 246, 280, 286, 340, 366, 370, 490] 44537433465001831: [0, 6, 18, 22, 28, 58, 60, 72, 82, 90, 102, 112, 156, 162, 186, 222, 232, 280, 286, 292, 340, 366, 412, 450, 490] q=20 Это полный квадрат Стенли (эталонный паттерн выведен в самом начале) 0 6 60 90 210 12 18 72 102 222 22 28 82 112 232 156 162 216 246 366 280 286 340 370 490 А это квадрат Стенли с 5 "дырками" 44537433465001831+ 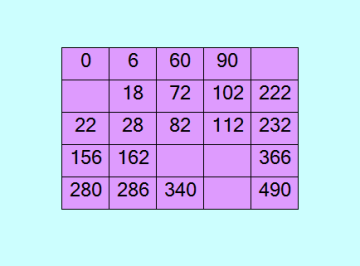 Замечательный квадратик! Таких у меня ещё не было :) Ждём теперь приближение с q=21. |

©2026 (C) Progger