Новые паттерны дали ещё приближения с q=17

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 126, 130, 138, 174, 270, 276, 330, 360, 396, 490, 496, 550, 580, 616]
27188587888558423: [0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 106, 126, 130, 238, 246, 306, 330, 364, 378, 444, 490, 496, 516, 580, 616]
q=17

[0, 4, 6, 10, 48, 54, 60, 64, 108, 126, 130, 174, 210, 214, 258, 270, 276, 330, 396, 480, 490, 496, 550, 616, 700]
27246163934733763: [0, 4, 24, 48, 54, 60, 64, 126, 130, 174, 210, 244, 258, 304, 396, 438, 444, 490, 496, 510, 550, 558, 616, 640, 700]
q=17

У второго приближения паттерн с круглым диаметром 700, симпатичный.

У - Р - А - А - А !
Найдено приближение с q=18, с новым паттерном с круглым диаметром 700 !

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 210, 214, 258, 270, 276, 330, 360, 480, 490, 496, 550, 580, 700]
27490106322352693: [0, 4, 6, 60, 90, 94, 96, 108, 138, 210, 214, 258, 264, 270, 276, 330, 336, 438, 480, 490, 496, 504, 544, 558, 700]
q=18

Не зря я искала новые теоретические паттерны для квадрата Стенли.

Итак, есть квадрат Стенли с 7 "дырками".
Надо его нарисовать :)

Теперь жду приближение с q=19.
Можно сразу с q=20 :)

Ещё теоретических паттернов для квадрата Стенли надо подбросить в этот поиск.
Понятно: чем больше будет теоретических паттернов, тем больше шансов найти квадрат.

Хороший у меня придумался алгоритм поиска теоретических паттернов для квадрата Стенли.
Можно хоть 1000 штук найти.

Это полный квадрат Стенли

0 4 48 270 490
6 10 54 276 496
60 64 108 330 550
90 94 138 360 580
210 214 258 480 700

S=1178

А это с 7 "дырками"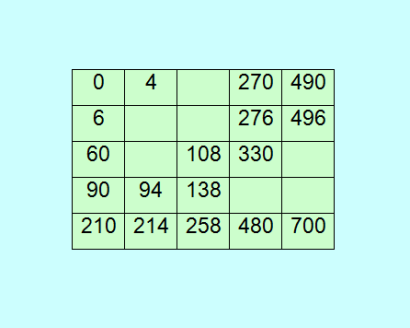



Построен из элементов кортежа

27490106322352693: [0, 4, 6, 60, 90, 94, 96, 108, 138, 210, 214, 258, 264, 270, 276, 330, 336, 438, 480, 490, 496, 504, 544, 558, 700]

Симпатяга!
Ну, дырявый немножко :)
Ничего, залатаем "дырки".

Замечу: у этого квадрата Стенли обалденный вектор смещений в столбце
[6, 60, 90, 210].
Между строками смещения: 6, 54, 30, 120.

Ещё найдено приближение с q=18 !

[0, 4, 6, 10, 36, 40, 48, 54, 60, 64, 84, 108, 120, 124, 168, 270, 276, 306, 330, 390, 490, 496, 526, 550, 610]
28748322529018783: [0, 6, 10, 54, 60, 64, 78, 108, 120, 124, 168, 208, 256, 270, 274, 276, 330, 370, 378, 390, 430, 496, 526, 550, 610]
q=18

Паттерн с другим диаметром, но тоже из новых.

Вчера нашла 507 новых допустимых паттернов для квадрата Стенли.

Все они различные и близки по структуре к этому паттерну

0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 210, 214, 258, 270, 276, 330, 360, 480, 490, 496, 550, 580, 700

на основе которого эти паттерны и строились.
При этом разброс диаметров паттернов от 280 до 700, вот примеры двух паттернов с такими диаметрами

0, 4, 6, 10, 18, 24, 28, 34, 60, 64, 70, 76, 78, 88, 90, 94, 108, 118, 130, 160, 210, 214, 228, 238, 280
0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 126, 132, 186, 210, 214, 216, 226, 336, 490, 496, 550, 580, 700

Добавила все новые паттерны в список теоретических паттернов для квадрата Стенли, теперь в этом списке 612 паттернов.
Запустила программу с новым списком паттернов.

Пока только с q=18

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 216, 220, 264, 270, 276, 330, 360, 486, 490, 496, 550, 580, 706]
29687208075440473: [0, 34, 48, 64, 78, 90, 94, 108, 138, 216, 220, 270, 276, 294, 360, 438, 480, 486, 490, 496, 550, 570, 580, 676, 706]
q=18

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 210, 214, 258, 270, 276, 330, 360, 480, 490, 496, 550, 580, 700]
27490106322352693: [0, 4, 6, 60, 90, 94, 96, 108, 138, 210, 214, 258, 264, 270, 276, 330, 336, 438, 480, 490, 496, 504, 544, 558, 700]
q=18

[0, 4, 6, 10, 36, 40, 48, 54, 60, 64, 84, 108, 120, 124, 168, 270, 276, 306, 330, 390, 490, 496, 526, 550, 610]
28748322529018783: [0, 6, 10, 54, 60, 64, 78, 108, 120, 124, 168, 208, 256, 270, 274, 276, 330, 370, 378, 390, 430, 496, 526, 550, 610]
q=18

[0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 210, 214, 228, 268, 274, 328, 358, 444, 450, 478, 504, 534, 654]
30248794845552313: [0, 4, 6, 24, 60, 64, 78, 90, 94, 220, 228, 240, 268, 276, 280, 328, 358, 444, 448, 450, 504, 534, 538, 550, 654]
q=18

Проверяем дальше.

Ещё с q=18

[0, 4, 6, 10, 48, 54, 60, 64, 70, 76, 90, 94, 108, 130, 138, 160, 210, 214, 258, 280, 330, 336, 390, 420, 540]
31089055920978613: [0, 4, 6, 10, 34, 48, 54, 60, 64, 76, 94, 108, 138, 160, 204, 210, 228, 258, 276, 336, 414, 420, 438, 480, 540]
q=18

[0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 210, 214, 226, 240, 246, 276, 282, 300, 330, 336, 366, 450, 486]
30983974152640567: [0, 4, 10, 22, 60, 64, 76, 90, 94, 112, 142, 154, 172, 210, 226, 240, 256, 276, 300, 330, 366, 430, 450, 456, 486]
q=18

И ещё

. . . . . . 
[0, 4, 6, 10, 28, 34, 60, 64, 88, 90, 94, 118, 160, 166, 210, 214, 220, 238, 250, 370, 468, 474, 528, 558, 678]
32137910019813463: [0, 34, 60, 64, 88, 90, 118, 160, 210, 214, 220, 238, 250, 358, 370, 378, 456, 474, 528, 558, 600, 606, 654, 666, 678]
q=18
[0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 186, 192, 210, 214, 226, 246, 276, 394, 396, 400, 454, 484, 604]
32086343066426707: [0, 4, 6, 10, 16, 60, 64, 90, 94, 186, 210, 220, 246, 330, 354, 394, 396, 400, 450, 454, 466, 484, 534, 574, 604]
q=18
pattern 152
pattern 153
pattern 154
pattern 155
pattern 156
pattern 157
pattern 158
pattern 159
pattern 160
[0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 210, 214, 226, 240, 246, 300, 330, 394, 400, 450, 454, 484, 604]
32086343066426707: [0, 4, 6, 10, 16, 60, 64, 90, 94, 186, 210, 220, 246, 330, 354, 394, 396, 400, 450, 454, 466, 484, 534, 574, 604]
q=18
. . . . . .

Интересны два последних решения: они одинаковые, но! они получены для разных исходных паттернов.
Я специально показала номера паттернов между этими решениями.

С q=19 пока нет решений.
Да-а-а, очень туго продвигаемся.
Думаю, что надо ещё подбросить теоретических паттернов.

Опять с q=18

[0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 210, 214, 226, 240, 246, 276, 282, 300, 330, 336, 366, 450, 486]
31398297675734047: [0, 4, 6, 10, 16, 34, 42, 64, 76, 90, 106, 210, 226, 246, 262, 276, 282, 330, 336, 340, 400, 442, 444, 450, 486]
q=18

Из бесконечной осенней хмари вынырнула мыслишка :)

Попробовала реализовать.
Вот что нашла (только три решения показываю для примера, найдено больше)

[0, 4, 6, 10, 18, 24, 28, 34, 60, 64, 78, 88, 90, 94, 108, 118, 210, 214, 228, 238, 268, 274, 328, 358, 478]
[0, 4, 6, 10, 18, 24, 28, 34, 60, 64, 88, 90, 94, 114, 118, 130, 156, 238, 240, 324, 328, 358, 478, 480, 514]
q=18
[0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 160, 166, 210, 214, 220, 228, 250, 358, 364, 370, 418, 448, 568]
[0, 4, 6, 18, 24, 60, 78, 90, 94, 108, 160, 166, 214, 216, 220, 228, 306, 348, 358, 370, 376, 390, 424, 430, 448]
q=18
[0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 160, 166, 210, 214, 220, 228, 250, 370, 424, 430, 484, 514, 634]
[0, 4, 6, 18, 24, 60, 78, 90, 94, 108, 160, 166, 214, 216, 220, 228, 306, 348, 358, 370, 376, 390, 424, 430, 448]
q=18

Догадайтесь сами, в чём суть :)

Думаю, что мыслишка полезная.

Новенькое с q=18

[0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 114, 120, 174, 204, 210, 214, 226, 280, 286, 324, 340, 370, 490]
33039797365287127: [0, 6, 10, 16, 22, 60, 64, 76, 90, 94, 114, 174, 204, 214, 226, 240, 286, 310, 324, 330, 342, 360, 396, 484, 490]
q=18

и ещё два

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 174, 180, 210, 214, 234, 258, 264, 384, 438, 444, 498, 528, 648]
33495633858310363: [0, 4, 6, 10, 54, 60, 64, 138, 174, 180, 210, 214, 234, 258, 264, 330, 340, 420, 438, 468, 498, 568, 570, 594, 648]
q=18

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 130, 136, 138, 190, 210, 214, 220, 258, 340, 364, 370, 424, 454, 574]
33228731435651953: [0, 10, 48, 54, 90, 94, 108, 130, 136, 138, 154, 190, 210, 214, 238, 258, 340, 364, 418, 430, 444, 454, 496, 526, 574]
q=18

А это новым методом:

из решения

[0, 4, 6, 10, 28, 34, 48, 54, 60, 64, 88, 90, 94, 108, 118, 138, 210, 214, 238, 258, 340, 346, 400, 430, 550]
33558532365345853: [0, 6, 10, 54, 60, 64, 90, 94, 108, 138, 208, 210, 214, 238, 264, 270, 340, 346, 378, 424, 430, 474, 480, 484, 550]
q=17

получено решение

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 210, 214, 258, 270, 276, 330, 340, 346, 360, 400, 430, 480, 550]
33558532365345853: [0, 6, 10, 54, 60, 64, 90, 94, 108, 138, 208, 210, 214, 238, 264, 270, 340, 346, 378, 424, 430, 474, 480, 484, 550]
q=18

Метод работает!

Из решения с q=18 может быть получено решение с q=19 и т. д.

Два новых приближения с q=18

[0, 4, 6, 10, 18, 24, 60, 64, 70, 76, 78, 90, 94, 108, 130, 148, 154, 160, 208, 210, 214, 228, 238, 280, 358]
34425966662322793: [0, 4, 18, 24, 60, 64, 70, 78, 90, 108, 160, 174, 208, 210, 214, 216, 228, 238, 280, 294, 328, 336, 346, 348, 358]
q=18

[0, 4, 6, 10, 36, 42, 60, 64, 76, 82, 90, 94, 96, 126, 136, 166, 210, 214, 246, 256, 262, 286, 316, 346, 466]
34094930567311717: [0, 6, 10, 34, 36, 54, 64, 76, 82, 90, 94, 96, 120, 126, 136, 166, 214, 244, 246, 294, 316, 346, 406, 442, 466]
q=18

И ещё

0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 118, 124, 138, 178, 190, 196, 208, 210, 214, 250, 258, 280, 328, 400]
34001747524286953: [0, 4, 6, 10, 24, 54, 60, 64, 94, 108, 124, 126, 138, 144, 154, 178, 190, 208, 250, 258, 276, 280, 364, 390, 400]
q=18

[0, 4, 6, 10, 28, 34, 60, 64, 88, 90, 94, 118, 210, 214, 238, 270, 276, 318, 324, 330, 360, 378, 408, 480, 528]
33749580351836533: [0, 6, 10, 34, 60, 88, 90, 94, 130, 136, 184, 210, 214, 238, 270, 276, 318, 360, 378, 384, 408, 420, 430, 448, 528]
q=18

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 138, 148, 154, 208, 210, 214, 238, 258, 358, 384, 390, 444, 474, 594]
33683958985210273: [0, 4, 6, 28, 48, 54, 60, 64, 90, 94, 108, 148, 154, 166, 174, 214, 256, 258, 298, 318, 358, 444, 474, 516, 594]
q=18

Первое приближение в этой порции симпатичное - с круглым диаметром.

В новой порции результатов опять только с q=18 максимальное приближение

[0, 4, 6, 10, 28, 34, 48, 54, 60, 64, 88, 90, 94, 108, 118, 138, 160, 166, 210, 214, 220, 238, 250, 258, 370]
34690805907035143: [0, 4, 6, 10, 28, 48, 60, 64, 66, 88, 94, 118, 138, 160, 180, 210, 214, 250, 258, 298, 316, 334, 340, 360, 370]
q=18

У - Р - Р - Р - А !

Сработал новый метод; назову этот метод постобработкой.

Из решения

[0, 4, 6, 10, 28, 34, 60, 64, 88, 90, 94, 118, 210, 214, 238, 268, 274, 328, 358, 424, 430, 478, 484, 514, 634]
35755687056730363: [0, 4, 6, 10, 28, 34, 60, 84, 88, 90, 118, 210, 214, 220, 238, 370, 424, 436, 448, 484, 490, 514, 604, 624, 634]
q=17

получено решение

[0, 4, 6, 10, 28, 34, 60, 64, 88, 90, 94, 118, 160, 166, 210, 214, 220, 238, 250, 370, 424, 430, 484, 514, 634]
35755687056730363: [0, 4, 6, 10, 28, 34, 60, 84, 88, 90, 118, 210, 214, 220, 238, 370, 424, 436, 448, 484, 490, 514, 604, 624, 634]
q=19

Сразу на два q увеличилось!

Это надо нарисовать :)
Уже осталось 6 "дырок" в приближении.

Ждём приближение с q=20.
Ну, конечно, от приближений толку мало, но всё равно они душу греют, надежду подают.

Постобработку проходили следующие приближения с q=17 (новые)

0, 4, 6, 24, 28, 64, 70, 78, 90, 94, 130, 160, 210, 214, 240, 280, 324, 330, 358, 360, 384, 408, 424, 426, 480;
0, 4, 6, 28, 34, 48, 64, 88, 90, 94, 114, 118, 184, 204, 214, 318, 324, 330, 384, 436, 468, 504, 550, 574, 588;
0, 4, 6, 10, 36, 42, 90, 96, 126, 130, 174, 210, 220, 264, 340, 382, 406, 412, 442, 466, 510, 526, 570, 600, 616;
0, 4, 46, 48, 64, 90, 94, 96, 108, 138, 148, 154, 208, 210, 216, 238, 270, 276, 348, 360, 396, 400, 414, 474, 480;
0, 4, 10, 60, 64, 84, 108, 120, 190, 228, 234, 276, 306, 330, 390, 430, 490, 496, 510, 526, 538, 550, 556, 606, 610;
0, 4, 6, 10, 28, 34, 60, 84, 88, 90, 118, 210, 214, 220, 238, 370, 424, 436, 448, 484, 490, 514, 604, 624, 634;
0, 4, 10, 18, 40, 48, 118, 120, 124, 148, 210, 238, 250, 270, 294, 334, 390, 490, 496, 516, 526, 610, 634, 658, 736;
0, 4, 10, 18, 24, 78, 88, 90, 94, 106, 108, 208, 214, 228, 244, 330, 390, 400, 406, 420, 438, 448, 510, 514, 540;
0, 4, 6, 10, 48, 54, 60, 64, 94, 118, 126, 138, 178, 208, 228, 246, 258, 280, 306, 316, 340, 364, 400, 498, 550;
0, 4, 6, 54, 60, 94, 118, 124, 126, 138, 178, 214, 258, 328, 334, 396, 400, 444, 448, 466, 498, 510, 514, 528, 648;

Это полный квадрат Стенли - из теоретического паттерна

0, 4, 6, 10, 28, 34, 60, 64, 88, 90, 94, 118, 160, 166, 210, 214, 220, 238, 250, 370, 424, 430, 484, 514, 634

0  4  28  160  424
6  10  34  166  430
60  64  88  220  484
90  94  118  250  514
210  214  238  370  634

Это квадрат Стенли с 6 "дырками"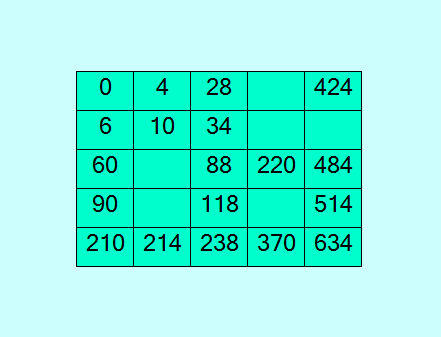



Квадрат построен из элементов кортежа

35755687056730363: [0, 4, 6, 10, 28, 34, 60, 84, 88, 90, 118, 210, 214, 220, 238, 370, 424, 436, 448, 484, 490, 514, 604, 624, 634]

Красавец!
"Дырок" пока многовато, ну ничего - залатаем "золотыми заплатами" :)

Не так уж и безнадёжен поиск по паттерну, как утверждает г. Петухов.
А если подбросить теоретических паттернов для квадрата Стенли, дело пойдёт ещё веселее.
Конечно, с увеличением количества теоретических паттернов замедляется поиск.
Но тут дело техники.

Напомню: у меня сейчас задействовано 612 теоретических паттернов для квадрата Стенли.
Надо бы ещё добавить, хотя бы до 1000 штук.

Напомню ещё, что решается одна подзадача: поиск квадрата Стенли, построенного из кортежа с любым диаметром.

Подзадача для минимального диаметра 156 пока не решается, ибо она очень трудная - так же, как задача 19-252.

На Ахиллесе-3 работает программа Белышева, один поток.
Это брутфорс, то есть и минимальный диаметр здесь тоже ищется, но, понятно, что он может появиться о-ч-е-н-ь не скоро, ибо до 10^20 решения для кортежа с минимальным диаметром точно нет, по утверждению Andersen.

Состояние поиска программой Белышева на данный момент

Поиск антимага Стенли 5-го порядка             130:55:10
Текущий интервал: [1045431537944346 ... 1045433537944346]
Проверено:  9803%%
Скорость:     85 Всего: 57824840 Подходящих: 11562966

Вы помните, господа, что программа Белышева абсолютно бесконечная*?
То есть запустили и пусть работает хоть тысячу/миллион лет - по-петуховски! :))
Правда, техника у нас к такой работе не годная, ибо вырубается постоянно.
Однако!
Вы помните и то, что в программе Белышева есть чекпоинт.

У меня Ахиллес-3 периодически вырубается.
Ничего, просто перезапускаю программу - и всё поехало дальше.

* Если Белышев использует генератор простых чисел primesieve, то конец в программе, конечно, наступит при достижении 2^64.

Сейчас сняла результаты с Ахиллеса-3.

Во-первых, найдены приближения с q=18

[0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 114, 120, 174, 204, 210, 214, 228, 238, 244, 298, 324, 328, 448]
35315732065362163: [0, 4, 6, 16, 18, 60, 64, 88, 90, 94, 108, 114, 120, 174, 220, 228, 238, 244, 286, 318, 324, 328, 408, 444, 448]
q=18

[0, 4, 6, 10, 48, 54, 60, 64, 90, 94, 108, 130, 136, 138, 190, 210, 214, 220, 258, 340, 364, 370, 424, 454, 574]
35317114904605273: [0, 4, 6, 60, 64, 90, 106, 108, 124, 130, 136, 138, 148, 190, 210, 214, 258, 270, 280, 340, 406, 424, 454, 498, 574]
q=18

Во-вторых, следующие приближения с q=17 и с q=18 прошли постобработку

0, 10, 36, 48, 54, 84, 124, 130, 168, 174, 178, 180, 270, 288, 306, 358, 378, 390, 466, 484, 490, 496, 526, 538, 616;
0, 4, 6, 16, 18, 60, 64, 88, 90, 94, 108, 114, 120, 174, 220, 228, 238, 244, 286, 318, 324, 328, 408, 444, 448;
0, 4, 6, 60, 64, 90, 106, 108, 124, 130, 136, 138, 148, 190, 210, 214, 258, 270, 280, 340, 406, 424, 454, 498, 574;
0, 4, 6, 18, 90, 94, 148, 150, 154, 186, 208, 210, 214, 216, 228, 238, 276, 288, 358, 390, 414, 444, 514, 588, 594;
0, 6, 18, 28, 34, 60, 70, 84, 90, 94, 108, 210, 238, 270, 276, 286, 330, 340, 346, 370, 400, 466, 480, 496, 550;
0, 10, 48, 60, 64, 88, 94, 108, 138, 144, 204, 210, 214, 246, 256, 274, 280, 328, 334, 336, 340, 364, 456, 466, 484;
0, 6, 10, 48, 54, 126, 130, 186, 210, 246, 270, 306, 318, 360, 396, 484, 490, 496, 516, 526, 588, 610, 616, 666, 736;
0, 10, 16, 22, 42, 60, 66, 106, 114, 120, 174, 204, 210, 214, 220, 226, 364, 370, 394, 406, 424, 442, 510, 520, 574;
0, 6, 18, 28, 34, 60, 64, 76, 78, 88, 90, 94, 108, 118, 160, 196, 198, 214, 228, 238, 336, 340, 346, 384, 430;
0, 6, 10, 22, 52, 60, 64, 94, 96, 126, 196, 202, 214, 252, 256, 264, 274, 280, 312, 334, 360, 364, 432, 454, 484;

Появилось ещё одно приближение с q=19 !
Замечательно!

Из решения

[0, 4, 6, 10, 18, 24, 28, 34, 60, 64, 78, 88, 90, 94, 108, 118, 210, 214, 220, 226, 228, 238, 280, 310, 430]
35020459259648893: [0, 6, 18, 28, 34, 60, 64, 76, 78, 88, 90, 94, 108, 118, 160, 196, 198, 214, 228, 238, 336, 340, 346, 384, 430]
q=17

получено решение

[0, 4, 6, 10, 18, 24, 28, 34, 60, 64, 78, 88, 90, 94, 108, 118, 210, 214, 228, 238, 340, 346, 400, 430, 550]
[0, 6, 18, 28, 34, 60, 64, 76, 78, 88, 90, 94, 108, 118, 160, 196, 198, 214, 228, 238, 336, 340, 346, 384, 430]
q=19

Ещё с q=18

[0, 4, 6, 10, 28, 34, 48, 54, 60, 64, 88, 90, 94, 108, 118, 138, 210, 214, 238, 258, 370, 376, 430, 460, 580]
35931617201764303: [0, 4, 10, 28, 34, 40, 48, 60, 88, 118, 138, 204, 210, 238, 258, 370, 376, 396, 418, 430, 460, 466, 538, 574, 580]
q=18

И одно приближение с q=18 найдено постобработкой от приближения с q=17, но это уже мало интересно.

Пока по-прежнему только с q=18 максимум приближения находятся

[0, 4, 6, 10, 16, 22, 60, 64, 76, 90, 94, 106, 126, 132, 186, 210, 214, 216, 226, 336, 364, 370, 424, 454, 574]
37090274655654817: [0, 4, 6, 10, 22, 60, 64, 76, 90, 94, 112, 126, 132, 186, 210, 214, 216, 310, 366, 370, 394, 462, 562, 564, 574]
q=18

[0, 4, 6, 10, 18, 24, 60, 64, 70, 76, 78, 90, 94, 108, 130, 160, 210, 214, 228, 280, 304, 310, 364, 394, 514]
36850466580240343: [0, 4, 10, 18, 60, 64, 70, 76, 78, 90, 94, 108, 130, 144, 210, 226, 228, 304, 310, 316, 420, 424, 444, 510, 514]
q=18

[0, 4, 6, 10, 18, 24, 60, 64, 78, 90, 94, 108, 114, 120, 174, 204, 210, 214, 228, 238, 244, 298, 324, 328, 448]
36354867012982933: [0, 6, 10, 24, 60, 64, 90, 94, 108, 114, 174, 210, 214, 216, 228, 244, 258, 268, 276, 324, 328, 340, 346, 444, 448]
q=18

Черепашка активно экспериментирует.

Сделала модернизацию алгоритма, должны быть улучшения, но программа выполняется очень медленно.
Пока только с q=17 идут приближения.