Хотя...
программа предпроверки построения квадрата Стенли из одного заданного паттерна (то есть из одной заданной 25-ки из последовательных простых чисел), которая показана в сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12915
выполняется мгновенно!

Если переписать программу предпроверки, будет ли сильный выигрыш в скорости?
По идее должен быть.
А вообще-то, надо писать проверку построения полного квадрата Стенли, не надо никаких предпроверок.
Можно просто выводить промежуточные результаты построения, то есть квадраты Стенли с "дырками".
Жалко, что промежуточные результаты не выводятся в программе Белышева.
Программа считает, считает... молча, ничего не выводит.
И кто её знает, чего она там считает и какие результаты получает.
Понятно, что полное решение не получается, иначе оно бы вывелось, я надеюсь :)

Как видите, задачу века решали многие весьма сильные программисты:
Макс Алексеев, Алексей Белышев, Progger.
Господин Петухов мимо проходил :)
Ещё Сергей Беляев решал.
Сейчас просматривала тему "Магические квадраты" и увидела его программу построения квадрата Стенли разных порядков (в том числе и 5-го порядка)
https://dxdy.ru/post904239.html#p904239

К сожалению, ссылка на программу ведёт неизвестно куда, а должна была вести на сайт Сергея.

Ну, и я тоже решала немножко; а в теме на форуме dxdy.ru пыталась убедить Макса, что надо использовать самый быстрый генератор простых чисел primesieve.
Но мне это, кажется, не удалось.
Он сказал, что я "бочку качу" на его генератор простых чисел.
Никаких бочек! Только объективная информация!
Генератор primesieve работает быстрее генераторов Белышева, Беляева и всех остальных, и Макса в том числе.
Белышев и Беляев это признали, а Макс не захотел.
Его вполне устаивает свой генератор.
Ну и чудесно!
Только тестирование скорости его генератора он так и не показал.

Вся программа содержит два этапа: генерацию простых чисел и проверку построения квадрата Стенли.
Каждый из этапов должен работать максимально быстро.
Это и ежу понятно.

Программа Сергея Беляева у меня в компьютере сохранилась.
Классная программа!
Запустила попробовать искать квадрат Стенли 5-го порядка из последовательных простых чисел.

Цитирую файл readme.txt

2. Как работать с программой

Сначала вводится порядок квадрата. Затем предлагается ввести имя рабочего
файла. Если ввести пустое имя, то происходит смена режима работы. В данный
момент всего два режима:
- Поиск примитивных квадратов
- Поиск простых чисел

После ввода имени рабочего файла запрашивается значение сегмента, с которого
начнется работа от 0 до 10^13. Для сегмента 10^13 начнется генерация простых
чисел примерно с 5.1*10^18.

Во время работы выводится информация о числе простых чисел, время работы и
значения si. Первое число (s0) это число найденных наборов последовательных
простых чисел, из которых можно правильно заполнить первую и последнюю строки
примитивного квадрата. Это число большое, поэтому для каждого сегмента
выводится свое число. Далее идет число найденных квадратов с 3 правильными
строками, с 4-мя и т.д. Последнее число это число правильных квадратов.
Найденные квадраты, с числом правильных строк от 3 до N-1 дополняются в
файл с именем SQ(N).txt, где N - порядок квадрата.
Найденные квадраты дополняются в файл с именем SQ_N.txt.

Для окончания работы программы достаточно нажать Esc, после этого
закончится проверка последнего диапазона и появится слово END, теперь для
выхода из программы нажмите Enter.

Посмотрела ещё раз алгоритм построения квадрата Стенли 5-го порядка.
Нашла экономию только одной свободной переменной.
Как у Белышева получилось обойтись перебором всего четырёх свободных переменных, ума не приложу.
А ведь мы с ним этот алгоритм подробно обсуждали!
Всё напрочь забыла.
У меня для построения полного квадрата Стенли требуется перебор шести свободных переменных из 23 (два элемента квадрата я фиксирую сразу - минимальный и максимальный).

Ну, можно написать программу построения полного квадрата Стенли (без предпроверки).
Пока крутится программа предпроверки.
Новых кандидатов с 8 "дырками" не найдено.
С 10 "дырками" кандидаты изредка появляются.

Кстати, в программе Сергея Беляева тоже выводятся кандидаты с 10 "дырками", но у него это квадраты с тремя заполненными строками.
Если появятся, покажу их.

Вот окно программы Сергея Беляева (работает на черепашке)

   Поиск примитивных квадратов              number=1682174617  seg=10000121133
 Порядок=5                                  number=1682344115  seg=10000121145
 file: out.txt                              number=1682514031  seg=10000121157
 Segment=10000001953                        number=1682683606  seg=10000121169
 5: 5105161846244460..5105161846754969      number=1682852846  seg=10000121181
 5: 5105161852370580..5105161852881089      number=1683022126  seg=10000121193
 5: 5105161858496700..5105161859007209      number=1683190955  seg=10000121205
 5: 5105161864622820..5105161865133329      number=1683359921  seg=10000121217
 5: 5105161870748940..5105161871259449      number=1683529161  seg=10000121229
 5: 5105161876875060..5105161877385569      number=1683698217  seg=10000121241
 5: 5105161883001180..5105161883511689      number=1683867184  seg=10000121253
 5: 5105161889127300..5105161889637809      number=1684036725  seg=10000121265
 5: 5105161895253420..5105161895763929      number=1684205881  seg=10000121277
 5: 5105161901379540..5105161901890049      number=1684360906  seg=10000121288
 5: 5105161907505660..5105161908016169      number=1684531007  seg=10000121300
 5: 5105161913631780..5105161914142289      number=1684700262  seg=10000121312
 5: 5105161919247390..5105161919757899      number=1684869464  seg=10000121324
 5: 5105161925373510..5105161925884019      number=1685038200  seg=10000121336
 5: 5105161931499630..5105161932010139      number=1685207230  seg=10000121348
 5: 5105161937625750..5105161938136259      number=1685376833  seg=10000121360
 5: 5105161943751870..5105161944262379
 5: 5105161949877990..5105161950388499      si=214,6,0,0
 5: 5105161956004110..5105161956514619      Time: 64501.08 sec

Начало проверки я задала с сегмента = 10.000.000.000, то есть с 51051*10^11.
Проверка выполнена до сегмента seg=10000121360.
Один сегмент равен 510510.
Хорошо продвинулись.

Если я правильно понимаю, найдено 6 квадратов Стенли с тремя заполненными строками, это квадраты с 10 "дырками".
Скоро прерву программу и посмотрю, что там в выходных файлах.

А это общее количество сгенерированных и проверенных простых чисел на данный момент
number=1685376833.

Господа!
Есть ли заинтересовавшиеся задачей?
Могу выложить программу Сергея Беляева.
На форуме dxdy.ru его ссылка на программу не работает.
Как мне кажется, программа интересная, написана на Паскале.
Работает хорошо, много памяти не требует в отличие от программы Белышева.

А это программа Сергея Беляева работает на Ахиллесе-3

  Џ®ЁбЄ ЇаЁ¬ЁвЁў­ле Єў ¤а в®ў              number=4626128433  seg=2000313171
 Џ®а冷Є=5                                  number=4626644967  seg=2000313206
 file: out.txt                              number=4627339141  seg=2000313253
 Segment=2000000000                         number=4627856921  seg=2000313288
 5: 1021179895305570..1021179895816079      number=4628550919  seg=2000313335
 5: 1021179919299540..1021179919810049      number=4629097382  seg=2000313372
 5: 1021179937167390..1021179937677899      number=4629688244  seg=2000313412
 5: 1021179961161360..1021179961671869      number=4630204515  seg=2000313447
 5: 1021179980050230..1021179980560739      number=4630795704  seg=2000313487
 5: 1021180000470630..1021180000981139      number=4631341844  seg=2000313524
 5: 1021180018338480..1021180018848989      number=4631932738  seg=2000313564
 5: 1021180038758880..1021180039269389      number=4632449688  seg=2000313599
 5: 1021180057647750..1021180058158259      number=4632966725  seg=2000313634
 5: 1021180078068150..1021180078578659      number=4633734974  seg=2000313686
 5: 1021180095936000..1021180096446509      number=4634325964  seg=2000313726
 5: 1021180113803850..1021180114314359      number=4634813794  seg=2000313759
 5: 1021180140350370..1021180140860879      number=4635360304  seg=2000313796
 5: 1021180160770770..1021180161281279      number=4635995936  seg=2000313839
 5: 1021180177617600..1021180178128109      number=4636542487  seg=2000313876
 5: 1021180196506470..1021180197016979      number=4637089235  seg=2000313913
 5: 1021180218458400..1021180218968909
 5: 1021180237347270..1021180237857779      si=708,55,0,0
 5: 1021180256236140..1021180256746649      Time: 36425.20 sec

Здесь поиск начат с Segment=2000000000.
Кириллица не печатается, но это мелочи.
Вроде бы найдено 55 квадратов Стенли с тремя заполненными строками.
Текущий проверяемый сегмент
seg=2000313913.

На Ахиллесе-3 программу не буду прерывать.
Посмотрим, что за ночь найдётся.
Вдруг найдётся квадрат с четырьмя заполненными строками, то есть с 5 "дырками".
Ну и мало ли... выскочит полный квадрат Стенли, как чёрт из табакерки, это же не простой квадрат, а дьявольский квадрат :)

Прервала программу на черепашке.
Вот квадраты Стенли с тремя заполненными строками, то есть с 10 "дырками"

5105103284867519: 0,48,180,198,240,50,98,230,248,290,*,*,*,*,*,*,*,*,*,*,332,380,512,530,572,
(0,1,*,*,4)
5105120277320759: 0,14,98,114,224,24,38,122,138,248,*,*,*,*,*,*,*,*,*,*,300,314,398,414,524,
(0,1,*,*,4)
5105121789393139: 0,42,202,330,384,30,72,232,360,414,*,*,*,*,*,*,*,*,*,*,420,462,622,750,804,
(0,1,*,*,4)
5105128140178399: 0,34,60,138,334,210,244,270,348,544,*,*,*,*,*,*,*,*,*,*,534,568,594,672,868,
(0,1,*,*,4)
5105139830834269: 0,4,18,120,144,90,94,108,210,234,*,*,*,*,*,*,*,*,*,*,714,718,732,834,858,
(0,1,*,*,4)
5105160943046833: 0,138,174,264,286,30,168,204,294,316,*,*,*,*,*,*,*,*,*,*,330,468,504,594,616,

Завтра я их проверю.

Сергей писал в файле readme.txt

Программа пока сырая и работа по ее улучшению (ухудшению :-) ) будет
продолжена.

Проверяю первый квадрат Стенли, найденный программой Сергея

5105103284867519: 0,48,180,198,240,50,98,230,248,290,*,*,*,*,*,*,*,*,*,*,332,380,512,530,572,

25-ка из последовательных простых чисел

{5105103284867519, 5105103284867567, 5105103284867569, 5105103284867603, 51051032
84867617, 5105103284867699, 5105103284867701, 5105103284867713, 5105103284867717
, 5105103284867723, 5105103284867749, 5105103284867759, 5105103284867767, 510510
3284867797, 5105103284867809, 5105103284867837, 5105103284867843, 51051032848678
51, 5105103284867899, 5105103284867941, 5105103284867987, 5105103284868007, 5105
103284868031, 5105103284868049, 5105103284868091}

паттерн

[0, 48, 50, 84, 98, 180, 182, 194, 198, 204, 230, 240, 248, 278, 290, 318, 324, 332, 380, 422, 468, 488, 512, 530, 572]

Квадрат Стенли с тремя заполненными строками

0 48 180 198 240
50 98 230 248 290
X X X X X
X X X X X
332 380 512 530 572

S=1374

Да, похоже.

Вроде бы у Сергея тоже зафиксированы два элементы квадрата: минимальный (нулевой) и максимальный (диаметр 25-ки).
Но проверка на возможность построения квадрата Стенли у него организована явно лучше, чем у меня, потому что программа работает быстрее моей.

В общем, программа очень интересная.
Я о ней совсем забыла; к счастью, вчера наткнулась на сообщение Сергея о программе в теме "Магические квадраты".
Программа написана в 2014 году!
И опять: умница моя черепашка, она всё хранит для меня :)

На Ахиллесе-3 пока без особых перемен.
Однако... квадратов Стенли с тремя заполненными строками найдено уже 93 шт.!
С четырьмя заполненными строками пока не найдено квадратов.

Программа продолжает работать.
В те давние времена я эту программу немного крутила, опробовала, но долго не крутила.
И квадрат с четырьмя заполненными строками тоже вроде бы не нашла, насколько помню.
Ну, и тем более не найден полный квадрат Стенли 5-го порядка.
Надо дальше посмотреть в теме "Магические квадраты", кажется, я там ещё писала о тестировании программы Сергея.
Потому что Сергей писал в файле readme.txt (к новой версии программы)

20.09.2014
Н.Макарова сообщила на форуме о повторах чисел. Увы, это так.
В процедуре перебора при переходе к новому числу строки у меня снималась метка
использования предыдущего числа. Сейчас это снятие убрано (превращено в
комментарий):
{ met[m[x]]:=false;met[m[x+NSM-NS]]:=false;}perm(u,x+1);

Сейчас и на черепашке запустила продолжение диапазона, начинающегося с seg=10000000000.
Интересно, что в этом диапазоне квадратов Стенли с тремя заполненными строками в разы меньше, нежели в диапазоне, проверяемом на Ахиллесе-3 (начинается с seg=2000000000).

Моя программа предпроверки тоже работает на Ахиллесе-3.

Новых кандидатов с 8 "дырками" пока не найдено.

Продолжила просмотр темы "Магические квадраты".
Вот какое сообщение встретила
https://dxdy.ru/post910778.html#p910778

В ожидании старта конкурса... что-то очень волнуюсь...

Вот решила пока сделать табличку для пандиагональных квадратов из последовательных простых чисел (порядки 4 - 10, задействованные в конкурсе) аналогичную этой табличке
<...>

Это был конкурс, организованный вместе с итальянским коллегой Stefano Tognon, по пандиагональным квадратам из последовательных простых чисел.

Ссылка на описание конкурса
https://primesmagicgames.altervista.org/wp/pandiagonal-squares-of-consecutive-primes/

На странице написано, что действительных решений никто не представил. поэтому победителя нет.
Не помню, участвовал ли вообще кто-нибудь в этом конкурсе.

Такая вот она - задача века!

Приведу ссылки со страницы описания конкурса

Help links

https://ru.wikipedia.org/wiki/Магический_квадрат
https://en.wikipedia.org/wiki/Magic_square
B. Rosser and R. J. Walker. The algebraic theory of diabolic magic squares
http://yadi.sk/d/tl-_Ab-o5AYhS
N. Makarova. Unconventional pandiagonal squares of primes
http://www.natalimak1.narod.ru/panpr.htm
http://www.natalimak1.narod.ru/pannetr.htm
http://www.natalimak1.narod.ru/pannetr2.htm
Contest “Pandiagonal Magic Squares of Prime Numbers” (from Al Zimmermann)
http://www.azspcs.net/Contest/PandiagonalMagicSquares/FinalReport
The smallest magic constant for any n x n magic square made from consecutive primes
http://oeis.org/A073520
The smallest magic constant of pan-diagonal magic squares which consist of distinct prime numbers
http://oeis.org/A179440

Знаменитая статья Россера на Яндекс.Диске лежит (оригинал на английском языке и перевод Сергея Беляева на русский язык).
Скачана 1 раз!
Такой поразительный не-интерес к интереснейшей статье о пандиагональных квадратах.
А потом некоторые дамы и господа говорят мне: "Да что же вы не публикуете свои статьи в научных журналах?
Так о ваших результатах никто не знает и знать не будет."
Тот, кто хочет знать, знать будет!
А тот, кому все эти квадраты пофигу, ничего о них знать не будет, даже если я опубликую все свои статьи в самых научных журналах.

PS. К сожалению, ссылка на этот замечательный конкурс по пандиагональным квадратам недействительна
Contest “Pandiagonal Magic Squares of Prime Numbers” (from Al Zimmermann).
Может быть, кто-нибудь знает, какая теперь ссылка на конкурсы у Al Zimmermann?

В этом конкурсе превосходно выступил Ярослав Врублевский, он нашёл много интереснейших результатов.
Но это были пандиагональные квадраты не из последовательных простых чисел.
Ярослав нашёл минимальный пандиагональный квадрат 7-го порядка из простых чисел.
Этот самый значимый результат конкурса.
Результат внесён в OEIS
https://oeis.org/A179440

a(7) from Jarek Wroblewski and new bounds from Al Zimmermann's contest, added by Max Alekseyev, Oct 11 2013

Это было 10 лет назад!
История.

Много ли выиграл форум dxdy.ru, заблокировав меня навечно?
Где развитие моей темы "Магические квадраты"?
Вот тему про симметричные кортежи из последовательных простых чисел господин Петухов пыжится развивать.
Ну, что-то пока сильного развития не наблюдается.
"Почти не дырявые" 19-ки с минимальным диаметром 252 - всё развитие!

Сегодня черепашка продолжала поиск в диапазоне, начатом с seg=10000000000.
Нашла 15 квадратов Стенли с тремя заполненными строками

5105167089670909: 0,84,88,318,340,60,144,148,378,400,*,*,*,*,*,*,*,*,*,*,360,444,448,678,700,
(0,1,*,*,4)
5105167464919007: 0,56,122,150,192,84,140,206,234,276,*,*,*,*,*,*,*,*,*,*,384,440,506,534,576,
(0,1,*,*,4)
5105170290397673: 0,38,360,398,426,48,86,408,446,474,*,*,*,*,*,*,*,*,*,*,438,476,798,836,864,
(0,1,*,*,4)
5105170376788331: 0,210,236,258,306,42,252,278,300,348,*,*,*,*,*,*,*,*,*,*,402,612,638,660,708,
(0,1,*,*,4)
5105171127779687: 0,6,150,170,174,66,72,216,236,240,*,*,*,*,*,*,*,*,*,*,396,402,546,566,570,
(0,1,*,*,4)
5105175083499091: 0,186,286,298,328,132,318,418,430,460,*,*,*,*,*,*,*,*,*,*,420,606,706,718,748,
(0,1,*,*,4)
5105176914495017: 0,114,140,162,306,210,324,350,372,516,*,*,*,*,*,*,*,*,*,*,330,444,470,492,636,
(0,1,*,*,4)
5105180309456393: 0,26,56,204,266,84,110,140,288,350,*,*,*,*,*,*,*,*,*,*,300,326,356,504,566,
(0,1,*,*,4)
5105180729430941: 0,146,230,290,308,12,158,242,302,320,*,*,*,*,*,*,*,*,*,*,330,476,560,620,638,
(0,1,*,*,4)
5105186190108383: 0,78,224,246,296,30,108,254,276,326,*,*,*,*,*,*,*,*,*,*,360,438,584,606,656,
(0,1,*,*,4)
5105187494375963: 0,18,56,108,150,78,96,134,186,228,*,*,*,*,*,*,*,*,*,*,438,456,494,546,588,
(0,1,*,*,4)
5105197392387583: 0,28,78,130,190,18,46,96,148,208,*,*,*,*,*,*,*,*,*,*,396,424,474,526,586,
(0,1,*,*,4)
5105218480088989: 0,48,84,238,322,30,78,114,268,352,*,*,*,*,*,*,*,*,*,*,360,408,444,598,682,
(0,1,*,*,4)
5105219897849881: 0,76,96,208,258,90,166,186,298,348,*,*,*,*,*,*,*,*,*,*,330,406,426,538,588,
(0,1,*,*,4)
5105221093844441: 0,78,258,278,338,42,120,300,320,380,*,*,*,*,*,*,*,*,*,*,372,450,630,650,710,

С четырьмя заполненными строками не нашла квадратов Стенли.

На Ахиллесе-3 продолжается проверка диапазона, начатого с seg=2000000000, без прерываний; вот окно программы

   Џ®ЁбЄ ЇаЁ¬ЁвЁў­ле Єў ¤а в®ў              number=14269612687  seg=2000966000
 Џ®а冷Є=5                                  number=14270129766  seg=2000966035
 file: out.txt                              number=14270676811  seg=2000966072
 Segment=2000000000                         number=14271223028  seg=2000966109
 5: 1021513171038360..1021513171548869      number=14271739800  seg=2000966144
 5: 1021513189927230..1021513190437739      number=14272257244  seg=2000966179
 5: 1021513208816100..1021513209326609      number=14272891867  seg=2000966222
 5: 1021513226683950..1021513227194459      number=14273409245  seg=2000966257
 5: 1021513244551800..1021513245062309      number=14273926678  seg=2000966292
 5: 1021513266503730..1021513267014239      number=14274620733  seg=2000966339
 5: 1021513284371580..1021513284882089      number=14275137281  seg=2000966374
 5: 1021513302239430..1021513302749939      number=14275653739  seg=2000966409
 5: 1021513326233400..1021513326743909      number=14276200475  seg=2000966446
 5: 1021513344101250..1021513344611759      number=14276746091  seg=2000966483
 5: 1021513361969100..1021513362479609      number=14277263131  seg=2000966518
 5: 1021513380857970..1021513381368479      number=14277780236  seg=2000966553
 5: 1021513399746840..1021513400257349      number=14278296874  seg=2000966588
 5: 1021513417614690..1021513418125199      number=14278813768  seg=2000966623
 5: 1021513435482540..1021513435993049      number=14279404403  seg=2000966663
 5: 1021513453350390..1021513453860899      number=14279920879  seg=2000966698
 5: 1021513471218240..1021513471728749
 5: 1021513491638640..1021513492149149      si=618,178,0,0
 5: 1021513509506490..1021513510016999      Time: 28372.08 sec

Найдено 178 квадратов Стенли с тремя заполненными строками!
В этих квадратах 10 "дырок".
И нет ни одного квадрата Стенли с четырьмя заполненными строками :(

В теме "Симметричные кортежи из последовательных простых чисел" наткнулась на сообщение
https://dxdy.ru/post1061692.html#p1061692
о задаче века.

Интересно: в сообщении рассматриваются ещё и симметричные 25-ки из последовательных простых чисел, из которых можно построить ассоциативные квадраты Стенли 5х5, которые превращаются в идеальные квадраты 5-го порядка.

Ну, до симметричных 25-ок нам ещё о-ч-е-н-ь далеко!

Ещё нашла интересную статью на моём сайте
ПАНДИАГОНАЛЬНЫЕ КВАДРАТЫ ИЗ ПРОСТЫХ ЧИСЕЛ
http://www.natalimak1.narod.ru/panpr.htm

Читайте, господа!
Это дьявольски интересно, потому что о дьявольских квадратах :)

Покажу скриншот фрагмента из этой статьи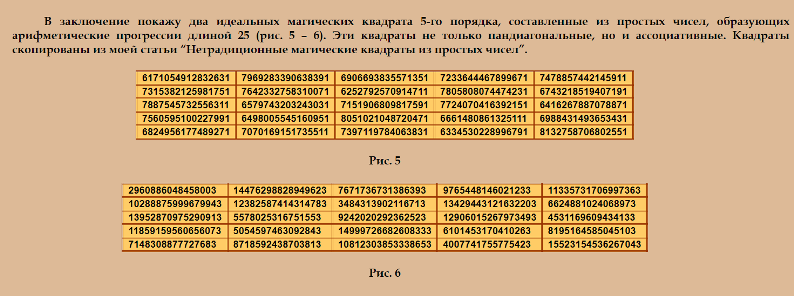



Это идеальные квадраты 5-го порядка (идеальные квадраты одновременно ассоциативные и пандиагональные).
25-ки тут симметричные из простых чисел, ибо это арифметические прогрессии из простых чисел!
Но! Они не из последовательных простых чисел.

К сожалению, ссылка на сайт, где я взяла арифметические прогрессии, недействительна.

Остановила свою программу предпроверки на возможность построения квадрата Стенли.
Кручу программу Сергея Беляева.

Посмотрите, что делается с самого начала диапазона простых чисел (задала Segment=1)

   Поиск примитивных квадратов              number=63991940653  seg=3402374
 Порядок=5                                  number=63994982998  seg=3402542
 file: pand5.txt                            number=63998028415  seg=3402710
 Segment=1                                  number=64001069677  seg=3402878
 5: 1737032226930..1737032737439            number=64004113293  seg=3403046
 5: 1737117992610..1737118503119            number=64007154238  seg=3403214
 5: 1737203758290..1737204268799            number=64010197053  seg=3403382
 5: 1737289523970..1737290034479            number=64013239797  seg=3403550
 5: 1737375289650..1737375800159            number=64016284113  seg=3403718
 5: 1737461055330..1737461565839            number=64019325892  seg=3403886
 5: 1737546821010..1737547331519            number=64022369067  seg=3404054
 5: 1737632586690..1737633097199            number=64025411418  seg=3404222
 5: 1737718352370..1737718862879            number=64028454724  seg=3404390
 5: 1737804118050..1737804628559            number=64031497293  seg=3404558
 5: 1737889883730..1737890394239            number=64034540506  seg=3404726
 5: 1737975649410..1737976159919            number=64039105229  seg=3404978
 5: 1738061415090..1738061925599            number=64042148702  seg=3405146
 5: 1738147180770..1738147691279            number=64045192884  seg=3405314
 5: 1738275829290..1738276339799            number=64048236000  seg=3405482
 5: 1738361594970..1738362105479            number=64051279316  seg=3405650
 5: 1738447360650..1738447871159
 5: 1738533126330..1738533636839            si=7848,5085,0,0
 5: 1738618892010..1738619402519            Time: 52950.08 sec

Найдено 5085 квадратов Стенли с тремя заполненными строками!
А с четырьмя заполненными строками по-прежнему нет и нет :(

Не сверяла скорость работы с программой Алексея Белышева.
Но у программы Сергея огромное преимущество: она выводит приближения к квадрату Стенли.
Можно видеть, как вообще эти квадраты строятся, насколько плохо или насколько хорошо.
Если бы появился квадрат Стенли с четырьмя заполненными строками - это уже всего 5 "дырок" в квадрате (одна строка)!
Но такого приближения пока не найдено.

Кстати, в сообщении
https://dxdy.ru/post1061692.html#p1061692
приведены паттерны для квадратов Стенли 5х5

0  4  18  22  48  52  60  64  70  78  82  84  88  90  102  108  118  130  132  138  144  148  150  162  168
0  20  30  36  38  48  56  60  66  74  80  84  90  98  108  120  126  140  146  150  156  158  164  168  174
0  6  10  16  30  66  72  76  82  84  90  94  96  100  114  126  132  136  142  144  150  154  156  160  174
0  12  30  36  42  46  58  60  72  76  82  88  90  96  102  126  130  138  142  156  160  162  166  168  172
0  12  30  36  42  54  64  66  76  84  90  94  96  100  106  120  124  132  136  150  154  156  160  162  166
0  10  24  34  48  60  66  70  76  84  90  94  100  108  114  120  126  130  136  144  150  154  160  168  174

Протестировала их программой предпроверки.
Всё в порядке, кандидаты с 8 "дырками" выводятся.

Надо добавить эти паттерны в общий список паттернов для квадратов Стенли 5х5, там нет таких паттернов.

Обновлённый список паттенов для квадратов Стенли 5х5
59 паттернов, отсортировано по диаметру

[0, 2, 6, 20, 30, 32, 36, 42, 50, 60, 62, 66, 72, 80, 84, 86, 90, 102, 104, 114, 116, 120, 126, 134, 156]
[0, 6, 14, 20, 30, 36, 42, 44, 50, 54, 56, 60, 72, 86, 90, 96, 102, 104, 116, 120, 132, 134, 144, 146, 156]
[0, 10, 12, 22, 24, 36, 40, 52, 54, 60, 66, 70, 84, 96, 100, 102, 106, 112, 114, 120, 126, 136, 142, 150, 156]
[0, 22, 30, 36, 40, 42, 52, 54, 66, 70, 72, 76, 84, 90, 94, 96, 106, 114, 120, 124, 126, 136, 150, 154, 156]
[0, 12, 30, 36, 42, 54, 64, 66, 76, 84, 90, 94, 96, 100, 106, 120, 124, 132, 136, 150, 154, 156, 160, 162, 166]
[0, 4, 18, 22, 48, 52, 60, 64, 70, 78, 82, 84, 88, 90, 102, 108, 118, 130, 132, 138, 144, 148, 150, 162, 168]
[0, 12, 30, 36, 42, 46, 58, 60, 72, 76, 82, 88, 90, 96, 102, 126, 130, 138, 142, 156, 160, 162, 166, 168, 172]
[0, 6, 10, 16, 30, 66, 72, 76, 82, 84, 90, 94, 96, 100, 114, 126, 132, 136, 142, 144, 150, 154, 156, 160, 174]
[0, 10, 24, 34, 48, 60, 66, 70, 76, 84, 90, 94, 100, 108, 114, 120, 126, 130, 136, 144, 150, 154, 160, 168, 174]
[0, 20, 30, 36, 38, 48, 56, 60, 66, 74, 80, 84, 90, 98, 108, 120, 126, 140, 146, 150, 156, 158, 164, 168, 174]
[0, 6, 18, 24, 28, 30, 34, 40, 46, 48, 54, 58, 60, 70, 84, 96, 114, 124, 126, 136, 144, 150, 154, 166, 180]
[0, 10, 18, 24, 28, 30, 34, 40, 48, 58, 66, 70, 84, 88, 90, 94, 96, 100, 114, 118, 136, 154, 160, 166, 184]
[0, 6, 18, 24, 28, 30, 34, 48, 54, 58, 60, 84, 88, 94, 96, 114, 118, 124, 126, 144, 150, 154, 180, 184, 214]
[0, 6, 10, 16, 28, 30, 34, 40, 58, 60, 66, 70, 76, 84, 88, 90, 94, 114, 144, 150, 154, 160, 184, 214, 220]
[0, 6, 12, 18, 20, 30, 32, 36, 50, 56, 60, 68, 72, 86, 90, 96, 102, 116, 152, 156, 162, 168, 182, 218, 222]
[0, 6, 8, 14, 24, 30, 36, 44, 50, 56, 60, 66, 74, 86, 90, 108, 114, 116, 126, 134, 144, 150, 174, 176, 234]
[0, 6, 12, 18, 20, 30, 32, 36, 50, 56, 68, 72, 78, 86, 92, 96, 102, 116, 128, 152, 156, 168, 186, 228, 252]
[0, 2, 6, 8, 12, 18, 30, 36, 42, 48, 60, 62, 72, 90, 102, 126, 128, 138, 156, 168, 216, 218, 228, 246, 258]
[0, 12, 20, 30, 32, 42, 48, 50, 56, 60, 62, 68, 72, 78, 86, 90, 92, 98, 120, 128, 188, 200, 218, 230, 260]
[0, 2, 6, 8, 20, 26, 30, 32, 42, 48, 50, 72, 86, 92, 116, 126, 128, 146, 168, 180, 182, 200, 212, 222, 266]
[0, 2, 6, 8, 30, 32, 42, 48, 60, 62, 72, 86, 92, 102, 116, 126, 128, 146, 156, 162, 168, 186, 212, 216, 282]
[0, 2, 6, 8, 12, 18, 30, 36, 48, 50, 60, 78, 90, 92, 102, 120, 126, 128, 138, 156, 252, 258, 300, 342, 378]
[0, 4, 36, 40, 64, 66, 70, 100, 130, 144, 180, 210, 252, 256, 270, 274, 294, 316, 330, 334, 360, 396, 414, 546, 564]
[0, 6, 20, 26, 48, 68, 92, 98, 102, 108, 140, 150, 186, 206, 216, 236, 278, 288, 308, 318, 440, 446, 488, 626, 656]
[0, 4, 18, 22, 30, 34, 48, 52, 144, 162, 198, 202, 228, 232, 342, 378, 382, 408, 412, 522, 564, 568, 594, 598, 708]
[0, 4, 6, 10, 48, 54, 60, 64, 108, 126, 130, 174, 246, 250, 270, 276, 294, 330, 396, 490, 496, 516, 550, 616, 736]
[0, 2, 12, 14, 30, 42, 60, 62, 90, 102, 104, 132, 134, 146, 194, 236, 260, 272, 320, 362, 480, 482, 510, 614, 740]
[0, 2, 18, 20, 30, 48, 96, 98, 126, 140, 158, 170, 188, 236, 266, 528, 530, 558, 576, 578, 606, 668, 698, 716, 746]
[0, 2, 30, 32, 42, 72, 74, 90, 92, 104, 132, 164, 200, 230, 240, 242, 282, 290, 314, 440, 552, 554, 594, 626, 752]
[0, 4, 18, 22, 30, 40, 48, 58, 84, 88, 114, 124, 240, 258, 270, 274, 300, 310, 324, 510, 534, 538, 564, 574, 774]
[0, 8, 12, 20, 38, 50, 144, 150, 152, 162, 180, 182, 188, 218, 270, 278, 294, 308, 330, 420, 518, 530, 662, 698, 788]
[0, 4, 60, 64, 66, 70, 120, 150, 154, 180, 186, 270, 336, 340, 354, 414, 420, 456, 460, 504, 520, 526, 610, 690, 796]
[0, 48, 86, 114, 134, 140, 188, 200, 204, 254, 260, 290, 308, 330, 344, 374, 378, 444, 464, 468, 534, 554, 608, 728, 798]
[0, 6, 8, 14, 18, 26, 78, 84, 96, 140, 146, 158, 278, 284, 296, 426, 434, 504, 546, 554, 566, 624, 686, 704, 824]
[0, 4, 6, 10, 34, 40, 66, 70, 100, 126, 130, 160, 174, 180, 240, 300, 360, 364, 394, 510, 516, 534, 576, 636, 870]
[0, 6, 14, 20, 30, 44, 68, 74, 98, 168, 174, 180, 194, 198, 224, 230, 248, 254, 348, 404, 660, 674, 728, 828, 884]
[0, 14, 24, 26, 38, 50, 54, 68, 80, 84, 98, 110, 114, 138, 168, 198, 200, 224, 254, 284, 684, 698, 710, 798, 884]
[0, 6, 8, 14, 30, 38, 50, 56, 80, 128, 134, 158, 210, 216, 240, 540, 548, 590, 668, 678, 686, 728, 750, 806, 888]
[0, 4, 18, 22, 24, 42, 60, 64, 84, 294, 298, 318, 360, 378, 420, 430, 448, 480, 484, 490, 504, 654, 724, 840, 910]
[0, 2, 8, 12, 14, 20, 90, 92, 98, 132, 134, 140, 308, 320, 398, 408, 420, 440, 498, 510, 512, 518, 540, 818, 918]
[0, 2, 12, 30, 32, 42, 108, 110, 120, 128, 158, 210, 212, 222, 236, 338, 348, 350, 360, 476, 572, 602, 680, 782, 920]
[0, 2, 6, 8, 50, 56, 66, 72, 90, 92, 126, 128, 140, 156, 176, 192, 420, 422, 470, 486, 500, 506, 590, 626, 920]
[0, 4, 24, 28, 30, 54, 64, 66, 70, 84, 88, 96, 108, 130, 150, 414, 418, 444, 478, 498, 864, 868, 894, 928, 948]
[0, 2, 12, 14, 30, 42, 44, 56, 90, 92, 120, 134, 350, 362, 440, 552, 554, 582, 596, 600, 602, 630, 644, 902, 950]
[0, 12, 30, 42, 80, 92, 110, 122, 128, 140, 158, 168, 170, 180, 198, 210, 420, 500, 530, 542, 548, 560, 572, 588, 950]
[0, 6, 10, 12, 18, 22, 36, 42, 46, 66, 78, 102, 166, 178, 202, 372, 378, 382, 438, 538, 792, 798, 802, 858, 958]
[0, 6, 10, 12, 16, 22, 30, 36, 40, 42, 48, 66, 390, 400, 426, 556, 562, 568, 570, 576, 582, 586, 600, 946, 960]
[0, 4, 12, 16, 30, 42, 60, 64, 90, 112, 124, 172, 240, 244, 270, 312, 316, 342, 352, 424, 660, 672, 720, 900, 972]
[0, 6, 36, 42, 66, 72, 76, 112, 114, 120, 142, 190, 240, 246, 316, 336, 372, 402, 450, 576, 736, 772, 802, 850, 976]
[0, 2, 6, 8, 12, 18, 56, 62, 182, 188, 216, 218, 228, 272, 398, 420, 422, 432, 476, 602, 816, 818, 828, 872, 998]
[0, 2, 12, 14, 18, 30, 120, 122, 138, 150, 152, 168, 308, 320, 428, 432, 434, 450, 458, 578, 590, 698, 728, 740, 1010]
[0, 4, 6, 10, 16, 22, 30, 34, 46, 60, 66, 90, 114, 120, 144, 450, 454, 466, 510, 564, 900, 904, 916, 960, 1014]
[0, 6, 12, 14, 20, 26, 50, 56, 62, 132, 146, 182, 300, 306, 312, 336, 350, 386, 432, 636, 680, 686, 692, 812, 1016]
[0, 6, 10, 16, 24, 30, 34, 36, 54, 84, 90, 100, 106, 108, 124, 210, 220, 240, 294, 310, 936, 946, 966, 1020, 1036]
[0, 6, 8, 14, 18, 26, 36, 44, 78, 84, 96, 114, 278, 284, 296, 314, 378, 386, 456, 656, 698, 704, 716, 734, 1076]
[0, 10, 12, 22, 24, 36, 276, 286, 300, 432, 442, 456, 492, 502, 516, 934, 946, 1210, 1284, 1296, 1366, 1426, 1560, 1716, 1776]
[0, 14, 24, 36, 38, 60, 114, 128, 150, 540, 554, 576, 686, 710, 800, 954, 968, 990, 1016, 1040, 1130, 1226, 1556, 1640, 1970]
[0, 12, 72, 86, 98, 150, 158, 236, 296, 308, 368, 446, 516, 602, 606, 618, 678, 756, 812, 1122, 1556, 1568, 1628, 1706, 2072]
[0, 6, 30, 36, 114, 126, 144, 156, 166, 172, 280, 292, 546, 552, 660, 672, 790, 796, 904, 916, 1386, 1416, 1552, 1932, 2176]

Господа!
Найдите хотя бы одну 25-ку из последовательных простых чисел, которая имеет один из этих паттернов, любой.
И задача века будет решена!

Для первых четырёх паттернов с минимальным диаметром 156, по утверждению Andersen, 25-ки из последовательных простых чисел не встречаются до 10^20.
Про остальные паттерны ничего неизвестно.

Список паттернов можно дополнять другими паттернами, их можно найти как угодно много.

Моя программа предпроверки на возможность построения квадрата Стенли находит кандидатов с 8 "дырками".
Я достраиваю эти кандидаты вручную.
Иногда удаётся получить квадрат Стенли с 7 "дырками".
Пример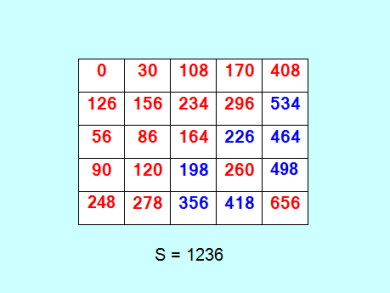



Сейчас я остановила свою программу предпроверки и кручу программу Сергея Беляева.
Эта программа пока выдаёт только квадраты Стенли с тремя заполненными строками - первая, вторая и пятая (10 "дырок" в таком квадрате).
Выше показаны такие кандидаты.

Вспомнила свою головоломку на сайте Carlos Rivera
https://www.primepuzzles.net/puzzles/puzz_681.htm

Читайте, господа, очень интересно там выступили Ярослав Врублевский и J. K. Andersen.
J. K. Andersen нашёл много решений для головоломки.

А это общая формула квадрата Стенли 5-го порядка, приведённая мной

For d=5, X26=S, e=17

x1=-x10-x15-x20-x22-x23-x24+2 x25+x26
x2=-x10-x15-x20-x21-x23-x24+2 x25+x26
x3=-x10-x15-x20-x21-x22-x24+2 x25+x26
x4=-x10-x15-x20-x21-x22-x23+2 x25+x26
x5=-x10-x15-x20-x21-x22-x23-x24+3 x25+x26
x6=x10+x21-x25
x7=x10+x22-x25
x8=x10+x23-x25
x9=x10+x24-x25
x11=x15+x21-x25
x12=x15+x22-x25
x13=x15+x23-x25
x14=x15+x24-x25
x16=x20+x21-x25
x17=x20+x22-x25
x18=x20+x23-x25
x19=x20+x24-x25

Здесь x1, x2, x3, ..., x24, x25 - элементы квадрата, x26 - индекс квадрата.
При построении квадрата Стенли 5-го порядка из заданного массива, состоящего из 25 чисел, индекс квадрата Стенли известен.

Эта общая формула квадрата Стенли 5-го порядка содержит 8 свободных и 17 зависимых переменных из 25 (x1, x2, x3, ..., x24, x25).
Если зафиксировать две переменные (x1 и x25), то свободных переменных будет 6 из 23.
Такое количество свободных переменных у меня и получилось при проверке возможности построения квадрата Стенли 5-го порядка, рассматриваемой в этой теме.

Кстати, выше показано построение пандиагонального квадрата 5-го порядка из квадрата Стенли с помощью простого преобразования.

Из этого обратимого квадрата, составленного из 25 последовательных натуральных чисел

1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25

можно построить классический идеальный квадрат, но преобразование для этого нужно другое.
[Напомню: обратимый квадрат всегда является квадратом Стенли, обратное неверно.]
Или же нужен другой исходный квадрат Стенли.

Читайте мою статью
ПОСТРОЕНИЕ ИДЕАЛЬНЫХ КВАДРАТОВ НЕЧЁТНОГО ПОРЯДКА ИЗ ОБРАТИМЫХ КВАДРАТОВ
http://www.klassikpoez.narod.ru/obratid.htm
В статье всё подробно написано о построении классического идеального квадрата 5-го порядка.

Покажу скриншот фрагмента статьи



Вы видите на скриншоте матрицу преобразования, которая переводит обратимый квадрат, показанный в начале сообщения, в идеальный квадрат, а также идеальный квадрат, полученный в результате данного матричного преобразования.

Попробуйте построить нетрадиционный идеальный квадрат 5-го порядка из арифметической прогрессии, например, из такой
a1 = 3, d = 4, с помощью показанного матричного преобразования.

Для этого сначала запишите обратимый квадрат из 25 членов этой прогрессии, записывая их по порядку.
Вот так

3 7 11 15 19
23 27 31 35 39
43 47 51 55 59
63 67 71 75 79
83 87 91 95 99

А теперь примените к этому обратимому квадрату матричное преобразование, которое показано выше.
Вы получите нетрадиционный идеальный квадрат 5-го порядка.

В сообщении
https://boinc.progger.info/odlk/forum_thread.php?id=260&postid=12947
показаны нетрадиционные идеальные квадраты 5-го порядка, построенные из арифметических прогрессий из простых чисел.