Возвращаюсь к теоретическому вопросу.

Это минимальный симметричный кортеж длины 15 из последовательных простых чисел с минимальным диаметром 180, найден Ярославом Врублевским в конкурсе по кортежам

3112462738414697093: 0 6 24 30 54 66 84 90 96 114 126 150 156 174 180

Ярослав нашёл ещё много 15-ок с минимальным диаметром 180, они показаны в теме
https://boinc.progger.info/odlk/forum_thread.php?id=226&postid=8458

Открываю свой старый рабочий файл, где работала с 15-ми, и вижу следующее

2: свободные (1) дополнения (1)
3: (1,2) (2,1)
5: (2,3) (3,2)
7: (1,4) (6,3)
11: (1,3) (10,8)
13: (3,8) (10,5)

ChineseRemainder[{1,2,3,6,10,10},{2,3,5,7,11,13}]
10163+30030n
ChineseRemainder[{1,2,3,6,10,5},{2,3,5,7,11,13}]
5543+30030n
ChineseRemainder[{1,2,3,6,8,10},{2,3,5,7,11,13}]
7433+30030n
ChineseRemainder[{1,2,3,6,8,5},{2,3,5,7,11,13}]
2813+30030n
ChineseRemainder[{1,2,3,3,10,10},{2,3,5,7,11,13}]
23033+30030n
ChineseRemainder[{1,2,3,3,10,5},{2,3,5,7,11,13}]
18413+30030n
ChineseRemainder[{1,2,3,3,8,10},{2,3,5,7,11,13}]
20303+30030n
ChineseRemainder[{1,2,3,3,8,5},{2,3,5,7,11,13}]
15683+30030n

Вот оно! То самое нахождение формул по паттерну!
Не уверена, что здесь найдены все формулы для данного паттерна.
Но уже видно, как это находилось.
Правда, я пока не понимаю – как именно.
Очевидно, что проверяются все простые меньше 15.
Думаю, что проверка идёт по элементам паттерна.

А дальше по результатам проверки строится функция ChineseRemainder и её значение вычисляется в ВольфрамАльфа.
Число 30030 – это праймориал_13.
ВСЁ!

Далее в рабочем файле написано, что минимальная 15-ка, показанная выше, находится по третьей формуле, то есть по этой

Q = 7433 + 30030n

при n = 103645112834322
Вот
Q = 7433 + 30030 * 103645112834322 = 3112462738414697093

Всё чётко.
Осталось совсем чуть-чуть, господа!

Кстати, о ВольфрамАльфа.
Я в последнее время не могу ничего там вычислить.
Вроде где-то читала, что этот сервис стал платным.
Это так?
А нет ли там режима Premium?
Могли бы и дать немного попользоваться бесплатно, ну недельку, например.

Ещё одна загадочная функция в ВольфрамАльфа (это тоже из рабочего файла)

matrix(table[Select[Range[0,200],PrimeQ[(n*30030+10163)+#]&],{n,40,50}])

n |
40 | {18, 26, 30, 44, 48, 60, 80, 114, 126, 138, 140, 168, 174, 180, 186, 200}
41 | {14, 20, 24, 30, 44, 54, 74, 84, 90, 96, 98, 114, 116, 156, 158, 164, 180, 186, 194}
42 | {6, 26, 48, 60, 80, 84, 90, 98, 108, 128, 138, 174, 180, 186}
43 | {0, 6, 14, 18, 44, 54, 74, 80, 86, 90, 98, 108, 128, 138, 150, 164, 168}
44 | {6, 14, 30, 38, 44, 66, 84, 90, 96, 104, 108, 114, 116, 128, 150, 158, 164, 174, 180, 200}
45 | {20, 60, 74, 80, 86, 90, 96, 116, 164, 186, 194, 200}
46 | {6, 14, 18, 20, 24, 30, 44, 54, 84, 86, 98, 104, 108, 110, 126, 158, 170, 186}
47 | {30, 38, 48, 54, 66, 74, 90, 96, 104, 116, 138, 158, 164, 168, 174, 186, 200}
48 | {0, 6, 20, 30, 38, 60, 74, 110, 114, 116, 126, 138, 140, 156, 164, 194}
49 | {30, 38, 60, 84, 86, 98, 110, 114, 116, 126, 140, 150, 164, 168, 186}
50 | {0, 6, 24, 26, 60, 74, 80, 84, 116, 128, 138, 156, 158, 200}

Кстати, ChineseRemainder Google переводит "Китайский остаток".
Здесь наверняка применяется китайская теорема об остатках, которую, к стыду своему, не знаю.
Но, кажется, я поняла, как формируется эта функция из данных

2: свободные (1) дополнения (1)
3: (1,2) (2,1)
5: (2,3) (3,2)
7: (1,4) (6,3)
11: (1,3) (10,8)
13: (3,8) (10,5)

По-моему, здесь

ChineseRemainder[{1,2,3,6,10,10},{2,3,5,7,11,13}]
10163+30030n
ChineseRemainder[{1,2,3,6,10,5},{2,3,5,7,11,13}]
5543+30030n
ChineseRemainder[{1,2,3,6,8,10},{2,3,5,7,11,13}]
7433+30030n
ChineseRemainder[{1,2,3,6,8,5},{2,3,5,7,11,13}]
2813+30030n
ChineseRemainder[{1,2,3,3,10,10},{2,3,5,7,11,13}]
23033+30030n
ChineseRemainder[{1,2,3,3,10,5},{2,3,5,7,11,13}]
18413+30030n
ChineseRemainder[{1,2,3,3,8,10},{2,3,5,7,11,13}]
20303+30030n
ChineseRemainder[{1,2,3,3,8,5},{2,3,5,7,11,13}]
15683+30030n

не все функции сформированы.
Должно получиться 32 варианта функции.

Что скажете, господа?

Ура-а-а-а-а!
ВольфрамАльфа сработал!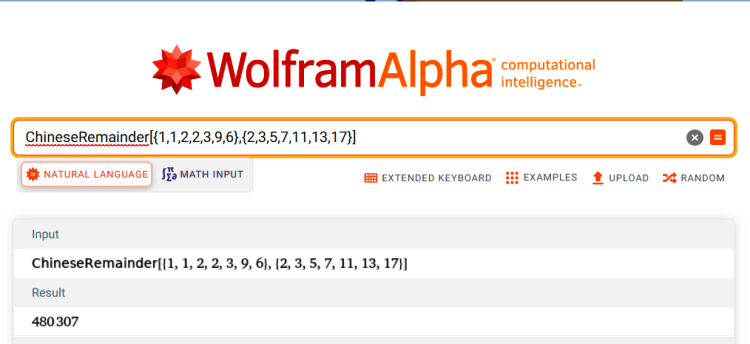



Это уже для 17-ки, есть у меня в рабочем файле и для 17-ки формулы, но опять же далеко не все.
Дальше покажу их.

Тэк-с, открыла тему на форуме MHP
"Получить формулы (китайская теорема об остатках)"
http://mathhelpplanet.com/viewtopic.php?f=62&t=77621

Авось, кто-нибудь поможет.

Итак, 17-ка с минимальным диаметром 240 (из найденных Ярославом Врублевским)

1006882292528806742267: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240

Вот что вижу в рабочем файле для данного паттерна

2: свободные (1), дополнения (1)
3: (1,2) (2,1)
5: (2,3) (3,2)
7: (4,5) (3,2)
11: (1,8) (10,3)
13: (2,4) (11,9)
17: (8,9,10,11) (9,8,7,6)

ChineseRemainder[{1,1,2,2,3,9,6},{2,3,5,7,11,13,17}]
480307+510510n
ChineseRemainder[{1,2,2,2,3,9,9},{2,3,5,7,11,13,17}]
470297+510510n

480307+510510n
420247+510510n
360187+510510n
300127+510510n
139967+510510n
79907+510510n
19847+510510n
470297+510510n
276103+510510n
216043+510510n
155983+510510n
95923+510510n

Показаны два примера функции ChineseRemainder, а затем несколько полученных формул.
Но формулы тоже ведь не все, их должно получиться 128, если я правильно поняла, как эта функция формируется.

Вот эту задачку и запостила на MHP: найти все 128 формул.

Господа!
Кто-нибудь может помочь решить эту задачку?

А после этого останется понять, как получаются эти данные

2: свободные (1), дополнения (1)
3: (1,2) (2,1)
5: (2,3) (3,2)
7: (4,5) (3,2)
11: (1,8) (10,3)
13: (2,4) (11,9)
17: (8,9,10,11) (9,8,7,6)

Ура!
На форуме MHP задачку решили!
Вот они - 128 значений функции ChineseRemainder, показываю несколько первых и последних

1 4223
2 19693
3 19847
4 21563
5 29417
6 29963
7 30403
8 38257
9 39973
10 40127
11 45433
12 55597
13 56143
. . . . . 
115 446273
116 454127
117 454673
118 464837
119 470143
120 470297
121 472013
122 479867
123 480307
124 480853
125 488707
126 490423
127 490577
128 506047

Замечательно!
Программку форумчанин написал на Питоне, смотрите сообщение
http://mathhelpplanet.com/viewtopic.php?p=445517#p445517

Итак, для 17-ки с паттерном

0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240

все 128 формул получены.

На очереди 19-ка.

Посмотрите на эти 17-ки, найденные Ярославом Врублевским

1) 1006882292528806742267: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240
Q = 510510k + 208427
k = 1972306698260184

2) 3954328349097827424397: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240
Q = 510510k + 103777
k = 7745839159071962

3) 4896552110116770789773: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240
Q = 510510k + 346433
k = 9591491077778634

4) 6751407944109046348063: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240
Q = 510510k + 430363
k = 13224829962408270

5) 7768326730875185894807: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240
Q = 510510k + 29417
k = 15216796401393089

6) 19252814175273852997757: 0 6 24 36 66 84 90 114 120 126 150 156 174 204 216 234 240
Q = 510510k + 234167
k = 37712903126821909

Все они с одним и тем же паттерном с минимальным диаметром 240, для каждой 17-ки я нашла формулу и значение k, для которого данный кортеж получен.
Очень интересен вопрос: есть ли между этими 17-ми другие 17-ки? Пусть и не с минимальным диаметром 240.
С минимальным диаметром, возможно, и нет, Ярослав, наверное, нашёл все подряд.
[Да, здесь не показаны 17-ки с другими паттернами с минимальным диаметром 240.]
Замечательные кортежи нашёл Ярослав!

Когда я организовала конкурс по кортежам, Бегемот и господин Петухов кричали, что конкурс бесполезный, ничего интересного в нём не найдено.
Зря кричали!
Ярослав нашёл очень много интересного и полезного.

PS. Проверила эти значения в формулах
208427, 103777, 346433, 430363, 29417, 234167
в списке значений, выданных программой форумчанина c MHP.
Все они имеются.

Проверила и значения в этих формулах (из моего рабочего файла)

480307+510510n
420247+510510n
360187+510510n
300127+510510n
139967+510510n
79907+510510n
19847+510510n
470297+510510n
276103+510510n
216043+510510n
155983+510510n
95923+510510n

Все они тоже имеются.

Игра "Угадай слово" за 12 июня

ДРОЖЬ
НУЖДА

Сегодня "двойка" :(
Опять пресловутая многовариантность.
К тому же, ошиблась в третьей попытке.

Новости "Пентадекатлона мечты"

Что-то уже два дня в теме молчание.
Господин Лецко писал в сообщении
https://dxdy.ru/post1557056.html#p1557056

Не помню сообщал ли: нашел 7-ку по 1000 делителей.
Запустил поиск 7-по по 340, 364 и 380 делителей.

По-моему, это уже извращение.
Гораздо интереснее заниматься минимизацией 14-ки и 15-ки с 12 делителями (чем занимается Антон).
Ну, или искать второй пентадекатлон - 15-ку с 36 делителями.

EUgeneUS и mathematician123 всё продолжают что-то доказывать.
Интересно, удастся ли им собрать эти многочисленные фрагменты воедино да ещё объединить их с фрагментами доказательств господина Лецко.
Ну, напишут монографию :)
Прикрепят к ней таблицу господина Лецко с сотнями (или тысячами) коротких цепочек с 1000, 10000, 100000 и т. д. делителей.
До миллиона делителей дойдут? :)

Возвращаюсь к своей проблеме.

Это программа на Питоне, которую написал форумчанин

from itertools import product
from math import prod

def chinese_remainder(primes, a):
    sum, mod = 0, prod(primes)
    for p_i, a_i in zip(primes, a):
        n = mod // p_i
        sum += a_i * mul_inv(n, p_i) * n
    return sum % mod
 
def mul_inv(a, b):
# extended Euclid algo. Return x such ax = 1 (mod b)
    b0 = b
    x0, x1 = 0, 1
    if b == 1: return 1
    while a > 1:
        q = a // b
        a, b = b, a%b
        x0, x1 = x1 - q * x0, x0
    if x1 < 0: x1 += b0
    return x1

m = [[1], [2,1], [3,2], [3,2], [10,3], [11,9], [9,8,7,6]]
primes = [2, 3, 5, 7, 11, 13, 17]

res = list(product(*m))
for i, v in enumerate(sorted([chinese_remainder(primes, x) for x in res]), 1):
    print(i,v)

Я попросила его сделать исполняемую программу.
Он сделал, смотрите сообщение
http://mathhelpplanet.com/viewtopic.php?p=445540#p445540

Но... программа у меня не работает.
Выдаётся ошибка, что в компьютере нет программы api-ms-win-core-path-l1-1-0.dll

Я скачала эту программу в Интернете, но не помогло, программа форумчанина всё равно не работает, ту же ошибку выдаёт.
Скачала другую версию - 32bit, и это не помогло.
Что делать? Пожалуйста, подскажите.
Форумчанин пропал, может, ещё вернётся и скажет что-нибудь.

Тэк-с, дали новый текст программы

from itertools import product
from math import prod

def chinese_remainder(primes, a):
    sum, mod = 0, prod(primes)
    for p_i, a_i in zip(primes, a):
        n = mod // p_i
        sum += a_i * mul_inv(n, p_i) * n
    return sum % mod


def mul_inv(a, b):
    # extended Euclid algo. Return x such ax = 1 (mod b)
    b0 = b
    x0, x1 = 0, 1
    if b == 1: return 1
    while a > 1:
        q = a // b
        a, b = b, a % b
        x0, x1 = x1 - q * x0, x0
    if x1 < 0: x1 += b0
    return x1


primes = list(map(int, input("Введите через пробел массив модулей: ").split()))
m = []
for i in primes:
    m.append(list(map(int, input(f"Введите через пробел набор остатков по модулю {i}: ").split())))

print('\n'.join(map(str, sorted([chinese_remainder(primes, x) for x in product(*m)]))))

и рекомендовали воспользоваться онлайн-компилятором
https://www.programiz.com/python-programming/online-compiler/

Проделала, всё получилось для рассматриваемого примера.

O!
Нашла в PARI/GP соответствующую функцию.

Это в ВольфрамАльфа

ChineseRemainder[{1,1,2,2,3,9,6},{2,3,5,7,11,13,17}]
480307

А это в PARI/GP

lift(chinese([Mod(1,2),Mod(1,3),Mod(2,5),Mod(2,7),Mod(3,11),Mod(9,13),Mod(6,17)]));
%5 = 480307

Теперь у меня задача: найти эти модули для паттерна

0 12 36 90 96 132 162 180 210 216 222 252 270 300 336 342 396 420 432

Кто знает алгоритм? Расскажите, пожалуйста.

Помню, что об этом писалось в теме на форуме dxdy.ru, и тогда это было абсолютно понятно. Я сама находила все эти модули.
Тема "Симметричные кортежи из последовательных простых чисел"
https://dxdy.ru/topic100750.html
Но... никак не хватает духу просмотреть тему и найти этот момент.
Надо собраться!
Теперь уже остался только один этот момент.
Дальше всё понятно.

gris написал, что разбирается в теме, после чего пропал.

Ау, gris!
У вас всё в порядке?
Или вы вдруг сорвались в путешествие? :)
Знаю вашу страсть к путешествиям.

Цитата из сообщения
https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=8906

Это минимальный симметричный кортеж длины 15 из последовательных простых чисел с минимальным диаметром 180, найден Ярославом Врублевским в конкурсе по кортежам

3112462738414697093: 0 6 24 30 54 66 84 90 96 114 126 150 156 174 180

Ярослав нашёл ещё много 15-ок с минимальным диаметром 180, они показаны в теме
https://boinc.progger.info/odlk/forum_thread.php?id=226&postid=8458

Открываю свой старый рабочий файл, где работала с 15-ми, и вижу следующее

2: свободные (1) дополнения (1)
3: (1,2) (2,1)
5: (2,3) (3,2)
7: (1,4) (6,3)
11: (1,3) (10,8)
13: (3,8) (10,5)

ChineseRemainder[{1,2,3,6,10,10},{2,3,5,7,11,13}]
10163+30030n
ChineseRemainder[{1,2,3,6,10,5},{2,3,5,7,11,13}]
5543+30030n
ChineseRemainder[{1,2,3,6,8,10},{2,3,5,7,11,13}]
7433+30030n
ChineseRemainder[{1,2,3,6,8,5},{2,3,5,7,11,13}]
2813+30030n
ChineseRemainder[{1,2,3,3,10,10},{2,3,5,7,11,13}]
23033+30030n
ChineseRemainder[{1,2,3,3,10,5},{2,3,5,7,11,13}]
18413+30030n
ChineseRemainder[{1,2,3,3,8,10},{2,3,5,7,11,13}]
20303+30030n
ChineseRemainder[{1,2,3,3,8,5},{2,3,5,7,11,13}]
15683+30030n

______________________________
конец цитаты

Протестировала программу форумчанина на этих данных.
Вот что получилось

Введите через пробел массив модулей: 2 3 5 7 11 13
Введите через пробел набор остатков по модулю 2: 1
Введите через пробел набор остатков по модулю 3: 1 2
Введите через пробел набор остатков по модулю 5: 2 3
Введите через пробел набор остатков по модулю 7: 3 6
Введите через пробел набор остатков по модулю 11: 8 10
Введите через пробел набор остатков по модулю 13: 5 10

283
1427
2813
3013
4157
5543
6817
7433
9547
9677
10163
11437
12407
12823
14167
14297
15553
15683
17027
17443
18413
19687
20173
20303
22417
23033
24307
25693
26837
27037
28423
29567

Всё верно, формулы у меня в рабочем файле найдены не все, всего будет 32 формулы.

Показанный кортеж получается по формуле
7433 + 30030n
при n = 103645112834322.

Игра "Угадай слово" за 13 июня

ПЕСНЯ
СЛОВО
СОСОК
СОДОМ
СОБОР

Сегодня "троечка" :)
Не повезло в первой попытке, поймалась одна буква не на своём месте да ещё очень распространённая.
Дальше думать почему-то не хотелось, быстренько нашлёпала ещё три слова.
Гимнастика для мозгов не очень хорошая получилась.

Ой, на форуме MHP есть форумчанин, который утверждает, что постиг все глубины простых чисел, понял все глобальные закономерности симметрии простых чисел.
Однако симметричную 19-ку из последовательных простых чисел показать не может, по той простой причине, что он её не знает.

Рисует разные красивые картинки и постит их в теме :)
Вот некоторые картинки









Говорит, что в этих картинках содержится разгадка всех симметрий простых чисел.
Разгадайте, господа! :)

Новости "Пентадекатлона мечты"

EUgeneUS писал в сообщении
https://dxdy.ru/post1557223.html#p1557223

По расчету цепочек с 84-ю делителями.
Досчитал для 1100e105, нашлось два кандидата в 10-ки. А дальше у меня начались сложности - за несколько суток из 4-х неизвестных чисел (их по два в каждом кандидате) у меня разложилось только одно
Прошу помочь с разложением, если это ещё возможно...

L2-167:923943599628522886780123718903641701760518481336568378962925588985768391997255110491590730792092886547562491: 42,  0, 84, 84, 84, 84, 84, 84, 84,  0, 84,  valids=8, maxlen=7/10, ALL (n+1 -?, n+9 -?)

L2-317:850110906168382371216057545387082625772983773608338698713882862297162247190308993041704075477374723603562491:  1,  0, 84, 84, 84, 84, 84, 84, 84,  0, 84,  valids=8, maxlen=7/10, ALL (n+1 - 84, n+9 -?)

Вот поэтому я и говорю, что увеличение количества делителей до бесконечности - извращение.
Здесь пока всего-то 84 делителя, и уже возникли сложности с подсчётом количества делителей.
Интересно, а как господин Лецко посчитал 1000 делителей?
И какой длины у него получились числа в цепочке?
Ну, как говорится, на вкус, на цвет ...

Господин Лецко помогает EUgeneUS посчитать количество делителей.
Кажется, вторая цепочка является правильной 10-ой с 84 делителями

850110906168382371216057545387082625772983773608338698713882862297162247190308993041704075477374723603562492: 84, 84, 84, 84, 84, 84,
84, 84, 84, 84

Форумчанин на MHP посчитал мне остатки
http://mathhelpplanet.com/viewtopic.php?p=445570#p445570
(Алгоритм пока не знаю, задала ему вопрос.)

"Bloodhound" wrote:

"Nataly-Mak" wrote:

Теперь мне надо найти эти множества для паттерна кортежа длины 19

0 12 36 90 96 132 162 180 210 216 222 252 270 300 336 342 396 420 432

2 (1,)
3 (1, 2)
5 (1, 2)
7 (4, 5)
11 (2, 6)
13 (4, 6)
17 (1, 9, 13, 14)
19 (8, 11, 13, 16)
23 (7, 12, 13, 15, 16, 21)

________________
конец цитаты

Только мне непонятно, почему он проверил по всем простым до 23 включительно; здесь вроде бы надо проверять до 19 включительно, потому что кортеж у нас длины 19.
Ну ладно, я сейчас получу формулы по остаткам до 19 включительно.