Для участников форума MHP
Message boards :
Cafe :
Для участников форума MHP
Message board moderation
Previous · 1 . . . 63 · 64 · 65 · 66 · 67 · 68 · 69 . . . 133 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Ахиллес нашёл во втором диапазоне вторую 13-ку, вот обе 13-ки в этом диапазоне 6000166649924711221: 0 12 60 90 132 138 180 222 228 270 300 348 360 6000201742565338057: 0 24 36 66 84 114 180 246 276 294 324 336 360 Очень симпатичные, как две сестрички - с одинаковым диаметром. Нет пока ни одной 15-ки. Ну, 15-ка, может, и появится, а вот до 17-ки, как до Луны пешком :) А мне-то 19-ка нужна! Статистика в обеих программах опубликована в сообщении https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=9875 Сейчас, конечно, прибавилось много 12-ок, 14-ок и 16-ок. 12-ки вообще пачками находятся, несколько штук сразу прибавляется. Одна новая 18-ка появилась. Остальное без изменений. Позже опубликую новую статистику. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
В первом диапазоне тоже появилась вторая 13-ка, вот обе 13-ки в этом диапазоне 5000174129811031207: 0 36 66 126 150 180 186 192 222 246 306 336 372 5000201877324953149: 0 12 42 54 60 90 132 174 204 210 222 252 264 Ахиллес усердно трудится! Но тут - как повезёт. Если 19-ка существует в проверяемых диапазонах, она будет найдена, потому что тотальный перебор и никуда она не денется. Закавыка в том, что нету её во всех уже проверенных брутфорсом диапазонах. Вот нету и всё! Кстати, о птичках... Как бы это супермен ускорил программу Алексея Белышева хотя бы раз в 100 :) Программа хорошая, но... работает медленно. Даже в BOINC-проекте TBEG проверка идёт медленно, а там ведь много машин работают. Программа Алексея не на PARI написана, но её можно и на PARI написать. Я уже пробовала давно; на PARI программа работает ещё медленнее программы Алексея. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Цитата из сообщения https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=9878 Запостила вопрос на форуме MHP Нет, никто не ответил :( Наверное, это условие не только мне не очевидно. А вот господину Лецко оно очевидно, потому что никаких доказательств (или хотя бы краткого разъяснения, почему это так) не приводится. Может быть, доказательство есть в его статьях по данной теме. Но тогда должна быть указана ссылка на статью, где это доказано. Мне вот очень интересно: для всех ли пентадекатлонов это условие является необходимым, или же это условие является необходимым только для системы паттернов господина Лецко? Если второе, то: поскольку господин Петухов использовал систему паттернов господина Лецко, то и во всех найденных по программам господина Петухова пентадекатлонах это условие тоже выполнено (что мы и наблюдаем). Похоже, ответ на этот вопрос я не узнаю никогда. PS. Итак, центральный элемент пентадекатлона ВСЕГДА равен 32p, где р - простое число (конечно, p<>2). Третий элемент пентадекатлона ВСЕГДА равен (32p - 5). Будет ли это число ВСЕГДА не кратно 7? Доказательство в студию! :) Впору писать программу и проверять числа вида (32p - 5) на кратность 7. Разумеется, надо ещё учитывать, что эти числа должны иметь ровно 12 делителей. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Цитата А в последний перезапуск на Ахиллесе ошиблась и вместо 2 миллиардов задала 20 миллиардов. Ахиллес грызёт 20 миллиардов в брутфорсе :) И сегодня утром появилась первая цепочка! В-о-о-о-т! На много миллиардов - цепочек с центральным элементом 32р и первым элементом, имеющим 12 делителей, кот наплакал. Теперь представим, что мы написали программу этого поиска, которая будет параллелиться (каким-нибудь способом, но программным), и запустили её на кластере, это 1000 ядер; может, в современных кластерах и больше. Представили? Думаю, что-то будет найдено за приемлемое время. Однако... программу пока не написали, кластера у нас нет. Остаётся только помечтать. BOINC-проекта тоже нет, ибо сервера нет (а может, и есть!), программу для BOINC-проекта супермен пока не написал. Пока супермен считает по своим программам с ускорителями. Это тоже неплохо. Но... есть одно но! Сколько бы ни было найдено пентадекатлонов этими программами, минимальность самого маленького придётся как-то доказывать, ибо минимальность эти программы не обеспечивают. А вот брутфорс обеспечивает минимальность! СтОит подумать о BOINC-проекте. PS. Кстати, кластер есть во многих вузах, а в некоторых, может, есть и суперкомпьютер. Помню, в проекте по ОДЛК10 Олег Заикин сообщал о некоторых вычислениях, выполняемых на кластере, который есть в вузе, где он работает. Возможно, кластер можно арендовать для разовой задачи. Но нужна хорошая программа. А сервер точно можно арендовать, если нет своего. А если есть свой, даже не самый мощный, то можно прямо сейчас запускать BOINC-проект. Замечательный пример у Progger! В BOINC-проекте не только пентадекатлон-12 можно искать, но и ещё много чего, например, пентадекатлон-36. Один товарищ сообщал на форуме MHP, что он не арендовал сервер, а купил, то есть сервер где-то там стоит, а он имеет к нему удалённый доступ, и сервер теперь считается его собственным. И когда он покупал, это было недорого, 8000 руб. с хвостиком. Но сейчас всё резко подорожало, в разы. Такой сервер, какой он купил, теперь стоит более 20000 рублей. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Заглянула в тему "Пентадекатлон мечты". На последней странице (134-й) о пентадекатлоне вообще не упоминается. На 133-ю страницу не стала переходить. Мне непонятно: тема о пентадекатлоне или о чём-то другом? Если о другом, тогда надо изменить название темы, дабы не вводить людей в заблуждение. Модерирование на форуме оставляет желать много лучшего! Я уж не говорю о драконовских методах модерирования. Полистала форум, обнаружила, что забаненных навечно пользователей больше активных в данный момент. При этом большинство забаненных пользователей были активными. Последние события на форуме добавили забаненных навечно. Политика... Так ведь политику можно запретить, прямо прописав это в Правилах форума. За нарушение Правил давать бан, но сначала временный. Нельзя сразу же навечно! Человек может исправиться. PS. Кстати, модераторов на форуме чуть ли не столько же, сколько активных пользователей (без учёта самих модераторов в активных пользователях). На форуме MHP один модератор, при этом не имеющий права банить. И она справляется! По мнению большинства форумчан. Я открыла тему - обращение к администратору с просьбой назначить второго модератора, так как один модератор очевидно не справляется с засильем ботов. Никто не поддержал моё обращение. Следовательно, все форумчане вполне довольны модерированием на форуме. Хотя было и такое сообщение, раньше моего обращения http://mathhelpplanet.com/viewtopic.php?p=449941#p449941 Mad_Math лучше бы Вам сложить свои модеаторские полномочия. Это сообщение было в теме "Оперативное реагирование", но Верховная самодура его снесла в тему "Удалено". Разумеется: критиковать Верховную самодуру непозволительно! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Цитирую gris Это наиболее достоверный путь к доказательству. Речь идёт о доказательстве необходимости условия для пентадекатлона: третье число пентадекатлона не кратно 7. "Достоверный путь" состоит в следующем. Пусть дана цепочка последовательных натуральных чисел a(1),a(2),a(3),a(4),a(5),a(6),a(7),a(8),a(9),a(10),a(11),a(12),a(13),a(14),a(15) в которой 1) a(8)=32p, где р - простое число, р<>2; 2) a(3)=32p-5 делится на 7 и имеет ровно 12 делителей. Доказать, что хотя бы одно число в цепочке имеет больше (или, может быть, меньше) 12 делителей, то есть цепочка не является пентадекатлоном. Кто смелый? :) Кстати, gris привёл примеры цепочек, удовлетворяющих указанным условиям 1) и 2). PS. Ломаем копья, а ведь, может быть, это доказано господином Лецко в его статьях. Я, конечно, не читала его статьи; знать бы, в какой именно статье это доказано, можно было бы и посмотреть в одной-то конкретной статье. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Встречный брутфорс В поиске пентадекатлона замечательно реализуется встречный брутфорс. Я давно пробовала этот способ в поиске симметричных кортежей из последовательных простых чисел. Но в этой задаче всё сложнее, так как начальный пункт встречного движения известен, а конечный пункт неизвестен. В поиске пентадекатлона известны оба пункта встречного движения. Начальный пункт: от нуля и вперёд. Можно не от нуля, а, скажем, от 28-значных чисел, как это делал господин Лецко - для начала. Конечный пункт: известный наименьший пентадекатлон, на данный момент 80215613469168729088982885848674841. И от этого пункта движение назад. Где-то встречаются эти два направления поиска. Встречный брутфорс делит всю задачу на две подзадачи, что, естественно, убыстряет поиск. Вот движение назад от наименьшего на данный момент пентадекатлона, работает черепашка . . . . . . . . продолжаю от 2506737920911522784030715175000000 до 2506737920911522784030715180000000 закончилась с результатом [80215613469168729088982885759996889, 80215613469168729088982885759996890, 80215 613469168729088982885759996891, 80215613469168729088982885759996892, 80215613469 168729088982885759996893, 80215613469168729088982885759996894, 80215613469168729 088982885759996895, 80215613469168729088982885759996896, 80215613469168729088982 885759996897, 80215613469168729088982885759996898, 80215613469168729088982885759 996899, 80215613469168729088982885759996900, 80215613469168729088982885759996901 , 80215613469168729088982885759996902, 80215613469168729088982885759996903] продолжаю, 10 миллионов от 2506737920911522784030715165000000 до 2506737920911522784030715175000000 законилась с результатом [80215613469168729088982885599996761, 80215613469168729088982885599996762, 80215 613469168729088982885599996763, 80215613469168729088982885599996764, 80215613469 168729088982885599996765, 80215613469168729088982885599996766, 80215613469168729 088982885599996767, 80215613469168729088982885599996768, 80215613469168729088982 885599996769, 80215613469168729088982885599996770, 80215613469168729088982885599 996771, 80215613469168729088982885599996772, 80215613469168729088982885599996773 , 80215613469168729088982885599996774, 80215613469168729088982885599996775] продолжаю 20 миллионов от 2506737920911522784030715145000000 до 2506737920911522784030715165000000 Диапазон поиска указывается для простых чисел p в формуле центрального члена: 32р. Как видите, постепенно увеличиваю диапазон, только начинаю. При движении вперёд черепашка легко берёт интервал в 500 миллионов, как я уже писала выше. При движении назад должно быть так же. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Вот так работает черепашка - движение вперёд (у меня начинается с 29-значных чисел) . . . . . . . . закончилась с результатом [10000000000000001675487996505, 10000000000000001675487996506, 10000000000000001 675487996507, 10000000000000001675487996508, 10000000000000001675487996509, 1000 0000000000001675487996510, 10000000000000001675487996511, 1000000000000000167548 7996512, 10000000000000001675487996513, 10000000000000001675487996514, 100000000 00000001675487996515, 10000000000000001675487996516, 100000000000000016754879965 17, 10000000000000001675487996518, 10000000000000001675487996519] продолжаю, 500 миллионов от 312500000000000052359000000 до 312500000000000052859000000 закончилась с результатом [10000000000000001691487997977, 10000000000000001691487997978, 10000000000000001 691487997979, 10000000000000001691487997980, 10000000000000001691487997981, 1000 0000000000001691487997982, 10000000000000001691487997983, 1000000000000000169148 7997984, 10000000000000001691487997985, 10000000000000001691487997986, 100000000 00000001691487997987, 10000000000000001691487997988, 100000000000000016914879979 89, 10000000000000001691487997990, 10000000000000001691487997991] продолжаю, 500 миллионов от 312500000000000052859000000 до 312500000000000053359000000 закончилась с результатом [10000000000000001707487998105, 10000000000000001707487998106, 10000000000000001 707487998107, 10000000000000001707487998108, 10000000000000001707487998109, 1000 0000000000001707487998110, 10000000000000001707487998111, 1000000000000000170748 7998112, 10000000000000001707487998113, 10000000000000001707487998114, 100000000 00000001707487998115, 10000000000000001707487998116, 100000000000000017074879981 17, 10000000000000001707487998118, 10000000000000001707487998119] Ахиллес при движении вперёд легко берёт 2 миллиарда. А сейчас у него задан интервал в 20 миллиардов! Пока обрабатывает, нашлась одна цепочка. Встреча двух направлений поиска неизбежна, минимальный пентадекатлон обязательно будет найден (сначала начиная от 29-значных чисел: потом надо будет искать от 0 и до найденного минимального; кстати, надо спросить у господина Лецко, почему он начинал с 28-значных чисел, а не с 20-значных, например). Отличная стратегия! Дарю главным стратегам :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Цитирую gris Кстати, насчёт сплошного поиска или как там он называется? Я вот провёл его до ста миллиардов. Нет пентов. Конечно, это мелочь. Но почему не потратить немножко времени на поиск с самого начала, а не с 28-восьми значных? Может быть есть некая доказанная нижняя граница? Наверное, серьёзные господа обладают сакральными знаниями или минимальный пентадекатлон давно никому не нужен? Ага, и я о том же :) ... кстати, надо спросить у господина Лецко, почему он начинал с 28-значных чисел, Я предполагаю, что господин Лецко что-то знает насчёт 28-значных чисел, но нам не скажет :) Наверняка есть какая-то доказанная теоретическая нижняя граница, ниже которой пентадекатлон не надо искать, потому что там его точно нет. PS. Рекомендовала gris задать этот вопрос в теме "Пентадекатлон мечты", но он стесняется. Я спросила бы, но у меня нет доступа на форум. Итак, обозначим первое число минимального пентадекатлона Pmin. Пишем X <= Pmin <= 80215613469168729088982885848674841 Полцарства за X :) Ах да... совсем забыла :) gris писал Я вот провёл его до ста миллиардов. Нет пентов. Пишем 10^11 <= Pmin <= 80215613469168729088982885848674841 Уже хорошо! Ниже 10^11 пентадекатлон не ищем. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
А вот что писал господин Петухов в сообщении https://dxdy.ru/post1562775.html#p1562775 Полный перебор снизу надо начинать от 7.2e9 (размещены простые по 13, только в квадратах), ускорителями несложно пройти скажем 1.4 триллиона шагов (по 64 паттернам), это до 1e22. Теперь уже не от 7.2e9 надо начинать, а от 10^11, с учётом результата gris. Господа! Вы можете увеличить нижнюю границу. Это очень просто сделать. Вот gris сделал это играючи. Верхнюю границу помогут уменьшить наши главные стратеги. Новый пентадекатлон не за горами. Вот-вот и взойдёт! (C) Замечание: то, о чём писал господин Петухов, вряд ли будет полным перебором, так как там упоминаются 64 паттерна. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Цитата Я предполагаю, что господин Лецко что-то знает насчёт 28-значных чисел, но нам не скажет :) Однако! В ответ на сообщение о новом пентадекатлоне 97648097903866012734106659998399641 господин Лецко писал Ого! https://dxdy.ru/post1562763.html#p1562763 Не вяжется, не правда ли? Сообщение господина Лецко похоже на сарказм, но... "дойдём до шестизначных". Это уже не научный сарказм. До шестизначных никогда не дойдём! Потому что, согласно результату gris, шестизначных пентадекатлонов не существует. Не думаю, что господину Лецко этот результат не был известен. С чего-то он начинал поиск пентадекатлонов с 28-значных чисел! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Результат gris замечательный, только он не показал, какие находились цепочки в этом начальном диапазоне 0 - 10^11. Стало любопытно, и я пошла дальше этого диапазона. Вот дырявая семёрка, в которой содержится непрерывная шестёрка 138595704921: 12, 32, 4, 12, 12, 12, 12, 12, 12, 24, 16, 6, 32, 16, 8 А что - уже 15-ка с 8 "дырками" :) На Ахиллесе и на черепашке программа крутится дальше, может, ещё интереснее цепочка найдётся. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Заглянула в тему "Пентадекатлон мечты". Там всё то же! А именно: восьмёрки господина Лецко. А где пентадекатлон? Закончился? :) Или мечта закончилась? :) Так и хочется воскликнуть вслед за М. Задорновым: - Ну тупые! Неужели нельзя привести название темы в соответствие с её содержанием? Ну, откройте, наконец, тему о минимизации цепочек с 12 делителями! Это ведь новая, большая задача, никак не связанная с восьмёрками, девятками и прочими -ками господина Лецко. Или модератор упёрся, как баран в ворота? Кстати, администратор форума dxdy.ru сообщил, что возможность редактирования сообщений по прошествии часа глобально отключена. Но у кого в этом есть необходимость, он эту возможность обещал дать. Вот и отлично! Не надо будет Антону просить господина Лецко редактировать свои таблицы в новой теме. Он сам может получить такую возможность. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Господин Лецко продолжает диалог с Hugo. Причём диалог периодически повторяется. Л. - Нашёл -ку. H. - Поздравляю! Л. - Спасибо! Это кому-то интересно? Мне нет. Ну, писал хотя бы алгоритмы для этих цепочек, как искал, и т. п. В каких статьях описывал теорию по каждой конкретной цепочке (для каждого k), как находил верхнюю оценку. Для тех, кто в теме, было бы хоть немного интересно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Ну вот, черепашка с Ахиллесом вместе быстренько увеличили нижнюю границу на порядок. Последняя дырявая семёрка, от черепашки 1086584178969: 12, 64, 4, 96, 16, 12, 12, 12, 12, 12, 4, 12, 32, 4, 8 Теперь пишем 1086584178969 <= Pmin <= 80215613469168729088982885848674841 Если моя программа не врёт, в проверенном диапазоне (от 10^11 до 1086584178969) нет пентадекатлона. Скорость выполнения программы в этом диапазоне побольше, потому что числа намного меньше. Пока останавливаю проверку в этом диапазоне. Возвращаюсь к встречному брутфорсу, о котором рассказано выше. Могу предложить gris продолжить проверку в начальном диапазоне. Предлагаю это также всем желающим. Пока мы ничего не знаем о теоретически доказанной нижней границе для пентадекатлона. Только добавлю, что надо искать в начальном диапазоне не только пентадекатлон, но и непрерывные цепочки меньшей длины - до 12 включительно. [Кажется, минимальность 11-ки Hugo уже доказал, насколько помню.] Вдруг найдётся минимальная цепочка меньшей длины. PS. У gris есть своя программа. Остальные желающие посчитать в начальном диапазоне, пожалуйста, пишите мне natalimak1@yandex.ru А также приглашаю желающих посчитать во встречном брутфорсе. gris говорит, что на больших числах у него программа сильно тормозит (у него 32-bit). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Интересное сообщение, не правда ли? https://dxdy.ru/post1566175.html#p1566175 Можно в это сообщение складывать все восьмёрки, ага. Их ведь будет много, сообщение превратится в большую скатерть. А потом вторая скатерть будет - из девяток. А раньше семёрки были, помните? Их и господин Петухов искал, иногда одни и те же вдвоём искали :) Восьмёрки господин Петухов почему-то не ищет. Восьмёрки господин Лецко считает "длинными цепочками", "высшие достижения", так сказать. А девятки будут наивысшими достижениями :) А помните, господа, у меня тема есть на форуме dxdy.ru, "Магические квадраты" называется? Эту тему все постоянно ругали. Но она была намного интереснее восьмёрок Лецко! Все мне в один голос говорили: "Таким темам не место на форуме. Заведите блог." Я послушалась и завела блог! :) Вы сейчас его читаете. А вот господина Лецко никто не ругает. Ну, он ЗУ, а ЗУ всё можно. PS. А куда же всё-таки подевался пентадекатлон мечты? Что с задачей минимизации цепочек с 12 делителями? Антон выдохся? Быстро! Не прошло и года! :))) Меня gris спрашивает: "Где Антон?", а я gris спрашиваю: "Где Антон?" :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Научная статистика от gris - оптимизация брутфорса 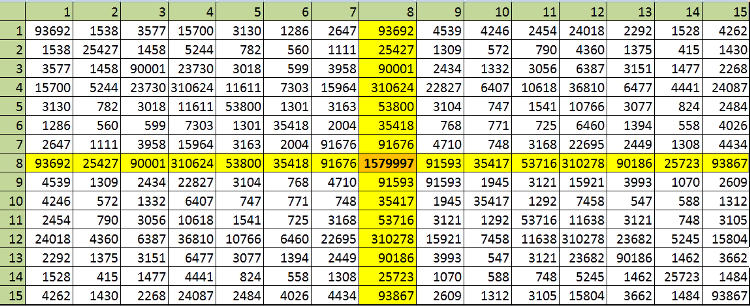 Цитата из письма (пояснение к таблице) Вот что это за таблица. Я рассматриваю все кортежи с 32р в центральном элементе в диапазоне от 12 млрд до 13 млрд. Их 1 579 997 штук. Теперь смотрю сколько там кортежей, в которых а(к) и а(п) имеют оба 12 делителей независимо от других элементом. а(8) всегда имеет 12, конечно.. gris проверил статистику для некоторых интервалов по миллиарду. Картина везде примерно одинаковая! Это интересно. На основе этой статистики gris выработал тактику поиска, убыстрив программу в несколько раз. Я сейчас изменила свои программки для встречного брутфорса, сделала так, как у gris. Считаю дальше. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Брутфорс по поиску симметричных кортежей из последовательных простых чисел работает на Ахиллесе Из интересного: 13-ки первый диапазон 5000174129811031207: 0 36 66 126 150 180 186 192 222 246 306 336 372 5000201877324953149: 0 12 42 54 60 90 132 174 204 210 222 252 264 второй диапазон 6000166649924711221: 0 12 60 90 132 138 180 222 228 270 300 348 360 6000201742565338057: 0 24 36 66 84 114 180 246 276 294 324 336 360 6000214362394303693: 0 6 66 78 108 126 168 210 228 258 270 330 336 6000232281466889321: 0 48 60 72 102 108 150 192 198 228 240 252 300 18-ки первый диапазон 5000212817639732531: 0 18 38 42 116 146 150 200 248 300 348 398 402 432 506 510 530 548 5000228393341722547: 0 6 10 94 142 180 220 250 312 334 396 426 466 504 552 636 640 646 5000228437608870541: 0 6 28 60 66 108 118 130 136 210 216 228 238 280 286 318 340 346 5000228498803578727: 0 24 30 64 66 120 126 142 154 222 234 250 256 310 312 346 352 376 5000240706672452753: 0 36 68 110 176 204 246 254 288 296 330 338 380 408 474 516 548 584 второй диапазон 6000168973577021471: 0 48 56 62 90 156 170 180 246 272 338 348 362 428 456 462 470 518 6000171231390006179: 0 20 68 98 104 120 138 192 210 242 260 314 332 348 354 384 432 452 6000176753966739833: 0 14 38 54 60 108 150 158 198 320 360 368 410 458 464 480 504 518 6000179806064597719: 0 40 52 54 60 174 202 208 250 312 354 360 388 502 508 510 522 562 6000191573499495347: 0 30 50 86 92 104 114 126 132 134 140 152 162 174 180 216 236 266 6000212066266836083: 0 8 18 56 80 84 128 206 240 254 288 366 410 414 438 476 486 494 Даже 15-ка ещё не появилась. Ох! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
В BOINC-проекте TBEG досчитался очередной диапазон. В заданиях пусто Tasks ready to send 0 https://boinc.tbrada.eu/server_status.php Перерыв. Уже сколько раз писала раньше администратору, что задания должны генерироваться непрерывно. Увы! Он не умеет генерировать задания непрерывно, а умеет только порциями. Ну что поделать, хорошо, что хоть так работает. Перерыв бывает долгим, а иногда и безобразно долгим - больше полугода. Понятно, что многие кранчеры за полгода разбежались, некоторые и забыли совсем об этом проекте. Кто-то вернулся сейчас и считает. Но проект очень плохо раскручен. Кстати, господа, пожалуйста, подключайтесь к этому BOINC-проекту. Вы поможете найти 19-ку! Её ищут очень долго, уже 8 лет. Она хорошо спряталась :) PS. Могу предложить господину Лецко и господину Петухову обратиться к администратору BOINC-проекта TBEG с предложением запустить второе Приложение в проекте - по поиску пентадекатлона-12. Программу, конечно, надо будет написать, не обязательно адаптированную к BOINC-платформе, администратор сам адаптирует. Разумеется, это должен быть брутфорс (со всеми возможными оптимизациями), ибо только брутфорс обеспечит нахождение минимального пентадекатлона. Не гарантирую, конечно, что администратор согласится. Но попытка - не пытка. Раньше в проекте работали два Приложения, значит, сервер потянет. Можно и к Progger обратиться с таким же предложением. Progger свой (не иностранец), может, быстрее согласится. Тем более что он совсем рядом - на форуме dxdy.ru. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16197 Credit: 0 RAC: 0 |
Ха-ха! Моё рацпредложение принято - восьмёрки складываются в сообщение https://dxdy.ru/post1566175.html#p1566175 Второе рацпредложение: может, их лучше на первой странице темы складывать? Или там, на первой странице, дать ссылку на файл с этими восьмёрками. Их же будет вагон и маленькая тележка! Неужели все будут в одно сообщение вываливаться? :) Не, ну высшие достижения! Как же их не показывать. Ой, что-то Hugo перестал поздравлять с восьмёрками. Устал, наверное :) Ну, хоть бы господин Петухов поздравил. Обидно же такое невнимание к высшим достижениям :) Меня с новыми магическими квадратами тоже никто не поздравлял, да ещё и ругали постоянно. Хотя достижения у меня тоже были и немало. Многие из них записаны в OEIS. И в области латинских квадратов у меня есть достижения, например, вот это  Результат тоже внесён в OEIS. Уверена, что этот результат никто на dxdy.ru не знает, в том числе и господин Лецко. Неудивительно! Я не знаю его цепочки, он не знает мои квадраты. Однако господин Лецко может публиковать свои высшие достижения на форуме dxdy.ru в неограниченном количестве, а я не могу. Замечу, что преступление моё перед форумом dxdy.ru было не столь велико, чтобы за него сразу забанить навечно. Уже писала раньше, что дважды обращалась к администратору форума dxdy.ru с просьбой разбанить меня. Увы! Администратор, видимо, не хочет создавать прецедент. |

©2025 (C) Progger