Для участников форума MHP
Message boards :
Cafe :
Для участников форума MHP
Message board moderation
Previous · 1 . . . 3 · 4 · 5 · 6 · 7 · 8 · 9 . . . 129 · Next
| Author | Message |
|---|---|
 Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
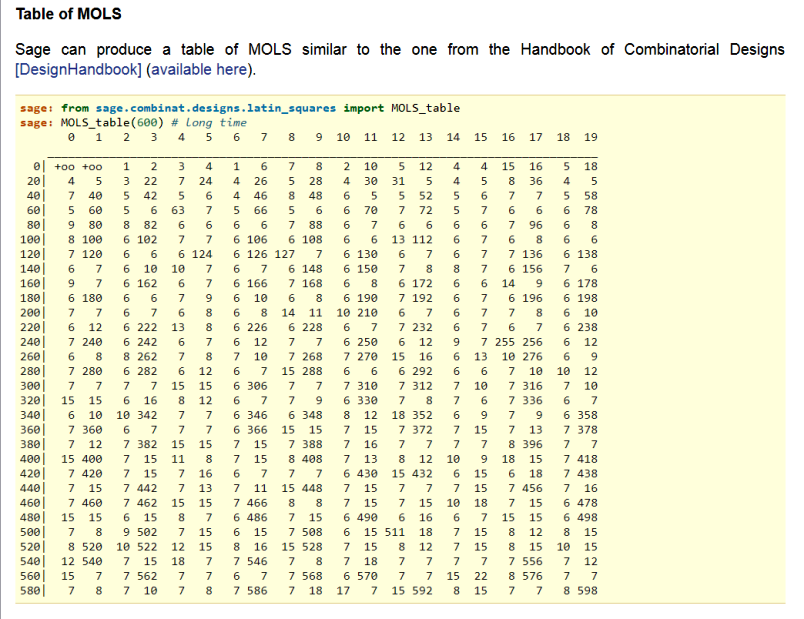
Могу ли я открывать новые темы для участников форума MHP? Как забанненная - не могу. Впрочем, и не забаненная не могла, потому что самодуре модераторше моя личность не понравилась. Зато теперь могу! Открываю новую тему "Уникальная группа MOLS 12-го порядка". Для вас, друзья с форума Math Help Planet! Результат я уже тут показала  Теперь расскажу подробно о получении этого результата. Сначала об аббревиатуре MOLS. Это очень известная аббревиатура. Если будете гуглить, найдёте очень много ссылок. Из списка статей о латинских квадратах первая попавшаяся статья на английском языке 1. "Mutually Orthogonal Latin Squares (MOLS)", авторы R. Julian R. Abel, Charles J. Colbourn, Jeffrey H. Dinitz. https://yadi.sk/i/x1w4tkQx3MsvHw (Яндекс.Диск) А это мои статьи о MOLS (на моём сайте) 1. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin squares (MOLS) http://www.natalimak1.narod.ru/grolk.htm 2. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin Squares (MOLS) Часть II http://www.natalimak1.narod.ru/grolk1.htm 3. ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin Squares (MOLS) Часть III http://www.natalimak1.narod.ru/grolk2.htm Кто хочет ознакомиться с этим понятием, пожалуйста, читайте статьи. Если что-то непонятно, спрашивайте, не стесняйтесь. Мои статьи написаны очень давно (2009 год), я тогда только начинала заниматься латинскими квадратами. Продолжение следует ID: 7677 · Rating: 0 · rate:
 /   |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Отзыв Чекрыгина о последнем посте ferma-T в теме "Сколько хорд можно провести на окружности?" Не скромничайте, не 3 копейки. Наговорили на 3 рубля, но мелочью. Привет хомяку. http://mathhelpplanet.com/viewreputation.php?id=35885 Да, не стоило разжёвывать ("мелочью"), надо было выдать Чекрыгину сразу три милльона! :) Однако, кажется, он успокоился. Я же говорила, что Пьер придумал утешительное для Чекрыгина. ID: 7678 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Хотя самодура модераторша делает жутко серьёзный вид, всё это выглядит балаганом. "mad_math" wrote: zalupkin2031, OlgaSvetlanovna, будьте любезны писать с одного аккаунта и не дублировать темы. http://mathhelpplanet.com/viewtopic.php?p=432363#p432363 На странице активных тем только темы-однодневки (с просьбой о помощи). Но и эти темы флудерасты умудряются превращать в балаган. Те вопрошающие, которые уже получили по мордасам, тоже отлично поддерживают балаган, о чём свидетельствует показанное замечание модераторши. В общем, на форуме о-ч-е-н-ь весело! ID: 7679 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Возвращаюсь к теме "Уникальная группа MOLS 12-го порядка". Надеюсь, что форумчане знают определение ортогональных латинских квадратов. Напомню - популярно. Берём два латинских квадрата одинакового порядка n (в дальнейшем - ЛК), накладываем их друг на друга (какой сверху, какой снизу - не имеет значения). Смотрим пары чисел, получившихся в соответствующих ячейках (ячейка под ячейкой). Если все n^2 пар чисел различные, то квадраты ортогональны. Возьмите с показанной выше иллюстрации любые два ЛК и наложите их друг на друга. Проверьте пары чисел в соответствующих ячейках. Понятно, что группа из нескольких ЛК называется группой MOLS, если все ЛК в этой группе попарно (взаимно) ортогональны. ID: 7680 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Математики уже лет 100 ищут группы MOLS для ЛК разных порядков. Всё бы хорошо, но вот ЛК порядка 10 не захотели дать группу MOLS даже из трёх ЛК! Кажется в книге Д. Кнута описывается, как Паркер нашёл ЛК, у которого более 12 миллионов ортогональных латинских квадратов (далее - ОЛК). Каково же было его расстройство, когда он проверил все эти ОЛК и не нашёл трёх взаимно ортогональных! Задача эта не решена до сих пор. Далее цитирую сообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2394 Сделала новый скриншот В этой таблице видим, что для порядка 12 найдена группа MOLS из пяти ЛК. Продолжение следует ID: 7681 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Это моё сообщение в тему http://mathhelpplanet.com/viewtopic.php?f=57&t=74812 У-р-р-р-а-а-а! У нас с черепашкой новый рекорд в двухцветной игре!  Мы побили рекорд Захара (1176). Теперь ему надо побить наш рекорд :) Господа! Всех приглашаю поиграть в эту интересную игру. Правда, очень интересно :) До Дмитрия Каменецкого (dimkadimon) не знаю, как достучаться. Пора мой новый рекорд внести в таблицу результатов :) Ну вот, с утра приблизились к предыдущему рекорду, а потом и побили этот рекорд. Госпожа Удача сегодня с нами :) На дворе беспросветный дождь хлещет, погода - только играть! Это у нас зима такая теперь :) *** ЗИМА ИЗ ДЕТСТВА Вот моя деревня; Вот мой дом родной; Вот качусь я в санках По горе крутой… И. З. Суриков Конец света что ль приближается, Иль на небе сошли все с ума? Там цунами, там наводнения, А в России пропала зима! Ах, как хочется белого снега Да морозца, чтоб с солнцем вместе!.. Воскресить бы ту сладкую негу, Что дарила зима в милом детстве! Снег пушист, белизны невозможной, А на окнах сплошные узоры. О, мороз был волшебный художник, Он умел очаровывать взоры! На дворе ослепительно бело, Бьёт луч солнца в меж ставней зазоры. Поскорее заканчивай дело, И – на санках на снежные горы! Ну, а дальше всё было, как в “Детстве”: Вот деревня, вот дом родной... Как я рада, что с маленьким Ваней Мы почти из деревни одной! 14 января 2007 г. https://stihi.ru/2007/01/14-624 ID: 7684 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Господа! А знакомы ли вам мои стихотворения? :) На форуме MHP есть тема "Стихи, стишки и стишочки", которая тоже, конечно, закрыта, как большинство моих тем. Нет, не потому, что это не математика, а потому, что самодуре модераторше моя личность не нравится. Сейчас на форуме есть тема "Стихосложение". Так себе тема, вялотекущая. Эту тему самодура не закрывает. Хорошая тема! Полезная! Покажу вам РОНДО Если скучно вам живётся, – “приколитесь”, Если вам сегодня грустно, – улыбнитесь. Если любите вы выпить, наливайте, Если рассказать хотите, начинайте! Я вас выслушать готова, право слово. Что же всё я о себе замолола! Этот плачет, тот смеётся, третий стонет, Но никто словечка вслух не проронит. Интересных штучек много в этом мире, Но не все они подвластны звонкой лире. Если рассказать хотите, начинайте! Если любите вы выпить, наливайте. Я зову сегодня в гости всех на свете, Посмеёмся и поплачем с вами вместе! Приходите, приходите, право слово, Вашу исповедь послушать я готова. Жить на свете очень трудно, я согласна. Но не надо так грустить понапрасну. Если вам сегодня грустно, – улыбнитесь, Если скучно вам живётся, – “приколитесь”. 5 марта 2007 г. https://stihi.ru/2007/03/05-628 Обратите внимание на рецензию: её написал мой лучший друг Жора :) ID: 7685 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
В теме "Стихи, стишки и стишочки" можете посмотреть мои стихотаорения http://mathhelpplanet.com/viewtopic.php?p=279961#p279961 http://mathhelpplanet.com/viewtopic.php?p=284214#p284214 http://mathhelpplanet.com/viewtopic.php?p=290061#p290061 http://mathhelpplanet.com/viewtopic.php?p=292013#p292013 http://mathhelpplanet.com/viewtopic.php?p=296097#p296097 Этот пост дублирую http://mathhelpplanet.com/viewtopic.php?p=304556#p304556 "Понравилось стихотворение в прозе Девочка-юность, когда я на тебя оглядываюсь, то вдруг понимаю, что не вижу пасмурных дней. Ты вне зоны и климата – сплошное солнце и радость – и уж точно вне времени: чем дальше, тем ближе ко мне. Я так помню тебя, моя далёкая девочка, так люблю тебя преданно в каждом движенье твоём: на экзамене в школе, в тусовке весёлой студенческой, в свете лампы настольной полночью за столом. Но без страха сужу и безжалостно не принимаю эту резкость прощаний, это вечное «всё или ничего», за бездарно утраченное я с тебя вины не снимаю, просто боль возвращается, так как в памяти ничто не мертво. И сейчас, на пороге противненького n-летия, я к тебе обращаюсь с таким вот открытым письмом. Знаешь, девочка-юность, а здорово, что я тебя встретила, ты вообще офигенная, как выяснилось потом. http://dxdy.ru/post1225140.html#p1225140 У меня ностальгическая боль о детстве... Осеню себя крестным знамением И с сумою пойду по Руси, Если сердце в разладе со временем И не видно другого пути. Мне бы только дойти до поляны, Где я в детстве счастливой была. Там цветы и высокие травы, Там прогретая солнцем земля. И на этой чудесной поляне, Где от века природный уют, Я прошу Тебя, Боже, пошли мне Мой последний надёжный приют. сентябрь 1991 г." В посте есть фотка. Пробую перетащить фотку  Получилось! ID: 7686 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Ой, господа, я отвлеклась от MOLS :) Но... поэзию очень люблю. Если бы не стала заниматься математикой, то занялась бы поэзией :) Однако математика победила. В общем, читайте тему "Стихи, стишки и стишочки". Это интересная тема, там форумчане выступали с разными стихами. Ну, ещё ведь есть тема "Стихосложение". Так что, любителям поэзии есть что читать и о чём писать. ID: 7687 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Ах ты батюшки! Чекрыгин не успокоился :) http://mathhelpplanet.com/viewtopic.php?p=432471#p432471 Ну, вот вам и третий способ "отображения хорды (отрезка)"! Я это предсказала :))) А если точку С выбирать на хорде АВ произвольными способами (которых будет бесконечно много, ну уж точно счётное множество), то и хорд АВ, построенных таким способом (по выбору точки С между точками А и В), будет бесконечно много. Браво, браво, браво! Чекрыгин строит новую геометрию, равную, например, геометрии Лобачевского. Ну, не его вина, что всякие закоснелые товарищи (вроде Макаровой и Захара) никак не хотят его понимать. Это их проблемы. Вот ferma_T понимает Чекрыгина! Честь и хвала ему. Так глядишь, они вдвоём и построят новую Геометрию. А мы с Захаром будем потом с завистью созерцать новую Геометрию и вспоминать, как мы мешали Чекрыгину её строить своим закоснелым "нельзя". ID: 7688 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
А вот вопрос: зачем вообще точки называть буквами? Без этого прекрасно можно хорду построить. Цитата Ладно, поделюсь, как я провожу хорду = отрезок, соединяющий две точки окружности (хотя меня и не спрашивают). Никаких тут нет букв А и В, а хорда построена по двум выбранным точкам на окружности! Но по Чекрыгину - нет! Пока не объявим буквы А и В (для хорды АВ) или буквы В и А для (хорды ВА), никакой хорды быть не может. А как только объявим эти буквы, так сразу появляются две хорды! А и Б сидели на трубе А упала, Б пропала, Что осталось на трубе? Ответ: хорда :) ***** Ой, господа, мне что-то так и захотелось запеть на мотив какой-то оперы - Дайте хорду мне, дайте хорду!... Не, не, не пугайтесь - "кукуха" не съехала, пока на месте :))) ***** PM to ferma_T Привет, Пьер! С величайшим душевным трепетом ожидаю вашего ответа Чекрыгину в теме "Сколько хорд можно провести на окружности?". Решается судьба новой Геометрии! ID: 7689 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Чекрыгин писал С глаголом «пипет» столкнулся впервые. Начал подбирать синонимы. Остановился на «интересует». Вроде, по смыслу подходит. Правда, есть еще одно «крепкое словечко»... ferma-T не писал "пипет", он писал "пипёт". Это две большие разницы, как говорят в Одессе. И вне всякого сомнения, это «крепкое словечко», которое тоже пишется через Ё, а не через Е (в окончании глагола). Носителю русского языка грех этого не знать; и букву Ё надо писать там, где она должна быть согласно правилам орфографии! Чекрыгину на заметку. ID: 7690 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Возвращаюсь к теме "Уникальная группа MOLS 12-го порядка". Предлагаю внимательно посмотреть тему "MOLS and MODLS of order 12" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120 В первом сообщении читаем Первую группу MOLS 12-го порядка из 5 ЛК я составила очень давно в своей статье (по известному алгоритму) Следующее сообщение дублирую Вторая группа MOLS 12-го порядка тоже из 5 ЛК получена программой SageMath. Команда sage: for x in designs.mutually_orthogonal_latin_squares(5,12): print(x,'\n') Группа MOLS 0 1 2 3 4 5 6 7 8 9 10 11 1 0 3 2 5 4 7 6 9 8 11 10 2 3 0 1 6 7 4 5 10 11 8 9 3 2 1 0 7 6 5 4 11 10 9 8 8 9 10 11 0 1 2 3 4 5 6 7 9 8 11 10 1 0 3 2 5 4 7 6 10 11 8 9 2 3 0 1 6 7 4 5 11 10 9 8 3 2 1 0 7 6 5 4 4 5 6 7 8 9 10 11 0 1 2 3 5 4 7 6 9 8 11 10 1 0 3 2 6 7 4 5 10 11 8 9 2 3 0 1 7 6 5 4 11 10 9 8 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 11 6 7 4 5 10 11 8 9 2 3 0 1 4 5 6 7 8 9 10 11 0 1 2 3 2 3 0 1 6 7 4 5 10 11 8 9 10 11 8 9 2 3 0 1 6 7 4 5 5 4 7 6 9 8 11 10 1 0 3 2 7 6 5 4 11 10 9 8 3 2 1 0 8 9 10 11 0 1 2 3 4 5 6 7 9 8 11 10 1 0 3 2 5 4 7 6 3 2 1 0 7 6 5 4 11 10 9 8 1 0 3 2 5 4 7 6 9 8 11 10 11 10 9 8 3 2 1 0 7 6 5 4 0 1 2 3 4 5 6 7 8 9 10 11 3 2 1 0 7 6 5 4 11 10 9 8 11 10 9 8 3 2 1 0 7 6 5 4 6 7 4 5 10 11 8 9 2 3 0 1 4 5 6 7 8 9 10 11 0 1 2 3 7 6 5 4 11 10 9 8 3 2 1 0 9 8 11 10 1 0 3 2 5 4 7 6 1 0 3 2 5 4 7 6 9 8 11 10 5 4 7 6 9 8 11 10 1 0 3 2 2 3 0 1 6 7 4 5 10 11 8 9 10 11 8 9 2 3 0 1 6 7 4 5 8 9 10 11 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 9 8 11 10 1 0 3 2 5 4 7 6 8 9 10 11 0 1 2 3 4 5 6 7 1 0 3 2 5 4 7 6 9 8 11 10 5 4 7 6 9 8 11 10 1 0 3 2 3 2 1 0 7 6 5 4 11 10 9 8 2 3 0 1 6 7 4 5 10 11 8 9 4 5 6 7 8 9 10 11 0 1 2 3 11 10 9 8 3 2 1 0 7 6 5 4 6 7 4 5 10 11 8 9 2 3 0 1 7 6 5 4 11 10 9 8 3 2 1 0 10 11 8 9 2 3 0 1 6 7 4 5 0 1 2 3 4 5 6 7 8 9 10 11 10 11 8 9 2 3 0 1 6 7 4 5 5 4 7 6 9 8 11 10 1 0 3 2 7 6 5 4 11 10 9 8 3 2 1 0 9 8 11 10 1 0 3 2 5 4 7 6 11 10 9 8 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 11 10 9 8 6 7 4 5 10 11 8 9 2 3 0 1 2 3 0 1 6 7 4 5 10 11 8 9 1 0 3 2 5 4 7 6 9 8 11 10 8 9 10 11 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 0 1 2 3 Утилита Harry White сообщает об этих ЛК Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
5 Latin
1 center symmetric
5 nfr
4 orthogonal pairКак видим, в этой группе тоже нет ДЛК. Итак, мы имеем две группы MOLS 12-го порядка из 5 ЛК (возможно, есть и другие, но мне не встречались) и не имеем тройки MODLS. Задача: найти тройку MODLS 12-го порядка. Это задача-минимум. Может быть, существуют группы MODLS 12-го порядка, содержание более трёх ДЛК. Но пока ставлю задачу - найти тройку MODLS. Не знаю, существует ли искомая тройка MODLS. Точно так же, как о тройке MOLS 10-го порядка ничего неизвестно (по крайней мере, до недавнего времени было неизвестно; может быть, уже что-то выяснили; математики работают, а мы не всегда знаем о полученных результатах). _______________________________ конец дублируемого сообщения Ну вот, здесь вы видите постановку задачи. Меня заинтересовала группа MODLS 12-го порядка, то есть группа взаимно ортогональных диагональных латинских квадратов (далее - ДЛК), состоящая из трёх или более ДЛК. Дальше в теме вы найдёте описание, как я решала данную задачу. Продолжение следует ID: 7691 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Чекрыгин писал Правда, можно придумать третий способ рисования отрезка по двум точкам. Критикую: а ещё забыли: отрезок АВ определён не по двум точкам, а как сумма отрезков ВС и СА! Это же будет совсем другой отрезок, согласно теории Чекрыгина. Не так ли? Пусть скажет мне спасибо за это существенное дополнение! :))) Санта Барбара продолжается! Пока в диалог вступил Захар. С нетерпением жду выступления ferma-T. ID: 7692 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Ой, ferma-T начал доказывать неспособность Захара абстрактно мыслить. ferma-T! Вы явно не в ту степь поехали. Оставьте Захара в покое. Уже давно понятно, что Захар и я мешаем вам с Чекрыгиным строить новую Геометрию. Я признаю, что мешаем. Захар не признаёт и никогда не признает. У него такой характер. Так игнорируйте его сообщения! Стройте свою новую Геометрию с Чекрыгиным, а мы понаблюдаем, что из этого получится. А насчёт Мега... Тера... Элементарно доказывается, что точек на окружности будет бесконечное счётное множество, а никакие Мега или Тера. Разделим окружность пополам любым диаметром, получим две точки на окружности (концы диаметра). Каждую полуокружность разделим пополам, получим 2^2 точек. Каждую полученную часть окружности снова разделим пополам, получим 2^3 точек. Надеюсь, процедура понятна. И так делим каждую часть, полученную на предыдущем шаге, пополам. Последовательность получаемых точек 2, 2^2, 2^3, 2^4, ..., 2^n, ... Теперь представляйте абстрактно, что n равно бесконечности. Представили? (Вы-то умеете абстрактно мыслить; в какой-то теме вы описывали, что такое n = oo) И сколько же мы получим точек на окружности при n равном бесконечности? Я считаю, что множество всех точек окружности бесконечное счётное. А по-вашему какова мощность множества всех точек на окружности? Неужели континуум? Тогда покажите, пожалуйста, способ выбора (расстановки) точек на окружности, при котором мощность множества всех точек окружности будет континуум. Я свой способ выбора точек показала. ID: 7693 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Если серьёзно, в теме "Сколько хорд можно провести на окружности?" сплошной идиотизм. Повторю это сообщение "searcher" wrote: "chekrygin" wrote:Сколько хорд можно провести на окружности? http://mathhelpplanet.com/viewtopic.php?p=431595#p431595 Но... вдруг с вашей помощью, ferma-T, из этого идиотизма действительно родится новая Геометрия. Все гении немножко идиоты :) Но далеко не все идиоты гении - хоть немножко! ID: 7694 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
PM to Alexdemath Alexdemath писал Надо отдохнуть пару месяцев, голубушка! Смотрите скриншот здесь https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=7586 Спасибо, голубчик! Я отдыхаю очень хорошо. Хочу предложить вам аннулировать результаты бурной деятельности модераторши в разделе "Репутация пользователя Nataly-Mak" Нет, меня "не пипёт" моя репутация на вашем форуме. [Понравилось выражение ferma-T, оно на вашем форуме в открытом доступе, имею полное право копировать.] Меня "пипёт" то, что вы своим бездействием одобряете противоправные действия вашей модераторши. Если же вы не одобряете эти противоправные действия, зайдите в мою репутацию и поставьте минус от своего имени. Тем самым вы аннулируете все результаты модераторши в этом разделе форума. Это не займёт у вас много времени, 2-3 минуты. Дата, подпись. Отвечайте, а не то напишу я в Спортлото! ID: 7695 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Возвращаюсь к теме "Уникальная группа MOLS 12-го порядка". Дублирую сообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2217 Я нашла группу MODLS 12-го порядка, состоящую из четырёх взаимно ортогональных ДЛК!! Сначала был найден набор из 16512 нормализованных ДЛК (работала программа перестановки строк и столбцов). Затем проверила этот набор на ортогональные пары программой GetOrthogonal. Ортогональных пар образовалось много, есть солидные группы ОДЛК: 48-ки, 32-ки. Таблица ортогональных пар получилась огромная. Программа SageMath много ругалась, то есть много выдала ошибок, но... клики размера 4 появились и их море! Вот скриншот 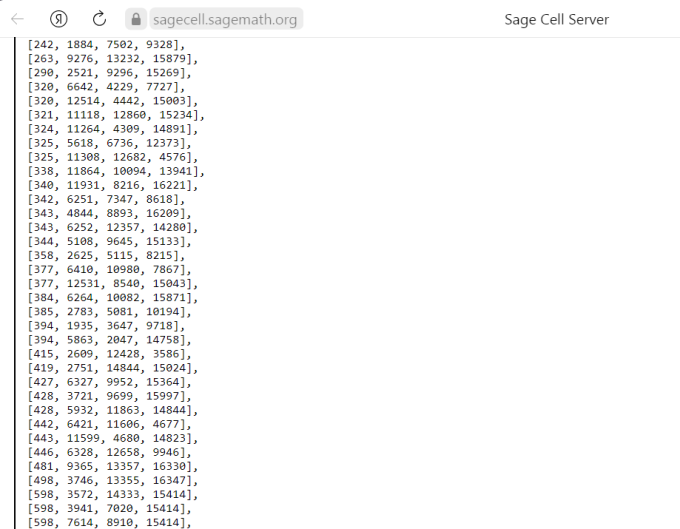 Надеюсь, что это максимальные клики и клики бОльшего размера нет. Но... надо бы это перепроверить, вдруг из-за множества ошибок клика бОльшего размера не найдена, но она есть. Я позже выложу таблицу ортогональных пар. Сложность ещё в преобразовании формата этой таблицы. Делала это в Ворде вручную, тоже могла ошибиться. Огромное количество клик размера 4 очень намекает на то, что есть клика размера 5 в этом наборе. Но, может быть, и нет клики размера 5. Показываю одну из многих групп MODLS 12-го порядка из 4-х взаимно ортогональных ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 1 3 5 0 9 7 4 2 11 6 8 10 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 7 2 3 5 10 0 11 1 6 8 9 4 11 10 9 8 7 6 5 4 3 2 1 0 3 0 7 1 6 2 9 5 10 4 11 8 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 9 6 11 4 3 10 1 8 7 0 5 2 10 8 6 11 2 4 7 9 0 5 3 1 0 1 2 3 4 5 6 7 8 9 10 11 2 5 0 7 8 1 10 3 4 11 6 9 3 0 7 1 6 2 9 5 10 4 11 8 11 10 9 8 7 6 5 4 3 2 1 0 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 6 4 10 9 0 8 3 11 2 1 7 5 4 9 8 6 1 11 0 10 5 3 2 7 7 2 3 5 10 0 11 1 6 8 9 4 1 3 5 0 9 7 4 2 11 6 8 10 0 1 2 3 4 5 6 7 8 9 10 11 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 0 1 2 3 4 5 6 7 8 9 10 11 7 2 3 5 10 0 11 1 6 8 9 4 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 Проверяю ДЛК этой группы программой GetOrthogonal Order? 12 Enter the name of the squares file: inp1 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp1-orthCounts.txt ..output file inp1-orthNos.txt squares 4 total orthogonal pairs 6 Maximum pairs for square 1: 3 There are 3 other squares with this maximum number of pairs. ..output file inp1-1orths.txt Pairs for square 1: 3 Всё верно: ДЛК образовали 6 ортогональных пар, и каждый ДЛК имеет 3 ОДЛК. Таблица ортогональных пар 1: 2 3 4 2: 1 3 4 3: 1 2 4 4: 1 2 3 Известна ли математикам группа MODLS 12-го порядка, состоящая из четырёх ДЛК? А из пяти ДЛК? Программа SageMath выдаёт группу MOLS данного порядка из 5 ЛК. Эта группа показана выше. Я искала группу MODLS на основе группы MOLS, построенной мной по известному алгоритму. В этой группе тоже 5 взаимно ортогональных ЛК. Выше показано, что сначала я нашла путём перестановок строк группу, в которой один ДЛК и 4 ЛК. Затем продолжила процесс перестановок строк. И вот - удача! ______________________________ конец дублируемого сообщения Итак, задача поиска группы MODLS 12-го порядка была решена. Найдена группа из четырёх взаимно ортогональных ДЛК 12-го порядка, и не одна, таких групп найдено много. Покажу иллюстрацию - одна из найденных групп MODLS 12-го порядка  Продолжение следует ID: 7696 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
"chekrygin" wrote: "3axap" wrote:Плохой совет. В свое время searcher решил пойти таким путем, http://mathhelpplanet.com/viewtopic.php?p=431595#p431595. http://mathhelpplanet.com/viewtopic.php?p=432493#p432493 Трудно понимать гениев, но рискну предположить, что на окружности радиуса R=1 можно выбрать всего 6 точек. Правильно понимаю? А на окружности радиуса R=2 можно выбрать 12 точек? На окружностях бОльших радиусов уже не берусь определять количество точек. Таким образом, количество точек, которые можно выбрать на окружности, зависит от её радиуса. Правильно ли понимаю? Боюсь, что неправильно. Ну, куда мне лезть в гениальные построения! Мой способ выбора точек на окружности, показанный выше, годится для окружности любого радиуса, при условии, что точка не имеет радиуса. Но мы же не решаем задачу: разместить на окружности радиуса R окружности радиуса r. Или как раз такую задачу и решаем? Похоже, я дальше этот идиотизм не читаю. PS. Всё больше склоняюсь к мысли, что это изощрённый троллинг. Чекрыгин задался целью раскрутить эту тему до 1000 ответов и 100000 просмотров. Цель при отсутствии нормальной модерации вполне достижимая. И вполне достойная для форума, на котором модераторша "накручивает" репутацию пользователя от 89 до -286. Каждый идиот развлекается по-своему. Главное, что все счастливы. ID: 7697 · Rating: 0 · rate:
/ |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 14341 Credit: 0 RAC: 0 |
Продолжаю тему "Уникальная группа MOLS 12-го порядка". Полученный результат (группа MODLS 12-го порядка из четырёх взаимно ортогональных ДЛК) внесён в OEIS, смотрите http://oeis.org/A328873 Цитата a(12) >= 4. - Natalia Makarova, May 30 2021 Цитата из сообщения Задала вопрос здесь Вопрос следующий Is there a known MODLS group of order 12 consisting of five diagonal Latin squares? Я сообщила, что нашла группу MODLS 12 порядка из четырёх взаимно ортогональных ДЛК, и затем спросила, известна ли группа MODLS данного порядка, состоящая из пяти взаимно ортогональных ДЛК. Ответ не получен. Указанные факты позволяют предположить, что найденная мной группа MODLS 12-го порядка из четырёх взаимно ортогональных ДЛК ранее не была известна математическому сообществу. Далее я продолжила поиск, пытаясь расширить найденную группу MODLS до пяти ЛК, хотя бы пятый квадрат при этом был ЛК, а не ДЛК. Это у меня получилось. Смотрите далее. ID: 7698 · Rating: 0 · rate:
/ |
©2024 (C) Progger