А вот совсем маленькое простое число из таблицы в статье: 171707099.

rp=52 для этого числа.
Проверим?

Запустила.

Это простое число программой г. Петухова проверяется, выводится удачная сумма (точнее - последний факториал удачной суммы)
[63088024]

Вот и результат тестирования

? \r gerbicz.txt
52
time = 1min, 58,500 ms.

Всё отлично!
И время небольшое.

Ну, хватит, пожалуй, тестировать.

Ой, gris прислал напоминание :)

У Пентадекатлона маленький юбилей - три года
https://oeis.org/A006558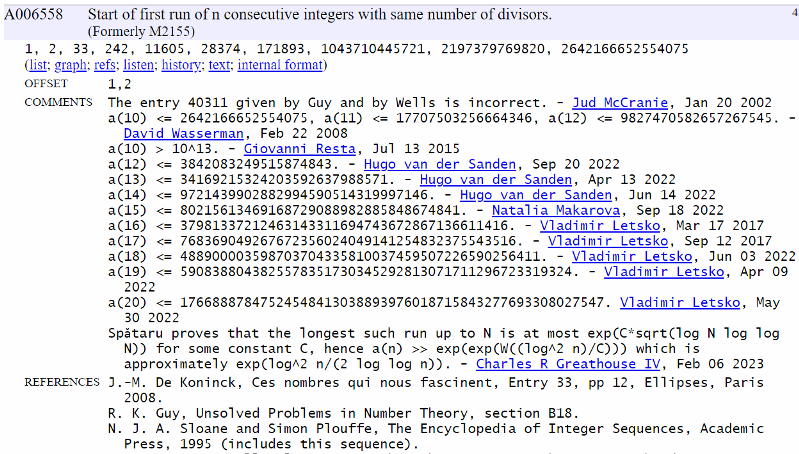



Да, было дело.
У меня тогда в удалённом управлении был мощный сервер, мне его дали потестировать, он был новый, только что пришёл.
Вот на нём я и нашла два пентадекатлона.
В OEIS показан меньший.
Это верхняя граница для пентадекатлона.

Г. Петухов писал
в сообщении
https://dxdy.ru/post1703098.html#p1703098

Если же речь про M48n21, то да, её на PARI искать можно (n20 же нашлась),

Очень интересно!
Так давайте поищем! :)

Насколько я помню, пентадекатлон искался с привлечением АСМ.
Ну, а потом Лецко ещё несколько решений нашёл, уже, видимо, только в PARI/GP.

И далее г. Петухов даже алгоритм набросал, парадигму, так сказать

Кстати про M48n21. Ведь при их поиске можно вообще отказаться от факторизации и разместить по всем местам столько малых простых, чтобы неизвестными остались лишь ровно по одному простому в каждой позиции. Искомые числа резко возрастут, вероятность нахождения ещё резче снизится, зато ispseudoprime сильно быстрее numdiv/factor. И что пересилит ещё вопрос.
Как и вопрос искать ли по одному паттерну или сразу по всем. VAL же ищет по одному (или нескольким, не уверен, но точно не по сотням тысяч) и находит, в том числе мировые рекорды, значит и такой подход имеет право на жизнь и может быть выгоднее перебора всех возможных паттернов (как делалось для пентадекатлона M12n15 и некоторых других).

Итак, найти группу паттернов из 21 последовательного натурального числа, в каждой позиции которых (паттернов) будет стоять число с одним неизвестным простым делителем, а остальные 47 делителей уже известные (ой, правильно ли я понимаю, что всего делителей должно быть 48? уже подзабыла малость).
И остаётся найти в каждой позиции ровно одно простое число, эти числа могут быть очень большими.

Что сказал бы Лецко о такой парадигме?
Насколько она хороша и что обещает в поиске?
По какой парадигме он искал 20-ку с 48 делителями?
Рассказал бы.
Может, у него получше парадигма, чем у г. Петухова.
Она (парадигма), между прочим, и результат дала у Лецко.

А группы паттернов составлять хорошо умеет Ядряра.

Насколько помню, именно по его группам паттернов искался пентадекатлон.
Это были очень хорошие группы паттернов, на мой дилетантский взгляд.

Ядряре и флаг в руки!

Может быть, всё-таки не 21 простое число оставлять неизвестными, а поменьше?
Это же очень много искать придётся простых чисел, причём очень больших.
Я, например, оставила бы половину неизвестных делителей, то есть 10 штук.
А всё остальное - известное.
Правда, не знаю, насколько просто найти 11 известных подходящих чисел с 48 делителями.

Ну, это вопрос к Лецко.
Он наверняка знает ответ.

https://dxdy.ru/topic161718-15.html

Как всегда, встречают в штыки.
Лженаука!

А как же Ванга, например?
Всё ложь???

Недавно смотрела интервью с А. Пугачёвой.
Она сказала, что у неё была "чуйка".
Знаете, что это такое?
Да - предчувствие!
Она что-то "видела" из 2027-го года.
Но на просьбу журналистки сказать об этом Пугачёва ответила: "Я знаю, что произойдёт, но не имею права говорить. Давайте доживём до 2027 года".

Это есть!
Несмотря на все протесты упёртых апологетов науки.
Это дано далеко не всем.
Но единицам дано.

Кстати, ещё интересно.
Вопрос журналистки к Пугачёвой: "А правда, что ваша прабабушка была колдунья?"
Ответ смотрите в интервью.
Интервью ищется, например, по запросу: "последнее интервью Аллы Пугачёвой".

Ну, в колдунов мы тоже не верим!
Лженаука!!!

Вещие сны тоже лженаука!
А знаете ли вы, к чему видеть во сне царя, да чтобы вы с ним были в контакте, то есть разговаривали?
В самом начале 2022 года я видела во сне нынешнего "царя", мы с ним были рядом вдвоём и... в общем, разговаривали.
До этого я ни разу его не видела ни во сне, ни наяву.

Проснулась я в сильном волнении, а когда осознала полностью сон, встревожилась ещё больше.

gris пишет, что Алиса теперь умеет оживлять фото.

Ничего подобного я не нашла.
Может, gris это за деньги делает.

Я нашла только "Нарисуй".
Задала ей: нарисуй мой портрет, я математик, очень серьёзный, старушка.

Вот портрет



Похожа? :)

Во всяком случае стеллаж с книгами точно мой, gris подтвердит :)

Ещё вариант, я попросила нарисовать меня за компьютером и в очках



Даю ссылки прямо на Алису, не знаю, как долго там хранятся изображения.
Ну, пока смотрите :)

Это моя дочь :)
Алиса нарисовала

Мы с Алисой дружим :)

Я спросила её сейчас, умеет ли она оживлять фото.
Она ответила, что пока не умеет.

Но там был анонс несколько дней назад, что "Оживить фото" Скоро.

А вот реальная фотография моей дочери



Качество плохое, чёткости нет.
А какой сервис умеет улучшать фотографии?

Я Алисе не заказывала нарисовать мою дочь; заказ был такой: "нарисуй амазонку на красивом коне в галопе".

А здесь оживлённое фото дочери
https://boinc.progger.info/odlk/forum_thread.php?id=196&postid=16654

А вот и ответ от Лецко
https://dxdy.ru/post1703161.html#p1703161

По поводу, что выгоднее: увеличивать количество простых или заморачиваться с факторизацией.
Три c половиной года назад мы это обсуждали. На основании накопленной статистики пришли к выводу, что для поиска 20-ки выгоднее всего 3 простых.
Конечно, этот рецепт не обязан быть универсален. Но мои поиски других относительно длинных цепочек показывают, что там, где паттерн с 3-я простыми возможен, он обычно срабатывает быстрее всего.

Очень ценно!

Он оставляет в паттерне неизвестными, как я понимаю, всего три простых.
Ну вот, такая парадигма мне нравится
А то искать 21 простое число, по-петуховски, запаришься!

И теперь дело за группой паттернов с такой парадигмой.
Это для Ядряры :)

И ещё Лецко написал (в том же сообщении) о количестве паттернов

Ищу по нескольким. Счет идет на единицы, максимум на десятки.

Цитата

Он оставляет в паттерне неизвестными, как я понимаю, всего три простых.

Посмотрела в теме "Пентадекатлон мечты" про паттерны.
Скорее всего, я неправильно понимаю, что хотел сказать Лецко, говоря о трёх простых.

Формирование паттерна очень сложная процедура.
Ядряра показал её подробно для 15-ки с 12 делителями.

В общем, как уже сказано выше, формирование паттернов для 21-ки отдаём Ядряре :)
Он мастер.
Ну, или самому автору проекта - Лецко.

Ой, а где я взяла про 48 делителей? :)
Всё забыла начисто!

Найденный мной петнтадекатлон с каким количеством делителей?
Вот этот

a(15) <= 80215613469168729088982885848674841. - Natalia Makarova, Sep 18 2022

Кстати, я считаю, что авторство указывается неправильно.
Надо обязательно указывать автора программы.
Моя роль чисто техническая, взяла готовую программу и запустила на удалённом компьютере.
И говорить, что это я нашла, неправильно.
Надо указать обязательно автора программы.

А, вот в этой цитате от г. Петухова

Если же речь про M48n21, то да, её на PARI искать можно (n20 же нашлась),

М48 что означает? Количество делителей?

Вот здесь, например,
https://www.primepuzzles.net/problems/prob_020.htm
явно указывается количество делителей

K = 10: A start is 14366256627859031643 with 24 divisors.
K = 11: A start is 193729158984658237901148 with 48 divisors.
K = 12: A start is 1284696910355238430481207644 with 24 divisors.

K - это длина цепочки, насколько могу понимать.

А это от Лецко (там же)

A run of 15 consecutive positive integers each having exactly 24 divisors starts at
176395563698184262497866317860996946591.

2017 год.
15-ка с 24 делителями.

Проверяю:

numdiv(14366256627859031643)

Да, это равно 24.

А найденный мной пентадекатлон получается всего с 12 делителями

numdiv(80215613469168729088982885848674841)=12

Ну, кое-что вспомнила :)

Последняя 20-ка от Лецко

a(20) <= 17668887847524548413038893976018715843277693308027547. Vladimir Letsko, May 30 2022

numdiv(17668887847524548413038893976018715843277693308027547) = 48

Больше трёх лет прошло, 21-ку никто не ищет.
Почему?
А может быть, кто-то ищет, просто мы об этом не знаем.
Проект-то имеет не одного автора.
Ещё Hugo, например, этим проектом занимался.
Что сейчас он ищет?

Забавно…

В 2008 сказали

a(10) <= 2642166652554075

в 2015 году сказали

a(10) > 10^13

https://oeis.org/A006558

numdiv(2642166652554075) = 24

И что?
Эту цепочку нельзя минимизировать?
Она настолько сложная?

Если минимизация невозможна, значит, должно быть

a(10) = 2642166652554075

А!
Так оно и есть

a(10) by Jud McCranie, Nov 27 2018

В 2018 году утсновили, что это минимальное решение.

Однако!
Обратите внимание: ни нижняя граница, ни верхняя граница для a(10) не удалены.
А почему, спрашивается?
Сейчас заставляют удалять верхнюю границу, если минимум установлен.
Или это двойной стандарт: где-то заставляют, где-то не заставляют?

Кстати, для минимизации там работы непочатый край.

Цепочка а(10) минимизирована в 2018 году.
И на этом всё остановилось.

А это решение

а(11) <= 17707503256664346

кто-нибудь пытался минимизировать?
Не поддаётся что ли?

numdiv(17707503256664346) = 24

А это про какую цепочку?

K = 11: A start is 193729158984658237901148 with 48 divisors.

https://www.primepuzzles.net/problems/prob_020.htm

Вроде в обоих источниках k - длина цепочки.
Таким образом. получается. что есть цепочка длины 11 с числом делителей 24, а также с числом делителей 48.
А в OEIS почему-то показана только одна цепочки - с числом делителей 24.

Как говорила мама: без пол-литра не разберёшься :)
Пойду чего-нибудь выпью, хотя бы чаю.

Ядряра писал в сообщении
https://dxdy.ru/post1703188.html#p1703188

Так что желающие могут потренироваться в снижении нынешних D48.

Почему тренироваться в минимизации надо именно для количества делителей 48?
Есть ведь более простые цепочки с количеством делителей 24.
Может быть, даже и с количеством 12 есть цепочки, минимальность которых не установлена.

Вот, например, цепочка с количеством делителей 24

а(11) <= 17707503256664346

Судя по последовательности OEIS её минимальность не установлена.

Цитата

Может быть, даже и с количеством 12 есть цепочки, минимальность которых не установлена.

Конечно, есть.
Например, найденный мной пентадекатлон

a(15) <= 80215613469168729088982885848674841

Но это сложная цепочка, потому что стартовое число огромное.
Минимизировать долго придётся.

Хотя...
был же найден мной первый пентадекатлон с 12 делителями в то же время.
В нём стартовое число ещё больше.
Значит, минимизации всё же поддаётся.

Кстати, первый пентадекатлон в OEIS, наверное, отсутствует.
В теме "Пентадекатлон мечты" должен быть.

Да, вот он
https://dxdy.ru/post1562121.html#p1562121

И снова рекорд в 259-м комплекте!

T(6,15) <= 5400788496821420197301806862543165145

А перед этим был ещё один, найденный г. Петуховым, он начинался с числа
66387422053662391209161093722597723545.

Хорошо минимизировали, но почему-то бросили.
И программа была быстрая, с использованием АСМ.

Минимизация шла так:

66387422053662391209161093722597723545
5400788496821420197301806862543165145
80215613469168729088982885848674841

Г. Петухов писал в сообщении
https://dxdy.ru/post1703221.html#p1703221

... такой кортеж исключительно редок, да?

У Супермена всё кверху ногами.
Кортежи он называет цепочками, цепочки - кортежами.

Не запутайтесь, господа! :)
Ноги - это нижние конечности, руки - это верхние конечности (у человека).
Не наоборот!

Ядряра писал

wrest, ровно наоборот. Я спрашиваю у тех, кто ещё вроде не очень разбирается в этих задачах, например у Вас, чтобы помочь освоиться.

А-а-а, ликбез, значит, открывается :))
То есть Ядряра знает ответ на этот вопрос.
Это он у нас - необразованных - спрашивает, чтобы нам помочь освоиться.
Так ведь, кто хочет освоиться, он сам спросит.

До чего же любит Ядряра учить!

Г. Петухов писал в сообщении
https://dxdy.ru/post1703252.html#p1703252

Подозреваю на большее количество делителей раскладывать заметно проще (и вероятнее).

Хм...
То есть, насколько понимаю, случайное натуральное число с большей вероятностью может иметь 48 делителей, нежели 24 делителя.

Что-то я в этом сильно сомневаюсь.