Приложение odlksym
Message boards :
News :
Приложение odlksym
Message board moderation
Previous · 1 · 2 · 3 · 4 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вторичная обработка 14 решений от симметричных ДЛК дала 47 уникальных КФ ОДЛК. Всего получено от этой порции решений 84 уникальные КФ ОДЛК. Обратите внимание, какой выход уникальных КФ ОДЛК от симметричных решений. В 6 раз в данном случае! И 6 уникальных четвёрок получено от этой порции решений. Отличный урожай! Спасибо участникам проекта! Ждём новых интересных решений. |
|
Send message Joined: 18 May 17 Posts: 24 Credit: 167,678 RAC: 0 |
Последние и более полные данные см. http://forum.boinc.ru/default.aspx?g=posts&t=2026&p=6 Здесь информация подается на основе частичных, куцых данных. |
|
Send message Joined: 18 May 17 Posts: 24 Credit: 167,678 RAC: 0 |
повторение |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вчера добавилось несколько новых решений от симметричных ДЛК, присланных помощником. Решили остановить его ветвь данного эксперимента. На данный момент в нашей БД имеется 1810 уникальных симметричных КФ ОДЛК (до запуска этого алгоритма их было 1672). Показываю первые 10 симметричных КФ ОДЛК в БД : 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 5 8 1 4 6 9 7 4 6 9 7 1 8 2 0 3 5 9 7 8 6 5 4 3 1 2 0 3 4 7 8 0 9 1 2 5 6 6 9 4 1 7 2 8 5 0 3 7 8 5 0 6 3 9 4 1 2 5 3 1 9 2 7 0 8 6 4 8 5 6 2 9 0 7 3 4 1 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 8 5 6 3 4 1 9 7 4 6 9 7 8 1 2 0 3 5 6 5 7 9 1 8 0 2 4 3 7 4 6 1 0 9 8 3 5 2 9 7 1 6 5 4 3 8 2 0 3 8 4 0 7 2 9 5 1 6 8 3 5 2 9 0 7 4 6 1 5 9 3 8 2 7 1 6 0 4 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 1 0 5 4 9 8 6 7 8 4 6 7 9 0 2 3 5 1 6 9 4 2 8 1 7 5 0 3 7 6 5 1 0 9 8 4 3 2 5 0 7 6 1 8 3 2 9 4 9 8 3 5 7 2 4 6 1 0 3 5 8 9 2 7 0 1 4 6 4 7 9 8 6 3 1 0 2 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 1 5 0 9 4 8 6 7 4 6 8 9 2 7 0 1 3 5 8 0 4 7 6 3 2 5 9 1 5 7 9 6 1 8 3 0 2 4 9 8 6 2 5 4 7 3 1 0 3 9 5 1 7 2 8 4 0 6 7 4 3 8 9 0 1 6 5 2 6 5 7 0 8 1 9 2 4 3 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 4 0 1 8 9 5 6 7 9 7 5 8 6 3 1 4 2 0 6 5 1 9 7 2 0 8 4 3 3 4 7 1 0 9 8 2 5 6 7 9 8 6 5 4 3 1 0 2 8 0 3 5 2 7 4 6 9 1 5 8 6 7 9 0 2 3 1 4 4 6 9 2 8 1 7 0 3 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 4 1 9 0 8 5 6 7 7 5 8 9 6 3 0 1 4 2 3 7 9 5 8 1 4 0 2 6 8 0 5 6 2 7 3 4 9 1 6 9 7 8 5 4 1 2 0 3 9 4 3 7 1 8 2 6 5 0 5 6 1 2 0 9 7 8 3 4 4 8 6 0 7 2 9 3 1 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 4 8 0 9 1 5 6 7 4 9 7 6 8 1 3 2 0 5 8 7 6 9 5 4 0 3 2 1 9 5 3 1 2 7 8 6 4 0 5 6 8 0 7 2 9 1 3 4 7 0 1 5 6 3 4 8 9 2 3 8 5 7 9 0 2 4 1 6 6 4 9 2 1 8 7 0 5 3 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 4 8 9 0 1 5 6 7 4 7 9 6 1 8 3 0 2 5 7 0 3 5 8 1 4 6 9 2 6 8 5 7 0 9 2 4 1 3 9 5 8 2 6 3 7 1 4 0 5 9 6 1 2 7 8 3 0 4 3 4 1 9 7 2 0 8 5 6 8 6 7 0 5 4 9 2 3 1 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 4 9 1 8 0 5 6 7 5 6 7 8 9 0 1 2 3 4 3 0 1 5 7 2 4 8 9 6 6 4 8 2 0 9 7 1 5 3 8 9 5 6 2 7 3 4 0 1 7 5 3 0 8 1 9 6 4 2 9 8 6 7 5 4 2 3 1 0 4 7 9 1 6 3 8 0 2 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 3 4 9 1 8 0 5 6 7 8 7 6 5 9 0 4 3 2 1 9 4 8 2 6 3 7 1 5 0 5 8 3 0 2 7 9 6 1 4 7 6 9 8 5 4 1 0 3 2 3 5 1 7 0 9 2 8 4 6 4 0 7 6 8 1 3 2 9 5 6 9 5 1 7 2 8 4 0 3 Если вы сравните эти КФ с первыми 10, показанными выше (из 1672), то увидите, что уже есть заполненные пропуски. Очень хорошо! И 138 новых симметричных КФ ОДЛК тоже замечательно. Интересно, что последняя на данный момент симметричная КФ ОДЛК была найдена очень давно (больше года назад): 0 1 2 3 4 5 6 7 8 9 2 3 1 4 0 9 5 8 6 7 4 7 9 1 3 6 8 0 2 5 7 6 8 5 9 0 4 1 3 2 6 9 5 2 8 1 7 4 0 3 9 8 7 6 5 4 3 2 1 0 3 0 4 7 1 8 2 5 9 6 1 5 3 0 2 7 9 6 4 8 5 2 0 8 6 3 1 9 7 4 8 4 6 9 7 2 0 3 5 1 Она является максимальной КФ в БД КФ ОДЛК первого формата, однако не доказано, что это глобальный максимум. Но держится уже больше года! Будет ли найден новый максимум? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
За 16 июля найдено 74 симметричные КФ ОДЛК, из них 14 уникальных. Представляю первую уникальную четвёрку на иллюстрации 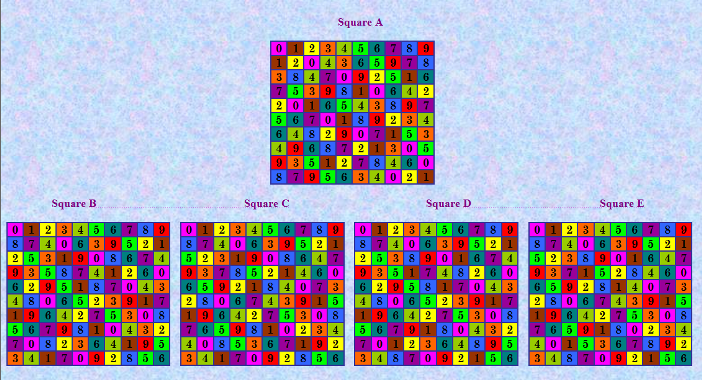 Square A - основной ДЛК четвёрки, это симметричный ДЛК. Четыре ортогональные пары: A - B, A - C, A - D, A - E. Отмечу особенность четвёрок, получаемых от симметричных ДЛК. Эти четвёрки дают три уникальные КФ, так как среди ортогональных соквадратов четвёрки есть две пары изоморфных ДЛК. Вот три уникальные КФ для показанной на иллюстрации четвёрки: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 3 8 4 7 0 9 2 5 1 6 7 5 3 9 8 1 0 6 4 2 2 0 1 6 5 4 3 8 9 7 5 6 7 0 1 8 9 2 3 4 6 4 8 2 9 0 7 1 5 3 4 9 6 8 7 2 1 3 0 5 9 3 5 1 2 7 8 4 6 0 8 7 9 5 6 3 4 0 2 1 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 7 8 9 3 6 8 4 5 9 2 6 0 1 7 3 4 3 8 1 6 9 2 0 5 7 7 8 1 2 9 0 5 3 6 4 2 9 6 7 8 3 4 5 1 0 3 5 9 6 1 8 7 4 0 2 9 0 4 8 7 1 3 6 2 5 6 7 3 5 0 2 9 8 4 1 5 6 7 0 3 4 1 2 9 8 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 7 8 9 3 6 9 4 5 8 2 6 0 1 7 3 4 3 9 1 6 8 2 0 5 7 7 8 1 2 9 0 5 3 6 4 2 9 6 7 8 3 4 5 1 0 3 5 8 6 1 9 7 4 0 2 8 0 4 9 7 1 3 6 2 5 6 7 3 5 0 2 9 8 4 1 5 6 7 0 3 4 1 2 9 8 Такая же четвёрка (от симметричного ДЛК) была получена в 1992 г. (первая!), опубликована в статье «Completion of the Spectrum of Orthogonal Diagonal Latin Squares» (John Wesley Brown, Fred Cherry, Lee Most, Mel Most, E. T. Parker and W. D. Wallis) 0 1 2 3 4 5 6 7 8 9 1 6 9 2 0 3 7 8 5 4 9 8 3 4 5 0 2 1 6 7 3 5 8 7 2 1 0 4 9 6 2 9 5 8 1 7 4 6 0 3 4 0 6 9 3 8 1 5 7 2 5 4 7 6 8 2 9 0 3 1 6 3 4 5 7 9 8 2 1 0 7 2 1 0 9 6 5 3 4 8 8 7 0 1 6 4 3 9 2 5 sq1 0 1 2 3 4 5 6 7 8 9 3 9 1 8 6 4 5 0 7 2 7 3 5 2 9 6 8 4 1 0 4 0 9 6 8 3 2 1 5 7 2 7 0 5 3 8 1 9 4 6 8 4 6 9 1 7 3 2 0 5 5 6 7 0 2 1 4 3 9 8 9 2 3 1 5 0 7 8 6 4 1 5 8 4 7 9 0 6 2 3 6 8 4 7 0 2 9 5 3 1 sq2 0 1 2 3 4 5 6 7 8 9 5 4 1 2 6 9 7 0 3 8 2 3 8 7 9 4 5 6 1 0 3 0 5 9 8 7 2 1 4 6 6 9 3 5 2 8 1 4 0 7 7 2 4 8 1 6 0 3 9 5 8 6 9 0 7 1 3 2 5 4 9 8 7 1 0 2 4 5 6 3 1 5 6 4 3 0 9 8 7 2 4 7 0 6 5 3 8 9 2 1 sq3 0 1 2 3 4 5 6 7 8 9 7 2 9 4 5 3 1 8 0 6 9 8 5 1 3 0 7 4 6 2 2 4 8 7 6 1 3 0 9 5 3 5 0 8 1 6 4 9 2 7 4 9 7 6 2 8 0 3 5 1 1 0 6 5 8 7 9 2 3 4 5 3 1 2 9 4 8 6 7 0 6 7 3 9 0 2 5 1 4 8 8 6 4 0 7 9 2 5 1 3 sq4 Square: 0 1 2 3 4 5 6 7 8 9 2 3 4 9 8 1 0 5 6 7 3 4 9 8 2 7 1 0 5 6 8 7 6 5 0 9 4 3 2 1 5 0 1 7 6 3 2 8 9 4 6 5 0 1 7 2 8 9 4 3 4 9 8 2 3 6 7 1 0 5 7 6 5 0 1 8 9 4 3 2 9 8 7 6 5 4 3 2 1 0 1 2 3 4 9 0 5 6 7 8 (все ДЛК преобразованы к нормализованному виду). Хотя тут очень интересный случай: в указанной статье приведена группа из двух пар ОДЛК: Square A 0 1 2 3 4 5 6 7 8 9 2 3 4 9 8 1 0 5 6 7 3 4 9 8 2 7 1 0 5 6 8 7 6 5 0 9 4 3 2 1 5 0 1 7 6 3 2 8 9 4 6 5 0 1 7 2 8 9 4 3 4 9 8 2 3 6 7 1 0 5 7 6 5 0 1 8 9 4 3 2 9 8 7 6 5 4 3 2 1 0 1 2 3 4 9 0 5 6 7 8 Square B 0 1 2 3 4 5 6 7 8 9 5 4 1 2 6 9 7 0 3 8 2 3 8 7 9 4 5 6 1 0 3 0 5 9 8 7 2 1 4 6 6 9 3 5 2 8 1 4 0 7 7 2 4 8 1 6 0 3 9 5 8 6 9 0 7 1 3 2 5 4 9 8 7 1 0 2 4 5 6 3 1 5 6 4 3 0 9 8 7 2 4 7 0 6 5 3 8 9 2 1 Square C 0 1 2 3 4 5 6 7 8 9 7 2 9 4 5 3 1 8 0 6 9 8 5 1 3 0 7 4 6 2 2 4 8 7 6 1 3 0 9 5 3 5 0 8 1 6 4 9 2 7 4 9 7 6 2 8 0 3 5 1 1 0 6 5 8 7 9 2 3 4 5 3 1 2 9 4 8 6 7 0 6 7 3 9 0 2 5 1 4 8 8 6 4 0 7 9 2 5 1 3 Ещё два ортогональных соквадрата были найдены О. Заикиным в 2016 г.: Square D 0 1 2 3 4 5 6 7 8 9 1 6 9 2 0 3 7 8 5 4 9 8 3 4 5 0 2 1 6 7 3 5 8 7 2 1 0 4 9 6 2 9 5 8 1 7 4 6 0 3 4 0 6 9 3 8 1 5 7 2 5 4 7 6 8 2 9 0 3 1 6 3 4 5 7 9 8 2 1 0 7 2 1 0 9 6 5 3 4 8 8 7 0 1 6 4 3 9 2 5 Square E 0 1 2 3 4 5 6 7 8 9 3 9 1 8 6 4 5 0 7 2 7 3 5 2 9 6 8 4 1 0 4 0 9 6 8 3 2 1 5 7 2 7 0 5 3 8 1 9 4 6 8 4 6 9 1 7 3 2 0 5 5 6 7 0 2 1 4 3 9 8 9 2 3 1 5 0 7 8 6 4 1 5 8 4 7 9 0 6 2 3 6 8 4 7 0 2 9 5 3 1 См. http://sat.isa.ru/pdsat/additional_solutions.php Эти два ортогональных соквадрата как раз изоморфны ортогональным соквадратам из группы двух пар ОДЛК Брауна. В результате получилась четвёрка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
17 июля найдено всего 6 симметричных КФ ОДЛК, уникальных нет. Жду решения за 18 июля. Пока немного занимаюсь вторичной обработкой решений от Приложения odlk3. Для этих решений очень мало получается добавлений при вторичной обработке, потому что в основном эти решения - однушки. Кое-что даёт обработка программой Канонизатор ЛК по ДЛК, программа-карусель ничего не даёт, ибо эта программа хороша для решений от симметричных ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
За 18 июля найдено 22 решения от симметричных ДЛК, уникальное только одно: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 7 8 3 5 9 0 4 6 1 2 9 4 7 1 6 3 8 2 5 0 2 9 6 8 5 4 1 3 0 7 4 6 8 7 0 9 2 1 3 5 6 0 4 2 1 8 7 5 9 3 5 3 1 9 2 7 0 8 6 4 8 5 9 6 7 2 3 0 4 1 3 7 5 0 8 1 9 4 2 6 Эта симметричная КФ ОДЛК даёт двушку, которая имеет парную двушку (как все двушки от симметричных ДЛК); основной ДЛК парной двушки - тоже симметричный: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 8 7 3 0 5 4 9 6 2 1 5 8 7 9 6 3 0 2 1 4 7 5 9 6 1 8 3 0 4 2 9 3 5 8 2 7 1 4 6 0 2 9 6 5 8 1 4 3 0 7 4 6 1 7 0 9 2 8 3 5 6 4 8 2 9 0 7 1 5 3 3 0 4 1 7 2 8 5 9 6 Хороший пример для изучения феномена парности двушек, полученных от симметричных ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
19 июля не найдено ни одной симметричной КФ ОДЛК. Сегодня (20 июля) они появились. На данный момент в нашей БД имеется 1814 уникальных симметричных КФ ОДЛК. Очень хороший вопрос: сколько их будет всего? Это минимальная симметричная КФ ОДЛК: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 5 8 1 4 6 9 7 4 6 9 7 1 8 2 0 3 5 9 7 8 6 5 4 3 1 2 0 3 4 7 8 0 9 1 2 5 6 6 9 4 1 7 2 8 5 0 3 7 8 5 0 6 3 9 4 1 2 5 3 1 9 2 7 0 8 6 4 8 5 6 2 9 0 7 3 4 1 Обратите внимание на первые две строки, они характеризуют первую группу симметричных КФ ОДЛК. Пока идут решения из этой группы. Когда поменяется вторая строка, пойдёт вторая группа решений; первые две строки во второй группе такие: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 Последняя (максимальная) известная на сегодня симметричная КФ ОДЛК: 0 1 2 3 4 5 6 7 8 9 2 3 1 4 0 9 5 8 6 7 4 7 9 1 3 6 8 0 2 5 7 6 8 5 9 0 4 1 3 2 6 9 5 2 8 1 7 4 0 3 9 8 7 6 5 4 3 2 1 0 3 0 4 7 1 8 2 5 9 6 1 5 3 0 2 7 9 6 4 8 5 2 0 8 6 3 1 9 7 4 8 4 6 9 7 2 0 3 5 1 Обратите внимание на вторую строку в этой группе. Долго идти до этой строки! И второй хороший вопрос: является ли текущая максимальная симметричная КФ ОДЛК глобальным максимумом в данном классе решений? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Появились симметричные КФ ОДЛК из второй группы (изменилась вторая строка)! 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 2 0 3 5 1 8 4 6 9 7 4 9 7 6 8 1 3 2 0 5 3 5 9 8 7 2 1 0 4 6 9 7 6 1 5 4 8 3 2 0 6 8 5 0 2 7 9 4 1 3 5 3 1 2 9 0 7 8 6 4 7 4 8 9 3 6 0 1 5 2 8 6 4 7 0 9 2 5 3 1 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 2 8 3 0 5 4 9 6 1 7 4 7 6 9 1 8 0 3 2 5 5 9 1 6 7 2 3 8 0 4 7 5 9 8 3 6 1 0 4 2 9 6 4 1 2 7 8 5 3 0 3 0 5 7 8 1 2 4 9 6 6 4 8 2 0 9 7 1 5 3 8 3 7 5 9 0 4 2 6 1 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 2 8 3 5 9 0 4 6 1 7 9 7 5 6 8 1 3 4 2 0 3 9 7 1 5 4 8 2 0 6 6 5 9 7 1 8 2 0 4 3 8 3 4 2 0 9 7 5 6 1 7 4 8 9 3 6 0 1 5 2 4 0 6 8 2 7 1 3 9 5 5 6 1 0 7 2 9 8 3 4 Решения пошли активнее. Это радует. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Взяла решения от симметричных ДЛК за 20 июля. Всего решений - 92, уникальных решений - 43, в том числе 8 четвёрок. Уже намного меньше повторенных решений! Первичная обработка решений дала 92 уникальные КФ. Отличный результат! Начинаю вторичную обработку решений. Прежде всего - найти все парные решения (обработка программой Белышева Канонизатор ЛК по ДЛК). Затем обработка моей программой карусель (метод перестановок элементов). |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вторичной обработкой 43 решений от симметричных ДЛК мне удалось получить 100 уникальных КФ. Вполне возможно, что это не предел. Всего 43 решения дали 192 уникальные КФ ОДЛК. На данный момент в нашей БД имеется 1882 уникальные симметричные КФ ОДЛК. Пока в BOINC-проекте найдены только группы из двух и четырёх пар ОДЛК. Ждём новых групп пар ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
307-ой вузучий :) (из решений за 21 июля) odlksym_11855_1500493057.929418, 307 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 3 7 1 5 9 0 4 8 2 6 7 9 4 6 8 1 3 5 0 2 9 5 6 8 7 2 1 3 4 0 5 3 8 7 0 9 2 1 6 4 2 4 9 1 3 6 8 0 5 7 6 0 5 2 1 8 7 4 9 3 8 6 7 9 5 4 0 2 3 1 4 8 3 0 2 7 9 6 1 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 3 7 1 5 9 0 4 8 2 6 7 9 4 6 8 1 3 5 0 2 9 5 6 8 7 2 1 3 4 0 5 8 3 7 0 9 2 6 1 4 2 4 9 1 3 6 8 0 5 7 6 0 5 2 1 8 7 4 9 3 8 6 7 9 5 4 0 2 3 1 4 3 8 0 2 7 9 1 6 5 odlksym_18781_1500493882.351777, 307 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 3 9 8 5 7 2 4 1 0 6 4 3 9 1 2 7 8 0 6 5 5 6 1 2 9 0 7 8 3 4 8 7 6 0 5 4 9 3 2 1 7 0 4 6 8 1 3 5 9 2 9 5 3 7 1 8 2 6 4 0 6 4 7 8 0 9 1 2 5 3 2 8 5 9 3 6 0 4 1 7 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 3 9 8 5 7 2 4 1 0 6 4 3 9 1 2 7 8 0 6 5 5 6 1 7 9 0 2 8 3 4 8 7 6 9 5 4 0 3 2 1 7 0 4 6 8 1 3 5 9 2 9 5 3 2 1 8 7 6 4 0 6 4 7 8 0 9 1 2 5 3 2 8 5 0 3 6 9 4 1 7 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
За 21 июля найдено 52 решения от симметричных ДЛК, уникальных только 12, все двушки. Первичная обработка дала 24 уникальные КФ, вторичная обработка - ещё 27 уникальных КФ. Всего от 12 решений мне удалось получить 51 уникальную КФ ОДЛК. |
|
Send message Joined: 18 May 17 Posts: 24 Credit: 167,678 RAC: 0 |
уникальные=повторные, уже ранее найденые |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
После добавления ршений за 21 июля в нашей БД имеется 1901 уникальная симметричная КФ ОДЛК. Сегодня решения идут хорошо, но... очень много повторенных, то есть таких, которые в БД уже есть. Сейчас в основном идут решения из второй группы - с первыми двумя строками 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 но есть и запоздавшие решения из первой группы, например: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 3 5 7 0 1 8 9 2 4 6 4 8 6 9 7 2 0 3 1 5 2 0 4 8 6 3 1 5 9 7 9 3 8 2 5 4 7 1 6 0 7 9 5 6 8 1 3 4 0 2 5 6 1 7 9 0 2 8 3 4 6 4 9 1 2 7 8 0 5 3 8 7 3 5 0 9 4 6 2 1 |
|
Send message Joined: 18 May 17 Posts: 24 Credit: 167,678 RAC: 0 |
... в нашей БД имеется 1901 уникальная симметричная КФ ОДЛК.[/code] уникальная - сами не запутались? |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
За 22 июля найдено 93 симметричные КФ ОДЛК. Увы, уникальных только 7 штук; есть две четвёрки. Первичная обработка этих 7 решений дала 17 уникальных КФ, вторичная обработка - 13 уникальных КФ. Всего получено от 7 решений 30 уникальных КФ ОДЛК. В БД теперь имеется 1911 уникальных симметричных КФ ОДЛК. |
|
Send message Joined: 18 May 17 Posts: 24 Credit: 167,678 RAC: 0 |
За 22 июля найдено 93 симметричные КФ ОДЛК. Увы, уникальных только 7 штук; есть две четвёрки. Не раскрыто, почему было 1901, нашли 7, стало 1911. С другой стороны найдено 7 штук уникальных, но остальные из 86=93-7 тоже уникальные, так как они есть среди 1901 уникальных симметричных КФ ОДЛК Т.е. все 93 уникальные, одна уникальней другой. Можно сказать сама Natalia Makarova уникальная ... ( далее каждый может вставить в меру своей испорченности, но в соответствие с законом) |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
23 июля найдено 31 решение от симметричных ДЛК. Уникальных только два, покажу их: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 8 7 3 5 9 0 4 6 2 1 2 5 6 9 8 1 0 3 4 7 3 8 4 0 7 2 9 5 1 6 7 9 5 1 3 6 8 4 0 2 9 6 7 8 5 4 1 2 3 0 4 0 1 6 2 7 3 8 9 5 6 4 8 7 0 9 2 1 5 3 5 3 9 2 1 8 7 0 6 4 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 8 7 3 5 9 0 4 6 2 1 3 5 8 9 7 2 0 1 4 6 9 4 7 6 1 8 3 2 5 0 7 9 6 1 5 4 8 3 0 2 6 8 5 2 0 9 7 4 1 3 5 0 1 7 3 6 2 8 9 4 2 3 4 0 8 1 9 5 6 7 4 6 9 8 2 7 1 0 3 5 Первичная обработка этих решений дала 5 уникальных КФ, вторичная обработка - 9 уникальных КФ. Здесь только двушки, четвёрок нет. После добавления этих решений в нашей БД стало 1916 уникальных симметричных КФ ОДЛК. Пока ещё идёт вторая группа решений с первыми двумя строками 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
24 июля найдено 3 симметричных КФ ОДЛК, уникальная только одна: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 3 5 9 7 8 3 7 4 1 9 0 8 5 2 6 8 0 7 5 3 6 4 2 9 1 2 4 9 6 8 1 3 0 5 7 9 3 5 8 2 7 1 4 6 0 5 6 8 0 7 2 9 1 3 4 4 9 3 2 1 8 7 6 0 5 7 8 6 9 5 4 0 3 1 2 6 5 1 7 0 9 2 8 4 3 КФ даёт двушку, у которой есть парная двушка. Здесь всё по минимуму: от одной КФ ОДЛК получено 4 уникальные КФ. И количество симметричных КФ ОДЛК в нашей БД стало 1917. |

©2026 (C) Progger