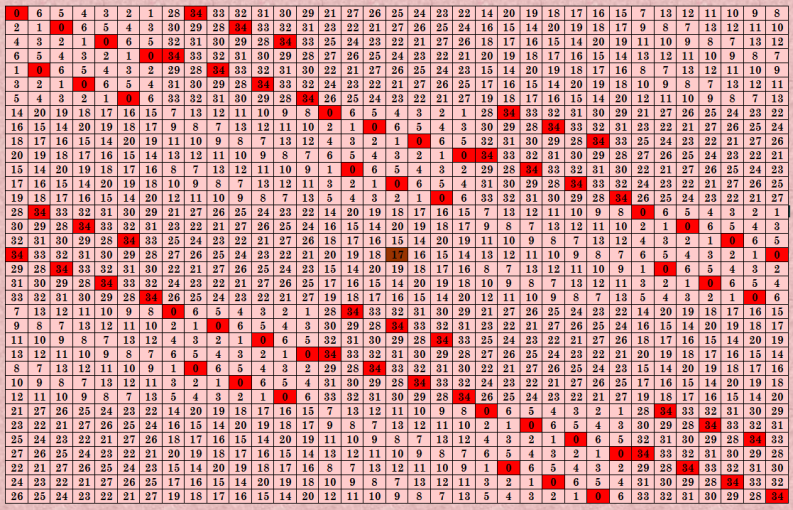
Начну эту тему с давнего построения методом составных квадратов.
Цитата

Кстати, методом составных квадратов можно строить не только дважды симметричные ДЛК.
Покажу построение этим методом идеального ДЛК 35-го порядка (ultra).
Исходные идеальные ДЛК взяла отсюда: 7-го и 5-го порядков (7-го порядка взяла левый квадрат на иллюстрации)





На выходе получила идеальный ДЛК 35-го порядка



Красавец! Этот ДЛК и ассоциативный, и пандиагональный.

На иллюстрациях вы видите идеальные ДЛК 7-го порядка (это из моей статьи) и разные ДЛК 5-го порядка (это с сайта Harry White).
Идеальные ДЛК - это одновременно ассоциативные и пандиагональные; их называют ultra по-английски.

Пандиагональные ДЛК интересуют меня очень давно. Далее будет понятно, почему они так интересны.
Пандиагональные ДЛК для порядков n=4k+2 (k=1, 2, 3, ...) не существуют.
Для порядка 10 я пыталась написать программу составления псевдопандиагональных ДЛК (то есть с небольшим нарушением пандиагональности), но на каком-то шаге зашла в тупик.
Может быть, банально ошиблась. Искать ошибку не стала.
В работе с ДЛК порядков 9 и 11 снова возник вопрос о пандиагональных ДЛК.
Решила посвятить им специальную тему.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Надо дать определение пандиагонального ДЛК.
Определение. ДЛК порядка n называется пандиагональным, если все его разломанные диагонали обоих направлений суть перестановка элементов 0, 1, ... , n-1.

Из определения понятно, что в каждой разломанной диагонали пандиагонального ДЛК нет повторяющихся элементов.

В статье OEIS https://oeis.org/A338620 дано такое определение пандиагонального ЛК

A pandiagonal Latin square is a Latin square in which the diagonal, antidiagonal and all broken diagonals and antidiagonals are transversals.

Да, в пандиагональном ЛК (а такой ЛК обязательно является ДЛК) все диагонали (главная, побочная и разломанные обоих направлений) являются трансверсалями.
Это следует из моего определения.
А в статье OEIS это сказано в самом определении.
И теперь понятно, почему пандиагональные ДЛК так интересны.
Для пандиагонального ДЛК элементарно составляется ортогональный ДЛК.
Есть готовый набор непересекающихся трансверсалей!

Таким образом, если бы мы сгенерировали много-много пандиагональных ДЛК 11-го порядка, все они сразу же были бы ОДЛК.
Однако... много-много не получилось, как я обнаружила с большим удивлением. Об этом напишу далее.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посмотрим на последовательность OEIS https://oeis.org/A338620

A338620 Number of pandiagonal Latin squares of order n with the first row in ascending order.
1, 0, 0, 0, 2, 0, 4, 0, 0, 0, 8, 0, 12386

Здесь приведено количество пандиагональных ДЛК до порядка n=13.
[В последовательности говорится о пандиагональных ЛК, но, как уже отмечено выше, пандиагональный ЛК обязательно является ДЛК.]
До порядка n=11 включительно пандиагональные ДЛК являются циклическими (конечно, для тех порядков, для которых они существуют), то есть строятся методом циклического сдвига.

Пример для n=5

0 1 2 3 4
2 3 4 0 1
4 0 1 2 3
1 2 3 4 0
3 4 0 1 2

0 1 2 3 4
3 4 0 1 2
1 2 3 4 0
4 0 1 2 3
2 3 4 0 1

Пример для n=7

0 1 2 3 4 5 6
2 3 4 5 6 0 1
4 5 6 0 1 2 3
6 0 1 2 3 4 5
1 2 3 4 5 6 0
3 4 5 6 0 1 2
5 6 0 1 2 3 4

0 1 2 3 4 5 6
3 4 5 6 0 1 2
6 0 1 2 3 4 5
2 3 4 5 6 0 1
5 6 0 1 2 3 4
1 2 3 4 5 6 0
4 5 6 0 1 2 3

0 1 2 3 4 5 6
4 5 6 0 1 2 3
1 2 3 4 5 6 0
5 6 0 1 2 3 4
2 3 4 5 6 0 1
6 0 1 2 3 4 5
3 4 5 6 0 1 2

0 1 2 3 4 5 6
5 6 0 1 2 3 4
3 4 5 6 0 1 2
1 2 3 4 5 6 0
6 0 1 2 3 4 5
4 5 6 0 1 2 3
2 3 4 5 6 0 1

Позже покажу и для порядка 11 все нормализованные пандиагональные ДЛК (8 штук).

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Кстати, на этой иллюстрации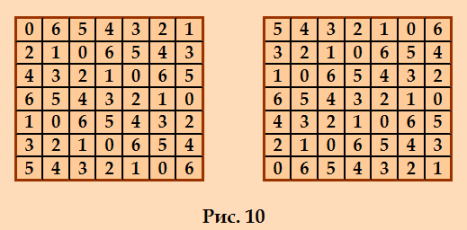



идеальный ДЛК слева тоже построен методом циклического сдвига, только он нормализованный не по первой строке, а по главной диагонали (сильно нормализованный по терминологии Белышева).
Идеальный ДЛК справа получен из левого ДЛК отражением (перестановкой строк). Он тоже циклический.
И это ортогональная пара, из которой в моей статье построен идеальный магический квадрат.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А далее мы посмотрим на ДЛК 9-го порядка.
Как видим в последовательности OEIS, нет пандиагональных ДЛК 9-го порядка.
Вот какая жалость :)
Но есть два вида псевдопандиагональных ДЛК 9-го порядка, точнее пандиагональных не в смысле данного выше определения, а в некотором другом смысле.
Расскажу о таких ДЛК дальше.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Итак, посмотрим на совершенный ДЛК 9-го порядка (показываю его в другой раскраске)



Это из моей статьи ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ.
Очень интересный квадратик!
Кстати, имеет максимальное количество Д-трансверсалей (333), как недавно установлено в двух BOINC-проектах по составлению полной БД КФ ОДЛК порядка 9 (Rake Search и Gerasim@Home).
А также имеет немало ортогональных диагональных соквадратов (308 штук).
На всякий случай покажу вывод программы Белышева ortogon_u

[DLK(308):1]
0 3 6 1 4 7 2 5 8
1 4 7 2 5 8 0 3 6
2 5 8 0 3 6 1 4 7
6 0 3 7 1 4 8 2 5
7 1 4 8 2 5 6 0 3
8 2 5 6 0 3 7 1 4
3 6 0 4 7 1 5 8 2
4 7 1 5 8 2 3 6 0
5 8 2 3 6 0 4 7 1

Теперь проверим этот ДЛК утилитой Harry White. Утилита выдаёт

Order? 9

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 weakly pandiagonal
         1 center symmetric
         1 self-orthogonal

Вот оно, свойство - weakly pandiagonal.
Это переводится как "слабо пандиагональный".
Что означает это свойство?
Оно означает пандиагональность в смысле пандиагональности магического квадрата.
То есть смотрим на ДЛК, как на магический квадрат.

Читаем в Википедии
https://wikipedia.tel/Магический_квадрат#Дьявольский_магический_квадрат

Дьявольский квадрат или пандиагональный квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям (англ.) (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.

Да, в смысле этого определения совершеннй ДЛК пандиагональный.
Но он не является пандиагональным в смысле определения пандиагонального ДЛК (см. выше).
Поэтому у Harry White это свойство названо "weakly pandiagonal".

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

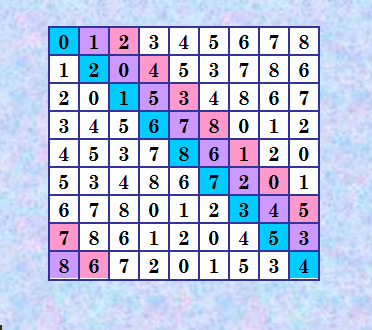
Кстати, обратите внимание в статье Википедии на эту иллюстрацию



Это я добавила очень давно, когда занималась магическими квдаратами.
Иллюстрация поможет понять, что такое разломанные диагонали, тем, кто встречается с этим понятием впервые.
Некоторые авторы называют разломанные диагонали "ломаными", но я привыкла к первому термину.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Второй пример псевдопандиагональности даже не в ДЛК, а в ЛК.
Цитата отсюда
https://boinc.progger.info/odlk/forum_thread.php?id=47&postid=1195

Пример
на иллюстрации изображён ЛК 9-го порядка и окрашены три трансверсали в этом ЛК



Конечно, элементы трансверсали не обязательно должны располагаться на диагонали ЛК (главной или разломанной). Просто в этом примере такое расположение.
Кстати, на всех диагоналях данного направления (главной и разломанных) в этом ЛК мы получим трансверсали. Их будет ровно 9 и они будут неперсекающимися. И мы имеем из этого набора трансверсалей готовый ортогональный соквадрат к приведённому ЛК:

0 2 1 6 8 7 3 5 4 
1 0 5 7 6 2 4 3 8 
2 4 3 8 1 0 5 7 6 
3 5 4 0 2 1 6 8 7 
4 3 8 1 0 5 7 6 2 
5 7 6 2 4 3 8 1 0 
6 8 7 3 5 4 0 2 1 
7 6 2 4 3 8 1 0 5 
8 1 0 5 7 6 2 4 3

Утилита Harry Whine отмечает в этом ЛК такие свойства

Order? 9

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 Latin
         1 center symmetric
         1 nfr
         1 nfc
         1 nfr nfc
         1 self-transpose

ЛК ассоцитативный и совпадает со своим транспонированным вариантом.
Псевдопандиагональность (пандиагональность в одном направлении) здесь не отмечена.
Я назвала бы этот ЛК полупандиагональным (semi-pandiagonal по-английски).
Как видим, к полупандиагональному ЛК тоже очень легко найти его ортогональный соквадрат.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Далее будем рассматривать нормализованные пандиагональные ДЛК 11-го порядка.
Их 8 штук, все они циклические и легко строятся вручную методом циклического сдвига.
Кроме того, все они входят в полную систему MOLS 11-го порядка.
Осталось их показать.

Вот они (построены мной вручную)

0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 0 1
4 5 6 7 8 9 10 0 1 2 3
6 7 8 9 10 0 1 2 3 4 5
8 9 10 0 1 2 3 4 5 6 7
10 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 0
3 4 5 6 7 8 9 10 0 1 2
5 6 7 8 9 10 0 1 2 3 4
7 8 9 10 0 1 2 3 4 5 6
9 10 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 0 1 2 3
8 9 10 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 0
5 6 7 8 9 10 0 1 2 3 4
9 10 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 0 1
6 7 8 9 10 0 1 2 3 4 5
10 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 0 1 2
7 8 9 10 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 0 1 2 3 4
10 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 0 1 2 3
9 10 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 0 1 2
8 9 10 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 0 1
7 8 9 10 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 0
6 7 8 9 10 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 0
7 8 9 10 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 0 1
8 9 10 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 0 1 2
9 10 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 0 1 2 3
10 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 0 1 2
10 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 0 1
9 10 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 0
8 9 10 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10
8 9 10 0 1 2 3 4 5 6 7
5 6 7 8 9 10 0 1 2 3 4
2 3 4 5 6 7 8 9 10 0 1
10 0 1 2 3 4 5 6 7 8 9
7 8 9 10 0 1 2 3 4 5 6
4 5 6 7 8 9 10 0 1 2 3
1 2 3 4 5 6 7 8 9 10 0
9 10 0 1 2 3 4 5 6 7 8
6 7 8 9 10 0 1 2 3 4 5
3 4 5 6 7 8 9 10 0 1 2

0 1 2 3 4 5 6 7 8 9 10
9 10 0 1 2 3 4 5 6 7 8
7 8 9 10 0 1 2 3 4 5 6
5 6 7 8 9 10 0 1 2 3 4
3 4 5 6 7 8 9 10 0 1 2
1 2 3 4 5 6 7 8 9 10 0
10 0 1 2 3 4 5 6 7 8 9
8 9 10 0 1 2 3 4 5 6 7
6 7 8 9 10 0 1 2 3 4 5
4 5 6 7 8 9 10 0 1 2 3
2 3 4 5 6 7 8 9 10 0 1

Как уже сказано, эти 8 ДЛК образуют группу MODLS, то есть все они взаимно ортогональны.

А теперь самое важное: не изоморфных ДЛК в этой группе всего два.
Я покажу их в оригинальном виде, а не в виде КФ

0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 0 1
4 5 6 7 8 9 10 0 1 2 3
6 7 8 9 10 0 1 2 3 4 5
8 9 10 0 1 2 3 4 5 6 7
10 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 0
3 4 5 6 7 8 9 10 0 1 2
5 6 7 8 9 10 0 1 2 3 4
7 8 9 10 0 1 2 3 4 5 6
9 10 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

Вот и всё! Больше никаких других (существенно различных) пандиагональных ДЛК 11-го порядка нет.
Это было для меня открытием.
Harry White предлагала поискать другие пандиагональные ДЛК 11-го порядка. Он поискал и тоже не нашёл других (не изоморфных двум показанным).

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Интересно: КФ пандиагональных ДЛК не пандагональные.
Показываю КФ первого формата для двух уникальных пандиагональных ДЛК 11-го порядка

 0  1  2  3  4  5  6  7  8  9 10
 2  3  1  4  5  6  7  9 10  8  0
 6  9  7  8 10  0  2  1  4  3  5
 7  8  9 10  0  2  1  3  5  4  6
 1  4  3  5  6  7  9  8  0 10  2
 9 10  8  0  2  1  3  4  6  5  7
 3  5  4  6  7  9  8 10  2  0  1
 8  0 10  2  1  3  4  5  7  6  9
10  2  0  1  3  4  5  6  9  7  8
 4  6  5  7  9  8 10  0  1  2  3
 5  7  6  9  8 10  0  2  3  1  4

 0  1  2  3  4  5  6  7  8  9 10
 2  3  4  5  1  7  8  9 10  6  0
 3  9  5  6  7  8  2 10  4  0  1
 5  6  7  8  9 10  4  0  1  2  3
 6  0  8  2 10  4  5  1  7  3  9
 8  2 10  4  0  1  7  3  9  5  6
10  4  0  1  2  3  9  5  6  7  8
 4  5  1  7  3  9 10  6  0  8  2
 1  7  3  9  5  6  0  8  2 10  4
 7  8  9 10  6  0  1  2  3  4  5
 9 10  6  0  8  2  3  4  5  1  7

КФ второго формата также не пандиагональные

 0  3  8  9  7  2 10  5  4  6  1
 6  1  4  7  8  3  5  0 10  2  9
 7 10  2  0  6  4  1  9  3  8  5
10  6  9  3  1  0  8  4  7  5  2
 2  9 10  8  4  1  0  6  5  3  7
 4  0  1  2  3  5  7  8  9 10  6
 3  7  5  4 10  9  6  2  0  1  8
 8  5  3  6  2 10  9  7  1  4  0
 5  2  7  1  9  6  4 10  8  0  3
 1  8  0 10  5  7  2  3  6  9  4
 9  4  6  5  0  8  3  1  2  7 10

 0  7  8  5  3  6  9  2 10  4  1
 4  1  6  7  5 10  3  9  0  2  8
 5  0  2 10  6  9  8  1  3  7  4
10  5  1  3  9  8  2  4  6  0  7
 8  9  5  2  4  7  0 10  1  6  3
 1  2  3  4  0  5 10  6  7  8  9
 7  4  9  0 10  3  6  8  5  1  2
 3 10  4  6  8  2  1  7  9  5  0
 6  3  7  9  2  1  4  0  8 10  5
 2  8 10  1  7  0  5  3  4  9  6
 9  6  0  8  1  4  7  5  2  3 10

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Канонизировала два нормализованных пандиагональных ДЛК 5-го порядка, КФ выдалась одна.
Таким образом, имеем один класс эквивалентности пандиагональных ДЛК 5-го порядка, вот его представитель

0 1 2 3 4
2 3 4 0 1
4 0 1 2 3
1 2 3 4 0
3 4 0 1 2

И далее канонизировала 4 нормализованных пандиагональных ДЛК 7-го порядка.
КФ тоже выдалась одна.
Это представитель класса эквивалентности пандиагональных ДЛК 7-го порядка

0 1 2 3 4 5 6
2 3 4 5 6 0 1
4 5 6 0 1 2 3
6 0 1 2 3 4 5
1 2 3 4 5 6 0
3 4 5 6 0 1 2
5 6 0 1 2 3 4

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Пандиагональных ДЛК 12-го порядка не существует.
А слабо пандиагональные существуют!

Мне удалось построить слабо пандиагональный ДЛК 12-го порядка.
Интересно, что для построения я применила метод трёх квадратов, который был найден мной при исследовании магических квадратов и описан в книге "Волшебный мир магических квадратов".
Скачать эту книгу можно с Яндекс.Диска
https://yadi.sk/d/ehakE2V6S5TzG

Метод трёх квадратов описан в главе 3.7 (стр. 38). Он назван "Преобразование трёх квадратов".
Сейчас я назвала бы его так: "Преобразование трёх квадрантов", но это сути преобразования не меняет.
Для магических квадратов данное преобразование превращает ассоциативный квадрат порядка n=4k в пандиагональный.
Вот я и решила попробовать - а что будет с ассоциативным ДЛК, если применить к нему это преобразование.
Преобразование сработало, только получился не пандиагональный ДЛК, а слабо пандиагональный. Такой результат я и ожидала.

Итак, я взяла ассоциативный ДЛК 12-го порядка

0 2 3 4 9 8 7 6 11 10 5 1
3 1 7 6 8 9 5 10 4 11 0 2
1 9 2 5 7 10 8 11 0 3 6 4
5 4 10 3 11 0 9 8 2 6 1 7
6 7 11 10 4 1 0 5 9 2 8 3
11 0 6 8 2 5 4 1 10 7 3 9
2 8 4 1 10 7 6 9 3 5 11 0
8 3 9 2 6 11 10 7 1 0 4 5
4 10 5 9 3 2 11 0 8 1 7 6
7 5 8 11 0 3 1 4 6 9 2 10
9 11 0 7 1 6 2 3 5 4 10 8
10 6 1 0 5 4 3 2 7 8 9 11

и применила к нему указанное преобразование трёх квадратов.
Получила такой ДЛК

0 2 3 4 9 8 1 5 10 11 6 7
3 1 7 6 8 9 2 0 11 4 10 5
1 9 2 5 7 10 4 6 3 0 11 8
5 4 10 3 11 0 7 1 6 2 8 9
6 7 11 10 4 1 3 8 2 9 5 0
11 0 6 8 2 5 9 3 7 10 1 4
10 6 1 0 5 4 11 9 8 7 2 3
9 11 0 7 1 6 8 10 4 5 3 2
7 5 8 11 0 3 10 2 9 6 4 1
4 10 5 9 3 2 6 7 1 8 0 11
8 3 9 2 6 11 5 4 0 1 7 10
2 8 4 1 10 7 0 11 5 3 9 6

Проверяю этот ДЛК утилитой Harry White

Order? 12

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 weakly pandiagonal
         1 self-orthogonal

ДЛК слабо пандиагональный, а ещё self-orthogonal.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Интересно, что транспонированный вариант этого ДЛК тоже слабо пандиагональный, вот он

 0  3  1  5  6 11 10  9  7  4  8  2
 2  1  9  4  7  0  6 11  5 10  3  8
 3  7  2 10 11  6  1  0  8  5  9  4
 4  6  5  3 10  8  0  7 11  9  2  1
 9  8  7 11  4  2  5  1  0  3  6 10
 8  9 10  0  1  5  4  6  3  2 11  7
 1  2  4  7  3  9 11  8 10  6  5  0
 5  0  6  1  8  3  9 10  2  7  4 11
10 11  3  6  2  7  8  4  9  1  0  5
11  4  0  2  9 10  7  5  6  8  1  3
 6 10 11  8  5  1  2  3  4  0  7  9
 7  5  8  9  0  4  3  2  1 11 10  6

И мы легко получаем пандиагональный магический квадрат методом латинских квадратов!
А пандиагональный магический квадрат 12-го порядка построить довольно сложно.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

О пандиагональных квадратах 13-го порядка в статье OEIS https://oeis.org/A338620
написано

For order n=13 this is not true and exists 12386 inequivalent squares; of these 10 are cyclic (in all directions) and 1560 are semi-cyclic (cyclic in a single direction).

Перевод в Google

Для порядка n = 13 это неверно и существует 12386 неэквивалентных квадратов; из них 10 являются циклическими (во всех направлениях) и 1560 являются полуциклическими (циклическими в одном направлении).

Что означает "12386 неэквивалентных квадратов", я не понимаю.
Ну, про 10 циклических, положим, понятно.
А вот что такое "полуциклические квадраты", я тоже пока не знаю. Как это: "циклические в одном направлении"?

Ладно, начну с того, что понятно, то есть с 10 циклических пандиагональных ДЛК 13-го порядка.
Они у меня тоже уже построены, когда строила полную систему MOLS 13-го порядка.
Сейчас найду их и покажу. Они образуют группу MODLS, то есть все взаимно ортогональны.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Показываю 10 циклических нормализованных пандиагональных ДЛК 13-го порядка (построены мной вручную методом циклического сдвига)

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

0 1 2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 0 1 2
6 7 8 9 10 11 12 0 1 2 3 4 5
9 10 11 12 0 1 2 3 4 5 6 7 8
12 0 1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12 0 1
5 6 7 8 9 10 11 12 0 1 2 3 4
8 9 10 11 12 0 1 2 3 4 5 6 7
11 12 0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 11 12 0
4 5 6 7 8 9 10 11 12 0 1 2 3
7 8 9 10 11 12 0 1 2 3 4 5 6
10 11 12 0 1 2 3 4 5 6 7 8 9

0 1 2 3 4 5 6 7 8 9 10 11 12
4 5 6 7 8 9 10 11 12 0 1 2 3
8 9 10 11 12 0 1 2 3 4 5 6 7
12 0 1 2 3 4 5 6 7 8 9 10 11
3 4 5 6 7 8 9 10 11 12 0 1 2
7 8 9 10 11 12 0 1 2 3 4 5 6
11 12 0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 11 12 0 1
6 7 8 9 10 11 12 0 1 2 3 4 5
10 11 12 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 11 12 0
5 6 7 8 9 10 11 12 0 1 2 3 4
9 10 11 12 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10 11 12
5 6 7 8 9 10 11 12 0 1 2 3 4
10 11 12 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11 12 0 1
7 8 9 10 11 12 0 1 2 3 4 5 6
12 0 1 2 3 4 5 6 7 8 9 10 11
4 5 6 7 8 9 10 11 12 0 1 2 3
9 10 11 12 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 11 12 0
6 7 8 9 10 11 12 0 1 2 3 4 5
11 12 0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 0 1 2
8 9 10 11 12 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10 11 12
6 7 8 9 10 11 12 0 1 2 3 4 5
12 0 1 2 3 4 5 6 7 8 9 10 11
5 6 7 8 9 10 11 12 0 1 2 3 4
11 12 0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 11 12 0 1 2 3
10 11 12 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 11 12 0 1 2
9 10 11 12 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 11 12 0 1
8 9 10 11 12 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 11 12 0
7 8 9 10 11 12 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10 11 12
7 8 9 10 11 12 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 11 12 0
8 9 10 11 12 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 11 12 0 1
9 10 11 12 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 11 12 0 1 2
10 11 12 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 11 12 0 1 2 3
11 12 0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 0 1 2 3 4
12 0 1 2 3 4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10 11 12
8 9 10 11 12 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 11 12 0 1 2
11 12 0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 11 12 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 11 12 0
9 10 11 12 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 11 12 0 1 2 3
12 0 1 2 3 4 5 6 7 8 9 10 11
7 8 9 10 11 12 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 11 12 0 1
10 11 12 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 11 12 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 0
10 11 12 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 0 1
11 12 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 0 1 2
12 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10 11 12
10 11 12 0 1 2 3 4 5 6 7 8 9
7 8 9 10 11 12 0 1 2 3 4 5 6
4 5 6 7 8 9 10 11 12 0 1 2 3
1 2 3 4 5 6 7 8 9 10 11 12 0
11 12 0 1 2 3 4 5 6 7 8 9 10
8 9 10 11 12 0 1 2 3 4 5 6 7
5 6 7 8 9 10 11 12 0 1 2 3 4
2 3 4 5 6 7 8 9 10 11 12 0 1
12 0 1 2 3 4 5 6 7 8 9 10 11
9 10 11 12 0 1 2 3 4 5 6 7 8
6 7 8 9 10 11 12 0 1 2 3 4 5
3 4 5 6 7 8 9 10 11 12 0 1 2

0 1 2 3 4 5 6 7 8 9 10 11 12
11 12 0 1 2 3 4 5 6 7 8 9 10
9 10 11 12 0 1 2 3 4 5 6 7 8
7 8 9 10 11 12 0 1 2 3 4 5 6
5 6 7 8 9 10 11 12 0 1 2 3 4
3 4 5 6 7 8 9 10 11 12 0 1 2
1 2 3 4 5 6 7 8 9 10 11 12 0
12 0 1 2 3 4 5 6 7 8 9 10 11
10 11 12 0 1 2 3 4 5 6 7 8 9
8 9 10 11 12 0 1 2 3 4 5 6 7
6 7 8 9 10 11 12 0 1 2 3 4 5
4 5 6 7 8 9 10 11 12 0 1 2 3
2 3 4 5 6 7 8 9 10 11 12 0 1

А не изоморфных ДЛК здесь всего три, вот эти

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

0 1 2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 0 1 2
6 7 8 9 10 11 12 0 1 2 3 4 5
9 10 11 12 0 1 2 3 4 5 6 7 8
12 0 1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12 0 1
5 6 7 8 9 10 11 12 0 1 2 3 4
8 9 10 11 12 0 1 2 3 4 5 6 7
11 12 0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 11 12 0
4 5 6 7 8 9 10 11 12 0 1 2 3
7 8 9 10 11 12 0 1 2 3 4 5 6
10 11 12 0 1 2 3 4 5 6 7 8 9

0 1 2 3 4 5 6 7 8 9 10 11 12
5 6 7 8 9 10 11 12 0 1 2 3 4
10 11 12 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11 12 0 1
7 8 9 10 11 12 0 1 2 3 4 5 6
12 0 1 2 3 4 5 6 7 8 9 10 11
4 5 6 7 8 9 10 11 12 0 1 2 3
9 10 11 12 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 11 12 0
6 7 8 9 10 11 12 0 1 2 3 4 5
11 12 0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 0 1 2
8 9 10 11 12 0 1 2 3 4 5 6 7

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Далее в статье OEIS https://oeis.org/A338620 приведён ДЛК 13-го порядка

7 1 0 3 6 5 12 2 8 9 10 11 4
2 3 4 10 0 7 6 9 12 11 5 8 1
4 11 1 7 8 9 10 3 6 0 12 2 5
6 5 8 11 10 4 7 0 1 2 3 9 12
8 9 2 5 12 11 1 4 3 10 0 6 7
3 6 12 0 1 2 8 11 5 4 7 10 9
10 0 3 2 9 12 5 6 7 8 1 4 11
1 7 10 4 3 6 9 8 2 5 11 12 0
11 4 5 6 7 0 3 10 9 12 2 1 8
5 8 7 1 4 10 11 12 0 6 9 3 2
12 2 9 8 11 1 0 7 10 3 4 5 6
9 10 11 12 5 8 2 1 4 7 6 0 3
0 12 6 9 2 3 4 5 11 1 8 7 10

который пандиагональный, но не циклический.
Этот квадрат взят из статьи
Vahid Dabbaghian, Tiankuang Wu, Constructing non-cyclic pandiagonal Latin squares of prime orders, Journal of Discrete Algorithms 30, 2015.
Ну и какой это квадрат? Полуциклический?
В общем, надо читать указанную статью, откуда взят этот квадрат.
И где бы это увидеть "12386 inequivalent squares" 13-го порядка?
Очень интересно на них посмотреть. А также выяснить в каком смысле эти квадраты "inequivalent".

Кстати, этот ДЛК даже не нормализован, прямо взят из статьи, в том виде, как он там опубликован.
Хотя в статье OEIS речь идёт о пандиагональных ЛК с первой строкой в порядке возрастания, то есть нормализованных

Number of pandiagonal Latin squares of order n with the first row in ascending order.

Нормализовала ДЛК

0 1 2 3 4 5 6 7 8 9 10 11 12
7 3 12 10 2 0 4 9 6 11 5 8 1
12 11 1 0 8 9 10 3 4 2 6 7 5
4 5 8 11 10 12 0 2 1 7 3 9 6
8 9 7 5 6 11 1 12 3 10 2 4 0
3 4 6 2 1 7 8 11 5 12 0 10 9
10 2 3 7 9 6 5 4 0 8 1 12 11
1 0 10 12 3 4 9 8 7 5 11 6 2
11 12 5 4 0 2 3 10 9 6 7 1 8
5 8 0 1 12 10 11 6 2 4 9 3 7
6 7 9 8 11 1 2 0 10 3 12 5 4
9 10 11 6 5 8 7 1 12 0 4 2 3
2 6 4 9 7 3 12 5 11 1 8 0 10

К трём уникальным пандиагональным ДЛК, показанным выше, добавился ещё один.
Это пока всё, что я могу сказать о пандиагональных ДЛК 13-го порядка.
Остальное смотрите в статье OEIS, а лучше - в статье, на которую указана ссылка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Пандиагональных ДЛК 14-го порядка не существует.
15-го порядка тоже, но для 15-го порядка должны быть слабо пандиагональные ДЛК.
Такой вывод делаю исходя из того, что существуют пандиагональные магические квадраты 15-го порядка.
Но для подтверждения вывода надо построить слабо пандиагональный ДЛК 15-го порядка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нашла интересную статью
https://onlinelibrary.wiley.com/doi/abs/10.1002/jcd.20143

Constructing orthogonal pandiagonal Latin squares and panmagic squares from modular n‐queens solutions
Jordan Bell
Brett Stevens

Abstract
In this article, we show how to construct pairs of orthogonal pandiagonal Latin squares and panmagic squares from certain types of modular n‐queens solutions. We prove that when these modular n‐queens solutions are symmetric, the panmagic squares thus constructed will be associative, where for an n × n associative magic square A = (aij), for all i and j it holds that aij + an−i−1,n−j−1 = c for a fixed c. We further show how to construct orthogonal Latin squares whose modular difference diagonals are Latin from any modular n‐queens solution. As well, we analyze constructing orthogonal pandiagonal Latin squares from particular classes of non‐linear modular n‐queens solutions. These pandiagonal Latin squares are not row cyclic, giving a partial solution to a problem of Hedayat. © 2007 Wiley Periodicals, Inc. J Combin Designs 15: 221–234, 2007

Особенно привлекает это

These pandiagonal Latin squares are not row cyclic, giving a partial solution to a problem of Hedayat.

Но статью там бесплатно не дают.

PS. Что это за проблема "a problem of Hedayat"?
Пожалуйста, расскажите, кто знает.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Написала комментарий на форуме MATHEMATICS

Weakly pandiagonal Latin square is pandiagonal as magic square. I found weakly pandiagonal Latin square of order 12. But I have not yet found the weakly pandiagonal Latin square of order 15.

https://math.stackexchange.com/questions/173127/no-pandiagonal-latin-squares-with-order-divisible-by-3/3962917#3962917

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ещё нашла статью
https://www.researchgate.net/publication/270398348_Constructing_Pandiagonal_Latin_Squares_from_Linear_Cellular_Automaton_on_Elementary_Abelian_Groups

Constructing Pandiagonal Latin Squares from Linear Cellular Automaton on Elementary Abelian Groups
December 2014
Vahid Dabbaghian
Journal of Combinatorial Designs 23(5)

Эту статью можно скачать (PDF).

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg