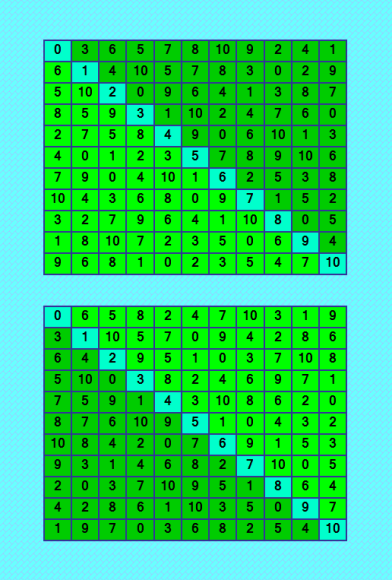
БД КФ ОДЛК порядка 11
Message boards :
Science :
БД КФ ОДЛК порядка 11
Message board moderation
Previous · 1 · 2 · 3 · Next
| Author | Message |
|---|---|
 Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Есть 30 тысяч КФ ОДЛК! БД растёт как на дрожжах :) Сейчас она содержит 30004 КФ ОДЛК. Покажу несколько первых и последних КФ ОДЛК текущего варианта БД 0 2 3 4 5 6 7 8 9 10 1 5 1 4 9 7 3 8 2 10 0 6 8 5 2 1 6 9 10 0 3 7 4 2 7 6 3 10 8 9 4 5 1 0 3 8 10 7 4 0 2 5 1 6 9 7 6 8 0 9 5 1 10 2 4 3 1 4 9 5 8 10 6 3 0 2 7 10 9 5 6 1 2 0 7 4 3 8 6 3 7 10 0 1 4 9 8 5 2 4 10 0 8 2 7 3 1 6 9 5 9 0 1 2 3 4 5 6 7 8 10 0 2 3 4 5 6 8 9 10 7 1 4 1 7 5 8 9 2 10 6 0 3 10 9 2 0 7 1 4 8 3 6 5 5 7 6 3 0 2 1 4 9 10 8 1 3 5 10 4 8 7 6 0 2 9 7 8 0 9 10 5 3 1 2 4 6 9 0 10 1 2 4 6 3 5 8 7 2 4 8 6 9 3 10 7 1 5 0 3 5 9 7 6 10 0 2 8 1 4 6 10 1 8 3 7 5 0 4 9 2 8 6 4 2 1 0 9 5 7 3 10 0 2 3 4 5 6 8 9 10 7 1 5 1 6 8 10 7 9 3 2 0 4 10 5 2 9 7 1 4 0 3 6 8 8 9 5 3 0 2 7 4 1 10 6 7 6 1 5 4 10 2 8 0 3 9 3 8 4 0 9 5 1 10 6 2 7 1 7 10 2 8 0 6 5 9 4 3 4 0 9 6 3 8 10 7 5 1 2 2 4 7 10 6 9 3 1 8 5 0 6 10 8 7 1 3 0 2 4 9 5 9 3 0 1 2 4 5 6 7 8 10 0 2 3 4 5 6 9 8 10 7 1 5 1 8 0 10 3 4 6 7 2 9 10 7 2 8 3 9 1 5 0 6 4 2 6 7 3 9 0 8 4 1 10 5 8 5 6 1 4 10 7 2 9 0 3 3 4 1 10 6 5 0 9 2 8 7 7 9 5 2 8 4 6 10 3 1 0 4 10 0 9 1 8 3 7 6 5 2 9 0 10 7 2 1 5 3 8 4 6 1 3 4 6 7 2 10 0 5 9 8 6 8 9 5 0 7 2 1 4 3 10 . . . . . . 0 10 9 8 7 6 2 3 5 4 1 10 1 8 6 5 7 0 9 3 2 4 1 8 2 7 3 4 9 5 0 10 6 7 5 1 3 2 8 10 4 6 0 9 6 3 0 10 4 9 7 8 1 5 2 9 7 3 1 6 5 4 2 10 8 0 2 0 4 5 8 1 6 10 9 3 7 8 2 6 9 0 10 5 7 4 1 3 4 9 10 2 1 0 3 6 8 7 5 5 6 7 4 10 3 1 0 2 9 8 3 4 5 0 9 2 8 1 7 6 10 0 10 9 8 7 6 4 2 5 3 1 4 1 3 2 6 7 5 10 9 0 8 9 5 2 7 1 8 10 6 3 4 0 5 9 7 3 0 2 8 4 1 10 6 1 6 5 0 4 10 7 3 2 8 9 10 3 0 1 9 5 2 8 7 6 4 3 0 8 10 2 9 6 5 4 1 7 8 2 1 9 10 4 0 7 6 5 3 2 4 10 6 3 0 1 9 8 7 5 7 8 6 4 5 1 3 0 10 9 2 6 7 4 5 8 3 9 1 0 2 10 0 10 9 8 7 6 4 2 5 3 1 9 1 3 4 2 10 5 6 7 0 8 7 4 2 9 10 0 1 5 3 8 6 10 6 5 3 1 8 0 4 2 7 9 2 8 0 6 4 1 7 9 10 5 3 4 3 7 2 6 5 8 1 9 10 0 3 7 10 5 9 2 6 8 0 1 4 5 0 1 10 8 3 9 7 6 4 2 1 9 6 0 5 4 3 10 8 2 7 6 2 8 1 3 7 10 0 4 9 5 8 5 4 7 0 9 2 3 1 6 10 0 10 9 8 7 6 4 5 2 3 1 4 1 8 10 6 3 5 9 7 0 2 9 8 2 6 10 4 0 1 3 7 5 8 5 0 3 9 2 1 4 6 10 7 3 0 1 5 4 10 7 2 9 8 6 7 9 6 2 1 5 8 3 10 4 0 1 4 7 0 8 9 6 10 5 2 3 10 2 5 9 0 1 3 7 4 6 8 6 3 10 4 5 7 2 0 8 1 9 5 6 3 7 2 0 10 8 1 9 4 2 7 4 1 3 8 9 6 0 5 10 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Если пропустить показанные в предыдущем посте КФ ОДЛК через программу Белышева ortogon_u, вот что получим на выходе [DLK(1):1] 0 2 3 4 5 6 7 8 9 A 1 5 1 4 9 7 3 8 2 A 0 6 8 5 2 1 6 9 A 0 3 7 4 2 7 6 3 A 8 9 4 5 1 0 3 8 A 7 4 0 2 5 1 6 9 7 6 8 0 9 5 1 A 2 4 3 1 4 9 5 8 A 6 3 0 2 7 A 9 5 6 1 2 0 7 4 3 8 6 3 7 A 0 1 4 9 8 5 2 4 A 0 8 2 7 3 1 6 9 5 9 0 1 2 3 4 5 6 7 8 A [DLK(1):2] 0 2 3 4 5 6 8 9 A 7 1 4 1 7 5 8 9 2 A 6 0 3 A 9 2 0 7 1 4 8 3 6 5 5 7 6 3 0 2 1 4 9 A 8 1 3 5 A 4 8 7 6 0 2 9 7 8 0 9 A 5 3 1 2 4 6 9 0 A 1 2 4 6 3 5 8 7 2 4 8 6 9 3 A 7 1 5 0 3 5 9 7 6 A 0 2 8 1 4 6 A 1 8 3 7 5 0 4 9 2 8 6 4 2 1 0 9 5 7 3 A [DLK(1):3] 0 2 3 4 5 6 8 9 A 7 1 5 1 6 8 A 7 9 3 2 0 4 A 5 2 9 7 1 4 0 3 6 8 8 9 5 3 0 2 7 4 1 A 6 7 6 1 5 4 A 2 8 0 3 9 3 8 4 0 9 5 1 A 6 2 7 1 7 A 2 8 0 6 5 9 4 3 4 0 9 6 3 8 A 7 5 1 2 2 4 7 A 6 9 3 1 8 5 0 6 A 8 7 1 3 0 2 4 9 5 9 3 0 1 2 4 5 6 7 8 A [DLK(1):4] 0 2 3 4 5 6 9 8 A 7 1 5 1 8 0 A 3 4 6 7 2 9 A 7 2 8 3 9 1 5 0 6 4 2 6 7 3 9 0 8 4 1 A 5 8 5 6 1 4 A 7 2 9 0 3 3 4 1 A 6 5 0 9 2 8 7 7 9 5 2 8 4 6 A 3 1 0 4 A 0 9 1 8 3 7 6 5 2 9 0 A 7 2 1 5 3 8 4 6 1 3 4 6 7 2 A 0 5 9 8 6 8 9 5 0 7 2 1 4 3 A [DLK(1):5] 0 A 9 8 7 6 2 3 5 4 1 A 1 8 6 5 7 0 9 3 2 4 1 8 2 7 3 4 9 5 0 A 6 7 5 1 3 2 8 A 4 6 0 9 6 3 0 A 4 9 7 8 1 5 2 9 7 3 1 6 5 4 2 A 8 0 2 0 4 5 8 1 6 A 9 3 7 8 2 6 9 0 A 5 7 4 1 3 4 9 A 2 1 0 3 6 8 7 5 5 6 7 4 A 3 1 0 2 9 8 3 4 5 0 9 2 8 1 7 6 A [DLK(1):6] 0 A 9 8 7 6 4 2 5 3 1 4 1 3 2 6 7 5 A 9 0 8 9 5 2 7 1 8 A 6 3 4 0 5 9 7 3 0 2 8 4 1 A 6 1 6 5 0 4 A 7 3 2 8 9 A 3 0 1 9 5 2 8 7 6 4 3 0 8 A 2 9 6 5 4 1 7 8 2 1 9 A 4 0 7 6 5 3 2 4 A 6 3 0 1 9 8 7 5 7 8 6 4 5 1 3 0 A 9 2 6 7 4 5 8 3 9 1 0 2 A [DLK(1):7] 0 A 9 8 7 6 4 2 5 3 1 9 1 3 4 2 A 5 6 7 0 8 7 4 2 9 A 0 1 5 3 8 6 A 6 5 3 1 8 0 4 2 7 9 2 8 0 6 4 1 7 9 A 5 3 4 3 7 2 6 5 8 1 9 A 0 3 7 A 5 9 2 6 8 0 1 4 5 0 1 A 8 3 9 7 6 4 2 1 9 6 0 5 4 3 A 8 2 7 6 2 8 1 3 7 A 0 4 9 5 8 5 4 7 0 9 2 3 1 6 A [DLK(1):8] 0 A 9 8 7 6 4 5 2 3 1 4 1 8 A 6 3 5 9 7 0 2 9 8 2 6 A 4 0 1 3 7 5 8 5 0 3 9 2 1 4 6 A 7 3 0 1 5 4 A 7 2 9 8 6 7 9 6 2 1 5 8 3 A 4 0 1 4 7 0 8 9 6 A 5 2 3 A 2 5 9 0 1 3 7 4 6 8 6 3 A 4 5 7 2 0 8 1 9 5 6 3 7 2 0 A 8 1 9 4 2 7 4 1 3 8 9 6 0 5 A Однушечки :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Утилиту модифицировала; теперь можно делать статистику по линейкам в БД КФ ОДЛК порядка 11. А тем временем БД у меня выросла до 33951 КФ ОДЛК. Покажу статистику по первым десяти линейкам для текущего варианта БД линейка 1 - 11 линейка 2 - 365 линейка 3 - 36 линейка 4 - 810 линейка 5 - 203 линейка 6 - 239 линейка 7 - 558 линейка 8 - 200 линейка 9 - 205 линейка 10 - 430 Можно для всех 67 линеек сделать, но пока нет смысла. Вот будет БД побольше, тогда сделаю полную статистику для всех линеек. Утилита выводит все выписанные из заданной линейки квадраты. Вот, например, КФ ОДЛК из линейки 1, их пока всего 11 штук 0 2 3 5 7 9 4 6 10 8 1 2 1 5 9 3 6 10 8 4 0 7 4 7 2 8 6 1 9 0 3 10 5 6 4 9 3 10 0 5 2 7 1 8 8 6 1 2 4 10 7 3 9 5 0 1 0 8 10 9 5 2 4 6 7 3 3 5 10 1 8 7 6 9 0 2 4 10 8 0 4 5 3 1 7 2 6 9 5 9 6 7 1 4 0 10 8 3 2 7 10 4 0 2 8 3 1 5 9 6 9 3 7 6 0 2 8 5 1 4 10 0 2 3 5 9 4 10 6 7 8 1 6 1 10 2 3 7 8 5 9 0 4 4 5 2 9 10 6 0 8 3 1 7 10 4 9 3 1 8 5 2 6 7 0 2 3 0 6 4 1 7 9 10 5 8 8 9 1 7 2 5 4 10 0 3 6 7 0 4 1 8 9 6 3 5 10 2 5 6 8 4 0 10 3 7 1 2 9 1 7 6 10 5 2 9 0 8 4 3 3 10 7 8 6 0 2 1 4 9 5 9 8 5 0 7 3 1 4 2 6 10 0 2 3 5 9 6 10 8 7 4 1 3 1 4 8 5 7 2 10 9 0 6 5 6 2 1 10 4 0 9 3 8 7 7 9 10 3 0 8 1 2 5 6 4 6 8 9 10 4 2 7 0 1 5 3 10 4 0 7 3 5 8 1 6 2 9 4 3 1 9 8 10 6 5 2 7 0 8 0 5 4 6 3 9 7 10 1 2 1 7 6 0 2 9 3 4 8 10 5 2 10 7 6 1 0 5 3 4 9 8 9 5 8 2 7 1 4 6 0 3 10 0 2 3 6 9 8 10 5 4 7 1 3 1 9 5 2 6 8 10 7 0 4 8 6 2 9 5 10 1 0 3 4 7 6 7 0 3 10 4 5 2 1 8 9 2 0 5 8 4 9 7 1 10 3 6 10 8 1 7 3 5 2 4 9 6 0 7 9 4 1 8 0 6 3 2 10 5 1 5 10 4 6 3 9 7 0 2 8 5 3 6 10 0 7 4 9 8 1 2 4 10 8 2 7 1 0 6 5 9 3 9 4 7 0 1 2 3 8 6 5 10 0 2 3 8 5 6 9 4 10 7 1 6 1 9 7 10 4 3 8 2 0 5 4 0 2 5 6 1 8 9 3 10 7 8 7 10 3 0 9 1 2 5 4 6 5 3 8 0 4 10 7 1 6 2 9 7 4 1 6 3 5 10 0 9 8 2 1 9 7 10 8 2 6 3 4 5 0 10 6 5 4 9 8 2 7 0 1 3 2 5 6 9 1 7 0 10 8 3 4 3 10 4 2 7 0 5 6 1 9 8 9 8 0 1 2 3 4 5 7 6 10 0 2 3 8 7 9 10 5 6 4 1 10 1 5 7 6 4 8 3 2 0 9 1 7 2 6 5 10 0 9 3 8 4 6 0 4 3 10 7 9 2 1 5 8 8 9 0 5 4 2 7 6 10 1 3 4 8 1 2 9 5 3 0 7 10 6 5 4 9 10 8 3 6 1 0 7 2 2 3 10 4 0 8 1 7 9 6 5 7 5 6 9 3 1 4 10 8 2 0 3 10 8 0 1 6 2 4 5 9 7 9 6 7 1 2 0 5 8 4 3 10 0 2 3 10 5 4 9 8 7 6 1 7 1 4 5 3 2 8 6 10 0 9 6 7 2 8 9 0 10 1 3 4 5 10 5 0 3 6 8 4 2 9 1 7 3 6 1 9 4 10 7 5 2 8 0 8 3 7 6 1 5 2 9 0 10 4 4 9 10 7 8 1 6 0 5 3 2 5 0 9 4 10 6 3 7 1 2 8 2 4 6 1 7 9 0 10 8 5 3 1 10 8 0 2 7 5 3 4 9 6 9 8 5 2 0 3 1 4 6 7 10 0 2 4 5 3 6 8 9 10 7 1 10 1 3 9 7 8 5 6 4 0 2 5 6 2 10 9 4 0 8 3 1 7 1 5 0 3 10 7 4 2 6 8 9 2 8 9 6 4 10 7 3 1 5 0 8 0 10 7 6 5 2 1 9 4 3 4 7 1 0 8 9 6 10 2 3 5 6 3 5 4 1 2 9 7 0 10 8 7 9 6 1 0 3 10 5 8 2 4 3 10 8 2 5 0 1 4 7 9 6 9 4 7 8 2 1 3 0 5 6 10 0 2 4 7 10 9 8 5 6 3 1 7 1 3 10 5 6 2 9 4 0 8 6 9 2 8 1 7 5 10 3 4 0 5 8 10 3 9 1 0 2 7 6 4 2 6 5 9 4 0 7 8 1 10 3 10 0 9 1 3 5 4 6 2 8 7 3 4 1 5 8 2 6 0 10 7 9 8 5 0 4 2 3 10 7 9 1 6 1 3 6 0 7 10 9 4 8 5 2 4 10 7 2 6 8 3 1 0 9 5 9 7 8 6 0 4 1 3 5 2 10 0 2 4 8 5 9 3 6 10 7 1 4 1 7 2 3 6 10 9 5 0 8 1 8 2 10 6 7 0 5 3 4 9 10 7 8 3 9 1 5 2 0 6 4 2 5 9 6 4 10 7 8 1 3 0 6 9 3 0 2 5 8 1 4 10 7 3 4 1 9 8 0 6 10 7 5 2 5 3 10 4 0 8 1 7 9 2 6 7 0 6 5 10 2 9 4 8 1 3 8 10 0 1 7 4 2 3 6 9 5 9 6 5 7 1 3 4 0 2 8 10 0 2 5 8 3 7 9 6 10 4 1 2 1 10 6 9 3 4 5 7 0 8 5 9 2 7 6 1 10 0 3 8 4 8 4 0 3 10 9 1 2 5 6 7 1 0 9 2 4 10 7 8 6 3 5 6 7 3 0 2 5 8 1 4 10 9 3 5 4 10 8 0 6 9 1 7 2 10 6 1 4 5 8 0 7 9 2 3 4 3 6 9 7 2 5 10 8 1 0 7 10 8 5 1 4 2 3 0 9 6 9 8 7 1 0 6 3 4 2 5 10 There are 11 squares in the rule 1 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Господа! Я тут старательно пишу, пишу... всё, что у меня в голове накопилось про ОДЛК 11-го порядка. А вы старательно молчите. Как было бы хорошо, если бы вы присоединились к обсуждению проблемы! Как говорится: одна голова - хорошо, а две - лучше. Вы можете писать по-английски, если по-русски вам трудно писать. На ваши вопросы по-английски я буду отвечать тоже по-английски. Итак, жду вторую голову :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Вот посмотрите, как написал citerra о проблемах https://boinc.ru/forum/topic/proekt-gerasimhome/?part=54#postid-3044 Не хватает времени у разработчиков. Есть такой сайт - Я плакал. Так вот: я плакала :) Как написал, а! Как написал! Оказывается, про тотальный поиск в проектах ОДЛК и ODLK1 знает. А про "бронепоезд на запасном пути" - как, а! А это --- ... но хочется решать интересные проблемы, те же новые структуры Я плакала... А это --- Сейчас заняты как исследовать квадраты больших порядков ( 11,12 и т.д.), алгоритмы генерации, области поиска, распределение заданий между проектами. Обалденно интересно! То есть мы накануне запуска BOINC-проектов по исследованию квадратов больших порядков. Вто-вот... и взлетит :) И господин Ватутин напишет: "Ну что там у Макаровой - курам смех. 1000 лет будет считать в один поток" ))))) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Цитата А это ортогональная пара ДЛК 11-го порядка - SODLS И вот второе очевидное направление поиска. У Harry White есть программа генерации SODLS 11-го порядка (и не только 11-го). Это готовый генератор ОДЛК! Один большой минус у этой программы - генерируется много изоморфных SODLS. Я уже немного покрутила эту программу в том варианте, который даёт ассоциативные SODLS. Некоторое количество уникальных SODLS найдено. Вопрос о количестве всех SODLS и DSODLS 11-го порядка открыт. Harry White не захотел заниматься этой проблемой, она ему не интересна. Francis Gaspalou ничего не ответил на моё предложение исследовать этот вопрос. Итак, два направления поиска ОДЛК 11-го порядка я уже указала, они лежат на поверхности, даже и изобретать ничего не надо. Включайте технику и - вперёд! Да, к сожалению, у меня один ПК с двумя ядрами. Но это не вина моя, а беда. Нехорошо смеяться над бедой. Зато у меня есть много интересных алгоритмов для поиска ОДЛК 9, 10, 11 порядков. Никаких проблем с разработкой алгоритмов, с генерацией заданий! Могла бы загрузить работой 10 BOINC-проектов легко! Три BOINC-проекта в своё время загрузила. Два из них работают, третий пока стоит. Долго ли будет стоять - одному Богу известно. Как загрузить четвёртый BOINC-проект, не знаю. Все мои попытки безуспешны. Платформу yoyo@home мне давно рекомендовали. Ну, вышла я на эту платформу, предложила свой проект https://www.rechenkraft.net/forum/viewtopic.php?f=16&t=17547&sid=df5ca590e50637f77f418e7a19682410 И что? А ничего! Им нужен готовый проект под BOINC, который они разместят на своей платформе. Но у меня нет готового проекта под BOINC-платформу. Господа! Я продолжаю поиск возможности запуска проекта БД КФ ОДЛК порядка 11 на BOINC-платформе. Подскажите, пожалуйста, где можно ещё поискать. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Интересный факт: все ассоциативные SODLS 11-го порядка являются DSODLS. И не только 11-го порядка. У меня гипотеза такая: все ассоциативные SODLS порядка n являются DSODLS. Доказательства нет, но и контрпример я пока не нашла. В предыдущем посте на иллюстрации показан ассоциативный SODLS 11-го порядка, он является также DSODLS. Программа Harry White легко генерирует ассоциативные SODLS 11-го порядка. А вот не ассоциативные не очень легко, но они тоже есть. Я один такой SODLS 11-го порядка нашла раньше (не по программе Harry White). My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Это я уже цитировала. Повторю. Взято отсюда https://boinc.ru/forum/topic/novosti-proekta-rakesearch/?part=6#postid-2042 Цитирую В тех приложениях, что сделал Даниэль, исходный код легко перекомпилируется для поиска квадратов с 11 по 16 порядка. Вот оригинальный текст с переводом: Написал форумчанин на boinc.ru И этот программист Даниэль тоже, наверное, сделал программы для поиска "перестановочных ОДЛК" больших порядков. Ну, их можно понять: они очень далеки от ДЛК и не понимают всей сути - чего надо искать. Форумчанину с boinc.ru, автору процитированного сообщения, я долго пыталась объяснить, что "перестановочные ОДЛК" 11-го порядка искть не надо, ибо они известны. Он на полном серьёзе заявил, что такие ОДЛК ещё никто не искал и поэтому никто не знает, существуют они или нет. Даже когда я показала ему эти "перестановочные ОДЛК" 11-го порядка, он их не увидел :) Даниэль, видимо, отличный программист, но вряд ли знаком с теорией ЛК/ДЛК/ОДЛК. Ему сказали: искать "перестановочные ОДЛК", вот он и пишет программы для такого поиска - аж до порядка 16 :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Не ассоциативный SODLS 11-го порядка, найденный мной, показан тут https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6121 Дублирую 0 9 4 5 7 10 8 6 2 3 1 6 1 8 0 5 9 10 3 4 2 7 5 10 2 7 1 8 4 0 3 6 9 2 5 9 3 6 7 1 4 10 8 0 10 3 5 8 4 6 0 9 7 1 2 4 0 1 2 3 5 7 8 9 10 6 9 2 0 10 8 3 6 1 5 7 4 1 4 6 9 10 2 3 7 0 5 8 3 7 10 6 0 1 9 2 8 4 5 8 6 7 4 2 0 5 10 1 9 3 7 8 3 1 9 4 2 5 6 0 10 Я начинала писать программу построения SODLS 11-го порядка, но не дописала её. Harry тогда написал о своей программе, ну я и начала по его программе генерировать SODLS. Однако, как уже отмечено, с не ассоциативными SODLS в программе Harry туго. А моя программа должна генерировать и не ассоциативные SODLS. Надо её дописать. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Цитата Показываю своё творчество Вот эту программу, пожалуй, надо дописать. Правда, есть проблема, о которой сказано в цитате. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Запустила сейчас программу Harry для поиска не ассоциативного SODLS 11-го порядка SODLS order? 11 Make SSSOLDS, y (yes) or n (no)? n .. writing SODLS to file SODLS11.txt Second \diagonal value, (2..10)? 2 Покручу немножко, может, найдёт хоть одно решение. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
У Harry White есть ещё одна программа, которая генерирует SODLS. Я рассказывала об этом в теме "ОДЛК для порядков n>10". Вот сейчас попробовала эту программу для порядка 11, моментально нашёлся такой SODLS 0 1 2 3 4 5 6 7 8 9 10 9 10 0 1 2 3 4 5 6 7 8 7 8 9 10 0 1 2 3 4 5 6 5 6 7 8 9 10 0 1 2 3 4 3 4 5 6 7 8 9 10 0 1 2 1 2 3 4 5 6 7 8 9 10 0 10 0 1 2 3 4 5 6 7 8 9 8 9 10 0 1 2 3 4 5 6 7 6 7 8 9 10 0 1 2 3 4 5 4 5 6 7 8 9 10 0 1 2 3 2 3 4 5 6 7 8 9 10 0 1 Этот ДЛК не только ассоциативный, но и пандиагональный, то есть ultra. Супер! Кстати, пандиагональные ДЛК 11-го порядка тоже весьма интересны! Подумайте о них на досуге :) Вот второй SODLS, найденный по этой же программе 0 2 3 4 10 7 9 8 6 5 1 3 1 6 7 9 8 4 5 10 0 2 1 8 2 9 7 4 5 10 3 6 0 5 0 8 3 2 10 7 4 9 1 6 7 6 5 10 4 1 2 9 0 3 8 6 3 9 8 0 5 10 2 1 7 4 2 7 10 1 8 9 6 0 5 4 3 4 9 1 6 3 0 8 7 2 10 5 10 4 7 0 5 6 3 1 8 2 9 8 10 0 5 6 2 1 3 4 9 7 9 5 4 2 1 3 0 6 7 8 10 Этот SODLS только ассоциативный (не пандиагональный). Интересно, а третий SODLS какой найдётся? :) Сейчас попробую. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Вот 0 10 9 8 7 6 5 4 3 2 1 2 1 0 10 9 8 7 6 5 4 3 4 3 2 1 0 10 9 8 7 6 5 6 5 4 3 2 1 0 10 9 8 7 8 7 6 5 4 3 2 1 0 10 9 10 9 8 7 6 5 4 3 2 1 0 1 0 10 9 8 7 6 5 4 3 2 3 2 1 0 10 9 8 7 6 5 4 5 4 3 2 1 0 10 9 8 7 6 7 6 5 4 3 2 1 0 10 9 8 9 8 7 6 5 4 3 2 1 0 10 Программа пишет "ultramagic", ну да: ассоциативный и пандиагональный. В первом случае SODLS тоже ассоциативный и пандиагональный, но ассоциативность - в моём определении; Harry называет такие квадраты центрально-симметричными; у меня нет отдельно центрально-симметричных и отдельно ассоциативных, это один класс квадратов - ассоциативные. Квадрат в первом случае имеет ассоциативную КФ второго формата, вот она 0 7 8 5 3 6 9 2 10 4 1 4 1 6 7 5 10 3 9 0 2 8 5 0 2 10 6 9 8 1 3 7 4 10 5 1 3 9 8 2 4 6 0 7 8 9 5 2 4 7 0 10 1 6 3 1 2 3 4 0 5 10 6 7 8 9 7 4 9 0 10 3 6 8 5 1 2 3 10 4 6 8 2 1 7 9 5 0 6 3 7 9 2 1 4 0 8 10 5 2 8 10 1 7 0 5 3 4 9 6 9 6 0 8 1 4 7 5 2 3 10 Но эта КФ не пандиагональна! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Цитата Запустила сейчас программу Harry для поиска не ассоциативного SODLS 11-го порядка Два часа программа работала и не нашла ни одного решения. Прерываю. Для не ассоциативных SODLS 11-го порядка нужна другая программа. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Я пока знаю два уникальных пандиагональных ОДЛК 11-го порядка 0 1 2 3 4 5 6 7 8 9 10 9 10 0 1 2 3 4 5 6 7 8 7 8 9 10 0 1 2 3 4 5 6 5 6 7 8 9 10 0 1 2 3 4 3 4 5 6 7 8 9 10 0 1 2 1 2 3 4 5 6 7 8 9 10 0 10 0 1 2 3 4 5 6 7 8 9 8 9 10 0 1 2 3 4 5 6 7 6 7 8 9 10 0 1 2 3 4 5 4 5 6 7 8 9 10 0 1 2 3 2 3 4 5 6 7 8 9 10 0 1 0 7 3 10 6 2 9 5 1 8 4 5 1 8 4 0 7 3 10 6 2 9 10 6 2 9 5 1 8 4 0 7 3 4 0 7 3 10 6 2 9 5 1 8 9 5 1 8 4 0 7 3 10 6 2 3 10 6 2 9 5 1 8 4 0 7 8 4 0 7 3 10 6 2 9 5 1 2 9 5 1 8 4 0 7 3 10 6 7 3 10 6 2 9 5 1 8 4 0 1 8 4 0 7 3 10 6 2 9 5 6 2 9 5 1 8 4 0 7 3 10 Первый получен по программе Harry White, второй построен мной вручную. Посмотрите-ка, какие это чудесные квадратики Order? 11
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
2 diagonal Latin
1 associative
2 pandiagonal
1 ultramagic
1 center symmetric
1 nfr
1 natural \diagonal
1 orthogonal pair
2 self-orthogonalЦелый букет свойств! КФ этих ОДЛК во втором формате 0 3 8 9 7 2 10 5 4 6 1 6 1 4 7 8 3 5 0 10 2 9 7 10 2 0 6 4 1 9 3 8 5 10 6 9 3 1 0 8 4 7 5 2 2 9 10 8 4 1 0 6 5 3 7 4 0 1 2 3 5 7 8 9 10 6 3 7 5 4 10 9 6 2 0 1 8 8 5 3 6 2 10 9 7 1 4 0 5 2 7 1 9 6 4 10 8 0 3 1 8 0 10 5 7 2 3 6 9 4 9 4 6 5 0 8 3 1 2 7 10 0 7 8 5 3 6 9 2 10 4 1 4 1 6 7 5 10 3 9 0 2 8 5 0 2 10 6 9 8 1 3 7 4 10 5 1 3 9 8 2 4 6 0 7 8 9 5 2 4 7 0 10 1 6 3 1 2 3 4 0 5 10 6 7 8 9 7 4 9 0 10 3 6 8 5 1 2 3 10 4 6 8 2 1 7 9 5 0 6 3 7 9 2 1 4 0 8 10 5 2 8 10 1 7 0 5 3 4 9 6 9 6 0 8 1 4 7 5 2 3 10 Эти ОДЛК входят в Топ-6 (смотрите выше в теме). Вот такие пандиагональные квадраты! PS. Для тех, кто не знает, что такое пандиагональный ДЛК. Это такой ДЛК, в котором во всех разломанных диагоналях (обоих направлений) элементы различны между собой. Для порядка 10 не существует ни ассоциативных, ни пандиагональных ДЛК. Я разработала алгоритм для псевдоассоциативных ДЛК 10-го порядка. А вот псевдопандиагональные ДЛК 10-го порядка у меня почему-то не получились, хотя пыталась написать генератор таких ДЛК. Может быть, банально ошиблась и программа у меня зашла в тупик. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
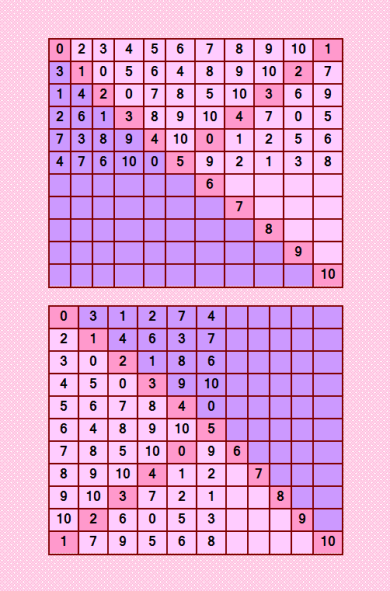
Оказывается, эти замечательные идеальные (то есть одновременно ассоциативные и пандиагональные) квадратики были известны мне в 2008 году. Успела за 12 лет очень хорошо забыть, но... не совсем. В памяти жёстко записалось (на жёстком диске!), что должно быть построение магических квадратов 11-го порядка с помощью латинских квадратов. И я нашла это построение! Смотрим мою статью ПОСТРОЕНИЕ ИДЕАЛЬНЫХ МАГИЧЕСКИХ КВАДРАТОВ НЕЧЁТНОГО ПОРЯДКА С ПОМОЩЬЮ ЛАТИНСКИХ КВАДРАТОВ http://www.klassikpoez.narod.ru/idlat.htm Вот они - эти чудесные квадратики, только в другом виде записаны  Кстати, наглядный пример "перестановочных ОДЛК", здесь хорошо это видно. И далее в статье показан идеальный магический квадрат, построенный из данной пары ортогональных ДЛК методом латинских квадратов. PS. А получила я эти квадратики тогда так: взяла известный идеальный магический квадрат 11-го порядка и разложила его на латинские квадраты. Никаких программ построения ортогональных ДЛК 11-го порядка у меня тогда, разумеется, не было. А магические квадраты я уже умела строить - всякие. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Моя БД КФ ОДЛК порядка 11 выросла до 35300 КФ ОДЛК. Новых рекордов не найдено. Пока генерирую SODLS программой Harry White, но очень много изоморфных SODLS генерируется, поэтому прирост БД небольшой сейчас. Надо начинать разработку нового алгоритма поиска ОДЛК. Алгоритм этот я уже выше указала: это поиск во множестве ассоциативных ДЛК. Надо написать генератор ассоциативных ДЛК. И далее - включаем технику, господа! Как говорится: дело техники, и ничего более!! Никаких премудростей и особенных эвристик. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Итак, линейка 16 - одна из трёх линеек, содержащих ассоциативные ДЛК 11-го порядка. Показываю три первых и три последних КФ ОДЛК из линейки 16 на данный момент 0 2 3 4 5 6 7 8 9 10 1 5 1 4 9 7 3 8 2 10 0 6 8 5 2 1 6 9 10 0 3 7 4 2 7 6 3 10 8 9 4 5 1 0 3 8 10 7 4 0 2 5 1 6 9 7 6 8 0 9 5 1 10 2 4 3 1 4 9 5 8 10 6 3 0 2 7 10 9 5 6 1 2 0 7 4 3 8 6 3 7 10 0 1 4 9 8 5 2 4 10 0 8 2 7 3 1 6 9 5 9 0 1 2 3 4 5 6 7 8 10 0 2 3 4 5 6 8 9 10 7 1 5 1 6 8 10 7 9 3 2 0 4 10 5 2 9 7 1 4 0 3 6 8 8 9 5 3 0 2 7 4 1 10 6 7 6 1 5 4 10 2 8 0 3 9 3 8 4 0 9 5 1 10 6 2 7 1 7 10 2 8 0 6 5 9 4 3 4 0 9 6 3 8 10 7 5 1 2 2 4 7 10 6 9 3 1 8 5 0 6 10 8 7 1 3 0 2 4 9 5 9 3 0 1 2 4 5 6 7 8 10 0 2 3 4 5 6 9 8 10 7 1 6 1 8 10 9 3 7 2 4 0 5 4 7 2 5 6 10 0 9 3 1 8 7 5 1 3 2 8 10 4 0 6 9 8 6 5 0 4 9 2 3 1 10 7 10 8 4 9 7 5 3 1 6 2 0 3 0 9 7 8 1 6 10 5 4 2 1 4 10 6 0 2 8 7 9 5 3 2 9 7 1 10 0 4 5 8 3 6 5 10 6 8 3 7 1 0 2 9 4 9 3 0 2 1 4 5 6 7 8 10 . . . . . 0 2 10 7 3 8 4 9 6 5 1 3 1 5 9 7 6 10 8 4 0 2 4 6 2 5 1 7 8 0 3 10 9 2 8 9 3 5 10 1 4 7 6 0 5 9 8 0 4 1 2 6 10 7 3 6 7 1 8 10 5 0 2 9 3 4 7 3 0 4 8 9 6 10 2 1 5 10 4 3 6 9 0 5 7 1 2 8 1 0 7 10 2 3 9 5 8 4 6 8 10 6 2 0 4 3 1 5 9 7 9 5 4 1 6 2 7 3 0 8 10 0 2 10 7 5 4 8 6 9 3 1 10 1 6 9 3 8 4 2 7 0 5 4 8 2 1 9 0 10 5 3 6 7 2 6 8 3 1 7 0 4 10 5 9 6 0 5 10 4 9 2 8 1 7 3 8 9 4 0 7 5 3 10 6 1 2 7 3 9 2 8 1 6 0 5 10 4 1 5 0 6 10 3 9 7 2 4 8 3 4 7 5 0 10 1 9 8 2 6 5 10 3 8 6 2 7 1 4 9 0 9 7 1 4 2 6 5 3 0 8 10 0 2 10 9 3 8 4 5 7 6 1 10 1 8 7 2 3 9 6 4 0 5 6 7 2 0 5 4 10 9 3 1 8 8 6 5 3 9 1 0 4 10 2 7 1 5 9 10 4 0 2 8 6 7 3 4 0 1 8 7 5 3 2 9 10 6 7 3 4 2 8 10 6 0 1 5 9 3 8 0 6 10 9 1 7 5 4 2 2 9 7 1 0 6 5 10 8 3 4 5 10 6 4 1 7 8 3 2 9 0 9 4 3 5 6 2 7 1 0 8 10 There are 1721 squares in the rule 16 Все показанные ОДЛК ассоциативные. Понятно, что в линейке могут быть и не ассоциативные ОДЛК. Линейка содержит на данный момент 1721 КФ ОДЛК, это довольно много для существующего ядра БД. КФ представлены во втором формате. Проверка всех ОДЛК из линейки 16 утилитой Harry White Order? 11
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
1721 diagonal Latin
1696 associative
1721 natural \diagonal
1580 self-orthogonalВидим: 1696 ассоциативных, 1580 self-orthogonal. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
А этот ассоциативный ДЛК 11-го порядка принадлежит другой линейке - 61-й  В этом представлении утилита Harry White называет ДЛК центрально-симметричным. Если же дать утилите КФ этого ДЛК во втором формате 0 7 8 5 3 6 9 2 10 4 1 4 1 6 7 5 10 3 9 0 2 8 5 0 2 10 6 9 8 1 3 7 4 10 5 1 3 9 8 2 4 6 0 7 8 9 5 2 4 7 0 10 1 6 3 1 2 3 4 0 5 10 6 7 8 9 7 4 9 0 10 3 6 8 5 1 2 3 10 4 6 8 2 1 7 9 5 0 6 3 7 9 2 1 4 0 8 10 5 2 8 10 1 7 0 5 3 4 9 6 9 6 0 8 1 4 7 5 2 3 10 она назовёт этот ДЛК ассоциативным. Уловили нюанс? :) Я уже писала об этом нюансе. По моему определению оба эти ДЛК ассоциативные. Надо начинать писать генератор ассоциативных ДЛК 11-го порядка. Начну с линейки 16. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Natalia Makarova Send message Joined: 6 Apr 17 Posts: 15279 Credit: 0 RAC: 0 |
Иллюстрация для сравнения 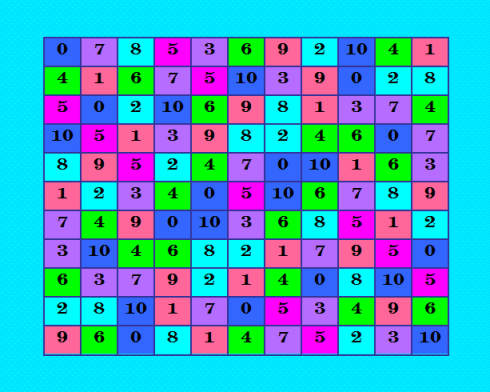 Это КФ ассоциативного ДЛК, показанного в предыдущем посте. В чём разница? Разница в том, что в КФ ассоциативного ДЛК сумма симметричных относительно центра квадрата элементов равна (n-1) (n - порядок квадрата). КФ ассоциативного ДЛК центрально-симметрична, центрально-симметричный ДЛК ассоциативен. В общем, оба они и центрально-симметричные, и ассоциативные, и не надо их разделять на центрально-симметричные и ассоциативные. Есть один термин для таких ДЛК - ассоциативные. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
©2025 (C) Progger