Я начинаю новый проект - БД КФ ОДЛК порядка 11, о чём объявлено тут
https://boinc.progger.info/odlk/forum_thread.php?id=175

Пока это ручной проект. Может быть, он таким и останется, потому что мне трудно найти желающих запустить проект на платформе BOINC.
Я уже столкнулась с этой трудностью в работе над проектом БД КФ ОДЛК порядка 9.
Но если у вас будут предложения по запуску проекта на BOINC-платформе, я готова рассмотреть их.

Итак, начинать всегда непросто.
БД КФ ОДЛК порядка 10 начиналась с этих пар ОДЛК



Эти пары ОДЛК были найдены в 1992 году.
Прошло 28 лет.
По меркам одной человеческой жизни это много.
Прогресс за эти 28 лет есть. В данный момент БД порядка 10 содержит более 10 миллионов КФ ОДЛК.
Однако одной человеческой жизни вряд ли хватит для полного решения этой проблемы.
Безусловно развитие техники позволит в дальнейшем решить эту задачу до конца.
Мы уже многое узнали об ОДЛК порядка 10.
Теперь у нас есть аналогия. Аналогия - сильнейшая вещь!
И я приступаю к составлению БД КФ ОДЛК порядка 11.
Да, эта проблема трудно решаема. Это всем понятно. Но частично она решаема, так же, как и проблема БД КФ ОДЛК порядка 10.
Будем смотреть на ОДЛК порядка 11. Это интересно! Не просто смотреть, а пристально смотреть, то есть исследовать.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Господа!
Если вы знаете интересные статьи и/или результаты по объявленному проекту, прошу вас сообщить о них.
Я имею на данный момент небольшое ядро БД порядка 11, состоящее из 28578 КФ ОДЛК.
Это количество постоянно увеличивается, то есть процесс наращивания БД легко запустить.
Далее об этом будет рассказано подробно.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Цитата

Встречайте: полная система взаимно ортогональных ЛК 11-го порядка, построенная вручную методом циклического сдвига

№1
0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 0
2 3 4 5 6 7 8 9 10 0 1
3 4 5 6 7 8 9 10 0 1 2
4 5 6 7 8 9 10 0 1 2 3
5 6 7 8 9 10 0 1 2 3 4
6 7 8 9 10 0 1 2 3 4 5
7 8 9 10 0 1 2 3 4 5 6
8 9 10 0 1 2 3 4 5 6 7
9 10 0 1 2 3 4 5 6 7 8
10 0 1 2 3 4 5 6 7 8 9

№2
0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 0 1
4 5 6 7 8 9 10 0 1 2 3
6 7 8 9 10 0 1 2 3 4 5
8 9 10 0 1 2 3 4 5 6 7
10 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 0
3 4 5 6 7 8 9 10 0 1 2
5 6 7 8 9 10 0 1 2 3 4
7 8 9 10 0 1 2 3 4 5 6
9 10 0 1 2 3 4 5 6 7 8

№3
0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

№4
0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 0 1 2 3
8 9 10 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 0
5 6 7 8 9 10 0 1 2 3 4
9 10 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 0 1
6 7 8 9 10 0 1 2 3 4 5
10 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 0 1 2
7 8 9 10 0 1 2 3 4 5 6

№5
0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 0 1 2 3 4
10 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 0 1 2 3
9 10 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 0 1 2
8 9 10 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 0 1
7 8 9 10 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 0
6 7 8 9 10 0 1 2 3 4 5

№6
0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 0
7 8 9 10 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 0 1
8 9 10 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 0 1 2
9 10 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 0 1 2 3
10 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 0 1 2 3 4

№7
0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 0 1 2
10 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 0 1
9 10 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 0
8 9 10 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 0 1 2 3

№8
0 1 2 3 4 5 6 7 8 9 10
8 9 10 0 1 2 3 4 5 6 7
5 6 7 8 9 10 0 1 2 3 4
2 3 4 5 6 7 8 9 10 0 1
10 0 1 2 3 4 5 6 7 8 9
7 8 9 10 0 1 2 3 4 5 6
4 5 6 7 8 9 10 0 1 2 3
1 2 3 4 5 6 7 8 9 10 0
9 10 0 1 2 3 4 5 6 7 8
6 7 8 9 10 0 1 2 3 4 5
3 4 5 6 7 8 9 10 0 1 2

№9
0 1 2 3 4 5 6 7 8 9 10
9 10 0 1 2 3 4 5 6 7 8
7 8 9 10 0 1 2 3 4 5 6
5 6 7 8 9 10 0 1 2 3 4
3 4 5 6 7 8 9 10 0 1 2
1 2 3 4 5 6 7 8 9 10 0
10 0 1 2 3 4 5 6 7 8 9
8 9 10 0 1 2 3 4 5 6 7
6 7 8 9 10 0 1 2 3 4 5
4 5 6 7 8 9 10 0 1 2 3
2 3 4 5 6 7 8 9 10 0 1

№10
0 1 2 3 4 5 6 7 8 9 10
10 0 1 2 3 4 5 6 7 8 9
9 10 0 1 2 3 4 5 6 7 8
8 9 10 0 1 2 3 4 5 6 7
7 8 9 10 0 1 2 3 4 5 6
6 7 8 9 10 0 1 2 3 4 5
5 6 7 8 9 10 0 1 2 3 4
4 5 6 7 8 9 10 0 1 2 3
3 4 5 6 7 8 9 10 0 1 2
2 3 4 5 6 7 8 9 10 0 1
1 2 3 4 5 6 7 8 9 10 0

У кого есть пакет Maple, проверьте.

Как видим, в полной системе только два ЛК не являются ДЛК: №1 и №10.
Подчёркиваю: это взаимно ортогональные ДЛК.
Так что, здесь уже имеется куча ортогональных пар ДЛК.

Да, порядок 11 интересен тем, что 11 - простое число и поэтому для данного порядка существует полная система MOLS, состоящая из 10 ЛК, из которых 8 являются ДЛК.
В приведённой цитате вы видите полную систему MOLS 11-го порядка, составленную мной вручную методом циклического сдвига.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

У меня имеется богатый инструментарий, созданный программистами Белышевым, Harry White и Tomas Brada.
Этот инструментарий даёт мне возможность составлять БД и исследовать новые решения.
Огромное спасибо этим замечательным программистам!
И приглашаю их в мой проект. Работы хватит всем.

Персональное приглашение Progger.
Progger, ау!
Может быть, этот проект заинтересует вас и вы запустите его в BOINC-платформе.
С предложением по проекту БД КФ ОДЛК порядка 9 я к вам обращалась в письме.
Ответа не получила.
Ну, конечно, вы подумали: "Какой смысл запускать проект, который уже запущен на BOINC-платформе?"
Смысл есть, я неоднократно писала об этом.
Но... не хочется дублировать.
Хорошо. Теперь предлагается совершенно новый проект.
Тоже не хочется? :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Возьмём группу MODLS 11-го порядка, состоящую из 8 взаимно ортогональных ДЛК, и с помощью утилиты Harry White составим таблицу ортогональных пар в этой группе

2:  1
3:  1 2
4:  1 2 3
5:  1 2 3 4
6:  1 2 3 4 5
7:  1 2 3 4 5 6
8:  1 2 3 4 5 6 7

Теперь мы можем изобразить эту группу ОДЛК в виде графа с 8 вершинами и 28 рёбрами.
Покажу две иллюстрации. Первая нарисована в программе Gephi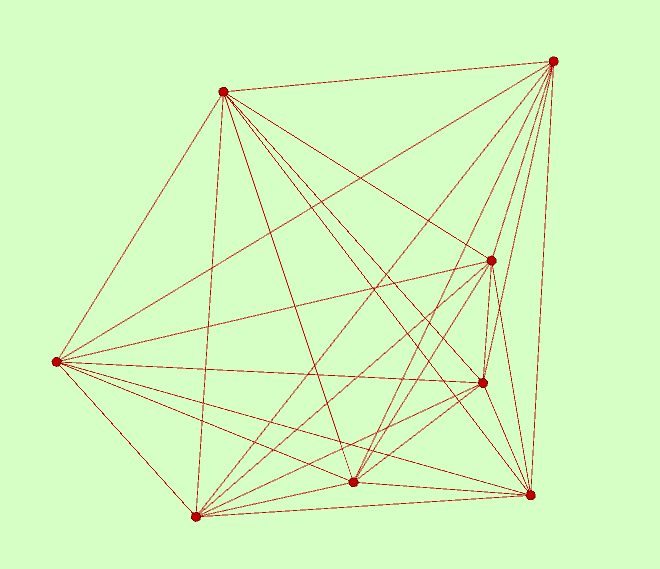



Вторая нарисована вручную, здесь хороша симметрия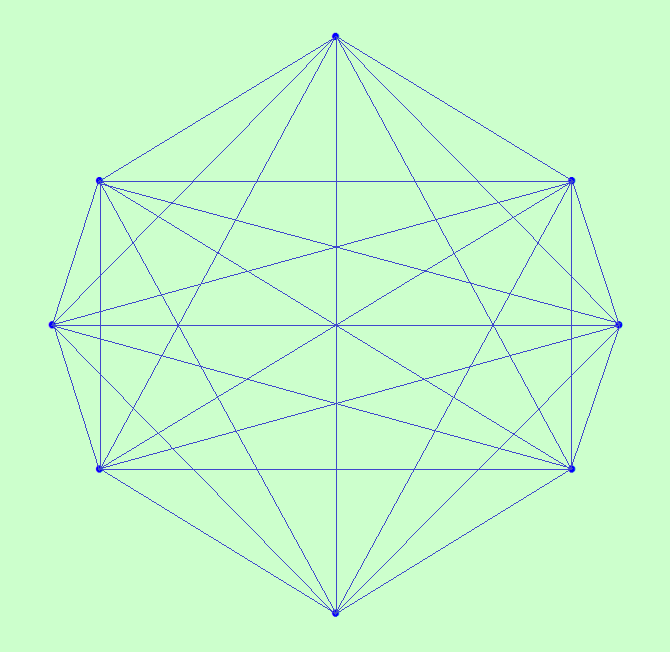



Можно нарисовать ещё более симметрично, взяв правильный восьмиугольник и проведя в нём все диагонали.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Максимальный размер группы MODLS порядка n мы видим в статье OEIS https://oeis.org/A328873
Там есть следующие оценки

a(10) >= 2; a(11) >= 8; a(12) >= 2; a(13) >= 10; a(14) >= 2; a(15) >= 4. - Natalia Makarova, Sep 03 2020

Я думаю, что a(11)=8, но у меня нет доказательства этой гипотезы.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Первый квадратик 11-го порядка (он из полной системы MOLS), который я проверила на ОДЛК программой Белышева ortogon_u



Этот ДЛК ассоциативный, пандиагональный (то есть ultra) и self orthogonal.
Раскраской показана ассоциативность.

Протокол работы программы Белышева

Проверка ДЛК11 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 4523
Соквадратов:     19139
Время в сек:     4250

Итак, показанный ДЛК 11-го порядка имеет 19139 ортогональных диагональных соквадратов.
Это не максимальное количество ОДЛК от одного ДЛК, известное мне на данный момент.
Дальше покажу Топ-6 групп ОДЛК 11-го порядка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот он - рекордный на данный момент ДЛК, который имеет 32462 ортогональных диагональных соквадрата

 0  9  4  5  7 10  8  6  2  3  1
 6  1  8  0  5  9 10  3  4  2  7
 5 10  2  7  1  8  4  0  3  6  9
 2  5  9  3  6  7  1  4 10  8  0
10  3  5  8  4  6  0  9  7  1  2
 4  0  1  2  3  5  7  8  9 10  6
 9  2  0 10  8  3  6  1  5  7  4
 1  4  6  9 10  2  3  7  0  5  8
 3  7 10  6  0  1  9  2  8  4  5
 8  6  7  4  2  0  5 10  1  9  3
 7  8  3  1  9  4  2  5  6  0 10

Этот ДЛК имеет 4828 диагональных трансверсалей (в дальнейшем буду писать: Д-трансверсалей) и 20763 общих трансверсалей.
Квадрат нашёл Tomas Brada, смотрите сообщение
https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4149

Этот ДЛК пока лидирует и по количеству Д-трансверсалей.
Смотрим последовательность OEIS https://oeis.org/A287648

Дальше продолжу Топ-6 групп ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Продолжаю Топ-6 групп ОДЛК 11-го порядка

№2
DLK(30198)
0 2 5 7 8 9 10 3 6 4 1
7 1 3 5 6 8 4 10 0 2 9
10 6 2 4 5 7 9 1 3 8 0
5 9 10 3 0 6 2 4 7 1 8
1 5 8 9 4 10 0 6 2 7 3
4 0 1 2 3 5 8 9 10 6 7
2 7 9 1 10 3 6 8 4 0 5
8 10 0 6 1 2 5 7 9 3 4
6 4 7 0 9 1 3 5 8 10 2
3 8 4 10 7 0 1 2 5 9 6
9 3 6 8 2 4 7 0 1 5 10
4813 Д-трансверсалей

№3 
DLK(26914)
0 3 8 9 7 2 10 5 4 6 1
6 1 4 7 8 3 5 0 10 2 9
7 10 2 0 6 4 1 9 3 8 5
10 6 9 3 1 0 8 4 7 5 2
2 9 10 8 4 1 0 6 5 3 7
4 0 1 2 3 5 7 8 9 10 6
3 7 5 4 10 9 6 2 0 1 8
8 5 3 6 2 10 9 7 1 4 0
5 2 7 1 9 6 4 10 8 0 3
1 8 0 10 5 7 2 3 6 9 4
9 4 6 5 0 8 3 1 2 7 10
4665 Д-трансверсалей

№4
DLK(24593)
0 7 3 8 5 2 10 9 6 4 1
5 1 6 4 7 3 8 10 0 2 9
6 5 2 10 0 4 9 1 3 8 7
1 10 5 3 9 0 2 4 7 6 8
8 2 9 5 4 1 0 6 10 7 3
9 8 7 6 10 5 3 2 1 0 4
10 4 1 0 8 7 6 3 9 5 2
3 0 4 9 6 8 1 7 2 10 5
4 3 10 7 2 9 5 0 8 1 6
2 6 8 1 3 10 7 5 4 9 0
7 9 0 2 1 6 4 8 5 3 10
4675 Д-трансверсалей

№5
DLK(19139)
0 7 8 5 3 6 9 2 10 4 1
4 1 6 7 5 10 3 9 0 2 8
5 0 2 10 6 9 8 1 3 7 4
10 5 1 3 9 8 2 4 6 0 7
8 9 5 2 4 7 0 10 1 6 3
1 2 3 4 0 5 10 6 7 8 9
7 4 9 0 10 3 6 8 5 1 2
3 10 4 6 8 2 1 7 9 5 0
6 3 7 9 2 1 4 0 8 10 5
2 8 10 1 7 0 5 3 4 9 6
9 6 0 8 1 4 7 5 2 3 10
4523 Д-трансверсалей

№6
DLK(18530)
0 4 9 6 3 8 7 2 10 5 1
4 1 0 8 10 7 3 9 5 2 6
9 0 2 1 7 6 8 5 3 10 4
6 8 1 3 2 10 5 4 9 0 7
3 10 7 2 4 9 0 8 1 6 5
8 7 6 10 9 5 2 1 0 4 3
2 9 5 4 8 1 6 10 7 3 0
10 5 3 9 1 0 4 7 6 8 2
5 2 10 0 6 4 1 3 8 7 9
1 6 4 7 5 3 10 0 2 9 8
7 3 8 5 0 2 9 6 4 1 10
4603 Д-трансверсалей

У Tomas Brada Топ-10 групп ОДЛК 11-го порядка

C1WSBL9yyhZmMTYSR5Fc8MSFU # 500 dtrans, 38 mates
Cxnb7rE3MdxM5afWEXYU41a1D5 # 533 dtrans, 38 mates
Cidd7mMU8d6NoGE9AhztKKdA9 # 550 dtrans, 47 mates
CAZRkazvwU9Po3vuRuswAgTj4 # 453 dtrans, 127 mates
CKm3qs57ahrTHAjZvEdUjyYx # 4603 dtrans, 18530 mates
CkWiTnTuCKwKk1AjqYvVT9kme3 # 4523 dtrans, 19139 mates
CFcPGHszAkh4MBHsnfDtAJqz5 # 4675 dtrans, 24593 mates
CWPTKSidjqhVrXPHRg8fVz9N4W3 # 4665 dtrans, 26914 mates
CsRcX7AMxNsp9r9mUwANzrWa # 4813 dtrans, 30198 mates
CBdLXkuMuUsLR2UMw31FGHxG64 # 4828 dtrans, 32462 mates

отсюда
https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4149

Квадраты №2 - №6 в моём списке мы нашли независимо друг от друга.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Система Tomas Brada кодирования ДЛК и конвертирования описана здесь
https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4132

Цитата

Diagonal Latin Square converter and normalizer
Windows: https://boinc.tbrada.eu/download/dlkconv.exe
Source on: https://github.com/tomasbrod/tbboinc

dlkconv.exe: (input-spec) [input] [(output-spec) [output]]
** Diagonal Latin Square converter and normalizer **
input-spec: Endoded/compressed (e), Alphanumeric (a), stdin (s) File (f).
 Encoded input can be passed immediately on command line.
 Othervise a NxN matrix of decimal numbers, or Alphanumeric (a) must be
 passed via stdin or file. Multiple orders (N) may be mixed on input.
 Empty lines and (one) trailing spaces are ignored.
output-spec: (e)(a)(f), stdout (s), Compact (c), Diagonal (d)
 LS normalized on first row are written to stdout by default.
 Space between output squares are ommited in Compact (c) mode.
 With (d), output matrix is normalized on main diagonal.
Example dlkconv.exe e 7yPG4 dc -- decode 7yPG4 and normalize diagonal
Author: Tomas Brada (GPL)

Я пользуюсь этой программой. Очень удобно для перевода из одного формата в другой.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Кстати, о форматах.
Мы рассматриваем представление ДЛК в следующих форматах

1. Нормализованные ДЛК
это ДЛК с первой строкой, упорядоченной в естественном порядке, то есть

0 1 2 3 4 5 6 7 8 9 10

Пример (здесь и далее в примерах представлен рекордный ДЛК 11-го порядка, имеющий 32462 ОДЛК)

0 1 2 3 4 5 6 7 8 9 10
7 10 6 0 3 1 5 9 2 8 4
3 5 8 4 10 6 2 0 9 7 1
8 3 1 9 7 4 10 2 5 6 0
5 9 3 6 2 7 0 1 4 10 8
2 0 10 8 9 3 4 6 1 5 7
1 8 0 5 6 9 7 10 3 4 2
10 2 7 1 5 8 9 4 0 3 6
9 4 5 7 0 10 1 8 6 2 3
6 7 4 2 8 0 3 5 10 1 9
4 6 9 10 1 2 8 3 7 0 5

2. Сильно нормализованные ДЛК
это ДЛК с упорядоченной в естественном порядке главной диагональю.

Пример

 0  9  4  5  7 10  8  6  2  3  1
 6  1  8  0  5  9 10  3  4  2  7
 5 10  2  7  1  8  4  0  3  6  9
 2  5  9  3  6  7  1  4 10  8  0
10  3  5  8  4  6  0  9  7  1  2
 4  0  1  2  3  5  7  8  9 10  6
 9  2  0 10  8  3  6  1  5  7  4
 1  4  6  9 10  2  3  7  0  5  8
 3  7 10  6  0  1  9  2  8  4  5
 8  6  7  4  2  0  5 10  1  9  3
 7  8  3  1  9  4  2  5  6  0 10

3. Буквенно-цифровой формат
в этом формате все элементы ДЛК больше 9 заменяются латинскими буквами (10=A, 11=B, 12=C, ...).
Данный формат вводится для ДЛК порядков n>10.

Пример

0 9 4 5 7 A 8 6 2 3 1
6 1 8 0 5 9 A 3 4 2 7
5 A 2 7 1 8 4 0 3 6 9
2 5 9 3 6 7 1 4 A 8 0
A 3 5 8 4 6 0 9 7 1 2
4 0 1 2 3 5 7 8 9 A 6
9 2 0 A 8 3 6 1 5 7 4
1 4 6 9 A 2 3 7 0 5 8
3 7 A 6 0 1 9 2 8 4 5
8 6 7 4 2 0 5 A 1 9 3
7 8 3 1 9 4 2 5 6 0 A

4. Закодированное имя ДЛК.
Для ДЛК порядка 10 мы имеем систему кодирования Белышева.
Система кодирования Tomas Brada пригодна для ДЛК любого порядка.

Пример

CBdLXkuMuUsLR2UMw31FGHxG64

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Рекордные ДЛК смотрим в последовательности OEIS https://oeis.org/A287695.
Для порядков 9 и 10 рекордные ДЛК (текущие рекорды) найдены мной.
Для порядка 11 я не внесла в OEIS текущий рекорд (он принадлежит Tomas Brada); думаю, что этот рекорд должен быть улучшен.

С текущим рекордом для порядка 9 скоро всё станет ясно, полная БД КФ ОДЛК порядка 9 составляется в двух BOINC-проектах (Gerasim@Home и Rake Search) и по сообщениям администраторов близка к завершению.

С текущим рекордом для порядка 10 пока всё в полном мраке, с апреля 2018 года держится текущий рекорд; 11-ка упорно не желает себя обнаружить, если она вообще существует.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Посмотрим иллюстрации рекордных групп ОДЛК порядков 9 и 10.

Найденная мной десяточка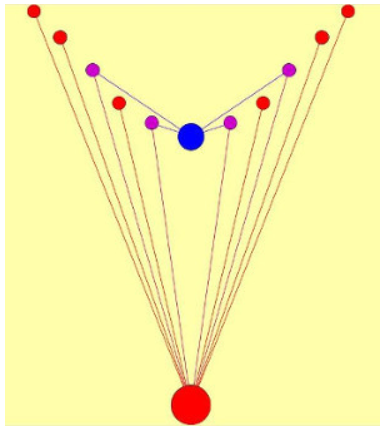



Рисовал Demis.

Рекордная группа ОДЛК 9-го порядка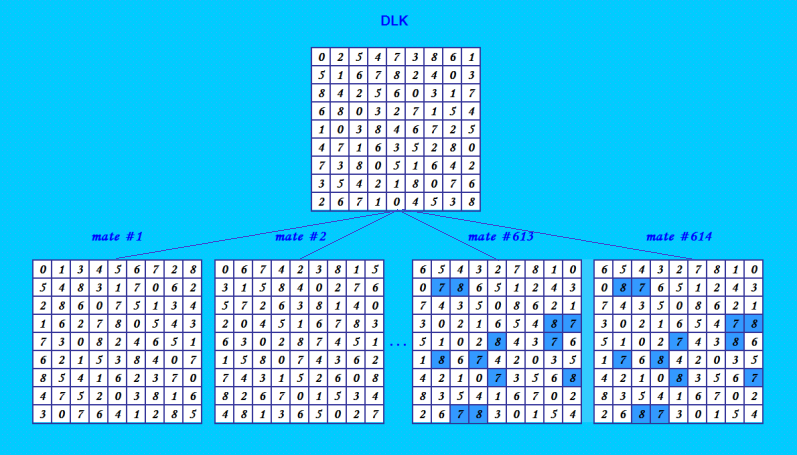



Аналогично можно изобразить текущий рекорд для порядка 11
ДЛК

 0  9  4  5  7 10  8  6  2  3  1
 6  1  8  0  5  9 10  3  4  2  7
 5 10  2  7  1  8  4  0  3  6  9
 2  5  9  3  6  7  1  4 10  8  0
10  3  5  8  4  6  0  9  7  1  2
 4  0  1  2  3  5  7  8  9 10  6
 9  2  0 10  8  3  6  1  5  7  4
 1  4  6  9 10  2  3  7  0  5  8
 3  7 10  6  0  1  9  2  8  4  5
 8  6  7  4  2  0  5 10  1  9  3
 7  8  3  1  9  4  2  5  6  0 10

и 32462 mates.
Но здесь, вполне вероятно, конфигурация будет не полной, потому что эти 32462 mates могут дать ещё ортогональные диагональные соквадраты, появится второй уровень; а потом, может быть, и третий уровень.
Впрочем, это относится и к конфигурации из ОДЛК порядка 9.
А вот конфигурация из ОДЛК порядка 10 полная.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Множество сильно нормализованных ДЛК (в дальнейшем - СН ДЛК) - очень интересное множество.
Вся суть в том, что это множество разбивается на K непересекающихся множеств, которые Белышев (создатель данной теории) назвал линейками.
Для порядка 10 существует 67 линеек.
Оказывается, СН ДЛК 11-го порядка настолько похожи на СН ДЛК 10-го порядка, что они тоже разбиваются на 67 линеек.
О количестве линеек для СН ДЛК порядка n смотрим последовательность OEIS https://oeis.org/A309283

Линейка - это множество всех СН ДЛК с одинаковой побочной диагональю.
Таким образом, линейки определяются побочной диагональю СН ДЛК.
Линейки для СН ДЛК 10-го порядка были найдены Белышевым.

Все линейки для СН ДЛК 11-го порядка были найдены мной эмпирически и подтверждены Harry White.
Смотрите список линеек (или побочных диагоналей, определяющих линейки) для СН ДЛК 11-го порядка здесь
https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6038

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Далее надо рассказать о канонизаторе.
Что это такое? Эта такая программа, которая преобразует любой ДЛК в его каноническую форму.
Я не буду здесь подробно объяснять, что такое каноническая форма (в дальнейшем - КФ) ДЛК и как она находится.
Кто работает с ДЛК, это уже хорошо знает.
Понятие КФ введено Белышевым. Это очень важное понятие.
Если очень кратко: КФ представляет класс эквивалентности ДЛК. Все ДЛК, принадлежащие одному классу эквивалентности (изоморфные), имеют одинаковую КФ.
Канонизотор для ДЛК порядков 9 и 10 был создан Белышевым.
Harry White создал канонизатор для ДЛК порядков до 15 включительно.
В теме "ОДЛК для порядков n>10" я давала ссылку на эту программу Harry White.

КФ может быть двух форматов.
Формат 1 - нормализованная КФ.
Формат 2 - сильно нормализованная КФ.
Между КФ двух этих форматов существует взаимно-однозначное соответствие.

Пример (для рекордного ДЛК 11-го порядка)

нормализованная КФ

 0  1  2  3  4  5  6  7  8  9 10
 1  2  3  5  6  9  7 10  0  4  8
 7 10  8  0  3  1  5  9  6  2  4
 3  5  9  4 10  6  8  0  2  7  1
 4  6  7 10  1  8  2  3  9  0  5
 5  9  4  6  8  7  0  1  3 10  2
10  8  0  1  5  2  9  4  7  3  6
 6  7 10  8  2  0  3  5  4  1  9
 8  0  1  2  9  3  4  6 10  5  7
 2  3  5  9  7  4 10  8  1  6  0
 9  4  6  7  0 10  1  2  5  8  3

сильно нормализованная КФ

 0  9  4  5  7 10  8  6  2  3  1
 6  1  8  0  5  9 10  3  4  2  7
 5 10  2  7  1  8  4  0  3  6  9
 2  5  9  3  6  7  1  4 10  8  0
10  3  5  8  4  6  0  9  7  1  2
 4  0  1  2  3  5  7  8  9 10  6
 9  2  0 10  8  3  6  1  5  7  4
 1  4  6  9 10  2  3  7  0  5  8
 3  7 10  6  0  1  9  2  8  4  5
 8  6  7  4  2  0  5 10  1  9  3
 7  8  3  1  9  4  2  5  6  0 10

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Как уже отмечено выше, процесс наращивания БД КФ ОДЛК 11-го порядка запустить легко.
И он у меня уже запущен!
Этот процесс имеет несколько очевидных направлений поиска ОДЛК.
Затем нужны разработки новых направлений.
Совершенно понятно что БД порядка 11 не для тотального поиска, хотя и такой поиск, разумеется, можно организовать.
Составить полную БД КФ ОДЛК порядка 11 в настоящее время не в состоянии даже 10 BOINC-проектов.
Это вам не квадратики порядка 9.
Поэтому решать проблему надо по частям. Каждое направление поиска даст свои результаты.
От эффективности алгоритмов будет зависеть, как много получится результатов.

А тем временем, у меня БД уже подросла до 29763 КФ ОДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Просто покажу некоторые КФ ОДЛК 11-го порядка, найденные только что; шеренга 32-шек, предваряемая 35-кой

. . . . . . .
[DLK(35):1068]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 0 8 A 4 5 9 2 7
7 A 2 4 1 9 5 8 3 6 0
2 6 9 3 0 8 7 4 A 1 5
1 3 A 8 4 7 0 9 2 5 6
8 7 6 A 9 5 1 0 4 3 2
4 5 8 1 A 3 6 2 0 7 9
5 9 0 6 3 2 A 7 1 4 8
A 4 7 2 5 1 9 6 8 0 3
3 8 1 5 6 0 2 A 7 9 4
9 0 5 7 2 4 3 1 6 8 A

[DLK(32):1103]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 0 8 A 4 5 9 2 7
7 A 2 4 1 9 5 8 3 6 0
2 6 9 3 0 8 7 4 A 1 5
1 7 A 8 4 3 0 9 2 5 6
8 3 6 A 9 5 1 0 4 7 2
4 5 8 1 A 7 6 2 0 3 9
5 9 0 6 3 2 A 7 1 4 8
A 4 7 2 5 1 9 6 8 0 3
3 8 1 5 6 0 2 A 7 9 4
9 0 5 7 2 4 3 1 6 8 A

[DLK(32):1135]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 0 8 A 4 5 9 2 7
7 A 2 4 1 9 5 8 3 6 0
8 6 9 3 0 2 7 4 A 1 5
1 7 A 8 4 3 0 9 2 5 6
2 3 6 A 9 5 1 0 4 7 8
4 5 8 1 A 7 6 2 0 3 9
5 9 0 6 3 8 A 7 1 4 2
A 4 7 2 5 1 9 6 8 0 3
3 8 1 5 6 0 2 A 7 9 4
9 0 5 7 2 4 3 1 6 8 A

[DLK(32):1167]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 0 8 A 4 5 9 2 7
7 A 2 4 9 1 5 8 3 6 0
2 6 9 3 0 8 7 4 A 1 5
1 7 A 8 4 3 0 9 2 5 6
8 3 6 A 1 5 9 0 4 7 2
4 5 8 1 A 7 6 2 0 3 9
5 9 0 6 3 2 A 7 1 4 8
A 4 7 2 5 9 1 6 8 0 3
3 8 1 5 6 0 2 A 7 9 4
9 0 5 7 2 4 3 1 6 8 A

[DLK(32):1199]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 0 8 A 4 5 9 2 7
7 A 2 4 9 1 5 8 3 6 0
8 6 9 3 0 2 7 4 A 1 5
1 7 A 8 4 3 0 9 2 5 6
2 3 6 A 1 5 9 0 4 7 8
4 5 8 1 A 7 6 2 0 3 9
5 9 0 6 3 8 A 7 1 4 2
A 4 7 2 5 9 1 6 8 0 3
3 8 1 5 6 0 2 A 7 9 4
9 0 5 7 2 4 3 1 6 8 A

[DLK(32):1231]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 A 8 0 4 5 9 2 7
7 A 2 4 1 9 5 8 3 6 0
8 6 9 3 0 2 7 4 A 1 5
1 7 A 8 4 3 0 9 2 5 6
2 3 6 0 9 5 1 A 4 7 8
4 5 8 1 A 7 6 2 0 3 9
5 9 0 6 3 8 A 7 1 4 2
A 4 7 2 5 1 9 6 8 0 3
3 8 1 5 6 A 2 0 7 9 4
9 0 5 7 2 4 3 1 6 8 A

[DLK(32):1263]
0 2 4 9 7 6 8 3 5 A 1
6 1 3 A 8 0 4 5 9 2 7
7 A 2 4 9 1 5 8 3 6 0
8 6 9 3 0 2 7 4 A 1 5
1 7 A 8 4 3 0 9 2 5 6
2 3 6 0 1 5 9 A 4 7 8
4 5 8 1 A 7 6 2 0 3 9
5 9 0 6 3 8 A 7 1 4 2
A 4 7 2 5 9 1 6 8 0 3
3 8 1 5 6 A 2 0 7 9 4
9 0 5 7 2 4 3 1 6 8 A
. . . . . . . 

Попутно замечу, что программа Белышева ortogon_u для порядка 11 работает с буквенно-цифровым форматом.
Белышев написал специальную утилиту, которая преобразует заданные ДЛК в буквенно-цифровой формат.
А вот для обратного преобразования он не написал утилиту (или я пропустила её).
Я пользуюсь для обратного преобразования программой Tomas Brada dlkconv.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Пожалуй, продублирую все линейки для СН ДЛК 11-го порядка

№1 1 0 3 2 7 5 8 4 6 10 9
№2 1 0 3 2 7 5 8 4 9 10 6
№3 1 0 3 2 7 5 8 6 4 10 9
№4 1 0 3 2 7 5 8 6 9 10 4
№5 1 0 3 2 7 5 8 9 10 4 6
№6 1 0 3 2 7 5 8 9 10 6 4
№7 1 0 3 2 7 5 9 4 10 6 8
№8 1 0 3 2 7 5 9 4 10 8 6
№9 1 0 3 2 7 5 9 6 10 4 8
№10 1 0 3 2 7 5 9 6 10 8 4
№11 1 0 3 2 7 5 9 8 4 10 6
№12 1 0 3 2 7 5 9 10 4 8 6
№13 1 0 3 2 7 5 9 10 6 8 4
№14 1 0 3 4 2 5 7 9 10 6 8
№15 1 0 3 4 2 5 7 9 10 8 6
№16 1 0 3 4 2 5 8 6 7 10 9
№17 1 0 3 4 2 5 8 6 9 10 7
№18 1 0 3 4 2 5 8 9 10 6 7
№19 1 0 3 4 2 5 8 9 10 7 6
№20 1 0 3 4 7 5 2 6 9 10 8
№21 1 0 3 4 7 5 2 9 6 10 8
№22 1 0 3 4 7 5 2 9 10 6 8
№23 1 0 3 4 7 5 2 9 10 8 6
№24 1 0 3 4 7 5 8 9 10 2 6
№25 1 0 3 4 7 5 8 9 10 6 2
№26 1 0 3 4 7 5 9 2 10 8 6
№27 1 0 3 4 7 5 9 6 10 2 8
№28 1 0 3 4 7 5 9 6 10 8 2
№29 1 0 3 4 7 5 9 8 10 2 6
№30 1 0 3 4 7 5 9 8 10 6 2
№31 1 0 3 4 7 5 9 10 6 2 8
№32 1 0 3 4 7 5 9 10 6 8 2
№33 1 0 3 4 8 5 2 9 10 6 7
№34 1 0 3 4 8 5 2 9 10 7 6
№35 1 0 3 4 8 5 9 6 10 2 7
№36 1 0 3 4 8 5 9 6 10 7 2
№37 1 0 3 4 9 5 7 10 6 2 8
№38 1 0 3 4 9 5 8 6 10 2 7
№39 1 0 3 4 9 5 8 6 10 7 2
№40 1 0 3 4 9 5 10 6 7 2 8
№41 1 0 3 4 9 5 10 6 7 8 2
№42 1 0 3 8 7 5 9 6 10 2 4
№43 1 0 3 8 7 5 9 6 10 4 2
№44 1 0 3 8 9 5 10 2 7 4 6
№45 1 0 3 8 9 5 10 2 7 6 4
№46 1 2 0 4 7 5 3 6 10 8 9
№47 1 2 0 4 7 5 3 8 10 6 9
№48 1 2 0 4 7 5 8 9 10 3 6
№49 1 2 0 4 7 5 8 9 10 6 3
№50 1 2 0 4 8 5 9 6 10 3 7
№51 1 2 0 4 8 5 9 6 10 7 3
№52 1 2 0 4 8 5 9 10 3 7 6
№53 1 2 0 4 8 5 9 10 6 7 3
№54 1 2 0 4 8 5 10 9 6 3 7
№55 1 2 0 4 8 5 10 9 7 6 3
№56 1 2 3 0 7 5 8 6 10 4 9
№57 1 2 3 0 7 5 8 9 10 6 4
№58 1 2 3 0 7 5 8 10 4 6 9
№59 1 2 3 4 0 5 8 6 10 7 9
№60 1 2 3 4 0 5 8 9 10 6 7
№61 1 2 3 4 0 5 10 6 7 8 9
№62 1 2 3 4 7 5 0 9 10 8 6
№63 1 2 3 4 7 5 8 6 10 0 9
№64 1 2 3 4 7 5 9 10 6 0 8
№65 1 2 3 4 7 5 10 9 0 6 8
№66 1 2 3 8 7 5 9 6 10 0 4
№67 1 2 3 8 7 5 10 6 4 0 9

Если мы имеем КФ ОДЛК второго формата (сильно нормализованную), легко определить по побочной диагонали в этой КФ, какой линейке она принадлежит.

Пример опять для рекордного ДЛК, это его КФ второго формата

 0  9  4  5  7 10  8  6  2  3  1
 6  1  8  0  5  9 10  3  4  2  7
 5 10  2  7  1  8  4  0  3  6  9
 2  5  9  3  6  7  1  4 10  8  0
10  3  5  8  4  6  0  9  7  1  2
 4  0  1  2  3  5  7  8  9 10  6
 9  2  0 10  8  3  6  1  5  7  4
 1  4  6  9 10  2  3  7  0  5  8
 3  7 10  6  0  1  9  2  8  4  5
 8  6  7  4  2  0  5 10  1  9  3
 7  8  3  1  9  4  2  5  6  0 10

Очевидно, что данная КФ принадлежит линейке №60.

Harry White написал утилиту GetDiagonals. которая выписывает из всех заданных КФ ОДЛК второго формата побочные диагонали и составляет список уникальных побочных диагоналей из выписанных.
С помощью этой утилиты мы можем определить, представители каких линеек есть в заданном множестве КФ ОДЛК.
Пример для текущей БД КФ ОДЛК, содержащей 29908 КФ ОДЛК

Order? 11
File? inp
Input file is inp.txt
.. writing squares to file inpDiags_2.txt
Which \ 1 or / 2? 2
squares 29908 diags 67

Таким образом, текущий вариант БД имеет представителей из всех 67 линеек.
Замечательное ядро БД!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Я написала утилиту, которая выписывает из заданного множества КФ ОДЛК все КФ ОДЛК из конкретной линейки.
С помощью этой утилиты я составляю статистику по линейкам для текущего варианта БД.
Надо модифицировать эту утилиту - для порядка 11; она у меня написана для порядков 9 и 10.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Эти три линейки для СН ДЛК 11-го порядка

№16 1 0 3 4 2 5 8 6 7 10 9
№46 1 2 0 4 7 5 3 6 10 8 9
№61 1 2 3 4 0 5 10 6 7 8 9

содержат ассоциативные ДЛК.

Пример



КФ этого ассоциативного ДЛК во втором формате

 0  7  8  5  3  6  9  2 10  4  1
 4  1  6  7  5 10  3  9  0  2  8
 5  0  2 10  6  9  8  1  3  7  4
10  5  1  3  9  8  2  4  6  0  7
 8  9  5  2  4  7  0 10  1  6  3
 1  2  3  4  0  5 10  6  7  8  9
 7  4  9  0 10  3  6  8  5  1  2
 3 10  4  6  8  2  1  7  9  5  0
 6  3  7  9  2  1  4  0  8 10  5
 2  8 10  1  7  0  5  3  4  9  6
 9  6  0  8  1  4  7  5  2  3 10

Очевидно, что эта КФ принадлежит линейке №61.

Очень хорошо, что ассоциативные ДЛК 11-го порядка существуют.
И вот первое направление поиска ОДЛК 11-го порядка - во множестве ассоциативных ДЛК.
Множество это огромное. Много ли оно даст КФ ОДЛК? Это покажет эксперимент.
И этот эксперимент можно запускать прямо сейчас.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg