Вот эту симпатичную конфигурацию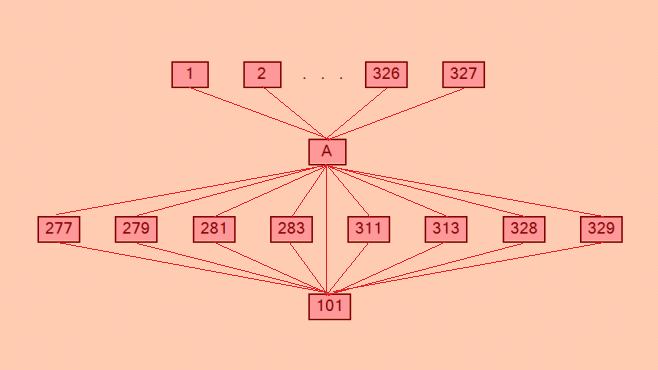



сейчас нарисую в Gephi.
Точно так же в верхнем ряду покажу только 4 квадрата, потому что если показать все квадраты, опять получится фигня, в которой ничего невозможно разобрать.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Странно! После применения импортирования программа перестала давать картинку с кривыми (дугообразными) рёбрами.
Только прямыми линиями рёбра рисуются. Сломалась на огромном количестве узлов и рёбер :)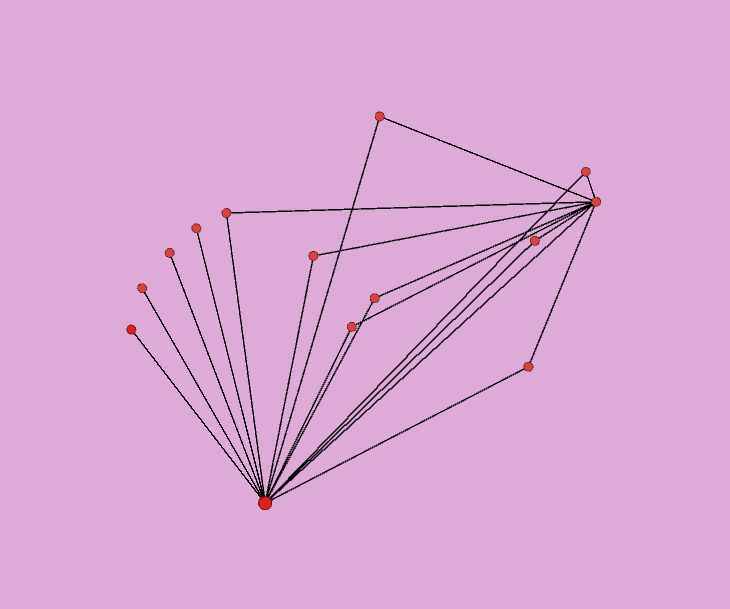



На этой картинке потренировалась перетаскивать узлы. Можно ещё узлы увеличивать; я увеличила узел, который является основным квадратом конфигурации (квадрат А).

Ну, ничем не лучше картинки, нарисованной нами с черепашкой вручную.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И ещё немного переставила узлы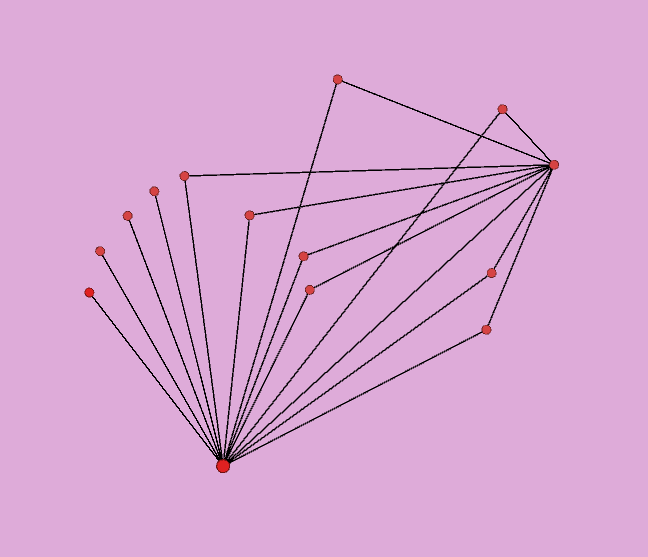



Ну, нарисовалась вдоволь :)

PS. В этой конфигурации интересны 8 троек MODLS. Их хорошо видно, это 8 треугольников.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Мне кажется, что на этой иллюстрации есть брак
https://boinc.progger.info/odlk/forum_thread.php?id=169&postid=6574
Отсутствуют два ребра. Либо я их не ввела (при ручном вводе), либо Gephi их не нарисовала.
Сейчас импортирую эту группу ОДЛК, таблица ортогональных пар

2:  1
3:  1 2
4:  1 2 3
5:  1 2 3 4
6:  1 2 3 4 5
7:  1 2 3 4 5 6
8:  1 2 3 4 5 6 7

Сначала попробую подкорректировать иллюстрацию вручную.

Вот подправила, красными линиями нарисовала два отсутствующих ребра.



Сейчас ещё порисую, может быть, удастся получше получить иллюстрацию.
Тут всего-то 8 узлов и 28 рёбер, всё должно быть чётко видно.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нарисовала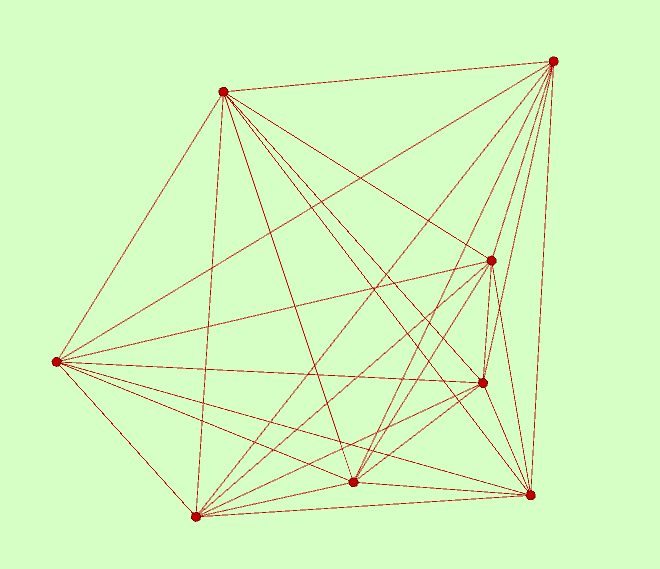



Немного корректировала узлы (перетаскивала), чтобы было чётко видно.
Вроде всё получилось.
Напомню: это MODLS 11-го порядка из 8 взаимно ортогональных ДЛК.
Живые квадраты конфигурации показаны выше. Они взяты из полной системы MOLS.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

А это MODLS 11-го порядка мы с черепашкой нарисовали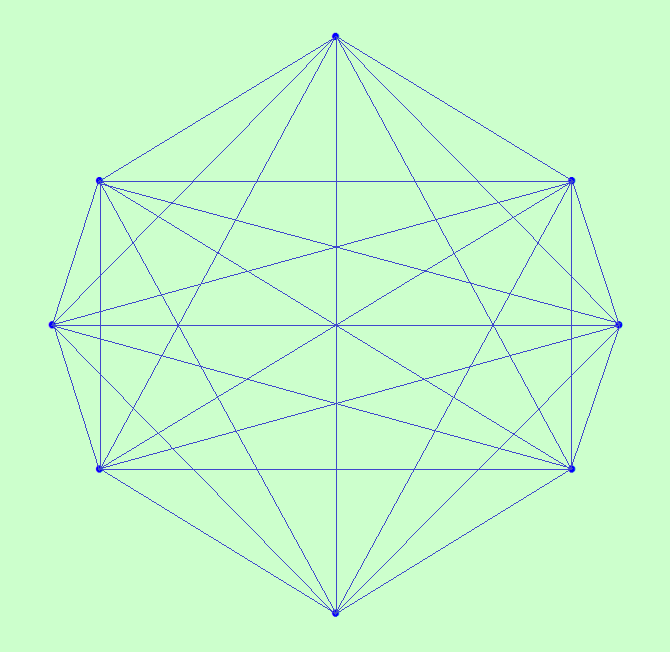



Как говорится: на вкус, на цвет...
Кому нравится симметричное изображение, а кому - ассиметричное (как в предыдущем посте).

Программа Gephi сама по себе не умеет симметрично рисовать. Может быть, у неё есть соответствующие настройки (?).
Но я не знаю о них, надо читать документацию.

Мне больше нравится симметричная иллюстрация.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Представляю группу MODLS 13-го порядка, состоящую из 10 взаимно ортогональных ДЛК
(группа взята из полной системы MOLS; система составлена мной вручную методом циклического сдвига; можно составить систему в матпакете Maple)

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

0 1 2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 0 1 2
6 7 8 9 10 11 12 0 1 2 3 4 5
9 10 11 12 0 1 2 3 4 5 6 7 8
12 0 1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12 0 1
5 6 7 8 9 10 11 12 0 1 2 3 4
8 9 10 11 12 0 1 2 3 4 5 6 7
11 12 0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 11 12 0
4 5 6 7 8 9 10 11 12 0 1 2 3
7 8 9 10 11 12 0 1 2 3 4 5 6
10 11 12 0 1 2 3 4 5 6 7 8 9

0 1 2 3 4 5 6 7 8 9 10 11 12
4 5 6 7 8 9 10 11 12 0 1 2 3
8 9 10 11 12 0 1 2 3 4 5 6 7
12 0 1 2 3 4 5 6 7 8 9 10 11
3 4 5 6 7 8 9 10 11 12 0 1 2
7 8 9 10 11 12 0 1 2 3 4 5 6
11 12 0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 11 12 0 1
6 7 8 9 10 11 12 0 1 2 3 4 5
10 11 12 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 11 12 0
5 6 7 8 9 10 11 12 0 1 2 3 4
9 10 11 12 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10 11 12
5 6 7 8 9 10 11 12 0 1 2 3 4
10 11 12 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11 12 0 1
7 8 9 10 11 12 0 1 2 3 4 5 6
12 0 1 2 3 4 5 6 7 8 9 10 11
4 5 6 7 8 9 10 11 12 0 1 2 3
9 10 11 12 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 11 12 0
6 7 8 9 10 11 12 0 1 2 3 4 5
11 12 0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 0 1 2
8 9 10 11 12 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10 11 12
6 7 8 9 10 11 12 0 1 2 3 4 5
12 0 1 2 3 4 5 6 7 8 9 10 11
5 6 7 8 9 10 11 12 0 1 2 3 4
11 12 0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 11 12 0 1 2 3
10 11 12 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 11 12 0 1 2
9 10 11 12 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 11 12 0 1
8 9 10 11 12 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 11 12 0
7 8 9 10 11 12 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10 11 12
7 8 9 10 11 12 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 11 12 0
8 9 10 11 12 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 11 12 0 1
9 10 11 12 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 11 12 0 1 2
10 11 12 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 11 12 0 1 2 3
11 12 0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 0 1 2 3 4
12 0 1 2 3 4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10 11 12
8 9 10 11 12 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 11 12 0 1 2
11 12 0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 11 12 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 11 12 0
9 10 11 12 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 11 12 0 1 2 3
12 0 1 2 3 4 5 6 7 8 9 10 11
7 8 9 10 11 12 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 11 12 0 1
10 11 12 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 11 12 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 0
10 11 12 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 0 1
11 12 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 0 1 2
12 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10 11 12
10 11 12 0 1 2 3 4 5 6 7 8 9
7 8 9 10 11 12 0 1 2 3 4 5 6
4 5 6 7 8 9 10 11 12 0 1 2 3
1 2 3 4 5 6 7 8 9 10 11 12 0
11 12 0 1 2 3 4 5 6 7 8 9 10
8 9 10 11 12 0 1 2 3 4 5 6 7
5 6 7 8 9 10 11 12 0 1 2 3 4
2 3 4 5 6 7 8 9 10 11 12 0 1
12 0 1 2 3 4 5 6 7 8 9 10 11
9 10 11 12 0 1 2 3 4 5 6 7 8
6 7 8 9 10 11 12 0 1 2 3 4 5
3 4 5 6 7 8 9 10 11 12 0 1 2

0 1 2 3 4 5 6 7 8 9 10 11 12
11 12 0 1 2 3 4 5 6 7 8 9 10
9 10 11 12 0 1 2 3 4 5 6 7 8
7 8 9 10 11 12 0 1 2 3 4 5 6
5 6 7 8 9 10 11 12 0 1 2 3 4
3 4 5 6 7 8 9 10 11 12 0 1 2
1 2 3 4 5 6 7 8 9 10 11 12 0
12 0 1 2 3 4 5 6 7 8 9 10 11
10 11 12 0 1 2 3 4 5 6 7 8 9
8 9 10 11 12 0 1 2 3 4 5 6 7
6 7 8 9 10 11 12 0 1 2 3 4 5
4 5 6 7 8 9 10 11 12 0 1 2 3
2 3 4 5 6 7 8 9 10 11 12 0 1

Здесь 10 узлов и 45 ортогональных пар.
Таблица ортогональных пар, как её выводит утилита Harry White

2:  1
3:  1 2
4:  1 2 3
5:  1 2 3 4
6:  1 2 3 4 5
7:  1 2 3 4 5 6
8:  1 2 3 4 5 6 7
9:  1 2 3 4 5 6 7 8
10:  1 2 3 4 5 6 7 8 9

Эту таблицу импортировала в программу Gephi; конечно, немного преобразовала.
Это иллюстрация, выданная Gephi



Ничего здесь не изменяла, оригинальный рисунок.
Довольно симпатичный. Тоже ассиметричный.
Ну, для симметричной иллюстрации нарисуйте правильный десятиугольник и соедините все его вершины между собой.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Представляю группу MODLS 8-го порядка, состоящую из 6 взаимно ортогональных ДЛК

0 1 2 3 4 5 6 7
2 3 0 1 6 7 4 5
4 5 6 7 0 1 2 3
6 7 4 5 2 3 0 1
5 4 7 6 1 0 3 2
7 6 5 4 3 2 1 0
1 0 3 2 5 4 7 6
3 2 1 0 7 6 5 4

0 1 2 3 4 5 6 7
3 2 1 0 7 6 5 4
6 7 4 5 2 3 0 1
5 4 7 6 1 0 3 2
1 0 3 2 5 4 7 6
2 3 0 1 6 7 4 5
7 6 5 4 3 2 1 0
4 5 6 7 0 1 2 3

0 1 2 3 4 5 6 7
4 5 6 7 0 1 2 3
5 4 7 6 1 0 3 2
1 0 3 2 5 4 7 6
7 6 5 4 3 2 1 0
3 2 1 0 7 6 5 4
2 3 0 1 6 7 4 5
6 7 4 5 2 3 0 1

0 1 2 3 4 5 6 7
5 4 7 6 1 0 3 2
7 6 5 4 3 2 1 0
2 3 0 1 6 7 4 5
3 2 1 0 7 6 5 4
6 7 4 5 2 3 0 1
4 5 6 7 0 1 2 3
1 0 3 2 5 4 7 6

0 1 2 3 4 5 6 7
6 7 4 5 2 3 0 1
1 0 3 2 5 4 7 6
7 6 5 4 3 2 1 0
2 3 0 1 6 7 4 5
4 5 6 7 0 1 2 3
3 2 1 0 7 6 5 4
5 4 7 6 1 0 3 2

0 1 2 3 4 5 6 7
7 6 5 4 3 2 1 0
3 2 1 0 7 6 5 4
4 5 6 7 0 1 2 3
6 7 4 5 2 3 0 1
1 0 3 2 5 4 7 6
5 4 7 6 1 0 3 2
2 3 0 1 6 7 4 5

Группа взята из полной системы MOLS.
Среди ДЛК группы только один уникальный, это КФ

0 2 5 7 6 4 3 1
3 1 6 4 5 7 0 2
7 5 2 0 1 3 4 6
4 6 1 3 2 0 7 5
2 0 7 5 4 6 1 3
1 3 4 6 7 5 2 0
5 7 0 2 3 1 6 4
6 4 3 1 0 2 5 7

Эта КФ имеет 824 ОДЛК.
Таким образом, имеем группу, состоящую из 825 ОДЛК (включая исходную КФ) и 834 ортогональных пар.
Группа MODLS (6 ОДЛК и 15 ортогональных пар) содержится в этой группе ОДЛК.
Таблицу ортогональных пар этой группы получила утилитой Harry White.
Сейчас попробую импортировать её в программу Gephi.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Импортировала, нарисовала



Вряд ли эта картинка даёт представление об изображённой группе ОДЛК.
Я даже не вижу, где расположилась группа MODLS, только предположительно.
Наглядности нет никакой в подобных иллюстрациях.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нашла интересную пятёрочку в БД КФ ОДЛК 9-го порядка

[DLK(5)]
0 2 3 4 6 7 8 5 1
8 1 4 7 3 6 2 0 5
1 7 2 5 8 0 3 4 6
6 5 7 3 1 2 0 8 4
5 6 1 0 4 8 7 2 3
4 0 8 6 7 5 1 3 2
2 4 5 8 0 3 6 1 7
3 8 6 2 5 1 4 7 0
7 3 0 1 2 4 5 6 8

На первом уровне это просто пятёрочка: 6 ОДЛК, из них 5 уникальных.
А вот второй уровень у этой пятёрочки интересный:

Order? 9

Enter the name of the squares file: inp
..output file inpPairs_5.txt
..output file inpPairNos_5.txt
squares 131 orthogonal pairs 323

Получена группа из 131 ОДЛК, в которой образовалось 323 ортогональные пары.
При этом группа ОДЛК второго уровня не бестолковая, толк есть, так как в группе 20 уникальных КФ ОДЛК (в группе первого уровня их было всего 5).
Покажу таблицу ортогональности для группы ОДЛК второго уровня

2:  1
3:  1
4:  1
5:  1
6:  1
7:  2 3 4 5 6
8:  2 6
9:  2 3 4 5 6
10:  2 3 4 5 6
11:  2 3 4 5 6
12:  3 9 11
13:  4 6 9 11
14:  2 3 4 5 6
15:  4
16:  4
17:  2 3 4 5 6 12 13
18:  2 3 4 5 6 12 13
19:  5 6
20:  2 3 4 5 6
21:  6
22:  6
23:  6
24:  6
25:  6
26:  6
27:  4 6 9 11 17 18
28:  6
29:  6
30:  6
31:  6
32:  6
33:  6
34:  6
35:  6
36:  6
37:  6
38:  6
39:  6
40:  6
41:  6
42:  6
43:  6
44:  6
45:  6
46:  6
47:  6
48:  6
49:  6 9 11 13 17 18 27
50:  6
51:  6
52:  6
53:  6
54:  6
55:  6
56:  6
57:  6
58:  6
59:  6
60:  6
61:  6
62:  6
63:  6
64:  6
65:  6
66:  6 44
67:  6
68:  6
69:  6
70:  2 6
71:  6
72:  6
73:  6
74:  6
75:  6 8 9 11 13 17 18 19 21 22
 23 24 25 26 27 28 29 30 31 32
 33 34 35 36 37 38 39 40 41 42
 43 44 45 46 47 48 49 50 51 52
 53 54 55 56 57 58 59 62 63 64
 65 66 67 68 69 70 71 72 73 74
76:  6 75
77:  6 75
78:  6 75
79:  6 75
80:  6 44 66 75
81:  6 75
82:  6 75
83:  6 75
84:  6 75
85:  6 75
86:  6 75
87:  6 75
88:  6 75
89:  6 75
90:  6 75
91:  6 75
92:  6 75
93:  6 75
94:  6
95:  5 6 75
96:  6 75
97:  2 3 4 5 6 12 13 27 49 75
98:  6
99:  2 3 4 5 6
100:  6 75
101:  6 75
102:  6 75
103:  6 75
104:  6 75
105:  6 75
106:  6 75
107:  6 75
108:  6 75
109:  6 75
110:  6 75
111:  6 75
112:  6 75
113:  6 75
114:  6 9 11 13 17 18 27 49 75 97
115:  6 75
116:  6 75
117:  6 75
118:  6
119:  6 44 66 75 80
120:  6 75
121:  6 75
122:  6 75
123:  6 75
124:  6 75
125:  6 75
126:  6 75
127:  6 75
128:  6 75
129:  6 75
130:  6 75
131:  6 75

Сейчас попробую нарисовать; выброшу все однушки - мало интересные ортогональные пары, только загромождают иллюстрацию.
Импортирую оставшиеся ортогональные пары и нарисую в Gephi.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Импортировала и нарисовала группу ОДЛК от пятёрочки (на втором уровне), но с выброшенными однушками, чтобы не сильно загромождали картинку



Всё равно мало что понятно тут.
Кажется, и однушки выброшены не все. Да... что-то в воздухе трепыхается :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Программа Gephi у меня рисует время от времени.
Новая иллюстрация


Живые квадраты конфигурации показаны здесь
https://boinc.progger.info/odlk/forum_thread.php?id=44&postid=6645

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ещё порисовали немножко :)



Живые квадраты конфигурации показаны здесь
https://boinc.progger.info/odlk/forum_thread.php?id=44&postid=6697

А вот вам задачка: есть ли в этой конфигурации MODLS?
Ну, одна тройка MODLS, конечно, есть; её видно сразу.
Есть ли ещё тройки MODLS? Сколько?
Есть ли MODLS из более трёх ОДЛК?
Задачку, разумеется, проще решать не по иллюстрации, а по таблице ортогональных пар.

Исправление этой иллюстрации смотрите здесь
https://boinc.progger.info/odlk/forum_thread.php?id=44&postid=6739

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg